Формула площади цилиндра через диаметр – Онлайн калькулятор площади цилиндра. Как узнать площадь цилиндра.

расчет боковой, полной поверхности цилиндра, формула нахождения

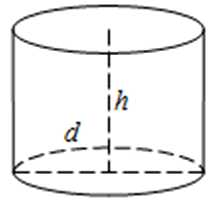
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.

Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.

Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.

Площадь поверхности цилиндра — онлайн калькулятор

Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.

Площадь боковой поверхности цилиндра

Сначала нужно представить, как выглядит развертка в двухмерном пространстве.

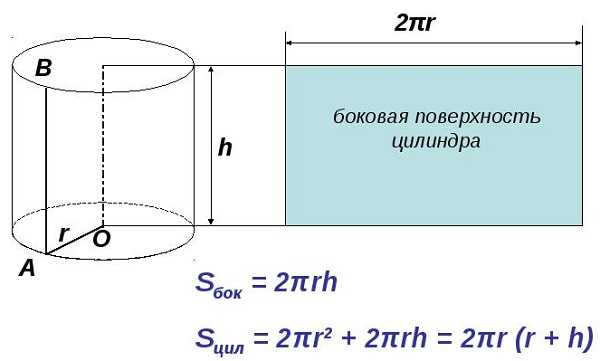
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r, где r — радиус окружности. Другая сторона прямоугольника равна высоте h. Найти искомое не составит труда.

S_бок = 2π * r * h,

где число π = 3.14.

Площадь полной поверхности цилиндра

Для нахождения полной площади цилиндра нужно к полученной

S_бокдобавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле S_о = 2π * r².

Конечная формула выглядит следующим образом:

S_пол = 2π * r² + 2π * r * h.

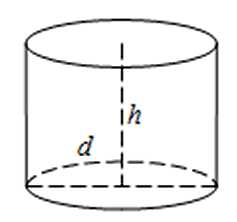
Площадь цилиндра — формула через диаметр

Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.

Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.

Sпол = 2π * r² + 2π * r * h = 2π * d²/4 + 2

π * h * d/2 = π * d²/2 + π * d * h,

Вместо r в полную формулу нужно вставить значение r = d/2.

Примеры расчета площади цилиндра

Вооружившись знаниями, приступаем к практике.

Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.

Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:

S_пол = 2 * 3.14 * 24² + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм²).

Переводим в привычные м² и получаем 0,01868928, приблизительно 0.02 м².

Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.

Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:

S_пол = 3.14 * 0.2²/2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м².

Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.

Один момент, есть формула:

S_бок = 2 * 3.14 * 1 * 1 = 6.28 м².

Заключение

В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.

Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.

1001student.ru

Площадь поверхности цилиндра — формулы, пример расчета

Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.

Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:

Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить формулу площади круга:
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.

Площадь боковой поверхности цилиндра

Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:

А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h = 4 см, r = 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:

Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.

Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.

Формула площади осевого сечения цилиндра выводится из формулы расчета площади прямоугольника:

Рассмотрим пример расчета площади осевого сечения цилиндра. Для этого возьмем условия из задачи, указанной выше. Чтобы найти величину нам потребуется диаметр. Мы знаем, что он равен двойному радиусу:

Подставим данные:

2mb.ru

периметр, площадь, содержание (формула и онлайн-расчет)

Расчет

Введите значения в желтые поля — другие отсчитывает себя.
При изменении информации в полях, отмеченные автоматически пересчитывается.
В качестве десятичной запятой можно использовать как запятую, так и точку.

 

Результат выводится в тех-же единицах, что и вводите данные.

Например если ввели в дециметрах, то и результат будет в них-же.

Обнаруженны NaN, проверьте, что вы ввели в поле
корректные данные, то есть без букв и других символов.

Формулы

Диаметр	d =	2 r	[m]
Окружность цилиндра	O =	π d = 2 π r	[m]
Площадь одной базы	P =	π d²/4 = π r²	[m²]
Поверхность цилиндра	Q =	π d h = 2 π r h	[m²]
Общая площадь	S =	2 P + Q = 2 π r (r + h)	[m²]
Объем	V =	π d²/4 h = π r² h	[m³]

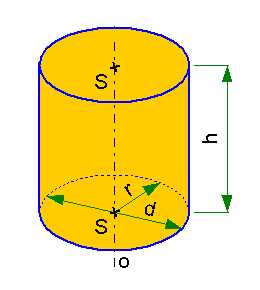
r … радиус = ½ диаметра

d … диаметр = 2 радиус

h … высота цилиндра

S … центр базовые цилиндра

o … ось цилиндра

π (Пи) = 3,14 (примерно)

Цилиндр и призмы

Скоро.

Принцип расчета

Общая площадь цилиндра состоит из поверхностей как основания и кожуха цилиндра. Оболочка цилиндра является произведением высоты и окружности цилиндра

Расчет объема/контента просто. о-первых, рассчитывать количество области цилиндра (то есть площадь круга), а затем умножив высоту.

Расчет цилиндра онлайн

Калькулятор окружности цилиндра или вычисление площади или поверхности цилиндра, содержание или объем цилиндра, узор валков площадь или длина окружности оболочки или содержимого. Расчет объема войны онлайн. Формула для вычисления цилиндра.

Ссылки

Как рассчитать …

Выделенные жирным шрифтом ссылки уже работают. Другие пока содержат только лишь формулу.

Могло бы вас заинтересовать

---

---

cilindr.wikina.ru

Как вычислить площадь цилиндра 🚩 площадь цилиндра через диаметр формула 🚩 Математика

27 декабря 2018

Автор КакПросто!

Цилиндр является пространственной фигурой и состоит из двух равных оснований, которые представляют собой круги и боковой поверхности, соединяющей линии, ограничивающие основания. Чтобы вычислить площадь цилиндра, найдите площади всех его поверхностей и сложите их.

Статьи по теме:

Вам понадобится

• линейка;
• калькулятор;
• понятие площади круга и длины окружности.

Инструкция

Определите площадь оснований цилиндра. Для этого измерьте при помощи линейки диаметр основания, затем поделите его на 2. Это будет радиус основания цилиндра. Вычислите площадь одного основания. Для этого возведите значение его радиуса в квадрат и умножьте на постоянную π, Sкр= π∙R², где R – радиус цилиндра, а π≈3,14. Найдите общую площадь двух оснований, исходя из определения цилиндра, которое говорит о том, что его основания равны между собой. Площадь одного круга основания умножьте на 2, Sосн=2∙Sкр=2∙π∙R². Вычислите площадь боковой поверхности цилиндра. Для этого найдите длину окружности, которая ограничивает одно из оснований цилиндра. Если радиус уже известен, то вычислите ее, умножив число 2 на π и радиус основания R, l= 2∙π∙R, где l – длина окружности основания.

Измерьте длину образующей цилиндра, которая равна длине отрезка, соединяющего соответствующие точки основания или их центры. В обычном прямом цилиндре образующая L численно равна его высоте H. Рассчитайте площадь боковой поверхности цилиндра, умножив длину его основания на образующую Sбок= 2∙π∙R∙L.

Вычислите площадь поверхности цилиндра, суммировав площадь оснований и боковой поверхности. S=Sосн+ Sбок. Подставив формульные значения поверхностей, получите S=2∙π∙R²+2∙π∙R∙L, вынесите общие множители S=2∙π∙R∙(R+L). Это позволит рассчитать поверхность цилиндра при помощи единой формулы.

Например, диаметр основания прямого цилиндра составляет 8 см, а его высота равна 10 см. Определите площадь его боковой поверхности. Вычислите радиус цилиндра. Он равен R=8/2=4 см. Образующая прямого цилиндра равна его высоте, то есть L=10 см. Для расчетов используйте единую формулу, это удобнее. Тогда S=2∙π∙R∙(R+L), подставьте соответствующие числовые значения S=2∙3,14∙4∙(4+10)=351,68 см².

Видео по теме

Источники:

• как посчитать площадь цилиндра

Совет полезен?

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru

Цилиндр. Формулы и свойства

Определение.

Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями (основами цилиндра).

Цилиндрическая поверхность — поверхность, получаемая при движении прямой (образующей L) параллельно самой себе, вдоль плоской кривой направляющей.

Основания цилиндра — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя плоскостями.

Круговой цилиндр

В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность, а основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.

Прямой круговой цилиндр

можно описать, как объёмного фигуру, образующуюся вращением прямоугольника вокруг своей стороны на 360°.

Определение. Радиус цилиндра r — это радиус основания цилиндра.

Определение. Диаметр цилиндра d — это диаметр основания цилиндра.

Определение. Высота цилиндра h — это расстояние между основаниями цилиндра.

Определение. Ось цилиндра — это прямая O₁O₂, которая проходит через центры оснований цилиндра.

Определение. Поверхность цилиндра состоит из цилиндрической поверхности и оснований цилиндра.

Определение. Осевое сечение цилиндра — это сечение цилиндра плоскостью, проходящей через ось цилиндра.

Определение. Касательная плоскость к цилиндру — это плоскость, которая проходит через образующую цилиндра и перпендикулярно к осевому сечении цилиндра.

Формула. Объём цилиндра:

V = πr2h = π	d2	h ,
	4

где r — радиус основы, h — высота цилиндра, d — диаметр основы. Формула. Площадь ,боковой поверхности цилиндра:

S_b = 2πrh = πdh

Формула. Полная площадь поверхности цилиндра:

S = 2πr(h + r)

Косой цилиндр — цилиндр, основы которого не параллельны (Рис.2)

Наклонный цилиндр — цилиндр, у которого образующие не перпендикулярно основам цилиндра (Рис.3 — наклонный круговой цилиндр).

ru.onlinemschool.com

Площадь поверхности цилиндра

Площадь поверхности цилиндра. В этой статье мы рассмотрим задания связанные с площадью поверхности цилиндра. На блоге уже рассмотрены задания с таким телом вращения как конус. Цилиндр тоже относится к телам вращения. Что требуется и нужно знать о площади поверхности цилиндра? Давайте посмотрим на развёртку цилиндра:

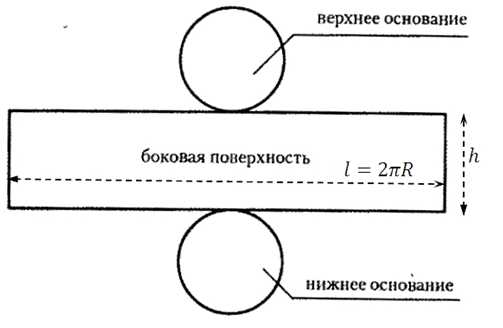
Верхнее и нижнее основание это два равных круга:

Боковая поверхность это прямоугольник. При чём одна сторона этого прямоугольника  равна высоте цилиндра, а другая длине окружности основания. Напомню, что длина окружности равна:

Итак, формула поверхности цилиндра:

*Учить эту формулу не нужно! Достаточно знать формулы площади круга и длины его окружности, тогда вы всегда сможете записать указанную формулу. Важно её понимание! Рассмотрим задачи:

Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту и площадь поверхности цилиндра (считайте, что число Пи равно 3,14 и результат округлите до десятых).

Площадь полной поверхности цилиндра:

Даны длина окружности основания и площадь боковой поверхности цилиндра. То есть,  нам дана площадь прямоугольника и одна его сторона, требуется найти  другую сторону (это есть высота цилиндра):

Требуется радиус и тогда мы сможем найти указанную площадь.

Длина окружности основания равна трём, тогда запишем:

Таким образом

Округляем до десятых, получаем 7,4.

Ответ: h = 2; S = 7,4

Площадь боковой поверхности цилиндра равна 72Пи, а диаметр основания — 9. Найдите высоту цилиндра.

Площадь боковой поверхности цилиндра находится по формуле:

Значит

Ответ: 8

Площадь боковой поверхности цилиндра равна 64Пи, а высота — 8 . Найдите диаметр основания.

Площадь боковой поверхности цилиндра находится по формуле:

Найдём радиус основания и далее определим диаметр:

Диаметр равен двум радиусам, значит:

Ответ: 8

27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на Пи.

Посмотреть решение

27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.

Посмотреть решение

27173. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на Пи.

Посмотреть решение

284361. Площадь боковой поверхности цилиндра равна 2Пи, а диаметр основания — 1. Найдите высоту цилиндра.

Посмотреть решение

284362. Площадь боковой поверхности цилиндра равна 2Пи, а высота — 1. Найдите диаметр основания.

Посмотреть решение

Будет ещё пару статей с цилиндрами, не пропустите!

На этом всё. Успеха Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Цилиндр, площадь цилиндра

Цилиндр (происходит из греческого языка, от слов «каток», «валик») – это геометрическое тело, которое ограничено снаружи поверхностью, называющейся цилиндрической, и двумя плоскостями. Данные плоскости пересекают поверхность фигуры и являются параллельными друг другу.

Цилиндрическая поверхность – это поверхность, которая получена поступательными движениями прямой линии в пространстве. Эти движения таковы, что выделенная точка этой прямой линии совершает движение вдоль кривой плоского типа. Такая прямая линия называется образующей, а кривая линия – направляющей.

Цилиндр состоит из пары оснований и боковой цилиндрической поверхности. Цилиндры бывают нескольких видов:

1. Круговой, прямой цилиндр. У такого цилиндра основания и направляющая перпендикулярны образующей линии, и имеется ось симметрии.

2. Наклонный цилиндр. У него угол между образующей линией и основанием не является прямым.

3. Цилиндр иной формы. Гиперболический, эллиптический, параболический и другие.

Площадь цилиндра, а также площадь полной поверхности любого цилиндра находится с помощью сложения площадей оснований этой фигуры и площади боковой поверхности.

Формула, по которой вычисляется полная площадь цилиндра для кругового, прямого цилиндра:

Sp = 2п Rh + 2п R2 = 2п R (h+R).

Площадь боковой поверхности ищется чуть сложнее, чем площадь цилиндра целиком, она вычисляется путем умножения длины образующей линии на периметр сечения, образованного плоскостью, которая перпендикулярна образующей линии.

Данная площадь поверхности цилиндра для кругового, прямого цилиндра узнается по развертке этого объекта.

Развертка – это прямоугольник, который имеет высоту h и длину P, которая приравнивается периметру основания.

Отсюда следует, что боковая площадь цилиндра является равной площади развертки и может быть вычислена по данной формуле:

Sb = Ph.

Если взять круговой, прямой цилиндр, то для него:

P = 2п R, а Sb = 2п Rh.

Если цилиндр наклонный, то площадь боковой поверхности должна быть равна произведению длины его образующей линии и периметра сечения, которое перпендикулярно данной образующей линии.

К сожалению, не существует простой формулы для выражения площади боковой поверхности наклонного цилиндра через его высоту и параметры его основания.

Чтобы вычислить площадь сечения цилиндра, необходимо знать несколько фактов. Если сечение своей плоскостью пересекает основания, то такое сечение всегда является прямоугольником. Но эти прямоугольники будут разными, в зависимости от положения сечения. Одна из сторон осевого сечения фигуры, которое перпендикулярно основаниям, равна высоте, а другая — диаметру основания цилиндра. А площадь такого сечения, соответственно, приравнивается произведению одной стороны прямоугольника на другую, перпендикулярную первой, или произведению высоты данной фигуры на диаметр его основания.

Если сечение будет перпендикулярно основаниям фигуры, но не будет проходить через ось вращения, то площадь этого сечения будет равна произведению высоты этого цилиндра и определенной хорды. Чтобы получить хорду, нужно построить окружность у основания цилиндра, провести радиус и отложить на нем расстояние, на котором находится сечение. А от этой точки нужно провести перпендикуляры к радиусу от пересечения с окружностью. Точки пересечения соединяются с центром. А основание треугольника – это искомая хорда, длина которой ищется по теореме Пифагора. Теорема Пифагора звучит так: «Сумма квадратов двух катетов равна гипотенузе, возведенной в квадрат»:

С2 = А2 + В2.

Если сечение не затрагивает основания цилиндра, а сам цилиндр круговой и прямой, то площадь этого сечения находится как площадь окружности.

Площадь окружности равна:

S окр. = 2п R2.

Чтобы найти радиус окружности R, нужно ее длину C разделить на 2п:

R = C \ 2п, где п – число пи, математическая постоянная, вычисленная для работы с данными окружности и равная 3,14.

fb.ru