Формула виета онлайн – Теорема Виета

Дискриминант. Теорема Виета

Дискриминант, как и квадратные уравнения начинают изучать в курсе алгебры в 8 классе. Решить квадратное уравнение можно через дискриминант и с помощью теоремы Виета. Методика изучения квадратных уравнений, как и формулы дискриминанта достаточно неудачно прививается школьникам, как и многое в настоящем образовании. Поэтому проходят школьные годы, обучение в 9-11 классе заменяет «высшее образование» и все снова ищут — «Как решить квадратное уравнение?», «Как найти корни уравнения?», «Как найти дискриминант?» и …

Формула дискриминанта

Дискриминант D квадратного уравнения a*x^2+bx+c=0 равен D=b^2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;
D=0 — уравнение имеет 1 корень (2 совпадающих корня):
D<0 – не имеет действительных корней (в школьной теории). В ВУЗах изучают комплексные числа и уже на множестве комплексных чисел уравнение с отрицательным дискриминантом имеет два комплексных корня.
Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра..

Общая формула для нахождения корней квадратного уравнения:

Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле

Вторая способ нахождения корней — это Теорема Виета.

Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни




До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком. Сумма корней равна 7 (коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».

Давайте попробуем разобраться, что описывает дискриминант?

В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0),

или парабола ветвями вниз (a<0).

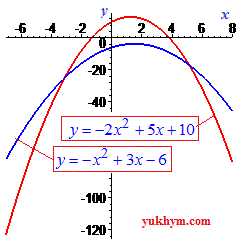Вершина параболы лежит посередине между корнями

Физический смысл дискриминанта:

Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox.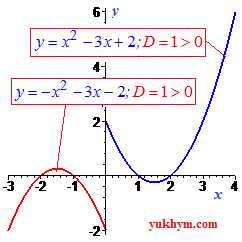
Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
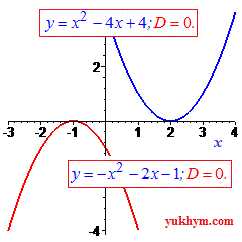И последний случай, когда дискриминант меньше нуля (D<0) – график параболы принадлежит плоскости над осью абсцисс (ветки параболы вверх), или график полностью под осью абсцисс (ветки параболы опущены вниз).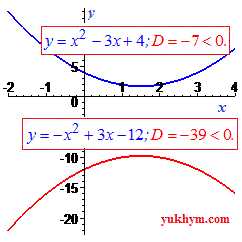

Неполные квадратные уравнения

Если в квадратном уравнении коэффициент при свободном члене или переменной равны нулю то такие уравнения называют неполными. Корни уравнений находим по упрощенной формуле
График функций всегда симметричен относительно начала координат. Стоит отметить, что уравнение имеет действительные корни только тогда, когда в уравнении чередуются знаки при коэффициентах «+, -» или «-, +».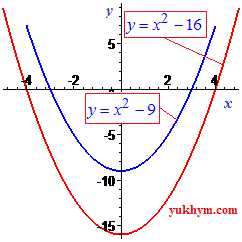
Неполное квадратное уравнение вида
одним из корней всегда имеет точку x=0.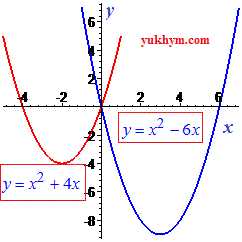
В таком контексте решения квадратных уравнений становится нужным, а при построении графиков парабол, еще и визуально интересным времяпрепровождением, особенно если речь идет о школьном занятии по анализу графика функций, или изучении темы парабол. Поэтому в 8, 9 классе рекомендуем эти две темы в алгебре сочетать.
Если материал помог Вам в обучении, просьба поделиться с друзьями ссылкой на статью!

yukhym.com

StudyPort.Ru — Теорема Виета

Теорема Виета:

1. Если x₁ и x₂ — корни квадратного уравнения

2. Если x₁ и x₂ удовлетворяют условиям , то они являются корнями квадратного уравнения.

Доказательство первого утверждения:

По формулам корней квадратного уравнения, имеем:

Доказательство второго утверждения:

Пусть x₁ и x₂ удовлетворяют условиям .

Подставим это выражение для  во второе условие, получим:

Умножим левую и правую часть, получившегося уравнения на a, имеем:

-b*x₂-ax₂²=c.

Перенесем все в правую часть:

-b*x₂-ax₂²-c=0.

Умножим левую и правую часть уравнения на -1 и поменяем местами слагаемые:

ax₂²+bx₂+c=0 — значит, x₂ является решением уравнения ax²+bx+c=0.

Аналогично докажем и для x₁

.

Примеры задач, которые решаются с помощью теоремы Виета:

1. Найти коэффициенты квадратного уравнения x²+bx+c=0, если его корни равны -2 и -3.

Решение:

Используем теорему Виета . В нашем случае a=1, значит,

Имеем: b=5 и c=6.

Ответ: уравнение имеет вид x²+5x+6=0.

2. Найти целые корни квадратного уравнения 2x²+10x+12=0.

Решение:

Это уравнение можно конечно, решить, используя формулы корней квадратного уравнения. Но, в условии сказано, что эти корни целые, при этом , по теореме Виета .

Шесть можно представить, как произведение 2*3, или (-2)*(-3), заметим, что -5=(-2)+(-3). Значит, по теореме Виета, -2 и -3 – целые корни квадратного уравнения.

Ответ: -2 и -3.

studyport.ru

Теорема Виета. Алгебра, 8 класс: уроки, тесты, задания.

1.	Теорема Виета Сложность: лёгкое	2
2.	Теорема Виета, составление уравнения Сложность: лёгкое	2
3.	Разложение на множители Сложность: лёгкое	1
4.	Корни квадратного уравнения Сложность: среднее	2
5.	Составление квадратного уравнения Сложность: среднее	2
6.	Разложение на множители квадратного трёхчлена Сложность: среднее	2
7.	Сокращение дроби Сложность: сложное	3
8.	Значение выражения Сложность: сложное	3
9.	Разность, сумма, произведение корней квадратного уравнения Сложность: сложное	3

www.yaklass.ru