Улитка Паскаля
Улитка Паскаля – плоская кривая. Ее можно определить как геометрическое место точек М и М1, расположенных на прямых пучка с центром в точке О, лежащей на данной окружности радиуса R, и находящихся на равном расстоянии а по обе стороны от точки пересечения Р прямых пучка с окружностью – см. рис., – где а < 2R. Улитка Паскаля изображена на нем красной линией.
Уравнение улитки Паскаля в полярных координатах имеет вид:
ρ = 2 Rcosφ + a,
где φ – полярный угол радиуса-вектора текущей точки.
Если а = 2R, то петля улитки Паскаля (сплошная линия внутри данной окружности на рис.) стягивается в точку, и улитка Паскаля вырождается в кардиоиду.
Если a > 2R, улитка Паскаля не имеет общих точек с данной окружностью (см. рис.).
(х2 + у2 – 2Rx)2 – a2(x2 + y2) = 0.
Поэтому она является алгебраической кривой четвертого порядка.
Как видно из рисунков, улитка Паскаля симметрична относительно оси абсцисс, начало координат при а > 2R – двойная точка; при а < 2R – узловая точка; при а = 2R – точка возврата I рода.
Площадь S, ограниченную улиткой Паскаля, можно подсчитать по формуле
;
при этом в случае а < 2R площадь внутренней петли считается по этой формуле дважды.
Улитка Паскаля – конхоида окружности диаметра 2 R; она же – частный случай декартова овала; она же – эпитрохоида.
Кривая названа в честь знаменитого французского ученого Б. Паскаля, изучавшего ее в первой половине XVII в.
school-collection.edu.ru
Плоские кривые — лемнискаты, циклоиды, гипоциклоиды, цепная линия, трохоида
ЛЕМНИСКАТЫ
Уравнение в полярных координатах:
r2 = a2cos2θ
Уравнение в прямоугольных координатах:
(x2 + y2)2 = a2(x2 — y2)
Угол между AB’ или A’B и осью x = 45o
Площадь одной петли = a2/2
ЦИКЛОИДА
Уравнения в параметрической форме:
Площадь одной дуги = 3πa2
Длина дуги одной арки = 8a
Это кривая, описываемая точкой Р на окружности радиусом а, которая катится вдоль оси х.
ГИПОЦИКЛОИДЫ С ЧЕТЫРЬМЯ ОСТРИЯМИ
Уравнение в прямоугольных координатах:
x2/3 + y2/3 = a2/3
Уравнения в параметрической форме:
Площадь, ограниченная кривой = 3πa2/8
Длина дуги целой кривой = 6a
Это кривая, описываемая точкой Р на окружности радиусом a/4, которая катится внутри окружности радиусом a.
КАРДИОИДА
Уравнение: r = a(1 + cosθ)
Площадь, ограниченная кривой = 3πa2/2
Длина дуги кривой = 8a
Это кривая, описываемая точкой Р на окружности радиусом a, которая катится снаружи окружности радиусом a. Эта кривая также является частным случаем улитки Паскаля.
ЦЕПНАЯ ЛИНИЯ
Уравнение:
y = a(ex/a + e-x/a)/2 = acosh(x/a)
Это кривая, по которой бы повисла цепь, подвешенная вертикально от точки А к В.
ТРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos3θ
Уравнение r = acos3θ подобно кривой, полученной вращением против часовой стрелки по кривой 30 o или π/6 радиан.
В общем, r = acosnθ или r = asinnθ имеет n лепестков если n является нечетным.
ЧЕТЫРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos2θ
Уравнение r = asin2θ подобно кривой, полученной вращением против часовой стрелки по кривой 45o или π/4 радиан.
В общем r = acosnθ или r = asinnθ имеет 2n лепестков если n — четное.
ЭПИЦИКЛОИДА
Параметрические уравнения:
Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а. Кардиоида является частным случаем эпициклоиды.
ОБЩАЯ ГИПОЦИКЛОИДА
Параметрические уравнения:
Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а.
Если b = a/4, кривая является гипоциклоидой с четырьмя остриями.
ТРОХОИДА
Параметрические уравнения:
Это кривая, описываемая точкой Р на дистанции b от центра окружности с радиусом а, когда она катится по оси x.
Если b укороченной циклоидой.
Если b > a, кривая имеет форму, показанную на рис. 11-11 и называется троходой.
Если b = a, кривая есть циклоидой.
ТРАКТРИСА
Параметрические уравнения:
Это кривая, описываемая конечной точкой Р натянутой струны длиной PQ, когда другой конец Q перемещается вдоль оси х.
ВЕРЗЬЕРА (ВЕРЗИЕРА) АНЬЕЗИ (ИНОГДА ЛОКОН АНЬЕЗИ)
Уравнение в прямоугольных координатах: y = 8a3/(x2 + 4a2)
Параметрические уравнения:
В. На рисунке переменная линия OA пересекающая y = 2a и круг с радиусом a с центром (0,a) в A и B соотвественно. Любая точка P на «локоне» определяется построением линий, параллельных к осям x и y, и через B и A соответственно и определяющие точку пересечения P.
ДЕКАРТОВ ЛИСТ
Уравнение в прямоугольных координатах:
Параметрические уравнения:
Площадь петли 3a2/2
Уравнение асимптоты: x + y + a = 0.
www.math10.com
Кардиоида и улитка Паскаля
При написании статьи использовались материалы сайта arbuz.ferghana.ru
Кардиоида (Cardioid)
Если использовать две окружности с одинаковыми радиусами и вращать одну вокруг другой, то получится кардиоида (греч.кардиа — сердце) — по мнению математиков, получаемая кривая отдаленно напоминает сердце
Формула r = 2a(1 + cos(theta)) рисует кардиоиду
Лимакона или Улитка Паскаля (Limacon of Pascal)
А как поведут себя кривые, если брать точку не самой катящейся окружности, а внутри ее, сместив в сторону от центра? Тогда мы получим кривую, получившуюся название Улитка Паскаля или лимакона
Лимакона
Формула r = b + 2a cos(theta) рисует лимакону (улитку Паскаля)
При b = 2a лимакона становится кардиодидом
Эффекты с кривыми
Итак, мы знаем формулы окружности, кардиоиды и улитки Паскаля. Видно, что формулы весьма схожи, осталось объединить их в один цикл для получения первого эффекта
Dim x As Single, y As Single, b As Single Dim twoPi As Single, I As Single, R As Single Dim col Cls twoPi = Atn(1) * 8 Scale (-25, 25)-(25, -25) For b = 0 To 8 Step 2 For I = 0 To twoPi Step 0.01 R = b + 6 * Cos(I) x = R * Cos(I) y = R * Sin(I) DrawWidth = 3 col = RGB(255 - 30 * b, 128 + (-1) ^ (b * 1) * b * 60, b * 110) Line (x, y)-Step(0, 0), col, BF Next I Next bВ нашем примере a — величина постоянная, а b меняется в цикле от b=0 до b=8. Вы видите, как меньшая петля вырождается в точку, а большая удваивает свой радиус, превращаясь в кардиоиду.
Доработаем рисунок. Изменим чуточку программу и получим красивый узор
Cls
pi = 4 * Atn(1)
scal = 15
a = 140
DrawWidth = 8
For l = 0 To 200 Step 13
For t = 0 To 360 Step 0.25
tt = t * pi / 180
x = a * Cos(tt) * Cos(tt) + l * Cos(tt)
y = a * Cos(tt) * Sin(tt) + l * Sin(tt)
red = 255 - 250 * Sin(0.31 * l)
green = 255 - 250 * Sin(0.3 * l)
blue = 255 - 250 * Sin(0.29 * l)
Col = RGB(red, green, blue)
If l Mod 2 = 0 Then
Col = RGB(0, 0, 0)
Else
Col = RGB(255, l, 255 - l)
End If
Line (x + 190, y + 250)-Step(ss, ss), Col, BF
PSet (x + 190, y + 250), Col
Next t
Next lКонхоида
Представим Улитку Паскаля как конхоиду. Не углубляясь в теорию кривых, дадим такое нестрогое определение: конхоида — это геометрическое место точек, полученное перемещением каждой точки первоначальной кривой вдоль определенным образом заданных поверхностей. Для Улитки Паскаля первоначальной кривой служит самая обычная окружность, а переносятся точки вдоль линий, проходящих через точку, лежащую на этой окружности. Поясним графически. На рисунке мы выбираем на окружности неподвижную точку Р и переменную точку М, которую мы сдвигаем вдоль линии, соединяющей точки Р и М на какое-то фиксированное расстояние а.
Полученные семейства точек и есть конхоида окружности относительно фиксированной точки. Программа позволяет получить ожидаемые картинки. Сначала назначим а=0.25R. (Постепенно увеличивайте эту величину). Обратите внимание на необходимость сделать два оборота (центральный угол, он же переменная f от 0 до 720 градусов) — один сдвигает точки наружу, а второй оборот — внутрь окружности. Основная тонкость переход от центрального угла окружности, по которому мы проходим в цикле (переменные f в градусах или t в радианах), к углу линии, соединяющей постоянную точку с текущей на окружности c горизонтальной осью (переменная alfa)
Form1.ScaleMode = vbPixels
Cls
pi = 4 * Atn(1)
scal = 15
'радиус окружности
R = 90
' точка на окружности
' в качестве разделителя используйте запятую для русской версии!
a = CSng(Text1.Text) * R
' a = 1.5 * r
' делаем оборот
For f = 1 To 720 Step 5
t = f * pi / 180
x = R * (1 + Cos(t))
y = R * Sin(t)
alfa = 0
If x > 0 Then alfa = Atn(y / x)
If f
Педальная кривая
Определение педальной кривой для первоначальной давать не будем, сразу перейдем к делу. В текущей точке окружности (пробегаемой в цикле по всей окружности) проведем касательную линию, а потом из фиксированной точки (в нашем случае лежащей на окружности) проводим перпендикуляр к этой касательной. Совокупность этих перпендикуляров огибает, как вы уже догадались, кардиоиду. Это в частном случае расположения фиксированной точки на окружности, при смещении этой точки внутрь окружности или наружу ее получим все семейство Улитки Паскаля. В приведенной программе все также счетчик цикла f центральный угол в градусах, t он же в радианах, beta угол наклона касательной в соответствующей точке цикла, k тангенс этого угла. Уравнение лини, как известно, y=kx+b, для каждой касательной находим b=y-kx. Для взаимно перпендикулярных прямых k1=-1/k, а b1=0 так как все перпендикуляры проходят через точку у которой y= 0. Решая совместно уравнения касательной и перпендикуляра к ней, находим координаты точки пересечения и рисуем в них маленький красный кружок. Эти кружки и нарисуют нам педальную кривую к окружности относительно точки.
Cls
Form1.ScaleMode = vbPixels
pi = 4 * Atn(1)
scal = 15
r = 180
a = 0 * r
DrawWidth = 1
Circle (190 + r, 250), r, RGB(0, 0, 200)
For f = 1 To 720 Step 3
t = f * pi / 180
x = r * (1 + Cos(t))
y = r * Sin(t)
beta = pi / 2 + t
k = Tan(beta)
b = y - k * x
k1 = -1 / k
b1 = k1 * a
X1 = (b1 - b) / (k - k1)
Y1 = k1 * X1 + b1
red = 255
green = 0
blue = 0
col = RGB(red, green, blue)
Circle (X1 + 190, Y1 + 250), 3, col ' Точка пересечения красная
Circle (x + 190, y + 250), 3, RGB(0, 155, 150) 'Точка на круге голубая
Line (190 - a, 250)-(X1 + 190, Y1 + 250), RGB(0, 155, 0)
Line (x + 190, y + 250)-(X1 + 190, Y1 + 250), RGB(0, 55, 150)
Next fСоздание шедевров
Будем брать точки все на той же нашей окружности, ставить в них иголку циркуля и рисовать новые окружности так, чтобы они все проходили через все ту же фиксированную точку на окружности. Общая огибающая (так называемая энвелопа) к полученным окружностям будет конечно, все уже догадались кардиоидой. А при смещении фиксированной точки получим всю гамму Улиток Паскаля. Этот процесс иллюстрирует картинка и программа, нарисовавшая ее. Маленькими черными кружками отмечены лежащие на исходной окружности точки центры проводимых окружностей. Здесь а смешение фиксированной точки для ваших экспериментов, пока равно нулю. Главное в этой программе посчитать радиус рисуемой в каждой точке цикла окружности, хотя для этого достаточно теоремы Пифагора, надо только уметь ее применить к месту. Как вы уже заметили, расцветка красивая, цвет окружностей меняется в течение цикла. Достаточно всего лишь уменьшить шаг цикла и мы получим красивую картину.
Form1.ScaleMode = vbPixels
Cls
pi = 4 * Atn(1)
scal = 15
r = 90
a = 0 * r
DrawWidth = 3
' попробуйте уменьшить шаг
For f = 1 To 360 Step 18
t = f * pi / 180 + pi
x = r * (1 + Cos(t))
y = r * Sin(t)
rr = Sqr((x - a) ^ 2 + y ^ 2)
red = 255 - 0.6 * f
green = 0.6 * f
blue = Abs(Int(0.0005 * f * (360 - f))) ^ 2
col = RGB(red, green, blue)
Circle (190 + x, 250 + y), rr, col
Circle (x + 190, y + 250), 4, RGB(0, 0, 0)
Next fТеперь нас отделяет от создания шедевра один маленький шаг делаем толщину линии побольше (например, 55 пикселей) и раскрашиваем каждый четный круг в желтый цвет, а нечетный в черный. И получаем шедевр поп-арта, которому позавидовал бы сам Малевич.
Form1.ScaleMode = vbPixels
Cls
pi = 4 * Atn(1)
scal = 5
r = 88
a = 0 * r
DrawWidth = 55
For f = 1 To 360 Step 17
t = f * pi / 180 + pi
x = r * (1 + Cos(t))
y = r * Sin(t)
rr = Sqr((x - a) ^ 2 + y ^ 2)
If f Mod 2 = 0 Then
col = RGB(255, 255, 10)
Else: col = RGB(0, 0, 0)
End If
Circle (190 + x, 260 + y), rr, col
Next fПродолжим наши опыты. Для текущей точки на окружности выделяем центральный угол с горизонтальной осью, под таким же углом проводим луч из фиксированной точки (все той же, на окружности), до пересечения с окружностью. Точку пересечения луча с окружностью соединяем с первоначальной точкой и находим середину полученной хорды. Вы будете смеяться, но эти середины хорд лежат на Улитке Паскаля.
Текущий центральный угол нам выделять не надо мы и так от него в цикле все и строим. Единственный технический момент нахождение точки пересечения окружности и линии, проходящей через фиксированную точку (параллельно радиусу, проведенному в текущую точку). Для нахождения координат точки пересечения линии, проходящей через фиксированную точку и окружности, надо совместно решить их уравнения. Уравнение линии y=kx+b, причем b=0 так как точка лежит на оси x, а k=tan(t), где t угол наклона линии в радианах. А уравнение окружности (x-r)2+y2=r2 так как центр сдвинут на величину r относительно начала координат, проходящего через фиксированную точку. Исключив y и решив относительно x, получим x=2r/(1-k2). Подставив это значение в уравнение линии, получим y точки на круге. А уж зная координаты двух точек найти координаты середины соединяющего их отрезка совсем просто они равны полусумме координат точек. Все это и реализовано в приведенной программе.
Form1.ScaleMode = vbPixels
Cls
pi = 4 * Atn(1)
R = 200
DrawWidth = 2
Circle (190 + R, 250), R, RGB(0, 0, 200)
x3 = 2 * R: y3 = 0
For f = 1 To 360 Step 6
t = f * pi / 180
x = R * (1 + Cos(t))
y = R * Sin(t)
k = Tan(t)
X1 = 2 * R / (1 + k ^ 2)
Y1 = k * X1
X2 = (X1 + x) / 2:
Y2 = (Y1 + y) / 2
DrawWidth = 2
Circle (X1 + 190, Y1 + 250), 4, RGB(0, 0, 250)
Circle (x + 190, y + 250), 4, RGB(0, 205, 0)
Circle (X2 + 190, Y2 + 250), 4, RGB(250, 0, 0)
Line (X2 + 190, Y2 + 250)-(x3 + 190, y3 + 250), RGB(250, 0, 0)
DrawWidth = 1
Line (190, 250)-(X1 + 190, Y1 + 250), RGB(0, 0, 250)
Line (190 + R, 250)-(x + 190, y + 250), RGB(0, 205, 0)
x3 = X2:
y3 = Y2
Next fПопробуем рассмотреть распространение волн и найти закономерности. Если мы заглянем в круглый зал и крикнем, то наверняка будут точки, в которые звук наш прилетит громче, чем в какие-то другие. Во всяком случае, мы можем построить модель распространения волн в такой комнате, или, что тоже самое, лучей в окружности, причем, будем рассматривать только первый отраженный луч. Вы, даже не читая дальше, поспорите, что отраженные лучи дадут кардиоиду. И будете совершенно правы! Из уважения к читателям программу не привожу после стольких тренировок не написать ее просто неприлично. Единственное, что нужно помнить, что угол падения равен углу отражения и что внутренний угол вдвое меньше центрального угла, опирающегося на ту же дугу.
Паутина
Любителям математических картинок известна так называемая паутина. На окружности берутся точки с определенным шагом, и каждая из них соединяется с такой же точкой, но сдвинутой по фазе в какое-то число раз (n). Это число можно задавать или брать случайным образом. Точки пересечения хорд сливаются в муаровый узор самых замысловатых форм. Идея так притягательна, что настоятельно рекомендую всем попробовать реализовать ее самостоятельно, чтобы поиграть с параметрами и насладиться эффектами. При n= 1 не нарисуется ничего, так как начальные и конечные точки линий совпадают, зато при увеличении n будут появляться фигуры с узлами, причем количество узлов равно n-1. Нас же особенно интересует случай для n= 2, при этом нарисуется фигура, хорошо уже изученная нами кардиоида. При n= 3 так называемая нефроида с двумя узлами. Если n-1 делитель числа 360, то картинка проявляет некоторую упорядоченность. Приводим картинки для значений n= 2 (наша любимая кардиоида)
Form1.ScaleMode = vbPixels
n = 2
xx = 380
yy = 380
R = 240
P = 3.1415926
Cls
For I = 0 To 360 Step 1
T = I * P / 180
x = R * Cos(T)
y = R * Sin(T)
X2 = R * Cos(n * T)
Y2 = R * Sin(n * T)
c = 255 / 360
Line (x + xx, y + yy)-(X2 + xx, Y2 + yy), RGB(0, 0, 0)
Next I
Использование таймера
Чтобы не вводить каждый раз вручную значения n, а поручить эту работу компьютеру, то можно наблюдать интересный калейдоскоп узоров
Dim a As Double
Private Sub Form_Load()
Форма1.WindowState = 2
a = 0
End Sub
Private Sub Timer1_Timer()
xx = 380
yy = 380
R = 330
P = 3.1415926
a = a + 0.03
Cls
For i = 0 To 360 Step 2
T = i * P / 180
x = R * Cos(T)
y = R * Sin(T)
X2 = R * Cos(a * T)
Y2 = R * Sin(a * T)
c = 255 / 360
Line (x + xx, y + yy)-(X2 + xx, Y2 + yy), RGB(0, 0, 0)
Next i
End Sub
www.rusproject.narod.ru
Улитка Паскаля Википедия
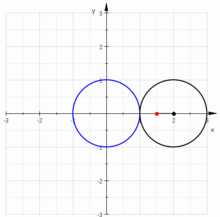
Три улитки Паскаля, конхоиды чёрной окружности: зелёная a>ℓ{\displaystyle a>\ell }, красная (кардиоида) a=ℓ{\displaystyle a=\ell } и синяя a<ℓ{\displaystyle a<\ell }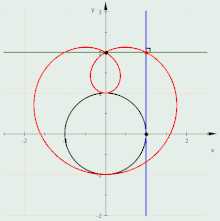
Анимация подеры окружностиУлитка Паскаля ― плоская кривая определённого типа. Названа по имени Этьена Паскаля (отца Блеза Паскаля), впервые рассмотревшего её.
Уравнения
Уравнение в прямоугольных координатах:
- (x2+y2+ay)2=ℓ2(x2+y2){\displaystyle (x^{2}+y^{2}+ay)^{2}=\ell ^{2}(x^{2}+y^{2})}
в полярных координатах:
- ρ=ℓ−asinϕ.{\displaystyle \rho =\ell -a\sin \phi .}
Параметрическое:
- x=2R⋅cos(t)−h⋅cos(2t){\displaystyle x=2R\cdot \cos(t)-h\cdot \cos(2t)}
- y=2R⋅sin(t)−h⋅sin(2t){\displaystyle y=2R\cdot \sin(t)-h\cdot \sin(2t)}
Здесь a — диаметр исходной окружности, а l — расстояние, на которое смещается точка вдоль радиус-вектора (см. конхоида).
При этом начало координат является
- узловой точкой при a>ℓ{\displaystyle a>\ell }.
- точкой возврата при a=ℓ{\displaystyle a=\ell } (в этом случае Улитка Паскаля называется кардиоидой).
- двойной точкой при a<ℓ{\displaystyle a<\ell }.
В случае ℓ=a2{\displaystyle \ell ={\frac {a}{2}}} улитка Паскаля также называется трисектри́са (также триссектри́са). Такое название она получила из за того, что если на плоскости задана трисектриса, то трисекцию угла можно построить с помощью циркуля и линейки. Уравнение трисектрисы:
- z=b(eit+e2it)=be3it2(eit2+e−it2)=2bcost2e3it2{\displaystyle z=b(e^{it}+e^{2it})=be^{3it \over 2}(e^{it \over 2}+e^{-it \over 2})=2b\cos {t \over 2}e^{3it \over 2}},
В полярных координатах:
- r=2bcosθ3{\displaystyle r=2b\cos {\theta \over 3}}
Построение улитки Паскаля.Свойства
- Улитка Паскаля является плоской алгебраической кривой 4-го порядка.
- Улитка Паскаля является обобщением кардиоиды
- Улитка Паскаля является подерой окружности.
- Улитка Паскаля является конхоидой окружности относительно точки на окружности.
- Улитка Паскаля является частным случаем Декартова овала.
- Улитка Паскаля является частным случаем эпитрохоиды.
- Улитка Паскаля является примером эквихордной кривой.
- Длина дуги выражается эллиптическим интегралом 2-го рода.
- Площадь, ограниченная улиткой Паскаля:
- S=πa22+πℓ2{\displaystyle S={\frac {\pi a^{2}}{2}}+\pi \ell ^{2}}
- при a>ℓ{\displaystyle a>\ell } площадь внутренней петли при вычислении по этой формуле считается дважды.
Литература
- Улитка Паскаля // Ужи — Фидель. — М. : Советская энциклопедия, 1956. — С. 188-189. — (Большая советская энциклопедия : [в 51 т.] / гл. ред. Б. А. Введенский ; 1949—1958, т. 44).
| Кривые | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Определения |
| ||||||||||||||||||
| Преобразованные |
| ||||||||||||||||||
| Неплоские |
| ||||||||||||||||||
| Плоские алгебраические |
| ||||||||||||||||||
| Плоские трансцендентные |
| ||||||||||||||||||
| Фрактальные |
| ||||||||||||||||||
wikiredia.ru
Улитка Паскаля — Википедия
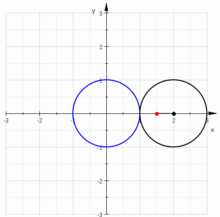
Три улитки Паскаля, конхоиды чёрной окружности: зелёная a>ℓ{\displaystyle a>\ell }, красная (кардиоида) a=ℓ{\displaystyle a=\ell } и синяя a<ℓ{\displaystyle a<\ell }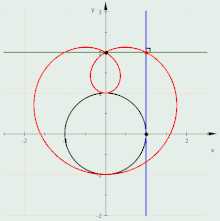
Анимация подеры окружностиУлитка Паскаля ― плоская кривая определённого типа. Названа по имени Этьена Паскаля (отца Блеза Паскаля), впервые рассмотревшего её.
Уравнения
Уравнение в прямоугольных координатах:
- (x2+y2+ay)2=ℓ2(x2+y2){\displaystyle (x^{2}+y^{2}+ay)^{2}=\ell ^{2}(x^{2}+y^{2})}
в полярных координатах:
- ρ=ℓ−asinϕ.{\displaystyle \rho =\ell -a\sin \phi .}
Параметрическое:
- x=2R⋅cos(t)−h⋅cos(2t){\displaystyle x=2R\cdot \cos(t)-h\cdot \cos(2t)}
- y=2R⋅sin(t)−h⋅sin(2t){\displaystyle y=2R\cdot \sin(t)-h\cdot \sin(2t)}
Здесь a — диаметр исходной окружности, а l — расстояние, на которое смещается точка вдоль радиус-вектора (см. конхоида).
При этом начало координат является
- узловой точкой при a>ℓ{\displaystyle a>\ell }.
- точкой возврата при a=ℓ{\displaystyle a=\ell } (в этом случае Улитка Паскаля называется кардиоидой).
- двойной точкой при a<ℓ{\displaystyle a<\ell }.
В случае ℓ=a2{\displaystyle \ell ={\frac {a}{2}}} улитка Паскаля также называется трисектри́са (также триссектри́са). Такое название она получила из за того, что если на плоскости задана трисектриса, то трисекцию угла можно построить с помощью циркуля и линейки. Уравнение трисектрисы:
- z=b(eit+e2it)=be3it2(eit2+e−it2)=2bcost2e3it2{\displaystyle z=b(e^{it}+e^{2it})=be^{3it \over 2}(e^{it \over 2}+e^{-it \over 2})=2b\cos {t \over 2}e^{3it \over 2}},
В полярных координатах:
- r=2bcosθ3{\displaystyle r=2b\cos {\theta \over 3}}
Построение улитки Паскаля.Свойства
- Улитка Паскаля является плоской алгебраической кривой 4-го порядка.
- Улитка Паскаля является обобщением кардиоиды
- Улитка Паскаля является подерой окружности.
- Улитка Паскаля является конхоидой окружности относительно точки на окружности.
- Улитка Паскаля является частным случаем Декартова овала.
- Улитка Паскаля является частным случаем эпитрохоиды.
- Улитка Паскаля является примером эквихордной кривой.
- Длина дуги выражается эллиптическим интегралом 2-го рода.
- Площадь, ограниченная улиткой Паскаля:
- S=πa22+πℓ2{\displaystyle S={\frac {\pi a^{2}}{2}}+\pi \ell ^{2}}
- при a>ℓ{\displaystyle a>\ell } площадь внутренней петли при вычислении по этой формуле считается дважды.
Видео по теме
Литература
- Улитка Паскаля // Ужи — Фидель. — М. : Советская энциклопедия, 1956. — С. 188-189. — (Большая советская энциклопедия : [в 51 т.] / гл. ред. Б. А. Введенский ; 1949—1958, т. 44).
| Кривые | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Определения |
| ||||||||||||||||||
| Преобразованные |
| ||||||||||||||||||
| Неплоские |
| ||||||||||||||||||
| Плоские алгебраические |
| ||||||||||||||||||
| Плоские трансцендентные |
| ||||||||||||||||||
| Фрактальные |
| ||||||||||||||||||
wiki2.red
Улитка паскаля Википедия
Три улитки Паскаля, конхоиды чёрной окружности: зелёная a>ℓ{\displaystyle a>\ell }, красная (кардиоида) a=ℓ{\displaystyle a=\ell } и синяя a<ℓ{\displaystyle a<\ell } Анимация подеры окружностиУлитка Паскаля ― плоская кривая определённого типа. Названа по имени Этьена Паскаля (отца Блеза Паскаля), впервые рассмотревшего её.
Уравнения
Уравнение в прямоугольных координатах:
- (x2+y2+ay)2=ℓ2(x2+y2){\displaystyle (x^{2}+y^{2}+ay)^{2}=\ell ^{2}(x^{2}+y^{2})}
в полярных координатах:
- ρ=ℓ−asinϕ.{\displaystyle \rho =\ell -a\sin \phi .}
Параметрическое:
- x=2R⋅cos(t)−h⋅cos(2t){\displaystyle x=2R\cdot \cos(t)-h\cdot \cos(2t)}
- y=2R⋅sin(t)−h⋅sin(2t){\displaystyle y=2R\cdot \sin(t)-h\cdot \sin(2t)}
Здесь a — диаметр исходной окружности, а l — расстояние, на которое смещается точка вдоль радиус-вектора (см. конхоида).
При этом начало координат является
- узловой точкой при a>ℓ{\displaystyle a>\ell }.
- точкой возврата при a=ℓ{\displaystyle a=\ell } (в этом случае Улитка Паскаля называется кардиоидой).
- двойной точкой при a<ℓ{\displaystyle a<\ell }.
В случае ℓ=a2{\displaystyle \ell ={\frac {a}{2}}} улитка Паскаля также называется трисектри́са (также триссектри́са). Такое название она получила из за того, что если на плоскости задана трисектриса, то трисекцию угла можно построить с помощью циркуля и линейки. Уравнение трисектрисы:
- z=b(eit+e2it)=be3it2(eit2+e−it2)=2bcost2e3it2{\displaystyle z=b(e^{it}+e^{2it})=be^{3it \over 2}(e^{it \over 2}+e^{-it \over 2})=2b\cos {t \over 2}e^{3it \over 2}},
В полярных координатах:
- r=2bcosθ3{\displaystyle r=2b\cos {\theta \over 3}}
Построение улитки Паскаля.Свойства
- Улитка Паскаля является плоской алгебраической кривой 4-го порядка.
- Улитка Паскаля является обобщением кардиоиды
- Улитка Паскаля является подерой окружности.
- Улитка Паскаля является конхоидой окружности относительно точки на окружности.
- Улитка Паскаля является частным случаем Декартова овала.
- Улитка Паскаля является частным случаем эпитрохоиды.
- Улитка Паскаля является примером эквихордной кривой.
- Длина дуги выражается эллиптическим интегралом 2-го рода.
- Площадь, ограниченная улиткой Паскаля:
- S=πa22+πℓ2{\displaystyle S={\frac {\pi a^{2}}{2}}+\pi \ell ^{2}}
- при a>ℓ{\displaystyle a>\ell } площадь внутренней петли при вычислении по этой формуле считается дважды.
Литература
- Улитка Паскаля // Ужи — Фидель. — М. : Советская энциклопедия, 1956. — С. 188-189. — (Большая советская энциклопедия : [в 51 т.] / гл. ред. Б. А. Введенский ; 1949—1958, т. 44).
| Кривые | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Определения |
| ||||||||||||||||||
| Преобразованные |
| ||||||||||||||||||
| Неплоские |
| ||||||||||||||||||
| Плоские алгебраические |
| ||||||||||||||||||
| Плоские трансцендентные |
| ||||||||||||||||||
| Фрактальные |
| ||||||||||||||||||
wikiredia.ru
Паскаля улитка Википедия
Три улитки Паскаля, конхоиды чёрной окружности: зелёная a>ℓ{\displaystyle a>\ell }, красная (кардиоида) a=ℓ{\displaystyle a=\ell } и синяя a<ℓ{\displaystyle a<\ell } Анимация подеры окружностиУлитка Паскаля ― плоская кривая определённого типа. Названа по имени Этьена Паскаля (отца Блеза Паскаля), впервые рассмотревшего её.
Уравнения
Уравнение в прямоугольных координатах:
- (x2+y2+ay)2=ℓ2(x2+y2){\displaystyle (x^{2}+y^{2}+ay)^{2}=\ell ^{2}(x^{2}+y^{2})}
в полярных координатах:
- ρ=ℓ−asinϕ.{\displaystyle \rho =\ell -a\sin \phi .}
Параметрическое:
- x=2R⋅cos(t)−h⋅cos(2t){\displaystyle x=2R\cdot \cos(t)-h\cdot \cos(2t)}
- y=2R⋅sin(t)−h⋅sin(2t){\displaystyle y=2R\cdot \sin(t)-h\cdot \sin(2t)}
Здесь a — диаметр исходной окружности, а l — расстояние, на которое смещается точка вдоль радиус-вектора (см. конхоида).
При этом начало координат является
- узловой точкой при a>ℓ{\displaystyle a>\ell }.
- точкой возврата при a=ℓ{\displaystyle a=\ell } (в этом случае Улитка Паскаля называется кардиоидой).
- двойной точкой при a<ℓ{\displaystyle a<\ell }.
В случае ℓ=a2{\displaystyle \ell ={\frac {a}{2}}} улитка Паскаля также называется трисектри́са (также триссектри́са). Такое название она получила из за того, что если на плоскости задана трисектриса, то трисекцию угла можно построить с помощью циркуля и линейки. Уравнение трисектрисы:
- z=b(eit+e2it)=be3it2(eit2+e−it2)=2bcost2e3it2{\displaystyle z=b(e^{it}+e^{2it})=be^{3it \over 2}(e^{it \over 2}+e^{-it \over 2})=2b\cos {t \over 2}e^{3it \over 2}},
В полярных координатах:
- r=2bcosθ3{\displaystyle r=2b\cos {\theta \over 3}}
Построение улитки Паскаля.Свойства
- Улитка Паскаля является плоской алгебраической кривой 4-го порядка.
- Улитка Паскаля является обобщением кардиоиды
- Улитка Паскаля является подерой окружности.
- Улитка Паскаля является конхоидой окружности относительно точки на окружности.
- Улитка Паскаля является частным случаем Декартова овала.
- Улитка Паскаля является частным случаем эпитрохоиды.
- Улитка Паскаля является примером эквихордной кривой.
- Длина дуги выражается эллиптическим интегралом 2-го рода.
- Площадь, ограниченная улиткой Паскаля:
- S=πa22+πℓ2{\displaystyle S={\frac {\pi a^{2}}{2}}+\pi \ell ^{2}}
- при a>ℓ{\displaystyle a>\ell } площадь внутренней петли при вычислении по этой формуле считается дважды.
Литература
- Улитка Паскаля // Ужи — Фидель. — М. : Советская энциклопедия, 1956. — С. 188-189. — (Большая советская энциклопедия : [в 51 т.] / гл. ред. Б. А. Введенский ; 1949—1958, т. 44).
| Кривые | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Определения |
| ||||||||||||||||||
| Преобразованные |
| ||||||||||||||||||
| Неплоские |
| ||||||||||||||||||
| Плоские алгебраические |
| ||||||||||||||||||
| Плоские трансцендентные |
| ||||||||||||||||||
| Фрактальные |
| ||||||||||||||||||
wikiredia.ru