Выборочная несмещенная дисперсия — statanaliz.info
Приветствую посетителей блога statanaliz.info. Это очередная статья из рубрики «вариация данных». Сегодня мы продолжаем знакомство со статистической непредсказуемостью.
Тема не нова, так как с таким показателями как размах значений, среднее линейное отклонение, дисперсия, среднее квадратическое (стандартное) отклонение, коэффициент вариации мы уже знакомы. Даже узнали, по каким формулам они рассчитываются и что обозначают. Дабы не тратить время, повторяться не буду, а те, кому интересно, могут перейти по соответствующим ссылкам.
Сразу разочарую: новых показателей вариации сегодня не будет. Зато мы возвращаемся к полюбившейся дисперсии и среднеквадратическому отклонению (корень из дисперсии), и на то есть веская причина.
Кто сталкивался с более-менее серьезным статистическим анализом, наверняка слышал термин «несмещенная дисперсия». Некоторые даже знают, чем расчет такой дисперсии отличается от обычной. Да-да, правильно – делим не на n, а на n-1. Думаю, многим будет интересно узнать, в чем различие и, собственно, кому это надо.
Из названия «выборочная несмещенная дисперсия» видно, что она как-то связана с выборкой. Действительно, выборочная дисперсия рассчитывается по выборке данных.
Понятие о сплошном и выборочном наблюдении
С точки зрения охвата объекта исследования, статистический анализ можно разделить на два вида: сплошной и выборочный. Сплошной статанализ предполагает изучение генеральной совокупности данных, то есть всего явления во всем его многообразии без распространения выводов на другие элементы, не входящие в анализируемую совокупность. Из названия данного типа явствует, что наблюдению подвергаются тотально все элементы. Результат анализа распространяется на всю генеральную совокупность без каких-либо допущений и поправок на ошибку. Данный тип статистического исследования является наиболее полным и точным, так как дополнительные знания почерпнуть уже неоткуда – информация собрана со всех элементов объекта исследования. Это бесспорный плюс.
Отличным примером сплошного наблюдения является перепись населения. «Всесоюзная перепись населения» — красиво звучало! Кстати, советская статистика, как и наука в целом, была одной из самых лучших в мире. Денег на проведение сплошных обследований не жалели, так как при СССР статистика выполняла свою прямую функцию – исследовала реальность, без чего невозможно было строить «светлое будущее». При этом советские ученые-статистики справедливо критиковали буржуазную статистику за то, что те скрывают от народа реальное положение дел и используют статистику для промывки мозгов. Об этом, кстати, писали и сами буржуи. Более практичный пример сплошного наблюдения – опрос жителей многоэтажного дома на предмет заваривания мусоропровода. Опрашиваются все, результат дает вполне однозначный ответ об отношении жителей к мусоропроводу. Ошибки в выводах маловероятны.
Как бы там ни было, у сплошного наблюдения есть отрицательное качество: на организацию и проведение исследования могут потребоваться значительные ресурсы. Одно дело взять пробу из партии товаров, другое – проверять всю партию. Одно дело опросить тысячу прохожих на улице, совсем другое – организовать перепись населения.
В противовес сплошному придумали выборочное наблюдение. Название метода точно отражает его суть: из генеральной совокупности отбирается и анализируется только часть данных, а выводы распространяют на всю генеральную совокупность. Отбор данных происходит таким образом, чтобы выборка была репрезентативной, то есть, сохранила внутреннюю структуру и закономерности генеральной совокупности. Если это условие не соблюдено, то дальнейший анализ во многом теряет смысл.
Сам анализ выборочных данных происходит так же, как и при сплошном наблюдении (рассчитываются различные показатели, делаются прогнозы и т.д.), только с поправкой на ошибку. Это значит, что рассчитывая тот или иной показатель, мы понимаем, что при повторной выборке его значение всегда будет иным. К примеру, провели опрос общественного мнения об отношении к кандидатам в президенты. Опрос показал, что за кандидата N желают проголосовать 60% опрошенных. Если провести еще один такой же опрос, даже в том же месте, то результат будет отличаться. То есть, взяв первое значение 60%, следует понимать, что с той или иной вероятностью оно могло быть, скажем, и 55%, и 65%. Точность и разброс выборочных показателей зависят от характера данных.
Пример изменчивости средней рассмотрен в статье о качестве средней величины при маленьком объеме данных. Там как раз речь идет о том, что средняя величина постоянно меняется и для решения проблемы предлагается увеличить выборку. Большая выборка, бесспорно, дает более надежные результаты, чем маленькая, но даже в этом случае ошибка сохранится, только станет меньше. А иногда и выбора нет, приходится иметь дело с маленькими выборками.
У выборочного наблюдения есть один существенный плюс и один минус, однако по сравнению со сплошным наблюдением крайности меняются местами. Плюс заключается в том, что для проведения выборочного обследования требуется гораздо меньше ресурсов. Минус – в том, что выборочное наблюдение всегда ошибочно. Поэтому основная задача проведения выборочного наблюдения – добиться максимальной точности при приемлемых затратах на его проведение.
Выборочная несмещенная дисперсия
{module 111}
И вот, стало быть, дисперсия. Дисперсия, как и доля или средняя арифметическая, также меняет свое значение от выборки к выборке, но здесь есть интересная особенность. Дисперсия ведь рассчитывается от средней величины, а она в свою очередь тоже рассчитывается по выборке, то есть является ошибочной. Как же это обстоятельство влияет на саму дисперсию?
Если бы мы знали истинную среднюю величину (по генеральной совокупности), то ошибка дисперсии была бы связана только с нерепрезентативностью, то есть с тем, что данные в выборке оказались бы ближе или дальше от средней, чем в целом по генеральной совокупности. При этом при многократном повторении данные стремились бы к своему реальному расположению относительно средней.
Выборочный показатель, который при многократном повторении выборки стремится к своему теоретическому значению, называется несмещенной оценкой. Почему оценкой? Потому что мы не знаем реальное значение показателя (по генеральной совокупности), и с помощью выборочного наблюдения пытаемся его оценить. Оценка показателя – это есть его характеристика, рассчитанная по выборке.
Примером из жизни могут служить оценки в школе. Учитель же не может влезть в мозг школьника и измерить объем знаний. Школьнику задаются вопросы, задачи, на основе чего оцениваются его знания (производится как бы выборочное наблюдение). Как и в эконометрике, оценка знаний школьника может быть ошибочна, что многие знают по себе. Почему-то только каждый считает, что его оценки занижают. Правда, учителя считают, что оценки завышают.
Теперь смотрим внимательно на выборочную среднюю. Выборочная средняя – это несмещенная оценка математического ожидания, так как средняя из выборочных средних стремится к своему теоретическому значению по генеральной совокупности. Где она расположена? Правильно, в центре выборки! Средняя всегда находится в центре значений, по которым рассчитана – на то она и средняя. А раз выборочная средняя находится в центре выборки, то из этого следует, что сумма квадратов расстояний от каждого значения выборки до выборочной средней всегда меньше, чем до любой другой точки, в том числе и до генеральной средней. Это ключевой момент. А раз так, то дисперсия в каждой выборке будет занижена. Средняя из заниженных дисперсий тоже даст заниженное значение. То есть при многократном повторении эксперимента выборочная дисперсия не будет стремиться к своему истинному значению (как выборочная средняя), а будет смещена относительно истинного значения по генеральной совокупности.
Отклонение выборочной средней от генеральной показано на рисунке.
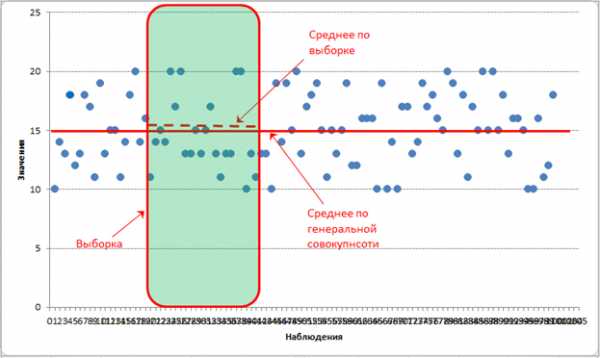
Несмещенность оценки – одна из важных характеристик статистического показателя. Смещенная оценка показателя заранее говорит о тенденции к ошибке. Поэтому показатели стараются оценивать таким образом, чтобы их оценки были несмещенными (как у средней арифметической). Для того, чтобы решить проблему смещенности оценки выборочной дисперсии в ее расчет вносят корректировку – домножают на n/(n-1), либо сразу при расчете в знаменатель ставят не n, а n-1. Получается так.
Выборочная смещенная дисперсия:
Выборочная несмещенная дисперсия:
Примечание. Для расчета выборочной и генеральной дисперсии в Excel есть специальная функция.
Под выборочной дисперсией понимают, как правило, именно несмещенный вариант.
Так как кредо данного блога – статистический анализ доступным языком, то несложное математическое доказательство того, что несмещенная дисперсия получается именно таким образом, опустим. В интернете можно легко найти и более детальную информацию, и доказательство. Зато вместо теоретического доказательства расскажу о практическом эксперименте. Как известно, практика – критерий истины (с).
Вначале я взял 100 случайных значений от 10 до 20 – это генеральная совокупность. Рассчитал дисперсию (по первой формуле). Потом сделал выборку из 20 значений и снова по той же формуле рассчитал дисперсию (генеральную). Как и ожидалась, дисперсия по выборке оказалась несколько меньше дисперсии по генеральной совокупности. Но это могло быть случайностью. Расчет повторил 100 раз. Получилось, что в 60 случаях из 100 дисперсия по выборке оказалась меньше, чем дисперсия генеральной совокупности. Эксперимент подтвердил, что дисперсия по выборке, рассчитанная по правилам генеральной, является смещенной оценкой (в сторону уменьшения).
Теперь посмотрим на практическую сторону использования той или иной формулы. Нас ведь практика интересует в первую очередь. Соотношение между выборочной и генеральной дисперсией составляет n/n-1. Несложно догадаться, что с ростом n (объема выборки) данное выражение стремится к 1, то есть разница между значениями выборочной и генеральной дисперсиями уменьшается.
Так, если мы возьмем выборку из 11 наблюдений, то 11/10 – это 10% относительной разницы. При 21 наблюдениях, отличие сокращается до 5%, при 31 наблюдении – до 3,3%, при 51 – до 2%, при 101 – до 1%. Короче, при достаточно большой выборке данных (50 и выше наблюдений) относительная разница между смещенной и несмещенной дисперсией практически исчезает. Оценка параметра, когда с ростом выборки его отклонение от теоретического значения уменьшается, называется асимптотически несмещенной оценкой.
При переходе к среднему квадратическому отклонению по выборке (оценка среднеквадратического отклонения, равная квадратному корню из выборочной дисперсии) разница становится еще меньше.
Таким образом, эффект смещенной дисперсии проявляется в небольших выборках. В больших выборках можно использовать генеральную дисперсию, что как бы не усложняет и не упрощает жизнь. Вручную сейчас никто не считает. Все легко посчитать в Excel. Но понимать различие в терминологии и в сути показателей все же следует.
Вот и все, что я хотел сегодня поведать. Из данной статьи неплохо бы усвоить следующее.
1. Формула генеральной дисперсии в выборке дает смещенную оценку.
2. Несмещенная оценка дисперсии рассчитывается по формуле, указанной выше.
3. При большом объеме выборки (от 100 наблюдений) разница между смещенной и несмещенной дисперсиями практически исчезает.
4. Среднеквадратическое отклонение по выборке – это корень из выборочной дисперсии.
Надеюсь, мне удалость развеять мифы о несмещенной (или выборочной) дисперсии.
До новых встреч на блоге statanaliz.info.
Поделиться в социальных сетях:
statanaliz.info
Оценка генеральной дисперсии по собственно-случайной выборке. Смещенность и состоятельность выборочной дисперсии (без вывода). Исправленная выборочная дисперсия.
На первый взгляд,
наиболее подходящей оценкой для
генеральной дисперсии 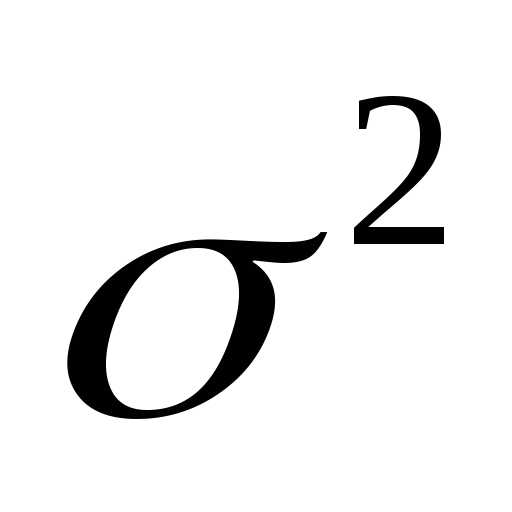 является выборочная дисперсия
является выборочная дисперсия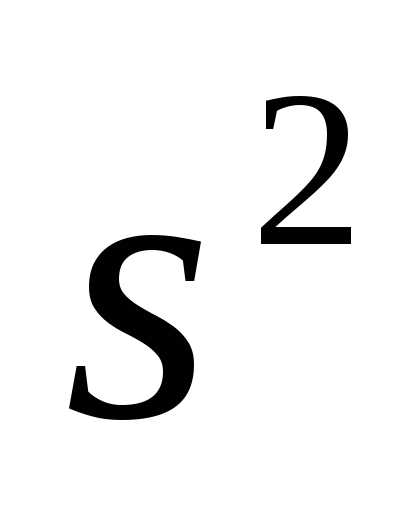 .
Следующая теорема свидетельствует о
том, что
.
Следующая теорема свидетельствует о
том, что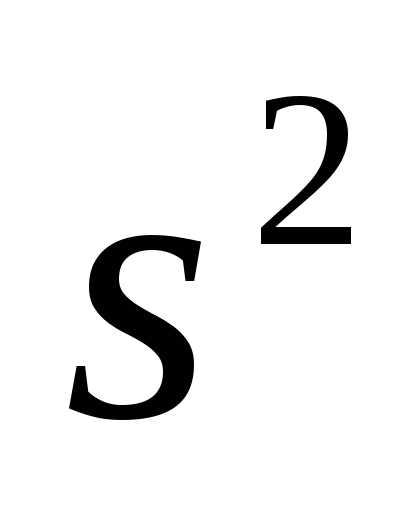 не является «наилучшей» оценкой.
не является «наилучшей» оценкой.
Теорема.
Выборочная дисперсия 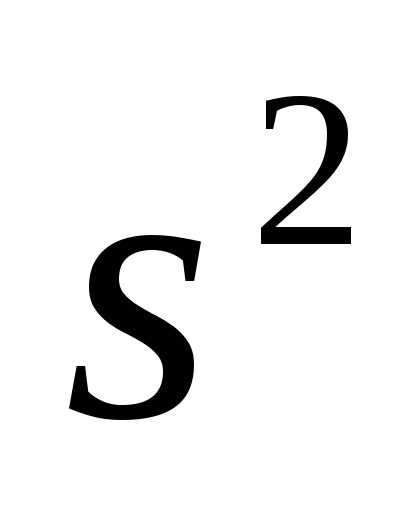 повторной и бесповторной выборок есть
смещенная и состоятельная оценка
генеральной дисперсии
повторной и бесповторной выборок есть
смещенная и состоятельная оценка
генеральной дисперсии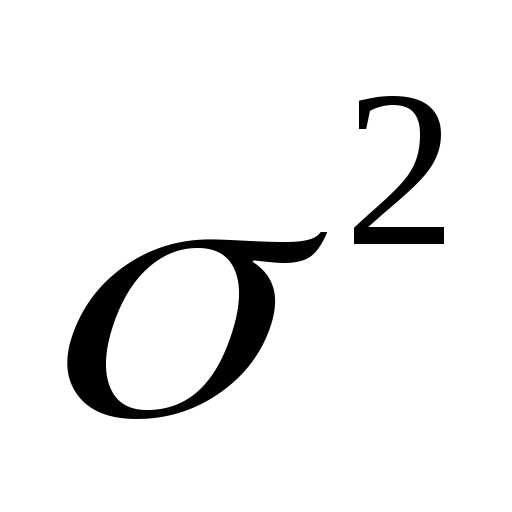 .
.
Δ Принимая без
док-ва состоятельность оценки 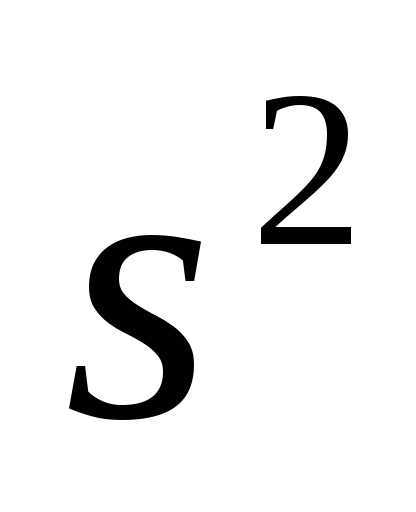
.
Полагая 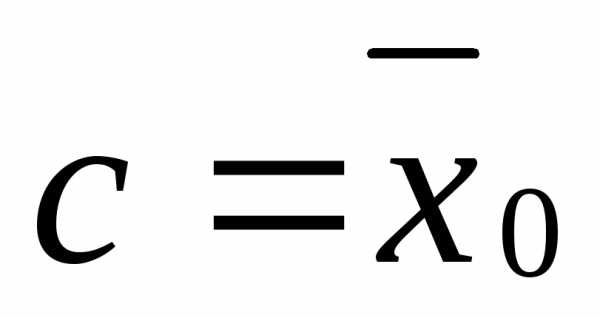 ,
получим.
,
получим.
а) Выборка повторная
Для повторной выборки выборочные значения рассматриваем как независимые случайные величины , каждая из к-ых имеет один и тот же закон распределения, что и у оценки генеральной средней с числовыми характеристиками (1) и (2), т.е.M,, k = 1,2,…,n.
Найдем мат-кое
ожидание оценки 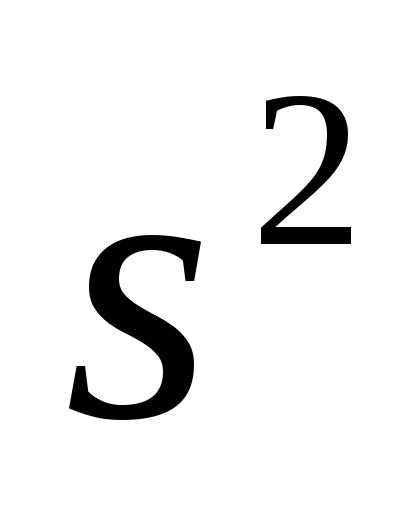 :
:
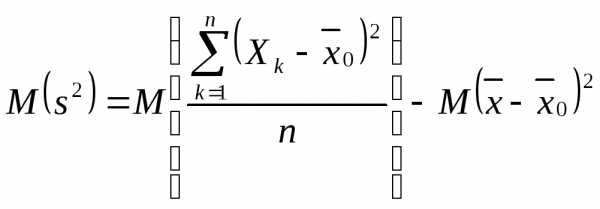 .
.
Первый член в правой части .
Второй член с учетом того, что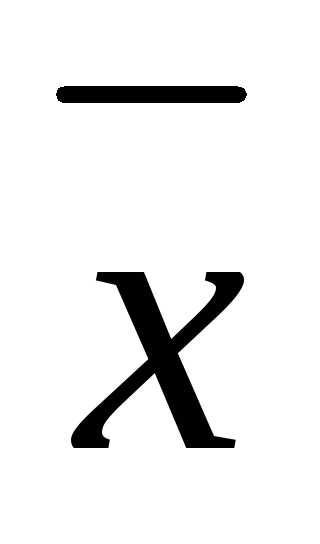 есть несмещенная оценка
есть несмещенная оценка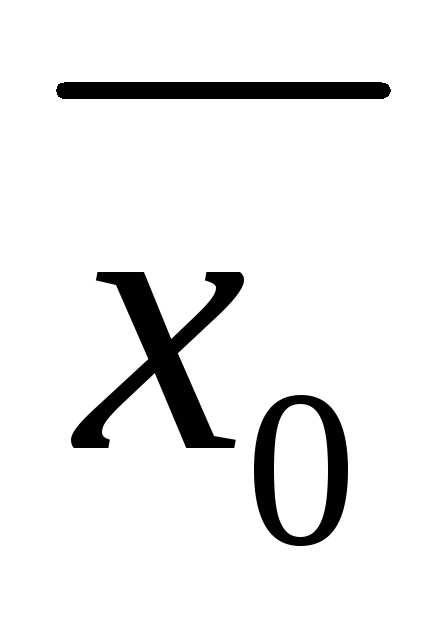 ,
т.е.
,
т.е.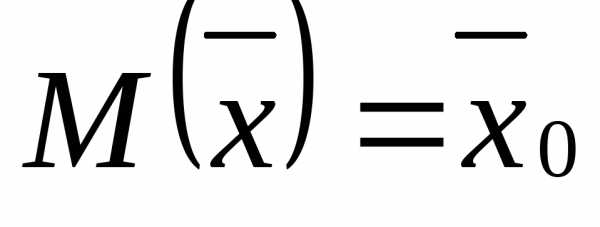 ,.
,.Поэтому .
б) Выборка бесповторная
Для бесповторной выборки — зависимые случайные величины. Можно показать, что
(т.к. объем генеральной совокупности N, как правило, большой и N ≈ N -1).
Итак, и для повторной
выборки, и для бесповторной 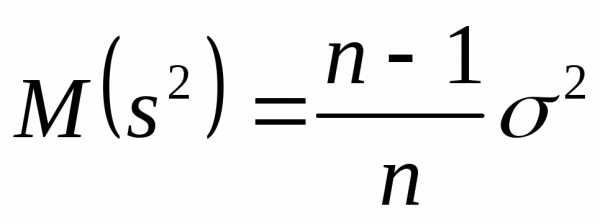 ,
т.е
,
т.е —
смещенная оценка
—
смещенная оценка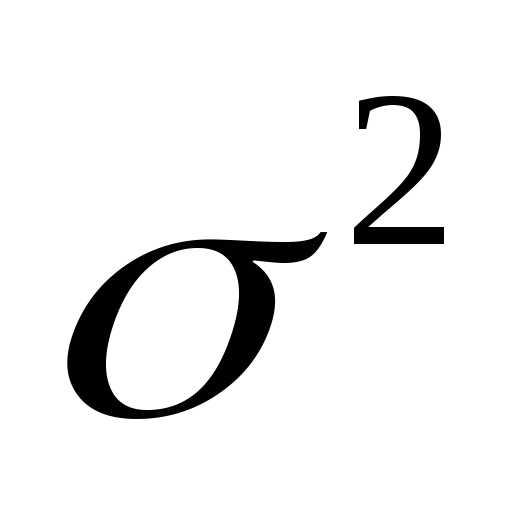 .
▲
.
▲
Т.к. 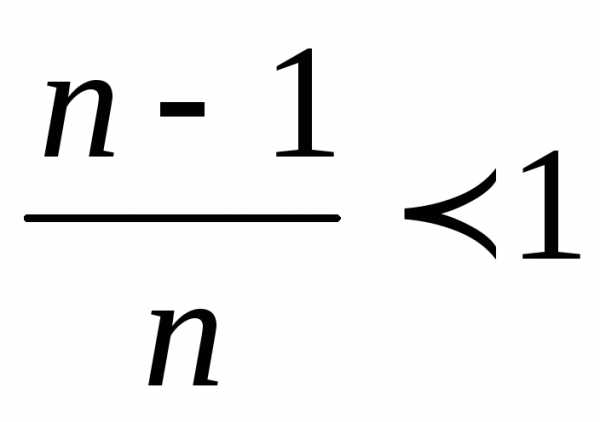 и,
то выборочная дисперсия (в n среднем,
полученная по разным выборкам) занижает
генеральную дисперсию. Поэтому, заменяя
и,
то выборочная дисперсия (в n среднем,
полученная по разным выборкам) занижает
генеральную дисперсию. Поэтому, заменяя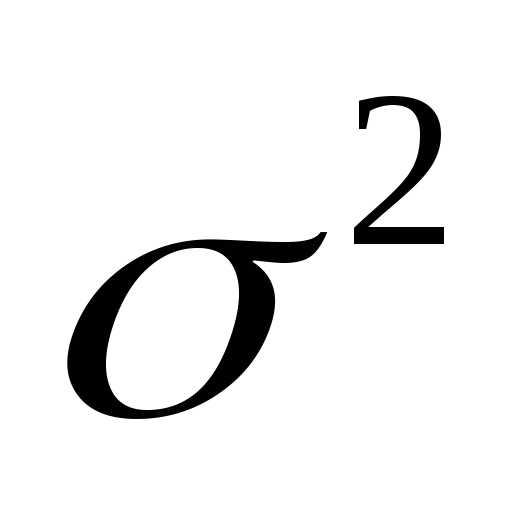
 ,
мы допускаем систематическую погрешность
в меньшую сторону. Чтобы ее ликвидировать,
достаточно ввести поправку, умножив
,
мы допускаем систематическую погрешность
в меньшую сторону. Чтобы ее ликвидировать,
достаточно ввести поправку, умножив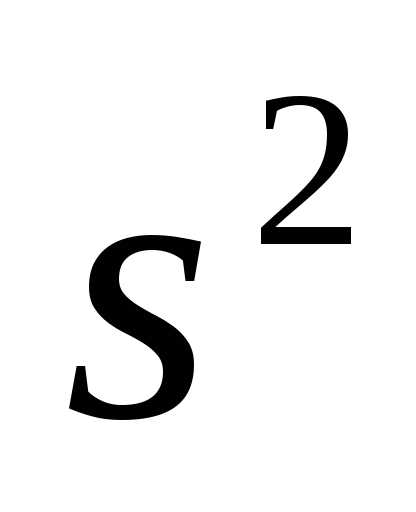 на
на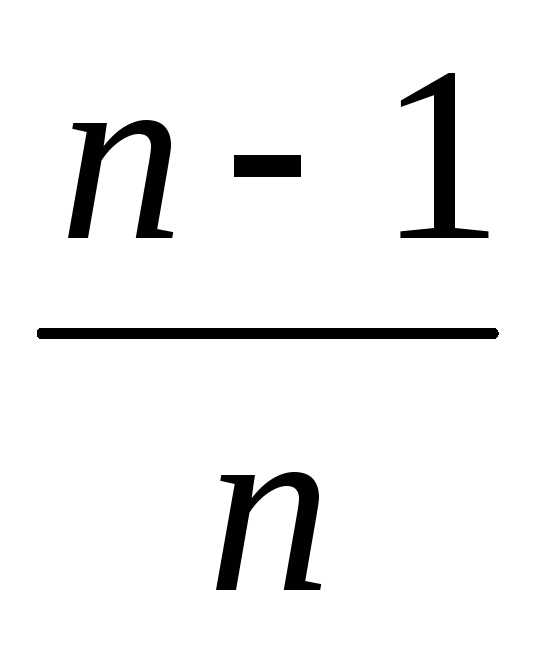 .
Тогда с учетом (
.
Тогда с учетом (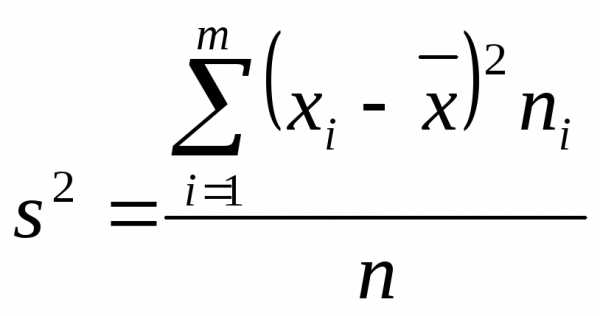 )
получим«исправленную»
выборочную дисперсию:
)
получим«исправленную»
выборочную дисперсию: 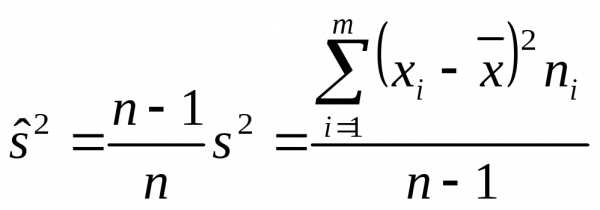 .
.
Очевидно, что .
Т.е.  является несмещенной и состоятельной
оценкой генеральной дисперсии
является несмещенной и состоятельной
оценкой генеральной дисперсии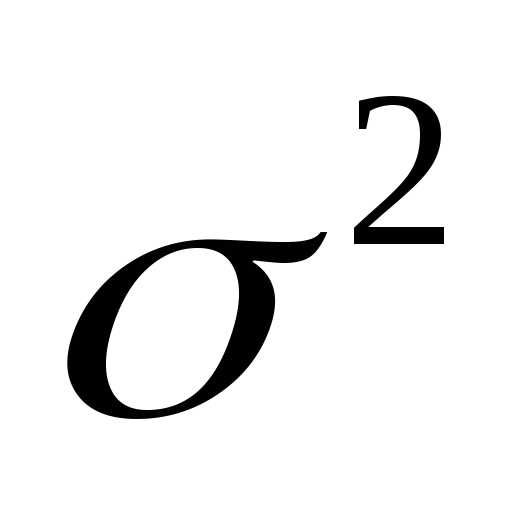
Понятие об интервальном оценивании. Доверительная вероятность и доверительный интервал. Предельная ошибка выборки. Ошибки репрезентативности выборки (случайные и систематические).
Интервальной
оценкой параметра θ называется числовой интервал 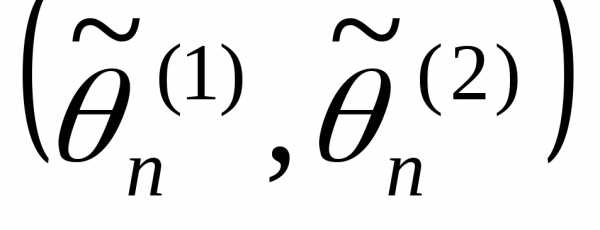 ,
к-ый с заданной вероятностью γ накрывает
неизвестное значение параметра θ.
,
к-ый с заданной вероятностью γ накрывает
неизвестное значение параметра θ.
Обращаем внимание на то, что границы интервала и его величина находятся по выборочным данным и потому являются случайными величинами в отличие от оцениваемого параметра θ — величины неслучайной, поэтому правильнее говорить о том, что интервал «накрывает», а не «содержит» значение θ.
Такой интервал 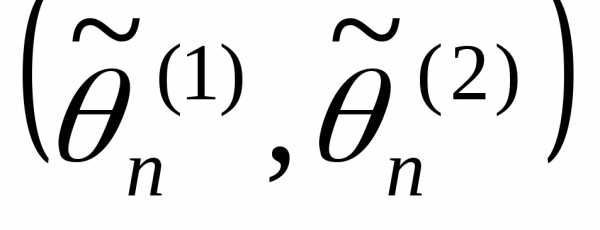 называетсядоверительным,
а вер-ть γ — доверительной
вер-тью, уровнем
доверия или надежностью
оценки.
называетсядоверительным,
а вер-ть γ — доверительной
вер-тью, уровнем
доверия или надежностью
оценки.
Величина доверительного интервала существенно зависит от объема выборки n (уменьшается с ростом n) и от значения доверительной вер-ти γ (увеличивается с приближением γ к 1).
Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно параметра θ, т.е. (θ-Δ,θ+Δ).
Наибольшее отклонение
Δ оценки 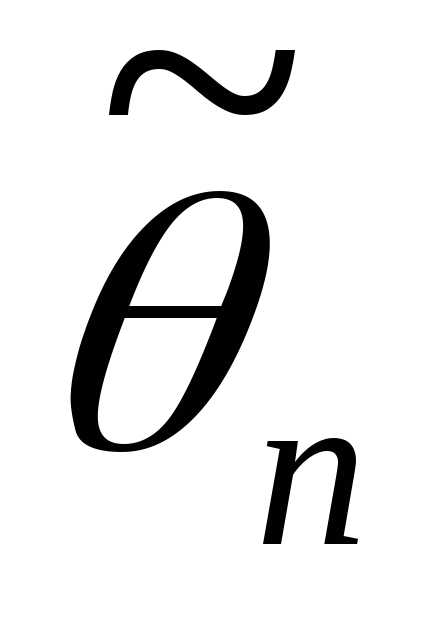 от оцениваемого параметра θ, в частности,
выборочной средней (или доли) от
генеральной средней (или доли), к-ое
возможно с заданной доверительной
вер-тью γ, называетсяпредельной
ошибкой выборки.
от оцениваемого параметра θ, в частности,
выборочной средней (или доли) от
генеральной средней (или доли), к-ое
возможно с заданной доверительной
вер-тью γ, называетсяпредельной
ошибкой выборки.
Ошибка Δ является ошибкой репрезентативности (представительства) выборки. Она возникает только вследствие того, что исследуется не вся совок-ть, а лишь часть, ее (выборка), отобранная случайно. Эту ошибку часто называют случайной ошибкой репрезентативности. Ее не следует путать с систематической ошибкой репрезентативности, появляющейся в рез-те нарушения принципа случайности при отборе элементов в выборку.
studfiles.net
Выборочное среднее, выборочная дисперсия.
Для
эмпирической случайной величины можно
построить ступенчатую функцию
распределения; она называется выборочной
функцией распределения. Кроме того, можно вычислить все числовые
характеристики выборочной случайной
величины 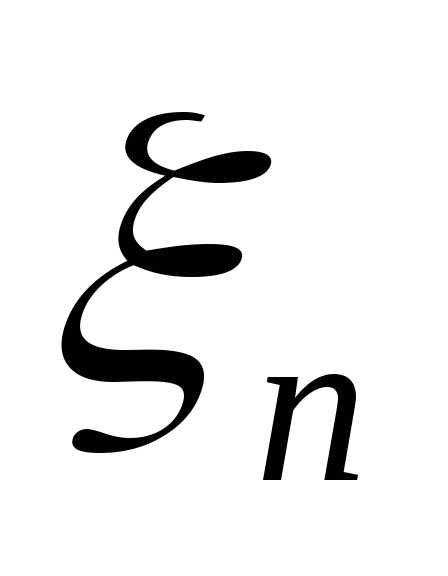 :
математическое ожидание, дисперсию,
среднеквадратичное отклонение
:
математическое ожидание, дисперсию,
среднеквадратичное отклонение  ,
начальные и центральные моменты, медиану,
коэффициенты асимметрии и эксцесса и
т.д. Все эти величины снабжаются
определением «выборочный»:выборочное
математическое ожидание
,
начальные и центральные моменты, медиану,
коэффициенты асимметрии и эксцесса и
т.д. Все эти величины снабжаются
определением «выборочный»:выборочное
математическое ожидание
 ) есть не что иное как среднее арифметическое
значений выборки:
.
Соответственно выборочная дисперсия
) есть не что иное как среднее арифметическое
значений выборки:
.
Соответственно выборочная дисперсия 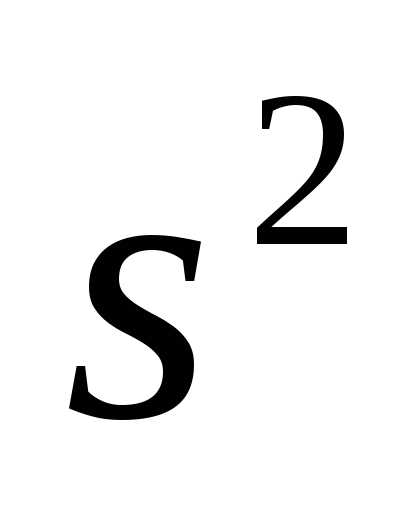 равна
равнаГистограмма и полигон
На
практике выборки большого объема из
непрерывных распределений обычно
подвергаются группировке: интервал
изменения значений выборки разбивается
на малые промежутки, а затем подсчитываются
частоты 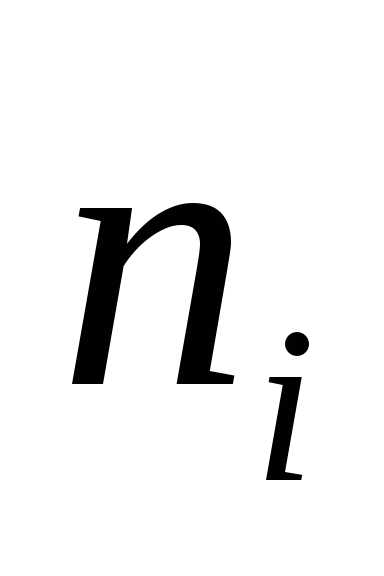 попадания значений выборки в каждыйi-й
промежуток. Для оценки плотности
распределения генеральной совокупности
используется специальный график — гистограмма. Гистограмма строится следующим образом.
Пусть длина каждого маленького промежутка
равна h. Построим на i-м промежутке как на основании прямоугольник
высотой
попадания значений выборки в каждыйi-й
промежуток. Для оценки плотности
распределения генеральной совокупности
используется специальный график — гистограмма. Гистограмма строится следующим образом.
Пусть длина каждого маленького промежутка
равна h. Построим на i-м промежутке как на основании прямоугольник
высотой 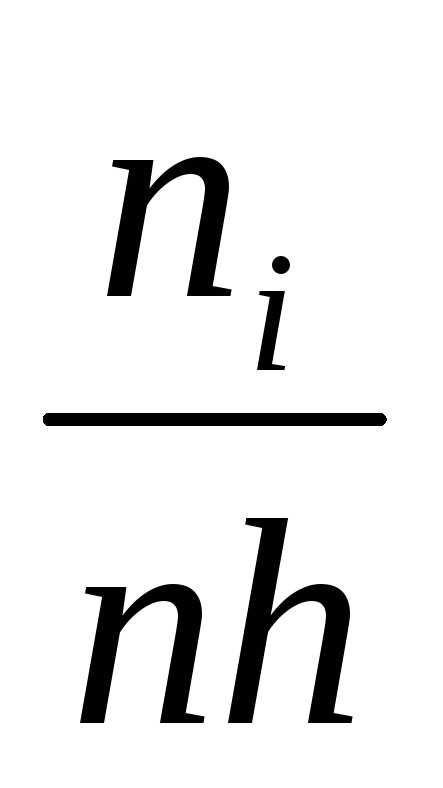 .
Тогда площадь прямоугольника будет
равна
.
Тогда площадь прямоугольника будет
равна 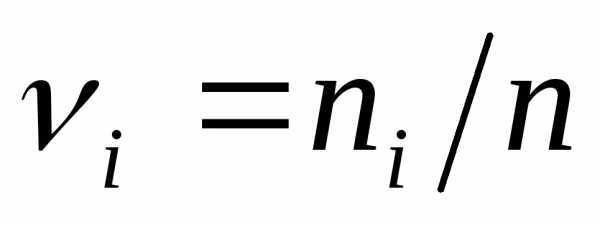 ,
то есть относительной частоте попадания
значений выборки в данный интервал.
Верхняя часть контура гистограммы дает
приближенное представление о графике
плотности распределения.
,
то есть относительной частоте попадания
значений выборки в данный интервал.
Верхняя часть контура гистограммы дает
приближенное представление о графике
плотности распределения.
Суммарная
площадь прямоугольников гистограммы
равна единице. Это статистический аналог
условия нормировки для плотности
распределения. Построенную гистограмму
было бы правильнее называть гистограммой
относительных частот. По аналогии с этой гистограммой строится гистограмма
частот: высота прямоугольников равна 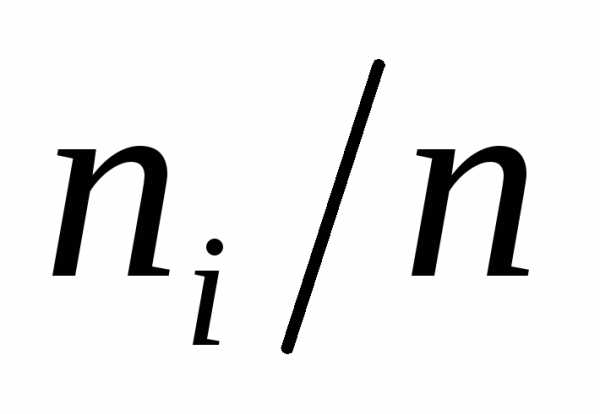 и площадь гистограммы совпадает с
объемом выборки n.
и площадь гистограммы совпадает с
объемом выборки n.
Если соединить отрезками середины верхних сторон прямоугольников гистограммы, получится еще одно графическое представление для плотности распределения —
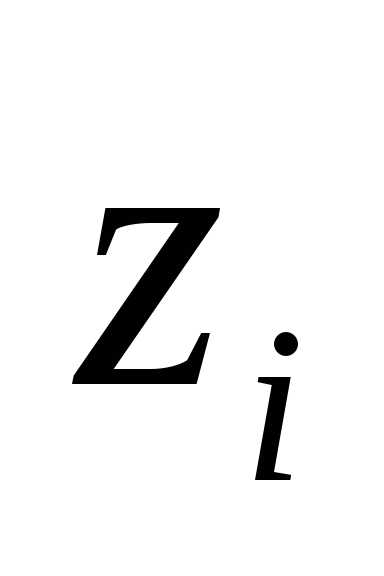 .
Полигоном соединяются точки с координатами
.
Полигоном соединяются точки с координатами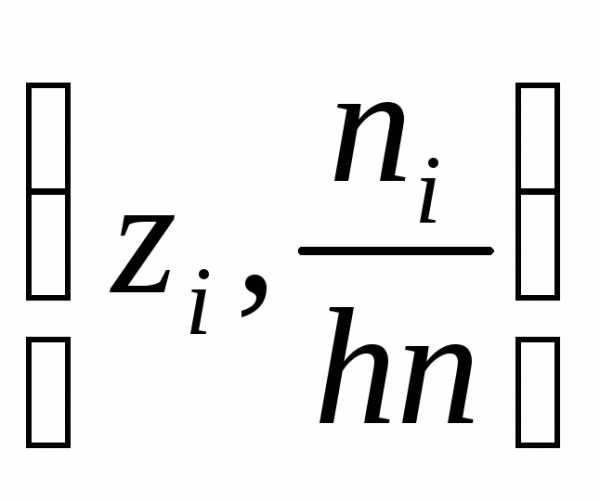 (полигон
относительных частот) или
(полигон
относительных частот) или 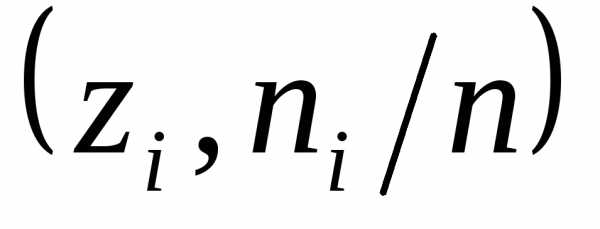 (полигон частот).
(полигон частот).В статистике используются также гистограммы и полигоны накопленных частот (накопленных относительных частот). Гистограмма накопленных относительных частот строится точно так же, как обычная гистограмма, но высота прямоугольника равна накопленной относительной частоте . Высота последнего прямоугольника равна единице. Сумма относительных частот приближенно равна сумме соответствующих вероятностей, то есть интегралу от плотности распределения от левой границы выборки до текущей точки. Гистограмма накопленных относительных частот (как и выборочная функция распределения) является аналогом функции распределения генеральной совокупности. Гистограмма накопленных частот и соответствующие полигоны строятся аналогично.
Оценка характеристик выборки.
Точечные оценки
Оценкой
(точечной оценкой) параметра  называется произвольная функция от
значений выборки
.
называется произвольная функция от
значений выборки
.
Оценка 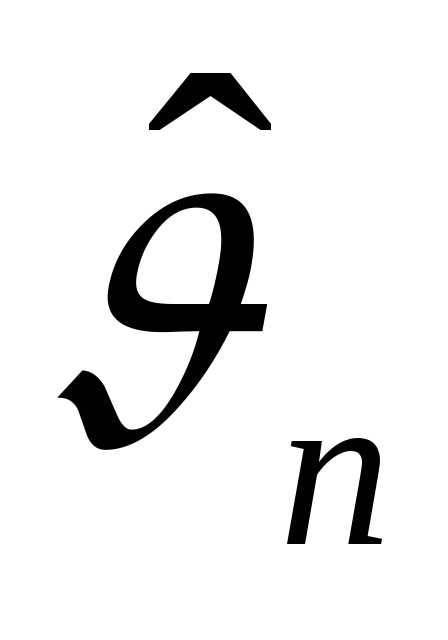 является случайной величиной.
является случайной величиной.
Оценка
называется несмещенной, если при любом объеме выборки п ее математическое ожидание совпадает
с истинным значением параметра: 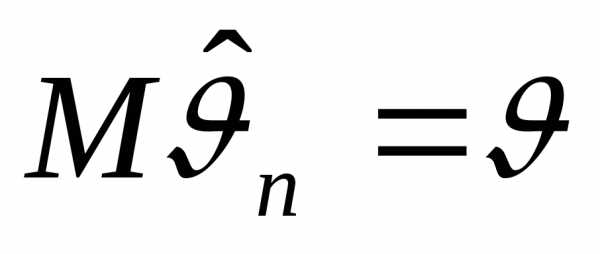 .
.
Разность называется смещением оценки 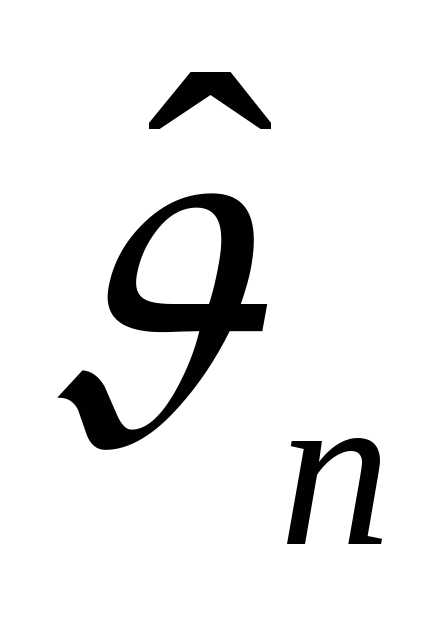
Оценка называется состоятельной, если при увеличении объема выборки вероятность того, что оценка мало отличается от истинного значения, приближается к единице. Формально это записывается в виде предельного соотношения:
Теорема. Если 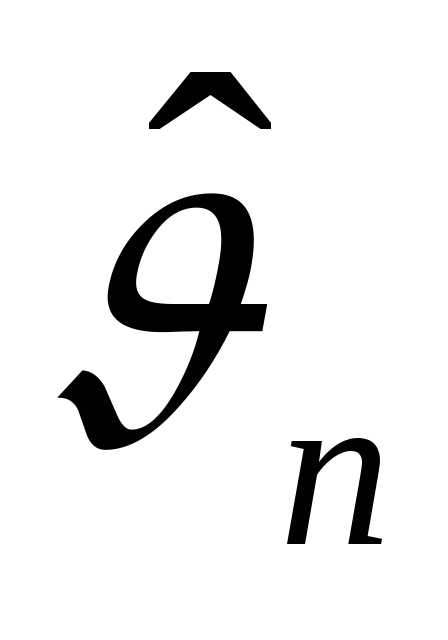 — несмещенная
оценка параметра и ее дисперсия стремится
к нулю при (), то данная
оценка является состоятельной.
— несмещенная
оценка параметра и ее дисперсия стремится
к нулю при (), то данная
оценка является состоятельной.
Качество оценки характеризуют средним квадратом ошибки:
Несмещенная оценка называется наиболее эффективной (или просто эффективной), если она имеет минимальную дисперсию среди всех несмещенных оценок данного параметра.
Относительная частота есть несмещенная, состоятельная и эффективная оценка вероятности.
Выборочная
функция распределения 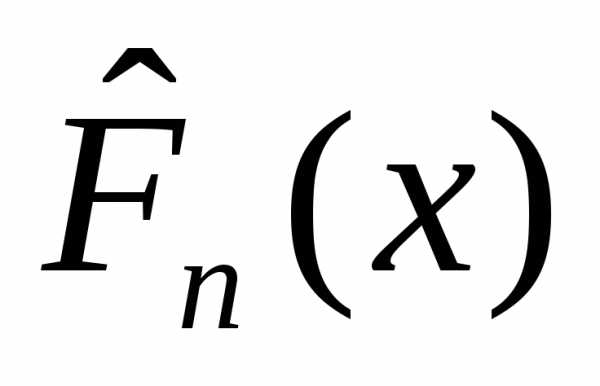 есть несмещенная, состоятельная и
эффективная оценка функции распределения:
есть несмещенная, состоятельная и
эффективная оценка функции распределения:
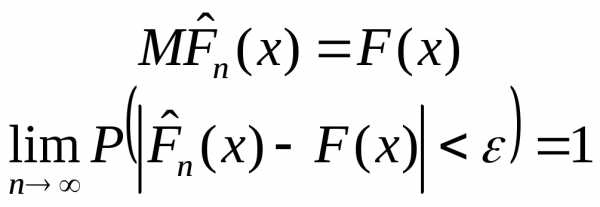
Выборочное среднее есть несмещенная состоятельная оценка математического ожидания.
Выборочная дисперсия

и величина (иногда ее называют исправленной дисперсией)
дают
состоятельные оценки дисперсии 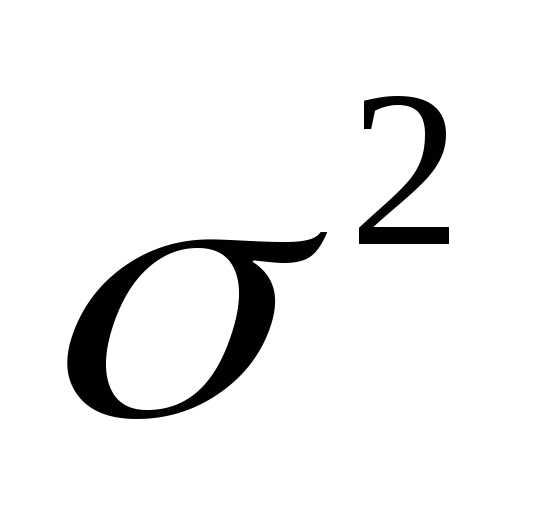 генеральной совокупности (соответственно
смещенную и несмещенную).
генеральной совокупности (соответственно
смещенную и несмещенную).
studfiles.net
Пример вычисления выборочной дисперсии и выборочного среднего квадратичного отклонения
Рассмотрим снова пример с делением отрезка. Ряд распределения частот мы построили выше и преобразовали его к дискретному виду, выбрав в качестве значений середины частичных отрезков.
Воспользуемся формулой для вычисления дисперсии. Для этого нам понадобится распределение квадратов :
k2 | 0,0550 | 0,1266 | 0,2209 | 0,3578 | 0,5175 |
W | 0,08 | 0,18 | 0,30 | 0,20 | 0,24 |
Среднее же квадрата величинымы вычисляем, как всегда, пользуясь определением выборочного среднего:
Следовательно, дисперсия величины — это следующая разность:
Для вычисления среднего квадратичного отклонения извлекаем квадратный корень из найденной дисперсии:
Метод описательной статистики
Иногда статистический анализ данных исследования ограничивается описательной частью:
по данным наблюдений строится статистическое распределение наблюдаемого признака,
и вычисляются его числовые характеристики.
Сами по себе они еще ничего не значат, но если речь идет о сравнении нескольких (как правило — двух) выборок, то по полученным результатам можно судить об их общих чертах или наоборот: об их различиях.
Действительно, если, например, среднее значение наблюдаемого показателя в экспериментальной выборке выше среднего в контрольной выборке, то можно предположить, что к повышению этого значения привело именно экспериментальное воздействие.
Однако, этого нельзя строго утверждать. Описательные статистические результаты позволяют лишь сформулировать статистические гипотезы, которые, в сою очередь, требуют дальнейшего статистического анализа с применением тех или иных статистических критериев.
Общие сведения о статистических критериях
Ключевой задачей статистического анализа является проверка статистической гипотезы.
Действительно, допустим, по экспериментальным данным мы построили статистическое распределение наблюдаемого показателя и даже, для наглядности, гистограмму этого распределения. Допустим, гистограмма до боли напоминает нам кривую Гаусса.
Ну и что? Имеем ли мы право утверждать, что наблюдаемое нами распределение подчинено нормальному закону?
Ведь для исследования мы использовали ограниченную выборку, и данные, полученные по другой выборке, могут сильно отличаться от того, что мы наблюдаем в данный момент.
Или пусть дисперсии двух выборок ипоказывают нам, что
.
Не является ли это неравенство, столь очевидное на первый взгляд, случайным? Не получим ли мы в другом исследовании на других выборках противоположное неравенство?
Запросто.
В любом случае, анализируя статистические данные, мы рискуем допустить ошибку и оказаться неверными в своих выводах.
Ошибка первого рода
Ошибка первого рода состоит в том, что отвергается основная гипотеза , при том, что на самом деле она является верной.
Ошибка второго рода
Ошибка второго рода состоит в том, что принимается конкурирующая гипотеза , при том, что на самом деле она является ложной.
Уровень значимости и мощность статистического критерия
Для того, чтобы статистический анализ приводил к корректным выводам, исследователю необходимо минимизировать по возможности вероятность допустить ошибку в своих выводах. Для этого применяются статистические критерии. Это очень широкий спектр самых разнообразных алгоритмов, применяемых для решения самых разнообразных задач. Но все они опираются на два показателя своей достоверности: уровень значимости (так называемый -уровень) и мощность (так называемый-уровень).
Уровнем значимости статистического критерия называется вероятность того, что в результате анализа допущена ошибка первого рода. Как правило, в качестве уровня значимости принимаетсяили.
Мощностью статистического критерия называется вероятность того, что в результате анализа отвергнута основная гипотеза, если верна конкурирующая. Другими словами, если — это вероятность допустить ошибку второго рода, то мощность критерия — это вероятность.
Понятно, что чем меньше вероятность и чем больше вероятность, тем лучше. Однако следует иметь в виду, что одновременно уменьшитьи повыситьневозможно. Единственный способ одновременного уменьшения вероятностей ошибок первого и второго рода состоит в увеличении объема выборки.
studfiles.net
Исправленная выборочная дисперсия — это… Что такое Исправленная выборочная дисперсия?
- Исправленная выборочная дисперсия
Выборочная дисперсия в математической статистике — это оценка теоретической дисперсии распределения на основе выборки. Различают выборочную дисперсию и несмещённую или исправленную выборочные дисперсии.
Определения
Пусть — выборка из распределения вероятности. Тогда
- ,
где символ обозначает выборочное среднее.
- Несмещённая (исправленная) дисперсия — это случайная величина
- .
Замечание
Очевидно,
- .
Свойства выборочных дисперсий
и
- ,
где обозначает сходимость по вероятности.
- Выборочная дисперсия является смещённой оценкой теоретической дисперсии, а исправленная выборочная дисперсия несмещённая:
- ,
и
- .
- .
Оценки СКО
Смотрите также
Wikimedia Foundation. 2010.
- Исправительный лагерь
- Исправленному верить
Смотреть что такое «Исправленная выборочная дисперсия» в других словарях:
Выборочная дисперсия — в математической статистике это оценка теоретической дисперсии распределения на основе выборки. Различают выборочную дисперсию и несмещённую, или исправленную, выборочные дисперсии. Содержание 1 Определения 2 Замечание … Википедия
Несмещённая оценка — в математической статистике это точечная оценка, математическое ожидание которой равно оцениваемому параметру. Определение Пусть выборка из распределения, зависящего от параметра . Тогда оценка называется несмещённой, если … Википедия
Несмещенная оценка — Несмещённая оценка в математической статистике это точечная оценка, математическое ожидание которой равно оцениваемому параметру. Определение Пусть выборка из распределения, зависящего от параметра . Тогда оценка называется несмещённой, е … Википедия
dic.academic.ru
Дисперсия выборочной средней — Энциклопедия по экономике
Поскольку, как правило, генеральная средняя ц неизвестна, этой формулой нельзя воспользоваться. Кроме того, в социально-экономических исследованиях из одной и той же совокупности выборки не проводятся многократно. Используют следующее соотношение квадрат средней ошибки (дисперсия выборочных средних) прямо пропорционален дисперсии признака х в генеральной совокупности а и обратно пропорционален объему выборки п [c.166]Дисперсия выборочной средней у [c.65]
Дисперсия выборочной средней для повторной выборки равна дисперсии изучаемого признака в генеральной совокупности, разделенной на объем выборки, т. е. [c.33]
Если из генеральной совокупности объема N производится бесповторная выборка объемом п, то дисперсия выборочной средней равна [c.33]
Когда дисперсия о2 генеральной совокупности неизвестна, тогда для больших значений п с большой вероятностью малой ошибки можно дисперсию выборочной средней вычислять приближенно по формуле [c.33]
Таким образом, для нахождения генеральных числовых характеристик необходим анализ всей генеральной совокупности. В силу того, что в реальности практически всегда имеют дело с выборками, приходится находить оценки указанных выше генеральных характеристик — выборочные числовые характеристики выборочное среднее, выборочную дисперсию, выборочное среднее квадратическое отклонение. [c.52]
Ошибка выборки или, иначе говоря, ошибка репрезентативности — это разница между значением показателя, полученного по выборке, и генеральным параметром. Так, ошибка репрезентативности выборочной средней равна ег = х — ц, выборочной относительной величины гг=р-п, дисперсии едЛ = s1 — а2, коэффициента корреляции ЕГ = г — р. [c.165]
Если представить, что было проведено бесконечное число выборок равного объема из одной и той же генеральной совокупности, то показатели отдельных выборок образовали бы ряд возможных значений выборочных средних величин х,, х-,, х3,. … относительных величин / ,, р2, ръ. … дисперсий s, s 2, s . .., и т. д. Каждая выборка имеет свою ошибку репрезентативности. Следовательно, можно построить ряды распределения выборок по величине ошибки репрезентативности для каждого показателя для средней, относительной величины и т.д. В таких распределениях улавливается тенденция к концентрации ошибок около центрального значения. Число выборок с той или иной величиной ошибки репрезентативности может быть симметрично или асимметрично относительно этого центрального значения. При бесконечно большом числе выборок получится кривая частот, которая представляет кривую выборочного распределения. Свойства таких распределений используются для получения статистических заключений, установления вероятности той или иной величины ошибки репрезентативности. [c.165]
Если п велико, то сомножитель п/(п — 1) 1 и можно принять выборочную дисперсию в качестве оценки величины генеральной дисперсии. Подставив выражение (7.10) в формулу средней ошибки выборочной средней, получим [c.169]
Табл. 7.2 содержит формулы средней ошибки выборки для выборочной средней и выборочной относительной величины для разных видов выборки. В приведенных формулах требуют пояснения выражения дисперсий выборочной относительной величины. [c.173]
Найдем дисперсию групповой средней у, представляющей выборочную оценку M Y). С этой целью уравнение регрессии (3.12) представим в виде [c.64]
В целях повышения однородности изучаемой совокупности и большей точности расчета совокупность стратифицируют, разбивают на ряд групп по какому-то признаку. В маркетинговом исследовании наиболее распространено деление по социальным группам (в частности, по уровню дохода). Формула численности выборки отличается от предыдущей только тем, что выборочная дисперсия заменяется средней из внутригрупповых дисперсий ( 2 ). Однако в этом случае целесообразно вести отбор по каждой группе пропорционально дифференциации признака (п.). Тогда формула численности выборки (по каждой группе) значительно упрощается [c.52]
Сущность метода состоит в том, что из всей совокупности (генеральной — N) отбирается малое число единиц п (выборочная совокупность не больше 20). Для каждой выборки вычисляются выборочная средняя (х) или доля (W) и выборочная дисперсия (о2) [c.170]
Когда распределение х в генеральной совокупности нормально, тогда выборочная средняя х подчинена также нормальному распределению со средней а и с дисперсией а =— [c.33]
Определение неизвестной генеральной средней по выборочной средней. Предположим, что сделана выборка из генеральной совокупности с нормальным распределением, среднее значение которой и дисперсия неизвестны. Необходимо по выборочному значению х и среднему квадратическому отклонению 5, вычисленному по этой же выборке объемом п, оценить генеральную среднюю а, задавшись некоторым уровнем гарантии Р и точностью е. [c.37]
Пусть случайная величина X имеет математическое ожидание JU и генеральную дисперсию математического ожидания и дисперсии по выборке (xl,X2,…,XN) будут выборочная средняя и выборочная дисперсия [c.65]
В момент проведения контроля с помощью выборки объема п выборочные среднее х и дисперсия S2 будут отличаться от математического ожидания MX vi дисперсии DX. Отклонения оценок от указанных параметров могут существенно отразиться на результатах контроля. Возникает вопрос оценки уровня входного качества контролируемой продукции с учетом этих отклонений, [c.139]
В данной главе речь идет о выборочной средней, выборочной дисперсии, выборочных коэффициентах связи, корреляции, регрессии. Мы будем обозначать выборочные величины теми же буквами, что и соответствующие им оценки генеральной совокупности, со значком над буквой. См. [11, 18, 27, 35]. [c.161]
Сначала рассмотрим относительно незначительные параметры с и 5. 5 -параметр положения. По существу, распределение может иметь средние значения, отличные от 0 (стандартного нормального среднего), что зависит от 5. В большинстве случаев исследуемое распределение нормализовано, и 5 = 0 то есть среднее распределения полагается равным 0. Параметр с — масштабный параметр. Он наиболее важен при сравнении реальных распределений. Опять же, в пределах понятия нормализации параметр с походит на выборочное отклонение он является мерой дисперсии. При нормализации выборочное среднее обычно вычитается (чтобы дать среднее равное 0) и делится на стандартное отклонение, так чтобы единицы были в терминах выборочного стандартного отклонения. Нормализация выполняется, чтобы сравнить эмпирическое распределение со стандартным нормальным распределением со средним равным 0 и стандартным отклонением равным 1. с используется, чтобы задать единицы, которыми распределение расширяется и сжимается около 5. Значение с по умолчанию равно 1. Единственная цель этих двух параметров — задать масштаб распределения относительно среднего и дисперсии. Они не являются действительно характерными для какого-либо из распределений, и поэтому они менее важны. Когда с = 1, а 5 = 0, распределение, как говорят, принимает приведенный вид. [c.193]
Разница заключается в том, что устойчивое распределение имеет среднее 0 и с = 1. Обычно мы нормализуем временной ряд, вычитая выборочное среднее и осуществляя деление на стандартное отклонение. Стандартизированная форма устойчивого распределения, по существу, является такой же. 8 — среднее распределения. Тем не менее, вместо деления на стандартное отклонение, мы делим на параметр масштабирования с. Вспомните из Главы 14, что дисперсия нормального распределения равна 2 с2. Следовательно, стандартизированное устойчивое распределение, где а = 2,0, не будет таким же, как стандартное нормальное распределение, поскольку коэффициент масштабирования будет другим. Устойчивое распределение изменяет масштаб на половину дисперсии нормального распределения. Мы начинаем со стандартизированной переменной, потому что ее логарифмическая характеристическая функция может быть упрощен. следующим образом [c.276]
Центральная предельная теорема может быть использована для доказательства утверждения о том, что выборочная средняя нормально распределена при условии, что объем выборки больше 30. В случае с малыми выборками необходимо допустить, что мы производим выборку из нормально распределенной совокупности для того, чтобы выборочная средняя была нормально распределена. Кроме того, только при выборках малого объема наша оценка генеральной дисперсии не будет надежной. В этом случае /-распределение позволит сделать поправку на эту дополнительную степень изменчивости. [c.232]
Что вы понимаете по терминами «выборочное распределение выборочной средней» и «выборочное распределение выборочной дисперсии». Рассчитайте стандартную ошибку средней по отношению к доходу по финансовому индексу со средним значением в 10% и средним квадратическим отклонением 16% на основе 60 наблюдений. [c.252]
Советская часть в ИСО проводит работы по преобразованию отечественных стандартов в международные, например, ГОСТ 20427—75 Статистическое регулирование технологических процессов методом кумулятивных сумм выборочного среднего и ГОСТ 20737—75 Статистическое регулирование технологических процессов методом групп качества в 1976 г. на 1-м заседании ИСО/ТК 69 П1 4 были одобрены и приняты за основу для разработки международных стандартов. На этом же заседании ИСО/ТК 69 ПК 4 была одобрена программа работ по стандартизации методов статистического регулирования технологических процессов, предложенная советскими специалистами. Программа предусматривает разработку международных стандартов, включающих методы с использованием контрольных карт средних арифметических значений, дисперсий или среднеквадратических отклонений, раз-махов при нормальном распределении контролируемого параметра, а также комбинированных контрольных карт. Предусмотрена также разработка стандартов на методы регулирования по альтернативному признаку, основанных на контрольных картах доли дефектности, числа дефектов, числа дефектных единиц продукции. [c.51]
Тейлор [159] изучил вопросы экономического обоснования контрольных карт кумулятивных сумм выборочного среднего для нормального распределения с известной дисперсией показателя качества. Он исходил из того, что контрольные карты кумулятивных сумм предназначаются для обнаружения разладки процесса формирования заданного показателя качества в предположении, что разладка наступает внезапно с известным смещением параметра. Ожидаемое время разладки предполагалось известным. Процесс прекращается для устранения неисправности. Если сигнал о разладке не является ошибочным, то требуется дополнительное время для обнаружения причины неполадки и ее устранения. Приближенно функция затрат основывалась на следующих допущениях [c.137]
При статистическом регулировании в качестве средних значений обычно используют выборочное среднее арифметическое х или выборочную медиану , а в качестве меры рассеяния — выборочное среднее квадратическое отклонение 5 или выборочную дисперсию S2 или размах R. [c.18]
Выборочными статистиками, значения которых накапливаются при статистическом регулировании методом кумулятивных сумм, могут быть выборочное среднее арифметическое значение, выборочная дисперсия или размах, а также число дефектов или число дефектных единиц продукции, и т. д. [c.23]
Дисперсия среднего выборки (выборочного среднего) на основании априорной информации может быть получена исходя из определения дисперсии [c.115]
Дисперсия среднего выборки представляет собой сумму дисперсии распределения математического ожидания про»-цесса и дисперсии среднего выборки при заданном частном значении математического ожидания процесса. Иными словами, мы можем представлять себе выборочное среднее состоящим из двух независимых аддитивных компонент. Оно равно сумме математического ожидания процесса и [c.115]
Если приведенные два сообщения эквивалентны, то тро и v должны быть независимы от получаемого сообщения. Если с=с(0)=с (1), то такая независимость действительно имеет место. Это сводит нашу проблему к проблеме, рассмотренной выше, когда было показано, что выборочное среднее является достаточным, за исключением того, что v (0) не обязательно будет равно v (1). Следовательно, в первом приближении можно сказать, что если мы имеем одинаково хорошую относительную информацию (измеряемую по с(0) и с(1)) о / и / ,, то наши два сообщения эквивалентны. Если же соотношение с— с(0)—с(1) не выполняется, то эти два сообщения в общем случае уже не эквивалентны следовательно, в этом случае Р уже нельзя считать достаточным сообщением. Интуитивно ясно, что сообщение о / о и R содержит больше информации . Если это толковать в том смысле, что апостериорная дисперсия для этого сообщения будет меньше, чем для сообщения Р, то без труда можно показать, что этот интуитивный вывод действительно подтверждается. [c.143]
ОР (т—/ns)—апостериорная плотность распределения т при заданном выборочном среднем т тро—апостериорное среднее значение т vpo — апостериорная дисперсия т [c.296]
X —наблюденное значение величины х (1= 1,2,…,/г) ms—выборочное среднее (среднее по выборке) LK(ms /п)—функция правдоподобия выборочного среднего ms V (ms)—дисперсия выборочного среднего E(ms)—ожидаемое значение выборочного среднего PR (т)—априорная плотность распределения от гПрГ—априорное среднее значение т Vpr—априорная дисперсия т [c.296]
Типический отбор используется в случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. При обследованиях населения такими группами могут быть, например, районы, социальные, возрастные или образовательные группы при обследовании предприятий — отрасль и подотрасль, форма собственности и т.п. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки, которая в этом случае определяется только внут-ригрупповой вариацией. [c.137]
Феллер (Feller, 1951) пришел к схожему результату, но он работал строго с откорректированным диапазоном R. Херст постулировал уравнение (5.1) для нормированного размаха, но оно фактически не было доказано в формальном смысле. Феллер работал с откорректированным диапазоном (то есть накопленные отклонения с удаленным выборочным средним) и пришел к ожидаемому значению R и его дисперсии. Нормированный размах, R/S, считался трудноразрешимым из-за поведения выборочного стандартного отклонения, особенно для небольших значений N. Существовало мнение, что результат был достаточно близок, так как откорректированный диапазон мог быть решен и должен был асимптотически (то есть в бесконечности) быть эквивалентным нормированному размаху. [c.74]
Для большинства индивидуумов, которые обучены стандартной гауссовой статистике, идея бесконечных среднего или дисперсии кажется абсурдной или даже извращенной. Мы всегда можем вычислить дисперсию или среднее выборки. Как оно может быть бесконечным Еще раз повторим, что мы применяем частный случай, гауссову статистику, ко всем случаям. В семействе устойчивых распределений нормальное распределение — частный случай, который существует, когда а = 2,0. В этом случае математическое ожидание и дисперсия действительно существуют. Бесконечная дисперсия означает, что не существует «дисперсии совокупности», к которой стремится распределение в пределе. Когда мы берем выборочную дисперсию, мы делаем это, согласно гауссову предположению, как оценку неизвестной дисперсии совокупности. Шарп (Sharpe, 1963) говорил, что беты (в смысле современной теории портфеля (МРТ)) должны рассчитываться на основании ежемесячных данных за пять лет. Шарп выбрал пять лет, потому что этот период дает статистически значимую выборочную дисперсию, необходимую для оценки дисперсии совокупности. Пятилетний период статистически значим, только если лежащее в основе распределение является гауссовым. Если оно не является гауссовым и а выборочная дисперсия ничего не говорит о дисперсии совокупности, потому что дисперсии совокупности нет. Выборочные дисперсии, как ожидалось бы, будут неустойчивыми и не будут стремиться ни к какому значению, даже при увеличении объема выборки. Если а [c.194]
В этой специальной асимптотике, которую мы в дальнейшем будем называть асимптотикой Колмогорова — Деева, нарушаются многие привычные свойства статистических процедур. Например, если X имеет многомерное нормальное распределение с нулевым вектором средних и независимыми координатами с дисперсией а2 и Хг- (/ — 1,. .., п) — независимая выборка объема п, то квадрат длины вектора выборочного среднего [c.155]
economy-ru.info
