Формулы и уравнения векторной алгебры
Формулы и уравнения векторной алгебры- Основные определения.
- Вектор (геометрический вектор) — это направленный отрезок (отрезок, у которого одна граничная точка считается начальной, другая – конечной).
На чертеже вектор обозначается стрелкой
над буквенным обозначением вектора также ставится стрелка .
Вектор, фигурирующий в определении, носит название связанного, или закрепленного вектора. - Закрепленный вектор — это направленный отрезок АВ, началом которого является точка А, а концом — точка В.
Свободный вектор — это множество всех закрепленных векторов, получающихся из фиксированного закрепленного вектора с помощью параллельного переноса. Обозначается .
Если же точка приложения вектора (точка A для вектора ) может быть выбрана произвольно, вектор называется свободным.
Если точка приложения может двигаться по линии действия вектора, говорят о скользящем векторе. Иначе говоря, свободный вектор является представителем бесконечного множества связанных или скользящих векторов. - Нулевой вектор — это вектор, у которого начало и конец совпадают:
- Коллинеарные векторы — это векторы, которые лежат на одной прямой, либо на параллельных прямых.
Нулевой вектор коллинеарен любому вектору. - Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов, то эти векторы компланарны. - Длина вектора (модуль) — это расстояние между началом и концом вектора. Обозначение: или
- Два вектора равны, если они коллинеарны, имеют одинаковую длину и направление. Например,
- Алгебраические операции над векторами.
- Операция сложения.
Суммой двух свободных векторов и называется свободный вектор , начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора и начало вектора .
Сумма двух векторов и () — это вектор, идущий из начала вектора в конец вектора при условии, что начало вектора приложено к концу вектора (правило треугольника).
Свойства операции сложения векторов:
1) Переместительное свойство: (коммутативность).
2) Сочетательное свойство: (ассоциативность).
3) Существует нулевой вектор , такой, что для любого вектора (особая роль нулевого вектора).
Нулевой вектор порождается нулевым закрепленным вектором, то есть точкой.
4) Для каждого вектора существует противоположный ему вектор , такой, что . Вектор называется вектором, противоположным вектору .
Правило параллелограмма (правило сложения векторов): если векторы и приложены к общему началу и на них построен параллелограмм, то сумма этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов и
Вычитание векторов определяется через сложение: .
Другими словами, если векторы и приложены к общему началу, то разностью векторов и будет вектор , идущий из конца вектора к концу вектора . - Операция умножения вектора на число.
Произведением вектора на число называется вектор такой, что:
1) если λ > 0, ≠ , то получается из растяжением в λ раз: ;
2) если λ < 0, ≠ , то получается из растяжением в |λ| раз и последующим отражением: ;
3) если λ = 0 или , то .
Свойства операции умножения:
1) Распределительное свойство относительно суммы чисел: для любых действительных и всех (дистрибутивность).
2) Распределительное свойство относительно суммы векторов: (дистрибутивность).
3) Сочетательное свойство числовых сомножителей: (ассоциативность).
4) Существование единицы: .
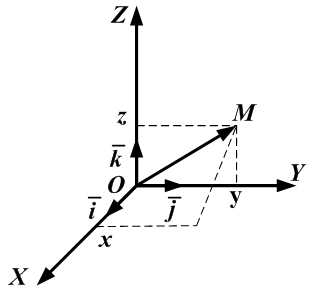
- Ортонормированный базис. Декартова прямоугольная система координат.
- Ортонормированный базис (ОНБ) — это три взаимно перпендикулярных вектора с длинами, равными единице.

Обозначения: - Базисные орты — это векторы .
- Зафиксированная точка О – это начало координат.
Отложим от точки O векторы .
Полученная система координат — это прямоугольная декартова система координат. - Декартовы координаты вектора — это координаты любого вектора в этом базисе:
Пример 11. - Координатные оси — это прямые линии, проведенные через начало координат (точку O) по направлениям базисных векторов:
– порождает Ox;
– порождает Oy;
– порождает Oz. - Абсцисса — это координата точки M (вектора в декартовой системе координат по оси
Ордината — это координата точки M (вектора в декартовой системе координат по оси Oy.
Аппликата — это координата точки M (вектора ) в декартовой системе координат по оси Oz. - Декартовы прямоугольные координаты x, y, z вектора равны проекциям этого вектора на оси Ox, Oy, Oz, соответственно. Иначе:
где α, β, γ – углы, которые составляет вектор с координатными осями Ox, Oy, Oz, соответственно, при этом cosα, cosβ, cosγ называются направляющими косинусами вектора . Пример 12.
Для направляющих косинусов справедливо соотношение: - Орт направления — это вектор единичной длины данного направления.
Формулы, уравнения, теоремы, примеры решения задач
matematika.electrichelp.ru
Раздел 2. Векторная алгебра на плоскости и в пространстве
2.1 Понятие о векторах и скалярах
Векторной величиной или вектором (в широком смысле), называется всякая величина, обладающая направлением. Скалярной величиной или скаляром называется всякая величина, направлением не обладающая. Например, сила, действующая на материальную точку, есть вектор, так как она обладает направлением. Скорость также является вектором. Температура тела – это скаляр, так как с этой величиной не связано никакое направление. Масса тела и его плотность – также скалярные величины.Если отвлечься от направления векторной величины, то ее, как и скалярную величину, можно измерить, выбрав соответствующую масштабную единицу. Но число, полученное в результате измерения, характеризует скалярную величину полностью, а векторную – лишь частично.
Векторную величину полностью можно охарактеризовать направленным отрезком, предварительно задав линейный масштаб.
2.2 Вектор в геометрии
Вектором называется направленный отрезок. Вектор
с началом в точке А и концом в точке В обозначается символом 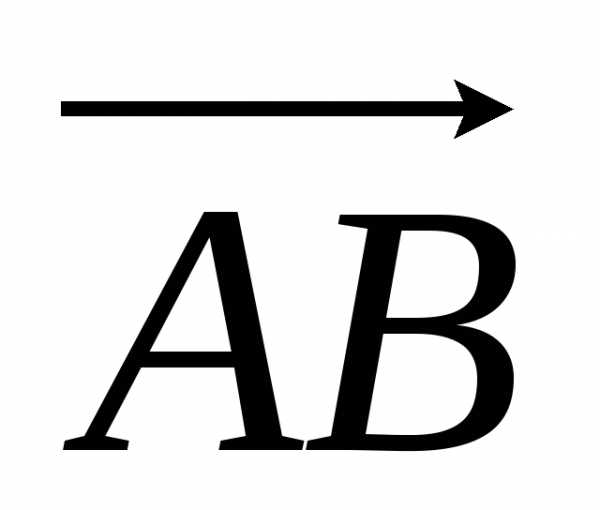 (или одной буквой,
(или одной буквой, ,
,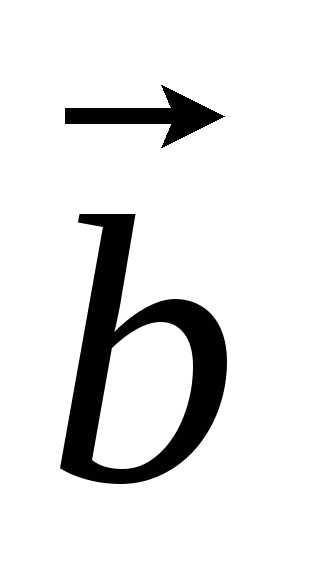 ,
…). Длина отрезкаАВ называется длиной, или модулем вектора
,
…). Длина отрезкаАВ называется длиной, или модулем вектора 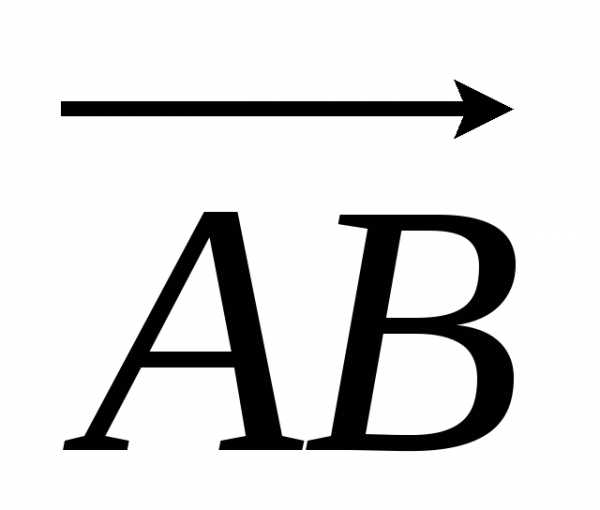 и обозначается
и обозначается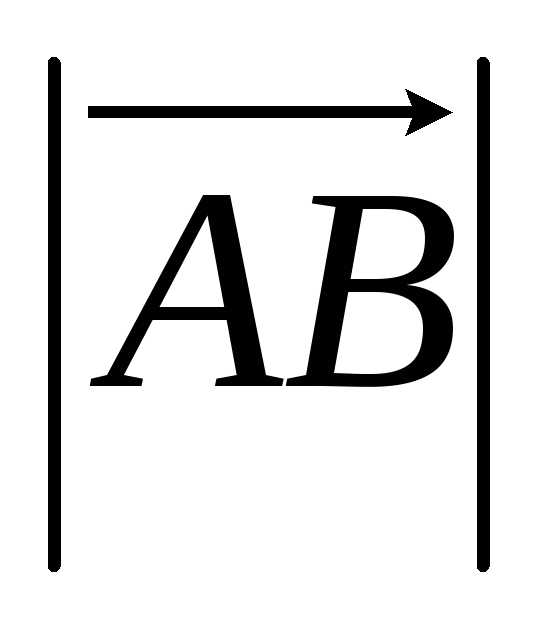 ,
,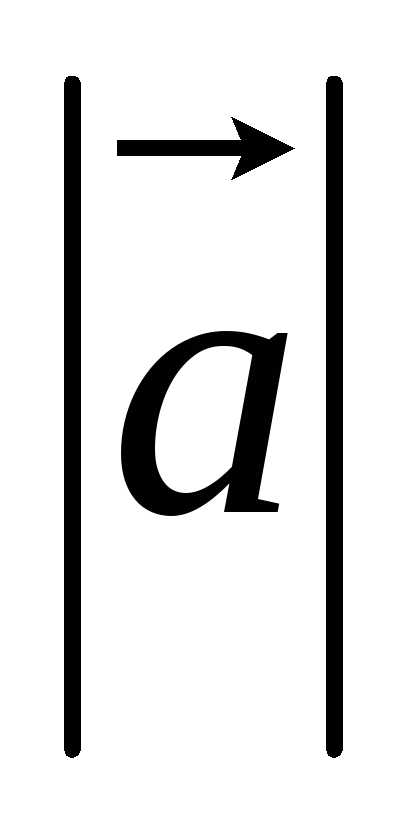 .
.
Векторы  и
и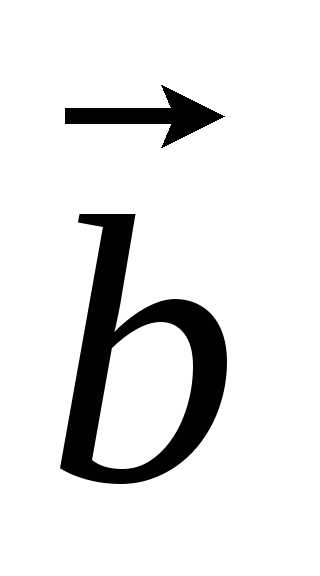 называютсяколлинеарными,
если они лежат на одной прямой или на
параллельных прямых; записывают
называютсяколлинеарными,
если они лежат на одной прямой или на
параллельных прямых; записывают 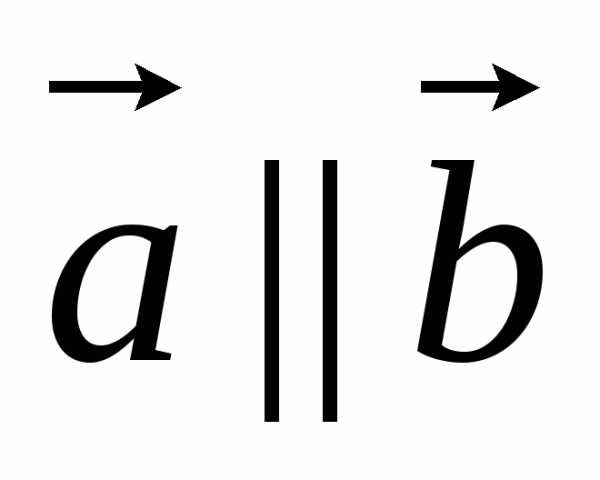
Три (и более) вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Вектор,
длина которого равна нулю, называется нулевым
вектором и обозначается 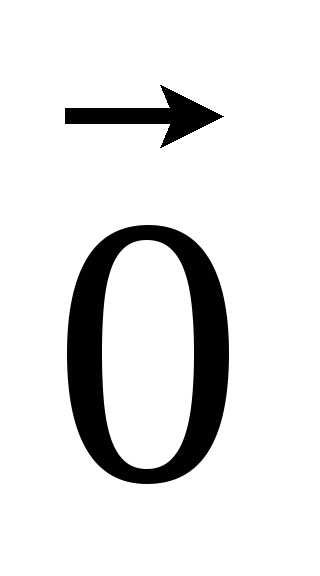 или просто 0. По определению нулевой
вектор не имеет направления и коллинеарен
любому вектору.
или просто 0. По определению нулевой
вектор не имеет направления и коллинеарен
любому вектору.
Вектор,
длина которого равна единице, называется единичным вектором
и обозначается через  .
.
Единичный
вектор, направление которого совпадает
с направлением вектора  ,
называетсяортом
,
называетсяортом
 и обозначается
и обозначается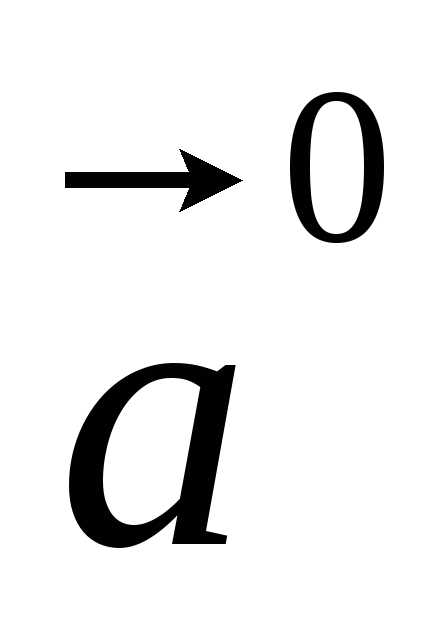 .
Два ненулевых вектора называютсяпротивоположными,
если они имеют одинаковую длину и
противоположные направления. Вектор,
противоположный вектору
.
Два ненулевых вектора называютсяпротивоположными,
если они имеют одинаковую длину и
противоположные направления. Вектор,
противоположный вектору  ,
обозначается
,
обозначается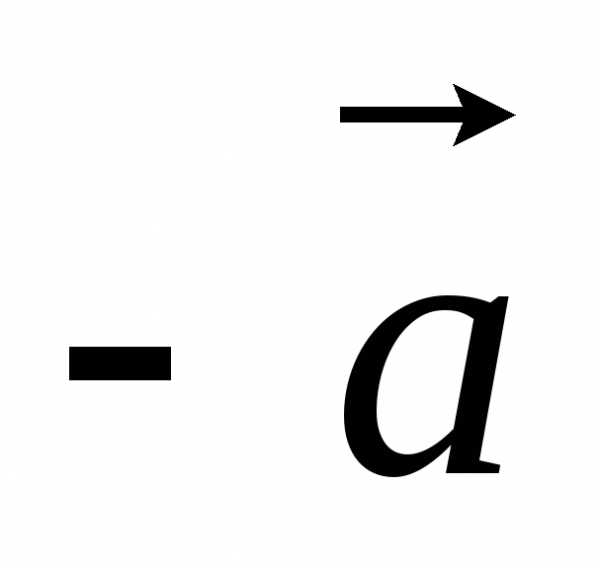 ;
вектор
;
вектор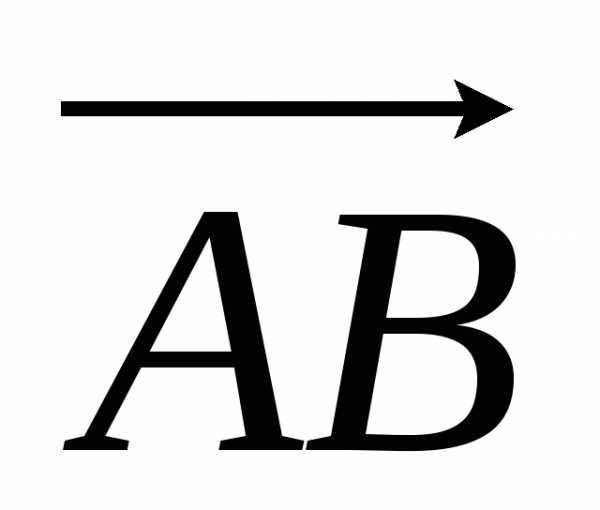 противоположен вектору
противоположен вектору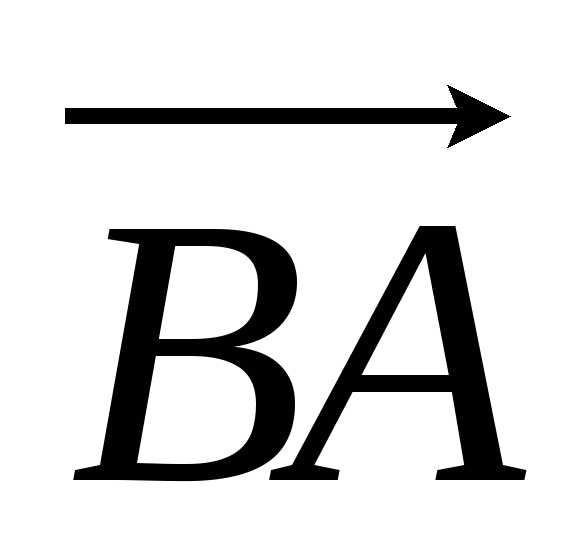 ().
(). Два
коллинеарных вектора  и
и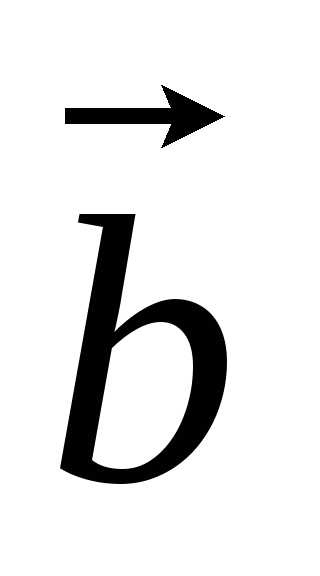 называютсяравными (
называютсяравными (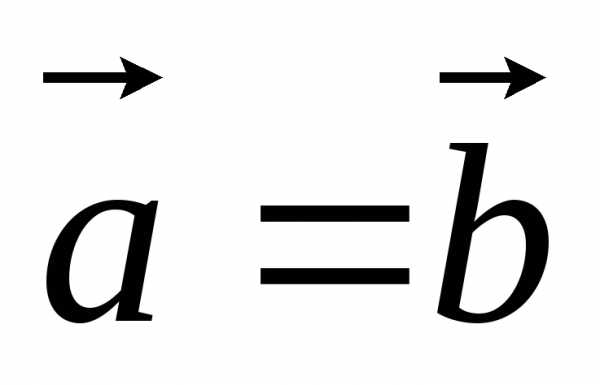 ),
если они сонаправлены и имеют равные
длины.
),
если они сонаправлены и имеют равные
длины.
Замечание
. Нельзя смешивать понятия «равенство отрезков» и «равенство векторов». Говоря: «отрезки равны», мы утверждаем, что их можно совместить наложением. Но для этого один из них может быть придется подвергнуть повороту. Два вектора будут равны лишь в том случае, когда их можно совместить, не применяя поворот. Совместим
параллельным переносом начала
неколлинеарных векторов  и
и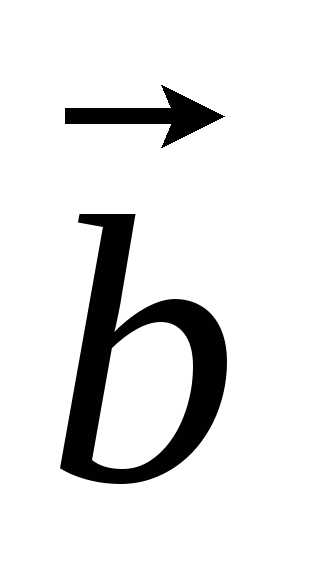 .
Начало и концы векторов образуют вершины
треугольника.Углом между векторами
.
Начало и концы векторов образуют вершины
треугольника.Углом между векторами  и
и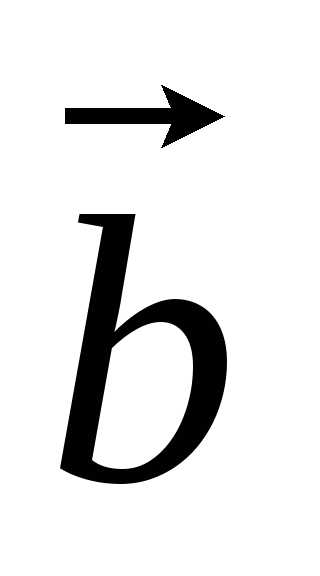 называется угол при вершине этого
треугольника, соответствующий началу
векторов. Если векторы сонаправлены,
то угол между ними равен нулю; если
противоположно направлены – угол между
ними равен 180°.
называется угол при вершине этого
треугольника, соответствующий началу
векторов. Если векторы сонаправлены,
то угол между ними равен нулю; если
противоположно направлены – угол между
ними равен 180°.
2.3 Векторная алгебра
Над векторами производят действия, называемые сложением, вычитанием и умножением векторов. Эти действия имеют много общих свойств с одноименными алгебраическими действиями. Поэтому учение о действиях над векторами называется векторной алгеброй.
Суммой двух векторов  и
и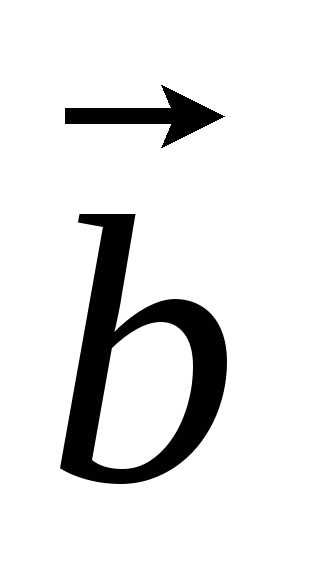 называется вектор
называется вектор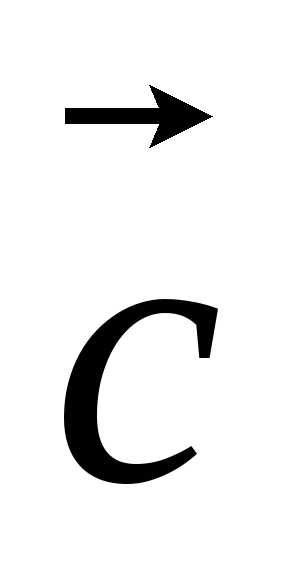 ,
соединяющий начало вектора
,
соединяющий начало вектора с концом вектора
с концом вектора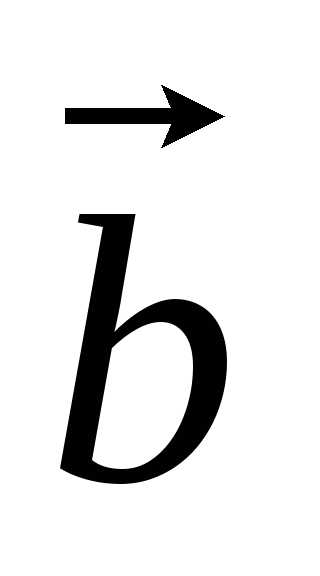 ,
отложенного от конца вектора
,
отложенного от конца вектора .
.
Обозначение: 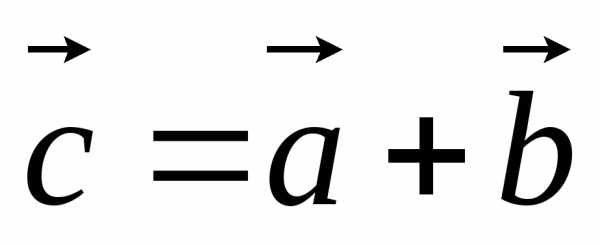 .
.
Д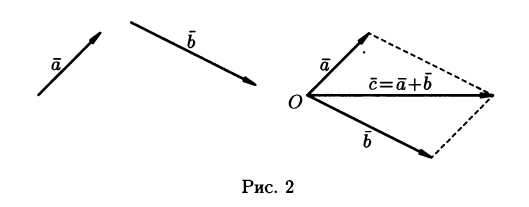 ля
геометрического представления суммы
векторов используют правила «треугольника»
и «параллелограмма», проиллюстрированные
на рис. 1 и 2 соответственно.
ля
геометрического представления суммы
векторов используют правила «треугольника»
и «параллелограмма», проиллюстрированные
на рис. 1 и 2 соответственно.
При сложении векторов имеют место неравенства:
1) 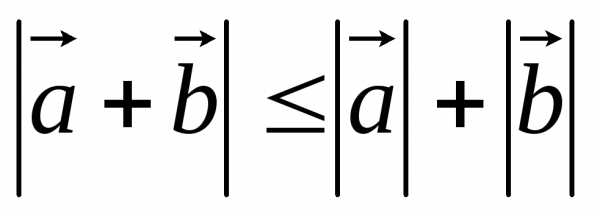 ,
,
2) 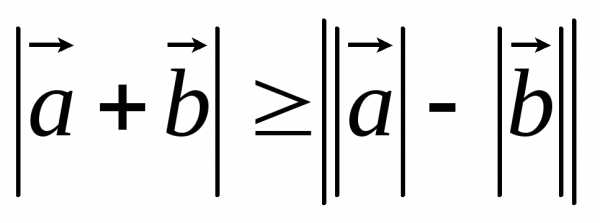 ,
,
выражающие, что сторона треугольника меньше суммы и больше разности двух других сторон (неравенство треугольника). В первой формуле равенство имеет место только для сонаправленных векторов, во второй – только для противоположно направленных векторов.
Сумма
противоположных векторов равна
нуль-вектору: 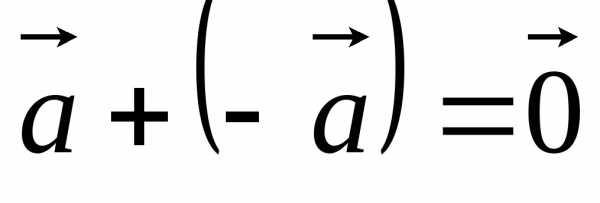 .
.
Суммой векторов
называется вектор, получающийся после
ряда последовательных сложений: к
вектору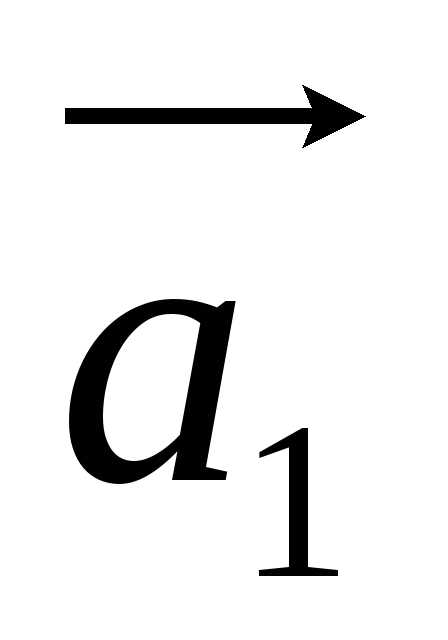 прибавляется вектор
прибавляется вектор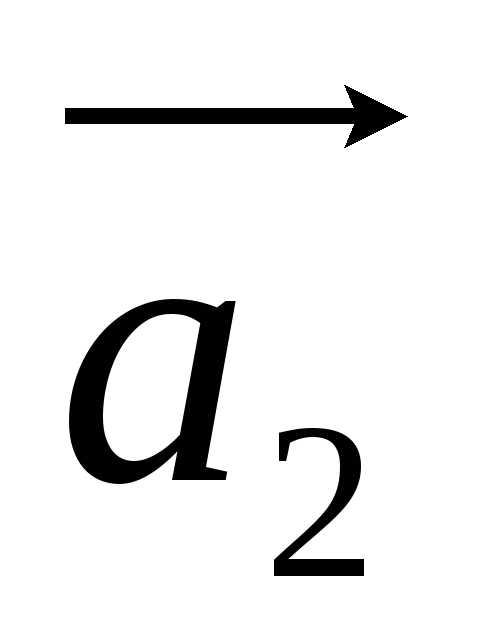 ,
к полученному вектору прибавляется
вектор
,
к полученному вектору прибавляется
вектор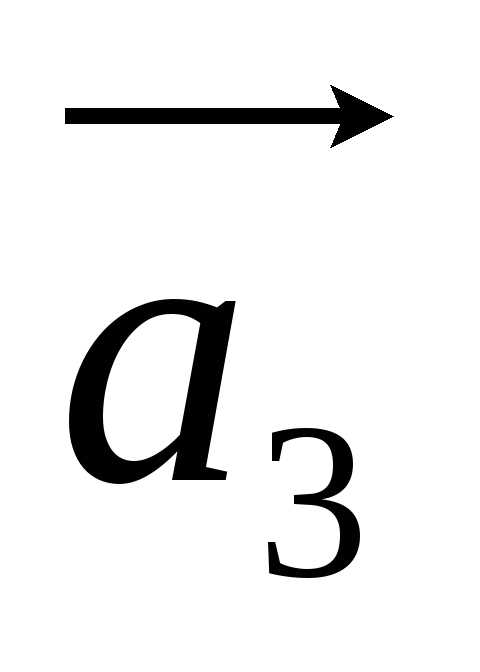 и так далее.
и так далее.
И з
определения вытекает следующее построение
(правило многоугольника или правило
цепи).
з
определения вытекает следующее построение
(правило многоугольника или правило
цепи).
Из
произвольного начала О откладываем вектор 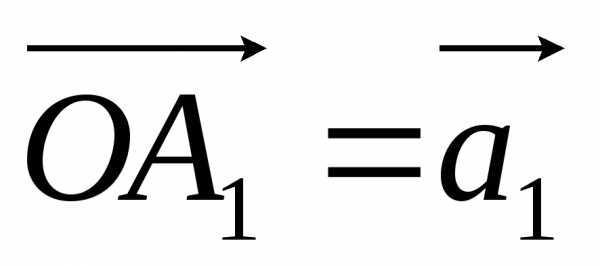 ,
из точкиА1,
как из начала, откладываем вектор
,
из точкиА1,
как из начала, откладываем вектор 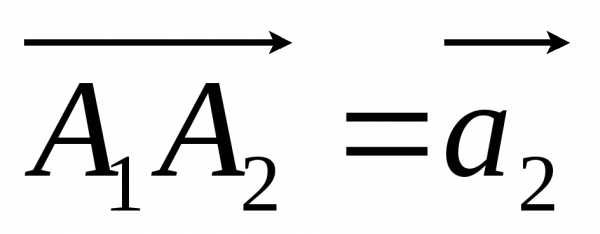 ,
из точкиА2 строим вектор
,
из точкиА2 строим вектор 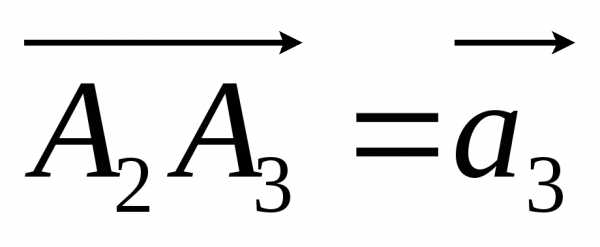 и так далее. Вектор
и так далее. Вектор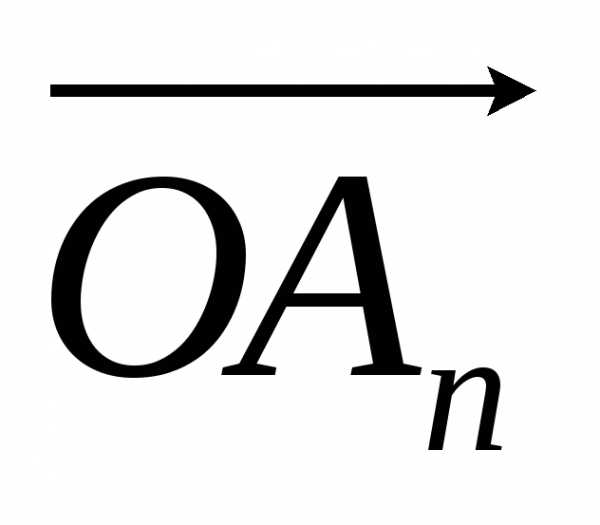 есть сумма векторов.
есть сумма векторов.
Сложение векторов подчиняется коммутативному и ассоциативному свойствам:
1) ,
2) .
Коммутативность и ассоциативность сложения векторов позволяет нам находить сумму векторов в любом удобном порядке.
П равило
параллелепипеда.
Если три вектора
,
равило
параллелепипеда.
Если три вектора
,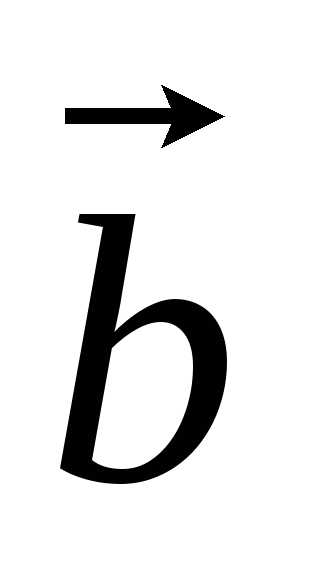 и
и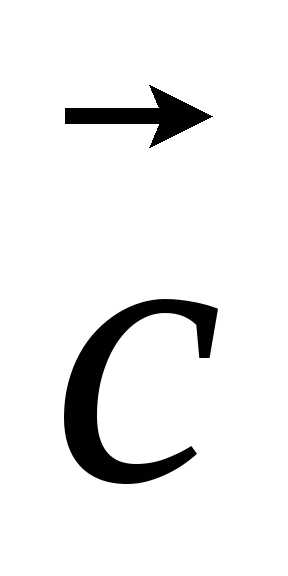 после приведения к общему началуне
лежат в одной плоскости, то сумму
после приведения к общему началуне
лежат в одной плоскости, то сумму 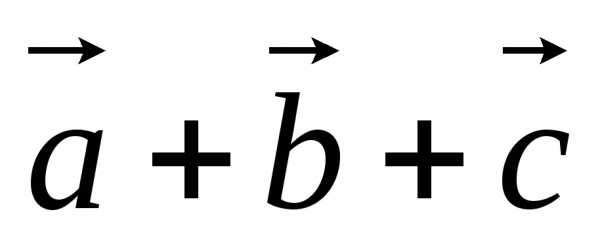 можно найти следующим построением. Из
общего началаО строим векторы
можно найти следующим построением. Из
общего началаО строим векторы 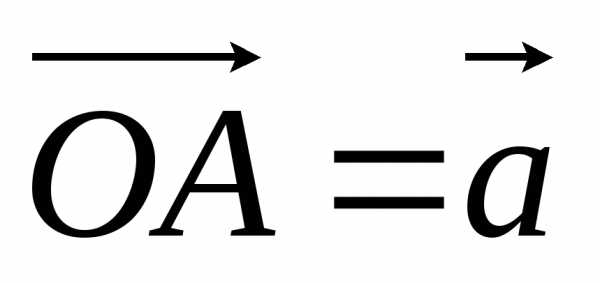 ,
,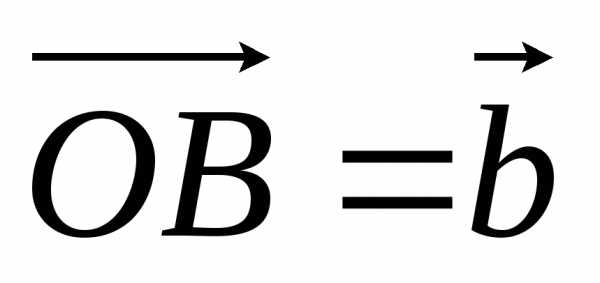 ,
,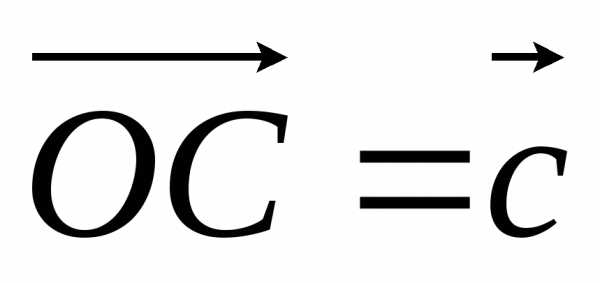 .
На отрезкахОА, ОВ, ОС,
как на ребрах, строим параллелепипед.
Вектор диагонали
.
На отрезкахОА, ОВ, ОС,
как на ребрах, строим параллелепипед.
Вектор диагонали 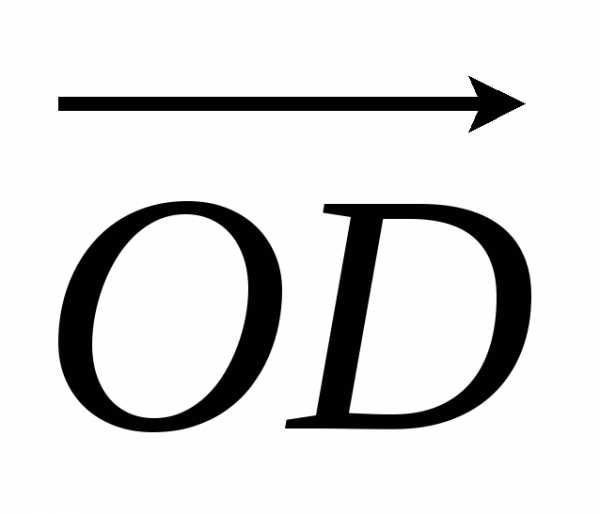 равен сумме векторов
равен сумме векторов ,
,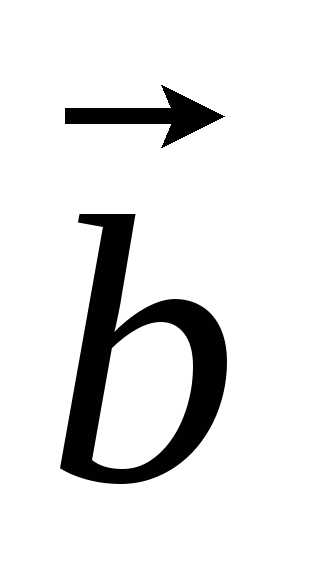 и
и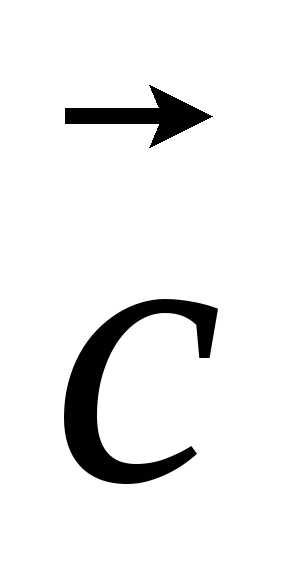 ,
так как
,
так как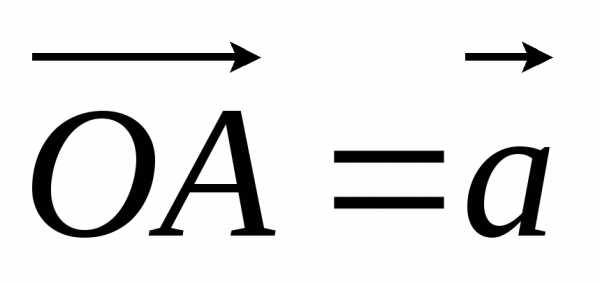 ,,и.
,,и.
Под
разностью векторов  и
и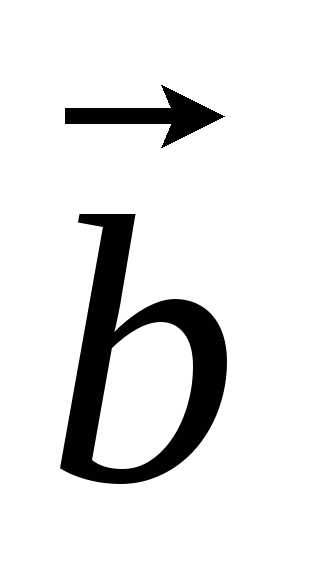 понимается вектор
понимается вектор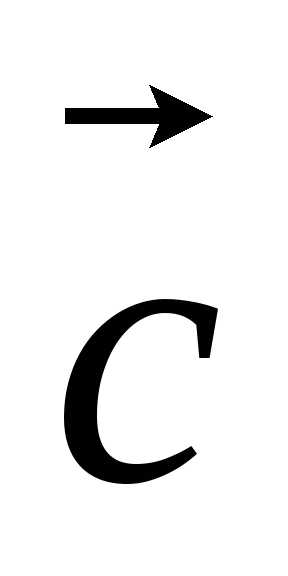 такой, что
такой, что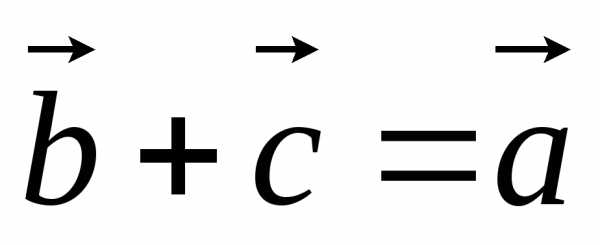 .
Обозначение:
.
Обозначение: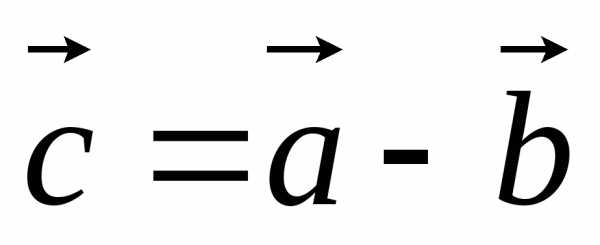 .
Справедливо равенство.
.
Справедливо равенство.
Произведением вектора 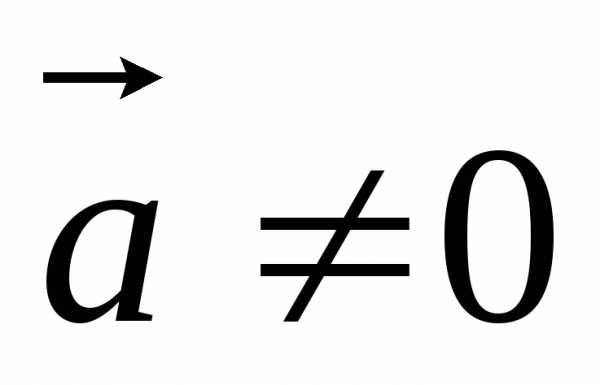 на число
на число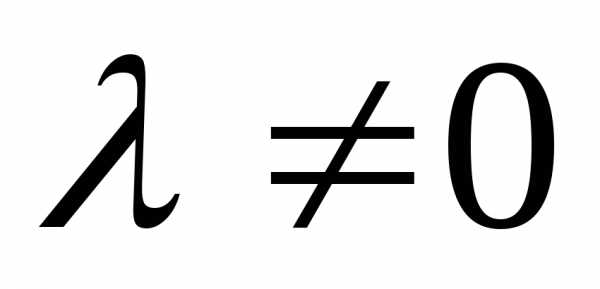 называется вектор, который имеет длину,
его направление если
называется вектор, который имеет длину,
его направление если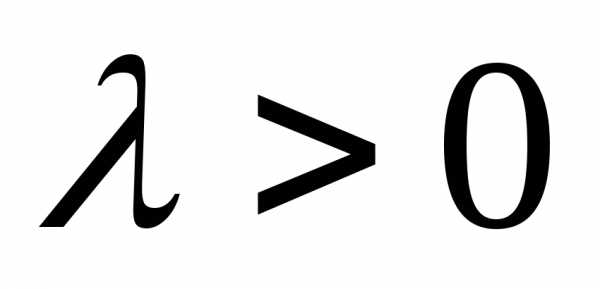 и противоположное направление, если
и противоположное направление, если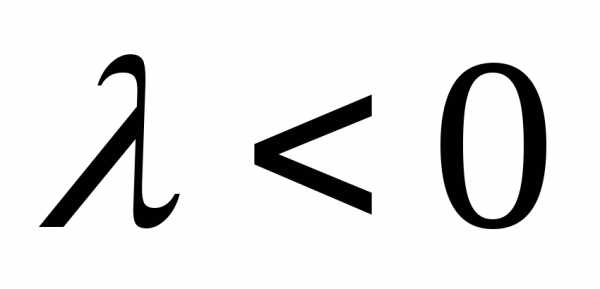 .
.
Обозначение: 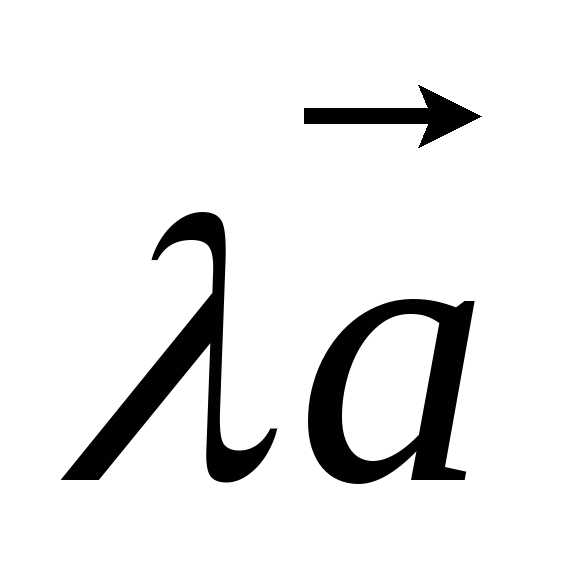 .
.
Отметим,
что 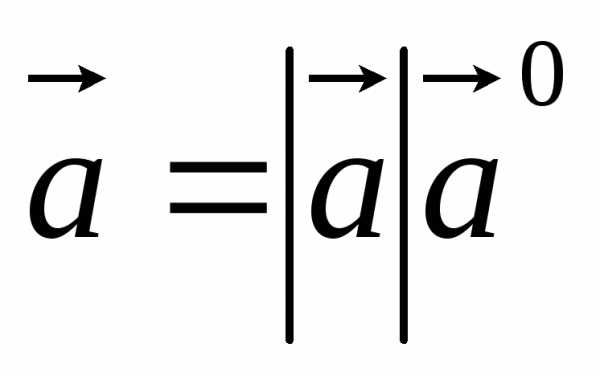 ,
т. е. каждый вектор равен произведению
его модуля на орт.
,
т. е. каждый вектор равен произведению
его модуля на орт.
Два
ненулевых вектора  и
и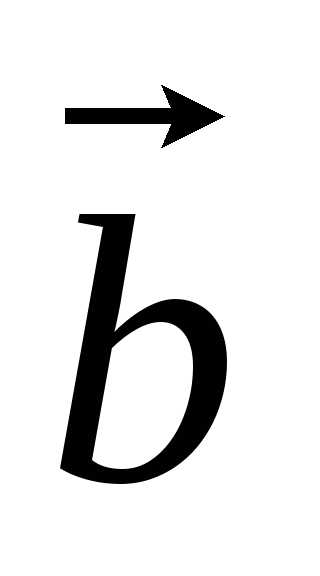 коллинеарны тогда и только тогда, когда
один из них есть произведение другого
на некоторое число, т. е.
коллинеарны тогда и только тогда, когда
один из них есть произведение другого
на некоторое число, т. е.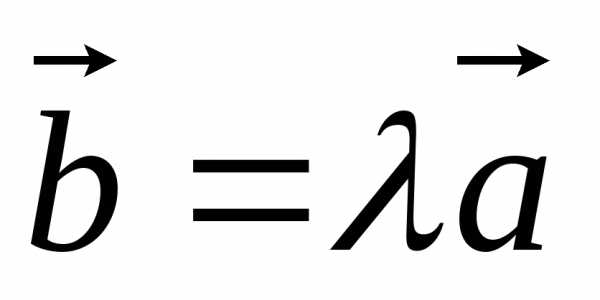 ,
λ – число (признак
коллинеарности векторов).
,
λ – число (признак
коллинеарности векторов).
Три
ненулевых вектора  ,
,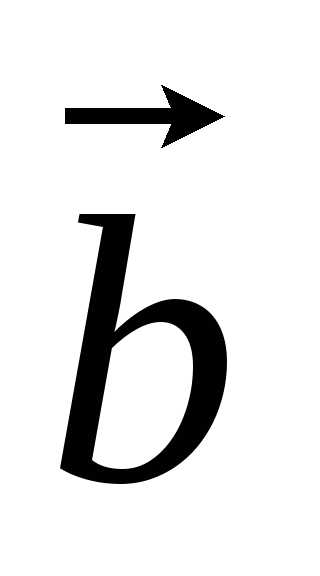 ,
,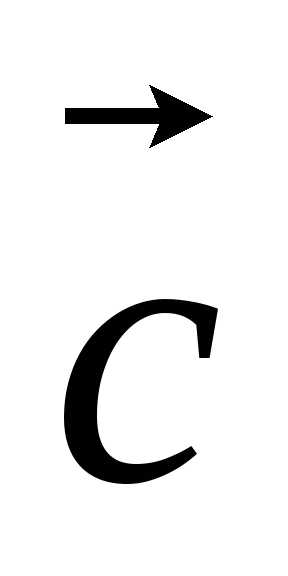 компланарны тогда и только тогда, когда
один из них является линейной комбинацией
других, например,(λ1,
λ2 – числа не равные нулю одновременно)
(признак
компланарности векторов).
компланарны тогда и только тогда, когда
один из них является линейной комбинацией
других, например,(λ1,
λ2 – числа не равные нулю одновременно)
(признак
компланарности векторов).
Умножение вектора на число подчиняется тем же законам, что и умножение чисел:
1. (дистрибутивный закон по отношению к числовому множителю).
2. (дистрибутивный закон по отношению к векторному множителю).
3. (ассоциативный закон).
Пример
1: В треугольнике ABC дано: 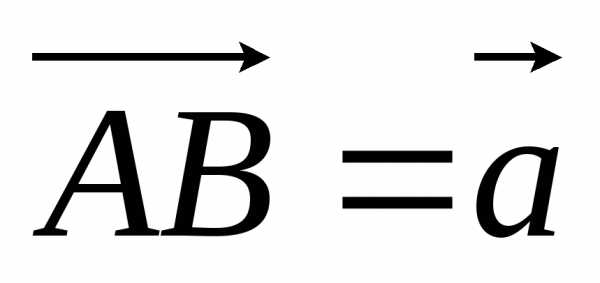 ,
,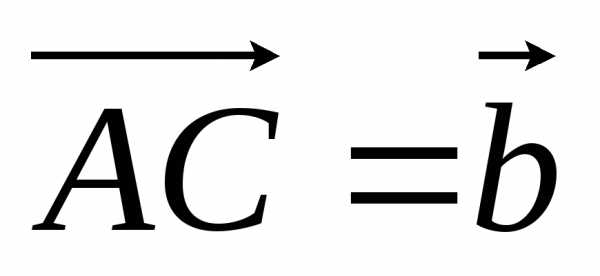 ,
точкаМ – середина стороны ВС.
Выразить вектор
,
точкаМ – середина стороны ВС.
Выразить вектор 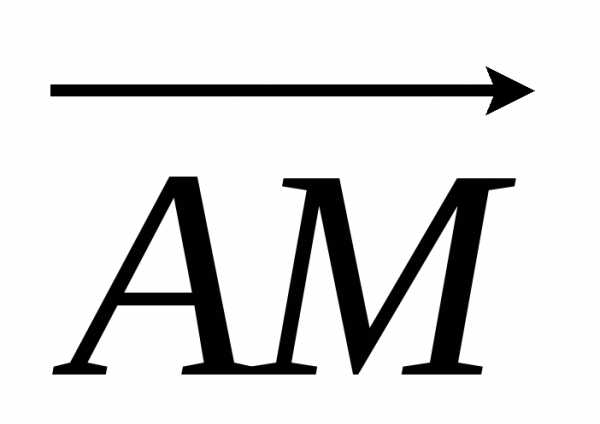 через векторы
через векторы и
и 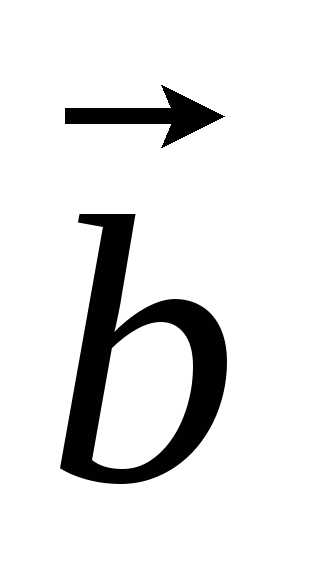 .
.
Решение:
Ч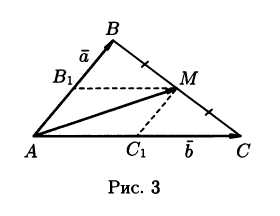 ерез
точкуМ проведем прямые, параллельные сторонам АВ и АС.
Получим параллелограмм АВ1МС1 (рис. 3), в котором AM является диагональю. Следовательно,
.
Но
ерез
точкуМ проведем прямые, параллельные сторонам АВ и АС.
Получим параллелограмм АВ1МС1 (рис. 3), в котором AM является диагональю. Следовательно,
.
Но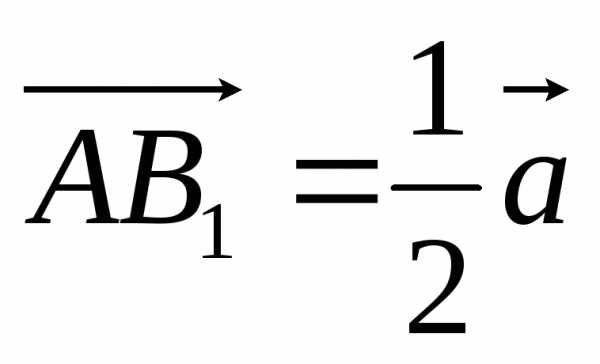 ,
,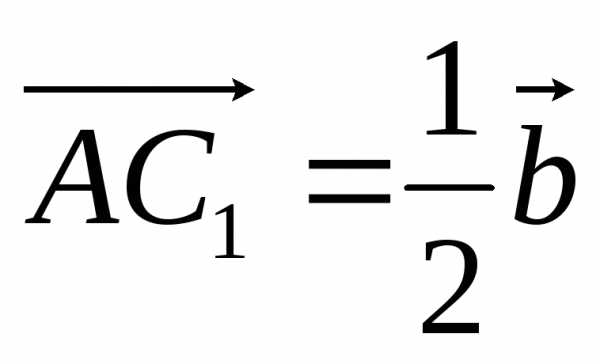 (B1M и C1M – средние линии, поэтому AB1 = B1B, AC1 = С1С).
Получаем
(B1M и C1M – средние линии, поэтому AB1 = B1B, AC1 = С1С).
Получаем 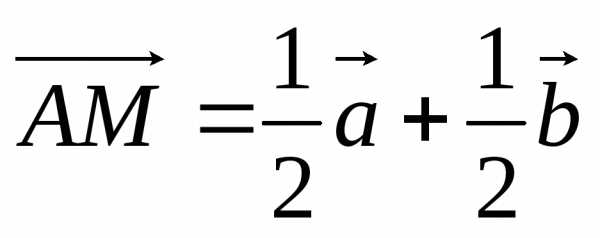 ,
т.е.
,
т.е.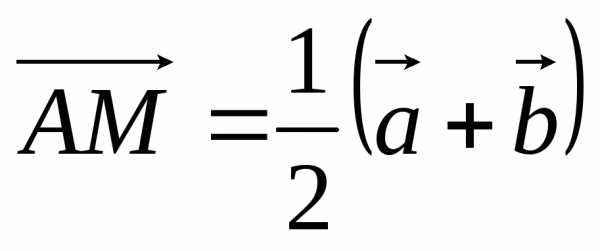 .
.
Пример
2: Какому условию должны удовлетворять
ненулевые векторы  и
и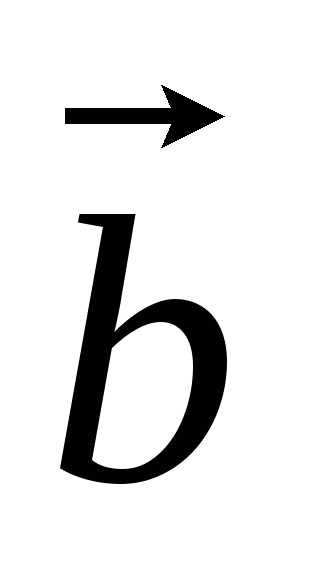 ,
чтобы имело место соотношение?
,
чтобы имело место соотношение?
Решение:
П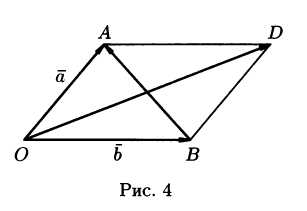 остроим
на векторах
остроим
на векторах и
и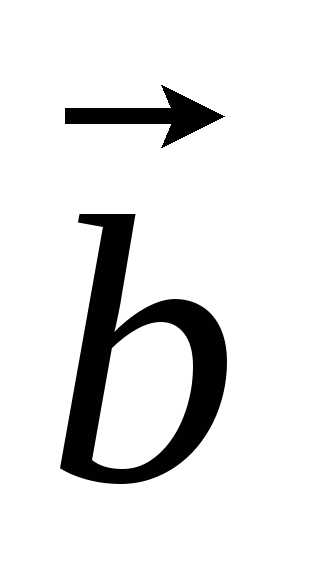 ,
отложенных от точкиО,
параллелограмм OADB (рис. 4). Тогда
,.
Равенство
,
отложенных от точкиО,
параллелограмм OADB (рис. 4). Тогда
,.
Равенство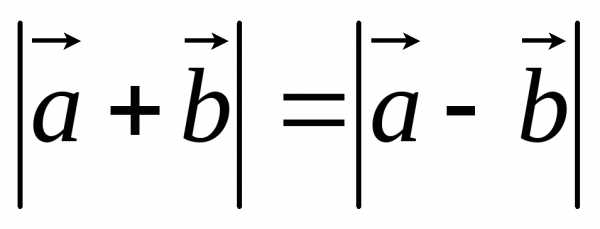 означает, что длины диагоналей
параллелограмма равны, т.е.
означает, что длины диагоналей
параллелограмма равны, т.е.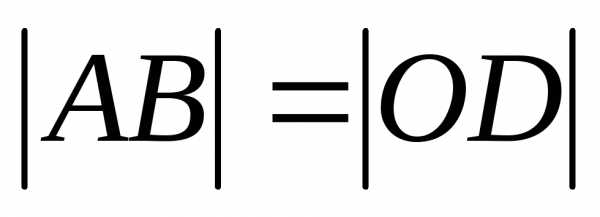 .
Отсюда следует, что данный параллелограмм
есть прямоугольник. Следовательно,
векторы
.
Отсюда следует, что данный параллелограмм
есть прямоугольник. Следовательно,
векторы и
и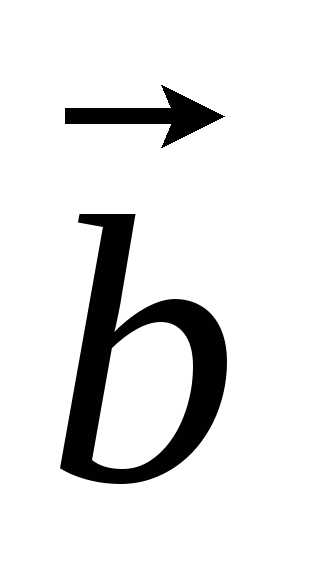 перпендикулярны.
перпендикулярны.
studfiles.net
Векторы. Начальные сведения
Определения
Вектор – это направленный отрезок, для которого указано, какая из его граничных точек является началом, а какая – концом.
Если \(A\) – начало вектора, \(B\) – его конец, то вектор обозначается как \(\overrightarrow{AB}\). Вектор также можно обозначать одной маленькой буквой: \(\overrightarrow{a}\).
Иногда говорят, что вектор – это перемещение из точки \(A\) в точку \(B\).
Длина (или модуль) вектора \(\overrightarrow{AB}\) – это длина соответствующего отрезка \(AB\).
Обозначение: \(|\overrightarrow{AB}|=AB\).
Если длина вектора равна нулю (совпадают начало и конец), то такой вектор называют нулевым.
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых (\(\overrightarrow a, \overrightarrow b\) и \(\overrightarrow c\)).
В противном случае векторы называются неколлинеарными (например, \(\overrightarrow a\) и \(\overrightarrow d\)).
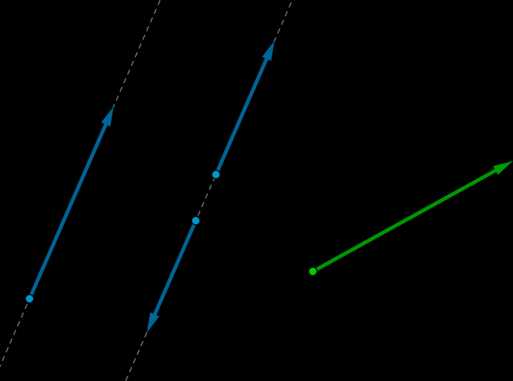
Причем если два коллинеарных вектора направлены в одну сторону, то они называются сонаправленными (\(\overrightarrow a\) и \(\overrightarrow c\)). В противном случае векторы называются противоположно направленными (\(\overrightarrow a\) и \(\overrightarrow
b\)).
Обозначение: \(\overrightarrow a \uparrow \uparrow \overrightarrow
c\), \(\overrightarrow a \uparrow \downarrow \overrightarrow b\).
Векторы называются равными, если они сонаправлены и их длины равны.
Правила сложения коллинеарных векторов:
\(\blacktriangleright\) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).
\(\blacktriangleright\) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).
Правила сложения неколлинеарных векторов \(\overrightarrow {a}\) и \(\overrightarrow{b}\):
\(\blacktriangleright\) Правило треугольника (рис. 3).
Нужно от конца вектора \(\overrightarrow {a}\) отложить вектор \(\overrightarrow {b}\). Тогда сумма \(\overrightarrow {a}+\overrightarrow {b}\) – это вектор, начало которого совпадает с началом вектора \(\overrightarrow {a}\), а конец – с концом вектора \(\overrightarrow {b}\).
\(\blacktriangleright\) Правило параллелограмма (рис. 4).
Нужно от начала вектора \(\overrightarrow {a}\) отложить вектор \(\overrightarrow {b}\). Тогда сумма \(\overrightarrow {a}+\overrightarrow {b}\) – вектор, совпадающей с диагональю параллелограмма, построенного на векторах \(\overrightarrow {a}\) и \(\overrightarrow {b}\) (начало которого совпадает с началом обоих векторов).
Определение
Вектор \(\overrightarrow {-b}\) – это вектор, противоположно направленный с вектором \(\overrightarrow {b}\) и совпадающий с ним по длине.
\(\blacktriangleright\) Для того, чтобы найти разность двух векторов \(\overrightarrow {a}-\overrightarrow{b}\), нужно найти сумму векторов \(\overrightarrow {a}\) и \(-\overrightarrow{b}\): \(\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})\) (рис. 5).
Свойства сложения векторов
1. Наличие нейтрального вектора: для любого вектора \(\overset{\rightarrow}{a}\) выполнено: \(\overset{\rightarrow}{a} + \overset{\rightarrow}{0} = \overset{\rightarrow}{a}\).
2. Наличие обратного вектора: для любого вектора \(\overset{\rightarrow}{a}\) выполнено \(\overset{\rightarrow}{a} + (-\overset{\rightarrow}{a}) = \overset{\rightarrow}{0}\).
3. Ассоциативность: для любых векторов \(\overset{\rightarrow}{a}\), \(\overset{\rightarrow}{b}\) и \(\overset{\rightarrow}{c}\) выполнено \((\overset{\rightarrow}{a} + \overset{\rightarrow}{b}) + \overset{\rightarrow}{c} = \overset{\rightarrow}{a} + (\overset{\rightarrow}{b} + \overset{\rightarrow}{c})\)
4. Коммутативность: для любых векторов \(\overset{\rightarrow}{a}\) и \(\overset{\rightarrow}{b}\) выполнено \(\overset{\rightarrow}{a} + \overset{\rightarrow}{b} = \overset{\rightarrow}{b} + \overset{\rightarrow}{a}\).
Замечание
Для того, чтобы сложить несколько вектором, можно отложить их последовательно: каждый следующий от конца предыдущего. Тогда суммой этих векторов будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего: \[\overrightarrow {a_1}+\overrightarrow {a_2}+\overrightarrow {a_3}+
\overrightarrow {a_4}=\overrightarrow {a}\]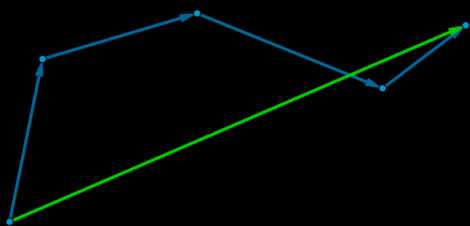
Определение
Произведением ненулевого вектора \(\overrightarrow {a}\) на число \(\lambda\) называется такой вектор \(\lambda\overrightarrow {a}\), длина которого равна \(|\lambda|\cdot |\overrightarrow {a}|\), причем векторы \(\overrightarrow {a}\) и \(\lambda \overrightarrow {a}\) сонаправлены, если \(\lambda>0\), и противоположно направлены, если \(\lambda<0\). Если \(\lambda=0\), то вектор \(\lambda\overrightarrow {a}\) равен нулевому вектору.
Свойства произведения вектора на число
1. Сочетательный закон: \(k(\lambda\overrightarrow {a})=(k\lambda)\overrightarrow {a}\);
2. Распределительный закон 1: \((k+\lambda)\overrightarrow {a}=k\overrightarrow {a}+\lambda\overrightarrow {a}\);
2. Распределительный закон 2: \(\lambda(\overrightarrow {a}+\overrightarrow {b})=\lambda\overrightarrow {a}+\lambda\overrightarrow {b}\).
Теорема
Если \(M\) – середина отрезка \(PQ\), \(O\) – произвольная точка плоскости, то \[\overrightarrow {OM}=\dfrac12 \left(\overrightarrow {OP}+\overrightarrow {OQ}\right)\]
shkolkovo.net
Векторы, Все о векторах
Вектор есть математическим объектом, который имеет величину и направление. Другими словами, это линия заданной длины и проведенная в заданном направлении. Величина вектора есть его длина и обозначающаяся ||.
Если два вектора , проведены в одном и том же направлении, тогда = n. где n — действительное число.
если 0 < n < 1 тогда || < ||
если 1 < n тогда || > ||
если n < 0 тогда || и направление противоположно направлению
Cложение двух векторов осуществляется размещением начала одного вектора к окончанию второго и построением вектора для получения треугольника, как показано на рисунке.
На рисунке внизу показано, как правило параллелограмма используется для построения векторов and который складывается с .
Скалярное произведение векторов

Пусть у нас есть два вектора. Скалярное произведение векторов определяется по формуле:
другие записи для скалярного произведеения есть or
(,)
Результатом скалярного умножения двух векторов всегда есть действительное число.
Свойства скалярного произведения
Если угол между двумя векторами , is 90°
тогда = 0, потому что cos(90°) = 0
= ||2 потому что угол между двумя векторами есть 180° и cos(180°) = 1
Задачи с векторами
1) Если = -1., что мы можем сказать об этих двух векторах?
Решение: Эти два вектора параллельны, одинаковой величины и с противоположными направлениями.
2) Чему равно скалярное произведение если || = 5, || = 7 и угол между этими двумя векторами равен 30°
3) Докажите, используя вектора, что для любого треугольника длина одной стороны меньше суммы двух других сторон.
www.math10.com
Сложение векторов, Сумма векторов | Формулы и расчеты онлайн
Правило треугольника
Сложение векторов, Сумма векторов, Правило треугольника
Сумма векторов a и b это третий вектор с, получаемый следующим построением: из произвольного начала О строим вектор OL, равный а; из точки L, как из начала строим вектор LM, равный b. Вектор с = ОМ есть сумма векторов a и b («правило треугольника»).
При сложении векторов справедливы неравенства
\[ |\vect{a} + \vect{b}| ≤ |\vect{a}| + |\vect{b}| \]
\[ |\vect{a} + \vect{b}| ≥ | |\vect{a}| — |\vect{b}| | \]
Эти неравенства показывают, что сторона OM треугольника OML меньше суммы и больше разности двух других сторон.
Неравенства при сложении векторов
В формуле (1) знак равенства имеет место только для равнонаправленных векторов, в формуле (2) – только для противоположного направленных векторов.
Сумма противоположных векторов
Из определения следует, что сумма противоположных векторов равна нуль-вектору.
\[ \vect{а} + (-\vect{а}) = 0 \]
Свойство переместительности
От перестановки слагаемых сумма не изменяется.
\[ \vect{а} + \vect{b} = \vect{b} + \vect{а} \]
Правило параллелограмма
Сумма векторов — Правило параллелограмма
Если слагаемые a и b не коллинеарны, то сумму a + b можно найти следующим построением:
из любого начала О строим векторы ОА = а и ОВ = b; на отрезках ОА, ОВ строим параллелограмм ОАСВ. Вектор диагонали ОС = с есть сумма векторов a и b (так как АС = OB = b и ОС = ОА + АС).
В помощь студенту
Сложение векторов, Сумма векторов |
стр. 171 |
|---|
www.fxyz.ru
Элементы линейной и векторной алгебры. Формулы Крамера. Геометрический вектор
1 ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
1.1 Определители
ОПР: Определителем второго порядка называется число, обозначаемое: .
ВЫЧИСЛЕНИЕ: .
ПРИМЕР: Вычислить определитель второго порядка:
|
а) |
; |
|
б) |
; |
|
в) |
. |
ОПР: Определитель третьего порядка – это число:
|
|
ВЫЧИСЛЕНИЕ:
*
* .
ПРИМЕР: Вычислить определитель третьего порядка:
УПРАЖНЕНИЯ:
|
а) |
; |
|
|
б) |
; |
|
|
в) |
; |
|
|
г) |
. |
1.2 Формулы Крамера
Дана линейная неоднородная система алгебраических уравнений с неизвестными ()
, где: , , – неизвестные; – коэффициенты уравнения;
, , – свободные члены.
ОПР: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы.
ОПР: , , – определители, составленные из главного определителя системы заменой столбца коэффициентов при неизвестных столбцом свободных членов.
.
.
.
ТЕОРЕМА: Если главный определитель системы линейных неоднородных уравнений с неизвестными отличается от нуля, то система совместна.
Решение этой системы можно найти по формулам Крамера:
.
ПРИМЕР: Решить систему по формулам Крамера:
.
РЕШЕНИЕ:
система совместна;
;
;
.

Ответ: .
УПРАЖНЕНИЯ: Решить систему по формулам Крамера
|
; |
1.3 Геометрические векторы
ОПР: Геометрическим вектором называется направленный отрезок прямой
ОБОЗНАЧЕНИЕ: или , точка A – начало вектора, точка B – конец вектора.
ОПР: Длиной отрезка AB называется длина (модуль) вектора .
ОБОЗНАЧЕНИЕ: или ,
ОПР: Векторы называются компланарными, если они принадлежат одной плоскости или параллельным плоскостям.
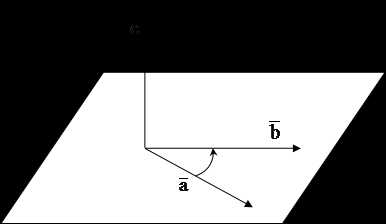 ОПР: Тройка векторов называется правой, если
смотря из конца третьего вектора кратчайший
поворот от первого вектора ко второму
будет виден как движение
против часовой стрелки.
ОПР: Тройка векторов называется правой, если
смотря из конца третьего вектора кратчайший
поворот от первого вектора ко второму
будет виден как движение
против часовой стрелки.
Если движение видно по часовой стрелке, то тройка векторов называется левой.
ОПР: Модуль вектора равен квадратному корню из суммы квадратов его координат.
Если , то .
ПРИМЕР: Найти длину вектора.
|
1) |
; |
|
2) |
. Вектор имеет координаты . ; |
|
3) |
. Вектор имеет координаты . . |
ОПР: Если вектор , где и , то:
.
ПРИМЕР: Даны точки и . Найти расстояние между двумя точками и .
РЕШЕНИЕ: Рассмотрим вектор , по формуле:
;
.
1.4 Линейные операции над векторами
1. Сложение векторов
Если , , то ;
2. Вычитание векторов
3. Умножение вектора на скаляр
Если , – число, то
.
ПРИМЕР:
Даны: , , .
Найти:
1) ;
2) ;
3) ;
4) ;
5) ;
6) .
РЕШЕНИЕ:
1) ;
2) ;
3) ;
4) ;
5) ,
;
6) ,
,
;
УПРАЖНЕНИЯ: Даны точки , , . Найти:
|
1) |
, |
; |
|
2) |
, |
; |
|
3) |
, |
; |
|
4) |
, |
; |
|
5) |
, |
; |
|
6) |
, |
; |
|
7) |
, |
; |
|
8) |
, |
. |
1.5 Скалярное произведение двух векторов
ОПР: Скалярным произведением вектора на называется число, равное произведению их модулей на косинус угла между ними.
ОБОЗНАЧЕНИЕ: .
Свойства скалярного произведения:
1. ;
2. ;
3.
4. – скалярный квадрат вектора равен квадрату его модуля;
5. ;
6. Условие ортогональности двух векторов и : Если и – ненулевые, то их скалярное произведение равно нулю тогда и только тогда, когда эти векторы ортогональны: ;
7. Скалярное произведение в координатной форме: Если векторы заданы своими координатами и , то . Скалярное произведение двух векторов равно сумме произведений их одноименных координат.
Геометрический смысл скалярного произведения:
ПРИМЕР: Найти скалярное произведение векторов, если ; ; .
РЕШЕНИЕ: По определению скалярного произведения , то .
ПРИМЕР: Найти скалярное произведение векторов, если ; .
РЕШЕНИЕ: По свойству №7 получим .
ПРИМЕР: Доказать что векторы и ортогональны, если ; .
РЕШЕНИЕ: По свойству №6 , если , векторы не являются ортогональными.
ПРИМЕР: Найти угол между двумя векторами и , если ; ; .
РЕШЕНИЕ: По свойству №5 , , .
ПРИМЕР: Найти скалярное произведение , если ; ; .
РЕШЕНИЕ: По определению скалярного произведения и свойству №3
ПРИМЕР: Найти , если , если ; ; .
РЕШЕНИЕ: По геометрическому смыслу скалярного произведения , по определению скалярного произведения ,
.
УПРАЖНЕНИЯ:
1.6 Векторное произведение
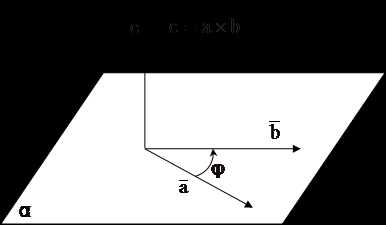
ОПР: Векторным произведением вектора на вектор называется такой вектор , который удовлетворяет условиям:
1) его модуль численно равен площади параллелограмма, построенного на векторах и как на сторонах;
2) и ;
3) тройка – правая
ОБОЗНАЧЕНИЕ:
.
 |
Свойства векторного произведения:
1) ;
2) ;
3) ;
4) Условие коллинеарности двух векторов:
Векторное произведение равно нуль–вектору тогда и только тогда, когда векторы коллинеарны , то | |, если , ;
5) Векторное произведение в координатной форме:
Если , , то
.
Геометрический смысл векторного произведения:
и .
ПРИМЕР: Найти модуль векторного произведения , если ; ; .
РЕШЕНИЕ: По определению векторного произведения .
ПРИМЕР: Найти площадь параллелограмма построенного на векторах и как на сторонах, если ; ; .
РЕШЕНИЕ:
.
ПРИМЕР: Найти , если , .
РЕШЕНИЕ: По свойству №5
,
.
УПРАЖНЕНИЯ:
1.7 Смешанное произведение трех векторов
ОПР: Смешанным произведением трех векторов называется их векторно–скалярное произведение.
ОБОЗНАЧЕНИЕ: или
Геометрический смысл векторного произведения:
Произведение трех векторов равно объему параллелепипеда, построенного на векторах как на ребрах, со знаком «+», если тройка правая, и со знаком «–», если тройка левая.
.
Свойства смешанного произведения:
1) ;
2) ;
3) Условие компланарности трех векторов:
Три вектора компланарные тогда и только тогда, когда их смешанное произведение равно нулю. ;
4) Вычисление смешанного произведения в координатной форме:
Если , , , то
;
5) Объем пирамиды: .
ПРИМЕР: Найти смешанное произведение , если , , .
РЕШЕНИЕ: по свойству №4:
.
ПРИМЕР: Доказать, что – компланарные, если , , .
РЕШЕНИЕ: по свойству №3:
векторы копланарные.
УПРАЖНЕНИЯ:
Даны: , , .
|
1) |
Найти смешанное произведение |
|
|
2) |
Установить компланарность |
|
|
3) |
Найти объем параллелепипеда |
|
|
4) |
Найти объем пирамиды |
|
|
5) |
Установить вид тройки векторов |
2 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
2.1 Прямая на плоскости
Если на плоскости задана декартова система координат, то прямую на плоскости можно задать как линию пересечения плоскостей и , т.е. уравнением:
1. Общее уравнение прямой на плоскости: ;
2. Уравнение прямой в отрезках: ;
3. Уравнение прямой, проходящей через две точки и :
4. Если известны угловой коэффициент прямой , и – отрезок, отсекаемый на оси , то уравнение прямой с угловым коэффициентом имеет вид: .
Если , то уравнение прямой имеет вид и прямая параллельна
vunivere.ru
Вектор (геометрия) — это… Что такое Вектор (геометрия)?
Под направленным отрезком в геометрии понимают упорядоченную пару точек, первая из которых — точка A — называется его началом, а вторая — B — его концом.
Определение
Вектором в простейшем случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Учитывая изоморфизм между множеством свободных векторов и множеством их параллельных переносов пространства, если операцию сложения отождествить с композицией переносов, можно использовать множество параллельных переносов пространства даже для определения вектора.
Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.
- Вектор, начало которого совпадает с его концом, называют нулевым:
- Вектор называют противоположным вектору .
- Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка: .
Свободные, скользящие и фиксированные векторы
Иногда, вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).
Определение. Говорят, что свободные векторы и равны, если найдутся точки E и F такие, что четырёхугольники ABFE и CDFE — параллелограммы.
- Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки A,B,C,D располагаются на одной прямой. В противном случае определение выглядит проще:
Определение. Говорят, что свободные векторы и , не лежащие на одной прямой, равны, если четырёхугольник ABDC — параллелограмм.
Определение. Говорят, что скользящие векторы и равны, если
- точки A,B,C,D располагаются на одной прямой,
- векторы и равны между собой как свободные векторы.
Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.
- Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на котой он лежит, не меняет момента силы ни относительно какой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.
Определение. Говорят, что фиксированные векторы и равны, если попарно совпадают точки A и C, B и D.
Операции над векторами
Сложение векторов
Два вектора u, v и вектор их суммы
Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.
Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Сложение коллинеарных скользящих векторов
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы и , расположенные на одной прямой. Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы
Прямые, на которых расположены векторы и , пересекаются всегда, за исключением случая, когда векторы и равны по величине и противоположны по направлению, в котором говорят, что векторы и образуют пару (векторов).
Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.
Произведение вектора на число
Произведением вектора и числа λ называется вектор, обозначаемый (или ), модуль которого равен , а направление совпадает с направлением вектора , если , и противоположно ему, если . Если же , или вектор нулевой, тогда и только тогда произведение — нулевой вектор.
- Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, .
Из определения произведения вектора на число легко вывести следующие свойства:
- если , то . Наоборот, если , то при некотором λ верно равенство ;
- всегда °, то есть каждый вектор равен произведению его модуля на орт.
Скалярное произведение
Скалярным произведением векторов и называют число, равное , где — угол между векторами и . Обозначения: или .
Если один из векторов является нулевым, то несмотря на то, что угол не определён, произведение равно нулю.
Свойства скалярного произведения векторов:
- — коммутативность.
- — дистрибутивность.
- — линейность по отношению к умножению на число.
- — норма вектора.
Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора с единичным вектором есть ортогональная проекция вектора на направление единичного вектора.
Векторное произведение
Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:
- длина вектора c равна произведению длин векторов a и b на синус угла φ; между ними
- вектор c ортогонален каждому из векторов a и b
- вектор c направлен так, что тройка векторов abc является правой.
Обозначение:
Геометрически векторное произведение есть ориентированная площадь параллелограмма, построенного на векторах , представленная псевдовектором, ортогональным этому параллелограмму.
Свойства векторного произведения:
- При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
- Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
- Векторное произведение обладает распределительным свойством:
Смешанное произведение
Сме́шанное произведе́ние векторов — скалярное произведение вектора на векторное произведение векторов и :
(равенство записано для разных обозначений скалярного и векторного произведения).
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение есть (ориентированный) объем параллелепипеда, построенного на векторах .
Условие перпендикулярности векторов
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
Пример
Даны два вектора и . Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.
Условие коллинеарности векторов
Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.
Пример
Даны два вектора и . Эти векторы коллинеарны, если x1 = λx2 и y1 = λy2, где
См. также
Ссылки
Wikimedia Foundation. 2010.
dic.academic.ru