| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Примерно 7-9 класс (13-15 лет)
| |||||||||||||||||||||||
dpva.ru
Парабола и гипербола 2019
Парабола против Гипербола
Парабола и гипербола — это два разных участка конуса. Мы можем иметь дело с их различиями в математическом объяснении или иметь дело с различиями в очень простом способе, который не только понимают математики, но и все. В этой статье мы попытаемся объяснить разницу между ними очень просто. Прежде всего, когда сплошная фигура, которая в этом случае является конусом, разрезается плоскостью, полученный участок называется коническим сечением. Конические участки могут быть кругами, эллипсами, гиперболами и параболами в зависимости от угла пересечения между осью конуса и плоскостью. Как параболы, так и гиперболы являются открытой кривой, что означает, что руки или ветви кривых продолжаются до бесконечности; они не являются замкнутыми кривыми, такими как круг или эллипс.
парабола Параболой является кривая, полученная, когда плоскость разрезается параллельно стороне конуса. В параболе линия, проходящая через центр и перпендикулярная к директрисе, называется «осью симметрии». Когда парабола пересекается точкой на «оси симметрии», ее называют «вершиной». Все параболы имеют форму одинаково, поскольку они разрезаются под определенным углом. Это характеризуется эксцентриситетом «1.». Именно поэтому они имеют одинаковую форму, но могут иметь разные размеры.
Парабола задается уравнением y2 = X Когда множество точек, присутствующих в плоскости, равноудалено от директрисы, данной прямой и равноудалено от фокуса, данная точка фиксирована, ее называют параболой. Параболы имеют много практических применений. Они используются для проектирования путей ракет, отражателей фар автомобилей, телескопов, радиолокационных приемников и спутниковых антенн.
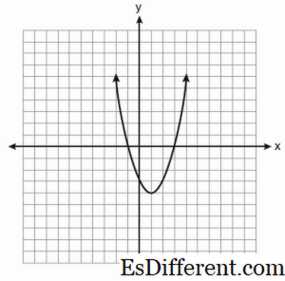
гипербола
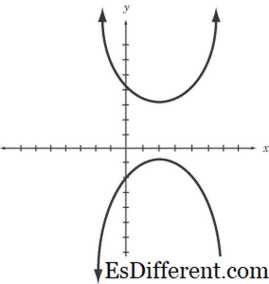
Гипербола — это кривая, полученная, когда плоскость разрезается почти параллельно оси. Гиперболы не идентичны по форме, так как между осью и плоскостью имеется много углов. «Вершины» — это точки на ближайших двух плечах; тогда как сегмент линии, соединяющий плечи, называется «большой осью». В параболе два плеча кривой, также называемые ветвями, становятся параллельными друг другу. В гиперболе два рычага или кривые не становятся параллельными. Центр гиперболы — это середина главной оси.
Гипербола задается уравнением XY = 1
Когда разность расстояний между множеством точек, присутствующих в плоскости до двух фиксированных фокусов или точек, является положительной константой, она называется гиперболой.
Резюме: Когда множество точек, присутствующих в плоскости, равноудалено от директрисы, данной прямой и равноудалено от фокуса, данная точка фиксирована, ее называют параболой. Когда разность расстояний между множеством точек, присутствующих в плоскости до двух фиксированных фокусов или точек, является положительной константой, она называется гиперболой. Все параболы имеют одинаковую форму независимо от размера; все гиперболы различной формы Парабола задается уравнением y2 = X; гипербола задается уравнением XY = 1 В параболе два плеча становятся параллельными друг другу, а в гиперболе — нет.
ru.esdifferent.com
Математическая гипербола. Как построить гиперболу?
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Математическая гипербола.
Функция заданная формулой \(y=\frac{k}{x}\), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции \(y=\frac{k}{x}\) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:
1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти. гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти
гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти
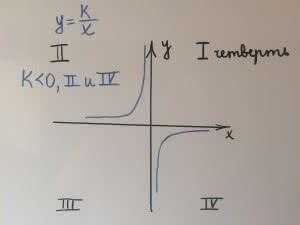 гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти
гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти
2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=\frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$y\neq\color{red} {\frac{1}{x}}+0$$
\(\frac{1}{x}\) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=\frac{1}{x+2}-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
$$y=\color{red} {\frac{1}{x+2}}-1$$
Дробь \(\color{red} {\frac{1}{x+2}}\) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):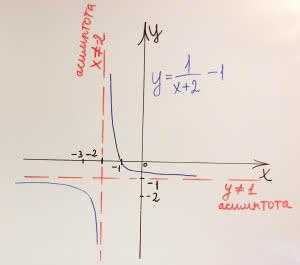
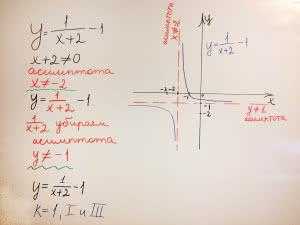
Пример №3:
$$\begin{align*}
&y=\frac{2+x}{1+x} \\\\
&y=\frac{\color{red} {1+1}+x}{1+x} \\\\
&y=\frac{1}{1+x}+\frac{1+x}{1+x}\\\\
&y=\frac{1}{1+x}+1\\\\
&y=\frac{1}{\color{red} {1+x}}+1
\end{align*}$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
$$y=\color{red}{\frac{1}{1+x}}+1$$
\(\color{red}{\frac{1}{1+x}}\) Дробь убираем.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
$$y=\frac{1}{x}$$
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.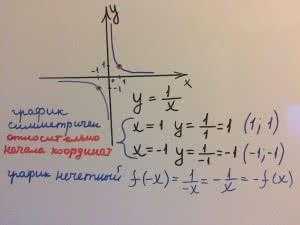
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
$$y=\frac{1}{x}$$
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.
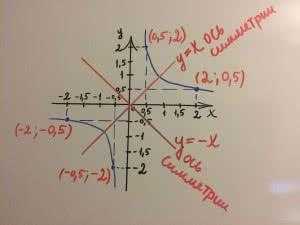
5. Гипербола нечетная функция.
$$f(-x)=\frac{1}{-x}=-\frac{1}{x}=-f(x)$$
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
$$y=\frac{-1}{x-1}-1$$
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
$$y=\color{red} {\frac{-1}{x-1}}-1$$
Дробь \(\color{red} {\frac{-1}{x-1}}\) удаляем.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).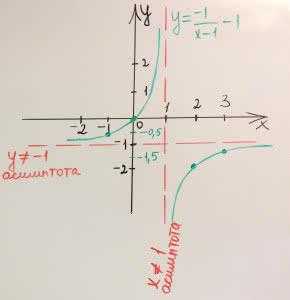

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.
8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама
tutomath.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра
Гипербола на координатной плоскости
Определение 1. Гиперболой (равносторонней гиперболой) называют график функции
| (1) |
где k – любое, отличное от нуля, число.
Функция (1) обладает следующими свойствами:
Рассмотрим теперь функцию, заданную формулой
| (2) |
где a, b, c, d – произвольные числа, а число c не равно нулю.
Определение 2. Дробно-линейной функцией называют функцию, заданную формулой (2), если дробь, стоящая в правой части формулы (2), несократима.
Графиком дробно–линейной функции является гипербола.
Примеры графиков дробно–линейных функций
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Уравнение гиперболы, формулы и примеры
Каноническое уравнение гиперболы
Каноническое уравнение гиперболы имеет вид
где – вещественная полуось, – мнимая полуось гиперболы.
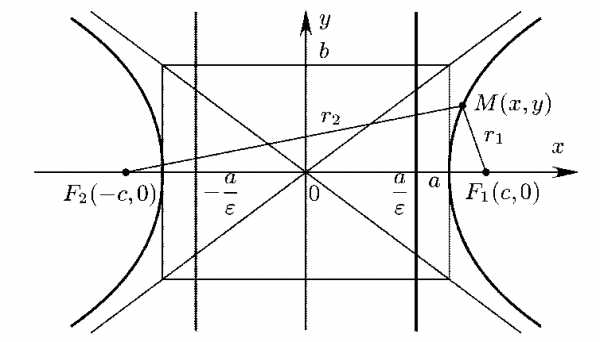
Вершины гиперболы находятся на вещественной оси и имеют координаты . Фокусы гиперболы имеют координаты и , где .
Примеры решения задач
ПРИМЕР 1| Задание | Составить уравнение гиперболы, если длина вещественной оси равна единице, а точка принадлежит гиперболе. |
| Решение | Из условия задачи известно, что длина вещественной оси равна единице, тогда параметр . Подставим полученное значение в каноническое уравнение гиперболы
Найдем значение параметра , подставив в уравнение координаты точки :
Подставим полученное значение в уравнение гиперболы
|
| Ответ | Уравнение гиперболы имеет вид: |
| Задание | В данной системе координат гипербола имеет каноническое уравнение. Составить это уравнение, если расстояние между вершинами равно 10, а расстояние между фокусами равно 12. |
| Решение | Вершины гиперболы имеют координаты , т.е. расстояние между ними равно . Из условия задачи следует, что
Фокусы гиперболы имеют координаты и , т.е. расстояние между ними равно . Тогда
Найдем значение параметра :
Теперь можно записать искомое уравнение гиперболы
|
| Ответ |
Построение гиперболы
Свойства гиперболы
Эксцентриситет гиперболы
Парабола
Формула вершины параболы
График параболы
Уравнение параболы
Кубическая парабола
ru.solverbook.com
Гипербола
Определение. Гипербола– геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная, равная большой оси гиперболы.
Эта разность по
модулю должна быть меньше расстояния
между фокусами  и отлична от нуля.
и отлична от нуля.
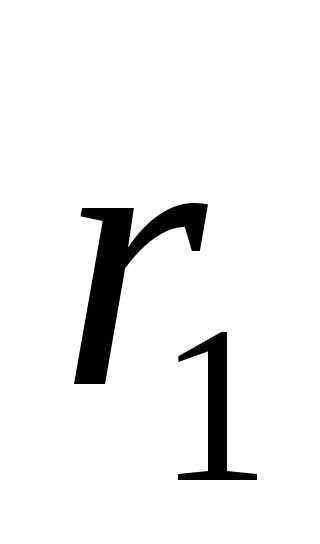
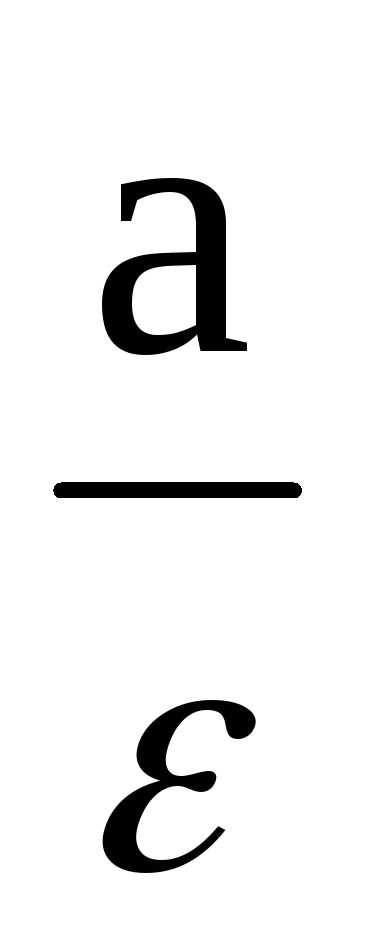
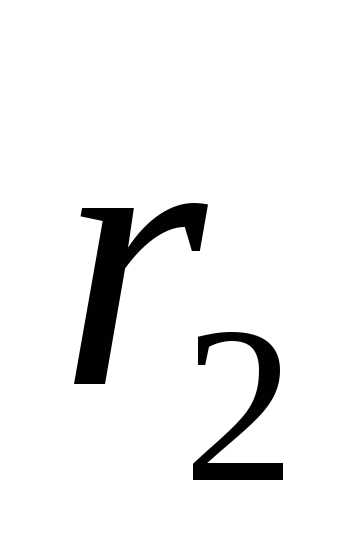 — фокусные радиусы точки
— фокусные радиусы точки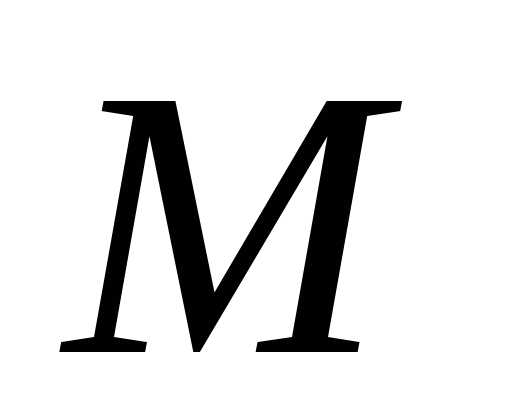 .
. 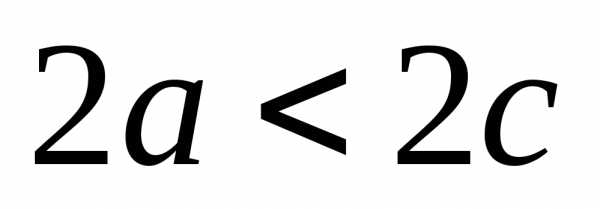 (по
определению) следовательно
(по
определению) следовательно  .
.
Гипербола состоит из двух отдельных частей, называемых ветвями.
Канонический вид уравнения
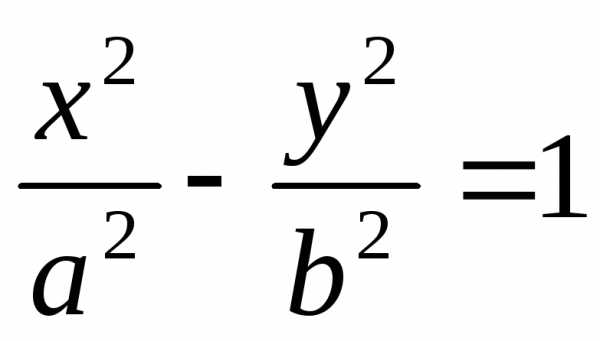 , (11)
, (11)
следовательно,
.
Уравнение 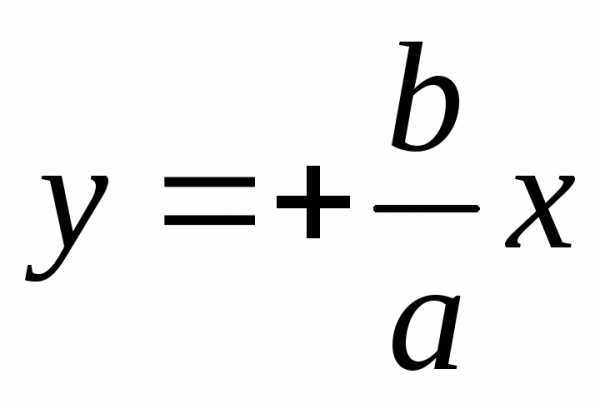 – это уравнение прямой с угловым
коэффициентом
– это уравнение прямой с угловым
коэффициентом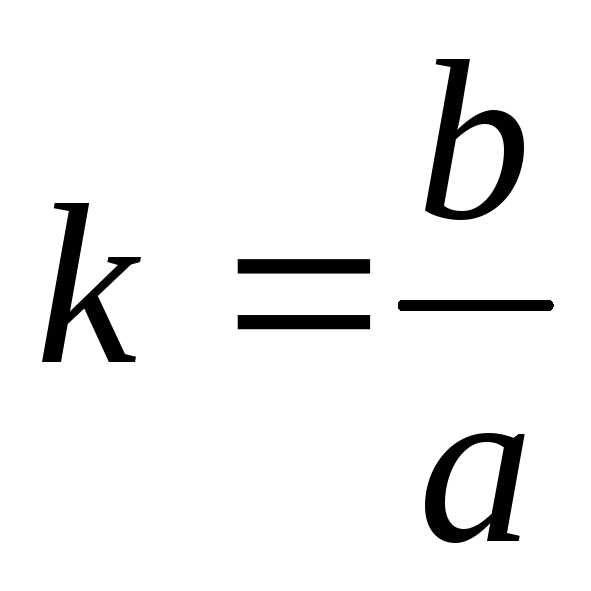 .
При.
.
При.
Прямые  называютсяасимптотамигиперболы.
называютсяасимптотамигиперболы.
Отрезки 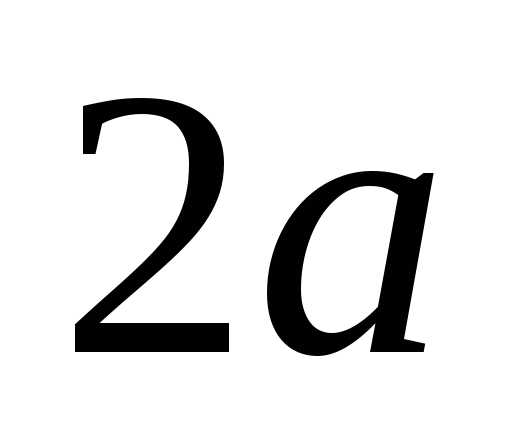 и
и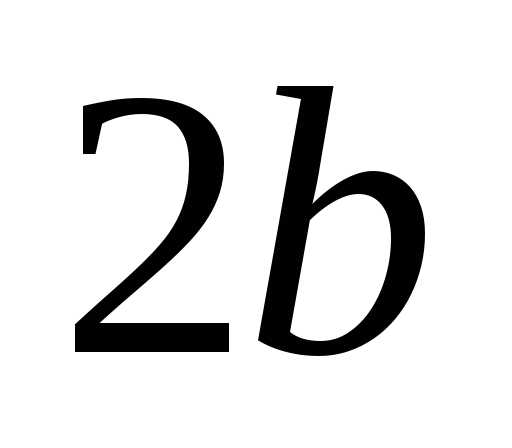 — оси гиперболы.
— оси гиперболы.
Уравнение вида 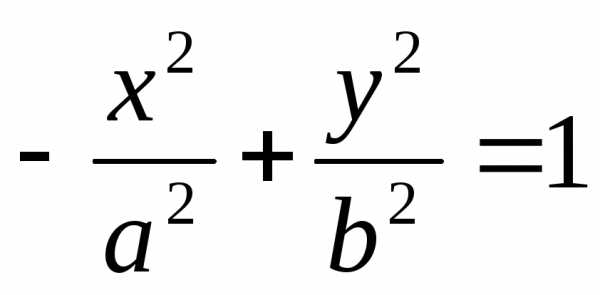 задает гиперболу, сопряженную с первой.
задает гиперболу, сопряженную с первой.
Гипербола с равными
полуосями 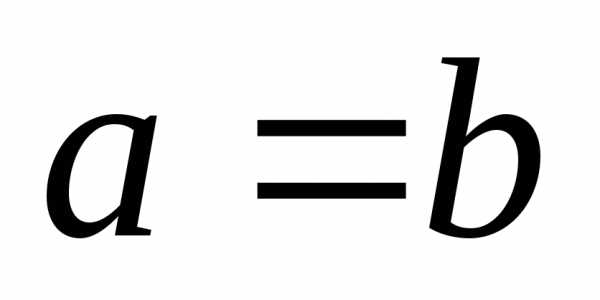 называется равносторонней:
называется равносторонней:
Определение.Эксцентриситетомгиперболы называется отношение расстояния между фокусами к расстоянию между вершинами:
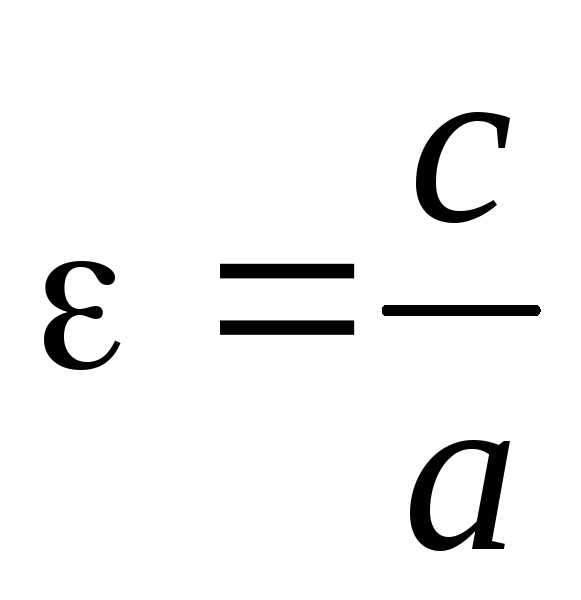 . (12)
. (12)
Определение.Две прямые, перпендикулярные к той оси
гиперболы, которая ее пересекает,
расположенные симметрично относительно
центра на расстоянии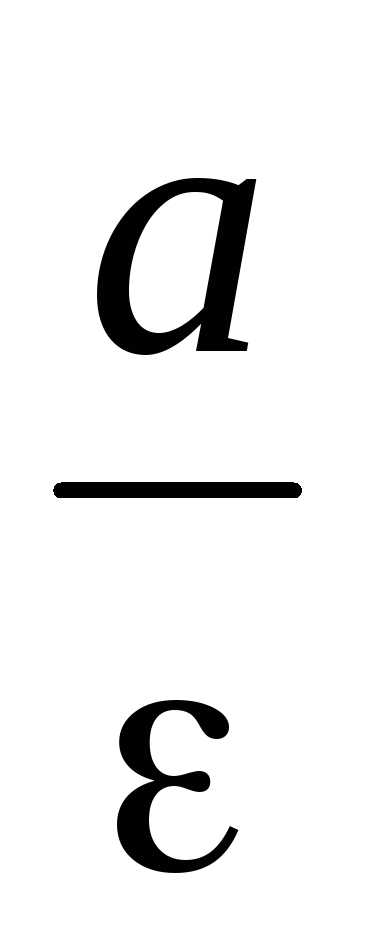 от него, называютсядиректрисамигиперболы.
от него, называютсядиректрисамигиперболы.
Теорема.Для любой точки эллипса и гиперболы справедливо соотношение
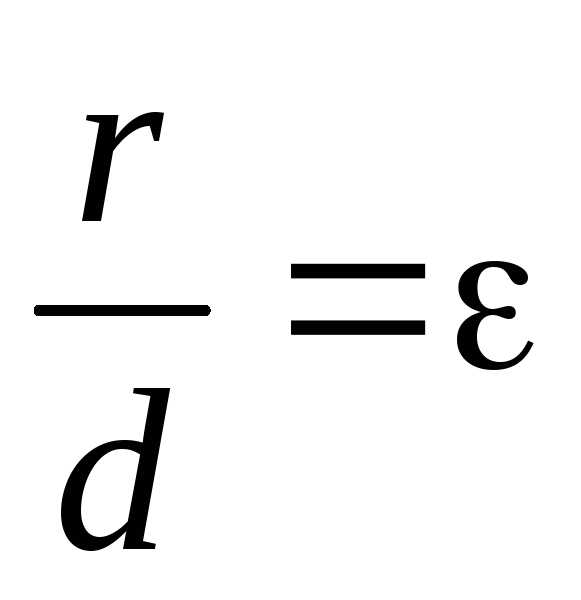 , (13)
, (13)
где 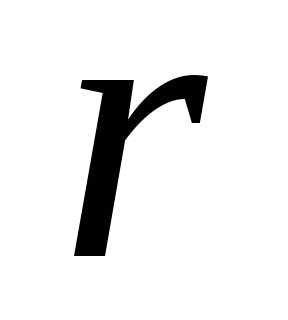 – расстояние от точки до фокуса
– расстояние от точки до фокуса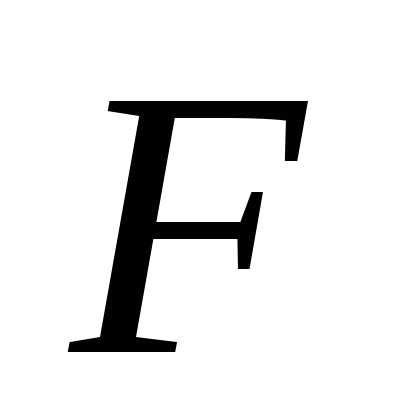 ,
а
,
а – расстояние до соответствующей
директрисы.
– расстояние до соответствующей
директрисы.
Парабола
Определение.Парабола– это геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой:
 .
(14)
.
(14)
 –фокус,
–фокус, 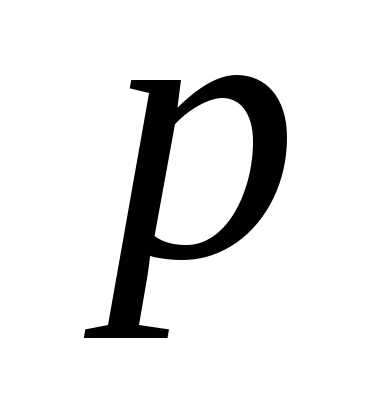 – расстояние от фокуса до директрисы
– параметр параболы,– фокальный радиус точки.
– расстояние от фокуса до директрисы
– параметр параболы,– фокальный радиус точки.
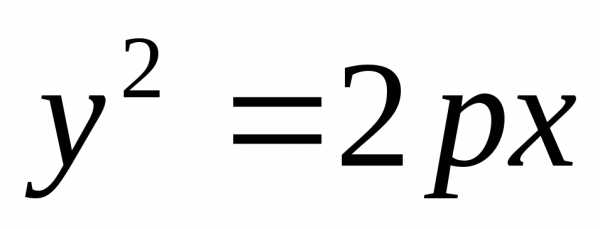 (15)
(15)
– каноническое
уравнение параболы, симметричной
относительно
оси О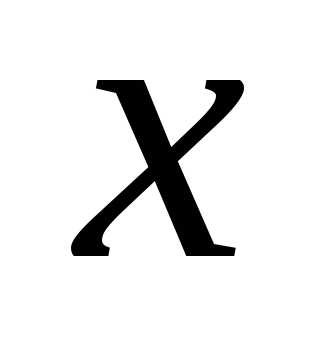 ,
при
,
при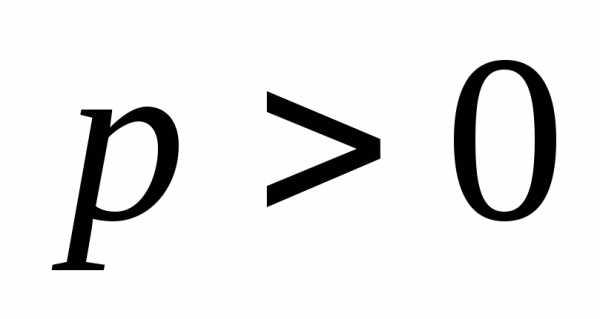 ветви параболы направлены вправо.
Уравнение
ветви параболы направлены вправо.
Уравнение
 задает параболу,
симметричную относительно оси ординат,
ветви которой при
задает параболу,
симметричную относительно оси ординат,
ветви которой при 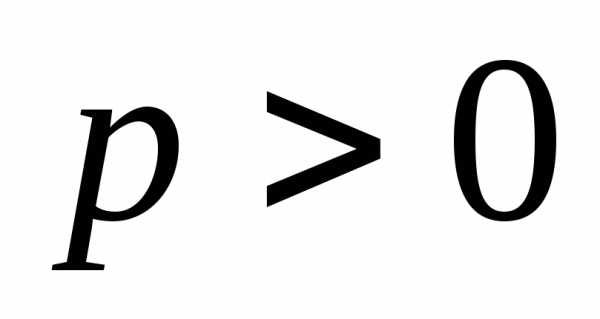 направлены вверх.
направлены вверх.
Примеры решения задач на тему «Кривые второго порядка».
Пример 1: Найти
координаты фокусов и эксцентриситет
эллипса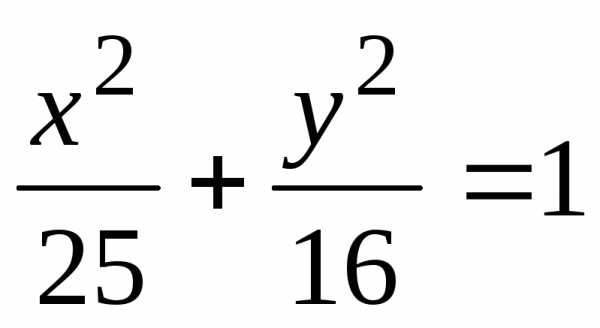
Решение: Для данного эллипсаи поэтому
Следовательно,
фокусы имеют координаты 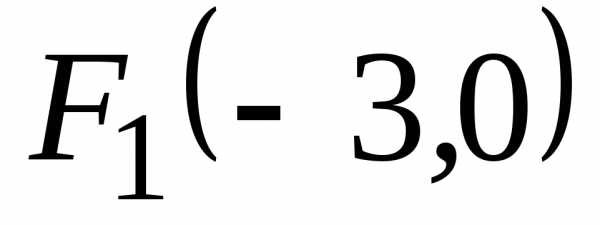 и
и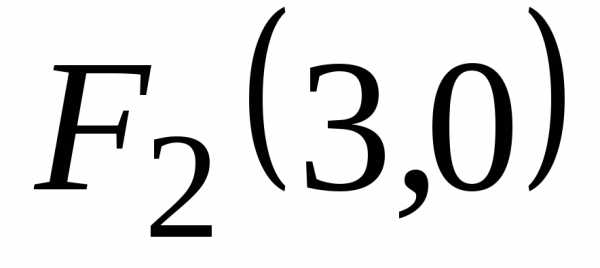 ,
эксцентриситет
,
эксцентриситет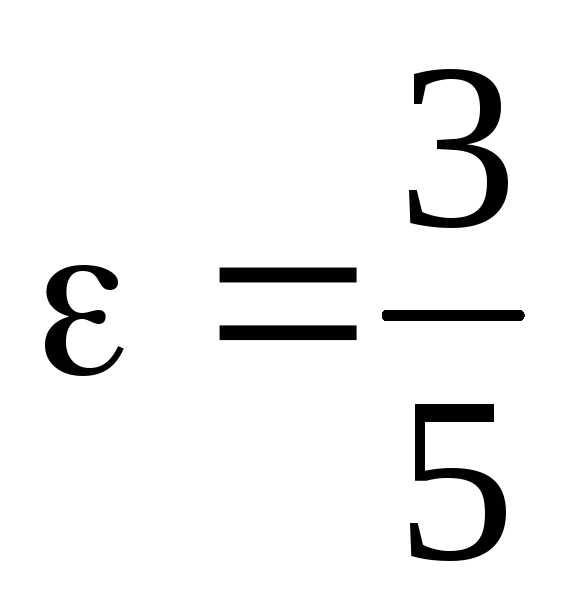
Пример 2: Найти полуоси, координаты фокусов и эксцентриситет эллипса
Решение: Разделив на 36, приведем данное уравнение к виду
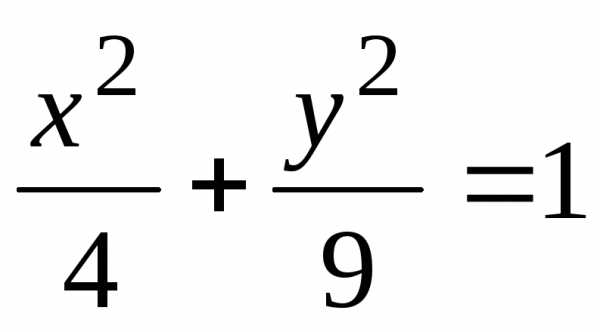
Отсюда следует,
что большая полуось эллипса 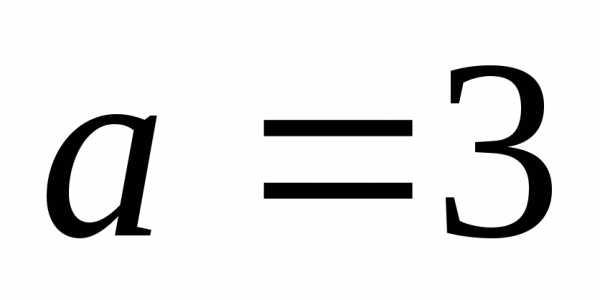 ,
а малая полуось
,
а малая полуось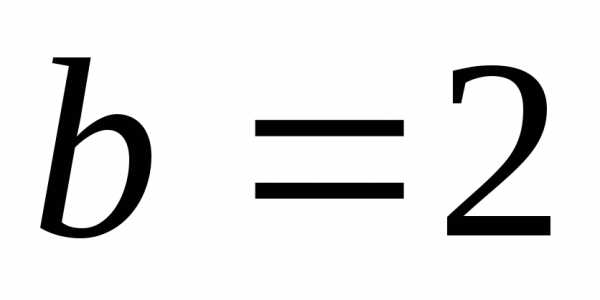 .
При этом ось эллипса и его фокусы
расположены на оси
.
При этом ось эллипса и его фокусы
расположены на оси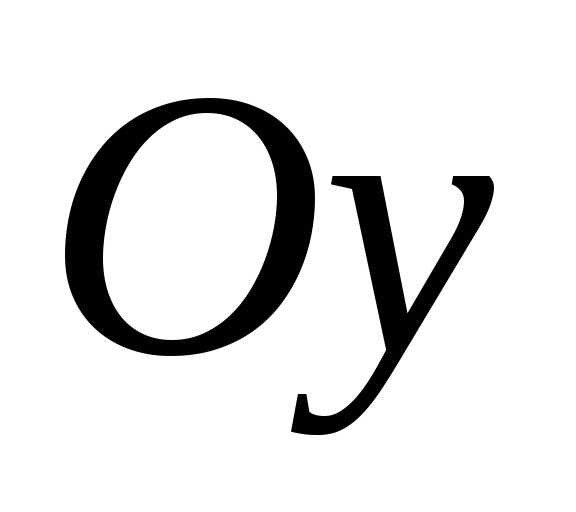 .
Найдем
.
Найдем по формуле
по формуле
.
Следовательно,
координаты фокусов  и
и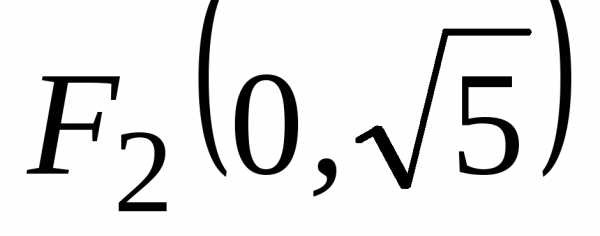 ,
а его эксцентриситет
,
а его эксцентриситет
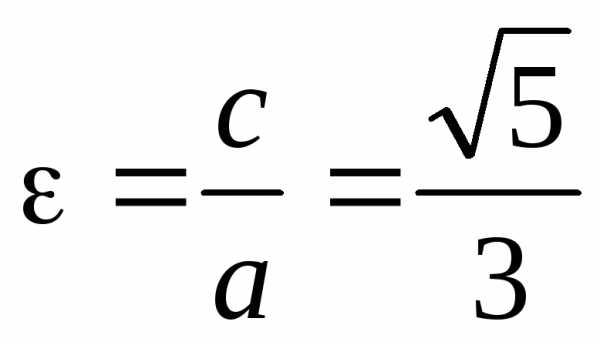
Пример 3: Составить
каноническое уравнение эллипса, зная,
что его большая полуось ,
а его эксцентриситет
,
а его эксцентриситет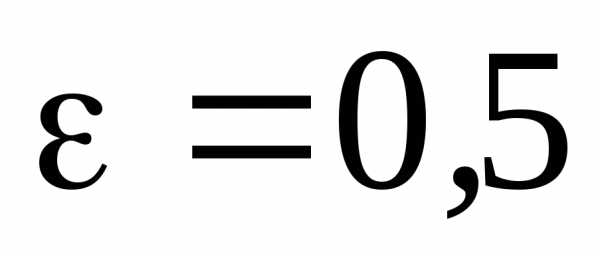 .
Найти расстояние между фокусами эллипса.
.
Найти расстояние между фокусами эллипса.
Решение: Воспользуемся формулой, выражающей эксцентриситет через отношение полуосей:
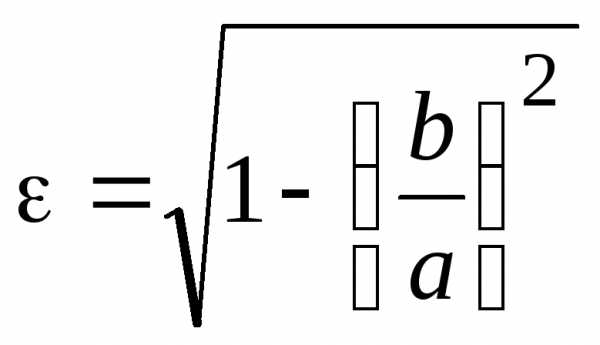 ,
или
,
или  ,
откуда.
,
откуда.
В данном случае
Следовательно, каноническое уравнение эллипса
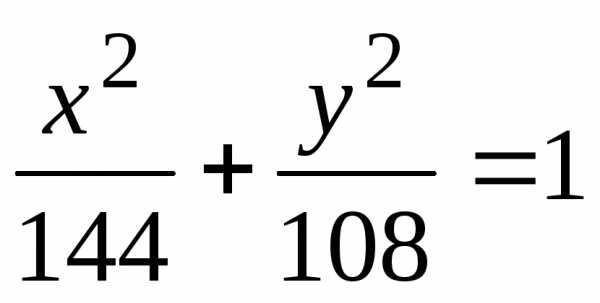 .
.
Так как 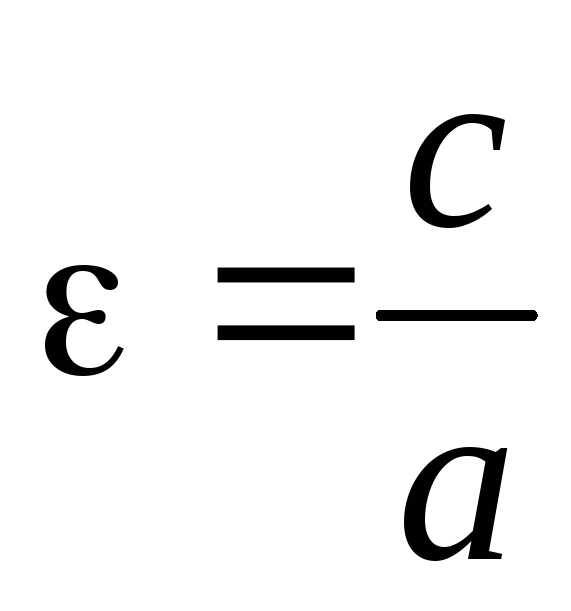 ,
то;и расстояние между фокусами
,
то;и расстояние между фокусами
Пример 4: Асимптоты гиперболы имеют уравнения, а расстояние между фокусами равно 20. Написать ее каноническое уравнение.
Решение: Разрешим
уравнения асимптот относительно и, сравнив с общей формулой асимптот,
найдем отношение
и, сравнив с общей формулой асимптот,
найдем отношение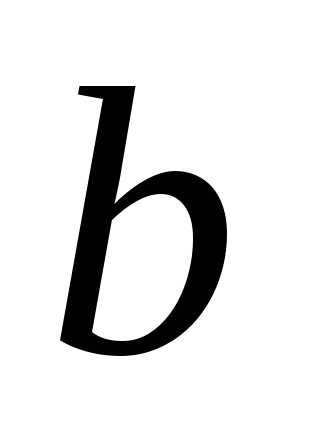 к
к :
:
Кроме того,
,
т.е. 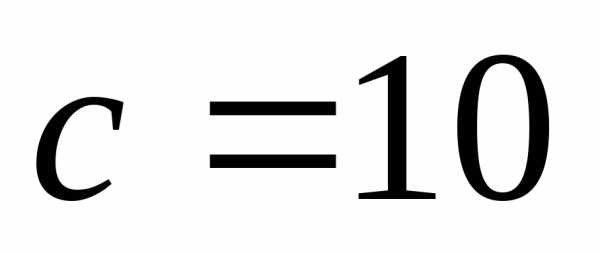 .
Так как для гиперболы,
то для нахождения
.
Так как для гиперболы,
то для нахождения и
и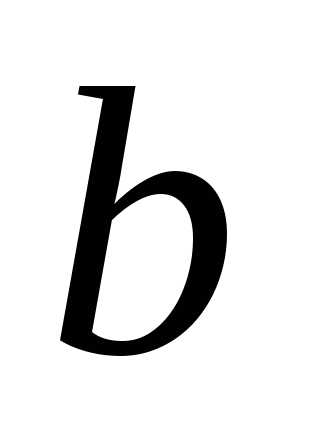 получим систему уравнений
получим систему уравнений
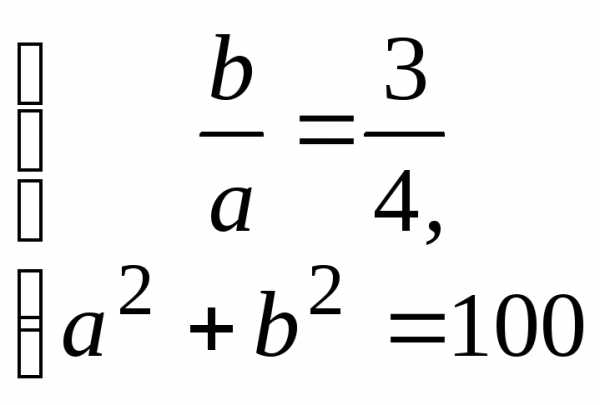
решая которую, найдем . Следовательно, каноническое уравнение гиперболы имеет вид
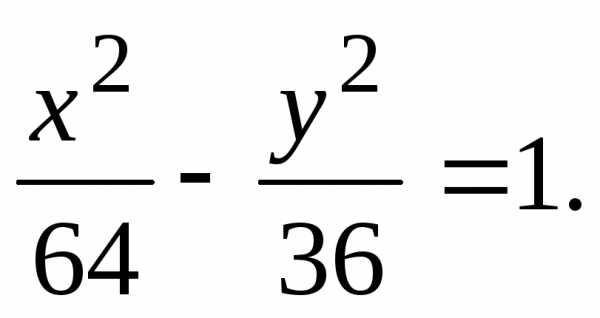
Пример 5: Парабола
с вершиной в начале координат проходит
через точку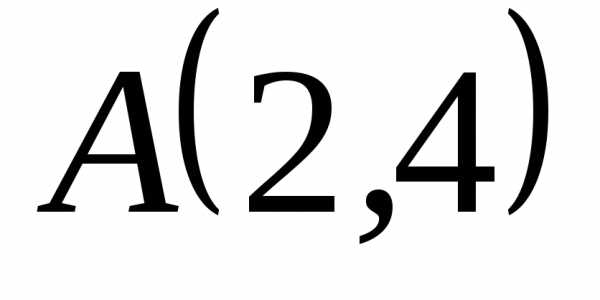 и симметрична относительно оси
и симметрична относительно оси .
Написать ее уравнение.
.
Написать ее уравнение.
Решение:Так как парабола симметрична
относительно оси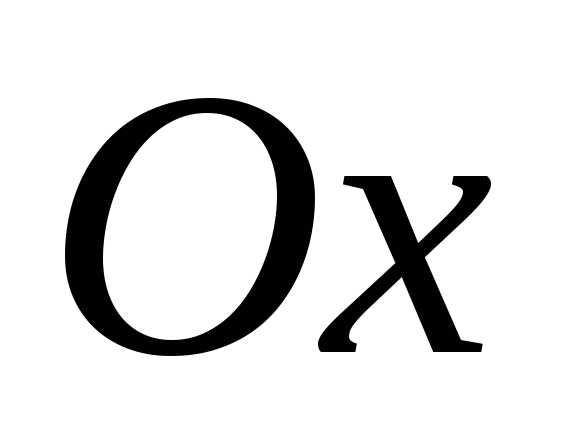 и проходит через точку
и проходит через точку с положительной абсциссой, то она имеет
вид, представленный на рис.
с положительной абсциссой, то она имеет
вид, представленный на рис.
Подставляя
координаты точки  в уравнение такой параболы
в уравнение такой параболы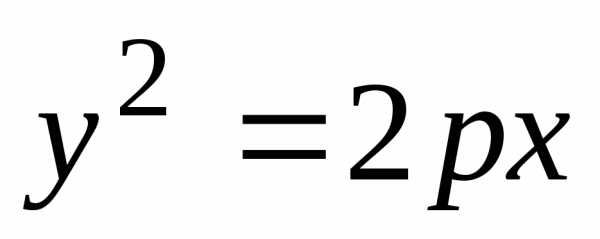 ,
получим,
т.е.
,
получим,
т.е.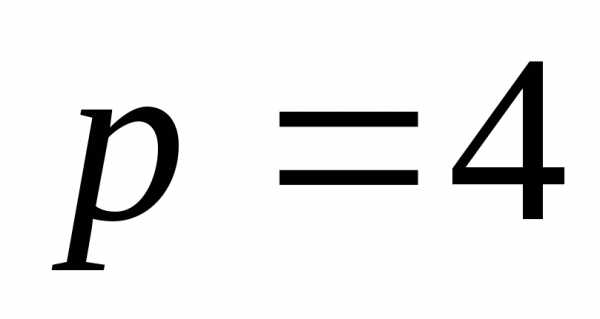 .
.
Следовательно, искомое уравнение
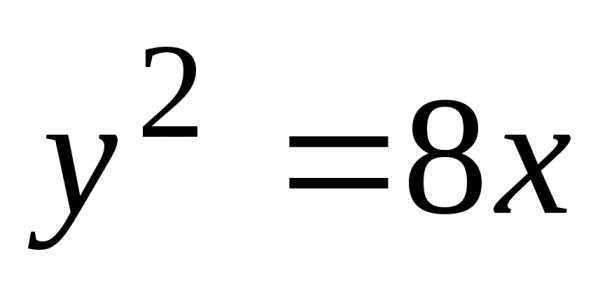
фокус этой параболы 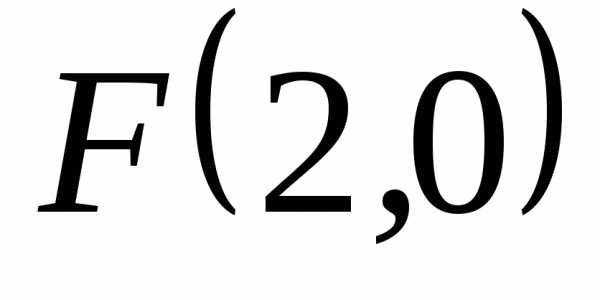 ,
уравнение директрисы
,
уравнение директрисы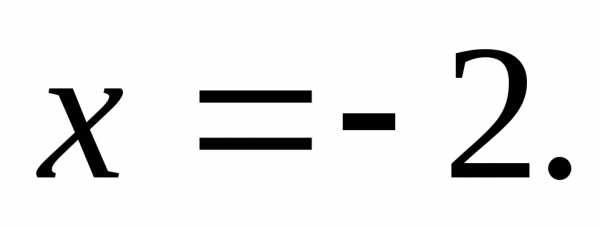
studfiles.net
III. Канонические уравнения окружности, эллипса, гиперболы и параболы.
Окружность.
Пусть
.
В этом случае в координатах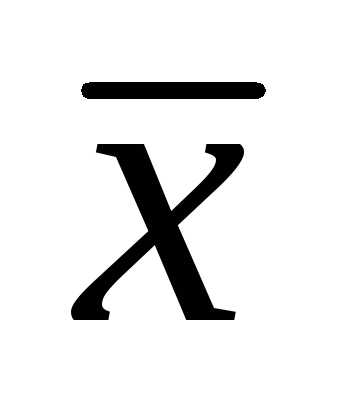 и
и получаем уравнение окружности
получаем уравнение окружности
радиуса 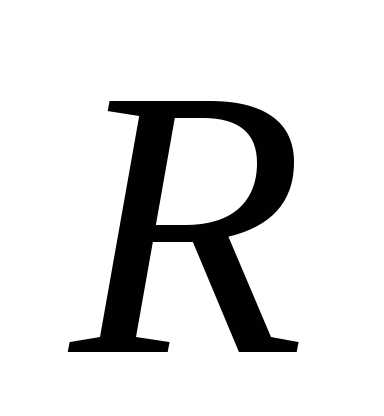 с центром в начале координат. Уравнение
окружности того же радиуса с центром в
точке
с центром в начале координат. Уравнение
окружности того же радиуса с центром в
точке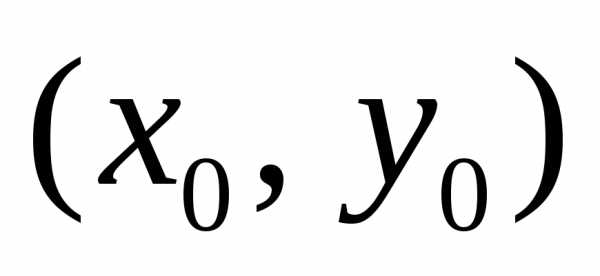 имеет вид
имеет вид
.
С геометрической
точки зрения окружность – геометрическое
место точек на плоскости, равноудаленных
от некоторой точки (центра окружности).
Если 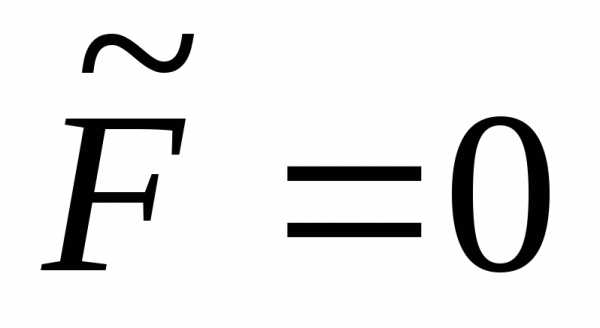 ,
то окружность вырождается в точку.
Наконец, если
,
то окружность вырождается в точку.
Наконец, если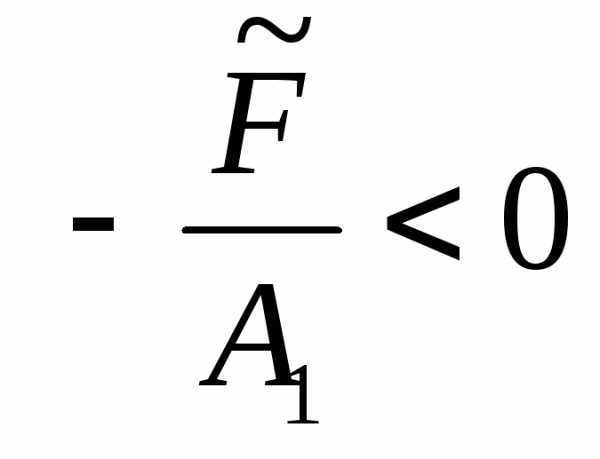 ,
то уравнениене определяет какой-либо кривой на
плоскости (мнимая окружность).
,
то уравнениене определяет какой-либо кривой на
плоскости (мнимая окружность).
2. Эллипс.
Запишем полученное уравнение центральной кривой в виде
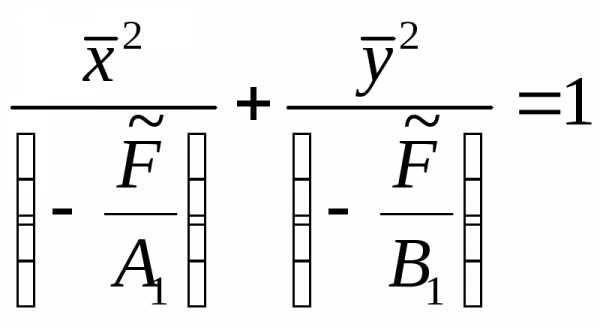 .
.
Пусть , получим каноническое уравнение эллипса
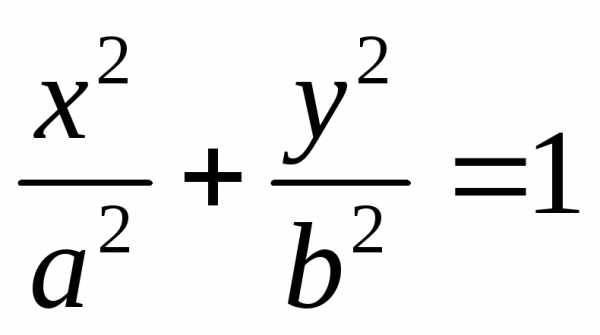 .
.
Оси 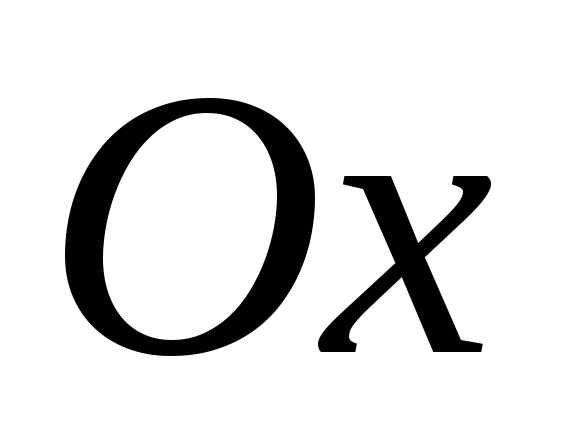 и
и называютсяосями
симметрии эллипса,
а точки
—вершинами
эллипса.
Пусть
называютсяосями
симметрии эллипса,
а точки
—вершинами
эллипса.
Пусть 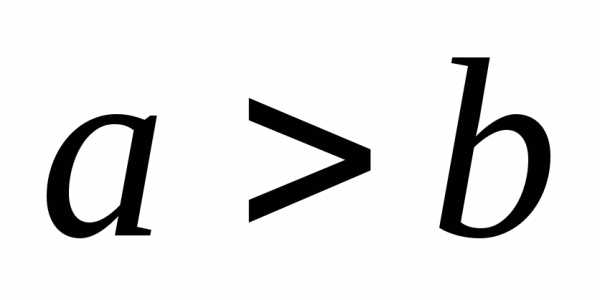 .
Отрезок
.
Отрезок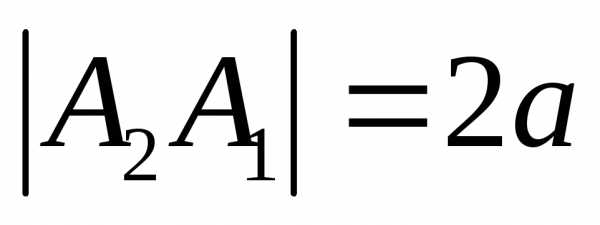 называетсябольшой
осью эллипса (
называетсябольшой
осью эллипса ( —большой
полуосью эллипса),
а отрезок
—большой
полуосью эллипса),
а отрезок  —малой осью
эллипса (
—малой осью
эллипса (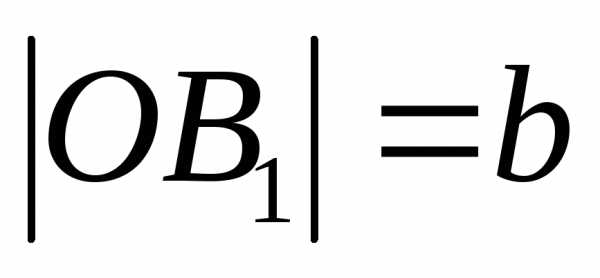 — малой
полуосью эллипса).
Эллипс имеет два фокуса ,
где.
Расстояние между фокусами равно
— малой
полуосью эллипса).
Эллипс имеет два фокуса ,
где.
Расстояние между фокусами равно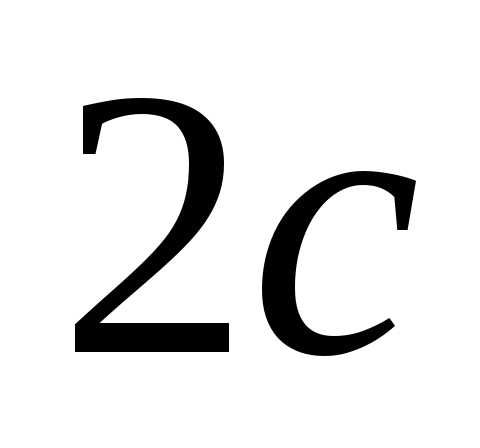 .
Форма эллипса зависит от отношения
.
Форма эллипса зависит от отношения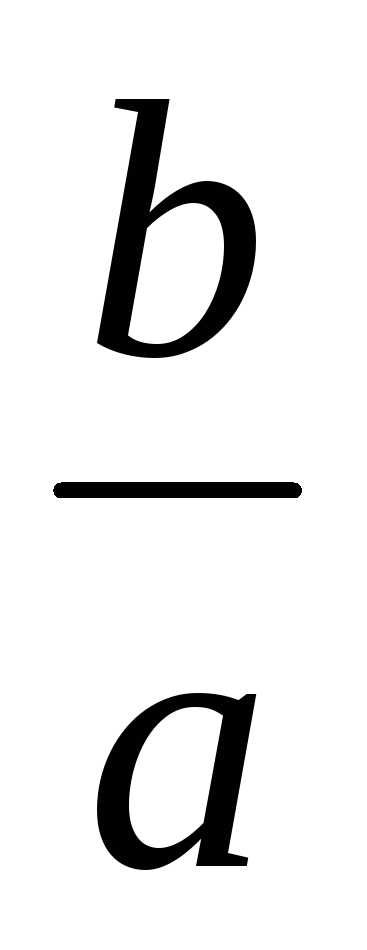 .
При
.
При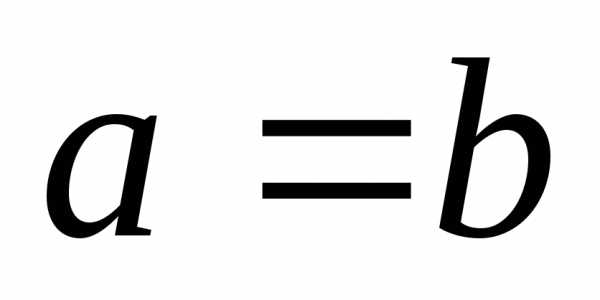 эллипс превращается в окружность.
Отклонение от окружности (сплющенность)
эллипса характеризуется параметром
эллипс превращается в окружность.
Отклонение от окружности (сплющенность)
эллипса характеризуется параметром ,
который называетсяэксцентриситетом
эллипса.
Для окружности
,
который называетсяэксцентриситетом
эллипса.
Для окружности 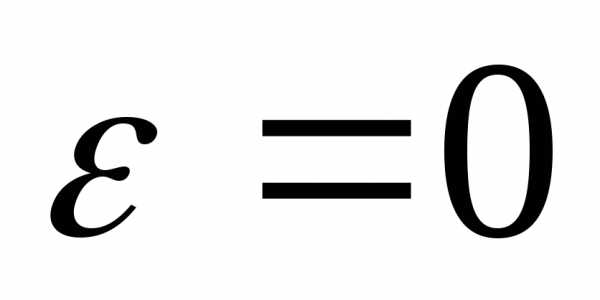 ,
для эллипса.
При
,
для эллипса.
При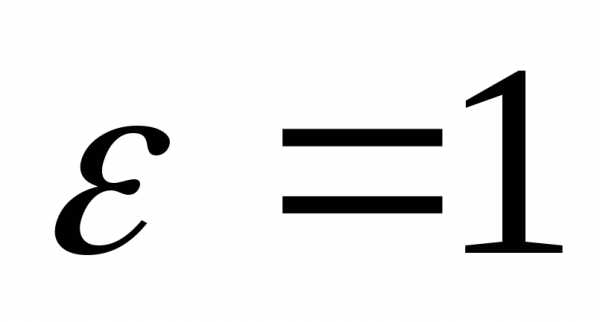 эллипс вырождается в отрезок (
эллипс вырождается в отрезок (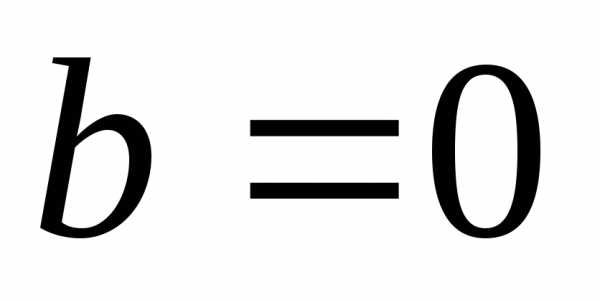 ).
Справедливость этих утверждений легко
увидеть из соотношения
).
Справедливость этих утверждений легко
увидеть из соотношения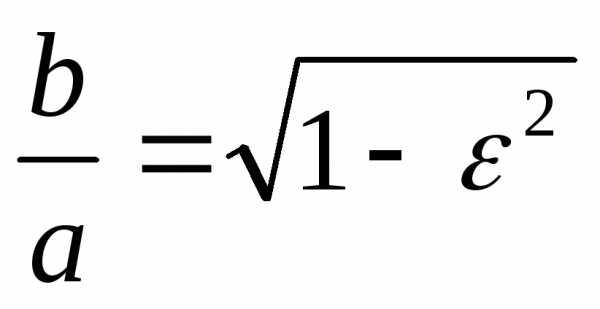 .
.
Рассмотрим точку  ,
лежащую на эллипсе. Длины
,
лежащую на эллипсе. Длины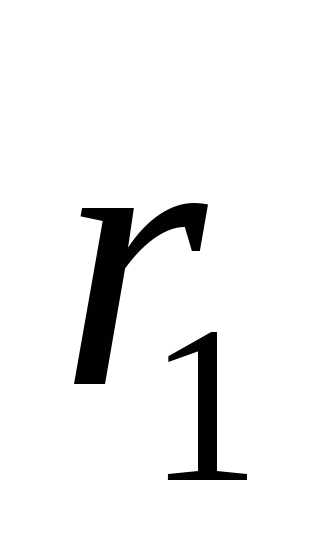 и
и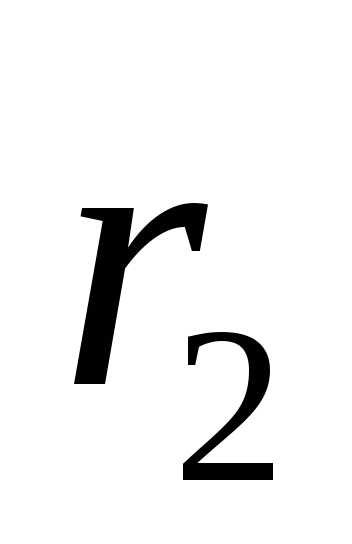 соответственно отрезков
соответственно отрезков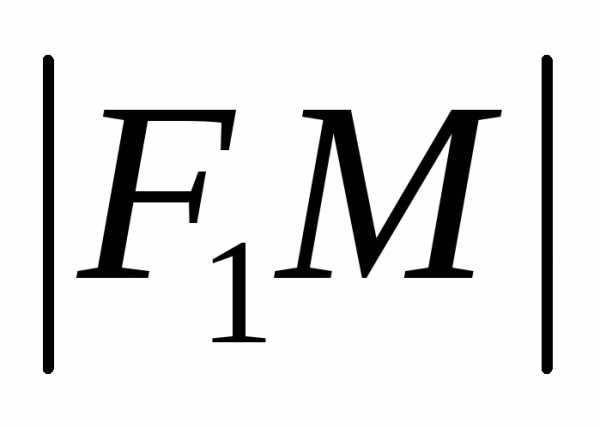 и
и называютсяфокальными
радиусами эллипса.
Заметим, что
.
Приведем соотношения, связывающие
фокальные радиусы с эксцентриситетом
эллипса:.
называютсяфокальными
радиусами эллипса.
Заметим, что
.
Приведем соотношения, связывающие
фокальные радиусы с эксцентриситетом
эллипса:.
Прямые 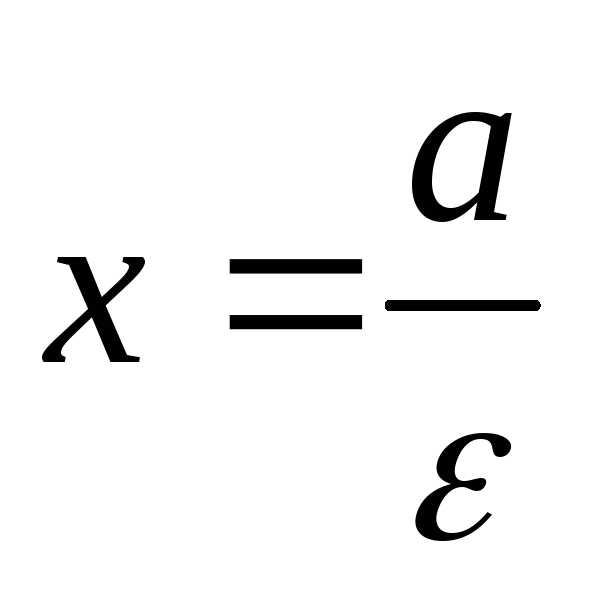 и
и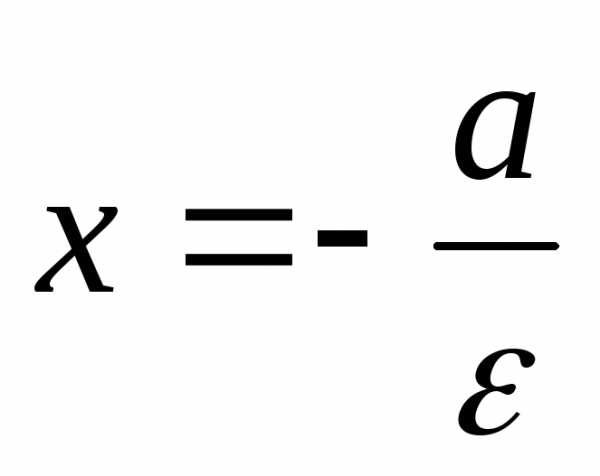 называютсядиректрисами
эллипса.
Рассмотрим правую директрису
называютсядиректрисами
эллипса.
Рассмотрим правую директрису 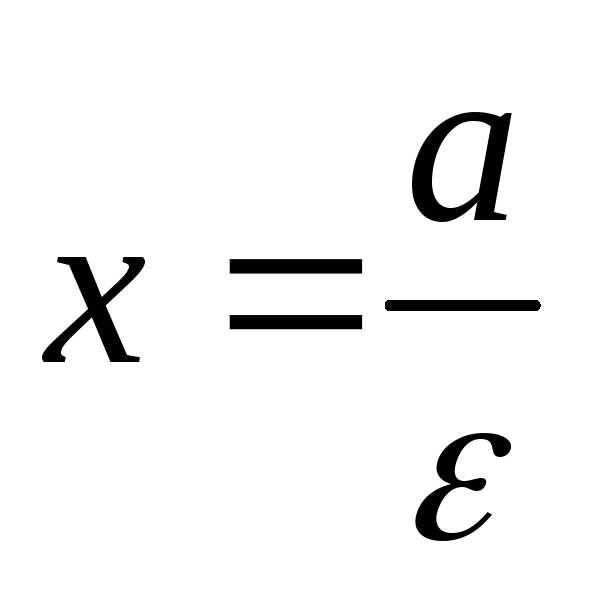 и правый же фокус эллипса
и правый же фокус эллипса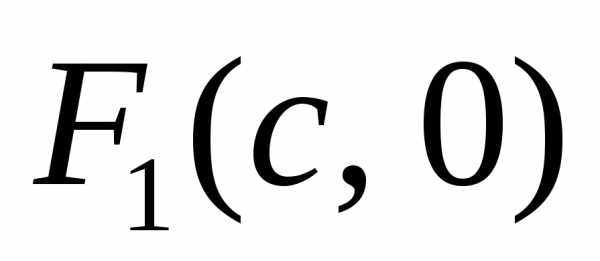 .
Точка
.
Точка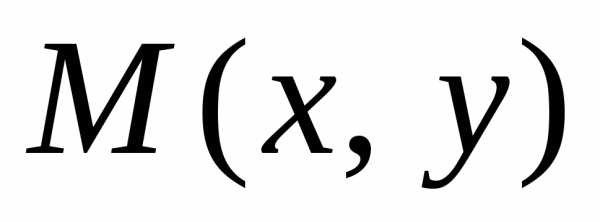 ,
лежащая на эллипсе, находится на
расстоянии
,
лежащая на эллипсе, находится на
расстоянии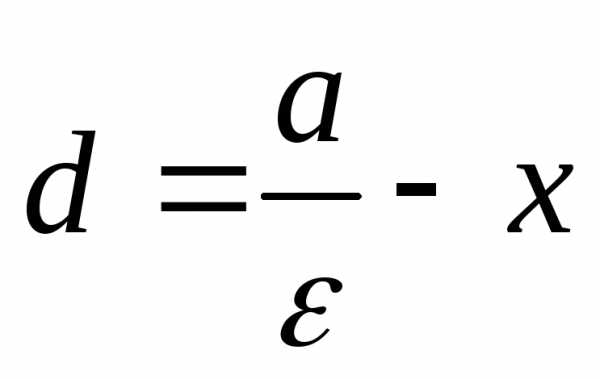 от рассматриваемой директрисы. Преобразуя
это равенство
от рассматриваемой директрисы. Преобразуя
это равенство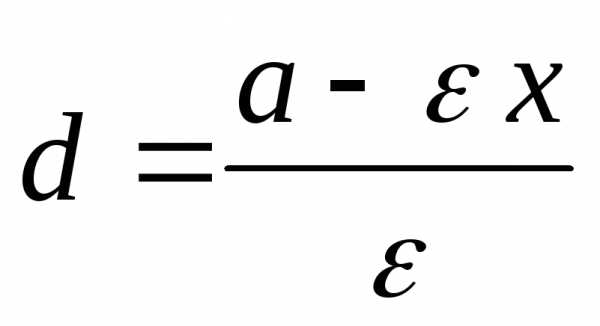 и замечая, что,
получим формулу
и замечая, что,
получим формулу (отношение фокального радиуса любой
точки эллипса к расстоянию между этой
точкой и соответствующей директрисой
есть величина постоянная, равная
эксцентриситету эллипса). Аналогичное
соотношение можно получить для другого
фокуса и другой директрисы.
(отношение фокального радиуса любой
точки эллипса к расстоянию между этой
точкой и соответствующей директрисой
есть величина постоянная, равная
эксцентриситету эллипса). Аналогичное
соотношение можно получить для другого
фокуса и другой директрисы.
Приведем
геометрическое определение эллипса.
Эллипсом называется множество всех
точек плоскости, сумма расстояний от
каждой из которых до двух данных точек
этой плоскости, называемых фокусами,
есть величина постоянная, большая, чем
расстояние между фокусами (, ).
).
Заметим, что если , то мы имеем мнимый эллипс.
Гипербола.
Вернемся к тому же каноническому виду кривой второго порядка
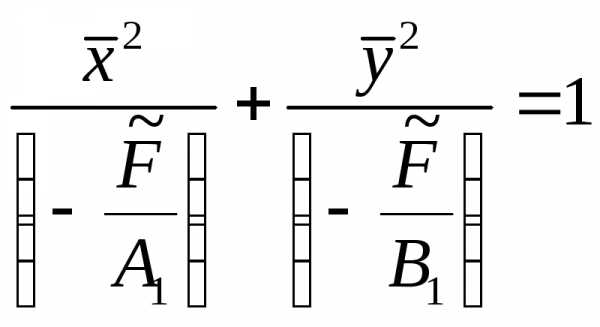 ,
,
но предположим, что знаменатели имеют разные знаки. Пусть для определенности .
Уравнение
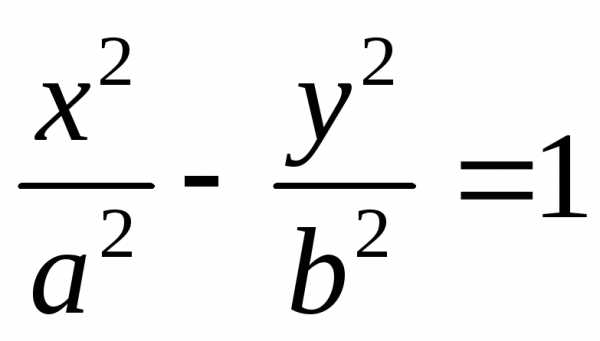
называется
каноническим уравнением гиперболы.
Точки пересечения гиперболы с координатной
осью 
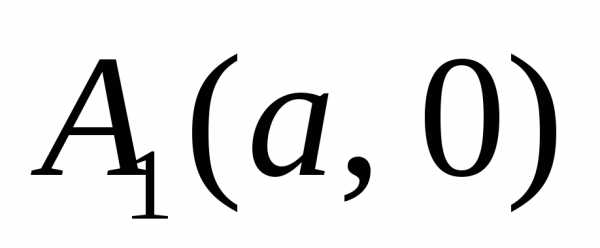 и
и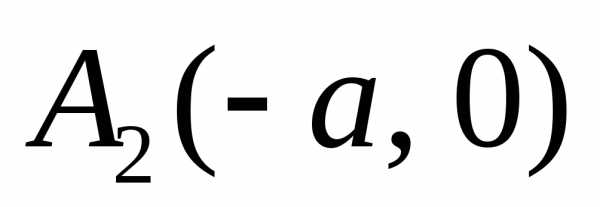 называютсявершинами
гиперболы,
а отрезок
называютсявершинами
гиперболы,
а отрезок 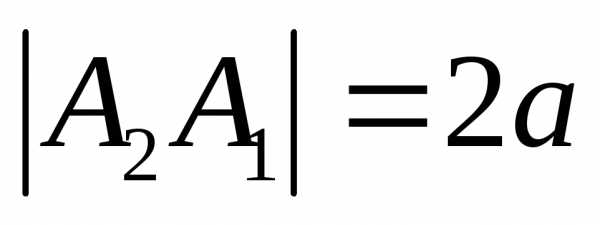 —действительной
осью гиперболы (
—действительной
осью гиперболы (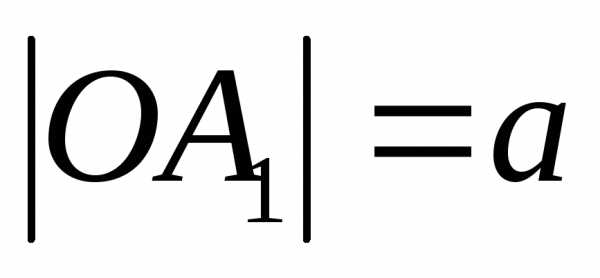 —действительной
полуосью гиперболы).
Точки
—действительной
полуосью гиперболы).
Точки  и
и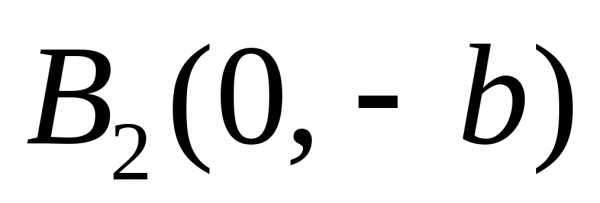 ,
лежащие на координатной оси
,
лежащие на координатной оси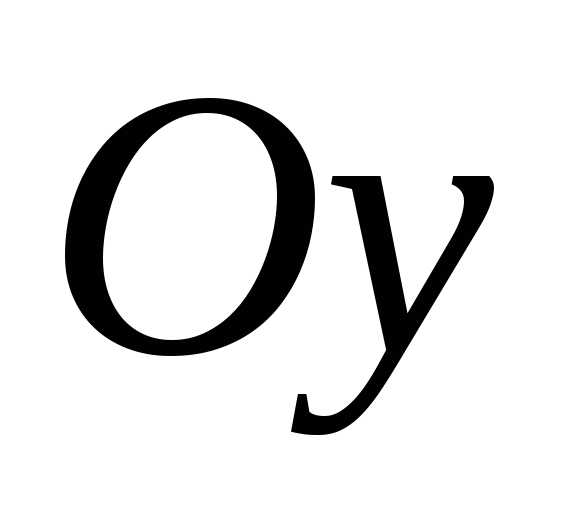 ,
можно назватьмнимыми вершинами
гиперболы,
а отрезок
,
можно назватьмнимыми вершинами
гиперболы,
а отрезок 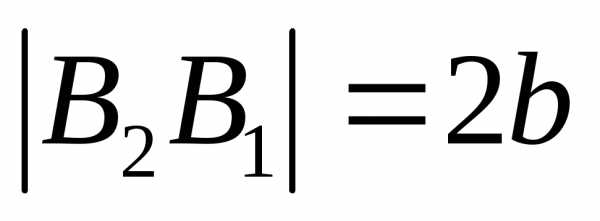 —мнимой
осью гиперболы (
—мнимой
осью гиперболы ( —мнимой
полуосью гиперболы).
Прямоугольник со сторонами
—мнимой
полуосью гиперболы).
Прямоугольник со сторонами 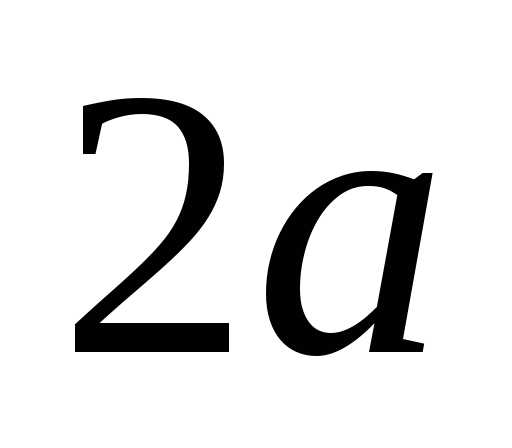 и
и ,
на которых лежат вершины гиперболы,
называютосновным
прямоугольником гиперболы. Прямые
,
на которых лежат вершины гиперболы,
называютосновным
прямоугольником гиперболы. Прямые 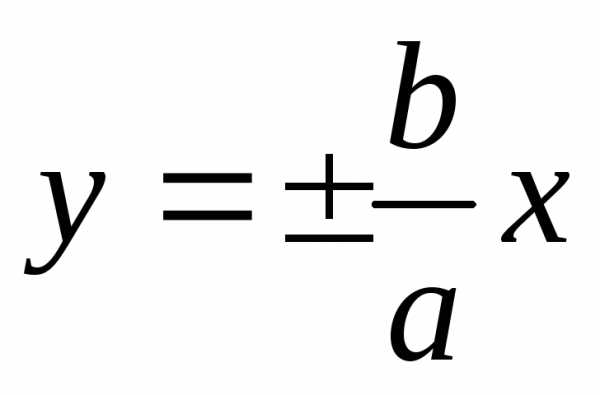 (частями которых являются диагонали
прямоугольника гиперболы) носят названиеасимптот
гиперболы.
Построение гиперболы удобно начинать
с построения прямоугольника и асимптот
гиперболы. Если
(частями которых являются диагонали
прямоугольника гиперболы) носят названиеасимптот
гиперболы.
Построение гиперболы удобно начинать
с построения прямоугольника и асимптот
гиперболы. Если 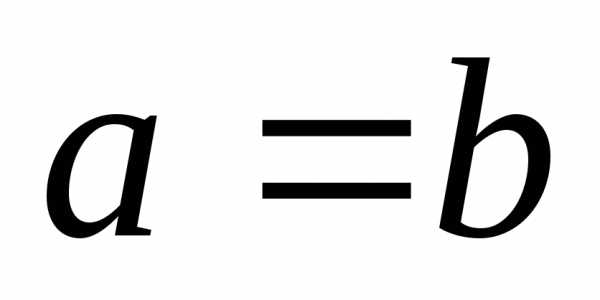 ,
то гипербола называетсяравносторонней,
ее уравнение имеет вид
.
Различаютправую
ветвь гиперболы (проходит
через вершину
,
то гипербола называетсяравносторонней,
ее уравнение имеет вид
.
Различаютправую
ветвь гиперболы (проходит
через вершину 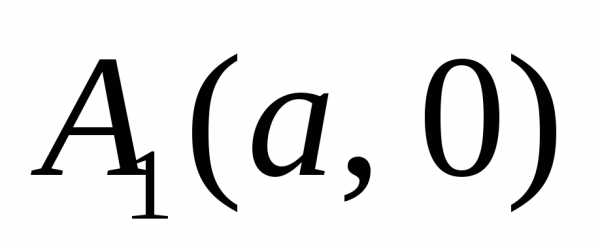 )
илевую
ветвь гиперболы (проходит
через вершину
)
илевую
ветвь гиперболы (проходит
через вершину 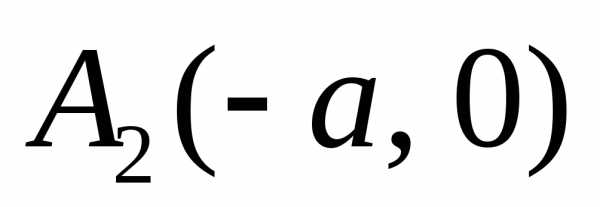 ).
).
Гипербола имеет
два фокуса ,
где.
Отношение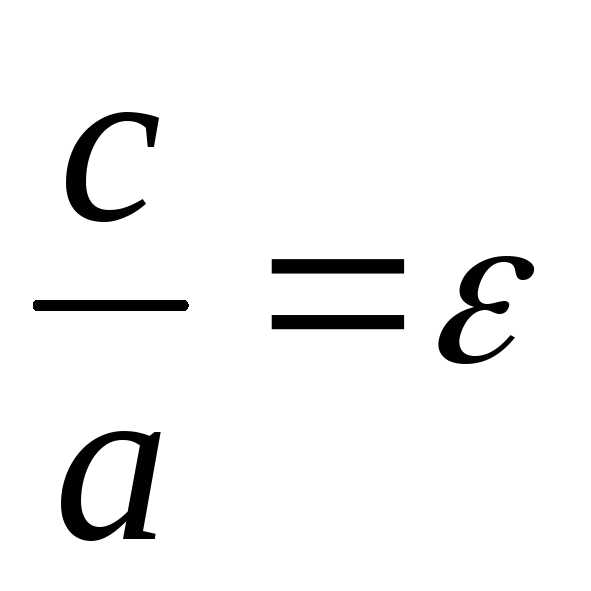 называетсяэксцентриситетом
гиперболы и
характеризует степень сжатости гиперболы.
Заметим, что
называетсяэксцентриситетом
гиперболы и
характеризует степень сжатости гиперболы.
Заметим, что 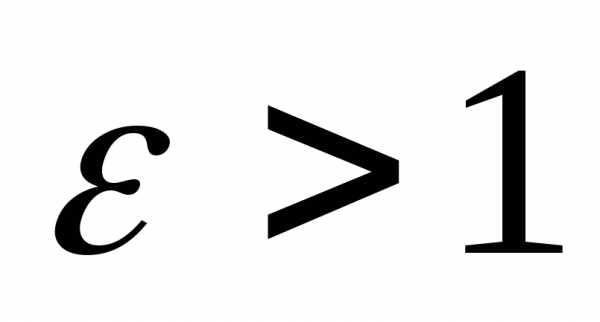 .
Отношение полуосей гиперболы является
функцией эксцентриситета
.
Отношение полуосей гиперболы является
функцией эксцентриситета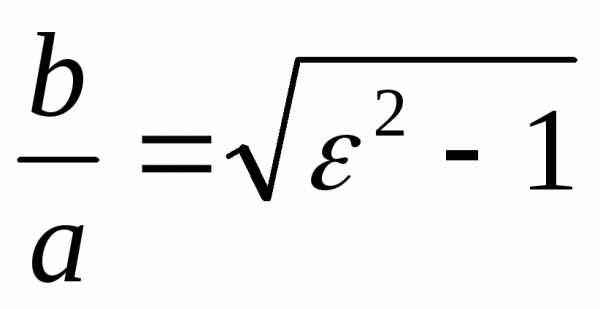 .
При
.
При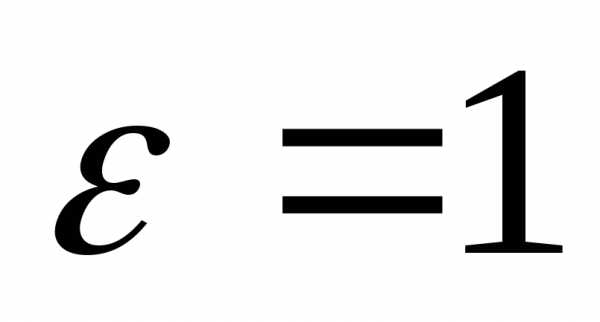 гипербола сжимается до двух лучей. При
росте эксцентриситета гипербола
«расправляется» и ее ветви стремятся
к прямым
гипербола сжимается до двух лучей. При
росте эксцентриситета гипербола
«расправляется» и ее ветви стремятся
к прямым .
.
Фокальные радиусы и для точек правой ветви гиперболы имеют вид и, а для левой -и.
Прямые 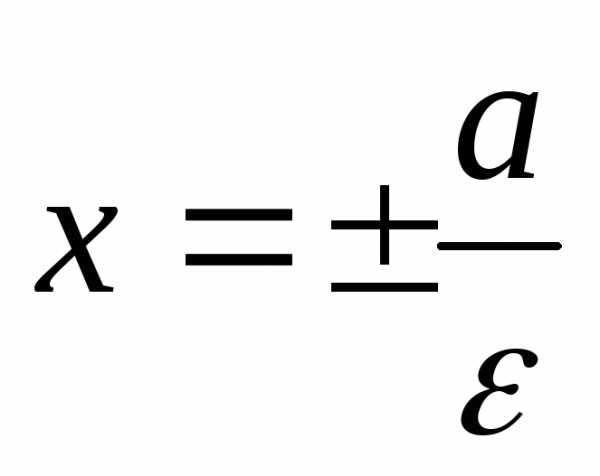 называютсядиректрисами
гиперболы.
Директрисы гиперболы имеют то же свойство
называютсядиректрисами
гиперболы.
Директрисы гиперболы имеют то же свойство 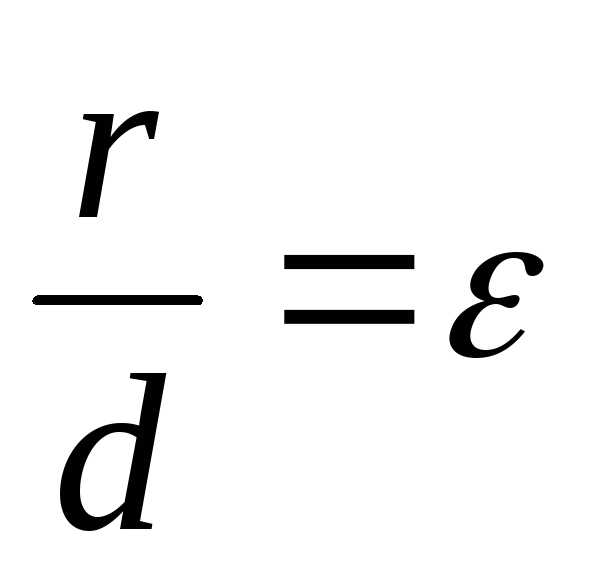 ,
что и директрисы эллипса.
,
что и директрисы эллипса.
Гиперболы 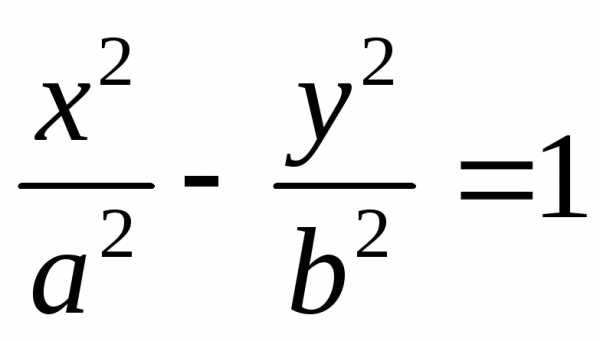 и
и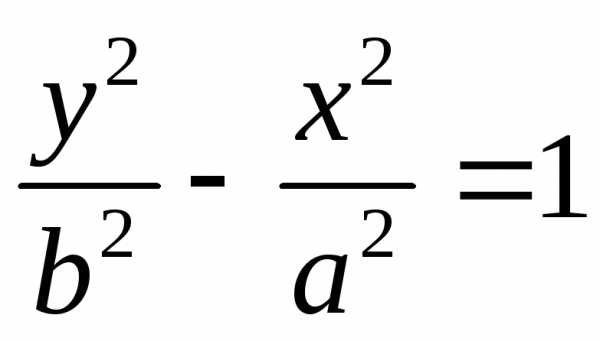 ,
имеющие разные действительные и мнимые
оси, но одинаковые асимптоты, называютсясопряженными гиперболами.
,
имеющие разные действительные и мнимые
оси, но одинаковые асимптоты, называютсясопряженными гиперболами.
Приведем
геометрическое определение гиперболы.
Гиперболой называется множество всех
точек плоскости, модуль разности
расстояний от каждой из которых до двух
данных точек этой плоскости, называемых
фокусами, есть величина постоянная,
меньшая, чем расстояние между фокусами
(, ).
).
Парабола.
Каноническим уравнением параболы называется уравнение вида
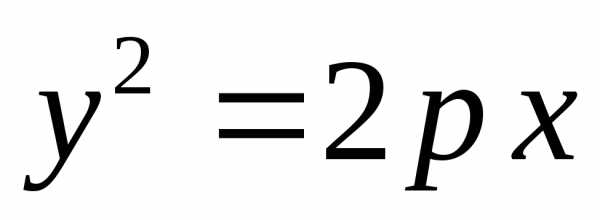 ,
,
где 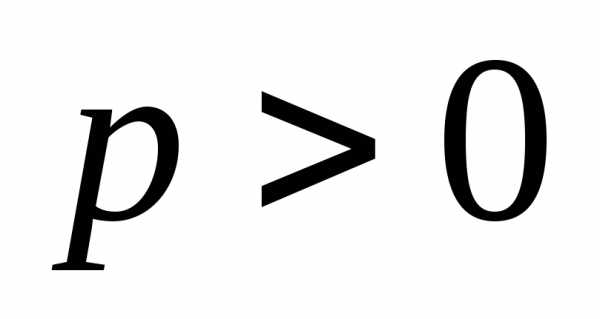 —параметр
параболы. Парабола
не является центральной кривой. Вершина
параболы находится в начале координат,
а фокус – в точке
—параметр
параболы. Парабола
не является центральной кривой. Вершина
параболы находится в начале координат,
а фокус – в точке 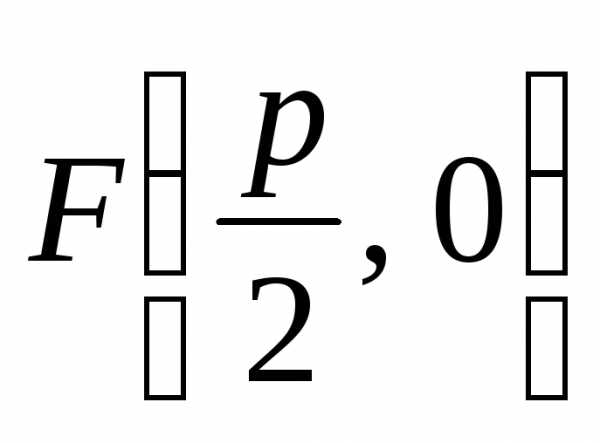 .
.
Уравнение директрисы
имеет вид 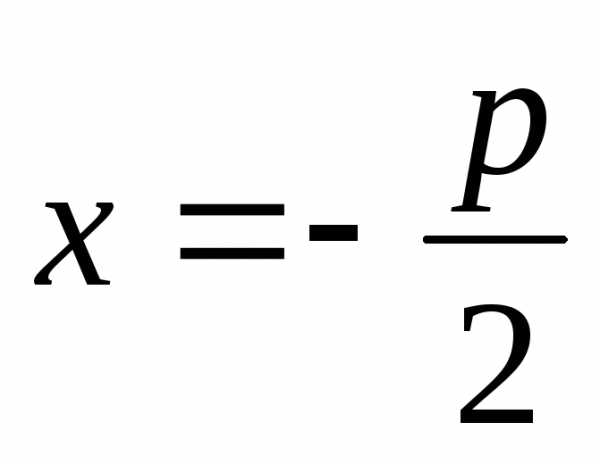 .
Ось
.
Ось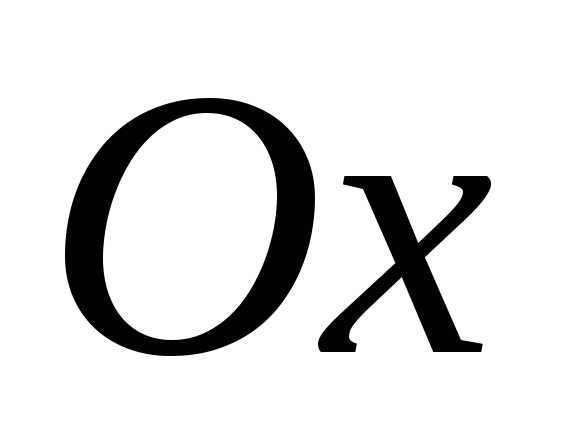 является осью симметрии параболы.
Фокальный радиус любой точки параболы
равен ее расстоянию до директрисы, т.е.
является осью симметрии параболы.
Фокальный радиус любой точки параболы
равен ее расстоянию до директрисы, т.е.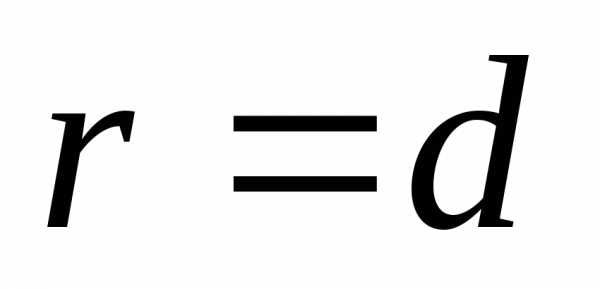 .
Об этом равенстве говорит геометрическое
определение параболы. Параболой
называется множество всех точек
плоскости, каждая из которых одинаково
удалена от данной точки, называемой
фокусом, и данной прямой, называемой
директрисой.
.
Об этом равенстве говорит геометрическое
определение параболы. Параболой
называется множество всех точек
плоскости, каждая из которых одинаково
удалена от данной точки, называемой
фокусом, и данной прямой, называемой
директрисой.
Возможны три других случая расположения параболы на плоскости: .
Замечание 1. При выводе канонического уравнения параболы следует первым сделать поворот координатных осей. Поскольку для параболы или, новые коэффициенты можно записать в виде:
.
Выбирая угол  из уравнения
из уравнения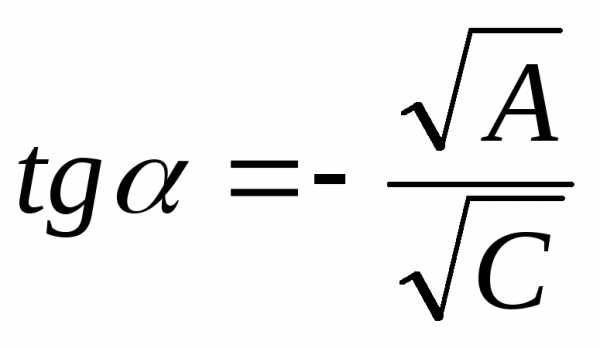 ,
можно обратить коэффициент
,
можно обратить коэффициент в нуль (если взять угол
в нуль (если взять угол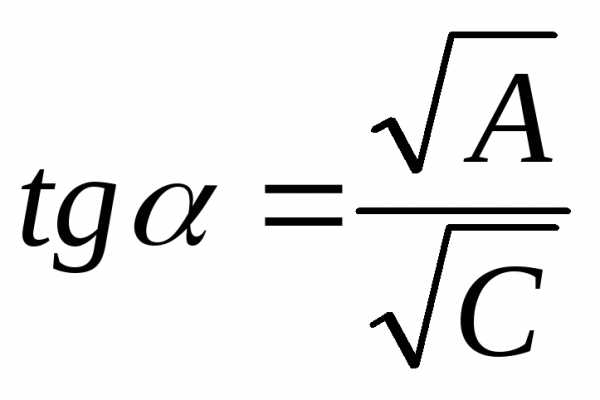 ,
то обратится в нуль
,
то обратится в нуль ).
В обоих случаях станет нулевым и
коэффициент
).
В обоих случаях станет нулевым и
коэффициент .
Далее совершая параллельный перенос
осей координат, можно найти координаты
вершины параболы и ее уравнение.
.
Далее совершая параллельный перенос
осей координат, можно найти координаты
вершины параболы и ее уравнение.
Замечание 2.
Если совершить поворот координатных
осей до их параллельного переноса с
выбором угла поворота, обращающего в
нуль коэффициент  ,
то общее уравнение кривой второго
порядка примет вид
,
то общее уравнение кривой второго
порядка примет вид
.
Это уравнение всегда определяет кривые:
1) окружность
при  ; 2) эллипс при
; 2) эллипс при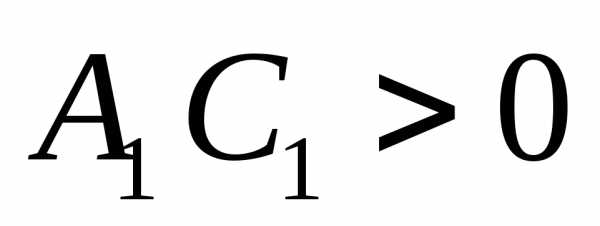 ;
;
3) гиперболу при 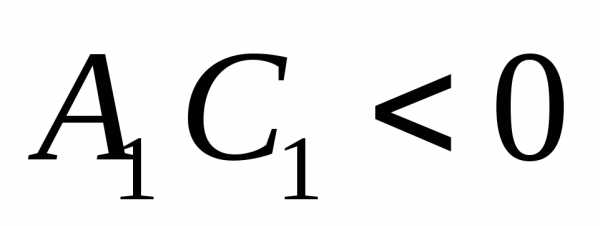 ;
;
4) параболу при 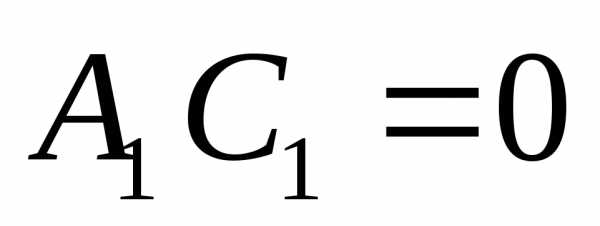 .
.
При этом возможны случаи вырождения:
окружности в точку или мнимую окружность;
эллипса в точку
 или в мнимый эллипс
или в мнимый эллипс ;
;гиперболы в пару пересекающихся прямых ;
параболы в пару параллельных прямых .
Замечание 3. Кривые второго порядка имеют следующие «оптические» свойства:
луч света, испущенный из одного фокуса эллипса и отраженный эллипсом, попадает в его второй фокус;
2) луч света, испущенный из одного фокуса гиперболы и отраженный гиперболой, пойдет по прямой линии, проходящей через второй фокус гиперболы;
3) луч света, испущенный из фокуса параболы и отраженный параболой, пойдет по прямой линии, параллельной оси симметрии параболы.
Замечание 4. Четыре кривые: окружность, эллипс, гиперболу и параболу называют коническими сечениями, поскольку эти кривые являются сечениями кругового конуса плоскостями.
ЗАДАЧИ
studfiles.net

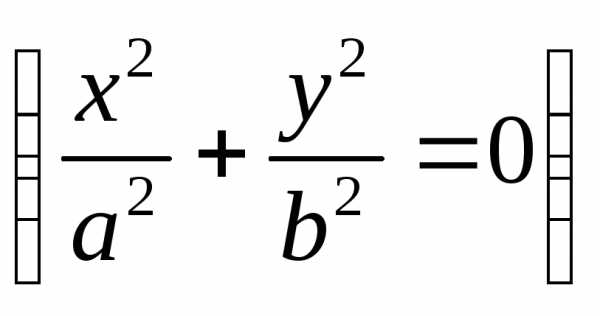 или в мнимый эллипс
или в мнимый эллипс ;
;