Формулы синуса косинуса и тангенса и котангенса – Синус, косинус и тангенс острого угла прямоугольного треугольника

Начальные сведения о синусе, косинусе, тангенсе и котангенсе

Определения

Синус острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к гипотенузе: \(\sin \alpha=\dfrac ac\)

 

Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к гипотенузе: \(\cos \alpha=\dfrac bc\)

 

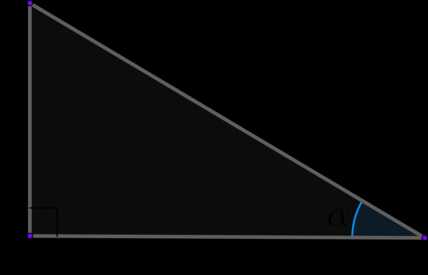
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к прилежащему катету: \(\mathrm{tg}\,\alpha=\dfrac ab\)

 

Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к противолежащему катету: \(\mathrm{ctg}\,\alpha=\dfrac ba\)

 

Утверждение

Синусы, косинусы, тангенсы и котангенсы равных углов соответственно равны.

 

Теорема

Из определений синуса, косинуса, тангенса и котангенса вытекают следующие формулы:

\[{\large{\begin{array}{|lcl|} \hline &&\\ \sin^2 \alpha+\cos^2 \alpha =1&\qquad& \mathrm{tg}\, \alpha \cdot \mathrm{ctg}\, \alpha =1\\ &&\\ \mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos \alpha}&&\mathrm{ctg}\, \alpha =\dfrac{\cos \alpha}{\sin \alpha}\\&&\\ \hline \end{array}}}\]

Утверждение

В прямоугольном треугольнике \(ABC\) с прямым углом \(\angle C\):

 

\(\sin \angle A=\cos \angle B\)

 

\(\mathrm{tg}\,\angle A=\mathrm{ctg}\,\angle B\)

 

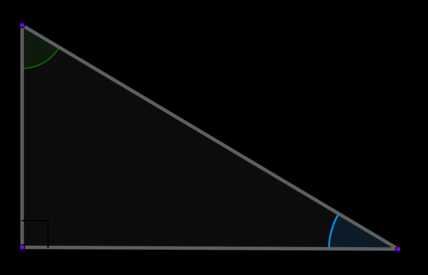
Доказательство

Утверждение следует непосредственно из определения синуса и косинуса острого угла в прямоугольном треугольнике.

 

Теорема

Для углов \(30^\circ, 45^\circ, 60^\circ\) верна следующая таблица:

\[{\large{\begin{array}{|c|c|c|c|} \hline & \phantom{000}30^\circ \phantom{000} & \phantom{000} 45^\circ \phantom{000} & \phantom{000} 60^\circ \phantom{000} \\[2pt] \hline &&&\\ \sin &\frac12&\frac{\sqrt2}2&\frac{\sqrt3}2\\[4pt] \cos &\frac{\sqrt3}2&\frac{\sqrt2}2&\frac12\\[4pt] \mathrm{tg} &\frac{\sqrt3}3&1&\sqrt3\\[4pt] \mathrm{ctg}&\sqrt3&1&\frac{\sqrt3}3\\[4pt] \hline \end{array}}}\]

Доказательство

1) Рассмотрим прямоугольный треугольник \(ABC\): \(\angle C=90^\circ, \angle A=60^\circ, \angle B=30^\circ\).

 

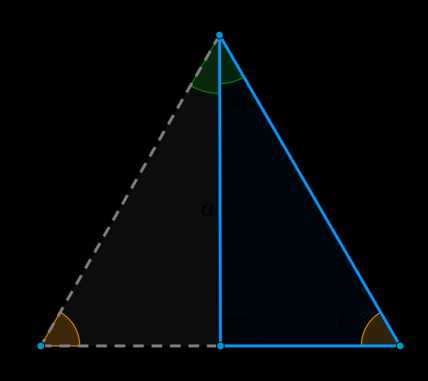
На стороне \(BC\) построим равный ему треугольник \(A’BC\), как показано на рисунке.

Полученный треугольник \(A’BA\) является правильным, т.к. \(\angle A’=\angle A=\angle A’BA=60^\circ\).
Следовательно, \(A’A=2b=AB=c\), откуда \(b=\dfrac12c\).

Тогда по теореме Пифагора \(a^2+b^2=c^2 \Rightarrow a=\dfrac{\sqrt3}2c\).

Теперь по определению \(\sin \angle A=\sin 60^\circ =\dfrac ac=\dfrac{\sqrt3}2\)

Т.к. по предыдущему утверждению \(\sin \angle A=\cos \angle B\), то \(\cos 30^\circ =\dfrac{\sqrt3}2\).

Т.к. \(\mathrm{tg}\,\alpha=\dfrac{\sin\alpha}{\cos\alpha}\), то \(\mathrm{tg}\,30^\circ=\mathrm{ctg}\,60^\circ=\dfrac{\sqrt3}3\), а \(\mathrm{tg}\,60^\circ=\mathrm{ctg}\,30^\circ=\sqrt3\).

 

2) Рассмотрим прямоугольный треугольник \(ABC\): \(\angle C=90^\circ, \angle A=45^\circ, \angle B=45^\circ\).

 

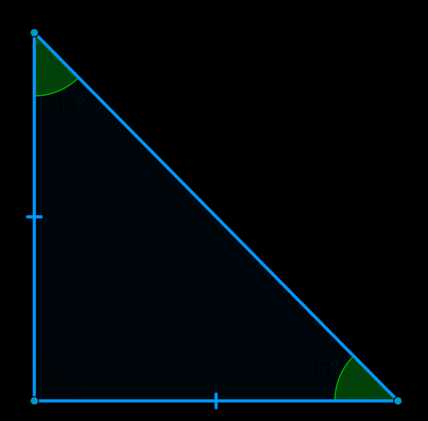
Этот треугольник равнобедренный, следовательно, \(BC=AC=a\).

Тогда по теореме Пифагора \(a^2+a^2=c^2 \Rightarrow a=\dfrac{\sqrt2}2c\).

Следовательно, \(\sin \angle A=\cos\angle A=\sin\angle B=\cos \angle B=\dfrac{\sqrt2}2\).

Из определения следует, что \(\mathrm{tg}\,45^\circ=\mathrm{ctg}\,45^\circ=1\).

 

Замечание

Для простоты запоминания таблицы можно записать ее в следующем виде:

\[{\large{\begin{array}{|c|c|c|c|} \hline & \phantom{000}30^\circ \phantom{000} & \phantom{000} 45^\circ \phantom{000} & \phantom{000} 60^\circ \phantom{000} \\[2pt] \hline &&&\\ \sin &\frac{\sqrt1}2&\frac{\sqrt2}2&\frac{\sqrt3}2\\[4pt] \cos &\frac{\sqrt3}2&\frac{\sqrt2}2&\frac{\sqrt1}2\\[4pt] \mathrm{tg} &\frac1{\sqrt3}&1&\sqrt3\\[4pt] \mathrm{ctg}&\sqrt3&1&\frac1{\sqrt3}\\[4pt] \hline \end{array}}}\]

То есть для синуса и косинуса число выглядит как \(\dfrac{\sqrt{\phantom{0}}}2\), где у синуса под корнем пишется \(1, 2, 3\), у косинуса – наоборот.

 

\[{\Large{\text{Синус, косинус, тангенс и котангенс тупого угла}}}\]

Теорема

Справедливы следующие формулы приведения:

\[\begin{aligned} \sin(180^\circ-\alpha)&=\sin\alpha\\ \cos(180^\circ-\alpha)&=-\cos\alpha\\ \mathrm{tg}\,(180^\circ-\alpha)&=-\mathrm{tg}\,\alpha\\ \mathrm{ctg}\,(180^\circ-\alpha)&=-\mathrm{ctg}\,\alpha \end{aligned}\]

Таким образом, если \(\alpha\) – острый угол, то с помощью этих формул можно найти синус, косинус, тангенс или котангенс тупого угла, смежного с \(\alpha\).

 

Пример

\(\sin 135^\circ=\sin(180^\circ-45^\circ)=\sin45^\circ=\dfrac{\sqrt2}2\)

shkolkovo.net

Свойства синуса, косинуса, тангенса и котангенса

В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.

Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α. Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и -α.

Yandex.RTB R-A-339285-1

Знаки тригонометрических функций по четвертям

Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?

Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A0(1, 0) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y). В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно. 

Для наглядности приведем иллюстрацию.

                                     

Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° — угол третьей четверти. Угол -45° —  это угол четвертой четверти.

При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.

Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.

Косинус — это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.

                                  

Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям. 

                                 

Важно помнить!

1. Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
2. Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
3. Тангенс угла 

zaochnik.com

Внеклассный урок — Синус, косинус, тангенс

Синус, косинус, тангенс, котангенс острого угла. Тригонометрические функции.

 

Синус острого угла α прямоугольного треугольника – это отношение противолежащего катета к гипотенузе.
Обозначается так: sin α.

Косинус острого угла α прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
Обозначается так: cos α.

Тангенс острого угла α – это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg α.

Котангенс острого угла α – это отношение прилежащего катета к противолежащему.
Обозначается так: ctg α.

 

Синус, косинус, тангенс и котангенс угла зависят только от величины угла.

 

Правила:

Катет b, противолежащий углу α, равен произведению гипотенузы на sin α: b = c · sin α Катет a, прилежащий к углу α, равен произведению гипотенузы на cos α: a = c · cos α Катет b, противоположный углу α, равен произведению второго катета на tg α: b = a · tg α Катет a, прилежащий к углу α, равен произведению второго катета на ctg α: a = b · ctg α

 

Основные тригонометрические тождества в прямоугольном треугольнике:

(α – острый угол, противолежащий катету b и прилежащий к катету a. Сторона с – гипотенуза. β – второй острый угол).

b                   sin α = —                               c	sin2 α + cos2 α = 1	α + β = 90˚
a                   cos α = —                                c	1            1 + tg2 α = ——                             cos2 α	cos α = sin β
b                   tg α = —                              a	1            1 + ctg2 α =  ——                                 sin2 α	sin α = cos β
a                   ctg α = —                                b	1            1             1  + ——  =  ——                     tg2 α      sin2 α	tg α = ctg β
sin α                   tg α = ——                             cos α

При возрастании острого угла sin α и tg α возрастают, а cos α убывает.

Для любого острого угла α:

sin (90° – α) = cos α

cos (90° – α) = sin α

Пример-пояснение:

Пусть в прямоугольном треугольнике АВС
АВ = 6,
ВС = 3,
угол А = 30º.

Выясним синус угла А и косинус угла В.

 

Решение.

1) Сначала находим величину угла В. Тут все просто: так как в прямоугольном треугольнике сумма острых углов равна 90º, то угол В = 60º:

В = 90º – 30º = 60º.

2) Вычислим sin A. Мы знаем, что синус равен отношению противолежащего катета к гипотенузе. Для угла А противолежащим катетом является сторона ВС. Итак:

               BC      3      1
sin A = —— = — = —
              AB      6       2

3) Теперь вычислим cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла В прилежащим катетом является все та же сторона ВС. Это значит, что нам снова надо разделить ВС на АВ – то есть совершить те же действия, что и при вычислении синуса угла А:

              BC       3      1
cos B = —— = — = —
              AB      6       2

 В итоге получается:
sin A = cos B = 1/2.

Или:

sin 30º = cos 60º = 1/2.

Из этого следует, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла – и наоборот. Именно это и означают наши две формулы:
sin (90° – α) = cos α
cos (90° – α) = sin α

Убедимся в этом еще раз:

1) Пусть α = 60º. Подставив значение α в формулу синуса, получим:
    sin (90º – 60º) = cos 60º.
    sin 30º = cos 60º.

2) Пусть α = 30º. Подставив значение α в формулу косинуса, получим:
    cos (90° – 30º) = sin 30º.
    cos 60° = sin 30º.

 

(Подробнее о тригонометрии — см.раздел Алгебра)

raal100.narod.ru

Свойства функций синуса, косинуса, тангенса и котангенса и их графики

Свойства функции y=sin(x) и ее график. 

График функции (синусоида)

Свойства функции

1.  Область определения: R (x — любое действительное число) т.е. 
2. Область значений:

3. Функция нечетная:

   (график симметричен относительно начала координат).

4. Функция периодическая с периодом 
5. Точки пересечения с осями координат:  
6. Промежутки знакопостоянства: 
7. Промежутки возрастания и убывания:   
   

 

Объяснение и обоснование

Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6)   промежутки знакопостоянства; 7) промежутки возрастания и убывания; 8) наибольшее и наименьшее значения функции.

Замечание

. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.

Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).

 

 Рис.1.

Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции — все действительные числа. Это можно записать так:

Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси орди­нат, и получить точку окружности, которая имеет рассматриваемую орди­нату. Таким образом, для функции область значений: . Это можно записать так:.Как видим,

наибольшее значение функции sin x равно единице. Это зна­чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при Наименьшее значение функции равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окруж­ности является точка B, то есть при.

Синус — нечетная функция: , поэтому ее график симметричен относительно начала координат.

Синус — периодическая функция с наименьшим положительным периодом : , таким образом, через промежутки длиной вид графика функции повторя­ется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной , а потом полученную линию парал­лельно перенести вправо и влево вдоль оси Ox на расстояние , где k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение , то есть график функции проходит через начало координат.

На оси значение . Поэтому необходимо найти такие значения , при которых , то есть ордината соответствующей точки единичной окруж­ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж­ности будут выбраны точки C или D, то есть при (см. рис. 1).

Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, при всех , а также, учитывая период, при всех .

Значения функции синус отрицательны (то есть ордината соответствую­щей точки единичной окружности отрицательна) в III и IV четвертях, поэто­му при .

Промежутки возрастания и убывания. Учитывая периодичность функции с периодом , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке . 

Если (рис. 3, а), то при увеличении аргумента  ордината соответствующей точки единичной окружности увеличивается (то есть , следовательно, на этом промежутке функция возрас­тает. Учитывая периодичность функции , делаем вывод, что она также возрастает на каждом из промежутков 

Рис.2                                                                            Рис.3

Если  (рис.3,б), то при увеличении аргумента  ордината соответствующей точки единичной окружности уменьшается (то есть ), таким образом, на этом промежутке функция убыва­ет. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков 

Проведенное исследование позволяет обоснованно построить график функции . Учитывая периодичность этой функции (с периодом ), достаточно сначала построить график на любом промежутке длиной , на­пример на промежутке . Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината соответствующей точки единичной окружности. На рисунке 4 показано построение графика функции на промежутке . Учитывая нечетность функции  (ее график симметричен относительно начала координат), для построения графика на промежутке отображаем полученную кривую симметрич­но относительно начала координат (рис. 5).

Рис.4

Рис.5

 

Поскольку мы построили график на промежутке длиной , то, учитывая периодичность синуса (с периодом ), повторяем вид графика на каждом промежутке длиной (то есть переносим параллельно график вдоль оси на , где k — целое число). Получаем график, который называется синусоидой .(Рис.6)

Рис.6

Замечание. Тригонометрические функции широко применяются в ма­тематике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой . Та­кие процессы называют гармоническими колебаниями

.

График функции можно получить из синусоиды сжатием или растяжением ее вдоль координатных осей и параллельным пере­носом вдоль оси . Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой , где А — амплитуда

колебания, — частота, — начальная фаза, — период колебания.

 

СВОЙСТВА ФУНКЦИИ И ЕЕ ГРАФИК

График функции  (косинусоида).

Свойства функции 

1. Область определения: R (x — любое действительное число).
2. Область значений: 

3. Функция четная:

   (график симметричен относительно оси ).

4. Функция периодическая с периодом  : 
5. Точки пересечения с осями координат 
6. Промежутки знакопостоянства: 
7. Промежутки возрастания и убывания: 
   

Объяснение и обоснование

Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции — все действительные числа. Это можно записать так:

.

Рис.7

Для точек единичной окружности абсциссы находятся в промежутке и принимают все значения от -1 до 1, поскольку через любую точку отрезка оси абсцисс (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции . Это можно записать так: .

Как видим, наибольшее значение функции равно единице. Это зна­чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при .

Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окруж­ности является точка B, то есть при .

Косинус — четная функция: , поэтому ее график симметричен относительно оси .

Косинус — периодическая функция с наименьшим положительным периодом : . Таким об­разом, через промежутки длиной вид графика функции повторяется.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение . На оси значение . Поэтому необходимо найти такие значения , при которых , то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при .

Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следова­тельно, 0 при , а также, учитывая период, при всех .

Значения функции косинус отрицательны (то есть абсцисса соответству­ющей точки единичной окружности отрицательна) во II и III четвертях, поэтому  при 

Промежутки возрастания и убывания. Учитывая периодичность функции , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .

Если (рис. 9, а), то при увеличении аргумента  абсцис­са соответствующей точки единичной окружности уменьшается (то есть ), следовательно, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков .

Если (рис. 9, б), то при увеличении аргумента  аб­сцисса соответствующей точки единичной окружности увеличивается (то есть ), таким образом, на этом промежутке функция  возрастает. Учитывая периодичность функции , делаем вывод, что она возрастает также на каждом из промежутков . 

Рис.8                                                                                                                          Рис.9

Проведенное исследование позволяет построить график функции аналогично тому, как был построен график функции . Но график функции можно также получить с помощью геометрических преобразований графика функции , используя формулу

Рис.10

Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки а также

абсциссы и ординаты этих точек. Так как , то при повороте

прямоугольника  около точки на угол — против часовой стрел­ки он перейдет в прямоугольник . Но тогда . Следовательно, 00.

Укажем также формулы, которые нам понадобятся далее:.

Тогда,

Таким образом, .

Учитывая, что , график функции можно полу­чить из графика функции его параллельным переносом вдоль оси на  (рис. 11). Полученный график называется косинусоидой (рис. 12).

Рис.11

Рис.12

График функции  (тангенсоида) 

Свойства функции :

1. Область определения: 

2. Область значений: 

3. Функция нечетная: 

4. Функция периодическая с периодом 

5. Точки пересечения с осями координат:   

6. Промежутки знакопостоянства:

7. Промежутки возрастания и убывания:

8. Наибольшего и наименьшего значений функция не имеет.

График функции  (котангенсоида)

Свойства функции :

1. Область определения:

2. Область значений:

3. Функция нечетная: 

4. Функция переодическая с периодом 
5. Точки пересечения с осями координат: 

6. Промежутки знакопостоянства: 

7. Промежутки возрастания и убывания:

 

8. Наибольшего и наименьшего значений функция не имеет.

 

ya-znau.ru

Основные тригонометрические тождества

Зависимость между синусом и косинусом

\sin^{2} \alpha+\cos^{2} \alpha=1

Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.

При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.

Нахождение тангенса и котангенса через синус и косинус

tg \alpha = \frac{\sin \alpha}{\cos \alpha},\enspace ctg \alpha=\frac{\cos \alpha}{\sin \alpha}

Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y является синус, а абсциссой x — косинус. Тогда тангенс будет равен отношению \frac{y}{x}=\frac{\sin \alpha}{\cos \alpha}, а отношение \frac{x}{y}=\frac{\cos \alpha}{\sin \alpha} — будет являться котангенсом.

Добавим, что только для таких углов \alpha, при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества tg \alpha = \frac{\sin \alpha}{\cos \alpha}, ctg \alpha=\frac{\cos \alpha}{\sin \alpha}.

Например: tg \alpha = \frac{\sin \alpha}{\cos \alpha} является справедливой для углов \alpha, которые отличны от \frac{\pi}{2}+\pi z, а ctg \alpha=\frac{\cos \alpha}{\sin \alpha} — для угла \alpha, отличного от \pi z, z — является целым числом.

Зависимость между тангенсом и котангенсом

tg \alpha \cdot ctg \alpha=1

Данное тождество справедливо только для таких углов \alpha, которые отличны от \frac{\pi}{2} z. Иначе или котангенс или тангенс не будут определены.

Опираясь на вышеизложенные пункты, получаем, что tg \alpha = \frac{y}{x}, а ctg \alpha=\frac{x}{y}. Отсюда следует, что tg \alpha \cdot ctg \alpha = \frac{y}{x} \cdot \frac{x}{y}=1. Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.

Зависимости между тангенсом и косинусом, котангенсом и синусом

tg^{2} \alpha + 1=\frac{1}{\cos^{2} \alpha} — сумма квадрата тангенса угла \alpha и 1, равна обратному квадрату косинуса этого угла. Данное тождество справедливо для всех \alpha, отличных от \frac{\pi}{2}+ \pi z.

1+ctg^{2} \alpha=\frac{1}{\sin^{2}\alpha} — сумма 1 и квадрат котангенса угла \alpha, равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого \alpha, отличного от \pi z.

Примеры с решениями задач на использование тригонометрических тождеств

Пример 1

Найдите \sin \alpha и tg \alpha, если \cos \alpha=-\frac12 и \frac{\pi}{2} < \alpha < \pi;

Показать решение

Решение

Функции \sin \alpha и \cos \alpha связывает формула \sin^{2}\alpha + \cos^{2} \alpha = 1. Подставив в эту формулу \cos \alpha = -\frac12, получим:

\sin^{2}\alpha + \left (-\frac12 \right )^2 = 1

Это уравнение имеет 2 решения:

\sin \alpha = \pm \sqrt{1-\frac14} = \pm \frac{\sqrt 3}{2}

По условию \frac{\pi}{2} < \alpha < \pi. Во второй четверти синус положителен, поэтому \sin \alpha = \frac{\sqrt 3}{2}.

Для того, чтобы найти tg \alpha , воспользуемся формулой tg \alpha = \frac{\sin \alpha}{\cos \alpha}. Соответствующие величины нам известны.

tg \alpha = \frac{\sqrt 3}{2} : \frac12 = \sqrt 3

Пример 2

Найдите \cos \alpha и ctg \alpha, если \sin \alpha=\frac{\sqrt3}{2} и \frac{\pi}{2} < \alpha < \pi.

Показать решение

Решение

Подставив в формулу \sin^{2}\alpha + \cos^{2} \alpha = 1 данное по условию число \sin \alpha=\frac{\sqrt3}{2}, получаем \left (\frac{\sqrt3}{2}\right )^{2} + \cos^{2} \alpha = 1. Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14.

По условию \frac{\pi}{2} < \alpha < \pi. Во второй четверти косинус отрицателен, поэтому \cos \alpha = -\sqrt\frac14=-\frac12.

Для того, чтобы найти ctg \alpha , воспользуемся формулой ctg \alpha = \frac{\cos \alpha}{\sin \alpha}. Соответствующие величины нам известны.

ctg \alpha = -\frac12 : \frac{\sqrt3}{2} = -\frac{1}{\sqrt 3}.

academyege.ru

Синус, косинус, тангенс, котангенс

В курсе геометрии 8 класса, мы с вами уже знакомились с понятиями синуса, косинуса, тангенса и котангенса для углов прямоугольного треугольника. Давайте вспомним их.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

 

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

 

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

;  

 

Еще мы с вами учили таблицу синусов, косинусов для углов в 30, 45 и 60 градусов. Давайте вспомним ее.

Сегодня на уроке мы познакомимся с понятиями синуса, косинуса, тангенса и котангенса произвольного угла из промежутка от 0 до 180º.

Построим в прямоугольной системе координат полуокружность радиус которой равен 1 так, чтобы центр этой полуокружности совпадал с началом координат.

Такую полуокружность мы назовем единичной полуокружностью. Из точки О давайте проведем произвольный луч h. Этот луч пересекает полуокружность с точке М (0;0). Угол между лучом h и положительным направлением оси Ox обозначим за α. Если луч h совпадает с положительным направлением оси Ox, то угол α равен 90º. Если луч h совпадает с осью Oy, то угол α= 90º. Если луч h совпадает с отрицательным направлением оси Ox, то угол α= 180º. Опустим из точки М перпендикуляр на ось Ox и рассмотрим прямоугольный треугольник ОМD.

Запишем элементы этого треугольника. Поскольку радиус полуокружности равен 1, значит, ОM=1. Так как координаты точки М равны x и y, то, очевидно, что МD=y, а ОD=x. Тогда , . Мы получили, что синус острого угла равен ординате точки М, а косинус угла α равен абсциссе точки М. По этим же формулам вычисляются синус и косинус для углов в 90º и 180º.

Для любого угла  синусом угла  называется ордината  точки , а косинусом угла  абсцисса  точки  

Поскольку речь у нас идет о единичной полуокружности, то ордината точки может изменятся от 0 до 1, значит, и синус угла α может принимать значения от 0 до 1. Абсцисса точки М может изменятся от -1 до 1, то есть и косинус угла α из промежутка от 0 до 180º может изменятся от -1 до 1.

Задача. Может ли:

а) абсцисса точки единичной полуокружности быть равна ?

б) ордината точки единичной полуокружности быть равна ?

Решение.

а) Поскольку полуокружность единичная, значит абсцисса точки должны принадлежать промежутку от -1 до 1, то есть абсцисса точки может быть равна , но не может быть равна 4 и 5.

б) Поскольку полуокружность располагается выше оси Ox, то ординаты точек могут быть только из промежутка от 0 до 1, то есть ордината точки может быть равна но не может быть равна .

Дополним известную нам таблицу синусов косинусов:

Для определения sin 0º и cos 0º давайте рассмотрим луч ОА. На единичной полуокружности точка А имеет координаты (1;0), значит , а .

Найдем теперь значение sin90 º и cos 90º. Этот угол задается лучом ОB. Координаты точки B равны (0;1), значит, , .

Проводя аналогичные рассуждения, получим , .

Задача. Определить координаты точки , если:

а) ;   б) ;   в) .

Решение.

а)

 

 

б)

 

 

в)

 

 

Ответ: ; ; .

Решим теперь обратную задачу.

Задача. Определить , , если:

а) ;   б) ;   в) .

Решение.

а)

 

б)

 

в)

 

Тангенсом острого угла мы называли отношение
. Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен  90º, то его cos 90º=0, а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому для угла в 90º тангенс не существует. Таким образом, мы немного уточнили определение тангенса.

Тангенсом угла , называется .

Котангенсом острого угла мы называли отношение . Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен 0º или 180º, то sin равен 0, а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому
,  –  не существует. Таким образом, мы немного уточнили определение котангенса.

Котангенсом угла , называется .

Задача. Определить , , если:

а) ;   б) ;   в) ;   г) ;   д) .

Решение.

 

а)

 

 

б)

 

 

в)

 

 

г)

 

 

д)

 

    

Давайте занесем полученные данные в таблицу и составим таблицу синусов, косинусов, тангенсов и котангенсов для углов 0º, 30º, 45º, 60º, 90º, 180º.

Подведем итоги урока. Сегодня на уроке мы определили, что Для любого угла  синусом угла  называется ордината  точки , а косинусом угла  абсцисса  точки  

Тангенсом угла ,  называется .

Котангенсом угла , называется .

Также мы дополнили известную нам таблицу значений синуса, косинуса и тангенсов для некоторых углов.

 

videouroki.net

Свойства функции синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса. Графики. Тест

Тестирование онлайн

• Функция синуса, косинуса

• Функция тангенса, котангенса

Функция синуса

На рисунке показано построение графика синуса на отрезе .

Рассмотрим основные свойства функции y=sinx:

1) Область определения функции — множество всех действительных чисел

2) Множеством значений функции является промежуток

3) Функция является нечетной, график симметричен относительно начала координат (0;0).

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) График функции пересекает ось Оy в точке (0; 0).

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция возрастает на промежутках

10) Функция убывает на промежутках

11) Точки минимума:

12) Точки максимума:

13) Графиком функции является синусоида

Функция косинуса

График косинуса получается из графика синуса с помощью параллельного переноса на расстояние влево.

Основные свойства функции y=cosx:

1) Область определения функции — множество всех действительных чисел

2) Множеством значений функции является промежуток

3) Функция является четной, график симметричен относительно оси Оу.

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) График функции пересекает ось Оy в точке (0; 1).

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция возрастает на промежутках

10) Функция убывает на промежутках

11) Точки минимума:

12) Точки максимума:

13) Графиком функции является косинусоида

Функция тангенса

Основные свойства функции y=tgx:

1) Область определения функции:

2) Множеством значений функции:

3) Функция является нечетной, график симметричен относительно начала координат (0;0).

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) График функции пересекает ось Оy в точке (0; 0).

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция возрастает на промежутках

10) Промежутки убывания отсутствуют.

11) Точек минимума нет.

12) Точек максимума нет.

13) Графиком функции является тангенсоида:

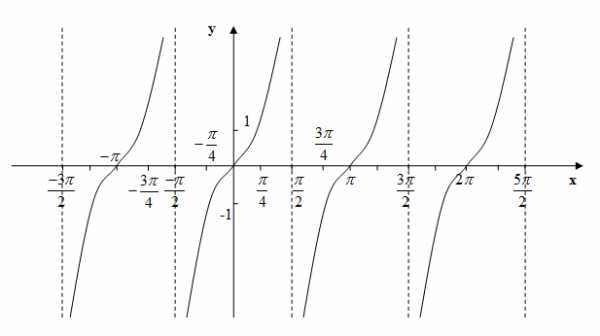
Функция котангенса

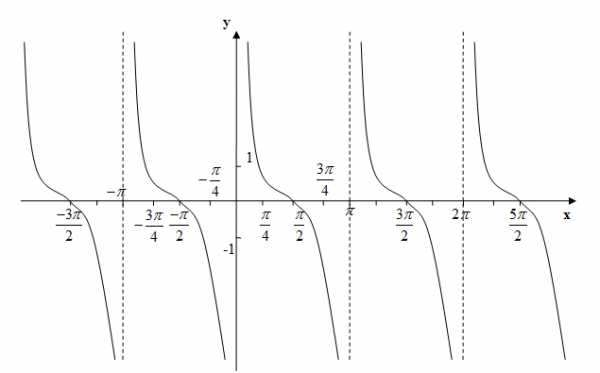
Основные свойства функции y=сtgx:

1) Область определения функции:

2) Множеством значений функции:

3) Функция является нечетной, график симметричен относительно начала координат (0;0).

4) Функция периодическая. Наименьший положительный период равен

5) График функции пересекает ось Ох (нули функции) в точках

6) Функции не пересекает ось Оy.

7) Функция принимает положительные значения на промежутках

8) Функция принимает отрицательные значения на промежутках

9) Функция не имеет промежутков возрастания.

10) Промежутки убывания:

11) Точек минимума нет.

12) Точек максимума нет.

13) Графиком функции является котангенсоида:

Период функции

1) Если T — основной период функции y=f(x), то число является основным периодом функции y=f(ax), где a — любое положительное число.

2) Если периодические функции y=f(x) и y=g(x) имеют один и тот же период T, то их сумма, разность и произведение тоже будет иметь период T.

3) Если периодические функции y=f(x) и y=g(x) имеют соизмеримые периоды T₁ и T₂, то они имеют общий период.

4) Период сложной функции y=g(f(x)) совпадает с периодом функции y=f(x).

fizmat.by

No related posts.