Функции параболы – Парабола, квадратичная функция. Как решаются квадратные уравнения?

Тестирование онлайн

• Квадратичная функция

Определение. График

Квадратичной (квадратной) функцией называется функция вида

где a, b, с — числа.

Графиком квадратичной функции является парабола.

Парабола имеет вершину, ось, проведенная через вершину и параллельная оси Оу, делит параболу на две симметричные части. Вершиной параболы называется точка

Если коэффициент а>0, то ветви параболы направлены вверх, если a, то ветви параболы направлены вниз.

Свойства квадратичной функции y=x²

1) Областью определения функции является множество всех действительных чисел, т.е.

2) Множеством значений функции является промежуток

3) Значение функции y=0 является наименьшим, а наибольшего значения функция не имеет.

4) Функция является четной, график симметричен относительно оси Оу.

5) Функция непериодическая.

6)Парабола имеет с осями координат единственную общую точку (0;0) — начало координат.

7) Значение аргумента x=0 является нулем функции.

8) На промежутке функция убывающая, а на промежутке — возрастающая.

9) Функция принимает положительные значения на множестве , т.е. все точки параболы, кроме начала координат.

Преобразование параболы

Функция y=x² — частный случай квадратичной функции.

Квадратичную функцию всегда можно привести у виду , а затем построить параболу с помощью ее геометрических преобразований.

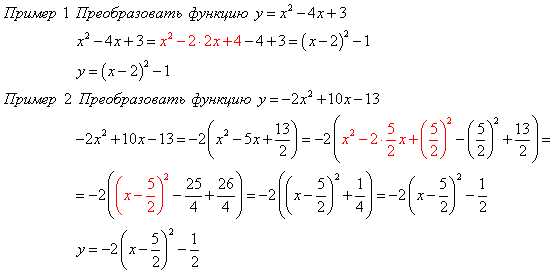
Для построения параболы необходимо:

1) Найти координаты вершины

2) Построить ось симметрии, проанализировать куда направлены ветви параболы

3) Найти точки пересечения параболы с осью Ox (нули), если они есть, решив уравнение

4) Найти точку пересечения с осью Оу, решив уравнение

Чтение графиков функций. Смещение параболы. Егэ решение.

Смещение по горизонтали параболы

Если мы прибаляем к функции \(y=x^2\) число 3 \(y=(x+3)^2\), то график смещается по оси \(0X\) на \(-3\) еденицы, если вычитаем число \(2\)  \(y=(x-2)^2\), то график сместится \(+2\)  относительно  \(0X\):

Если мы отнимем от \(y=(x+3)^2\) 3 , то \(y=(x+3)^2-3\), то график начнет смещаться уже по вертикали вниз на \(3\) единицы, а именно по оси \(0Y\):

Задача 

Здесь нам пригодятся знания нахождения формулы вершины параболы  \(x=\frac{ — b}{2a}\), она не такая  и тяжелая, так что запомните ее. Если мы видим на графике параболу, то сразу представляем уранение вида \(y = ax^2 + bx + c \). По графику выше определяем вершина равна -1:

\(\frac{-b}{2a}=-1\)  \(—>\) \(b=2a\)

Как видно из рисунка парабола пересекает \(OY\) в точке 3, поэтому \(с=3\)  и \(y = ax^2 + 2ax + 3\), так как \(b=2a\). Находим любую точку проходящую через параболу, возьмем вершину параболы \((-1; 2)\) и подставим в уравнение:

\(2 = (-1)x^2 + 2(-1)x + 3\) \(—>\) \(2=-a+3\) \(—>\) \(a=1\)

Ответ: 2)1.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

myalfaschool.ru

Свойства параболы, с примерами

Парабола является графиком квадратичной функции, которая задается уравнением

и обладает следующими свойствами:

– если коэффициент и вершина параболы имеет координаты , то

Область определения – .

Область значений – .

Функция убывает при , возрастает при .

Функция непрерывна и выпукла вниз.

Минимум функции .

– если коэффициент a, а вершина параболы имеет координаты , то

Область определения – .

Область значений – .

Функция убывает при , возрастает при .

Функция непрерывна и выпукла вверх.

Максимум функции .

Примеры решения задач

ru.solverbook.com

Квадратичная функция

Квадратичная функция — функция вида:

f(x)=ax²+bx+c

или

y(x)=ax²+bx+c

Где  a≠0.

В уравнении квадратичной функции:

a –старший коэффициент

b – второй коэффициент

с  свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции

y(x)=x²

или

f(x)=x²

.

Имеет вид и строится по «базовым точкам»:

a>0

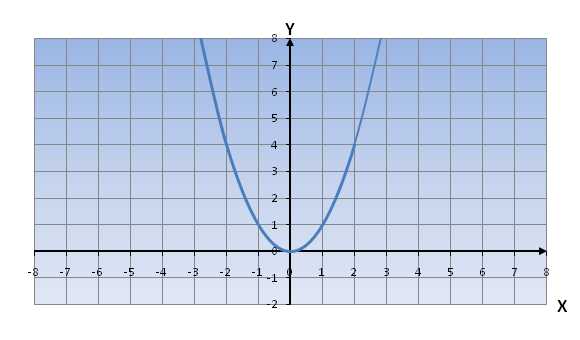
Парабола состоит из 2 частей: одна находится в I четверти, где значения X и Y положительные, а вторая часть – во II четверти, где значения X отрицательные, а значения Y  положительные.

y(x)>0, при x∈(-∞;0)∪(0;+∞)

Если двигаться по одной ветви параболы от -∞ к 0

Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как y(x)=x² при любых значениях остальных коэффициентов.

График функции

y(x)=-x² 

Имеет вид и строится по «базовым точкам»:

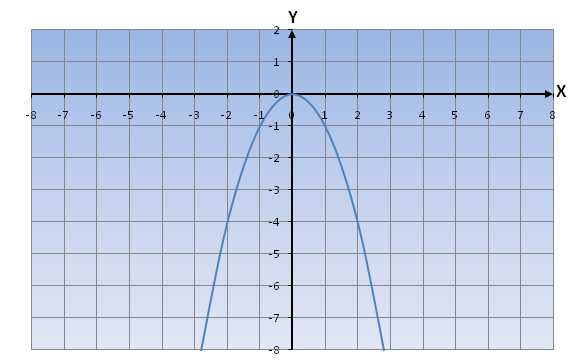
Парабола состоит из 2 частей: одна находится в III четверти, где значения X и Y  отрицательные, а вторая часть – в IV четверти, где значения X  положительные, а значения Y отрицательные.

y(x)<0, при x∈(-∞;0)∪(0;+∞)

Если двигаться по одной ветви параболы от  -∞ к 0

Свойства функции y(x)=x²:

1)    Область определения функции:

D(f)=(-∞;0)∪(0;+∞). 

2)Область значения функции:

Если a<0

E(f)=(-∞;0].

Если a>0

E(f)=[0;+∞).

3)Наибольшее и наименьшее значение функции:

Если a<0, то Y_наиб=0,Y_наим нет.

Если a>0, тоY_наим=0, Y_наиб нет.

4)Y(x)=x²— четная функция(т.к.f(-x)=x²=(-x)²=f(x) ).

График симметричен относительно оси oY  .

5) Ограниченность функции:

Если a>0, функция ограничена снизу.

Если a<0, функция ограничена сверху.

6) Функция пересекает оси oX и oY в точке (0;0)

Перемещение параболы y(x)=x²

Если добавить константу d (где d любое число), в качестве слагаемого к X, то произойдет перемещение параболыпо оси  (вместе с вертикальной асимптотой).

В таком случае уравнением функции станет:

y(x)=(x±d)²

Если d>0 (y(x)=(x+d)²), то график функции передвигается по оси oX  влево.

Для примера возьмем уравнение y=(x+2)²

Если d<0 (y(x)=(x-d)²), то график функции передвигается по оси oX 

Для примера возьмем уравнение y=(x-2)²

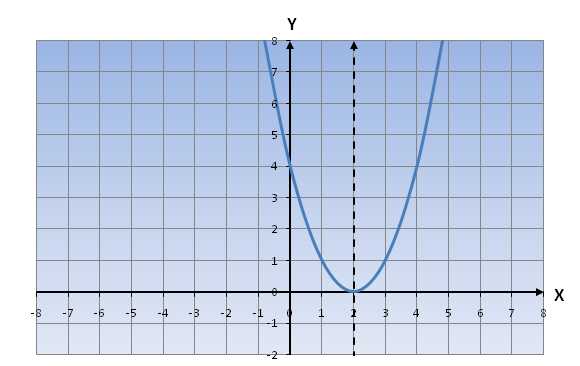
Если добавить константу c(где cлюбое число) к X² в качестве слагаемого, то произойдет перемещение параболы по оси oY (вместе с горизонтальной асимптотой)

В таком случае уравнением функции станет:

 y(x)=(x)²±c

 Если  c>0 (y(x)=(x)²+c), то график функции передвигается по оси oY вверх.

Для примера возьмем уравнение y=(x)²+2

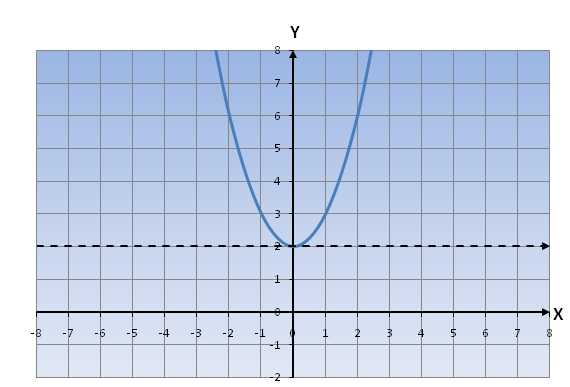
Если  c<0 (y(x)=(x)²-c), то график функции передвигается по оси oY вниз.

Для примера возьмем уравнение y=(x)²-3

Дискриминант и нахождение корней

y=ax²+bx+c

ax²+bx+c=0

D=(b)²-4ac

1) 1) Если D>0 то уравнение ax²+bx+c=0 имеет 2 решения,  уравнение y=ax²+bx+c имеет 2 точки пересечения с осью oX:

Если a>0, график функции будет иметь примерный вид:

2) Если D=0, то уравнение ax²+bx+c=0 имеет 1 решение,=> уравнениеy=ax²+bx+c имеет 1 точку пересечения с осью oX.

Если a>0, график функции будет иметь примерный вид:

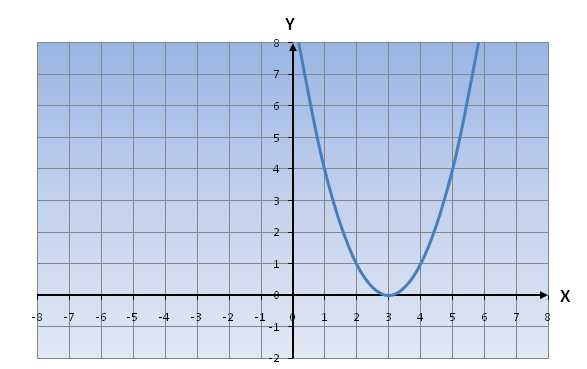
3) Если  D<0, то уравнение ax²+bx+c=0 не имеет решения, => уравнениеy=ax

Если a>0, график функции будет иметь примерный вид:

Координаты вершины параболы

Координаты вершины параболы находятся через данные формулы:

Прямая, проходящая через вершину параболы является осью симметрии параболы.

   Точка пересечения с осью oY

Так как абсцисса любой точки, лежащей на оси oY равна нулю, чтобы найти точку пересечения параболы y=ax²+bx+c с осью oY, нужно в уравнение параболы вместо Xподставить 0, тогда y(0)=c. 

Алгоритм построения квадратичной параболы

1) Направление ветвей.

2) Координаты вершины параболы.

3) Корни дискриминанта.

4) Дополнительные точки.

5) Построение графика.

Разложениеквадратного трехчлена

Пример №1

Построим функцию y=x²-6x+15

В квадратичном трехчлене x²-6x+15, чтобы выразить квадрат разности, используем формулу сокращенного умножения.

Базовая формула: (a±b)²=x²±2ab+b²,

Выразим квадрат разности: x²-6x+15=(x²-6x+9)+6,

Соберем формулу: (x²-6x+9)+6=(x-3)²+6,

У нас получилась функция y=(x-3)²+6,

Мы замечаем, что график функции смещен на 3 по оси oX вправо и на 6 по оси oY вверх.

Следовательно, график функции y=(x-3)²+6 будет выглядеть таким образом:

Пример №2

Построим функцию y=x²+8x+17

В квадратичном трехчлене x²+8x+17,чтобы выразить квадрат разности, используем формулу сокращенного умножения.

Базовая формула: (a±b)²=x²±2ab+b²,

Выразим квадрат разности: x²+8x+17=(x²+8x+16)+1,

Соберем формулу: (x²+8x+16)+1=(x+4)²+1,

У нас получилась функция y=(x+4)²+1,

Мы замечаем, что график функции смещен на 4 oX влево и на 1 по оси oY вверх.

Следовательно, график функции y=(x+4)²+1 будет выглядеть таким образом:

Итог:

Чтобы разложить квадратный трехчлен, использую такой алгоритм:

1) Выразим квадрат разности из данного трехчлена, с помощью формул сокращенного умножения;

2) Соберем, получившуюся формулу;

3) «Прочитаем» график, на смещение, относительно осей координат;

4) Построим график.

Автор статьи: Мажаров Данила Михайлович

Редакторы: Агеева Любовь Александровна, Гаврилина Анна Викторовна

www.teslalab.ru

Квадратичная функция и ее график

На уроках математики в школе Вы уже познакомились с простейшими свойствами и графиком функции y = x². Давайте расширим знания по квадратичной функции.

Задание 1.

Построить график функции y = x². Масштаб: 1 = 2 см. Отметьте на оси Oy точку F(0; 1/4). Циркулем или полоской бумаги измерьте расстояние от точки F до какой-нибудь точки M параболы. Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс (рис. 1). Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?

Результат: какую бы точку на параболе y = x² вы не взяли, расстояние от этой точки до точки F(0; 1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число – на 1/4.

Можно сказать иначе: расстояние от любой точки параболы до точки (0; 1/4) равно расстоянию от той же точки параболы до прямой y = -1/4. Эта замечательная точка F(0; 1/4) называется фокусом параболы y = x², а прямая y = -1/4 – директрисой этой параболы. Директриса и фокус есть у каждой параболы.

Интересные свойства параболы:

1. Любая точка параболы равноудалена от некоторой точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.

2. Если вращать параболу вокруг оси симметрии (например, параболу y = x² вокруг оси Oy), то получится очень интересная поверхность, которая называется параболоидом вращения.

Поверхность жидкости во вращающемся сосуде имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если сильно помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.

3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе (рис. 2).

4. Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола (рис. 3).

5. В парках развлечений иногда устраивают забавный аттракцион «Параболоид чудес». Каждому, из стоящих внутри вращающегося параболоида, кажется, что он стоит на полу, а остальные люди каким-то чудом держаться на стенках.

6. В зеркальных телескопах также применяют параболические зеркала: свет далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокус.

7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи, отразившись от параболического зеркала, образуют параллельный пучок.

Построение графика квадратичной функции

На уроках математики вы изучали получение из графика функции y = x² графиков функций вида:

1) y = ax² – растяжение графика y = x² вдоль оси Oy в |a| раз (при |a| < 0 – это сжатие в 1/|a| раз, рис. 4).

2) y = x² + n – сдвиг графика на n единиц вдоль оси Oy, причем,  если n > 0, то сдвиг вверх, а если n < 0, то вниз, (или же можно переносить ось абсцисс).

3) y = (x + m)²  – сдвиг графика на m единиц вдоль оси Ox: если m < 0, то вправо, а если m > 0, то влево, (рис. 5).

4) y = -x²  – симметричное отображение относительно оси Ox графика  y = x².

Подробнее остановимся на построении графика функции y = a(x – m)² + n.

Квадратичную функцию вида y = ax² + bx + c всегда можно привести к виду

y = a(x – m)² + n, где m = -b/(2a), n = -(b² – 4ac)/(4a).

Докажем это.

Действительно,

y = ax² + bx + c = a(x² + (b/a) x + c/a) =

= a(x² + 2x · (b/a) +  b²/(4a²) – b²/(4a²) + c/a) =

= a((x + b/2a) ² – (b² – 4ac)/(4a²)) = a(x + b/2a) ² – (b² – 4ac)/(4a).

Введем новые обозначения.

Пусть m = -b/(2a), а n = -(b² – 4ac)/(4a),

тогда получим y = a(x – m)² + n или y – n = a(x – m)².

Сделаем еще замены: пусть y – n = Y, x – m = X (*).

Тогда получим функцию Y = aX², графиком которой является парабола.

Вершина параболы находится в начале координат. X = 0; Y = 0.

Подставив координаты вершины в (*), получаем координаты вершины графика y = a(x – m)² + n: x = m, y = n.

Таким образом, для того, чтобы построить график квадратичной функции, представленной в виде

y = a(x – m)² + n

путем преобразований, можно действовать следующим образом:

a) построить график функции y = x²;

б) путем параллельного переноса вдоль оси Ox на m единиц и вдоль оси Oy на n единиц – вершину параболы из начала координат перевести в точку с координатами (m; n) (рис. 6).

Запись преобразований:

y = x² → y = (x – m)² → y = a(x – m)² → y = a(x – m)² + n.

Пример.

С помощью преобразований построить в декартовой системе координат график функции y = 2(x – 3)²– 2.

Решение.

Цепочка преобразований:

y = x²(1) → y = (x – 3)²(2) → y = 2(x – 3)²(3) → y = 2(x – 3)² – 2 (4).

Построение графика изображено на рис. 7.

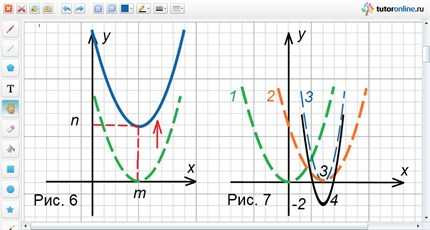Вы можете практиковаться в построении графиков квадратичной функции самостоятельно. Например, постройте в одной системе координат с помощью преобразований график функции y = 2(x + 3)² + 2. Если у вас возникнут вопросы или же вы захотите получить консультацию учителя, то у вас есть возможность провести бесплатное 25-минутное занятие с онлайн репетитором после регистрации. Для дальнейшей работы с преподавателем вы сможете выбрать подходящий вам тарифный план.

 Остались вопросы? Не знаете, как построить график квадратичной функции?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Квадратичная функция



Квадратичная функция (парабола)

если а < 0, ветви параболы направлены вниз

osiktakan.ru

квадратичной функции

В уравнении квадратичной функции:

a – старший коэффициент

b – второй коэффициент

с  — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции  имеет вид:

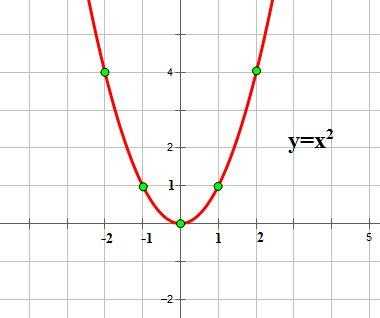
Обратите внимание на точки, обозначенные зелеными кружками – это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.

График  функции  имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции  симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвленывверх.

Если старший коэффициент a<0, то ветви параболы напрaвленывниз.

Второй параметр для построения графика  функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции  — это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю,чтобы найти координаты  точек  пересечения графика функции с осью ОХ, нужно решить уравнение.

В случае квадратичной функции  нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение  не имеет решений, и, следовательно, квадратичная парабола  не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:

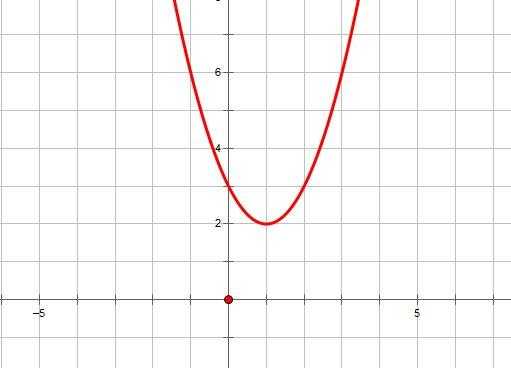
2. Если ,то уравнение  имеет одно решение, и, следовательно, квадратичная парабола   имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:

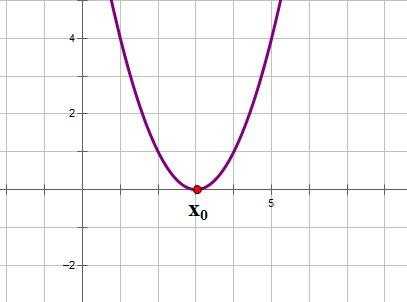
3.  Если ,то уравнение  имеет два решения, и, следовательно, квадратичная парабола   имеет две точки пересечения с осью ОХ:

,  

Если ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

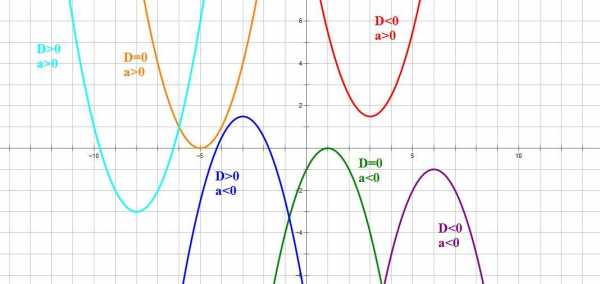
Следующий важный параметр графика квадратичной функции –координаты вершины параболы:

Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы.

И еще один параметр, полезный при построении графика функции –точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы  с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны  на рисунке:

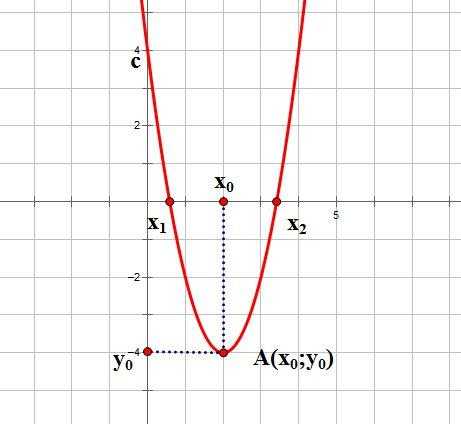
Рассмотрим несколько способов построения квдартичной параболы.В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

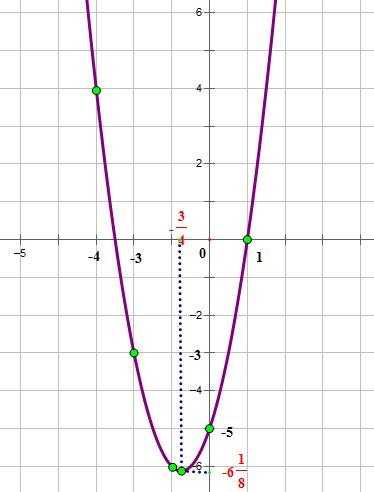
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции 

1. Направление ветвей параболы.

Так как ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена 

Дискримнант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение: 

,  

3.   Координаты  вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем коодинаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные  слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы  соответственно 0;1;2

Подствим значения х в уравнение функции, найдем ординаты этих точек и занесем их  в таблицу:

Нанесем эти точки на кординатную плоскость и соединим плавной линией:

2.  Уравнение квадратичной функции имеет вид  – в этом уравнении – координаты вершины параболы

или в уравнении квадратичной функции  , и второй коэффициент – четное число.

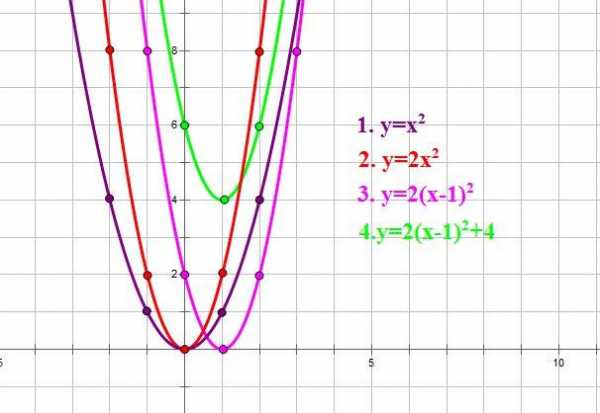
Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

• сначала построить график функции ,

• затем одинаты всех точек графика умножить на 2,

• затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,

• а затем вдоль оси OY на 4 единицы вверх:

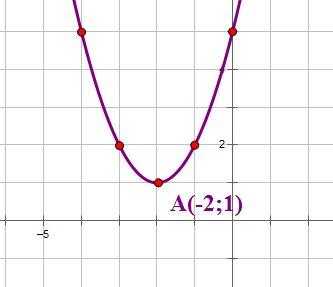
Теперь рассмотрим построение  графика функции . В уравнении этой функции, и второй коэффициент – четное число.

Выделим в уравнении функции полный квадрат: 

Следовательно,  координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3.  Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции – точки пересечения графика функции с осью ОХ:

(х-2)(х+4)=0, отсюда 

2. Координаты вершины параболы: 

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на  координатную плоскость и построим график:

studfiles.net