Проверка статистических гипотез — Электронный учебник K-tree
Что это и кому это нужно?
Проверка (тест) статистической гипотезы — это способ математического определения верности некоторого утверждения на основе
закона распределения. Освоив этот метод, Вы сможете делать математически обоснованные выводы, например:
Пример #1
Вы изготавливаете кубики для игры в кости и чтобы убедиться, что кубик отлично сбалансирован, Вы проводите тест — бросаете кости 600 раз и решаете, что если каждое число выпало 100±10 раз, то кубик сбалансирован.
Пример #2
На производстве 5% продукции отбраковывается, Вы разработали новую технологию и хотите проверить, уменьшится ли количество брака.
Основные термины, определения и формулы
Нулевая и альтернативная статистические гипотезы
Математически, условие статистического теста записывается в виде основной (нулевой) гипотезы H0 и альтернативной (конкурирующей) гипотезы H1. Основная гипотеза подразумевает некое значение параметра. Альтернативная гипотеза используется для обозначения области, которая нам также может быть интересна.
Теперь в примерах:
В первом примере мы хотим узнать, будет ли количество каждого выброшенного числа равно 100±10, при этом для нас неудачным будет как больше 110 так и меньше 90
H0: μ = 100±10
H1: μ ≠ 100±10научная запись выглядит так:
H0: μ = 100
H1: μ ≠ 100
α = 0.1
Во втором примере мы хотим узнать, новая технология лучше старой? При этом нас не интересует, стала ли она хуже, а только есть ли улучшения. Предположим, что если количество брака осталось на уровне 5±0.25%, то процесс не стал лучше, если количество брака меньше 4.75%, то улучшения есть:
H0: p = 5±0.25%
H1: p < 4.75%научная запись выглядит так:
H0: p = 0.05
H1: p < 0.05
α = 0.05
Критическая область и две ошибки
Область значений, в которой основная гипотеза неверна — это критическая область, размер этой области задаётся в виде уровня значимости α:
Мы имеем значения от 100 до 200 и хотим проверить,
мы предполагаем, что в критической области основная гипотеза неверна, если наше предположение неверно — значит мы ошиблись, такая ошибка называется ошибка первого рода. Для альтернативной гипотезы мы также можем допустить ошибку, такая ошибка будет называться ошибка второго рода
Почему?
Мы формулируем гипотезу так, что бы неверное отвержение основной гипотезы являлось для нашего решения более существенным, чем неверное принятие альтернативной, вот пример:
Проводится исследование, есть ли связь между курением и заболеванием раком, основная гипотеза выдвигается такая: курение вызывает рак. Если мы отвергнем это утверждение, а оно окажется верным — мы ставим под угрозу человеческие жизни (ошибка первого рода). При этом, если курение не вызывает рак, а в ходе эксперимента мы утвердили, что вызывает, то особых последствий это не вызовет (ошибка второго рода).
В условиях принятия решения мы хотим контролировать уровень ошибки первого рода, т.е. если нам необходимо принять решение относительно некоего утверждения, мы должны задаться некоторым уровнем значимости α и последующие расчёты будут зависеть от этого параметра.
Необходимо проверить,
Уровень значимости, статистическая мощность
Уровень значимости α — это вероятность допустить ошибку первого рода. Уровень значимости и ошибка первого рода — это одно и то же. Статистическая мощность связана с ошибкой второго рода (β), статистическая мощность — это вероятность отвергнуть основную гипотезу, когда верна альтернативная. Вероятность ошибки второго рода и статистическая мощность в сумме дают 100%, соответственно, чем больше статистическая мощность, тем меньше вероятность допустить ошибку второго рода.
Итак, мы имеем:
Проверка статистической гипотезы — математическое представление некоего утверждения
Нулевая гипотеза (H0) — предположение о некоем параметре θ, H0: θ = θ0
Альтернативная гипотеза (H1) — предположение о некоем параметре θ, H1: θ = θ0
Критическая область — область, в которой основная гипотеза H0 неверна
Ошибка I рода — вероятность отвергнуть основную гипотезу, когда она верна
Ошибка II рода — вероятность принять основную гипотезу, когда она неверна
Пример
Математическая запись гипотезы, что среднее значение генеральной совокупности равно 2
H1 : μ ≠ 2
Ещё пример
Математическая запись гипотезы, что среднее значение выборки А и среднее значение выборки В равны
H0 : μA = μB
H1 : μA ≠ μB
Что бы уж точно
Математическая запись гипотезы, что среднее значение выборки А меньше среднего значения выборки В
H0 : μA < μB
H1 : μA ≥ μB
Уровень значимости α
Уровень значимости (его также можно было бы назвать «Степень доверия») — это параметр, который означает, какова вероятность,
что верная гипотеза не будет принята. Этот параметр может быть получен, а может быть заранее задан условием, привожу два примера:
- Можем ли мы быть уверены на 90% (уровень значимости 10%), что машину не надо будет сдавать в ремонт в течение года? После проверки гипотезы мы получим результат «да» или «нет»
- На сколько мы можем быть уверены, что машину в течение года не надо будет сдавать в ремонт? После проверки гипотезы мы получим результат в процентах
Ошибки гипотезы
Когда мы делаем утверждение относительно некой гипотезы, мы можем допустить две ошибки:
Ошибка первого рода α
Например, мы провели тест некой выборки и по результатам решили, что параметр X не соответствует генеральной совокупности. Если выборка была
сделана некорректно и параметр X описывает генеральную совокупность, то мы совершили ошибку первого рода — отказались от главной гипотезы
когда она верна.
α = P(ошибка первого рода) = P(отказ от H0 | H0 верна)
Ошибка первого рода и уровень значимости это абсолютно одно и то же.
Пример
Предположим, что вес кролика подчиняется нормальному закону, тогда:
σ = 0.5/√(10) = 0.16
μ = 5.1
Условие гипотезы:
α = P(H0 неверна | H0 верна) = P(x < )
Ошибка второго рода β
Обратный случай ошибке первого рода — это когда мы приняли главную гипотезу, но она оказалась неверна
β = P(ошибка второго рода) = P(принятие H0 | H0 ошибочна)
Проверка статистической гипотезы
Проверка статистической гипотезы обозначает выполнение следующих шагов:
1. Построение случайной выборки
2. Расчёт параметра X выборки
3. Проверика гипотезы с использованием полученного значения X
k-tree.ru
Статистическая проверка статистических гипотез.
Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определенный вид (назовем его А), выдвигают гипотезу: генеральная совокупность распределена по закону А. Таким образом, в этой гипотезе речь идет о виде предполагаемого распределения.
Возможен
случай, когда закон распределения
известен, а его параметры неизвестны.
Если есть основания предположить, что
неизвестный параметр  равен определенному значению
равен определенному значению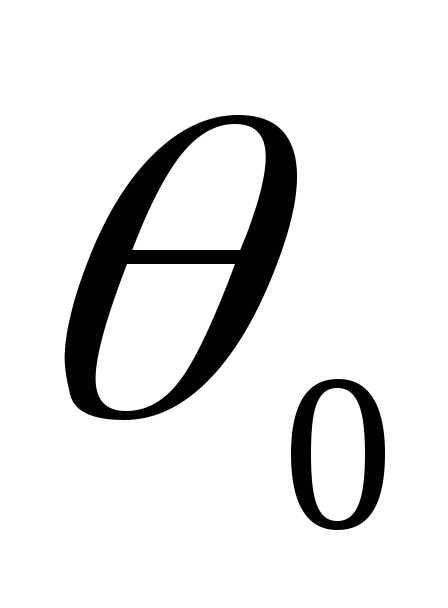 ,
выдвигают гипотезу:
,
выдвигают гипотезу:
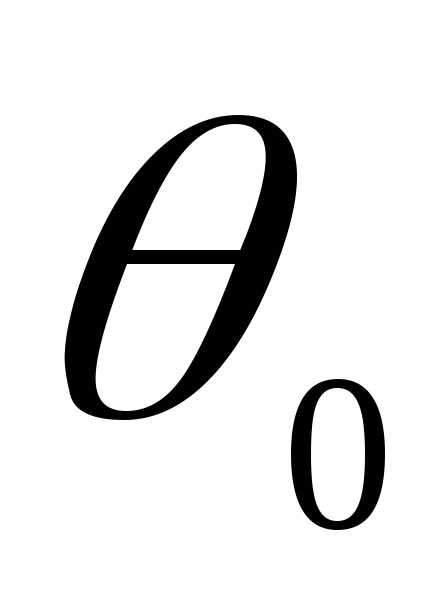 .
Таким образом, в этой гипотезе речь идет
о предполагаемой величине параметра
одного известного распределения.
.
Таким образом, в этой гипотезе речь идет
о предполагаемой величине параметра
одного известного распределения.Возможны и другие гипотезы: о равенстве параметров двух или нескольких распределений, о независимости выборок и многие другие.
Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.
Например, статистическими являются гипотезы:
генеральная совокупность распределена по закону Пуассона;
дисперсии двух нормальных совокупностей равны между собой.
В первой гипотезе сделано предположение о виде неизвестного распределения, во второй —о параметрах двух известных распределений.
Гипотеза «на Марсе есть жизнь» не является статистической, поскольку в ней не идет речь ни о виде, ни о параметрах распределения.
Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.
Нулевой (основной) называют выдвинутую гипотезу H0.
Конкурирующей (альтернативной) называют гипотезу Н1, которая противоречит нулевой.
Например,
если нулевая гипотеза состоит в
предположении, что математическое
ожидание а нормального распределения
равно 10, то конкурирующая гипотеза, в
частности, может состоять в предположении,
что а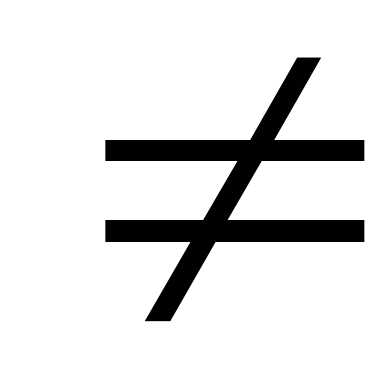 10.
Коротко это записывают так:H0:а=10;
Н1 а=10.
10.
Коротко это записывают так:H0:а=10;
Н1 а=10.
Различают гипотезы, которые содержат только одно и более одного предположений.
Простой называют гипотезу, содержащую только
одно предположение. Например, если  параметр показательного распределения,
то гипотезаH0:
параметр показательного распределения,
то гипотезаH0:  =5
–простая. Гипотеза: математическое
ожидание нормального распределения
равно 3 (
=5
–простая. Гипотеза: математическое
ожидание нормального распределения
равно 3 ( известно) — простая.
известно) — простая.
Сложной называют гипотезу, которая состоит из
конечного или бесконечного числа простых
гипотез. Например, сложная гипотеза Н
:  > 5 состоит из бесчисленного множества
простых видаHi:
> 5 состоит из бесчисленного множества
простых видаHi:  = вi,
где вi – любое число, большее 5. Гипотеза :
математическое ожидание нормального
распределения равно 3 (
= вi,
где вi – любое число, большее 5. Гипотеза :
математическое ожидание нормального
распределения равно 3 ( неизвестно) — сложная.
неизвестно) — сложная.
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т. Е. могут быть допущены ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Подчеркнем, что последствия этих ошибок могут оказаться весьма различными. Например, если отвергнуто правильное решение «продолжать строительство жилого дома», то эта ошибка первого рода повлечет материальный ущерб; если же принято неправильное решение «продолжать строительство», несмотря на опасность обвала стройки, то эта ошибка второго рода может повлечь гибель людей. Можно привести примеры, когда ошибка первого рода влечет более тяжелые последствия, чем ошибка второго рода.
Замечание 1. Правильное решение может быть принято также в двух случаях:
1) гипотеза принимается, причем и в действительности она правильная;
гипотеза отвергается, причем и в действительности она неверна.
Замечание 2. Вероятность совершить ошибку первого рода
принято обозначать через а; ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости, равный 0,05, то это означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода (отвергнуть правильную гипотезу).
Для
проверки нулевой гипотезы используют
специально подобранную случайную
величину, точное или приближенное
распределение которой известно. Эту
величину обозначают через U
или Z,
если она распределена нормально, F
или v2 – по закону Фишера – Снедекора, Т — по
закону Стьюдента, 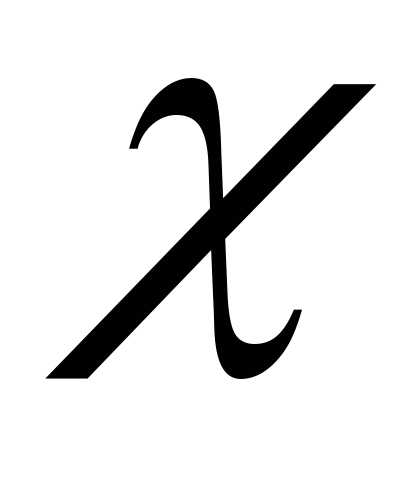 —
по закону «хи квадрат» и т. Д. Поскольку
вид распределения во внимание приниматься
не будет, обозначим эту величину в целях
общности черезK.
—
по закону «хи квадрат» и т. Д. Поскольку
вид распределения во внимание приниматься
не будет, обозначим эту величину в целях
общности черезK.
Статистическим критерием (или просто критерием) называют случайную величину K, которая служит для проверки нулевой гипотезы.
Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия К принимают отношение исправленных выборочных дисперсий:
Эта величина случайная, потому что в различных опытах дисперсии принимают различные, наперед неизвестные значения, и распределена по закону Фишера – Снедекора.
Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают частное (наблюдаемое) значение критерия.
Наблюдаемым
значением Кнабл называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсии s = 20 и s
= 20 и s = 5, то наблюдаемое значение критерия F
= 5, то наблюдаемое значение критерия F
После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая — при которых она принимается.
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезы (областью допустимых
значений) называют совокупность значений критерия, при
которых гипотезу принимают.
Основной принцип проверки статистических гипотез
можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области, гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.
Поскольку критерий К- одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют.
Критическими точками (границами) kкр называют точки, отделяющие критическую область от области принятия гипотезы.
studfiles.net
Тема 5. Проверка статистических гипотез
42
5.1 Основные понятия, используемые при проверке гипотез
5.1.1 Статистические гипотезы
Статистическая гипотеза – любое предположение, касающееся неизвестного распределения случайных величин (элементов), соответствующее некоторым представлениям об изучаемом явлении. В частном случае это может быть утверждение о значениях параметров распределения генеральной совокупности.
Различают нулевую и альтернативную гипотезы. Нулевая гипотеза – гипотеза, подлежащая проверке. Альтернативная гипотеза – каждая допустимая гипотеза, отличная от нулевой. Нулевую гипотезу обозначают Н0, альтернативную – Н1 (от Hypothesis – «гипотеза» (англ.)).
Конкретная задача проверки статистической гипотезы полностью описана, если заданы нулевая и альтернативная гипотезы. При обработке реальных данных большое значение имеет правильный выбор гипотез. Принимаемые предположения, например, нормальность распределения, должны быть тщательно обоснованы, в частности, статистическими методами. Необходимо помнить, что в подавляющем большинстве конкретных прикладных задач распределение результатов наблюдений в той или иной степени отлично от нормального.
5.1.2 Уровень значимости и мощность критерия. Ошибки при проверке гипотез
При проверке статистической гипотезы возможны ошибки. Есть два рода ошибок.
Ошибка первого рода заключается в том, что отвергают нулевую гипотезу, в то время как в действительности эта гипотеза верна. Вероятность ошибки первого рода называется уровнем значимости и обозначается α.
Ошибка второго рода состоит в том, что принимают нулевую гипотезу, в то время как в действительности эта гипотеза неверна.
Обычно используют не вероятность ошибки второго рода, а ее дополнение до 1. Эта величина носит название мощности критерия. Итак, мощность критерия – это вероятность того, что нулевая гипотеза будет отвергнута, когда альтернативная гипотеза верна.
Понятия уровня значимости и мощности критерия объединяются в понятии функции мощности критерия – функции, определяющей вероятность того, что нулевая гипотеза будет отвергнута.
Наглядным способом интерпретации ошибок является их графическое представление.
Предположим, что проверяется гипотеза Н0: о равенстве среднего значения генеральной совокупности заданной величине(известной, например, из предыдущих экспериментов).
Для этого берется выборка объема n, находится ее среднее арифметическое и по его величине судят о справедливости гипотезы Н0.
Распределение среднего арифметического при условии, что верна гипотеза Н0, будет. Это распределение качественно представлено на рис. 4.1.
Распределение среднего арифметического при условии, что верна альтернативная гипотеза Н1:, буде уже другим —.
Будем считать, что гипотеза Н0 отвергается, если выборочное среднее арифметическое окажется больше некоторого критического значения, т. е., как показано на рис.
Рис. 6.1. Ошибки первого и второго рода
Область непринятия гипотезы Н0 называется критической областью критерия. Она показана па рисунке наклонной штриховкой. Уровень значимости будет соответствовать площади критической области.
Вероятность ошибки второго рода будет равна площади под кривой распределения, показанной на рисунке. вертикальной штриховкой.
Величина называется мощностью критерия.
Исследователь всегда должен формулировать гипотезу и задавать уровень значимости до получения экспериментальных данных, по которым эта гипотеза будет проверяться.
При выборе уровня значимости исследователь исходит из практических соображений, отвечая на вопрос: какую вероятность ошибки он считает допустимой для его конкретной задачи?
Обычно считают достаточным уровень значимости 0,05 (5%), иногда 1% или 10%, редко 0,1%.
studfiles.net
87. Проверка статистических гипотез. Примеры гипотез.
Статистическая гипотеза. Основные понятия.
Под статистическими гипотезами понимается предположения о неизвестном законе распределения или неизвестных параметрах известных законах распределения.
К примерам статистических гипотез можно отнести:
1) Генеральный признак Х имеет нормальный закон распределения.
2) Математическое ожидание нормально распределенной случайной величины = 5.
3) Дисперсия двух биномиально распределенных признаков равны между собой.
Выдвинутую гипотезу, которую необходимо принять или отвергнуть называют нулевой или основной гипотезой. Обозначают . В предыдущих примерах:
1) -Х имеет нормальный закон распределения
2) : а=5
3) : Д(х)=Д(у)
Вместе с выдвинутой гипотезой всегда рассматривается противоречащая гипотеза, которая называется конкурирующей и обозначается .
В предыдущих примерах:
1) -Х имеет другое распределение
2) : а не=5 или а>5
3) : Д(х) не=Д(у)
Гипотезы бывают:
— простая содержит 1 элементарное предположение :
— сложная – более 1 предположения:
Для проверки любой статист гипотезы рассм-ся нек-я СВ, закон распределения к-й заранее известен и эту СВ наз-ют критерием проверки гипотезы. k- критерий. Все значения критерия делят числ прямую на 2 области: 1)область применения, 2)критическая область. Область принятия гипотезы наз-ся все зн-я критерия, при к-х нулевая гипотеза принимается. Критич область-множ-во знач-й критерия, при к-х нулевая гипотеза отвергается.
Сущ-ет 3 вида критич областей: 1)правосторонняя критич область, к-я задается нер-вом , 2)левосторонняя крит область, 3)двусторонняя крит область. Критическими точками наз-ся знач-я критерияk, разделяющая критич обл и обл принятия гипотезы. Суть метода проверки любой статистич гипотезы состоит в том, чтобы определить знач-е критерия и проверить принадлежность знач-я к критич области. Если крит обл- отвергается. Есликрит обл- принимается. При проверке любой гипотезы расс-ся нек-й уровень значимости, под к-м понимается небольшая вероятность попадания Х к крит обл. Для правосторонней крит обл 3 уровня знач-я, для левострон крит обл, для двусторонней крит обл выдвигают 2 требования. Т.е. любая гипотеза проверяется любым заданным уровнем значимости, если-маленькая вероятность попадания критерия в в крит обл, то 1— это большая вер-ть попадания критерия обл принятия гипотезы.
Гипотеза о равенстве дисперсии 2-х нормально распределенных признаков.
Рассмотрим 2 генер призанка Х и У, имеющих норм законы распределения и выдвинем гипотезу о рав-ве дисперсии этих признаков . Такая гипотеза обычно выдвигается при проверке вычислений 2 методами или точности самих методов. В качестве критерия рассмотрим СВF равная отношению исправленных выборочных дисперсий этих признаков. , где–исправленная выборочная дисперсия, найденная по выборке с большим объемом.м-т соответ-ет Х или У. Пусть генер сов-ти Х сделана выборка
Также из У:
Известно, что по данным выборок м-о определить исправленной выбор дисперсии ии большая из этих знач-й.
Критерий F содержит испр выб дисп т к именно они явл-ся точечными оценками генер дисперсией, т.е , поэтому нулевую гипотезу иногда записывают в виде:или.
Критерий F имеет закон распределения Фишера-Снедекора со степенями свободы и, где,, причемсоот-ет той выборке, у к-й большаясоот-ет. Для распределения Фишера-Снедекора сущ-ет спец табл значений при заданном уровне значения. Выбор критич обл зависит от вида конкурирующей гипотезы. В связи с выбором конкурирующей гипотезы сущ-ет 2 правила проверки гипотезы:
Пусть нулевой гипотезывыдвигается конкурирующая гипотеза. В этом случае строится правосторонняя крит обл исходя из исследованиявер-ть попадания крит обл очень мала. Справедливо правило для того, чтобы при задан уровне знач-япроверитьпринеобходимо: 1) вычислить наблюдаемое знач-е критерия по формуле; 2) найти крит точку из табл распр-я Фишера-Снедекора при заданном уровне знач-яи степенях свободыи,; 3)Если, то-принимается, если, то-отвергается.
Пусть нулевой гипотезы ставится конкурирующая гипотеза, то в этом случае строится двусторонняя крит обл, причем для распр-я Фишера-Снедекора крит точки расположены симметрично отн-но начала координат, тогда если уровень значимости- это маленькая вер-ть попасть в крит обл, то достаточно рассм-ть одну крит точку для симметрич. Если вер-ть попасть в двустороннюю обл=, то вер-ть попасть в правую обл=/2. Справедливо след правило: для того, чтобы при уровне значимостипроверитьпринеобходимо: 1) вычислить наблюдаемое значение критерия по формуле ; 2) найти крит точку из табл распред-я Фишера-Снедекора при уровне/2 :; 3) сделаем вывод:- принимается,- отвергается.
studfiles.net
Проверка статистических гипотез.
Лекция №3.
Статистическая гипотеза — это предположение о генеральной совокупности, высказанное на основании статистических выборочных данных.
Статистическая проверка гипотез — это процедура обоснованного сопоставления высказанной гипотезы с имеющимися выборочными данными.
Например: исследуем влияние нового лекарственного препарата на снижение артериального давления.
X{x1, x2, … xn1} — контрольная группа (выборка, объёмом n1)
Y{y1, y2, … yn2} — опытная группа (выборка объёмом n2)
Высказываются две альтернативные гипотезы:
Н0: — различия между выборками не достоверны (т.е. носят случайный характер).
Н: — различия между выборками достоверны (т.е. влияние препарата достоверно (эффективно))
Чтобы принять или опровергнуть эти предположения, используют статистические критерии или критерии достоверности.
Статистический критерий — это случайная величина, закон распределения которой известен, т.е. каждому значению критерия поставлена в соответствие вероятность, с которой он эти значения принимает.
Для каждого критерия существует таблица, в которой содержатся критические значения критерия. Каждое критическое значение соответствует определённому уровню значимости α и числу степеней свободы (или к)
где а — число наложенных связей или ограничений.
α=1-РД — это вероятность принять ошибочную гипотезу.
Критические значения позволяют определить вероятность нулевой гипотезы: Р(Н0).
Гипотеза Н0 принимается, если в результате проверки выяснилось, что её вероятность больше выбранного уровня значимости.
если Р(Н0)>α , то Н0 принимаем,
если Р(Н0)<α , то Н0 отвергаем.
Например: Хотим доказать достоверность различия между выборками X{x1, x2, … xn1} и Y{y1, y2, … yn2} с РД=0,95 (это значит, что влияние препарата достоверно (эффективно) на 95%).
Если в результате проверки выяснилось, что Р(Н0)˃α , (т.е. ˃0,05), то мы вынуждены принять гипотезу Н0, так как Р(Н)<РД
Р(Н)<0,95.
Основные этапы проверки статистических гипотез.
1).Выдвигается гипотеза Н0.
2).Выбирается величина уровня значимости α (α=1-РД).
3).По заданному α и числу степеней свободы ν(или к) в таблице находим критическое (табличное) значение критерия.
4).Подсчитывается экспериментальное значение критерия по имеющимся выборкам (для каждого критерия существует формула для определения значения критерия).
5).С помощью сравнения экспериментального и критического значений делается вывод о правомерности гипотезы Н0.
6).Если Н0 принимается, следовательно гипотеза Н (о достоверности различий) не верна.
Если Н0 отвергается, следовательно верна гипотеза Н..(Н0 и Н — противоположные события).
Критерии достоверности подразделяются на параметрические и непараметрические.
Параметрические критерии для вычисления экспериментального значения используют статистические параметры: . Они могут использоваться для выборочных совокупностей, распределённых по закону близкому к нормальному (Гаусса).
Непараметрические критерии не требуют вычисления выборочных параметров, они менее точны, дают более грубую оценку, чем параметрические критерии, но:
1). Их можно применять к выборкам, закон распределения которых неизвестен (не обязательно нормальное распределение).
2). Они проще и позволяют быстрее производить проверку рассматриваемых гипотез.
studfiles.net
6.6. Статистическая проверка гипотез | Решение задач по математике и др
Во многих случаях результаты наблюдений используются для проверки предположений (гипотез) относительно либо самого вида распределения генеральной совокупности, либо значения параметров уже известного распределения — статистических гипотез. Пусть известно распределение СВ X (например, это нормальный закон), и по выборке необходимо проверить гипотезу о значении некоторого параметра (хг, Dr или стг) этого распределения.
В дальнейшем выдвигаемую и проверяемую гипотезу будем называть нулевой гипотезой (или основной) и обозначать ее через Н0. Наряду с Н0 рассматривают также одну из альтернативных (конкурирующих) гипотез Н1. Например, если проверяется гипотеза о равенстве параметра в некоторому заданному значению в0, т. е. Н0′. в = в0, то в качестве альтернативной гипотезы можно рассмотреть одну из следующих: а) Н1: в > в0;
б) Н1: в < в0; в) Н1: в ф в0; г) Н1: в = в1, где в1 — другое заданное значение параметра в.
Выдвинутая гипотеза Н0 может соответствовать истине или нет. При проверке гипотезы Н0 по результатам выборки могут быть допущены ошибки двух родов: 1) ошибка первого рода — отвергнута правильная гипотеза; 2) ошибка второго рода — принята неправильная гипотеза. Последствия этих ошибок неравнозначны, и роль каждой оценивается до конца по условиям конкретной задачи. Например, если при проверке качества партии деталей по выборке из нее в качестве Н0 принята гипотеза, что доля брака не более 0,1%, то при допущении здесь ошибки первого рода будет забракована годная продукция, а допустив ошибку второго рода, выпустим потребителю партию деталей с долей
брака больше допустимого. Перед началом анализа выборки фиксируют очень малое число а. Вероятность совершить ошибку первого рода называется уровнем значимости а. Обычно берут а = 0,05; 0,01; 0,005.
Правило, по которому принимается решение принять или отклонить гипотезу #0, называется критерием или статистическим критерием К. Выбор К зависит от конкретной задачи.
Обычно критерий проверки гипотезы реализуется с помощью некоторой статистической характеристики, определенной по выборке, т. е. с помощью некоторой статистики в. Здесь в — некоторая СВ, закон распределения которой известен.
В множестве всех возможных значений статистики д критерия К выделим подмножество а 0, при котором гипотеза #0 отклоняется. Это подмножество называется критической областью. То подмножество значений в, при котором гипотезу #0 не отклоняют, называется областью принятия гипотезы (допустимой областью). Точки, разделяющие эти области, называются критическими точками. Для определения критических точек используют принцип практической невозможности событий, имеющих малую вероятность. При этом задаются достаточно малой величиной а, называемой уровнем значимости критерия, и определяют критическую область как множество тех значений в, вероятность которых принадлежать к области а 0 равнялась бы а, т. е.
Р {в е а0 } = а.
Если по данным выборки при данном уровне значимости получается, что в £ а 0, то это может служить основанием для отклонения гипотезы #0.
Рассмотрим проверку гипотезы о нормальном распределении генеральной совокупности X. Пусть распределение X неизвестно, но есть основание предположить, что X имеет нормальное распределение, т. е. выдвигается нулевая гипотеза #0 о нормальности СВ X. Статистический критерий, с помощью которого проверяется нулевая гипотеза, называется критерием согласия. Имеется несколько критериев согласия. Обычно в них используют статистики, имеющие таблицы распределений, подготовленные заранее: статистику с нормальным нормированным распределением, статистику у и статистику Фишера. Рассмотрим критерий согласия Пирсона (критерий согласия у Пирсона, у2 — «хи квадрат»).
Пусть для X получена выборка объема п, заданная в виде статистического ряда с равноотстоящими вариантами:
Найдем по данным выборки величины хв и стБ. Предполагая, что X имеет нормальное распределение, вычислим величины п :
называемые теоретическими частотами, в противоположность чему п; здесь называют эмпирическими частотами.
В качестве статистики в выбирают СВ % 2:
2 =^ (п; — пі )2
% Пі ‘
;=1 ;
Она подчиняется распределению % 2 с числом степенной свободы п = ^ — г — 1, где ^ — число различных значений х;; г — число параметров, от которых зависит распределение. Для нормального за-
кона таких параметров два: а = хв = М(X) и <у = $ = Вв—, т. е.
V п-1’
г = 2, и п = $ — 3. Если эмпирическое и теоретическое распределения совпадают, то с2 = 0. По данному уровню значимости а и числу степеней свободы пв таблице распределения с 2 находят критическое значение Срит. и определяют критическую область: с2 < скурит., «0 = {с2 : С2 ^ скурит.}. Затем вычисляют наблюдаемое значение с 2, т. е. с^абл. по формуле
(п — п )2
г =1
Если окажется, что < Х2рит. то нулевую гипотезу Н0 о том, что X имеет нормальное распределение, принимают. В этом случае опытные данные выборки хорошо согласуются с гипотезой о нормальном распределении генеральной совокупности.
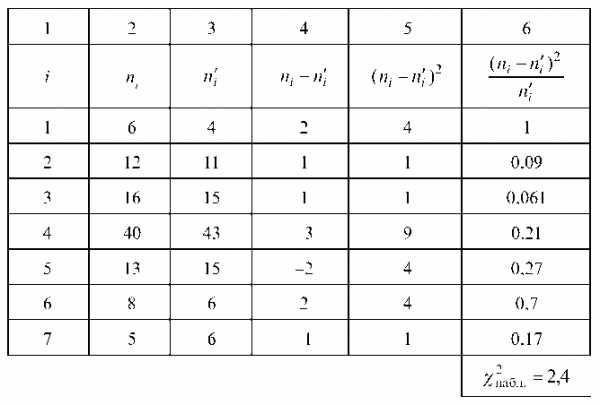
Пример 6.37. При уровне значимости a = 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
Так как %набл. < %2р. то нулевая гипотеза о нормальности генеральной совокупности принимается.
Решение. Число различных вариант m равно 7, значит число степеней свободы распределения с2 равно 7 — 3 = 4. По таблице критических точек распределения %2, по уровню значимости a = 0,05 и числу степеней свободы 4 находим %^р = 9,5. Вычислим %набл., для чего составим расчетную таблицу.
Пример 6.38. Дано статистическое распределение выборки:
Решение.
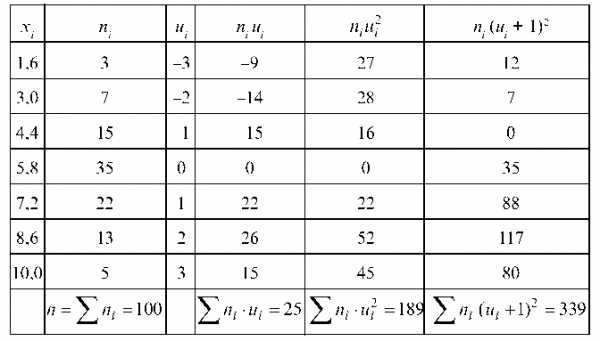
1.Найдем методом произведений выборочные: среднюю, дисперсию и среднее квадратическое отклонение. Воспользуемся методом произведений, для чего составляем табл. 1.
Таблица 1
В качестве ложного нуля принимаем С = 5,8 — варианта с наибольшей частотой 35. Шаг выборки h = х2 — х1 = 3,0 — 1,6 = 1,4. Тогда условные варианты определяем по формуле
Подсчитываем условные варианты щ и заполняем все столбцы.
Последний столбец служит для контроля вычислений по тождеству:
Контроль: 339 = 189 + 2 ¦ 25 + 100.
Вычисления произведены верно. Найдем условные моменты.
Вычисляем выборочную среднюю:
Находим выборочную дисперсию:
Определяем выборочное среднее квадратическое отклонение:
2. Строим нормальную кривую.
Для облегчения вычислений все расчеты сводим в табл. 2.

Заполняем первые три столбца.
В четвертом столбце записываем условные варианты по формуле, указанной в «шапке» таблицы. В пятом столбце находим значения функции
Функция j (u.) четная, т. е. j (u.) = j (-u.).
Значения функции j (u.) в зависимости от аргумента u. (берутся положительные u., т. к. функция j (u.) четная) находим из таблицы.
Теоретические частоты теоретической кривой находим по формуле
и заполняем последний столбец. Отметим, что в последнем столбце частоты n’ округляются до целого числа и
В системе координат (x.; y. = n’) строим нормальную (теоретическую) кривую (рис. 81) по выравнивающим частотам n’ (они
отмечены кружками) и полигон наблюдаемых частот (они отмечены крестиками). Полигон наблюдаемых частот построен в системе координат (x.; y. = n.).
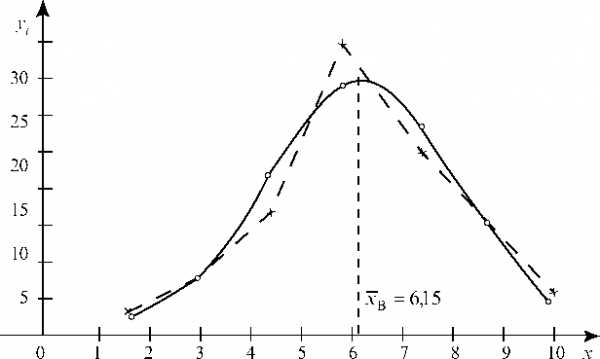
3. Проверяем гипотезу о нормальности X при уровне значимости a = 0,05.
Вычислим, для чего составим расчетную таблицу 3.
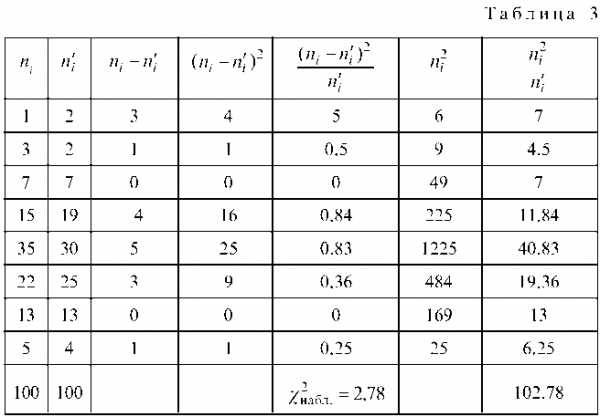
Суммируя числа пятого столбца, получаем Суммируя числа последнего столбца, получаем 102,78.
Контроль:
Совпадение результатов подтверждает правильность вычислений.
Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариантов) 7. v = 7 — 3 = 4.
По таблице критических точек распределения % 2, по уровню значимости a = 0,05 и числу степеней свободы v = 4 находим %Кр. = 9,5.
Так как %набл. < %Кр. то нет оснований отвергать нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
4. Найдем доверительный интервал для оценки неизвестного МО М (X), полагая, что X имеет нормальное распределение, среднее квадратическое отклонение s = sx = стВ = 1,89 и доверительная вероятность g = 0,95.
Известен объем выборки: n = 100, выборочная средняя хВ= 6,15.
Из соотношения 2Ф (t) = g получим Ф (t) = 0,475. По таблице находим параметр t = 1,96.
Найдем точность оценки
Доверительный интервал таков:
или
Надежность g = 0,95 указывает, что если произведено достаточно большое число выборок, то 95% из них определят такие доверительные интервалы, в которых параметр действительно заключен.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Решение задач математической статистики по теме «Проверка статистических гипотез»
Подобный материал:- Лекция 13, 99.82kb.
- Темы, которые мы обсуждали на предыдущей лекции: Прообраз=(Тадж Махал)=Неизвестный, 97.53kb.
- Первый. Предмет и история юридической статистики 7 Глава, 5134.73kb.
- Проверка статистических гипотез, 59.38kb.
- «Исследование скорости сходимости распределений статистик критериев проверки статистических, 116.56kb.
- Проверка статистических гипотез о законах распределения, 59.19kb.
- Решение задач описательной статистики средствами ms excel содержание, 164.81kb.
- Лекции №10 Выборочные методы математической статистики, 60.62kb.
- Задачи (научить) изучить базовые разделы математической статистики; развить навыки, 49kb.
- Волгоградская Государственная Сельскохозяйственная Академия Описание проекта Название, 110.24kb.
Пример (предложен студенткой Аленой Бут):
На основании предшествующих исследований было известно, что доля крупных западноевропейских бизнесменов, имеющих счета в швейцарских банках, составляет примерно 78%. Исследовательский центр Германии «Meinungsumfrage» отобрал 670 крупных бизнесменов Западной Европы и установил, что 510 из них хранят свои сбережения на счетах в швейцарских банках.
На основе применения доверительного интервала проверить справедливость утверждения, что и в настоящее время доля крупных бизнесменов, имеющих счета в швейцарских банках, составляет 78%.
Решить эту же задачу, применяя традиционную постановку задачи с введением основной и альтернативной гипотез.
Во обоих случаях принять уровень доверия равным 1%.
Решение:
Экспериментальные данные: n = 670, k = 510, α = 0,01
Поскольку выборка большая, то доверительный интервал находится по формуле
Вычислим доверительный интервал:
Данный доверительный интервал с вероятностью 99% накрывает генеральную долю западноевропейских бизнесменов, хранящих свои сбережения в швейцарских банках.
Поскольку значение генеральной доли 0.78, заданное условием задачи, попадает в этот доверительный интервал, то, следовательно, с уровнем доверия в 99% (или с уровнем значимости в 1%) можно принять нулевую гипотезу как не противоречащую опытным данным.
Решим этот же пример на основе традиционного алгоритма проверки статистических гипотез.
Постановка задачи:
H0: Wг = 0,78, здесь р0=0.78
H1: Wг
Экспериментальные данные: n = 670, k =510; кроме того, α = 0,01.
Вычислим значение критерия, который при справедливости основной гипотезы имеет стандартное нормальное распределение:
Найдем границу левосторонней критической области:
P (tкр л + ) = 0,99→P (tкр л + )= Ф0 (+) — Ф0 (tкр л)=
=0.5 — Ф0 (tкр л)=0.99→Ф0 (tкр л) = — 0,49→Ф0 (-tкр л) = 0,49→ tкр л ≈-2,32
На основе данного графика, сравнивая взаимное расположение наблюдаемого значения критерия и границы левосторонней критической области, следует сделать вывод о принятии нулевой гипотезы как не противоречащей экспериментальным данным с уровнем доверия в 1%.
Замечание: получены одинаковые выводы независимо от способа решения на основе использования доверительного интервала и на основе традиционного алгоритма проверки статистической гипотезы.
Пример (предложена студентом):
Главный врач ветеринарной клиники утверждает, что не менее 70 % его пациентов после приёма новейших лекарств верно служат своим хозяевам не болея на протяжении трех лет. Можно ли считать это утверждение верным, если из 100 пациентов ветеринарной клиники 59 остаются здоровыми после приема таблеток ещё три года? Принять уровень значимости 5%.
Решение:
Постановка задачи:
H0: p = 0,70 (р0 = 0,70)
H1: p
Вычислим наблюдаемое значение критерия:
Так как n>30, то находим tкрс помощью функции Лапласа:
P (tкр л + ) = 0,95 →P (tкр л + )=: Ф0 (+) — Ф0 (tкр л) =
=0,5 + Ф0(-tкр л) = 0,95 → Ф0 (-tкр л) = 0,45 → tкр л = -1,65
Поскольку наблюдаемое значение критерия попало в область критических значений критерия, то отвергаем нулевую гипотезу как противоречащую экспериментальным данным и принимаем альтернативную гипотезу H1, т.е. можно сказать, что менее 70% пациентов после приёма лекарств верно прослужат своим хозяевам ещё три года (утверждение врача клиники чрезмерно оптимистично).
Проверка гипотезы о равенстве математических ожиданий (о равенстве генеральных средних) двух нормально распределенных генеральных совокупностей
Пусть имеются две нормально распределенные генеральные совокупности, причем в первой совокупности изучаемый признак X~N(m1;s1), во второй совокупности изучаемый признак Y~N(m2;s2).
Мы в дальнейшем будем рассматривать ситуации, относящиеся к случаям больших выборок из этих двух генеральных совокупностей: n1>30, n2>30. Случаи малых выборок анализируются в соответствующих разделах учебников, но такие ситуации здесь не рассматриваются.
Постановка задачи:
Решим конкретную задачу, в которой реализуется описанный выше подход.
Пример:
Проводится сравнение роста 20-летних юношей, проживающих в Москве и в Новосибирске. На основе двух случайных выборок, выполненных в двух городах, были получены следующие данные. В Москве отобрали 75 юношей, по величинам ростов которых были вычислены две характеристики: средний рост юношей, который оказался равным 179 см, и стандартное отклонение, которое оказалось равным 8 см; в Новосибирске были случайно отобраны 57 юношей, их средний рост оказался равным 176 см со стандартным отклонением 10 см. На основе этих экспериментальных данных следует проверить гипотезу о примерном равенстве ростов московских и новосибирских 20-летних юношей. Принять доверительную вероятность равной 90%. Предполагается, что рост юношей подчиняется нормальному закону распределения.
Иная постановка вопроса к тем же исходным данным может звучать так:
Следует выяснить, значимо или же незначимо отличаются друг от друга выборочные средние значения. Если будет показано, что выборочные средние отличаются незначимо, то отсюда можно будет сделать вывод о справедливости нулевой гипотезы о примерном равенстве ростов юношей, проживающих в различных городах. В противном случае будет сделать вывод о существенном различии ростов юношей из этих городов.
Решение:
Постановка задачи:
При такой постановке задачи следует строить двустороннюю критическую область.
Вычислим границы этой области на основе табличного решения уравнения:
Вычислим на основе экспериментальной информации наблюдаемое значение критерия:
Изобразим результаты графически:
Поскольку наблюдаемое значение критерия попало в критическую область значений параметра, то следует отвергнуть основную гипотезу в пользу альтернативной гипотезы и сказать, что средний рост московских и новосибирских 20-летних юношей отличается значимо.
Решим эту же задачу с теми же самыми исходными данными в случае иной, более естественной в данном случае альтернативной гипотезы. Ее естественность обусловлена конкретными экспериментальными значениями.
Постановка задачи:
Такая постановка задачи требует построения правосторонней критической области.
Найдем границу правосторонней критической области:
В данном случае наблюдаемое значение критерия не меняется.
График показывает, что наблюдаемое значение критерия попало в критическую область, поэтому следует сделать тот же вывод, который был получен ранее: средний рост московских и новосибирских юношей значимо отличается.
Проверка гипотезы о равенстве вероятностей биномиального закона распределения (о равенстве долей признака) двух генеральных совокупностей
Рассмотрим две генеральные совокупности.
Из первой генеральной совокупности делается случайная выборка объемом n1, и на основе этой выборки выясняется, сколько объектов выборки обладает изучаемым признаком – этих объектов k1.
Из второй генеральной совокупности делается случайная выборка объемом n2; количество объектов выборки, обладающих изучаемым признаком, — k2.
Выборочные доли признака равны соответственно
w1= k 1 / n1 ; w2= k 2 / n2
В данном пункте мы ограничимся лишь случаем, когда выборки достаточно большие: n1>30, n2>30.
Постановка задачи:
В этой ситуации в качестве критерия используется случайная величина вида
При справедливости гипотезы H0 данная случайная величина имеет стандартный нормальный закон распределения.
Рассмотрим пример, в котором реализуется рассмотренная выше ситуация.
Пример:
Перед экспертами поставлена задача оценить сравнительную активность электората Москвы и Санкт-Петербурга при избрании депутатов Государственной Думы. С этой целью была сделана случайная выборка в двух этих городах из состава населения, которое имеет право голоса. Было выяснено, какая часть выборки реально пришла на избирательный участок для участия в выборах. Данные оказались следующими: в Москве из 1500 потенциальных случайно выбранных избирателей реально в выборах приняли участие 480 человек, а в Санкт-Петербурге из 1630 потенциальных избирателей на избирательные участки пришли 490 человек. На уровне значимости α=10% проверить гипотезу о равенстве генеральных долей избирателей в двух этих городах, реально принявших участие в выборах.
Решение:
Постановка задачи:
Вычислим на основе экспериментальных данных выборочные доли:
Вычислим на основе экспериментальных данных наблюдаемое значение критерия:
Найдем границы двусторонней критической области, таблично (с помощью таблицы функции Лапласа) решив следующее уравнение:
Покажем все найденные значения на графике плотности стандартного нормального закона распределения, который описывает поведение случайной величины t при справедливости нулевой гипотезы.
Поскольку наблюдаемое значение критерия попало в область естественных для данного закона распределения значений (в данном случае стандартного нормального закона распределения), то гипотеза H0 принимается как не противоречащая экспериментальным данным с уровнем доверия 90%, т.е. генеральные доли электората, реально принявших участие в выборах в Москве и Санкт-Петербурге, значимо не отличаются, т.е. их можно считать одинаковыми.
Проверка гипотезы о значимости выборочного коэффициента корреляции Пирсона.
Рассматривается двумерная нормально распределенная генеральная совокупность (X,Y), т.е. случайные величины X и Y в ней распределены нормально Из этой совокупности извлечена выборка объемом n пар (xi , yi) и по ней вычислен выборочный коэффициент корреляции Пирсона, который оказался отличным от нуля. Возникает вопрос, объясняется ли это действительно существующей линейной связью между случайными величинами X и Y в генеральной совокупности или является следствием случайности отбора переменных в выборку. Можно ли при этом заключить, что и коэффициент корреляции r между случайными величинами X и Y во всей генеральной совокупности также отличен от нуля?
Напоминание:
Постановка задачи:
H0: ρ=0
H1: ρ≠0
Если нулевая гипотеза отвергается, то это означает, что коэффициент корреляции в генеральной совокупности значимо отличается от нуля (кратно говоря «значим»), и, следовательно, в генеральной совокупности признаки X и Y связаны линейной зависимостью. Если же принимается нулевая гипотеза, то генеральный коэффициент корреляции незначим, и, следовательно, признаки X и Y в генеральной совокупности не связаны линейной зависимостью.
В качестве критерия проверки нулевой гипотезы используется случайная величина
Показано, что эта случайная величина при справедливости нулевой гипотезы имеет распределение Стьюдента с k = n — 2 степенями свободы. Число степеней свободы на две единицы меньше объема выборки, поскольку в выражении для r задействованы две связи, заданные формулами для вычисления средних значений по выборке:
;
Ясно также, что при больших объемах выборки (n>30) можно вместо распределения Стьюдента использовать стандартный нормальный закон распределения.
Поскольку конкурирующая гипотеза имеет вид ρ≠0, то следует строить двустороннюю критическую область.
Определив, куда попадает вычисленное значение tнабл, делаем вывод о справедливости нулевой или же альтернативной гипотезы:
если | tнабл |кр, то принимается гипотеза H0,
если | tнабл |³ tкр , то принимается гипотеза H1.
Пример:
По выборке объема n=7, извлеченной из нормальной двумерной генеральной совокупности, был вычислен коэффициент корреляции Пирсона r=0,57. При уровне значимости α=10% проверить гипотезу H0 о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе ρ≠0.
Решение:
Постановка задачи:
H0: ρ=0
H1: ρ≠0
Найдем наблюдаемое значение критерия:
Определим значения границ двусторонней критической области из условия, что при малых объемах выборок критерий t распределен (при справедливости нулевой гипотезы) по закону распределения Стьюдента с числом степеней свободы k=7-2=5.
Привлечем таблицу «Критические точки распределения Стьюдента»; в таблице используем ту ее часть, которая относится к двусторонней критической области, задаем =0.10 и k=5→ tкр =2.01.
Полученные результаты покажем графически:
Поскольку наблюдаемое значение критерия попало в область принятия нулевой гипотезы, то следует принять нулевую гипотезу с уровнем значимости 10%. Это означает, что генеральный коэффициент корреляции равен нулю, т.е. в генеральной совокупности между случайными величинами X и Y линейная связь отсутствует. В этом случае не следует использовать уравнение линейной регрессии для прогнозирования значения одной случайной величины по значению другой случайной величины.
Рассмотрим аналогичный пример, но существенно увеличим в нем объем выборки.
Пример:
По выборке объема n=112, извлеченных их нормальной двумерной генеральной совокупности, был вычислен коэффициент корреляции Пирсона r=0,57. При уровне значимости α=10% проверить гипотезу H0 о равенстве генерального коэффициента корреляции нулю (ρ=0) при конкурирующей гипотезе ρ≠0.
Решение:
Постановка задачи:
H0: ρ=0
H1: ρ≠0
Найдем наблюдаемое значение критерия:
Определим значения границ двусторонней критической области из условия, что при больших объемах выборок критерий t распределен по стандартному нормальному закону распределения при справедливости нулевой гипотезы:
tкр : =1-=1-0.10=0.90→Ф0(tкр) = = =0,45 => tкр=1,65
a/2=0.05
a
a/2=0.05
a
Поскольку наблюдаемое значение критерия попало в критическую область, то следует отклонить нулевую гипотезу в пользу альтернативной гипотезы, т.е. принять, что коэффициент линейной корреляции в генеральной совокупности значим. Из этого утверждения следует, что между двумя случайными величинами X и Y в генеральной совокупности имеется линейная связь, которая позволяет использовать уравнение линейной регрессии для прогнозирования, т.е., задавая конкретное значение величины X, получать значение другой случайной величины Y.
Получился интересный результат, который надо иметь в виду. Он заключается в том, что при больших объемах выборок то же самое значение коэффициента корреляции является значимым, т.е. показывает наличие линейной связи между случайными величинами в генеральной совокупности. В то же время при малых объемах выборок это же значение коэффициента корреляции не является значимым и не позволяет сделать вывод о том, что между случайными величинами в генеральной совокупности имеется линейная связь, поскольку для получения такого вывода в случае малых выборок имеется недостаточное количество экспериментальных данных.
Проверка гипотезы о значимости выборочного коэффициента корреляции Спирмена
Постановка задачи
Напоминание:
Формулы для вычисления коэффициента Спирмена:
Пояснения к приведенным формулам можно посмотреть на странице Дружининской И.М.в файле « Очень краткое изложение курса лекций по теории вероятностей и математической статистике для факультета менеджмента».
При проверке значимости коэффициента корреляции Спирмена поступают совершенно аналогично тому, как мы поступали, работая с коэффициентом Пирсона. Формулы для вычислений используются те же самые с учетом небольших изменений:
Если объем выборки совсем маленький (n), то для выяснения значимости коэффициента корреляции нужны специальные таблицы, которые приводятся в специальных руководствах (этот случай мы рассматривать не будем).
Если объем выборки n ³ 9, то при справедливости гипотезы H0 критерий
имеет распределение Стьюдента с k = n — 2 степенями свободы;
tкр находим по таблице критических точек распределения Стьюдента по значениям a и k для двусторонней критической области. Вычисляем tнабл на основе приведенной выше формулы. Если | tнабл |кр, то принимается гипотеза H0, если | tнабл |³ tкр, то принимается гипотеза H1, т.е. в этом случае считаем доказанным утверждение, что коэффициент корреляции является значимым и в генеральной совокупности между порядковыми качественными признаками имеется корреляционная связь.
Если объем выборки n >30, то вместо закона Стьюдента используем стандартный нормальный закон распределения.
geum.ru
