Что такое окружность как геометрическая фигура: основные свойства и характеристики
Чтоб в общих чертах представить для себя, что такое окружность, посмотрите на кольцо либо обруч. Можно также взять круглый стакан и чашечку, поставить ввысь дном на лист бумаги и обвести карандашом. При неоднократном увеличении приобретенная линия станет толстой и не совершенно ровненькой, и края ее будут размытыми. Окружность как геометрическая фигура не имеет таковой свойства, как толщина.
 Окружность: определение и главные средства описания
Окружность: определение и главные средства описания
Окружность – это замкнутая кривая, состоящая из огромного количества точек, расположенных в одной плоскости и равноудаленных от центра окружности. При всем этом центр находится в той же плоскости. Обычно, он обозначается буковкой О.
Расстояние от хоть какой из точек окружности до центра именуется радиусом и обозначается буковкой R.
Если соединить две любые точки окружности, то приобретенный отрезок будет называться хордой. Хорда, проходящая через центр окружности, – это поперечник, обозначаемый буковкой D. Поперечник разделяет окружность на две равные дуги и по длине в два раза превосходит размер радиуса. Таким макаром, D = 2R, либо R = D/2.
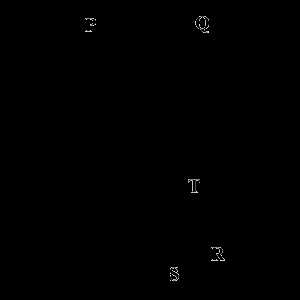
Характеристики хорд
- Если через две любые точки окружности провести хорду, а потом перпендикулярно последней – радиус либо поперечник, то этот отрезок разобьет и хорду, и дугу, отсеченную ею, на две равные части. Правильно и оборотное утверждение: если радиус (поперечник) разделяет хорду напополам, то он перпендикулярен ей.
- Если в границах одной и той же окружности провести две параллельные хорды, то дуги, отсеченные ними, также заключенные меж ними, будут равны.
- Проведем две хорды PR и QS, пересекающиеся в границах окружности в точке T. Произведение отрезков одной хорды всегда будет равно произведению отрезков другой хорды, другими словами PT х TR = QT х TS.
Длина окружности: общее понятие и главные формулы
Одной из базисных черт данной геометрической фигуры является длина окружности. Формула выводится с внедрением таких величин, как радиус, поперечник и константа “π”, отражающая всепостоянство дела длины окружности к ее поперечнику.
Таким макаром, L = πD, либо L = 2πR, где L – это длина окружности, D – поперечник, R – радиус.
Формула длины окружности может рассматриваться как начальная при нахождении радиуса либо поперечника по данной длине окружности: D = L/π, R = L/2π.
Что такое окружность: главные постулаты
1. Ровная и окружность могут размещаться на плоскости последующим образом:
- не иметь общих точек;
- иметь одну общую точку, при всем этом ровная именуется касательной: если провести радиус через центр и точку касания, то он будет перпендикулярен касательной;
- иметь две общие точки, при всем этом ровная именуется секущей.
2. Через три произвольные точки, лежащие в одной плоскости, можно провести менее одной окружности.
3. Две окружности могут соприкасаться исключительно в одной точке, которая размещена на отрезке, соединяющем центры этих окружностей.
4. При всех поворотах относительно центра окружность перебегает сама в себя.
5. Что такое окружность исходя из убеждений симметрии?
- однообразная кривизна полосы в хоть какой из точек;
- центральная симметрия относительно точки О;
- зеркальная симметрия относительно поперечника.
6. Если выстроить два случайных вписанных угла, опирающихся на одну и ту же дугу окружности, они будут равны. Угол, опирающийся на дугу, равную половине длины окружности, другими словами отсеченную хордой-диаметром, всегда равен 90°.
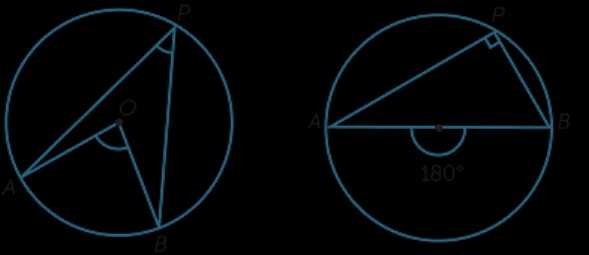
7. Если ассоциировать замкнутые кривые полосы схожей длины, то получится, что окружность отграничивает участок плоскости большей площади.
Окружность, вписанная в треугольник и описанная около него
Представление о том, что такое окружность, будет неполным без описания особенностей связи этой геометрической фигуры с треугольниками.
- При построении окружности, вписанной в треугольник, ее центр всегда будет совпадать с точкой скрещения биссектрис углов треугольника.
- Центр окружности, описанной около треугольника, размещается на скрещении срединных перпендикуляров к каждой из сторон треугольника.
- Если обрисовать окружность около прямоугольного треугольника, то ее центр будет находиться на середине гипотенузы, другими словами последняя будет являться поперечником.
- Центры вписанной и описанной окружностей будут находиться в одной точке, если базой для построения является равносторонний треугольник.
Главные утверждения об окружности и четырехугольниках
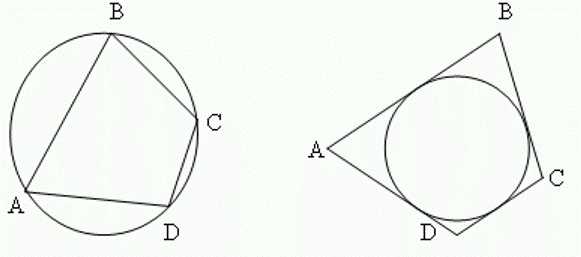
- Вокруг выпуклого четырехугольника можно обрисовать окружность только тогда, когда сумма его обратных внутренних углов приравнивается 180°.
- Выстроить вписанную в выпуклый четырехугольник окружность можно, если схожа сумма длин его обратных сторон.
- Обрисовать окружность вокруг параллелограмма можно, если его углы прямые.
- Выстроить окружность через углы трапеции можно, только если она равнобедренная. При всем этом центр описанной окружности будет размещаться на скрещении оси симметрии четырехугольника и срединного перпендикуляра, проведенного к боковой стороне.
tipsboard.ru
Что такое окружность как геометрическая фигура: основные свойства и характеристики
Чтобы в общих чертах представить себе, что такое окружность, взгляните на кольцо или обруч. Можно также взять круглый стакан и чашку, поставить вверх дном на лист бумаги и обвести карандашом. При многократном увеличении полученная линия станет толстой и не совсем ровной, и края ее будут размытыми. Окружность как геометрическая фигура не имеет такой характеристики, как толщина.
 Окружность: определение и основные средства описания
Окружность: определение и основные средства описания
Окружность – это замкнутая кривая, состоящая из множества точек, расположенных в одной плоскости и равноудаленных от центра окружности. При этом центр находится в той же плоскости. Как правило, он обозначается буквой О.
Расстояние от любой из точек окружности до центра называется радиусом и обозначается буквой R.
Если соединить две любые точки окружности, то полученный отрезок будет называться хордой. Хорда, проходящая через центр окружности, — это диаметр, обозначаемый буквой D. Диаметр делит окружность на две равные дуги и по длине вдвое превышает размер радиуса. Таким образом, D = 2R, или R = D/2.
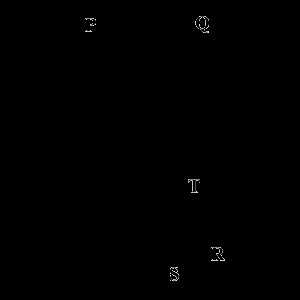
Свойства хорд
- Если через две любые точки окружности провести хорду, а затем перпендикулярно последней – радиус или диаметр, то этот отрезок разобьет и хорду, и дугу, отсеченную ею, на две равные части. Верно и обратное утверждение: если радиус (диаметр) делит хорду пополам, то он перпендикулярен ей.
- Если в пределах одной и той же окружности провести две параллельные хорды, то дуги, отсеченные ними, а также заключенные между ними, будут равны.
- Проведем две хорды PR и QS, пересекающиеся в пределах окружности в точке T. Произведение отрезков одной хорды всегда будет равно произведению отрезков другой хорды, то есть PT х TR = QT х TS.
Длина окружности: общее понятие и основные формулы
Одной из базовых характеристик данной геометрической фигуры является длина окружности. Формула выводится с использованием таких величин, как радиус, диаметр и константа «π», отражающая постоянство отношения длины окружности к ее диаметру.
Таким образом, L = πD, или L = 2πR, где L – это длина окружности, D – диаметр, R – радиус.
Формула длины окружности может рассматриваться как исходная при нахождении радиуса или диаметра по заданной длине окружности: D = L/π, R = L/2π.
Что такое окружность: основные постулаты
1. Прямая и окружность могут располагаться на плоскости следующим образом:
- не иметь общих точек;
- иметь одну общую точку, при этом прямая называется касательной: если провести радиус через центр и точку касания, то он будет перпендикулярен касательной;
- иметь две общие точки, при этом прямая называется секущей.
2. Через три произвольные точки, лежащие в одной плоскости, можно провести не более одной окружности.
3. Две окружности могут соприкасаться только в одной точке, которая расположена на отрезке, соединяющем центры этих окружностей.
4. При любых поворотах относительно центра окружность переходит сама в себя.
5. Что такое окружность с точки зрения симметрии?
- одинаковая кривизна линии в любой из точек;
- центральная симметрия относительно точки О;
- зеркальная симметрия относительно диаметра.
6. Если построить два произвольных вписанных угла, опирающихся на одну и ту же дугу окружности, они будут равны. Угол, опирающийся на дугу, равную половине длины окружности, то есть отсеченную хордой-диаметром, всегда равен 90°.
7. Если сравнивать замкнутые кривые линии одинаковой длины, то получится, что окружность отграничивает участок плоскости наибольшей площади.
Окружность, вписанная в треугольник и описанная около него
Представление о том, что такое окружность, будет неполным без описания особенностей взаимосвязи этой геометрической фигуры с треугольниками.
- При построении окружности, вписанной в треугольник, ее центр всегда будет совпадать с точкой пересечения биссектрис углов треугольника.
- Центр окружности, описанной около треугольника, располагается на пересечении срединных перпендикуляров к каждой из сторон треугольника.
- Если описать окружность около прямоугольного треугольника, то ее центр будет находиться на середине гипотенузы, то есть последняя будет являться диаметром.
- Центры вписанной и описанной окружностей будут находиться в одной точке, если базой для построения является равносторонний треугольник.
Основные утверждения об окружности и четырехугольниках
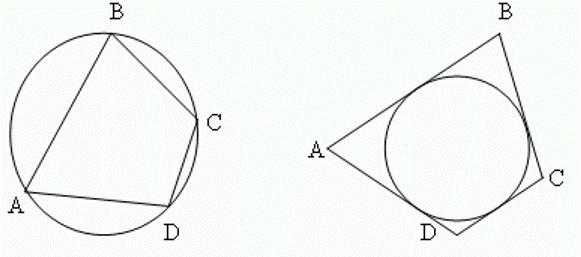
- Вокруг выпуклого четырехугольника можно описать окружность лишь тогда, когда сумма его противоположных внутренних углов равняется 180°.
- Построить вписанную в выпуклый четырехугольник окружность можно, если одинакова сумма длин его противоположных сторон.
- Описать окружность вокруг параллелограмма можно, если его углы прямые.
- Вписать в параллелограмм окружность можно в том случае, если все его стороны равны, то есть он является ромбом.
- Построить окружность через углы трапеции можно, только если она равнобедренная. При этом центр описанной окружности будет располагаться на пересечении оси симметрии четырехугольника и срединного перпендикуляра, проведенного к боковой стороне.
ОКРУЖНОСТЬ И КРУГ — ОКРУЖНОСТЬ И КРУГ. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ — Учебник Геометрия 7 класс Бевз Г.П. — Возрождение 2015 год
Круг — первая самая простая и самая совершенная фигура.
Прокл
РАЗДЕЛ 4 ОКРУЖНОСТЬ И КРУГ. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
В этом разделе вы расширите и углубите свои знания о круге и круг, приобретенные в предыдущих классах, узнаете о взаимное расположение на плоскости прямой и окружности, двух окружностей; о свойствах касательной к окружности, касательных окружностей; окружности вписанные и описанные вокруг треугольника А еще поймете, что такое геометрическое место точек, научитесь выполнять основные геометрические построения и решать более сложные задачи на построение циркулем и линейкой.
§ 17. ОКРУЖНОСТЬ И КРУГ
Круг — это фигура, состоящая из всех точек плоскости, равноудаленных от данной точки. Эту точку называют центром окружности.
Отрезок, соединяющий любую точку окружности с его центром, называют радиусом. Отрезок, соединяющий две произвольные точки окружности, называют хордой круга.
Хорду, проходящую через центр окружности, называют диаметром (рис. 209). Каждый Диаметр окружности состоит из двух радиусов, поэтому его длина вдвое больше длины радиуса. Если хорда не проходит через центр окружности, ее длин а меньшая от длины диаметра. (Почему?)
Круг на бумаге изображают с помощью циркуля.
Считают, что из данного центра на плоскости можно описать только одну окружность данного радиуса (рис. 210).
Прямая и окружность могут иметь две общие точки (рис. 211, а), одну общую точку (мат. 211,6) или не иметь ни одной (рис. 211, в).
Прямую, имеющую с окружностью две общие точки, называют секущей.
Прямую, имеющую с окружностью только одну общую точку, называется касательной к окружности. Их общую точку называют точкой касания. (Речь идет о фигуры на одной плоскости.) Точка касания лежит на круге, поэтому касательная удалена от центра круга на расстояние, равное длине радиуса. Поскольку все остальные точки касательной лежат вне круга, расстояния от них до центра окружности больше длины радиуса. Из этого следует, такое утверждение.
Рис. 209
Рис. 210
Касательная к окружности перпендикулярна к ного радиуса, проведенного в точку касания.
Рис.211
Чтобы через данную на окружности точку К провести касательную к этой окружности, надо провести радиус ОК, а потом — прямую KM, перпендикулярную этому радиусу (рис. 212).
Если два круга имеют две стальные точки, то говорят, что данные окружности пересекаются в этих точках. Точки пересечения двух кот лежат по разные стороны от прямой, которая проходит через центры этих окружностей. На рисунке 213 изображены круги с центрами О и O, пересекаются в точках А и В.
Если две окружности имеют только одну общую точку, говорят, что они соприкасаются в этой точке. Касание двух окружностей может быть внешним (рис. 214) или внутренним (рис. 215). В обоих случаях точка касания и центры окружностей лежат на одной прямой.
Два круга одной плоскости, имеющих общий центр, называются концентрическими кругами (рис. 216).
Обычно круги чертят, пользуясь циркулем. Но иногда удобнее это делать с помощью специальных шаблонов с вырезанными кругами разных радиусов.
Окружность делит плоскость на две части (области). Объединение круга с его внутренней областью называют кругом. Граница круга — окружность. Центром, радиусам, диаметром, хордой круга называют соответственно центр, радиус, диаметр, хорду окружности, которая является границей данного круга (рис. 217).
Рис. 212
Рис. 213
Рис. 214
Рис. 215
Рис. 216
Рис. 217
Форму круга имеет обруч, форму круга — дно ведра, видимый диск Солнца и тому подобное. Колесо на рельсе — материальная модель круга, что примыкает к прямой. На схематическом изображении подшипника (рис. 218) есть несколько соприкасающихся кругов.
Как вам известно из предыдущих классов, длину С окружности и площадь S круга выражается через радиус r следующим формулам:
С = 2 пг, S = пг2.
Строгие доказательства этих формул будут рассматриваться в старших классах.
Рис. 218
Для любознательных
Слово круг — древнеукраинское. Оно масс один корень со словами колода, колоть, колотить, сколоть. Околотами называли праукраинцев, которые жили на землях современной Украины за скифов и еще раньше. А еще слово коло в русском языке служит предлогом, как и вокруг, вокруг. Если к забитому в землю колу (кола) привязывали животное, то она ходила вокруг, вокруг.
Раньше круг также называли кругом, например, пели: «Ой сойди, сойди, ясень месяцу, как мельничный круг». Хоть и полнолуние, и камень в мельнице имеют форму круга, а не круга. Нередко круг называли также колесом; кое-кто считает, что первые колеса научились делать мастеровые люди в наших краях.
В геометрии круг играет важную роль. Существует даже отдельная часть геометрии — геометрия кругов, в которой исследуются важные и интересные свойства геометрических фигур, связанных с кругом.
Вопросы и задания для самоконтроля
1. Что такое круг; центр окружности; радиус; диаметр; хорда?
2. Что такое круг? Чем отличается круг от окружности?
3. Сколько общих точек могут иметь: а) прямая и окружность; б) два круга?
4. Сформулируйте определение касательной к окружности. Какое свойство имеет касательная к окружности?
5. Какие круги называют касательными? Что такое точка соприкосновения?
6. Как могут соприкасаться два круга?
7. Какие окружности называют концентрическими?
Выполним вместе
1. Докажите, что точки касания окружности к сторонам угла равноудалены от его вершины.
— Пусть круг с центром О касается сторон угла А в точках В и С (рис. 219). Докажем, что АВ = АС.
Радиусы OD и ОС, проведенные в точки касания, перпендикулярны к соответствующим касательным и уровне. Поэтому прямоугольные треугольники АВО и АСО равны по гипотенузой и катетом.
Следовательно, АВ = АС.
2. Докажите, что диаметр окружности, проведенный через середину хорды, отличной от диаметра, перпендикулярен к хорде.
Пусть АВ — хорда окружности, не проходящая через центр О окружности, а КР — диаметр круга, КОТОРЫЙ проходит через середину М хорды АВ (рис. 220). Треугольник ОАВ равнобедренный, так как ОА = ОВ. А медиана ОМ равнобедренного треугольника, проведенная к его основанию, является также высотой треугольника. Поэтому ОМ ⏊ АВ, а следовательно, и КР ⏊ АВ.
3. Найдите площадь кольца, ограниченного двумя концентрическими окружностями радиусов r и r1 (рис. 221) .
Площадь S кольца равна разности площадей кругов радиусов r и r1:
S = пг2 — пг2 = п (r2 – r21).
Рис. 219
Рис. 220
ЗАДАЧИ И УПРАЖНЕНИЯ
Выполните устно
497. Сколько разных окружностей можно провести через: а) одну точку; б) две точки; в) три точки?
498. Сколько общих точек могут иметь: а) окружность и прямая; б) два круга;
в) круг и треугольник; г) круг и плоскость?
499. Дано окружность с центром О. Сколько общих точек имеет окружность с: а) прямой ОА; б) лучом ОМ?
500. Сколько различных касательных к данной окружности можно провести через данную точку, лежащую: а) на окружности; б) вне окружности; в) внутри круга?
501. Сколько пар соприкасающихся кругов на рисунке 218? А сколько пар концентрических кругов?
Рис. 221
А
502. Начертите круг. Проведите его радиус, диаметр, хорду.
503. Докажите, что диаметр — наибольшая из хорд данного круга.
504. Даны окружность и отрезок, меньшинств от диаметра. Проведите хорду, длина которой равна длине данного отрезка.
505. Найдите расстояние между центрами окружностей радиусов 5 м и 7 м, которые касаются:
а) внешним способом; б) внутренним способом.
506. Имеют ли общие точки две окружности, радиусы которых равны 3 см и 4 см, если расстояние между их центрами равно 5 см?
507. АВ и CD — равные хорды окружности с центром О. Докажите, что ∆АВО = ∆CDO.
508. Окружности с центрами О и О1 пересекаются в точках А и В. Докажите, что:
1) ∆ОАО1 = ∆ОВО1; 2) ∆ОАВ и О1АВ — равнобедренные.
509. Окружности с центрами О и О1 пересекаются в точках А и В, причем каждое из них проходит через центр другой. Найдите ∠AOB и ∠OAO1.
Бы
510. Каждое из трех окружностей проходит через центры двух других. Докажите, что их центры — вершины равностороннего треугольника.
511. Докажите, что равные хорды окружности равноудалены от центра.
512. Как построить касательную к данной окружности:
а) параллельную данной прямой;
б) перпендикулярную к данной прямой?
513. Садовник описывает круг для клумбы с помощью колышков и веревки (рис. 222).
Почему описанная таким способом фигура — круг? Получится круг, если веревка намотуватиметься на колышек?
Рис. 222
514. Найдите радиусы двух соприкасающихся окружностей, если они относятся как 1 : 3, а расстояние между центрами окружностей равно 16 см. Рассмотрите два случая.
515. Из точки А к окружности с центром О проведены касательные АВ и АС. Докажите, что АО — биссектриса угла ВАС.
516. Из точки А к окружности с центром О проведены две касательные, угол между которыми равен 60°. Найдите радиус окружности, если ОА = 10 см.
517. Из точки А к окружности проведены две касательные. Найдите угол между ними, если расстояние от точки А до точки касания равно радиусу круга.
518. Круг касается сторон угла А в точках В и С так, что АВ = ВС. Найдите меру угла А.
519. Три равные окружности с центрами O1, О2, О3 попарно касаются друг друга в точках К, Р и Т. Докажите, что:
1 )В1В2 = В2В3 = В2В1; 2) КР = РТ = ТК.
520. Из центра круга провели три луча, которые разбили данное окружность на три дуги, длина каждой из которых равна 3 см. Найдите углы между этими лучами и радиус круга.
521. Докажите, что площадь кольца, ограниченного двумя концентрическими окружностями радиусов r и r1 равна среднему арифметическому длин этих окружностей, умноженному на разницу радиусов, то есть S = lm (рис. 223).
Рис. 223
Практическое задание
522. Подготовьте презентацию на тему: а) «Круг вокруг нас»; б) «Круг вокруг нас».
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
523. Отрезок длиной а поделен на 3 равные части. Какую часть составляет расстояние между серединами первой и третьей частей?
524. Найдите длину биссектрисы треугольника с периметром 40 см, если она разбивает его на два треугольника с периметрами 20 см и 30 см.
525. Найдите площадь квадрата ABCD, если АС = 10 см.
schooled.ru
Геометрическое место точек. Круг и окружность | Учеба-Легко.РФ
Геометрическое место точек – это множество всех точек, удовлетворяющих определённым заданным условиям.
П р и м е р 1. Срединный перпендикуляр любого отрезка есть геометрическое
место точек (т.е. множество всех точек), равноудалённых от
концов этого отрезка. Пусть PO AB и AO = OB :
Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d .
Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
П р и м е р 2. Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон.
П р и м е р 3. Окружность есть геометрическое место точек (т.е. множество
всех точек), равноудалённых от её центра ( на рис. показана одна
из этих точек – А ).
Окружность — это геометрическое место точек (т.е. множество всех точек) на плоскости, равноудалённых от одной точки, называемой центром окружности. Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности ( AmB, рис.39 ) называется дугой. Прямая PQ, проходящая через точки M и N окружности ( рис.39 ), называется секущей, а её отрезок MN, лежащий внутри окружности — хордой.
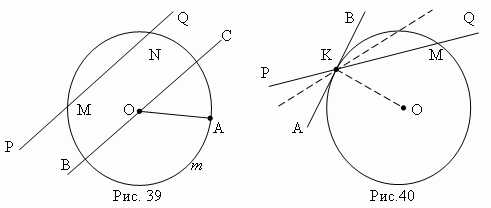
Хорда, проходящая через центр круга ( например, BC, рис.39 ), называется диаметром и обозначается d или D . Диаметр – это наибольшая хорда, равная двум радиусам ( d = 2 r ).
Касательная. Предположим, секущая PQ ( рис.40 ) проходит через точки K и M окружности. Предположим также, что точка M движется вдоль окружности, приближаясь к точке K. Тогда секущая PQ будет менять своё положение, вращаясь вокруг точки K. По мере приближения точки M к точке K секущая PQ будет стремиться к некоторому предельному положению АВ. Прямая AB называется касательной к окружности в точке K. Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.
uclg.ru

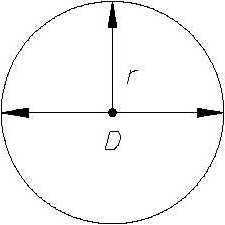 Окружность: определение и главные средства описания
Окружность: определение и главные средства описания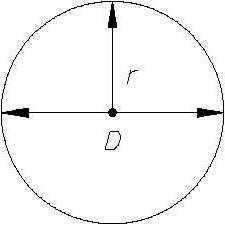 Окружность: определение и основные средства описания
Окружность: определение и основные средства описания