Транспонированная матрица пример – Транспонированная матрица.

Содержание

транспонирование матриц — ПриМат

1. Выполнить сложение матриц:
.
Для сложения матриц нам необходимо каждый элемент первой матрицы сложить с соответствующим элементом из второй:
.

Следует также отметить, что операция сложения матриц коммутативна и ассоциативна. Например, пусть даны матрицы , и . Тогда:

Покажем выполнение ассоциативности сложения матриц:

;
.
;
.

Как видим, .

2. Выполнить умножение матрицы на число:
.
Для умножения матрицы на число мы умножаем каждый элемент матрицы на данное число:
.

Операция умножения матрицы на число ассоциативна, то есть , . Покажем это на конкретном примере:
Пусть дана матрица и .
Тогда ;
.
;
.
Как видим, .

3. Вычислить произведение матриц:
.
Для удобства будем называть первую матрицу а вторую матрицу . Для начала убедимся, что произведение данных матриц возможно. Даны матрицы размерностей и , следовательно умножение возможно, так как количество столбцов первой матрицы равно количеству строк второй. Для вычисления первого элемента результирующей матрицы умножим каждый элемент первой строки матрицы на соответствующие элементы первого столбца матрицы . Полученные значения сложим. Данную последовательность действий можно проиллюстрировать следующим образом:

Получим следующее:
.
Далее вычисляем первый элемент второго столбца результирующей матрицы. Умножаем все элементы первой строки матрицы на соответствующие им элементы из второго столбца матрицы и складываем полученные значения:
.
Для вычисления первого элемента второй строки результирующей матрицы мы будем аналогично умножать элементы второй строки матрицы на элементы первого столбца матрицы , складывая результаты:
.
Оставшиеся элементы вычисляются аналогично:
.
Отметим, что произведение матриц в общем случае некоммутативно и покажем это на примере.
Пусть даны матрицы .

Тогда .
.
Как видим, .

4. Возвести матрицу в степень:
.
Для возведения в степень необходимо данную матрицу умножить саму на себя. Заметим, что возводить в степень можно только квадратные матрицы.
.

5. Транспонировать матрицу:
.
Для транспонирования матрицы достаточно записать строки столбцами, а столбцы строками:
.

Таблица лучших: Действия над матрицами. Групповые свойства некоторых матриц

максимум из 9 баллов
Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

Действия над матрицами. Групповые свойства некоторых матриц

Лимит времени: 0

Информация

Тест на тему «Действия над матрицами. Групповые свойства некоторых матриц».

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 4

Ваше время:

Время вышло

Средний результат
Ваш результат

Ваш результат был записан в таблицу лидеров

С ответом
С отметкой о просмотре

Задание 1 из 4
Количество баллов: 3
Правильно
Неправильно
Задание 2 из 4
Количество баллов: 1
Транспонировать матрицу

ib.mazurok.com

Транспонирование матриц в MS EXCEL. Примеры и методы

Транспонирование матрицы

— это операция над матрицей, при которой ее строки и столбцы меняются местами. Для этой операции в MS EXCEL существует специальная функция ТРАНСП() или англ. TRANSPOSE.

Если матрица A имеет размер n×m, то транспонированная матрица A^t имеет размер m×n.

В MS EXCEL существует специальная функция ТРАНСП() для нахождения транспонированной матрицы.

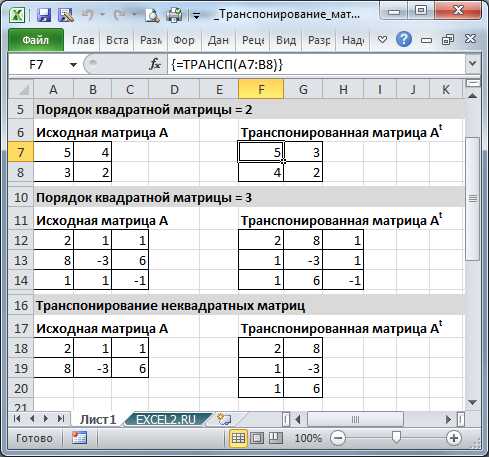
Если элементы исходной матрицы 2 х 2 расположены в диапазоне А7:В8, то для получения транспонированной матрицы нужно:

выделить диапазон 2 х 2, который не пересекается с исходным диапазоном А7:В8
в строке формул ввести формулу =ТРАНСП(A7:B8) и нажать комбинацию клавиш CTRL+SHIFT+ENTER, т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2)

Если исходная матрица не квадратная, например, 2 строки х 3 столбца, то для получения транспонированной матрицы нужно выделить диапазон из 3 строк и 2 столбцов. В принципе можно выделить и заведомо больший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.

СОВЕТ: В статьях раздела про транспонирование таблиц (см. Транспонирование) можно найти полезные приемы, которые могут быть использованы для транспонирования матриц другим способом (через специальную вставку или с использованием функций ДВССЫЛ(), АДРЕС(), СТОЛБЕЦ()).

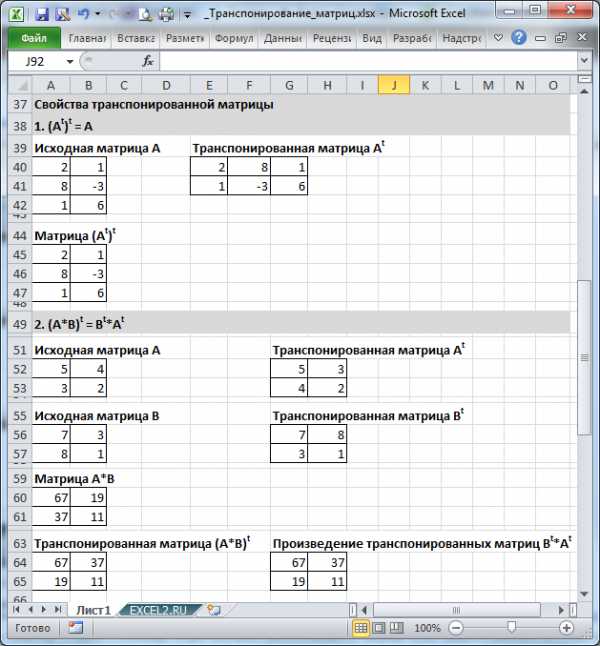
Напомним некоторые свойства транспонированных матриц (см. файл примера).

(A^t)^t = A
(k · A)^t = k · A^t(про умножение матриц на число и сложение матриц см. статью Сложение и вычитание матриц, умножение матриц на число в MS EXCEL)
(A + B)^t = A^t + B^t
(A · B)^t = B^t · A^t (про умножение матриц см. статью Умножение матриц в MS EXCEL)

excel2.ru

Транспонирование матрицы, онлайн калькулятор

Наш онлайн калькулятор позволяет транспонировать любую матрицу всего в два кликов. Для нахождения транспонированной матрицы выберите ее размеры (матрица не обязательно должна быть квадратной), введите значения всех элементов матрицы и нажмите кнопку «Вычислить», калькулятор выдаст подробное решение и ответ! Каждый шаг будет подробно расписан, это поможет вам понять, как был получен ответ.

Заполните элементы матрицы Решили сегодня: раз, всего раз

Понравился сайт? Расскажи друзьям!

Как найти транспонированную матрицу онлайн

Транспонирование матрицы через данный онлайн калькулятор не займёт у вас много времени, но зато быстро даст результат и поможет лучше разобраться в самом процессе.

Иногда в алгебраических вычислениях возникает потребность поменять местами строки и столбцы матрицы. Такая операция именуется транспонированием матрицы. Строки по порядку становятся столбцами, а сама матрица – транспонированной. В данных вычислениях есть определённые правила, и чтобы в них разобраться и наглядно ознакомиться с процессом, воспользуйтесь данным онлайн калькулятором. Он существенно облегчит вам задачу и поможет лучше усвоить теорию транспонирования матриц. Значительным плюсом данного калькулятора является демонстрация развёрнутой и детального решения. Таким образом, его использование способствует получению более глубоких и осознанных представлений об алгебраических расчётах. K тому же, с его помощью всегда можно проверить, насколько успешно вы справились с задачей, производя транспонирование матриц вручную.

Пользоваться калькулятором очень просто. Чтобы найти транспонированную матрицу онлайн укажите размер матрицы нажатием на иконки «+» или «-» до получения нужных значений числа столбцов и строк. Далее в поля вводятся необходимые цифры. Ниже расположена кнопка «Вычислить» — её нажатие выводит на экран готовое решение с подробной расшифровкой алгоритма.

ru.solverbook.com

Сопряжённо-транспонированная матрица Вики

Эрми́тово-сопряжённая ма́трица или сопряжённо-транспони́рованная ма́трица — это матрица A{\displaystyle A}^* с комплексными элементами, полученная из исходной матрицы A{\displaystyle A} транспонированием и заменой каждого элемента комплексно-сопряжённым ему.

Эрмитово-сопряжённые матрицы во многом играют ту же роль при изучении комплексных векторных пространств, что и транспонированные матрицы в случае вещественных пространств.

Определение и обозначения[ | код]

Если исходная матрица A{\displaystyle A} имеет размер m×n{\displaystyle m\times n}, то эрмитово-сопряжённая к A{\displaystyle A} матрица A∗{\displaystyle A^{*}} будет иметь размер n×m,{\displaystyle n\times m,} а её (i,j){\displaystyle (i,j)}-й элемент будет равен:

(A∗)ij=Aji¯,{\displaystyle \left(A^{*}\right)_{ij}={\overline {A_{ji}}},}

где z¯{\displaystyle {\overline {z}}} обозначает комплексно-сопряжённое число к z{\displaystyle z} (сопряжённое число к a+bi{\displaystyle a+bi} есть a−bi{\displaystyle a-bi}, где a{\displaystyle a} и b{\displaystyle b} — вещественные числа).

Эрмитово-сопряжённую матрицу обычно обозначают как A∗{\displaystyle A^{*}} или AH{\displaystyle A^{H}} (H от англ. Hermitian — эрмитова), но иногда используются и другие обозначения:

A†{\displaystyle A^{\dagger }} — в квантовой механике;
A+{\displaystyle A^{+}} — но это обозначение может быть спутано с обозначением для псевдообратной матрицы;
A¯T{\displaystyle {\overline {A}}^{\text{T}}}.

Пример[ | код]

Если

A=[3+i52−2ii]{\displaystyle A={\begin{bmatrix}3+i&5\\2-2i&i\end{bmatrix}}}

тогда

A∗=[3−i2+2i5−i].{\displaystyle A^{*}={\begin{bmatrix}3-i&2+2i\\5&-i\end{bmatrix}}.}

Связанные определения[ | код]

Если матрица A{\displaystyle A} состоит из вещественных чисел, то эрмитово-сопряжённая к ней матрица — это просто транспонированная матрица:

A∗=AT,{\displaystyle A^{*}=A^{T},} если aij∈R.{\displaystyle a_{ij}\in \mathbb {R} .}

Квадратная матрица A{\displaystyle A} называется:

Свойства[ | код]

(A+B)∗=A∗+B∗{\displaystyle (A+B)^{*}=A^{*}+B^{*}} для любых двух матриц A{\displaystyle A} и B{\displaystyle B} одинаковых размеров.
(cA)∗=c¯A∗{\displaystyle (cA)^{*}={\overline {c}}A^{*}} для любого комплексного скаляра c∈C{\displaystyle c\in \mathbb {C} }.
(AB)∗=B∗A∗{\displaystyle (AB)^{*}=B^{*}A^{*}} для любых матриц A{\displaystyle A} и B{\displaystyle B}, таких, что определено их произведение AB{\displaystyle AB}. Обратите внимание, что в правой части равенства порядок перемножения матриц меняется на противоположный.
(A∗)∗=A{\displaystyle (A^{*})^{*}=A} для любой матрицы A{\displaystyle A}.
Собственные значения, определитель и след меняются на сопряжённые у эрмитово-сопряжённой матрицы, по сравнению с исходной.
A{\displaystyle A} обратима тогда и только тогда, когда обратима матрица A∗{\displaystyle A^{*}}. При этом:
(A∗)−1=(A−1)∗{\displaystyle (A^{*})^{-1}=(A^{-1})^{*}}
⟨Ax,y⟩=⟨x,A∗y⟩{\displaystyle \langle Ax,y\rangle =\langle x,A^{*}y\rangle } для любой матрицы A{\displaystyle A} размера m×n{\displaystyle m\times n} и любых векторов x∈Cn{\displaystyle x\in \mathbb {C} ^{n}} и y∈Cm{\displaystyle y\in \mathbb {C} ^{m}}. Обозначение ⟨⋅,⋅⟩{\displaystyle \langle \cdot ,\cdot \rangle } обозначает стандартное скалярное произведение векторов в комплексном векторном пространстве.
Матрицы AA∗{\displaystyle AA^{*}} и A∗A{\displaystyle A^{*}A} являются эрмитовыми и положительно-полуопределёнными для любой матрицы A{\displaystyle A} (необязательно квадратной). Если A{\displaystyle A} квадратная и невырожденная, то эти две матрицы будут положительно-определёнными.

См. также[ | код]

Сопряжённый оператор — обобщение понятия эрмитово-сопряжённой матрицы для бесконечномерных пространств.

Ссылки[ | код]

Транспонированная матрица Википедия

Транспонированная матрица — матрица AT{\displaystyle A^{T}}, полученная из исходной матрицы A{\displaystyle A} заменой строк на столбцы.

Формально, транспонированная матрица для матрицы A{\displaystyle A} размеров m×n{\displaystyle m\times n} — матрица AT{\displaystyle A^{T}} размеров n×m{\displaystyle n\times m}, определённая как AijT=Aji{\displaystyle A_{ij}^{T}=A_{ji}}.

Например,

[1234]T=[1324]{\displaystyle {\begin{bmatrix}1&2\\3&4\end{bmatrix}}^{\mathrm {T} }\!\!\;\!=\,{\begin{bmatrix}1&3\\2&4\end{bmatrix}}} и [123456]T=[135246]{\displaystyle {\begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}}^{\mathrm {T} }\!\!\;\!=\,{\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}}\;}

То есть для получения транспонированной матрицы из исходной нужно каждую строчку исходной матрицы записать в виде столбца в том же порядке.

Свойства транспонированных матриц[ | ]

Дважды транспонированная матрица А равна исходной матрице А.

(AT)T=A{\displaystyle (A^{T})^{T}=A}

Транспонированная сумма матриц равна сумме транспонированных матриц.

(A+B)T=AT+BT{\displaystyle (A+B)^{T}=A^{T}+B^{T}}

Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.

ru-wiki.ru

Действие третье. Транспонирование матрицы — КиберПедия

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Пример:
Транспонировать матрицу

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

– транспонированная матрица.

Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Пошаговый пример:
Транспонировать матрицу

Сначала переписываем первую строку в первый столбец:

Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.

Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Пример:
Сложить матрицы и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

Пример:
Найти разность матриц ,

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

Действие пятое. Умножение матриц.

Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.

Какие матрицы можно умножать?

Чтобы матрицу можно было умножить на матрицу необходимо, чтобы число столбцов матрицы равнялось числу строк матрицы .

Пример:
Можно ли умножить матрицу на матрицу ?

, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно, и вообще, такая запись не имеет смысла

Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, и возможно как умножение , так и умножение

Как умножить матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

Пример:
Умножить матрицу на матрицу
Я буду сразу приводить формулу для каждого случая:

– попытайтесь сразу уловить закономерность.

Пример сложнее:

Умножить матрицу на матрицу

Формула:

В результате получена так называемая нулевая матрица.

Попробуйте самостоятельно выполнить умножение (правильный ответ ).

Обратите внимание, что ! Это почти всегда так!

Таким образом, переставлять матрицы в произведении нельзя!

Если в задании предложено умножить матрицу на матрицу , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка: