2. Градиент, дивергенция, ротор
Если каждой точке М пространства или некоторой его области V поставлена в соответствие скалярная величина u(М), то говорят, что в этой области задано скалярное поле. В декартовой системе координат задание скалярного поля эквивалентно заданию функции трех переменных u(М) = u(x,y,z). Примерами скалярных полей могут служить поле температур данного тела, поле атмосферного давления и т.д. Пусть функция u(x, y, z) является непрерывно дифференцируемой в области V. В каждой точке этой области определен вектор, проекциями которого на оси координат являются значения частных производных функции u(x,y,z):
Вектор grad u направлен в сторону наибыстрейшего возрастания скалярного поля
Если
каждой точке М некоторой области V поставлен в соответствие определенный
вектор 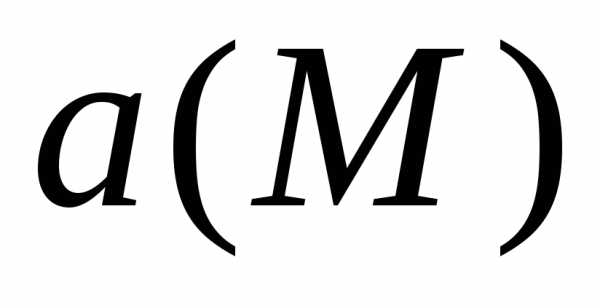 ,
то говорят, что в этой области задано
векторное поле. В декартовой системе
координат задание векторного поля
равносильно заданию трех скалярных
функций:P(x,y,z), Q(x,y,z)
и R(x,y,z)
– проекций этого вектора на оси координат.
Вектор
,
то говорят, что в этой области задано
векторное поле. В декартовой системе
координат задание векторного поля
равносильно заданию трех скалярных
функций:P(x,y,z), Q(x,y,z)
и R(x,y,z)
– проекций этого вектора на оси координат.
Вектор 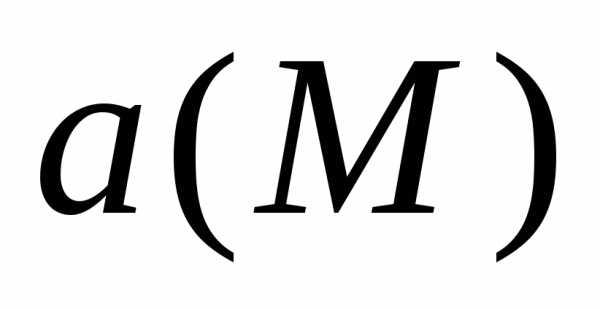 в этом случае записывается в виде
в этом случае записывается в виде

а функции P(x,y,z
), Q(x,y,z) и R(x,y,z) являются непрерывно дифференцируемыми в области V. В качестве примера векторного поля можно рассмотреть поле скоростей стационарного потока жидкости. Дивергенцией векторного поля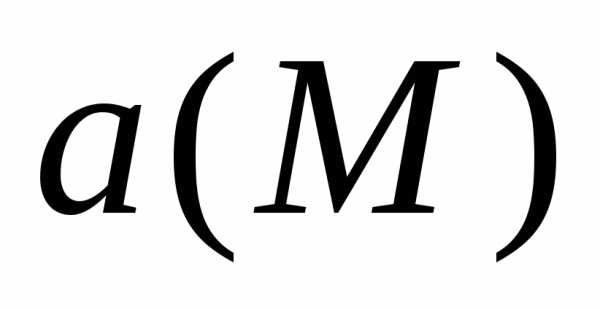 называется скаляр
называется скаляр Ротором
(вихрем) векторного поля 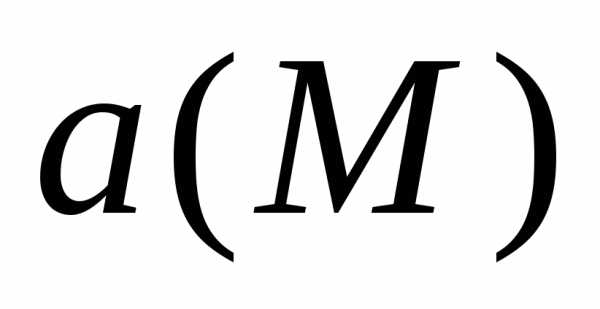 называется
вектор
называется
вектор
Все
рассмотренные величины полей: grad u,
div  иrot
иrot  вычисляются с помощью частного
дифференцирования скалярного поляu и компонентов P, Q, R векторного поля
вычисляются с помощью частного
дифференцирования скалярного поляu и компонентов P, Q, R векторного поля .
Таким образом, мы имеем дело с
дифференциальными операциями первого
порядка. Наряду с ними можно рассмотреть
дифференциальные операции второго
порядка:grad
div
.
Таким образом, мы имеем дело с
дифференциальными операциями первого
порядка. Наряду с ними можно рассмотреть
дифференциальные операции второго
порядка:grad
div 
 иdiv
grad u.
Рассмотрим последнюю операцию:
иdiv
grad u.
Рассмотрим последнюю операцию:Эту операцию можно записать кратко, вводя оператор Лапласа
Для векторного поля
3. Экстремум функции нескольких переменных
Максимумом
(минимумом) функции
называется такое значение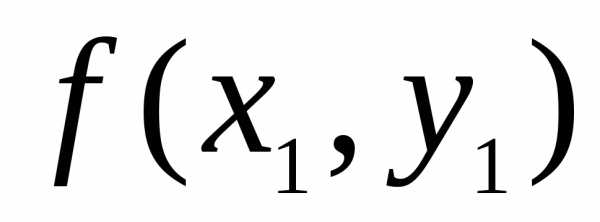 этой функции, которое больше (меньше)
всех ее значений
этой функции, которое больше (меньше)
всех ее значений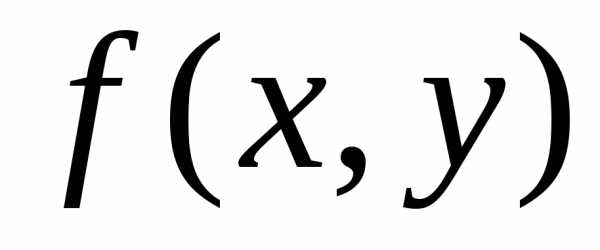 ,
принимаемой данной функцией в точках
некоторой окрестности точки
,
принимаемой данной функцией в точках
некоторой окрестности точки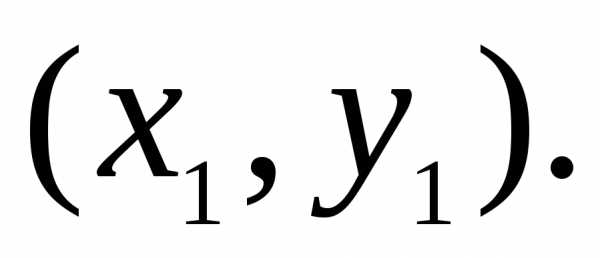 Максимум или минимум функции
Максимум или минимум функции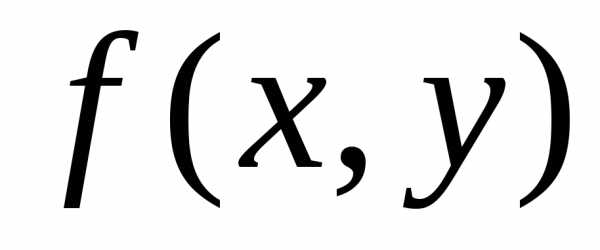
а)
Необходимый признак экстремума: в точке
экстремума функции нескольких переменных
каждая ее частная производная первого
порядка либо равна нулю, либо не существует 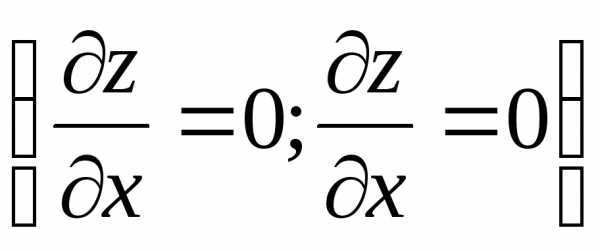 .
Точки, в которых частные производные
первого порядка равна нулю, либо не
существуют, называются критическими;
.
Точки, в которых частные производные
первого порядка равна нулю, либо не
существуют, называются критическими;
б)
Достаточный признак экстремума: если
точка
– критическая точка функциии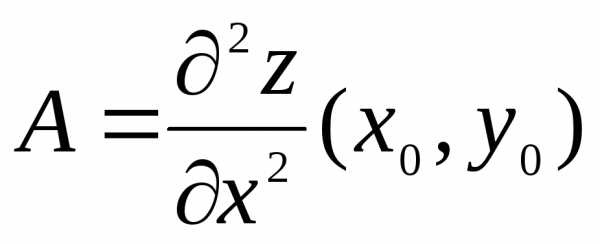 ,
,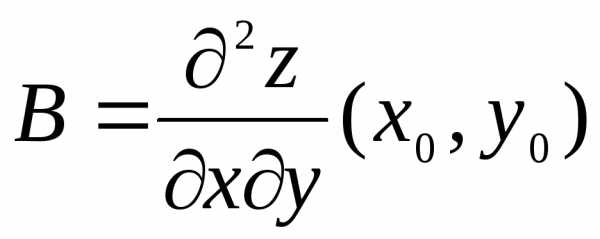 ,
,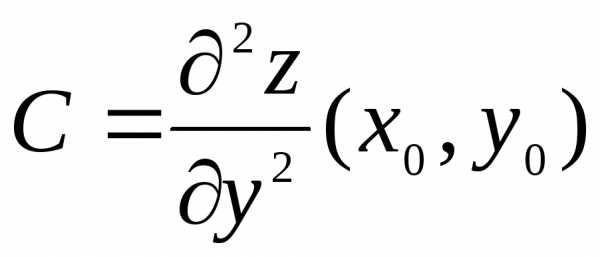 ,,
тогда:
,,
тогда:
1)
если 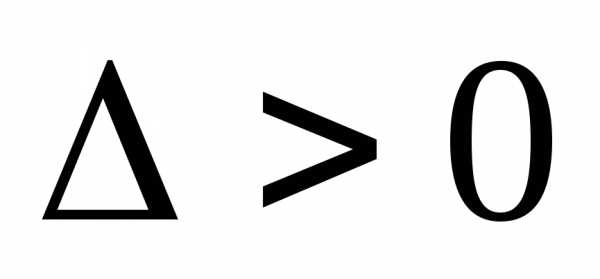 ,
то функция имеет экстремум в точке,
а именно максимум, если,
и минимум, если;
,
то функция имеет экстремум в точке,
а именно максимум, если,
и минимум, если;
2)
если 
3)
если 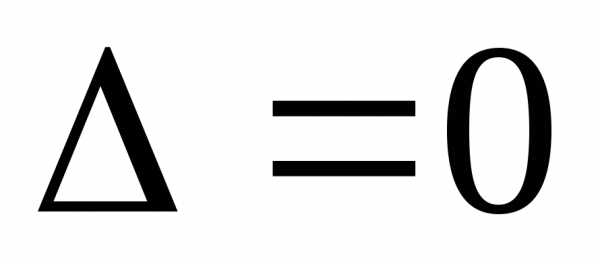 ,
то вопрос о наличии экстремума в точкетребует дополнительного исследования.
,
то вопрос о наличии экстремума в точкетребует дополнительного исследования.
Пример 3.1. Исследовать на экстремум функцию .
а) Найдем критические точки:
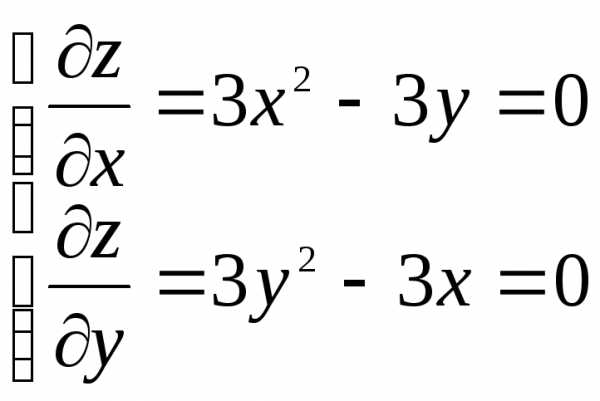

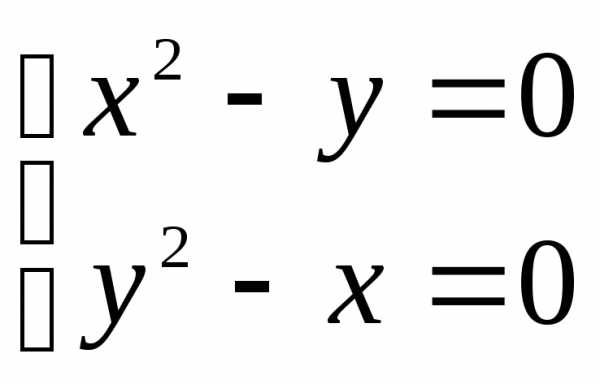

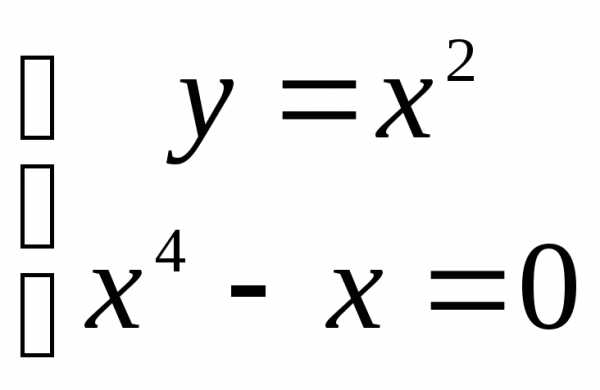

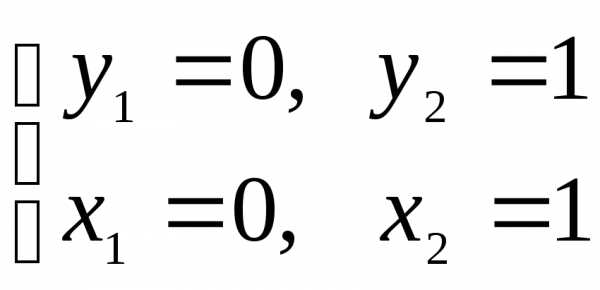
Таким
образом, имеем две критические точки 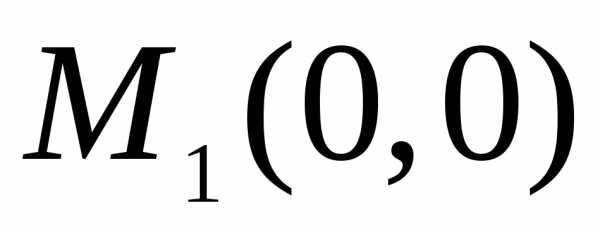 и
и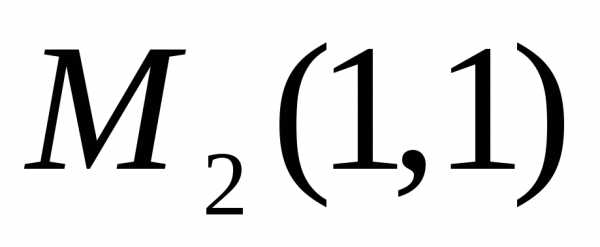
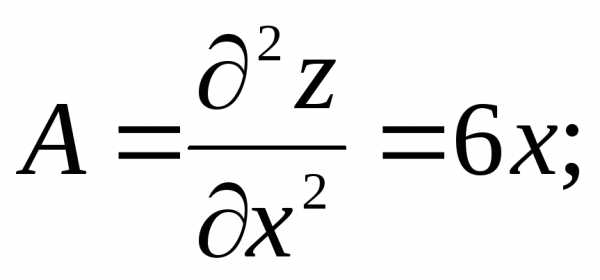
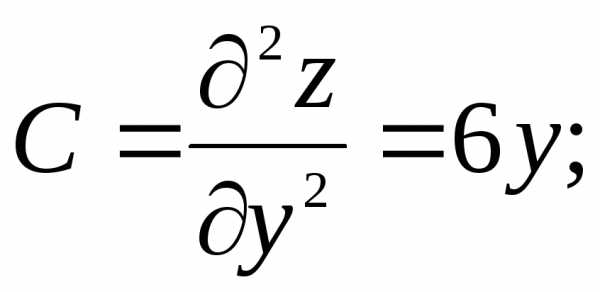
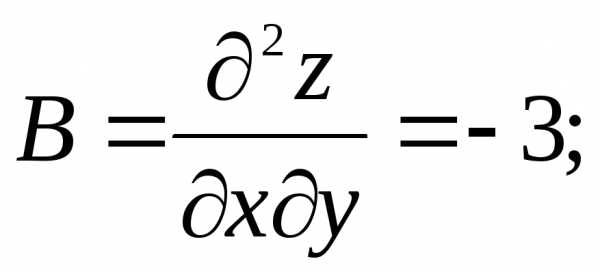 .
. В
точке
,
т.е. в этой точке экстремума нет. В точке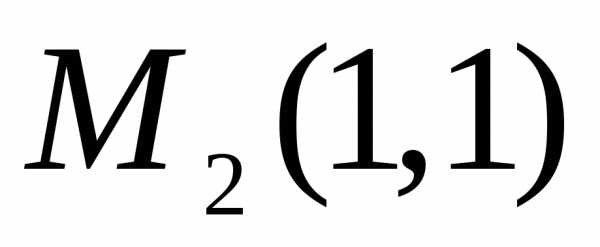 и,
следовательно, в этой точке функция
имеет локальный минимум:.
и,
следовательно, в этой точке функция
имеет локальный минимум:.
studfiles.net
Градиент, ротор, дивергенция пространства.
!Это дохуя сложная тема, тут будет много определений и формул!!Векторы я буду обозначать *!
Чтобы начать говорить про эти штуки, нам нужно вспомнить оператор набла. Грубо говоря, эта штука нужна, чтобы разложить пространство, на пространственные единичные вектора и дать нам возможность выполнять с ними всякую хуйню. Допустим, у нас есть четырёхмерное пространство А, с координатами п, и, д, р, записывается это так А(п,и,д,р) – запомним.
Если мы захотим записать оператор набла, то выглядит это так:
• ∇=∂/(∂х1)е1*+∂/(∂х2)е2*+..+∂/(∂хn)еn*
Где х1..хn – координаты, e* – единичный пространственный вектор, n – размерность этого пространства.
Итак, градиент.
Если мы хотим (ну просто за каким-то хуем, у всех такое бывает) записать какое-то пространство в виде векторов, которые показывают, как изменяется геометрия этого пространства, где векторы указывают на точку изменения, а длина вектора – скорость изменения геометрии пространства (звучит пезда занудно). Записать это можно так:
• grad(A)=∇A=∂A/(∂п)п*+∂А/(∂и)и*+ ∂А/(∂д)д*+∂А/(∂р)р*
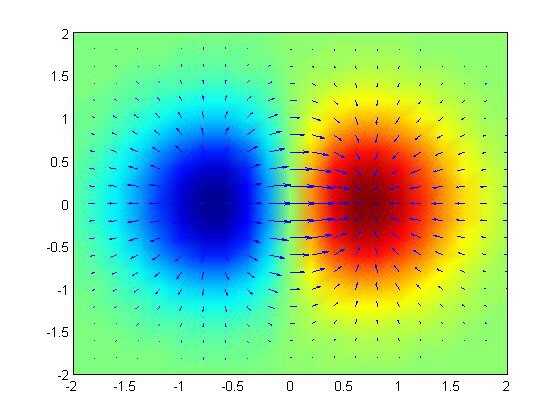
Эта хуета используется в физике для !УПРОЩЕНИЯ!, а также в уравнениях Максвелла. Чтобы это понять, можно это представить так (картинка 1): 2 области температуры: синяя – холодная, красная – горячая. Так вот, векторы будут показывать насколько быстро меняется температура, потом эти векторы без изменений переносят на новое пространство и вуаля – градиент.
Ротор пространства. Усложняем.
Эта хуета показывает нам вращение какого-либо объекта в «искривлении» пространства. Записать это можно так:
• rot(А)=∇хА(векторное умножение)=2ω(угловые скорости)
Полную формулу писать я не буду – ее вы можете увидеть на 2 картинке.
Для понимания можно взять в пример пылинку, которую вращают потоки ветра.
Эта хуйня очень важна для физики, так как присутствует в уравнениях Максвелла.
Дивергенция пространства.
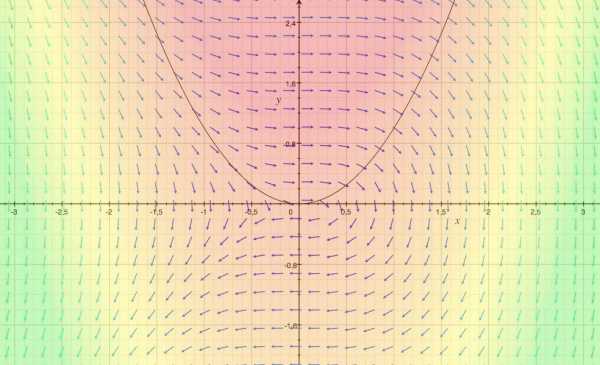
Эта поебота показывает расхождение векторного и скалярного полей. Сча поясню: у нас есть некоторая функция (допустим, парабола), если мы ее будем отображать (то есть магическим образом переносить) на скалярное (числовое) поле, то числа, которые будут образовывать нашу функцию (параболу) будут преобразовывать поток поля на повышение или понижение (3 картинка – красная область образуют параболу и является повышением потока, а зелёная – понижением; векторы указывают на направление потока). Записывается это так:
Эта неебически сложная хуета также входит в уравнения Максвелла.
Спасибо за то, что дочитали эту хуйню до конца.
С любовью, Рителлинг
Спасибо за то, что вы с нами.
С любовью, Рителлинг favorite
retell.in
Лекция №41
6
ЛЕКЦИЯ №41
14. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
ЭЛЕКТРОМАГНИТНОГО ПОЛЯ14.1. Основные операторы и векторные операции
Электромагнитное поле – это вид материи, определяемый во всех точках двумя векторными величинами, которые характеризуют две его стороны, называемые электрическим полем и магнитным полем, и оказывающий силовое воздействие на заряженные частицы, зависящее от их скорости и заряда (ГОСТ 19880-74).
Основным математическим аппаратом при расчете электромагнитного поля является векторный анализ, включающий в себя понятия: скаляр, вектор и тензор. В общем случае скаляры и векторы являются функциями координат точки и времени. При анализе электромагнитного поля применяют линейный, поверхностный и объемный интегралы, а также дифференциальные операторы.
Оператор – это символ, характеризующий действие над вектором или скаляром, расположенным после символа.
Дифференциальные операторы позволяют сократить запись различных операций над скалярными и векторными величинами.
14.1.1. Линейный, поверхностный и объемный интегралы
Пусть имеется кривая l, ограничивающая поверхность S, которая находится в электромагнитном поле (рис. 14.1).
Линейный по кривой l интеграл является скалярной величиной
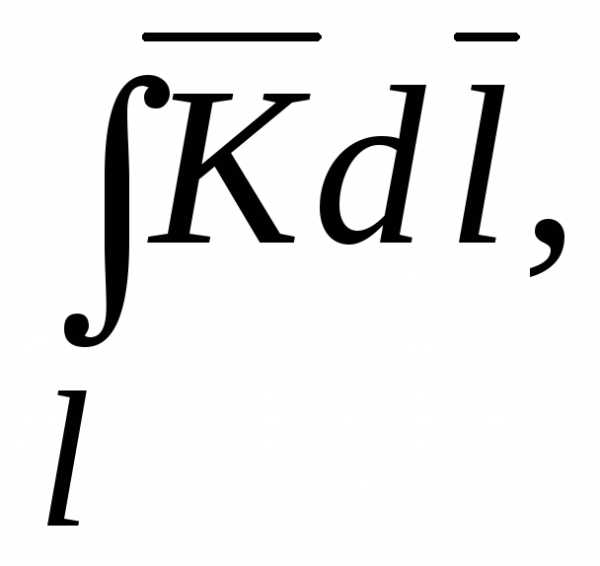 (14.1)
(14.1)
где  – вектор электромагнитного поля.
– вектор электромагнитного поля.
Вектор 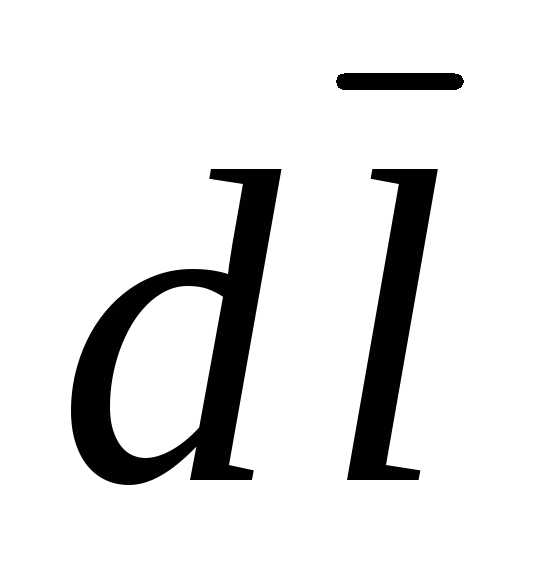 имеет направление, касательное к элементу
кривой интегрированияl.
имеет направление, касательное к элементу
кривой интегрированияl.
Циркуляцией
вектора  по замкнутой кривойl называется интеграл вида:
по замкнутой кривойl называется интеграл вида: 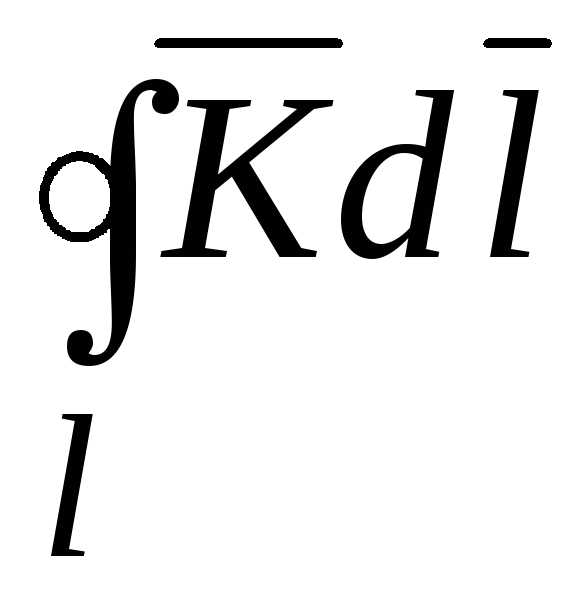 . (14.2)
. (14.2)
Поверхностный интеграл по поверхности S (рис. 14.2) имеет вид:
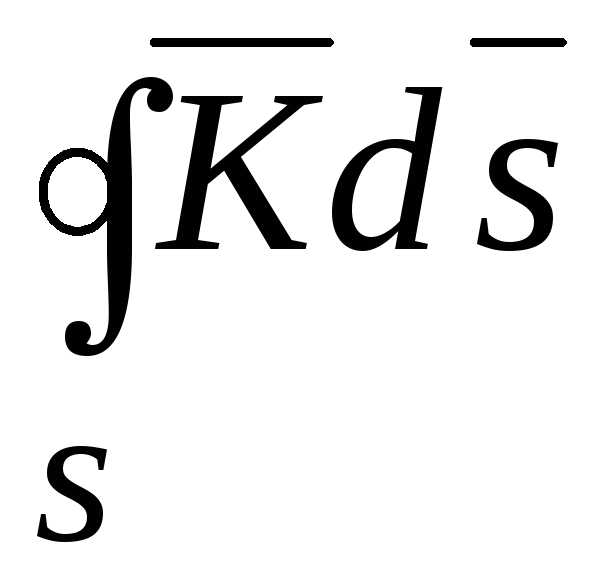 .
(14.3)
.
(14.3)
Рис. 14.2. К пояснению поверхностного интеграла
Его
часто называют потоком вектора  через поверхностьS.
через поверхностьS.
Вектор 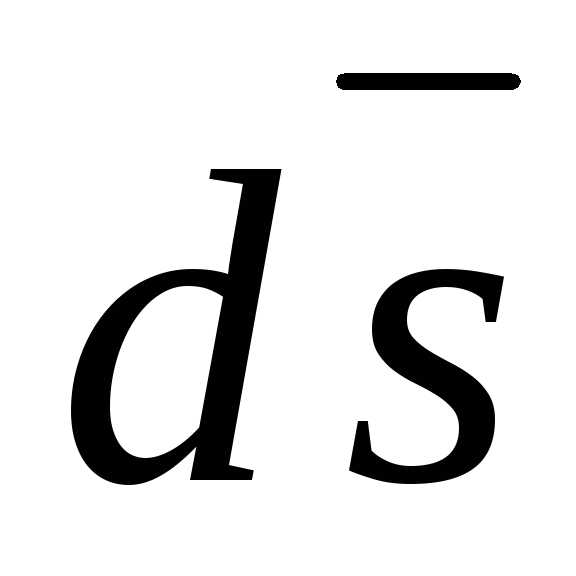 имеет направление, совпадающее с
направлением внешней нормали
имеет направление, совпадающее с
направлением внешней нормали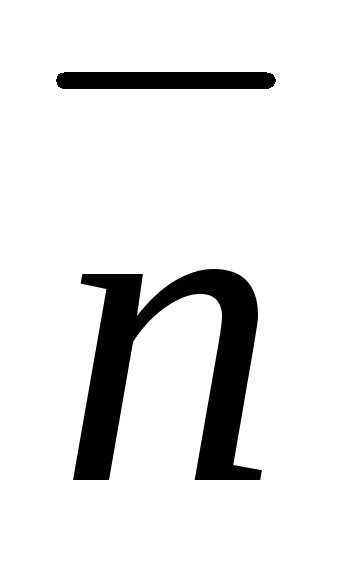 к элементу замкнутой поверхности. Он
численно равен элементу поверхностиds.
к элементу замкнутой поверхности. Он
численно равен элементу поверхностиds.
Объемный интеграл по объему V:
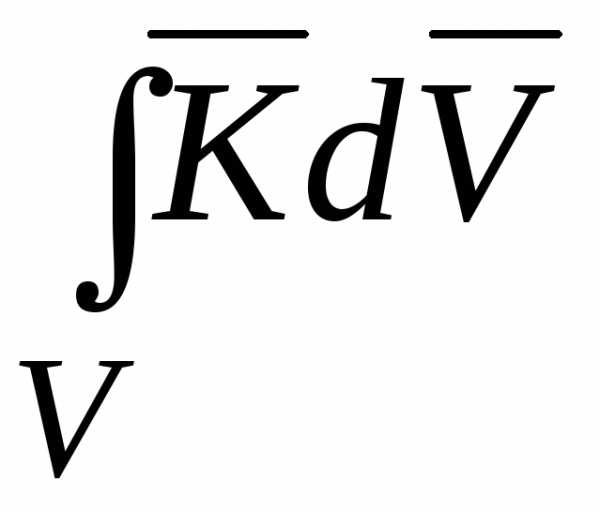 .
(14.4)
.
(14.4)
Элемент
объема  – это физически бесконечно малый объем,
который может иметь форму куба, сферы
и т.д.
– это физически бесконечно малый объем,
который может иметь форму куба, сферы
и т.д.
14.1.2. Дифференциальные операторы набла и Лапласа
Оператор набла (оператор Гамильтона) – это символический вектор, сочетающий в себе векторные и дифференцирующие свойства. Поэтому при действии с оператором необходимо применять правила векторной алгебры.
В декартовой системе координат оператор записывается:
Существует запись его в цилиндрической и сферической системах координат.
При оперировании со сложными функциями используют правила дифференцирования сложных функций:
(14.5)
Использование оператора позволяет упростить запись некоторых векторных операций. Так умножение оператора на скалярную функцию означает градиент этой функции
. (14.6)
Скалярное умножение и вектора приводит к дивергенции вектора
. (14.7)
Векторное произведение на вектор дает ротор вектора
. (14.8)
Оператор
Лапласа  (лапласиан) – это скалярный дифференциальный
оператор, определяемый как дивергенция
градиента скалярной функции (уравнение
Лапласа).
(лапласиан) – это скалярный дифференциальный
оператор, определяемый как дивергенция
градиента скалярной функции (уравнение
Лапласа).
В
декартовой системе координат оператор  запишется:
запишется:
(14.9)
Если
применить оператор  к вектору
к вектору ,
то
,
то
(14.10)
где
Векторное
уравнение 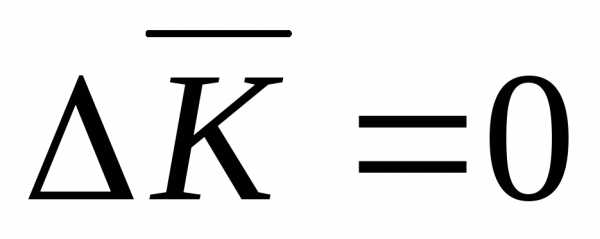 можно представить тремя скалярными
уравнениями:
можно представить тремя скалярными
уравнениями:
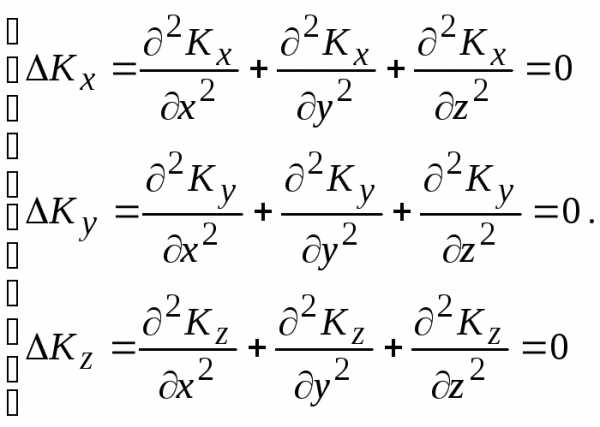 (14.11)
(14.11)
14.1.3. Понятие о градиенте, дивергенции и роторе
Градиент скалярной функции – это вектор, указывающий направление наиболее быстрого возрастания скалярной функции и по абсолютному значению равный наибольшей скорости возрастания этой функции.
(14.12)
Градиент направлен по нормали к поверхности равного уровня скалярной функции в данной точке. Градиент скалярного потенциала постоянного во времени поля равен:
(14.13)
где 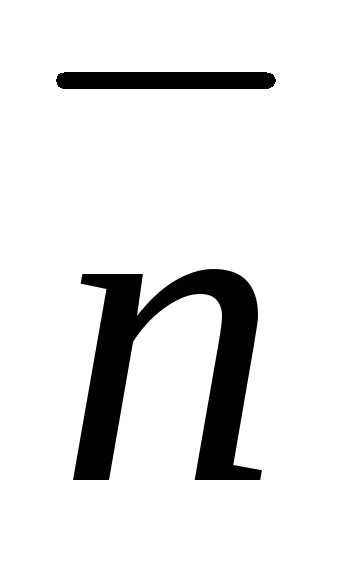 – нормаль к эквипотенциальной поверхности
в данной точке поля.
– нормаль к эквипотенциальной поверхности
в данной точке поля.
Градиент
скалярного потенциала
в каждой точке совпадает с касательной
к силовой линии напряженности
электрического поля  в данной точке и имеет направление,
противоположное вектору
в данной точке и имеет направление,
противоположное вектору (рис.
14.3).
(рис.
14.3).
Рис. 14.3. Картина электрического поля
Дивергенция (расхождение вектора) – это алгебраическая скалярная величина, характеризующая источники поля в рассматриваемой точке поля или указывающая на отсутствие источников
.
Численно дивергенцию в данной точке определяют как предел, к которому стремится отношение потока вектора через замкнутую поверхность к объему, ограниченному этой поверхностью, при стремлении этого объема к нулю
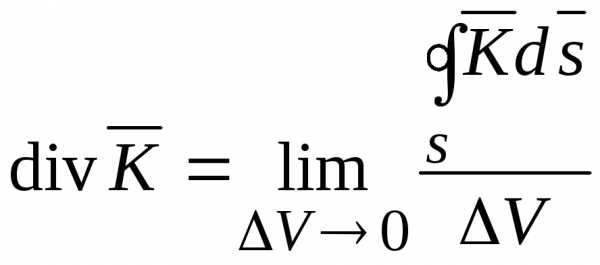 . (14.14)
. (14.14)
Если
div  > 0, то имеются источники поля и линии
вектора
> 0, то имеются источники поля и линии
вектора расходятся из данной точки. Точка
наблюдения служит началом (истоком)
линий вектора
расходятся из данной точки. Точка
наблюдения служит началом (истоком)
линий вектора .
.
Если
div  < 0, то в точке наблюдения линии вектора
< 0, то в точке наблюдения линии вектора сходятся, т.е. она служит стоком линий
вектора
сходятся, т.е. она служит стоком линий
вектора .
.
Если
div  = 0, то в рассматриваемой точке отсутствует
источник линий вектора
= 0, то в рассматриваемой точке отсутствует
источник линий вектора .
.
Картина
электрического поля при наличии и
отсутствии зарядов показана на рис. 14.4.
Например, если имеется объемный
положительный заряд +,
то он является истоком вектора
электрического смещения 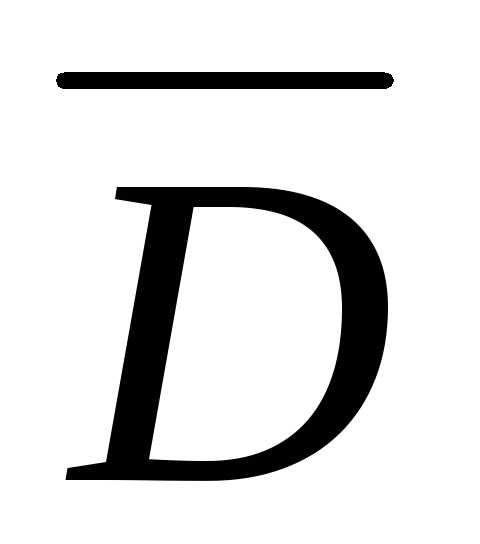 .
.
Рис. 14.4. Электрическое поле при наличии и отсутствии электрических зарядов
Дивергенция
вектора магнитной индукции 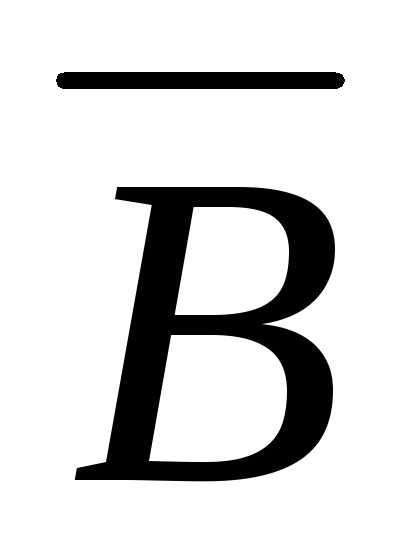 всегда равна нулю, так как линии вектора
всегда равна нулю, так как линии вектора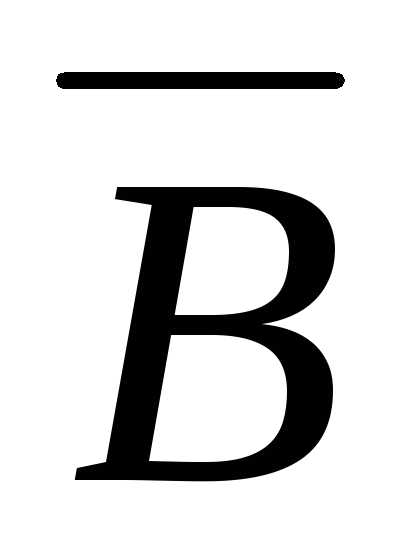 замкнуты (не имеют начала и конца).
замкнуты (не имеют начала и конца).
В декартовой системе координат
(14.15)
Ротор
(вихрь) вектора поля rot  – это вектор, характеризующий интенсивность
вихревых полей в каждой точке. Ротор
проявляет себя как вихрь, поэтому он
имеет ось. Направление оси определяет
направление вектора, изображающего
ротор.
– это вектор, характеризующий интенсивность
вихревых полей в каждой точке. Ротор
проявляет себя как вихрь, поэтому он
имеет ось. Направление оси определяет
направление вектора, изображающего
ротор.
Численно
составляющую ротора в направлении
нормали 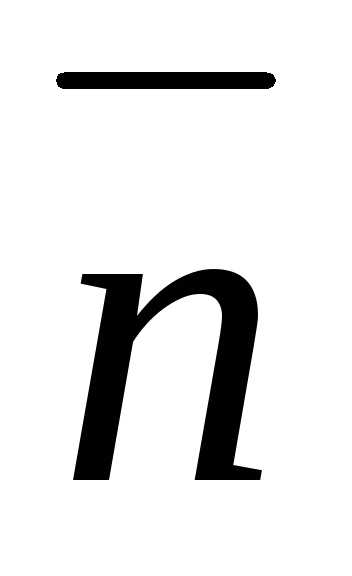 к плоской площадкеs определяют как предел, к которому
стремится отношение циркуляции вектора
к площадке s,
ограниченной контуром интегрирования,
при стремлении ее к нулю (рис. 14.5)
к плоской площадкеs определяют как предел, к которому
стремится отношение циркуляции вектора
к площадке s,
ограниченной контуром интегрирования,
при стремлении ее к нулю (рис. 14.5)
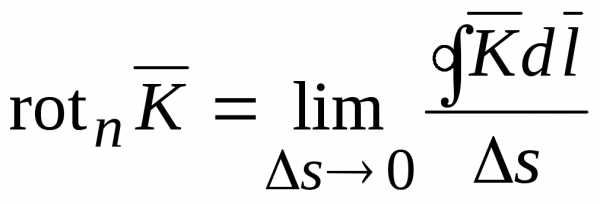 .
(14.16)
.
(14.16)
Если
вихревое поле в некоторой области не
имеет внутри источников векторных
линий, то rot 
0 (div
0 (div  = 0).
= 0).
Запишем ротор вектора в декартовой системе координат
(14.17)
Рис. 14.5. К пояснению определения ротора вектора
где: 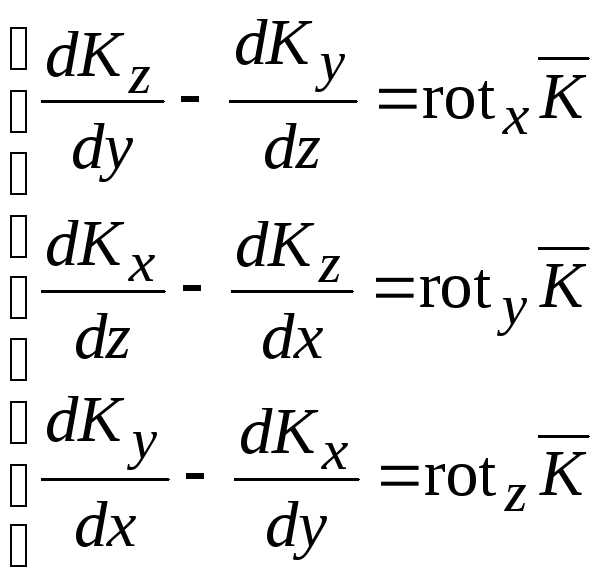 .
(14.18)
.
(14.18)
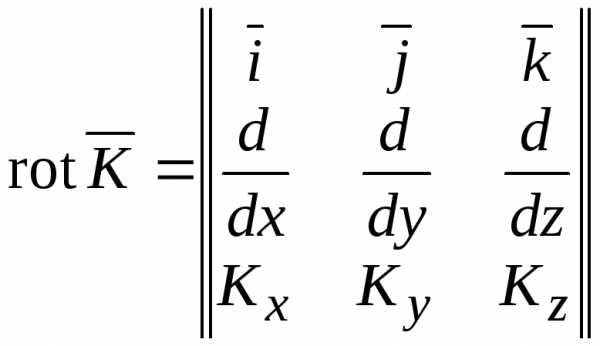 (14.19)
(14.19)
14.1.4. Запись основных векторных операций с помощью оператора
Пространственные производные grad, div и rot можно записать с помощью оператора . При этом умножение оператора на скалярную функцию равносильно взятию градиента этой функции = grad . Скалярное умножение оператора и вектора дает дивергенцию этого вектора , а векторное их умножение образует ротор вектора. Применение оператора облегчает выполнение сложных векторных операций. В табл.14.1 приведены примеры символической записи наиболее часто встречающихся векторных операций.
studfiles.net
градиент, поток вектора, циркуляция, дивергенция, ротор. Примеры.
Градиент — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».
Формальное определение выглядит следующим образом:
Для случая трёхмерного пространства, градиентом называется векторная функция с компонентами , , , где — некоторая скалярная функция координат x, y, z.
градиент Определяет направление и скорость скорейшего возрастания скалярного поля
Поток векторного поля — однопараметрическое семейство диффеоморфизмов Γt определямых дифференциальным уравнением
Поток векторного поля через гиперповерхность — поверхностный интеграл второго рода по поверхности S. По определению
где — векторное поле (вектор-функция векторного аргумента — точки пространства), — единичный вектор положительной нормали к поверхности (положительное направление выбирается для ориентируемой поверхности условно, но одинаково для всех точек — т.е. для дифференцируемой поверхности — так, чтобы было непрерывно; для неориентируемой поверхности это не важно, т.к. поток через неё всегда ноль), dS — элемент поверхности В трёхмерном случае ,а гиперповерхность — есть обычная двумерная поверхность.
Иногда, особенно в физике, применяется обозначение
тогда поток записывается в виде
Циркуля́цией ве́кторного по́ля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру Γ. По определениюгде — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ, — бесконечно малое приращение радиус-вектора вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру.
Дивергенция — это дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.
Оператор дивергенции, применённый к полю , обозначают как или .
Дивергенция Характеризует расходимость, источники и стоки векторного поля.
Ротор— векторный оператор векторного поля, показывает насколько и в каком направлении закручено поле в каждой точке. Ротор Характеризует вихревую составляющую векторного поля.
4.Теорема Остроградского — Гаусса. Электрическое поле заряженной плоскости, цилиндрической и сферической поверхности.
Теорема Остроградского — Гаусса — утверждение интегрального исчисления функций многих переменных, устанавливающее связь между n-кратным интегралом по области и (n − 1)-кратным интегралом по её границе. Пусть V = (v1,v2,…,vn) есть векторное поле на , такое что функции vi вместе со своими частными производными интегрируемы по Лебегу в ограниченной области Ω, граница которой является объединением конечного множества кусочно гладких (n − 1)-мерных гиперповерхностей, ориентированных с помощью внешней единичной нормали ν.
Тогда формула Остроградского имеет вид
где- есть дивергенция поля V.
Формула Остроградского — Гаусса в векторной форме имеет вид
,то есть интеграл от дивергенции векторного поля , распространённый по некоторому объёму T, равен потоку вектора через поверхность S, ограничивающую данный объём.
Формула применяется для преобразования объёмного интеграла в интеграл по поверхности, ограничивающей данный объём, то есть замкнутых, таких как поверхность воздушного шарика, и не применима к поверхностям, таким как воздушный шар с подогревом.
В работе Остроградского формула записана в следующем виде,,
где ω и s дифференциалы объёма и поверхности. В современной записи ω = dΩ — элемент объема, s = dS — элемент поверхности. — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.
studfiles.net
36. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.
Пусть в некоторой области D задано непрерывное векторное поле (M)=(x,y,z). Потоком векторного полячерез ориентированнуюкусочно-гладкую
поверхность S, расположенную в области D, называется интеграл , где– единичный вектор нормали к поверхности S, указывающий на ее
ориентацию, а – элемент площади поверхности S.
Векторное поле называется соленоидальным в области D, если поток этого поля через любуюкусочно-гладкуюнесамопересекающуюся поверхность, расположенную в D и представляющую собой границу некоторой ограниченной подобласти области D, равен нулю.
| Векторные | Если дивергенция равна нулю, то есть | , то поле вектора называется соленоидальным. |
| линии | ||
|
|
| |
S | S |
|
|
2 |
|
| |
3 | Векторная |
|
|
трубка |
|
| |
S |
|
| |
|
|
| |
1 |
| , поэтому поток везде, на каждом сечении трубки, одинаков. | |
|
| ||
Для того чтобы непрерывно дифференцируемое векторное поле было соленоидальным вобъемно-односвязнойобласти D, необходимо и достаточно, чтобы во всех точках D выполнялось равенство. Где дивергенцией (“расходимость”) векторного поля
называется скалярная функция
Циркуляцией векторного поля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру L:
Где — векторное поле (иливектор-функция),определенное в некоторой области D, содержащей в себе
контур L,— бесконечно малое приращениерадиус-векторавдоль контура. Окружность на
символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую
поверхность в отдельности, то есть
– формула Стокса в векторном виде.
Вихревым вектором (вихрем) или ротором векторного поля называется вектор, имеющий
координаты:
Ротор в декартовых координатах:
Если , то векторное поленазывается безвихревым или потенциальном.
37. Оператор Гамильтона. (набла) его применение (примеры).
Оператор набла (оператор Гамильтона) – векторный дифференциальный оператор, обозначаемый символом . Для трёхмерного евклидова пространства в
прямоугольных декартовых координатах оператор набла определяется следующим образом:
Для трёхмерного евклидова пространства в прямоугольных декартовых координатах. оператор набла определяется следующим образом: , где— единичные векторы по осям x, y, z.
Через оператор набла естественным способом выражаются основные операции векторного анализа: grad (градиент), div (дивергенция), rot (ротор), а также
оператор Лапласа (см. ниже). Широко употребляется в описанном смысле в физике и математике (хотя иногда графический символ используется также для обозначения некоторых других, хотя в некотором отношении не совсем далеких от рассмотренного, математических объектов, например, ковариантной производной).
Под n-мернымоператором набла подразумевается вектор с компонентамивn-мерномпространстве.
studfiles.net
Потенциальное и вихревое поле
Различают два основных типа векторных полей: потенциальные (безвихревые) и вихревые (соленоидальные) поля. Физические свойства их различны.
Потенциальное поле тесно связано со своим источником, линии поля имеют начало (исток) и конец (сток). Линии вихревого поля всегда непрерывны и не имеют источников (рисунок Рисунок 12 ).
−Потенциальное и вихревое поля
Для потенциального поля  имеем
имеем
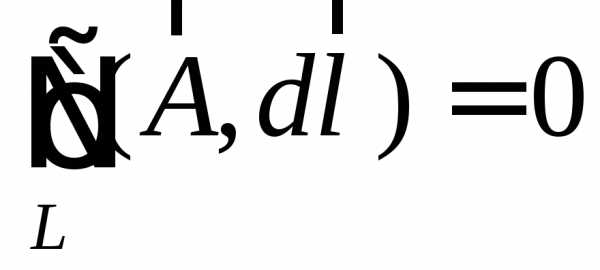 ,
,
то есть циркуляция вектора  по любому замкнутому контуру
по любому замкнутому контуру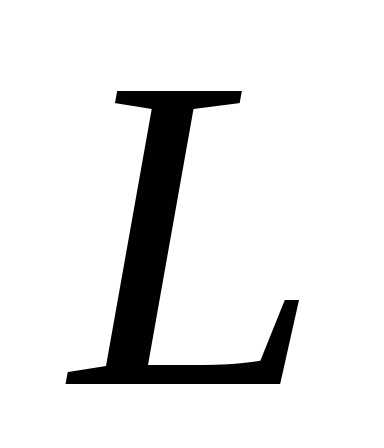 равна нулю.
равна нулю.
Если поле является вихревым, то поток
вектора  через любую замкнутую поверхность равен
нулю:
через любую замкнутую поверхность равен
нулю:
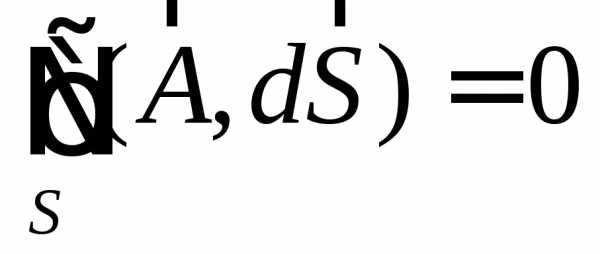 .
.
В дальнейшем будет показано, что электростатическое поле является только потенциальным, магнитное – вихревым.
Градиент, оператор Гамильтона
Далее мы рассмотрим некоторые дифференциальные операции с векторыми и скалярными полями, а именно градиент, дивергенцию (расхождение) и ротор (вихрь). Эти операции потребуются нам при рассмотрении уравнений Максвелла.
Каждое поле порождает собой еще три поля, которые мы и будем рассматривать: векторные поля градиента и ротора и скалярное поле дивергенции.
Градиентом скалярного поля  называется вектор, имеющий направление
быстрейшего увеличения
называется вектор, имеющий направление
быстрейшего увеличения и по величине равный производной по
этому направлению.
и по величине равный производной по
этому направлению.
В векторном анализе часто удобно использовать условный вектор, т.н. оператор Гамильтона. В декартовых координатах он имеет вид
 .
.
Тогда можно записать
.
Градиент совпадает по направлению с
нормалью к поверхности уровня  и направлен в ту сторону, куда
и направлен в ту сторону, куда возрастает (рисунок Рисунок 13 ).
возрастает (рисунок Рисунок 13 ).
−Градиент
Градиент будет применяться при анализе потенциальных векторных полей. Другое применение вектора градиента – численная оптимизация функций.
Дивергенция, физический смысл дивергенции
Для анализа явлений, происходящих в электромагнитном поле, важно знать, где находятся источники того или иного вектора. За меру источника можно выбрать поток вектора через замкнутую поверхность, но внутри данной замкнутой поверхности могут быть источники разных знаков, взаимно уничтожающие свое действие. Чтобы выявить распределение источников в пространстве, можно устремить эту замкнутую поверхность к нулю, но тогда поток вектора через эту бесконечно малую поверхность будет бесконечно малым. Это затруднение ликвидируется тем, что поток вектора через замкнутую поверхность делят на объем, окруженный этой поверхностью. Устремляя объем к нулю, получим предел этого отношения, который и называется дивергенцией.
Дивергенция дает возможность точно указать, в каких точках пространства расположились источники вектора.
Возьмем какую-либо точку поля 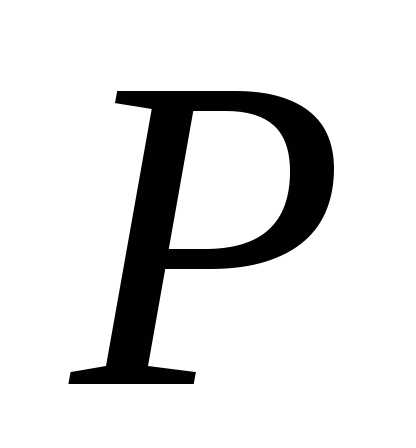 ,
окружим ее малым объемом
,
окружим ее малым объемом и вычислим поток вектора
и вычислим поток вектора через поверхность
через поверхность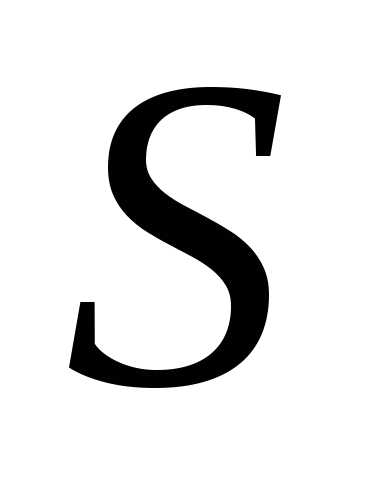 ,
ограничивающую объем
,
ограничивающую объем .
Разделим этот поток на
.
Разделим этот поток на ,
чтобы отнести его к единице объема и
перейдем к пределу, устремляя к нулю
все размеры
,
чтобы отнести его к единице объема и
перейдем к пределу, устремляя к нулю
все размеры ,
что мы будем обозначать символом
,
что мы будем обозначать символом .
При этом объем
.
При этом объем будет стягиваться к точке
будет стягиваться к точке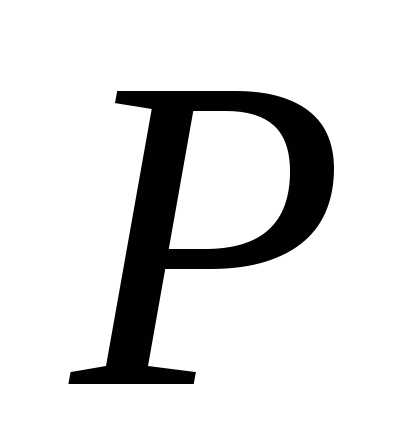 .
В результате получится некоторое число,
зависящее от поведения
.
В результате получится некоторое число,
зависящее от поведения вблизи точки
вблизи точки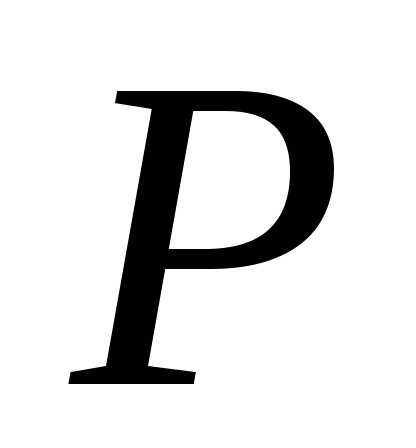 ,
и характеризующее степень истечения
из точки
,
и характеризующее степень истечения
из точки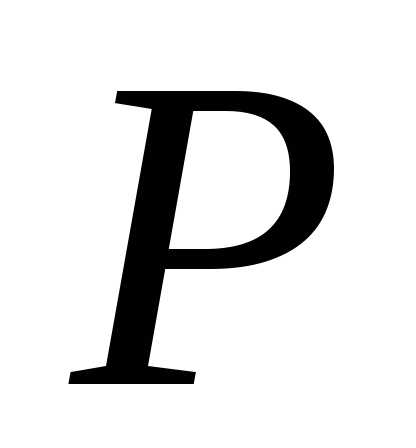 .
Это число называется расхождением, или
дивергенцией вектора
.
Это число называется расхождением, или
дивергенцией вектора в точке
в точке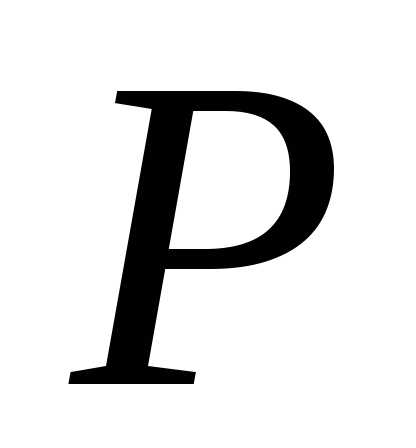 .
Дивергенция обозначается символом
.
Дивергенция обозначается символом .
Таким образом,
.
Таким образом,
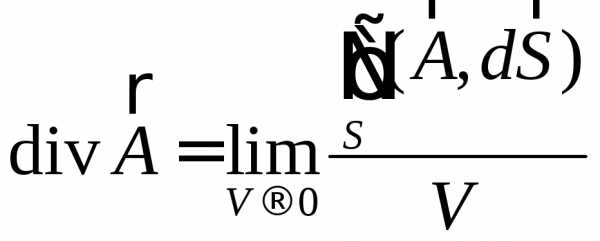
В векторном анализе доказывается, что
или, с применением оператора Гамильтона,
,
т.е., скалярное произведение оператора
набла на вектор  .
.
Рассмотрим значения дивергенции для
разных случаев поля  (рисунок Рисунок 14 ).
(рисунок Рисунок 14 ).
−Дивергенция
При положительной в точке 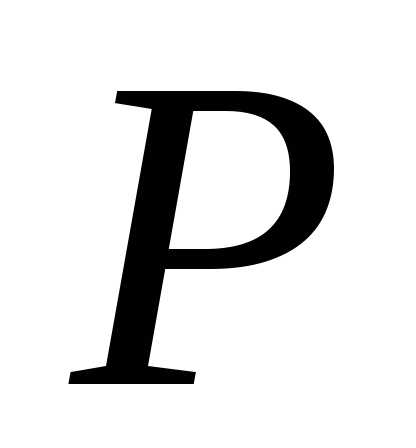 дивергенции внутри области
дивергенции внутри области поток вектора
поток вектора через ограничивающую поверхность больше
нуля, то есть линии вектора расходятся
из этой области. Таким образом, внутри
через ограничивающую поверхность больше
нуля, то есть линии вектора расходятся
из этой области. Таким образом, внутри находятся источники вектора
находятся источники вектора .
При отрицательной дивергенции, наоборот,
линии вектора сходятся в область
.
При отрицательной дивергенции, наоборот,
линии вектора сходятся в область и тогда внутри нее находятся стоки
векторного поля.
и тогда внутри нее находятся стоки
векторного поля.
Если же во всех точках некоторой области поля дивергенция оказывается равной нулю, что силовые линии поля либо пронизывают ее, либо являются замкнутыми.
studfiles.net
5. Дивергенция векторного поля
Продолжим изучение характеристик векторных полей.
Определение 23. Дивергенцией векторного поля A = {Ax, Ay, Az}, где
Ax, Ay, Az – функции от x, y, z, называется
. (107)
Замечание 1. Из определения видно, что дивергенция является скалярной функцией.
Замечание 2. Слово «дивергенция» означает «расходимость», так как дивергенция характеризует плотность источников данного векторного поля в рассматриваемой точке.
Рассмотрим формулу Гаусса-Остроградского с учетом определений потока и дивергенции векторного поля. Тогда в левой части формулы (67) стоит тройной интеграл по объему V от дивергенции векторного поля {P, Q, R}, а в правой – поток этого вектора через ограничивающую тело поверхность S:
(108)
Докажем, что величина дивергенции в данной точке не зависит от выбора системы координат. Рассмотрим некоторую точку М, которую окружает трехмерная область V, ограниченная поверхностью S. Разделим обе части формулы (108) на V и перейдем к пределу при стягивании тела V к точке М. Получим:
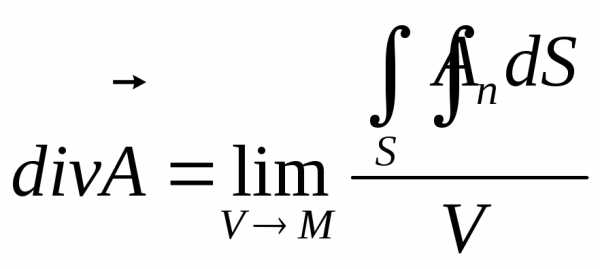 .
(109)
.
(109)
Это равенство можно считать инвариантным определением дивергенции, то есть определением, не зависящим от выбора координатной системы.
Пример 28.
Определить дивергенцию и ротор векторного поля .
6. Оператор Гамильтона, его использование и свойства.
Дифференциальные операции второго порядка
Вспомним определение градиента скалярной функции u = u(x, y, z):
grad u =
Определим оператор, стоящий в скобках в правой части этого равенства, так:
Определение 24. Оператор
(110)
называется оператором Гамильтона или набла-оператором и обозначается символом («набла»).
При применении оператора Гамильтона удобно рассматривать его как «символический вектор» и использовать различные операции над векторами. Например:
1) если умножить «вектор» на скалярную функцию и, то получим градиент этой функции:
u = grad u; (111)
2) составив скалярное произведение на вектор A = {Ax, Ay, Az}, получим дивергенцию вектора A:
· A = ; (112)
3) перемножим теперь векторы и А векторным образом. Результатом будет ротор вектора А:
А =
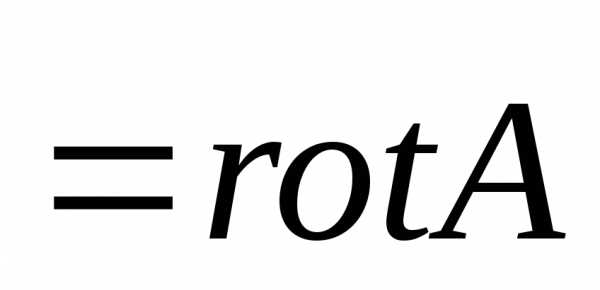 (113)
(113)
4) рассмотрим скалярное произведение векторов и u = grad u:
· (u) = div (grad u) = =
Определение 25. Оператор
Δ
= · = ²
= 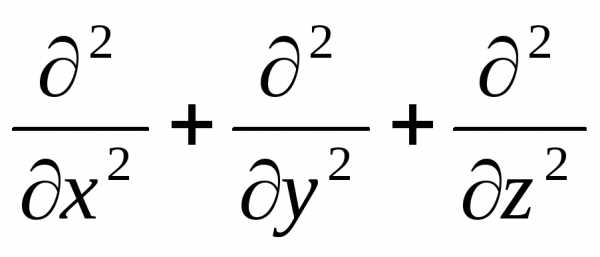 (114)
(114)
называется оператором Лапласа и обозначается символом Δ («дельта»).
Определение 26. Уравнение
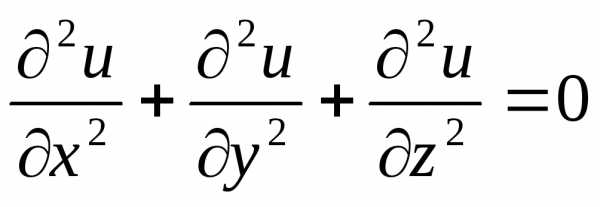 (115)
(115)
называется уравнением Лапласа, а функция, удовлетворяющая ему – гармонической функцией.
Отметим еще раз, результатом применения к скалярной функции и оператора Гамильтона является вектор, а оператора Лапласа – скаляр.
По аналогии с производной по направлению от скалярной функции и:
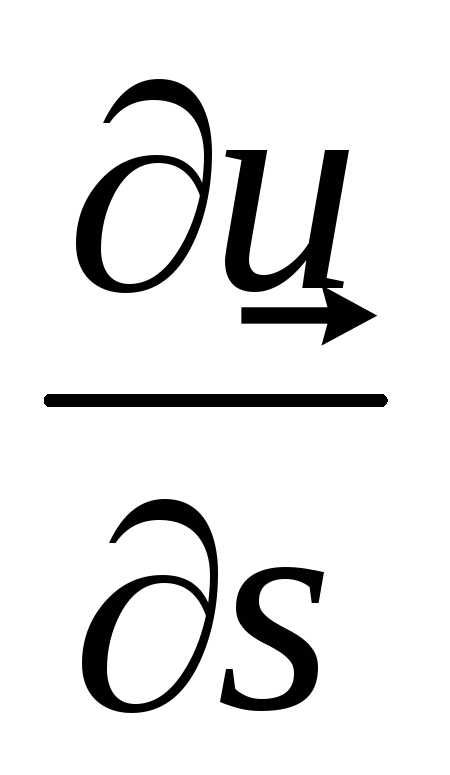 введем понятие
производной по направлению единичного
вектора
введем понятие
производной по направлению единичного
вектора  от векторной функции:
от векторной функции:
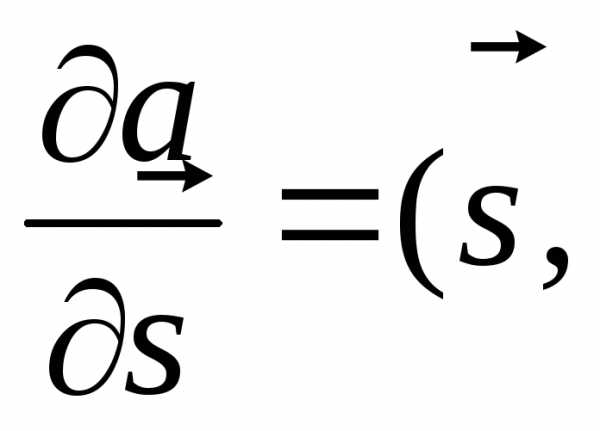 )
)
. (116)
Производная по
направлению любого произвольного
вектора 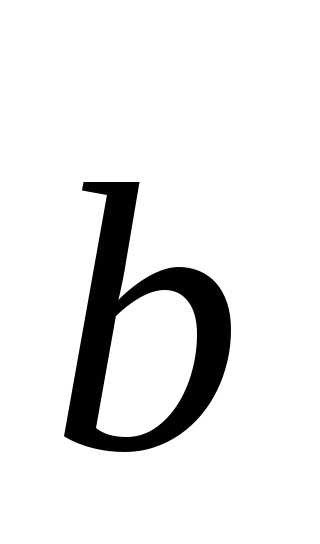 отличается от производной по направлению
единичного вектора лишь тем, что в нее
входит дополнительный скалярный
множитель
отличается от производной по направлению
единичного вектора лишь тем, что в нее
входит дополнительный скалярный
множитель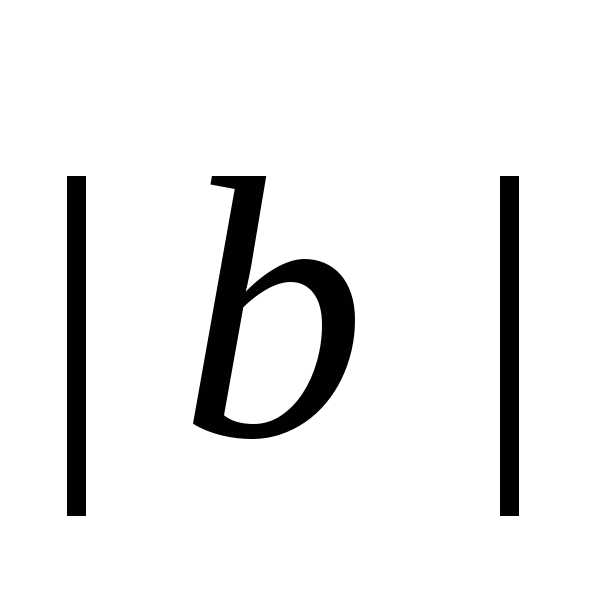 :
:
(117)
Таким образом, с помощью оператора Гамильтона можно образовать пять дифференциальных операций второго порядка:
div grad u = (,) u = 2u
rot grad u = [,] u
grad div
 =(,
=(, )
(118)
)
(118)
div rot
 = (,[,
= (,[, ])
])
rot rot
 =
=
Кроме того, операцию
2 можно применять и к векторным полям,
рассматривая 2 .
.
Результатом
применения второй и четвертой операции
всегда является нуль: rot
grad u = [,] u ≡ 0, div
rot  = (,[,
= (,[, ])
≡ 0. Это следует
из векторного смысла оператора :
во второй операции присутствует векторное
произведение коллинеарных векторов
(более подробное доказательство этого
утверждения будет проведено далее, на
стр. 70), а в четвертой операции – смешанное
произведение коллинеарных векторов.
])
≡ 0. Это следует
из векторного смысла оператора :
во второй операции присутствует векторное
произведение коллинеарных векторов
(более подробное доказательство этого
утверждения будет проведено далее, на
стр. 70), а в четвертой операции – смешанное
произведение коллинеарных векторов.
Пример 29.
Определить rot rot a, где a = {x2y, y2z, z2x}.
Известно, что rot
rot  =
=  =
=
Здесь
Проведем последовательные вычисления:
Окончательно получим:
studfiles.net

 =(,
=(, )
(118)
)
(118) = (,[,
= (,[, ])
]) =
=