2.1.4. Размещения с повторениями
Задача.
Определить количество всех упорядоченных
наборов длиныr,
которые можно составить из элементов
множестваX (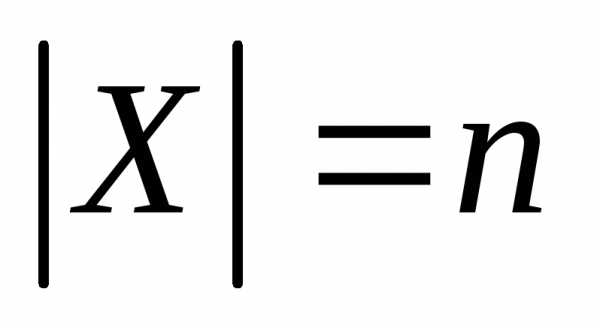 ),
если выбор каждого элемента,
производится из всего множестваX.
),
если выбор каждого элемента,
производится из всего множестваX.
Упорядоченный
набор – это элемент декартова произведения
,
состоящего изrодинаковых множителейX.
По правилу произведения количество
элементов множества равно
равно 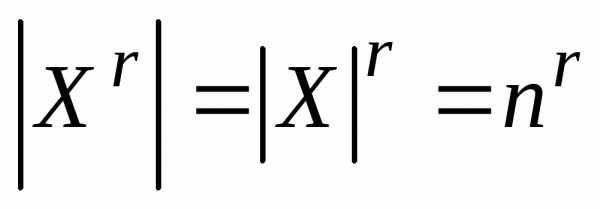 .
Мы вывели формулу
.
Мы вывели формулу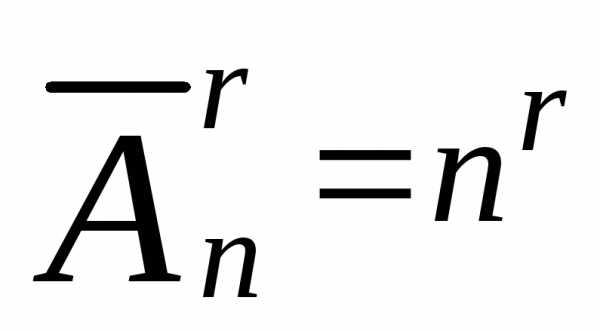 .
.
Пример. Сколько четырехзначных телефонных номеров можно составить, если использовать все десять цифр?
2.1.5. Размещения без повторений
Задача. Сколько упорядоченных наборовможно составить изnэлементов множестваX, если все элементы набора различны?
Первый элемент 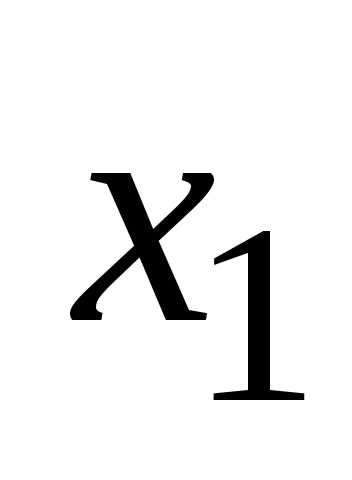 можно выбратьnспособами. Если первый элемент уже
выбран, то второй элемент
можно выбратьnспособами. Если первый элемент уже
выбран, то второй элемент можно выбрать лишь
можно выбрать лишь способами,
а если уже выбран
способами,
а если уже выбран элемент,
то элемент
элемент,
то элемент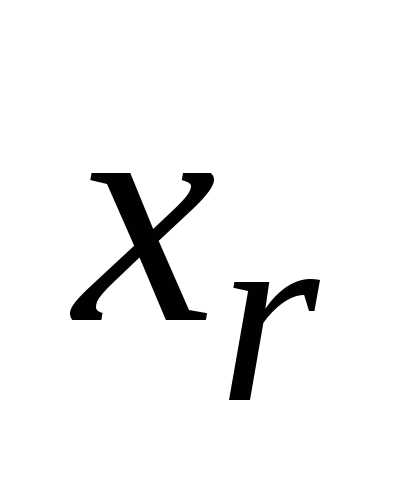 можно
выбратьспособами
(повторение уже выбранного элемента не
допускается). По правилу произведения
получаем
можно
выбратьспособами
(повторение уже выбранного элемента не
допускается). По правилу произведения
получаем
Эта формула записывается иначе с использованием обозначения . Так как
то
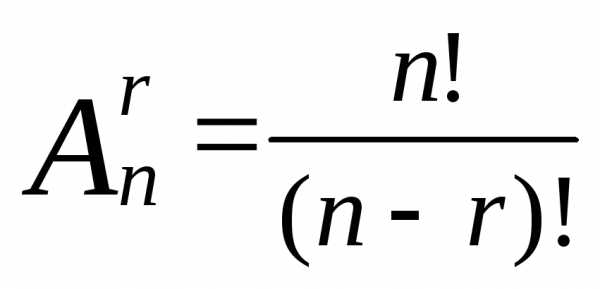
Пример. Сколько может быть различных списков победителей олимпиады (первое, второе, третье место), если участвовало 20 человек?
Здесь , искомым является число
2.1.6. Перестановки без повторений
Рассмотрим
частный случай размещения без повторений:
если 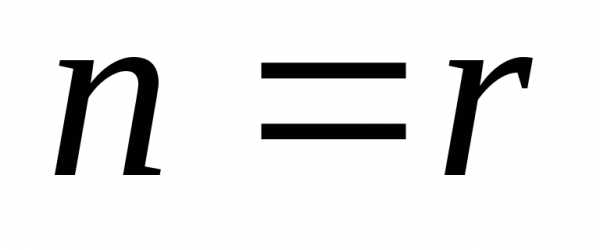 ,
то в размещении участвуют все элементы
множестваX,
т.е. выборки имеют одинаковый состав и
отличаются друг от друга только порядком
элементов. Такие выборки называютсяперестановками. Количество
перестановок изnэлементов обозначают
,
то в размещении участвуют все элементы
множестваX,
т.е. выборки имеют одинаковый состав и
отличаются друг от друга только порядком
элементов. Такие выборки называютсяперестановками. Количество
перестановок изnэлементов обозначают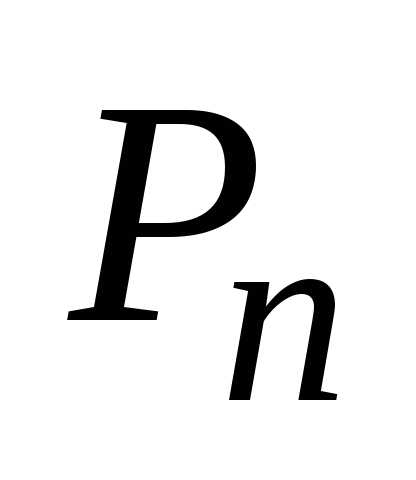 :
:
Пример. Сколькими способами можно выстроить очередь в кассу, если хотят получить зарплату шесть человек?
.
2.1.7. Перестановки с повторениями
Пусть множество Xсостоит изkразличных элементов:.Перестановкой с повторениями составабудем называть упорядоченный набор
длины,
в котором элемент
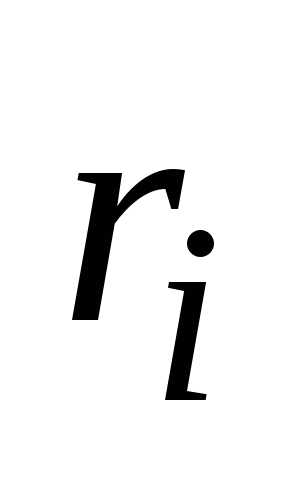 раз .
Количество таких перестановок обозначается.
раз .
Количество таких перестановок обозначается.Пример. Из
букв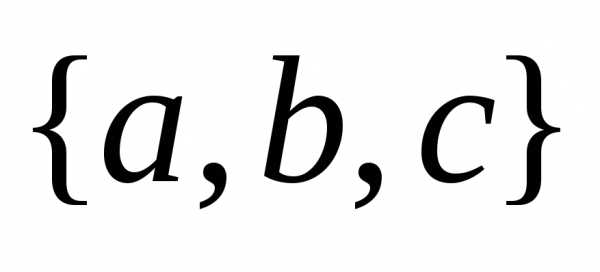 запишем перестановку с повторением
состава
запишем перестановку с повторением
состава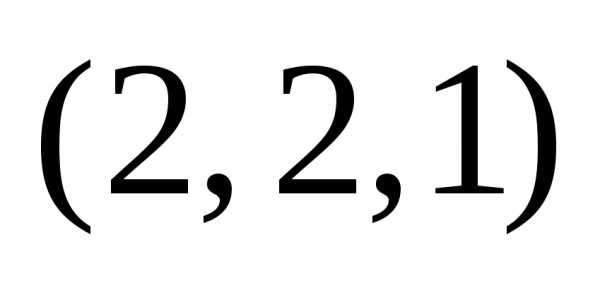 .
Ее длина,
причем букваaвходит 2 раза,b– 2 раза,c– один раз. Такой перестановкой будет,
например,или.
.
Ее длина,
причем букваaвходит 2 раза,b– 2 раза,c– один раз. Такой перестановкой будет,
например,или.
Выведем формулу
количества перестановок с повторениями.
Занумеруем все одинаковые элементы,
входящие в перестановку, различными
индексами, т.е. вместо перестановки
получим.
Теперь все элементы перестановки
различны, а количество таких перестановок
равно.
Первый элемент встречается в выборке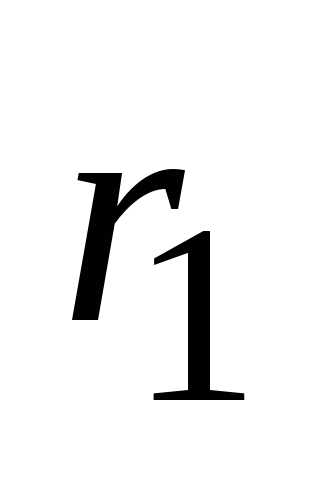
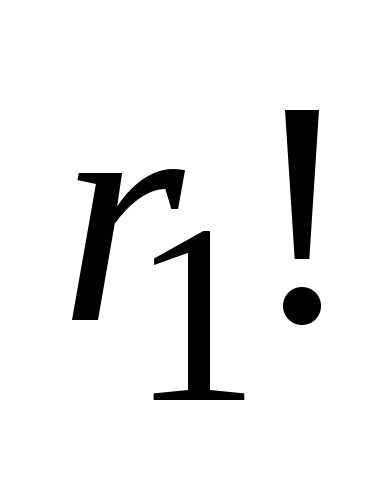 раз, т.к. при изменении порядка одинаковых
элементов наша выборка не изменится.
Уберем индексы у второго элемента –
число перестановок уменьшится в
раз, т.к. при изменении порядка одинаковых
элементов наша выборка не изменится.
Уберем индексы у второго элемента –
число перестановок уменьшится в 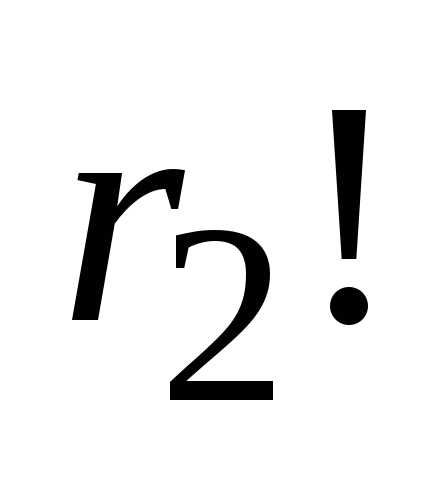 раз. И так далее, до элемента с номеромk– число перестановок уменьшится в
раз. И так далее, до элемента с номеромk– число перестановок уменьшится в 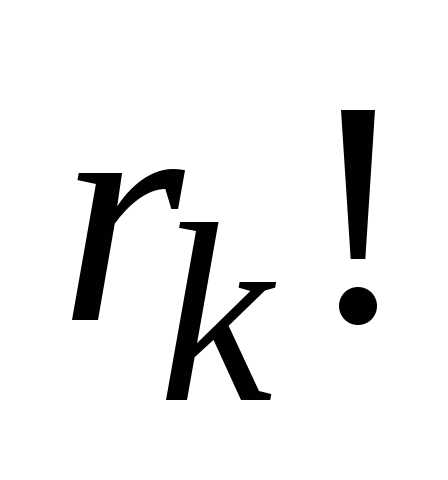 раз. Получим формулу
раз. Получим формулуПример. Сколько различных “слов” можно получить, переставляя буквы слова “передача” ?
В этом слове буквы “е” и “а” встречаются два раза, остальные по одному разу. Речь идет о перестановке с повторением состава длины. Количество таких перестановок равно
.
2.1.8. Сочетания
Задача. Сколько различных множеств изrэлементов можно составить из множества, содержащего
Будем составлять
вначале упорядоченные наборы по rэлементов в каждом. Количество таких
наборов (это размещения изnэлементов поr)
равно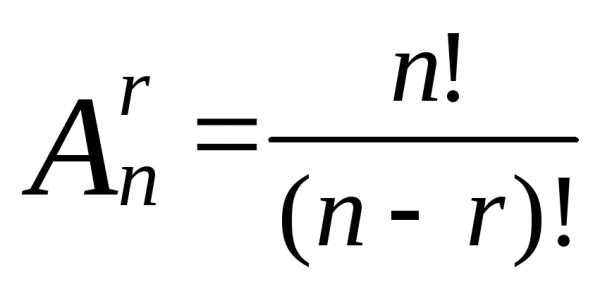 .
Теперь учитываем, что порядок записи
элементов нам безразличен. При этом из
.
Теперь учитываем, что порядок записи
элементов нам безразличен. При этом из различных размещений, отличающихся
только порядком элементов, получим одно
сочетание. Например, два различных
размещения
различных размещений, отличающихся
только порядком элементов, получим одно
сочетание. Например, два различных
размещения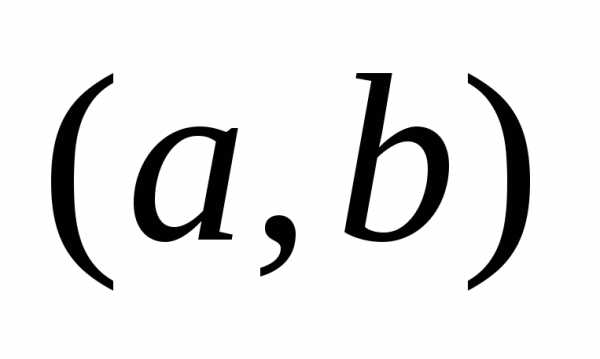 и
и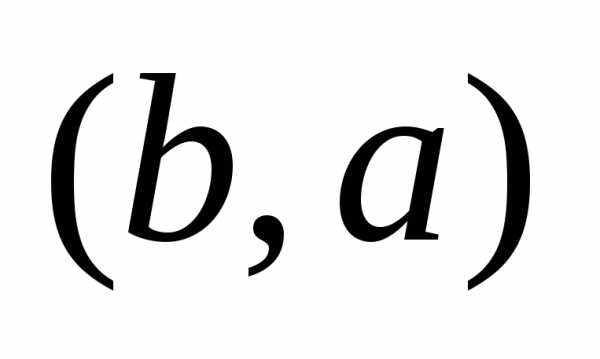 из двух элементов соответствуют одному
сочетанию
из двух элементов соответствуют одному
сочетанию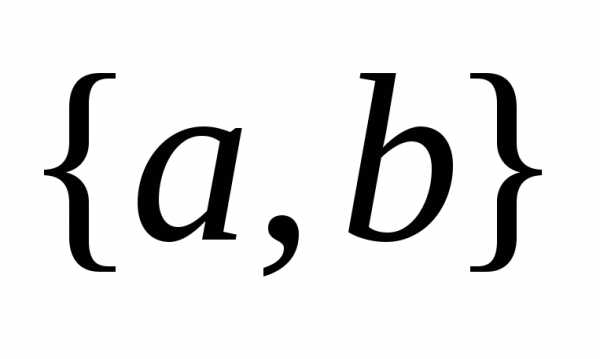 .
Таким образом, число сочетаний
.
Таким образом, число сочетаний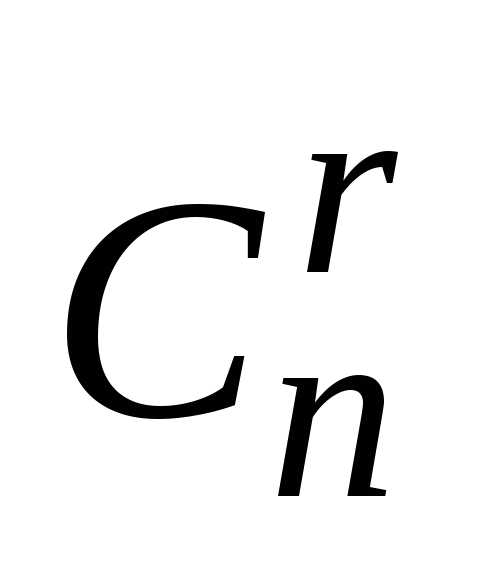 в
в
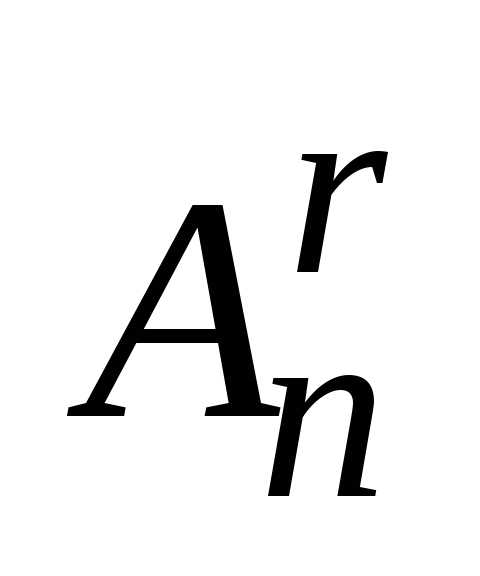 :
:
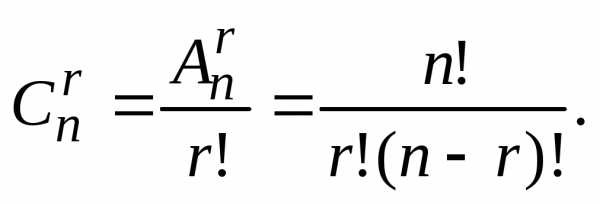
Пример. Количество способов, которыми мы можем выбрать из восьми дворников троих равно
studfiles.net
Комбинаторика в MS EXCEL. Примеры и методы
Подсчитаем в MS EXCEL количество Размещений из n по k и с помощью формул выведем на лист соответствующие варианты размещений (английский перевод термина: partial permutation или sequence without repetition).
Размещением (partial permutation) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.
Например, из множества содержащего 3 (n) различных элемента (a, b, c) можно сформировать 6 упорядоченных наборов по 2 (k) различных элемента (т.е. 6 размещений из 3 по 2): ab, ac, ba, bc, ca, cb. В отличие от Размещений с повторениями повторы элементов в наборах не допускаются, т.е. наборы аа, bb и сс не допустимы. В отличие от Сочетаний наборы ac и ca считаются различными (важен порядок).
Очевидно, что k=<n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются).
Примечание: О Размещениях с повторениями (с возвращением элементов) можно прочитать в статье Размещения c повторениями: Комбинаторика в MS EXCEL.
Для вычисления количества Размещений в MS EXCEL имеется специальная функция ПЕРЕСТ(). Чтобы подсчитать количество Размещений из 3 (n) по 2 (k) нужно записать формулу =ПЕРЕСТ(3;2)
Примечание: Если k=n, то количество Размещений из n по n равно числу Перестановок из n элементов, т.е. n!=ФАКТР(n)=ПЕРЕСТ(n;n).
В файле примера MS EXCEL приведен подсчет количества Размещений с помощью функции =ПЕРЕСТ(n;k) и альтернативной формулы =ФАКТР(n)/ФАКТР(n-k).
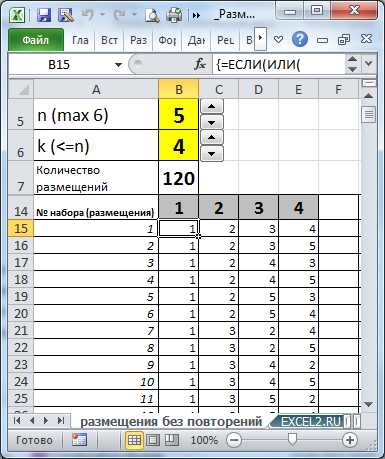
Кроме того, в файле примера создана универсальная формула для вывода всех Размещений для заданных n и k.
Задавая с помощью элементов управления Счетчик количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формулы массива можно вывести все Размещения.
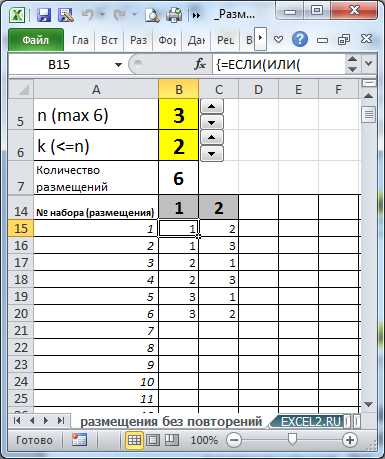
Задача
6 машин разных марок участвуют в гонках на выживание: LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo. Определить число возможных вариантов распределения 3-х призовых мест между участниками.
Нам нужно определить число размещений 6 машин на 3-х призовых местах (понятно, что порядок размещения машин на призовых местах важен). Т.е. n=6, а k=3. Оказывается, что таких вариантов =ПЕРЕСТ(6;3) равно 120.
Воспользуемся файлом примера, чтобы наглядно убедиться, что мы решили задачу правильно.
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …
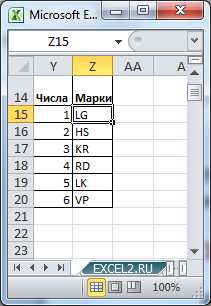
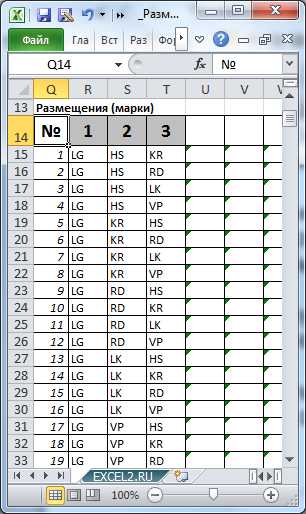
Выставив в ячейках В5 и В6 значения 6 и 3, определим все варианты размещений машин на призовых местах.

В столбцах Q:T числовым значениям сопоставлены марки машин.
Примечание: О Перестановках можно прочитать в статье Перестановки без повторений: Комбинаторика в MS EXCEL, а о Сочетаниях в статье Сочетания без повторений: Комбинаторика в MS EXCEL.
Примечание: В данной статье рассмотрена выборка элементов из одного массива, в котором содержится n элементов. В статье Комбинации элементов из нескольких множеств составлены все возможные комбинации элементов таким образом, чтобы в комбинации присутствовал один и только один элемент из каждого множества.
excel2.ru
Размещения без повторений.
Назовём множество, содержащее nэлементов,n-множеством. Последовательность(x1, x2, …, xk )длиныkбез повторяющихся элементов из элементов данногоn-множества назовём k-размещением без повторений элементов. Обозначим символомчисло размещений изnпоkэлементов (от фран. «arrangement» — размещение). Используя правило произведения, вычислим число. Пусть произвольное размещение длиныk имеет вид(x1, x2, …, xk ). Элемент x1можно выбратьnспособами. После каждого выбораx1элементx2 можно выбрать (n — 1) способами. После каждого выбора элементов x1 иx2элементx3 можно выбрать (n — 2) способами, и т.д. После каждого выбора элементов x1 , x2, …, xk-1элементxkможно выбрать (n —(k — 1)) = (n — k + 1) способами. Тогда, по правилу произведения, последовательность(x1, x2, …, xk)можно выбрать числом способов, равнымn(n — 1)(n — 2) … (n — k + 1) . Произведение умножим и разделим на (n — k)!, получим:
. (2)
Если в форуме (2) k = n, тоесть числоPnперестановок изnэлементовPn = n!.
Сочетания без повторений .
k-подмножество из неповторяющихся элементов данногоn-множества называетсяk-сочетанием без повторений. Обозначим черезчислоk-сочетаний из данных nэлементов. Формулу для числа сочетаний получим, рассуждая следующим образом. Если каждое сочетание упорядочить всеми возможными способами, то получим все k-последовательностей из nэлементов, без повторений, то есть все k-размещения. Иными словами,Откуда , полагая, чтоnиk— целые положительные числа и0!=1.:(3)
Основные свойства сочетаний.
Условились, что
Сочетания и размещения широко используются при вычислении классической вероятности случайных событий.
Пример. В корзине находятся 20 орехов, из которых 7 грецких. Наудачу выбирают 5 орехов. Найти вероятность того, что среди выбранных орехов содержатся 2 грецких.
Решение. Число исходов опыта. Случайное событиеA— среди пяти выбранных орехов содержатся 2 грецких ореха. Число исходов, благоприятствующих событиюA, равно:. Искомая вероятность.
Задачи.
Найти вероятность того, что случайно выбранное 5-значное (десятичное) число не содержит цифры 5.
Предприятие располагает 5 вакансиями для мужчин, 5 вакансиями для женщин и 4 вакансиями для работников любого пола. В отдел кадров предприятия обратилось 20 человек, среди которых 12 мужчин и 8 женщин. Сколькими способами предприятие может заполнить имеющиеся вакансии?
В классе 25 учеников, из которых 13 юношей и 12 девушек. Сколькими способами 25 учеников могут встать в шеренгу так, чтобы юноши после удаления из строя девушек, оказались построенными по росту; аналогично девушки после удаления из строя юношей оказались построенными по росту?
В современной литературе наиболее употребителен для обозначения числа k-сочетаний изnэлементов символ,nназывают верхним индексом,k— нижним индексом. Используя свойства сочетаний 1, 2, 4, составим таблицу1.
Таблица 1.Треугольник Паскаля
n | |||||||||||
0 | 1 |
|
|
|
|
|
|
|
|
|
|
1 | 1 | 1 |
|
|
|
|
|
|
|
|
|
2 | 1 | 2 | 1 |
|
|
|
|
|
|
|
|
3 | 1 | 3 | 3 | 1 |
|
|
|
|
|
|
|
4 | 1 | 4 | 6 | 4 | 1 |
|
|
|
|
|
|
5 | 1 | 5 | 10 | 10 | 5 | 1 |
|
|
|
|
|
6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 |
|
|
|
|
7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
|
|
|
8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
|
|
9 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 |
|
10 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
Заметим, что Блез Паскаль называл числовой треугольник, начало которого содержится в таблице1, арифметическим. Паскаль посвятил свойствам арифметического треугольника основополагающий «Трактат об арифметическом треугольнике» (1654). Справедливости ради, стоит упомянуть, что биномиальные коэффициенты были хорошо известны в Азии за много веков до рождения Паскаля. В Италии треугольник Паскаля называют треугольником Тартальи. Сочетания имеют многочисленные интерпретации и приложения. Сочетанияявляются биномиальными коэффициентами в разложении бинома
(1.4)
В этой интерпретации индексы могут принимать вещественные значения. Используя свойства биномиальных коэффициентов (при разных ограничениях на выбор верхних и нижних индексов), доказано громадное число комбинаторных тождеств, составивших самостоятельный раздел комбинаторной математики. В частности, из формулы 1.4 при x = 1, получим, приx = -1, n > 0, получим, продифференцировав равенство 1.4, получим приx = 1,и т.д. Существует тесная связь между подмножествами множества и разложениями целого (положительного) числа.Разложение n есть представление числа nв виде упорядоченной суммы положительных целых чисел. Например, существует восемь разложений числа 4, именно: 1+1+1+1 3+1 2+1+1 1+3 1+2+1 2+2 1+1+2 4 Если разложениесодержит в точности kслагаемых, то говорят, чтоимеет k частей и называетсяk-разложением. Дляk-разложениячисла n: a1 + a2 + …+ an— определим (k — 1)-подмножество(), (n — 1)-множества {1, 2, …, n-1}, формулой.
() ={a1,a1+a2,…,a1+a2+…+ak-1} (1.5)
Эта формула устанавливает биекцию между всеми k-разложениями числаnи (k — 1)-подмножествами (n — 1)-множества. Следовательно, существуетk-разложений числаnи2n-1разложений числаn. Биекциючасто схематично изображают строкой, состоящей изnточек иk — 1разделяющей вертикальной черты. Точки разделились поkлинейно упорядоченным «купе»; числа точек в «купе» соответствуют слагаемым вk-разложении числаn. Например, строка|||||соответствует разложению 1+2+1+1+3+2. Другая проблема, тесно связанная с разложениями, есть задача подсчёта числаN(n,k) решений уравнения
x1 + x2 +…+xk = n(1.6)
Неотрицательные целые решенияуравнения 1.6 называются слабымиk-разложениями числаn. Число неотрицательных целых решений уравнения 1.6 равно числуположительных решений уравнения
y1 + y2 +… + yk = n + k,
то есть числу k-разложений числаn + k. Таким образом,N(n,k) =.
Если k-сочетание содержит повторяющиеся элементы, то такоеk-сочетание называютk-мультимножеством. Число всехk-сочетаний с повторениями из данногоn-элементного множества обозначим через, где
(1.7)
Сочетание можно интерпретировать, как распределение элементовn-множестваSмежду двумя категориями, первая из которых содержитkэлементов, вторая содержитn — kэлементов. Обобщим это представление. Пусть (a1,a2, …,am)- последовательность неотрицательных целых чисел, сумма которых равнаn. РассмотримmкатегорийC1,C2, …Cm. Обозначим символом(1.8) число способов распределения nэлементов среди категорийC1,C2, …Cmтак, чтобы категорииCiпринадлежало точноaiэлементов. Тогда(1.9)
studfiles.net
Размещения без повторений
Сколькими способами в группе студентов из 34 человек можно выбрать старосту и казначея? Если известно, что один человек не может занимать две должности сразу. Если известно, что один человек может занимать две должности сразу.
В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост?
Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, если имеется материя шести различных цветов?
Забор состоит из 100 дощечек. У Тома Сойера есть краски 150 различных цветов. Сколько существует различных раскрасок забора, если все дощечки покрашены в разный цвет? Та же задача, но дощечки могут быть покрашены в одинаковый цвет.
Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили два различных числа?
Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4 и 5? Тот же вопрос, но при условии, что ни одна цифра не повторяется?
У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если общее число имен равно 300, а ему дают ровно три имени?
У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если общее число имен равно 300, а ему дают не более трех имен?
Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов? А если одна полоса обязательно должна быть красной?
Сколькими способами можно составить расписание на день из 5 различных уроков, если изучается 14 предметов?
В комнате студенческого общежития живут трое студентов. У них есть 4 чашки, 5 блюдец и 6 чайных ложек (все чашки, блюдца и ложки отличаются друг от друга). Сколькими способами они могут накрыть стол для чаепития (каждый получает одну чашку, одно блюдце и одну ложку)?
На полке стоят 5 книг. Сколькими способами можно выложить в стопку несколько из них (стопка может состоять и из одной книги)?
Докажите, что .
На группу из 34 человек выделено две путевки в Сочи и Евпаторию. Сколькими способами можно распределить путевки? Известно, что один человек не может получить две путевки сразу. Известно, что один человек может получить две путевки сразу.
Сколько существует трехзначных чисел, в записи которых цифры 1, 2, 3 встречаются ровно по одному разу?
Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
В ряду зрительного зала 15 кресел. Сколькими способами можно разместить на них 15 человек?
На полке n различных книг. Скольким способами их можно переставить?
Сколькими способами можно рассадить за круглым столом 6 мужчин и 6 женщин таким образом, чтобы мужчины и женщины чередовались?
Сколько существует перестановок из n различных элементов, в которых один данный элемент идет непосредственно впереди другого данного элемента?
Сколько можно сделать перестановок из n различных элементов, в которых данные два стоят рядом?
Сколько можно сделать перестановок из n различных элементов, в которых данные два не стоят рядом?
Лингвисты расшифровывают записи некоторого племени. Известно, что каждый символ обозначает один звук. Всего в алфавите 26 символов. Сколькими способами можно сопоставить звуки и знаки письма? Во сколько раз уменьшится количество возможных вариантов, если ученым удалось найти 7 знаков, обозначающих гласные, и 19 – согласные?
Сколько существует различных последовательностей длины 5, составленных из трех 1 и двух 0?
Сколько существует различных пятизначных чисел, составленных из трех 1 и двух 0?
Бусы – это кольцо, на которое нанизаны бусины. Бусы можно поворачивать, но не переворачивать. Сколько различных вариантов бус можно сделать из 13 разноцветных бусин?
Предположим теперь, что бусы можно и переворачивать. Сколько тогда различных бус можно сделать из 13 разноцветных бусин?
Сколькими способами на доске из n вертикалей и горизонталей можно расположить n ладей так, чтобы они не могли бить друг друга? Ответьте на вопрос задачи, если все ладьи одинаковы и если все они различны.
Слово – любая конечная последовательность букв русского алфавита. Выясните, сколько различных слов можно составить из слов: а) «ВЕКТОР»; б) «ЛИНИЯ»; в) «ПАРАБОЛА»; г) «БИССЕКТРИСА»; д) «МАТЕМАТИКА», используя все буквы.
studfiles.net
Размещения с повторениями и без повторений — Мегаобучалка
Симметрическая разность.
A D B:= (A \ B) И (B \ A) = (A И B) \ (A З B)
Свойства операций над множествами.
- Коммутативность.
A И B=B И A
A З B=B З A
- Ассоциативность.
(A И B) И C=A И (B И C)
(A З B) З C= A З (B З C)
- Дистрибутивность.
(A И B) З C = (A З C) И (B З C)
(A З B) И C= (A И C) З (B И C)
- A И A=A, A З A=A
A И Ж = A, A З Ж= Ж - Законы де Моргана (законы двойственности).
1) A И B= A З B
2) A З B= A И B
28.Мощьность множества. Декартово произведение.
Мощность множества, кардинальное число— характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.
Прямое или декартово произведение двух множеств — это множество, элементами которого являются всевозможные упорядоченные пары элементов исходных множеств.
29.Наглядное представление задаваемых множеств. Диаграмма Эйлера-Венна.
Диаграмма Венна (иногда диаграмма Эйлера — Венна) — схематичное изображение всех возможных пересечений нескольких (часто — трёх) множеств
30.Упорядоченные и неупорядоченные выборки.
Выборками называются подмножества какого-либо множества.
Упорядоченными выборками называются выборки, в которых важен порядок элементов.
Если в выборке поменяют местами два элемента и получится другая выборка, то данная выборка является упорядоченной.
Неупорядоченными выборками называются выборки, в которых не важен порядок элементов.
Размещения с повторениями и без повторений.
Размещение с повторениями или выборка с возвращение — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз.
32.Сочитания с повторениями и без повторений.
Сочетаниями без повторений из n различных элементов по k элементов называются комбинации, которые составлены из данных n элементов по k элементов и отличаются хотя бы одним элементом .
Пусть имеются предметы n различных видов предметов, и из них составляются наборы, содержащие k элементов. Такие выборки называются сочетаниями с повторением.
.
33. перестановки с повторениями и циклические перестановки.
Всякое размещение с повторениями, в котором элемент повторяется раз, элемент повторяется раз и т.д. элемент повторяется раз, где , , , — данные числа, называется перестановкой с повторениями порядка
Определение циклической перестановки. Пусть a1; a2; : : : ; ak — попар-
но различные элементы Xn. Перестановку ‘, действующую по правилу
‘(a1) = a2; ‘(a2) = a3; : : : ; ‘(ak) = a1;
‘(j) = j при j =2 fa1; a2; : : : ; akg;
называют циклической перестановкой элементов a1; a2; : : : ; ak или циклом
из элементов a1; a2; : : : ; ak. Обозначение:
‘ = (a1 a2 : : : ak)n.
34.Основные понятия теории графов: вершины, ребра, инцидентность, смежность.
Вершина — верхняя точка чего-либо.
Ребро — любой отрезок, являющийся стороной какого-либо многогранника
Матрица смежности — один из способов представления графа в виде матрицы. это квадратная матрица размерностью n x n, (где n – число вершин графа ), однозначно представляющая его структуру.
ИНЦИДЕНТНОСТЬ — геометрический термин, употребляемый для обозначения отношения принадлежности (связи, соединения) между основными объектами геометрии: точками, прямыми, плоскостями. Свойства И. характеризуются так наз. аксиомами принадлежности
Матрица инцидентности представляет собой прямоугольную матрицу размером n x m, где n – количество вершин графа, а m– количество дуг графа.
35.Типы графов: элементарный граф, граф с петлями, мультиграф, псевдограф, орграф.
Определение: (p,q) – граф, есть система объектов. G=(V,E), где V={v1, v2,…,vp} – множество вершин, E={ e1=(vi1,vj1), e2=(vi2,vj2),…, eq=(viq,vjq)}ik ≠ jk k=1,2,3,..,q – множество неориентированных ребер ik≠j1, k=1..q.Мультиграф допускает кратные ребра, но не допускает петель. Песевдограф допускает и кратные ребра, и петли.
Петля это дуга, начальная и конечная вершина которой совпадают.
мультиграф, у которых две вершины могут быть соединены двумя и более рёбрами.
36.Связанные и несвязанные графы. Компоненты связанности.
Неориентированный граф считается связным, если из любой вершины есть путь в любую другую вершину (путь может состоять из любого количества рёбер).
Граф считается не связанным, если из одной вершины нельзя будет провести ни в какую другую вершину.
Компонента связности — множество вершин такое, что из любой вершину этого множества есть путь в любую другую вершину этого множества, но ни из какой вершины этого множества нельзя попасть в некоторую вершину вне этого множества.
37.Способы описания графов.
Граф описывается перечислением множества вершин и дуг.
38. Способы задания множеств. Понятие мощность множества.
Считают, что множество задано своими элементами, т.е. множество задано, если о любом объекте можно сказать: принадлежит он этому множеству или не принадлежит. Задавать множество можно следующими способами:
1) Если множество конечно, то его можно задать перечислением всех его элементов.
2) Множество можно задать указанием характеристического свойства его элементов. Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, не принадлежащий ему.
Мощность множества или кардинальное число множества — это обобщение понятия количества (числа элементов множества), которое имеет смысл для всех множеств, включая бесконечные.
42. Операции над подстановками.
подстановка — это операция синтаксической замены подтермов данного терма другими термами, согласно определённым правилам.
megaobuchalka.ru
Понятие размещения. Число размещений с повторениями и без повторений
В комбинаторике размещением из n по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества. Или иначе, размещение из n по k – это k-элементное подмножество n-элементного множества.
Число размещений из n по k без повторений
Пусть у нас есть множество X, состоящее из n элементов:
и – некоторое размещение элементов этого множества.
1-й элемент этого множества мы можем выбрать n способами;
2-й элемент – n-1 способами;
3-й элемент – n-2 способами.
Размещая таким образом элементы множества X до k-го, мы получим, что k-й элемент мы можем выбрать n-(k-1) способами.
Тогда мы получаем, что по правилу произведения количество этих k-элементных упорядоченных подмножеств множества Х будет равно
.
То есть получаем, что число размещений из n элементов по k без повторений равно:
.
То есть получаем формулу для вычисления числа размещений без повторений из n элементов по k:
Замечание! (читается «n факториал»).
Число размещений из n по k с повторениями
Пусть у нас есть множество X, состоящее из n элементов:
и – некоторое размещение элементов этого множества, однако на этот раз элементы в данном размещении могут повторяться. Обозначим (или ) число размещений с повторениями.
Тогда 1-й элемент мы можем выбрать n способами; 2-й элемент – n способами; 3-й элемент – n способами, и т.д., и k-й элемент мы можем выбрать тоже n способами.
Таким образом, мы получаем, что число размещений с повторениями можно вычислить следующим образом:
То есть получаем формулу: .
Число подмножеств конечного множества
Рассмотрим его на примере данного множества A, состоящего из трех элементов: . Перечислим все подмножества множества А:
;
;
;
;
;
;
;
.
Обозначим множество всех подмножеств множества А. Тогда получаем,что число элементов множества равно 8, при условии, что число элементов множества А равно 3.
Пусть множество .
Каждому подмножеству множества А поставим в соответствие n-элементный набор, состоящий из 0 и 1:
;
;
;
;
И т.д.
.
Тогда число всех подмножеств равно числу всех таких наборов, а оно, в свою очередь, вычисляется по формуле:
Выводы к главе 1
Комбинаторика формировалась как наука в течение довольно долгого периода, и она все еще развивается. Она широко используется как в обиходе (например, в играх), так и в других науках, и тесно связана с различными областями математики (алгеброй, геометрией, теорией вероятностей и др.). Иногда в широком понимании под комбинаторикой подразумевают более обширную область дискретной математики, включающую, в том числе, и теорию графов. Однако наиболее знакомой для нас является вероятностная и перечислительная комбинаторика. Первая изучает вопрос вероятности обладания некоторого множества конкретным свойством, вторая же рассматривает задачи о перечислении или исчислении количества различных конфигураций (перестановок, размещений, сочетаний). Данная работа сфокусирована на размещениях и исследовании их теоретических и практических особенностей.
По окончанию первой главы мы можем заключить, что комбинаторика имеет интересную историю собственного становления как науки. А ее различные разделы имеют широкий спектр применения в различных сферах знаний.
Глава 2. Примеры решения задач по комбинаторике
cyberpedia.su
А. Размещения без повторений — КиберПедия
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком следования.
Упорядоченные подмножества из n элементов по k элементов каждое, называются размещениями из n элементов по k элементов (или кратко: размещениями из n по k). Таким образом, размещения отличаются либо составом элементов, либо их порядком.
Пусть дано множество, состоящее из п элементов. Размещением из п элементов по к (к < п) элементов называется упорядоченное подмножество, содержащее к различных элементов данного множества Все эти подмножества отличаются друг от друга или составом элементов, или порядком их распределения. Но число элементов во всех этих подмножествах равно к.
Размещениями изn поmназываются всевозможные упорядоченные подмножества, содержащие m элементов из данных n. Обозначаются и вычисляются по формуле:
Пример 10.Сколько можно составить четырехзначных чисел, содержащих различные цифры из 5 цифр.
Решение: Четырехзначное число – это упорядоченная последовательность цифр, т.е. имеем дело с размещениями без повторений: А54=5!/(5-4)!=5!/1!=5×4×3×2=120.
Пример 11. В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами может быть составлено расписание на 1 день?
Решение:
Пример 12. Сколькими способами можно выбрать 3 из 10 различных шаров?
Ответ: А103=720.
B. Размещения с повторениями
Размещением с повторениями из m элементов по k элементов называется такое упорядоченное множество, которое содержит k элементов, причем один и тот же элемент может входить в это множество несколько раз (от нуля до k). Число всех размещений с повторениями из m по k равно mk, т.е. Ākm= mk
Размещениями с повторениями из n элементов по k элементов называются упорядоченные множества, каждое из которых содержит k необязательно различных элементов из данного множества n элементов. Число размещений с повторениями вычисляется по формуле:
Пример 13.Сколько различных пятизначных чисел можно составить при помощи цифр 1, 2, 3?
Решение.Согласно предыдущему, искомое число равно Ā53 =35=243
Пример 14.Кодовый замок имеет на диске 12 букв. Секретное слово состоит из 5 букв. Сколько неудачных попыток можно сделать? Общее число комбинаций Ā512 =125=248832. Число неудачных попыток 248832-1=248831.
Пример 15. В стену здания вмонтированы 8 гнезд для флажков. В каждое гнездо вставляется либо голубой, либо красный флажок. Сколько различных случаев распределения флажков на здание.
Решение: Так как порядок расположения элементов важен и не все элементы используются в данном соединении, то это размещение. А так как всего 8 гнезд, а флажков 2 вида (голубой и красный), то они будут повторяться, т.е. это размещение с повторением.
Сочетания
A. Сочетания без повторений
Определение.Подмножества из n элементов по k элементов каждое, отличающиеся хотя бы одним элементом, называются сочетаниями из n элементов по k элементов (или кратко: сочетания из n по k). Таким образом, сочетания отличаются только составом элементов. Число сочетаний из n по k обозначается: Ckn.
Пусть дано множество, состоящее из п элементов. Сочетанием из п элементов по к (0 < к < п) элементов называется любое подмножество, которое содержит к различных элементов данного множества. Таким образом, различными подмножествами считаются только те, которые отличаются составом элементов. Подмножества, отличающиеся друг от друга лишь порядком следования элементов, не считаются различными. Число всех возможных сочетаний из п элементов по к обозначается Ckn. Так как число перестановок из к равно k!, то число размещений из п элементов по к — Аknбудет в к! раз больше, чем число сочетаний из п
элементов по к — Сkn , т.е. Аkn =n! × Ckn.
Отсюда: Ckn = Аkn /k!= n!/(n-k)! ×k!
Пусть имеются n различных элементов. k- сочетаниями без повторений из n элементов называют k-расстановки, составленные из этих элементов, и отличающиеся друг от друга составом, но не порядком элементов. Число k-сочетаний без повторений из n различных элементов обозначается Сkn.
Сочетаниями изn поmназываются всевозможные подмножества данных nэлементов, состоящие из m элементов. Для подсчета их числа используются следующие обозначение и формула:
Сочетанием называют комбинации, составленные из n –различных элементов по m элементов, которые отличаются только составом элементов и не зависят от порядка следования.
Пример 16. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?
Решение: Так как порядок выбранных четырех человек не имеет значения, то это можно сделать C425 способами: C425 = 25!/(25-4)! ×4!=12650
Пример 17. Сколькими способами можно выбрать при игре в спортлото 6 из 49 номеров?
Ответ: C649=69919080
Пример 18. В кондитерской продавалось 4 вида пирожных: наполеоны, эклеры, песочные, слоеные. Сколькими способами можно купить 7 пирожных?
Ответ: C47=
B. Сочетания с повторениями
Сочетанием с повторениями из m элементов по k элементов (или короче: сочетанием с повторениями из m по k) называется множество, содержащее k элементов, причем каждый элемент принадлежит к одному из m типов. Число всех вышеупомянутых сочетаний с повторениями из m по k обозначается Ĉkm (обратите внимание на отличие от обозначения числа сочетаний из n по k – черта сверху).Число сочетаний с повторениями из т по k равно:
Пусть имеется n различных типов предметов. Сколько k-расстановок можно составить, которые отличаются друг от друга составом, но не порядком входящих элементов? Такие k -расстановки называются k-сочетаниями с повторениями из n типов предметов. Число k -сочетаний с повторениями из n типов предметов обозначается Ĉkm.
Сочетания из n элементов, в каждое из которых входит m элементов, причем один и тот же элемент может повторяться в каждом сочетании любое число раз, но не более m, называются сочетаниями с повторениями. Число сочетаний с повторениями вычисляется по формуле:
Пример 19. На почте продаются открытки 10 сортов. Сколько вариантов существует для покупки 12 открыток.
Решение: Порядок расположения элементов не имеет значения, следовательно, это сочетание. А так как открытки в наборе могут повторяться, то это сочетание с повторениями.
.
Таким образом, из 10 открыток можно выбрать набор из12 штук 293930 способами.
Пример 20.Число различных бросаний двух одинаковых кубиков равно
Пример 21.Напишем все сочетания с повторениями из трех элементов А, В, С по 3. Сколько их?
Вот они: ААА ВВВ ССС, АВВ ВСС, АСС ВВС, ААВ, ААС, АСВ. Их 10 штук, т.е.Ĉ33.=10.
Свойства сочетаний
1) Сkn = Сn—kn
2) Сkn = Сk-1n-1+ Сkn-1
3) С0n + С1n + С2n + …+ Сnn = 2n
4) Сkn * Сm—kn—k= Сkm+ Сmn
Все сочетания легко вычисляются, если записать их в виде треугольной таблицы (треугольника Паскаля ):
1 Со°
1 1 C10 С11
1 2 1 С20 С21 С22
1 3 3 1 С30С31 С32С33
1 4 6 4 1 С40 С41С42С43С44
1 5 10 10 5 1 С50С51С52С53С54С55
На основании данной таблицы можно увидеть справедливость указанных выше свойств сочетаний.
При определении вида комбинации удобно пользоваться схемой:

КОМБИНАТОРНЫЕ ЗАДАЧИ
Задача 1. Максимально возможное количество матчей, которое можно организовать в высшей лиге футбольного дивизиона страны не должно превышать 160 в один круг. Сколько (максимально) команд можно включить в состав высшей лиги.
Решение. Обозначим возможное количество команд через n, тогда число сыгранных матчей равно C2n . По условию C2n ≤ 160. Пусть C2n = 160, тогда:
n!/(n-2)!* 2!=160. Тогда n=18,4;-17,4.
Число команд должно быть натуральным числом, поэтому n = 18.
Ответ. 18 команд.
Задача 2. Имеется 4 сорта чая, 5 сортов конфет и 6 сортов печенья. Сколькими способами можно организовать чаепитие-дегустацию на трех человек, если каждый может выпить одну чашку чая определенного сорта с одной конфетой и одним печеньем?
Решение. Используя правило произведения, подсчитаем, что:
1) число способов распределить сорта чая для трех дегустаторов равно 43;
2) число способов распределить по одной конфете определенного сорта для трех дегустаторов равно 53;
3) число способов распределить по одному печенью определенного для трех дегустаторов равно 63.
Применяя еще раз правило произведения, мы получим, что число способов организовать данное чаепитие-дегустацию равно 43* 53* 63= 1 728 000.
Задача 3. В соревнованиях принимают участие 16 команд Сколькими способами могут распределиться три первых места, т е необходимо найти число всех подмножеств, состоящих из трех элементов, отличающихся составом (номерами команд) или порядком их размещения (подмножества № 1, № 2, № 3 и № 2, № 1, № 3 являются разными). Таким образом, имеем дело с размещением. Тогда искомое число равно A316=3360
Задача 4. В отделении 10 солдат. Необходимо составить наряд из 4-х человек. Сколько существует способов составления такого наряда?
Решение. Поскольку порядок, в котором мы выбираем участников наряда, не важен, то мы имеем дело с сочетаниями их 10 по 4. Итак, C410=210
Задача 5. Сколько существует четырехзначных чисел, состоящих из различных цифр?
Решение. Ноль не может быть первой цифрой, следовательно, есть 9 возможностей выбрать первую цифру. Далее может следовать любая упорядоченная тройка оставшихся цифр, а для этого есть A39 способов. Итого, получаем 9* A39=4536
Задача 6. Сколькими способами можно раскрасить диаграмму из 4 столбцов четырехцветной ручкой так, чтобы каждый столбец был окрашен в определенный цвет.
Решение: Порядок расположения элементов имеет значение и в диаграмме 4 столбца, а ручка тоже четырехцветная, т.е. все элементы присутствуют в соединении, следовательно, это соединение – перестановка. А так как окраска столбцов не повторяется (в условии сказано, что столбцы имеют разные цвета), то это перестановка без повторения. Итак, Pn = n! = 4! = 1×2×3×4 = 24 Ответ: столбцы можно закрасить 24 способами.
Задача 7. Имеется 5 кружков: 3 белых и 2 черных. Сколько различных узоров можно получить, располагая кружки в ряд.
Решение: Порядок расположения элементов имеет значение и в узоре 5 кружков, т.е. все элементы присутствуют в соединении, следовательно, это соединение – перестановка. А так как окраска кружков повторяется (в условии сказано, что 3 белых и 2 черных), то это перестановка с повторением. Итак,
Ответ: узор можно составить 10 способами.
Задача 8. Сколько словарей надо издать, чтобы можно было непосредственно выполнить перевод с любого из 5 языков на любой из 5 языков.
Решение: Порядок имеет значение (так как русско-английский и англо-русский словари различны) и не все элементы присутствуют в соединении (а только 2 из 5), значит, это размещение. Так как языки различны, то это размещение без повторения. Итак, . Ответ: надо составить 20 словарей.
Задача 9. На железнодорожной станции имеется 5 светофоров. Сколько может быть дано различных комбинаций их сигналов, если каждый светофор имеет 3 состояния.
Решение: Порядок имеет значение и не все элементы присутствуют в соединении, значит, это размещение. Так как цвета повторяются, то это размещение с повторением. Итак, . Ответ: может быть дано 243 различных комбинаций цветов.
Задача 10. 12 человек играли в городки. Сколькими способами они могут разбиться на команды по 4 человека в каждой.
Решение: Порядок расположения игроков в команде не имеет значения, следовательно, это сочетание. А так как игроки не повторяются (все члены команды различные люди), то это сочетание без повторения. Итак, .
Ответ: игроки могут разбиться на команды по 4 человека в каждой 495 способами.
Задача 11. В цветочном магазине продаются цветы 6 видов. Сколько можно составить букетов из 10 цветов в каждом (букеты отличающиеся лишь расположением цветов считать одинаковыми).
Решение: Порядок расположения цветов в букете не имеет значения, следовательно, это сочетание. А так как цветы повторяются, то это сочетание с повторением. Итак, . Ответ: букеты можно составить 3003 способами.
Задача 12. В группе 25 студентов, из которых 5 отличников, 11 хорошистов и остальные троечники. Сколькими способами можно выбрать группу для выполнения лабораторной работы, состоящей из 3 хорошистов, 1 отличника и 1 троечника.
Решение: Сначала узнаем сколькими способами можно выбрать 3 хорошистов из 11 человек. Порядок расположения студентов не важен, значит, это сочетание. А так как люди в группе не повторяются, то это соединение – сочетание без повторения. Итак, одного хорошиста можно выбрать способами. Аналогично рассуждая, приходим к тому, что 1 отличника можно выбрать способами и одного троечника можно выбрать способами. Так как команда для выполнения лабораторной работы выбирается одновременно, т.е. 5 хорошистов, затем 1 отличник, затем 1 троечник, то, применив правило произведения, получим: способами. Ответ: группу для выполнения лабораторной работы можно составить 3300 способами.
Задача 13: Имеется 4 чашки, 5 блюдец, 6 ложек (все чашки, блюдца, ложки различны). Сколькими способами можно накрыть стол к чаю на 3 человека, если каждый получает 1 чашку, 1 блюдце и 1 ложку.
Решение: Выберем для 3 человек чашки из 4 имеющихся. Порядок расположения элементов имеет значение, и не все элементы входят в соединение, значит, это размещение. Но так чашки не повторяются, то это размещение без повторения. Итак, из 4 чашек 3 можно выбрать способами. Аналогично рассуждая, получим, что из 5 блюдец 3 можно выбрать способами, а из 6 ложек 3 можно выбрать способами. Так блюдце, чашка и ложка входят в набор одновременно, то стол можно накрыть способами. Ответ: стол можно накрыть 172800 способами.
Задача 14. Группу из 20 студентов можно разместить в аудитории по 2 человека за каждой партой. Порядок их размещения имеет значения.
Решение. Количество возможных вариантов размещений вычисляется по формуле:
Задача 15. Найти количество трехзначных чисел с неповторяющимися цифрами, которые можно составить из цифр: 1, 2, 3, 4, 5.
Решение. Количество трехзначных чисел в данном примере определяется по формуле размещений (3) и равно:
Задача 16. Группу из 20 студентов следует рассадить в аудитории по 2 человека за каждой партой. Порядок их размещения не имеет значения. Определить количество возможных вариантов сочетаний.
Решение. Количество возможных вариантов сочетаний вычисляется по формуле 4):
Задача 17. Флаг государства может комбинироваться из трёх полос разного цвета. Определить число комбинаций из пяти разных цветов, которые можно получить, выбирая из них три полосы разного цвета.
Решение. Если учитывать порядок в комбинации, то число вариантов равно:
Если же порядок в комбинации не имеет значения, то количество разных вариантов равно:
cyberpedia.su
