График функции y 5x – Постройте график функции y=5/x

Постройте график функции y = –5/x

Задание.
Постройте график функции у = —5 / x.

Решение.
Функции с дробями мало кому нравятся, но на самом деле их график построить совсем не сложно.
Немного ознакомимся с функцией.
Функция записана в виде дроби, причем в числителе находится конкретное число, а вот в знаменателе — переменная, которая может принимать различные значения. Для таких случаев необходимо проверить, все ли значения может принимать данная переменная.
Вспоминаем правило: делить на ноль нельзя!
Соответственно для заданной дроби в знаменателе не должно быть нуля, поэтому переменная х не может быть равной нулю:

   

Больше никаких ограничений для данной функции не существует, поэтому можно приступать к ее построению.
Чтобы понимать, как будет вести себя график функции, проверим саму функцию на четность / нечетность:

   

Следовательно, функция является нечетной.
Определим точки, через которые пройдет график функции.

Ранее было определено, что функция существует для любых значений переменной х, исключая 0. Поэтому можно выбрать произвольные значения этой переменной и подставить их в уравнение:

   

   

Точка (—5; 1)

   

   

Точка (—2; 2,5)

   

   

Точка (—1; 5)

   

   

Точка (—0,5; 10)
Этих точек достаточно, чтобы провести часть кривой графика. Так как определили, что функция является нечетной, то другую часть графика можно провести симметрично началу координат.
Получаем гиперболу у = —5 / x.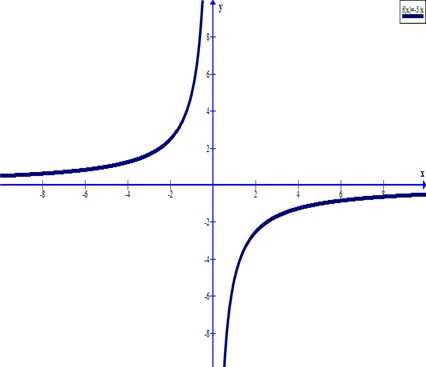

ru.solverbook.com

Постройте график функции y = x|x|-5|x|-3x

Задание.
Постройте график функции y = x|x| — 5|x| — 3x.
 
Решение.
На первый взгляд построить данную функцию не так просто, но на самом деле она строится не намного сложнее других.

Разберемся со знаком модуля, который входит в данную функцию. Как известно, под этим знаком может стоять хоть положительное, хоть отрицательное число, но в любом случае результат будет положительным. Следовательно, необходимо рассмотреть два варианта:
1) когда под знаком модуля будет стоять отрицательное число;
2) когда под знаком модуля будет стоять положительное число.
В случае отрицательного числа получим следующую функцию после открытия модуля:

   

Графиком такой функции будет парабола с ветвями, которые направлены вниз, так как перед квадратом переменой х стоит знак «минус».
Найдем координаты вершины параболы:

   

Найдем значение функции для этой точки:

   

Полученная вершина первой параболы для отрицательных значений х имеет координаты (—1; 1).
Пересекаться парабола с осями будет в следующих точках:
Ось Ох:

   

   

   

   

или
Получилось две точки — (0; 0) и (—2; 0).
В случае положительного х получим такую функцию после открытия модуля:

   

График функции — парабола с ветвями, которые направлены вверх, так как перед квадратом х стоит знак «плюс».
Координаты ее вершины:

   

Найдем значение функции для этой точки:

   

Полученная вершина второй параболы для положительных значений х имеет координаты (4; —16).
Пересечение параболы с осями будет в следующих точках:
Ось Ох:

   

   

   

или
Получилось две точки — (0; 0) и (8; 0).
Не забывая об ограничениях из-за модуля, наносим точки на график.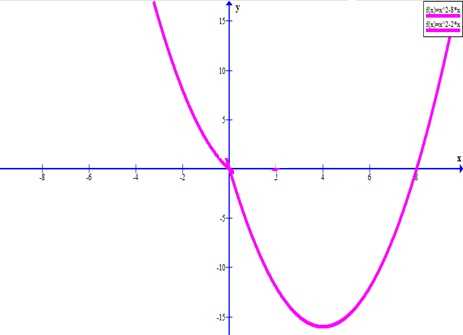

ru.solverbook.com

Постройте график функции y = (x+5)^2

Задание

.
Постройте график функции y = (x + 5)^2.

Решение.
Построить график любой функции можно простым подбором координат точек, которые будут принадлежать этой функции. Но зачастую проще сделать небольшой анализ уравнения функции, чтобы понять что за кривая должна получиться, а также такой анализ поможет более быстро и точно построить этот график.
Рассмотрим заданное уравнение:

   

Видим квадрат от суммы двух чисел, одно из которых является неизвестным. В таких случаях можно представить с помощью формул сокращенного умножения данную функцию в следующем виде:

   

Получаем квадратную функцию, графиком которой является парабола. Ветви этой параболы будут направлены вверх, так как перед квадратом х нет отрицательного коэффициента.
У каждой параболы есть вершина. Найдем ее абсциссу с помощью простой формулы:

   

Полученное значение абсциссы подставим в уравнение заданной функции и найдем нужное значение ординаты точки вершины:

   

Имеем, что вершина параболы с координатами (—5; 0).
В принципе это видно из начального уравнения функции, а именно из выражения (х + 5) под знаком квадрата.
Найдем дополнительные точки, чтобы построить параболу. Относительно своей вершины она симметрична, поэтому можно найти точки для построения одной ветви, а вторую достроить симметрично ей.
Выберем х = —4:

   

Координаты первой точки (—4; 1).
Выберем х = —3:

   

Координаты второй точки (—3; 4).
При х = —2 функция — третья точка (—2; 9)
Нанесем точки на плоскость, соединим их плавной кривой и достроим вторую ветвь параболы симметрично ее вершине.

ru.solverbook.com

Постройте график функции y=0,5x(в квадрате)

Задание.
Постройте график функции y = 0,5x(в квадрате).

Решение.
Для начала запишем функцию в более привычном для математики виде:

   

Так будет проще воспринимать саму функцию.
Итак, из ее записи видно, что графиком будет парабола. На это указывает квадрат аргумента х. Далее из коэффициента 0,5 перед квадратом аргумента определяет, что ветви параболы будут направлены вверх, так как коэффициент — положительный.
Определим четность функции:

   

Получается, что значения функции для положительных и отрицательных значений аргумента будут совпадать, то есть функция является четной, а ее график будет симметричен оси Оу.
Найдем вершину параболы. Поскольку функция располагается симметрично оси Оу, то ее вершина будет лежать на этой оси. А это значит, что абсцисса точки вершины равна 0 (х = 0). Подставим это значение в функцию и найдем значение у:

   

Получается, что вершина параболы в начале координат.
Найдем несколько точек, через которые пройдет парабола. Будем находить значения функции только для положительных х, а для отрицательных, как мы выяснили, значения будут такими же.
Выберем первую точку х = 1. Тогда . Получили точку (1; 0,5).
Выберем вторую точку х = 2. Тогда . Получили точку (2; 2).
Выберем третью точку х = 3. Тогда . Получили точку (3; 4,5).
Построим точки и симметричные им и проведем параболу.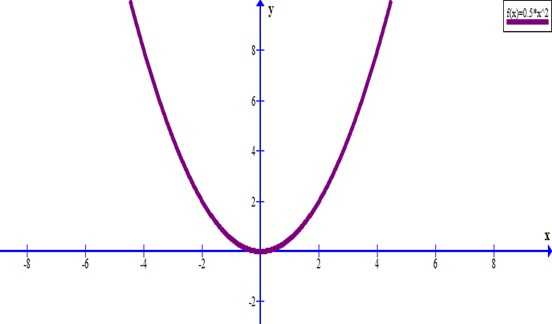

ru.solverbook.com

Постройте график функции y = |-2

Задание.
Постройте график функции y = |-2 – |x + 5||.

Решение.
Страшная на первый взгляд функция на самом деле строиться не так уж сложно.
Чтобы разобраться в ее построении вспомним, что представляет собой модуль. Как известно из алгебры, модулем любого числа (то ли оно положительное, то ли отрицательное) всегда будет положительное число. Также модуль называют расстоянием, а как известно, расстояние не может быть отрицательным – это всегда положительное число.
Под знаком модуля в заданной функции стоит сумма неизвестного числа х и числа 5, которая может быть как положительной, так и отрицательной. Поэтому для построения графика этой функции нужно рассмотреть обе возможности.
Пусть сумма (х + 5) будет положительным числом. Тогда, при открытии знака модуля, функция примет следующий вид:
y = |–2 – |x + 5|| = |-2 – x – 5| = |– x – 7|
Здесь также возможны два варианта:
1) –х – 7 – положительное, тогда у = –х – 7
2) –х – 7 – отрицательное, тогда у = х + 7
Таким образом, при х > –5:
1) –х – 7 > 0
При x < –7 функция существовать не будет
2) –х – 7 < 0
При x > –7 функция будет существовать для х > –5, а тогда:
у (–4) = –4 + 7 = 3 – точка (–4; 3)
у (0) = 0 + 7 = 7 – точка (0; 7)

Пусть сумма (х + 5) будет отрицательным числом. Тогда, открыв знак модуля, получим:
y = |–2 – |x + 5|| = |-2 + x + 5| = |x + 3|

Здесь также возможны два варианта:
1) х + 3 – положительное, тогда у = х + 3
2) х + 3 – отрицательное, тогда у = – х – 3
Таким образом, при х < –5:
3) х + 3 > 0
При x > –3 функция у = х + 3 существовать не будет
4) х + 3 < 0
При x < –3 функция будет существовать для х < –5. Тогда:
у (–6) = –(–6) – 3 = 3 – точка (–6; 3)
у (–10) = –(–10) – 3 = 7 – точка (–10; 7)
Нанесем полученные точки на плоскость.

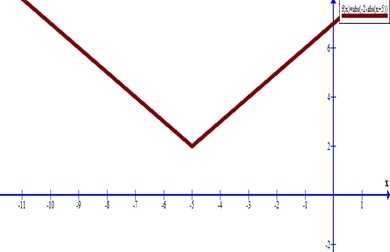
ru.solverbook.com