Методом интервалов решите неравенство – Метод интервалов: решение простейших строгих неравенств

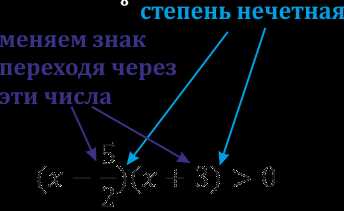
Решение неравенств методом интервалов

Статья посвящена разбору примеров решения неравенств методом интервалов. При том, что этот метод решения неравенств достаточно универсален, важно помнить, что не всегда применение данного метода оправдано с точки зрения объема вычислений. Иногда бывает удобнее воспользоваться некоторыми другими методами решения неравенств. Все рассмотренные в статье неравенства взяты из реальных вариантов ЕГЭ по математике разных лет. Присутствует подробный видеоразбор одного из заданий.

 

Метод интервалов

Пусть заданное неравенство имеет вид: Для решения этого неравенства используется так называемый метод интервалов (метод промежутков), который состоит в следующем.

Во-первых, на числовую ось наносят точки разбивающие ее на промежутки, в которых выражение определено и сохраняет знак («плюс» или «минус»). Такими точками могут быть корни уравнений и Соответствующие этим корням точки отмечают на числовой оси: закрашенными кружками — точки, удовлетворяющие заданному неравенству, а светлыми кружками — не удовлетворяющие ему.

Во-вторых, определяют и отмечают на числовой оси знак выражения для значении , принадлежащих каждому из полученных промежутков. Если функции и являются многочленами и не содержат множителей вида где  то достаточно определить знак функции в любом таком промежутке, а в остальных промежутках знаки «плюс» и «минус» будут чередоваться.

Если же в числителе или знаменателе дроби  имеется множитель вида  где  то непосредственной проверкой выясняют, удовлетворяет ли значение заданному неравенству.

Изменение знаков удобно иллюстрировать с помощью волнообразной кривой (кривой знаков), проведенной через отмеченные точки и лежащей выше или ниже числовой оси в соответствии со знаком дроби в рассматриваемом промежутке. Промежутки, которые содержат точки, удовлетворяющие данному неравенству, иногда покрывают штрихами. На ту же ось помещают и точки, соответствующие Заштрихованная область в совокупности с полученными точками будет являться ответом к неравенству.

Общий вид прямой знаков в методе интервалов

Примеры решения неравенств методом интервалов

Пример 1. Решите неравенство:

   

Решение. Упрощаем неравенство путем равносильных преобразований:

При умножении или делении обеих частей неравенства на отрицательное число, меняется знак неравенства!

   

   

Выражения, стоящие в числителе и знаменателе, можно разложить на множители, тогда неравенство примет вид:

   

Далее по алгоритму решения неравенств методом интервалов находим корни уравнений и . Из первого получаем Из второго получаем Наносим на числовую прямую получившиеся точки, причем точки и обозначаем закрашенными кружочками (для них неравенство выполняется), а точки и — светлыми (для них неравенство не выполняется, при этих значениях, выражение, стоящее слева от знака неравенства, вообще не имеет смысла):

Числовая прямая с отмеченными точками

Определяем теперь знаки выражения на полученных промежутках (подставляем любое значение из каждого полученного промежутка в данное выражение), изображаем кривую знаков, заштриховываем те промежутки, на которых исходное неравенство выполняется:

Кривая знаков для исходного неравенства

Итак, исходному неравенству удовлетворяют следующие значения:

Ответ: 

Задача для самостоятельного решения №1. Решите неравенство:

   

Показать ответ

Ответ: Пример 2. Решите неравенство:

   

Решение. Подкоренное выражение, как известно, не может принимать отрицательных значений, также не допускается нахождение в знаменателе дроби нуля. Следовательно, область допустимых значений данного неравенства определяется неравенством и тем условием, что Решаем уравнения и Из первого уравнения получаем, что Из второго уравнения получаем, что Наносим область допустимых значений неравенства и полученные точки на числовую прямую, причем эти точки будет светлыми, поскольку ни одно из значений и не удовлетворяет неравенству. Сразу определяем знаки выражения в каждом из полученных промежутков и рисуем кривую знаков:

yourtutor.info

Метод интервалов: примеры, решения

Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.

Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.

Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.

Yandex.RTB R-A-339285-1

Алгоритм

Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x)<0 (знак неравенства может быть использован любой другой, например, ≤, > или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:

• произведение линейных двучленов с коэффициентом 1 при переменной х;
• произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.

Приведем несколько примеров таких неравенств:

(x+3)·(x2−x+1)·(x+2)3≥0,

(x-2)·(x+5)x+3>0 ,

(x−5)·(x+5)≤0,

(x2+2·x+7)·(x-1)2(x2-7)5·(x-1)·(x-3)7≤0 .

Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:

• находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
• определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
• определяем знаки выражения f(x) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
• наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки < или ≤ изображается, штрихуются «минусовые» промежутки, если же мы работаем с неравенством, имеющим знаки > или ≥, то выделяем штрих

zaochnik.com

Метод интервалов, решение неравенств

Решение неравенств

Метод интервалов

Перенос знаков

Выбор точек

Система и совокупность

Точка знакопостоянства

---

Что нельзя делать в неравенстве, даже под пытками:

1) Домножать на знаменатель.

2) Умножать/делить на отрицательное число, не меняя знак.

3) Убирать бездумно логарифм или основание.

Начнем с простого: 

Линейные уравнения решаются обычным переносом, один только очень важный момент (домножение или деление на отрицательное число):

Ответ: x ∈ ( −4; +oo).

Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:

Ответ: x ∈ ( 0; +oo).

Следующий пример уже с дробью:

Приравняем числитель к нулю, и скажем, что знаеменатель не равен нулю:

Раставляем корни числителя и знаменателя на одной прямой. Попробуем подставить х = 0, чтобы определить знаки: 

Там, где «0», ставим знак «−», а дальше знаки чередуем: 

Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+»:

Когда мы включаем точку (корень числителя) ставим «[ ]» — квадратную скобку. Если не включаем (корень знаменатля), или знак строгий (>, <),  скобки круглые «( )» .

Ответ: x ∈  (2; 7].

Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения, или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности: 

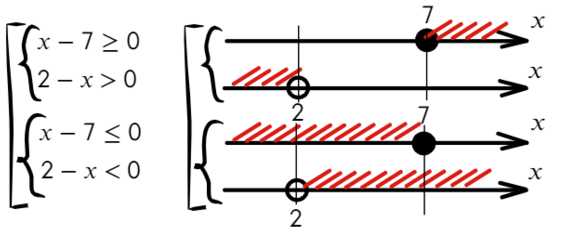
Отметим на прямой решение каждого неравенства.

Решением системы «{» является тот участок, который подходит обоим неравенствам.

Решением совокупонсти «[» является тот участок, который включен хотя бы в одно неравенство.

Мой любимый пример: 

Покажу мастер-класс, как делать не надо. Дома не повторять!

А теперь через метод интервалов разберемся, как сделать правильно:

Там, где ноль, ставим знак «−», а дальше чередуем:

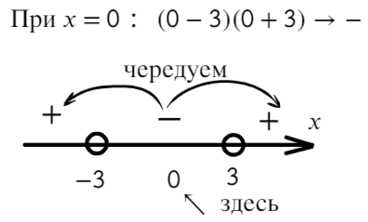
В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».

Ответ: x ∈ (−3; 3).

Перейдем к квадратному уравнению:

Разложим на множители и подставим x = 10, чтобы определить знак: 

Нам требуются положительные значения: 

Неравенство можно также решить, разложив на множители: 

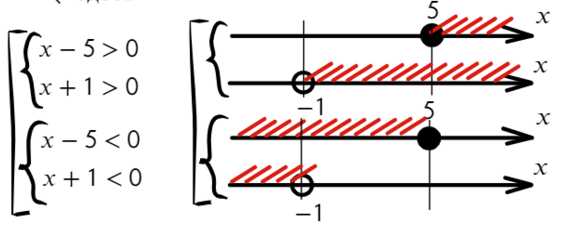
Ответ: x ∈ (−oo; −1) ∪ (5; +oo).

А теперь простой, но крайне показательный пример:

Убирать квадрат ни в коем случае нельзя. Простенький контрпример: 

Надеюсь, убедил. Вместо знака больше поставим знак равно и попробуем решить методом интервалов:

Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).

Проверим это:

В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».

Только точка «0» не подходит, 0 > 0 — неверно!

Ответ: x ∈ R \ {0} или x ∈ (−oo; 0) ∪ (0; +oo).

Переходим на новый уровень:

Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)

По методу координат найдем корни числителя и знаменателя:

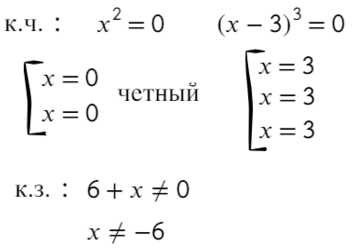
Отметим все корни на одной прямой. Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота.

Требуется найти промежутки, где выражение больше или равно нулю. Нам подойдут все «промежутки», где знак плюс. А что по поводу точки x = 0, эта точка нам подойдет? Подставим:

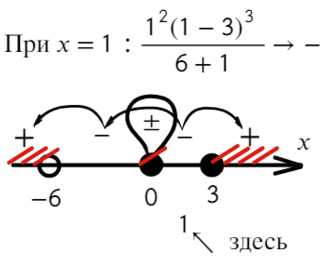
Вот для чего ставить в восклицательном знаке ±. Чтобы не потерять отдельные точки, в данном случае 0.

Ответ: (−oo; − 6) ∪ {0} ∪ [ 3; +oo).

Дальше интереснее:

По той же схеме корни числителя и знаменателя:

Определим знак при x = 10 и расставим знаки: 

Ответ:  {−3} ∪ (−2; +oo).

Закрепляем последовательность:

Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя? 

Подставим x = 10 и расставим знаки:

Ответ: [ −5; 3) ∪ [ 5; +oo).

Все скользкие моменты разборали, стало понятнее?

Резюме: 

1. Если знак строгий (>, <), все точки выколотые (в круглые скобки).
2. Если знак нестрогий (≥, ≤), корни числителя закрашенные, точки знаменателя выколотые [в квадратные скобки].
3. Если корень является решением уравнения четное кол-во раз (2, 4, 6, 8), то в этой точке знак меняться не будет.
4. Отдельная точка записывается {в фигурных скобках}.

Нашел ошибку/опечатку — напиши.

Группа с полезной информацией и легким математическим юмором.

ik-study.ru

Неравенства методом интервалов

Рассмотрим, как решать неравенства методом интервалов, на конкретных примерах.

   

Используем алгоритм метода интервалов. Приравниваем к нулю левую часть:

   

   

   

Полученные точки отмечаем на числовой прямой:

Для проверки знака берем 0 (желательно на числовой прямой отметить взятую точку, чтобы потом не забыть, куда ставить знак). Подставляем 0 в последнее неравенство: (2∙0-14)(5∙0+25)= -14∙25, то есть (-)∙(+)= -. Таким образом, в промежуток, из которого взяли нуль, ставим знак «-«, остальные знаки чередуем в шахматном порядке. Поскольку решаем неравенство ≥0, выбираем промежутки со знаком «+» и записываем ответ.

Ответ:

   

   

Приравниваем к нулю левую часть:

   

   

Полученные точки отмечаем на числовой прямой:

Для проверки знака берем 0 и подставляем его в последнее неравенство. По знакам получаем:

   

В промежуток, которому принадлежит 0, ставим «+», остальные знаки расставляем в шахматном порядке. Поскольку решаем неравенство ≤0, в ответ выбираем промежутки со знаком «-«. (Не забываем, когда точки закрашенные, а когда — выколотые. Те точки, в которых знаменатель обращается в нуль, выколотые всегда).

Ответ:

   

   

Приравниваем к нулю левую часть:

   

По теореме, обратной теореме Виета

   

Полученные точки отмечаем на числовой прямой:

Для определения знака берем 0 и подставляем его в последнее неравенство. Получает (-)/(-)=(+). Остальные знаки расставляем в шахматном порядке. Поскольку решаем неравенство ≥0, выбираем промежутки со знаком «+» и записываем ответ.

Ответ:

   

   

Переносим все слагаемые в левую часть, приводим к наименьшему общему знаменателю и упрощаем: 

   

   

   

   

После упрощения решаем неравенство методом интервалов.

Приравниваем к нулю левую часть:

   

   

Точек, в которых числитель обращается в нуль, нет. На числовой прямой отмечаем только одну точку:

Для проверки берем нуль. Подставляя его в последнее неравенство, получаем «+». На другом интервале — «-«. Нам нужен интервал с «-«.

Ответ:

   

Как решать более сложные неравенства методом интервалов, рассмотрим в следующий раз.

www.uznateshe.ru

Метод интервалов

 

Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f(x) > 0. Алгоритм состоит из 5 шагов:

 

1. Решить уравнение f(x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
2. Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
3. Найти кратность корней. Если корни четной кратности, то над корнем рисуем петлю. (Корень считается кратным, если существует четное количество одинаковых решений)
4. Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) любое число, которое будет правее всех отмеченных корней;
5. Отметить знаки на остальных интервалах, чередуя их.

После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f(x) > 0, или знаком «−», если неравенство имеет вид f(x) < 0.

В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) = 0;

 

Пример 1:

 

Решить неравенство:

(x — 2)(x + 7) < 0

Работаем по методу интервалов.

Шаг 1: заменяем неравенство уравнением и решаем его:

(x — 2)(x + 7) = 0

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:

x — 2 = 0 => x = 2

x + 7 = 0 => x = -7

Получили два корня.

 

Шаг 2: отмечаем эти корни на координатной прямой. Имеем:

 

 

Шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). 

Получим:

f(x) = (x — 2)(x + 7)

x = 3

f(3)=(3 — 2)(3 + 7) = 1*10 = 10

Получаем, что f(3) = 10 > 0 (10 – это положительное число), поэтому в самом правом интервале ставим знак плюс.

 

Шаг 4:  нужно отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус. Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. 

 

 

Вернемся к исходному неравенству, которое имело вид:

(x — 2)(x + 7) < 0

Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.

 

Пример 2:

 

Решить неравенство:

(9x² — 6x + 1)(x — 2) ≥ 0

Решение: 

Для начала необходимо найти корни уравнения 

(9x² — 6x + 1)(x — 2) = 0

Свернем первую скобку, получим:

(3x — 1)²(x — 2) = 0

Отсюда:

x — 2 = 0; (3x — 1)² = 0

Решив эти уравнения получим:

x₁ = 2; x₂ = ; x₃= ;

Нанесем точки на числовую прямую:

Т.к. x₂ и x₃ – кратные корни, то на прямой будет одна точка и над ней “петля”.

Возьмем любое число меньшее самой левой точки   и подставим в исходное неравенство. Возьмем число -1.

(9*(-1)² — 6*(-1) + 1)(-1 — 2) = -12

Т.к. решение уравнения при x = -1 отрицательное (-12), то на графике в крайнем левом интервале пишем -, и далее чередуя знак записываем его в следующие интервалы:

Далее выбираем отрицательные интервалы, т.к. знак нашего неравенства ≤.

Не забываем включать решение уравнения (найденные X), т.к. наше неравенство нестрогое.

Ответ: {} U [2;+∞)

 

Пример 3:

 

Решить неравенство:

(9x² — 6x + 1)(x — 2) > 0

Все, чем данное неравенство отличается от предыдущего – вместо нестрогого неравенства (≥) стоит строгое (>). Как ни странно, решение данного неравенства будет иным.

Найдем корни уравнения (9x² — 6x + 1)(x — 2) ≠ 0 (знак ≠ означает, что найденные корни не могут быть решениями нашего неравенства, т.к. оно строгое). Проделав все этапы, что и в предыдущем примере получим:

x₁= 2; x_2,3 =;

Вынесем наши решения на числовую прямую (обратите внимания, что данные точки не включены, т.к. неравенство строгое, т.е. левая часть неравенства не равна нулю)

Обратите внимание, что корни x₂ и x₃ совпадают, корень “” является кратным. Соответственно, в данной точке на числовой прямой рисуем петлю.

Возьмем число -1.

(9*(-1)² — 6*(-1) + 1)(-1 — 2) = -12

Т.к. решение уравнения при x = -1 отрицательное (-12), то на графике в крайнем левом интервале пишем -, и далее чередуя знак записываем его в следующие интервалы:

Далее выбираем отрицательные интервалы, т.к. знак нашего неравенства <.

Найденные корни не включаем в ответ.

Ответ: (2;+∞).

ya-znau.ru

Метод интервалов — материалы для подготовки к ЕГЭ по Математике

Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.

1. Рассмотрим, например, такое неравенство

Метод интервалов позволяет решить его за пару минут.

В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.

Метод интервалов основан на следующем свойстве дробно-рациональной функции.

Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.

Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).

Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида  .

, где  и  — корни квадратного уравнения .

Получим:

Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.

Нули знаменателя и  — выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя). Нули числителя и  — закрашены, так как неравенство нестрогое. При  и  наше неравенство выполняется, так как обе его части равны нулю.

Эти точки разбивают ось на промежутков.

Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».

И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например, и проверим знак выражения в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак .

Следующий промежуток: . Проверим знак при . Получаем, что левая часть поменяла знак на .

. Возьмем . При выражение положительно — следовательно, оно положительно на всем промежутке от до .

При  левая часть неравенства отрицательна. 

И, наконец, . Подставим и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак .

Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:

Ответ: .

Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.

Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:

, или , или , или .

(в левой части — дробно-рациональная функция, в правой — нуль).

Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.

Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.

Ты нашел то, что искал? Поделись с друзьями!

2. Рассмотрим еще одно неравенство.

Снова расставляем точки на оси . Точки и  — выколотые, поскольку это нули знаменателя. Точка  — тоже выколота, поскольку неравенство строгое.

При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например, . Левая часть имеет знак :

При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак :

При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак :

Наконец, при все множители положительны, и левая часть имеет знак :

Ответ: .

Почему нарушилось чередование знаков? Потому что при переходе через точку «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.

Вывод: если линейный множитель  стоит в чётной степени (например, в квадрате), то при переходе через точку  знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.

3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:

Левая часть та же, что и в предыдущей задаче. Та же будет и картина знаков:

Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.

Ответ: .

В задаче на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!

4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:

Квадратный трехчлен  на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения при всех одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.

И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех . Придём к равносильному неравенству:

— которое легко решается методом интервалов.

Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.

5. Рассмотрим еще одно неравенство, на вид совсем простое:

Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.

Мы поступим по другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:

И после этого — применим метод интервалов.

---

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Метод интервалов. Как решать неравенства с помощью метода интервалов

Метод интервалов применяется при решении огромного количества самых разных неравенств – квадратных,  дробно-рациональных, показательных, логарифмических…

Примеры неравенств, которые удобно решать методом интервалов:

\((2x-5)(x+3)≤0\)	\(\frac{-14}{x^2+2x-15}\)\(≤0\)
\(x^2<361\)	\(\frac{x^2-6x+8}{x-1}\)\(-\)\(\frac{x-4}{x^2-3x+2}\)\(≤0\)
\(\frac{x-2}{3-x}\)\(≤0\)	\(\frac{2}{5^x-1}\)\(+\)\(\frac{5^x-2}{5^x-3}\)\(≥2\)
\(x^2 (-x^2-64)≤64(-x^2-64)\)	\(\frac{5\log^2_{2}⁡x-100}{\log^2_{2}⁡x-25}\)\(≥4\)

Как решать неравенства методом интервалов (алгоритм с примерами)

1. Равносильными преобразованиями приведите неравенство к виду: \(\frac{(x-x_1 )^n (x-x_2 )^k…}{(x-x_3 )^l (x-x_4 )^m…}\)\(∨0\) или \((x-x_1 )^n (x-x_2 )^k…∨0\) (\(∨\) — любой знак сравнения; \(n,k,l,m\) – любые натуральные числа большие нуля, в том числе и \(1\))

   Пример:

   \((2x+5)(x-2)>5\)
   \(2x^2-4x+5x-10-5>0\)
   \(2x^2+x-15>0\)
   \(D=1-4 \cdot 2 \cdot (-15)=121=11^2\)
   \(x_1=\frac{-1-11}{2 \cdot 2}=-3;\)      \(x_2=\frac{-1+11}{2 \cdot 2}=\frac{5}{2}\)
   \(2(x-\frac{5}{2})(x+3)>0\)          \(|:2\)
   \((x-\frac{5}{2})(x+3)>0\)                

   Отметим, что здесь применено разложение на множители квадратного трехчлена.

   
   

2. Найдите корни числителя и знаменателя (т.е. такие значения икса, которые превратят их в ноль).

   \(x=\frac{5}{2}; x=-3\)

   
   

3. Нанесите найденные значения на числовую ось.

   Если неравенство строгое, то корни числителя обозначьте «выколотой» точкой, если нет — закрашенной. Корни знаменателя «выколоты» всегда, независимо от строгости знака сравнения. 

4. Расставьте знаки на интервалах числовой оси. Напомню правила расстановки знаков:

   — В крайнем правом интервале ставим знак плюс;

   — Дальше двигаемся влево;

   — Переходя через число:		— меняем знак, если скобка с этим числом была в нечетной степени (1, 3, 5…)
   		— не меняем знак, если скобка с этим числом была в четной степени (2, 4, 6…)

   
   
   

5. Выделите нужные промежутки.
   Если есть отдельно стоящий корень, то отметьте его флажком, чтоб не забыть внести этот корень в ответ (такая ситуация рассмотрена в одном из примеров ниже).

   
   

6. Запишите в ответ выделенные промежутки и корни, отмеченные флажком (если они есть).

   Ответ: \((-∞;-3)∪(\frac{5}{2};∞)\)

Пример. (задание из ОГЭ)  Решите неравенство методом интервалов   \((x-7)^2< \sqrt{11}(x-7)\)
Решение:

\((x-7)^2< \sqrt{11}(x-7)\)		Чтобы в неравенстве справа был \(0\), перенесем выражение из правой части в левую.
\((x-7)^2- \sqrt{11}(x-7)<0\)		Вынесем за скобку \((x-7)\).
\((x-7)(x-7-\sqrt{11})<0\)		Находим корни.
\(x=7;\)        \(x=7+\sqrt11\)		Расставляем на числовой оси корни, затем знаки и закрашиваем нужные интервалы
		Записываем ответ

Ответ: \((7;7+\sqrt{11})\)

Пример. Решите неравенство методом интервалов    \(\frac{(4-x)^3 (x+6)(6-x)^4}{(x+7,5)}\)\(≥0\)
Решение:

\(\frac{(4-x)^3 (x+6)(6-x)^4}{(x+7,5)}\)\(≥0\)		Здесь на первый взгляд все кажется нормальным, а неравенство изначально приведенным к нужному виду. Но это не так – ведь в первой и третьей скобке числителя икс стоит со знаком минус. Преобразовываем скобки, с учетом того, что четвертая степень — четная (т.е. уберет знак минус), а третья – нечетная (т.е. не уберет). \((4-x)^3=(-x+4)^3=(-(x-4))^3=-(x-4)^3\) \((6-x)^4=(-x+6)^4=(-(x-6))^4=(x-6)^4\) Вот так. Теперь возвращаем скобки «на место» уже преобразованными.
\(\frac{-(x-4)^3 (x+6)(x-6)^4}{(x+7,5)}\)\(≥0\)		Теперь все скобки выглядят как надо (первым идет иск без знака и только потом число). Но перед числителем появился минус. Убираем его, умножая неравенство на \(-1\), не забыв при этом перевернуть знак сравнения
\(\frac{(x-4)^3 (x+6)(x-6)^4}{(x+7,5)}\)\(≤0\)		Готово. Вот теперь неравенство выглядит как надо. Можно применять метод интервалов.
\(x=4;\) \(x=-6;\) \(x=6;\) \(x=-7,5\)		Расставим точки на оси, знаки и закрасим нужные промежутки.
		В промежутке от \(4\) до \(6\), знак не надо менять, потому что скобка \((x-6)\) в четной степени (см. пункт 4 алгоритма). Флажок будет напоминанием о том, что шестерка — тоже решение неравенства. Запишем ответ.

Ответ: \((-∞;7,5]∪[-6;4]∪\left\{6\right\}\)

Пример. (Задание из ОГЭ) Решите неравенство методом интервалов    \(x^2 (-x^2-64)≤64(-x^2-64)\)
Решение:

\(x^2 (-x^2-64)≤64(-x^2-64)\)		Слева и справа есть одинаковые выражения – это явно не случайно. Первое желание – поделить на \(-x^2-64\), но это ошибка, т.к. есть шанс потерять корень. Вместо этого перенесем \(64(-x^2-64)\) в левую сторону
\(x^2 (-x^2-64)-64(-x^2-64)≤0\)		Вынесем за скобку общий множитель.
\((-x^2-64)(x^2-64)≤0\)		Вынесем минус в первой скобки и разложим на множители вторую
\(-(x^2+64)(x-8)(x+8)≤0\)		Обратите внимание: \(x^2\) либо равно нулю, либо больше нуля. Значит, \(x^2+64\) – однозначно положительно при любом значении икса, то есть это выражение никак не влияет на знак левой части. Поэтому можно смело делить обе части неравенства на это выражение. Поделим неравенство так же на \(-1\) , чтобы избавиться от минуса.
\((x-8)(x+8)≥0\)		Теперь можно применять метод интервалов
\(x=8;\)   \(x=-8\)		Запишем ответ

Ответ: \((-∞;-8]∪[8;∞)\)

Смотрите также:
Квадратные неравенства
Дробно-рациональные неравенства

Скачать статью

cos-cos.ru