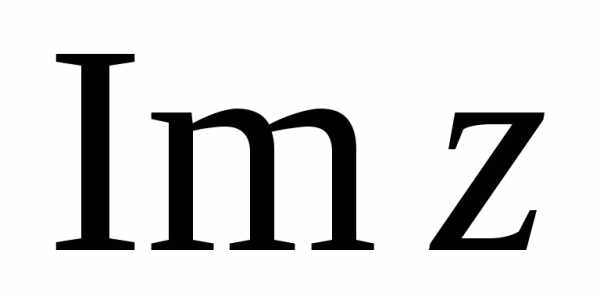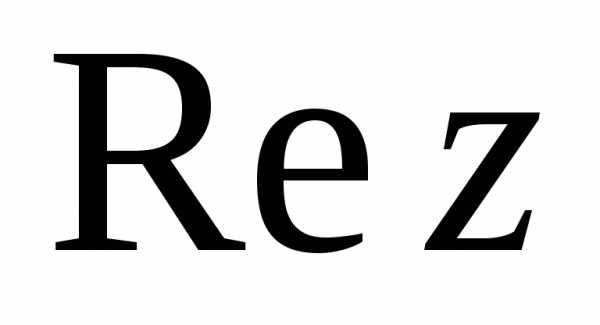3.2. Комплексные числа
В поле действительных чисел неразрешимо простейшее уравнение
x2 + 1 = 0.
Для устранения этой проблемы вводится новое число i (мнимая единица) такое, что i2 = –1.
Определение. Полем комплéксных чисел называется минимальное поле, содержащее в качестве подполя поле действительных чисел, и в котором содержится элемент, квадрат которого равен – 1. Это поле обозначают буквой С
Символ вида z = a + bi , где a и b – действительные числа, а i – мнимая единица, называется комплексным числом с действительной частью a = Rez и мнимой частью b = Imz. Сложение и умножение в множестве C комплексных чисел осуществляется по правилам:
(a + bi)(c + di) = (ac – bd) + (ad + bc) i .
Не сложно проверить, что все аксиомы поля для множества таких чисел с введёнными операциями выполняются. В частности обратный элемент для любого отличного от 0 числа может быть найден следующим образом:
(a + bi)-1 = 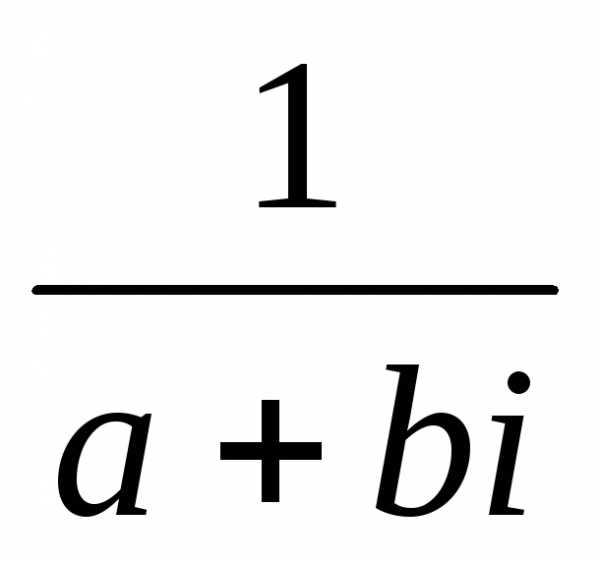 =.
=.
Корректность данного способа проверяется умножением числа на обратное к нему. Действительное число a можно трактовать как комплексное число a + 0i, так что поле действительных чисел является подмножеством множества C.
Числами вида a + bi исчерпывается все поле комплексных чисел. Поскольку поле является устойчивым относительно сложения и умножения, то вместе с любыми двумя действительными числами a и b, а также мнимой единицей i , оно должно содержать и любое выражение вида z = а + bi, так что построенное поле удовлетворяет условию минимальности. Данная форма комплексного числа называется алгебраической. а называется действительной частью числа, а b – мнимой частью числа.
Идея геометрического представления комплексных чисел заключается в том, что комплексному числу х + yi сопоставляется точка плоскости с координатами (x, y). Данную модель впервые предложил К. Вессель (1799). Другой вариацией является представление комплексного числа матрицей:
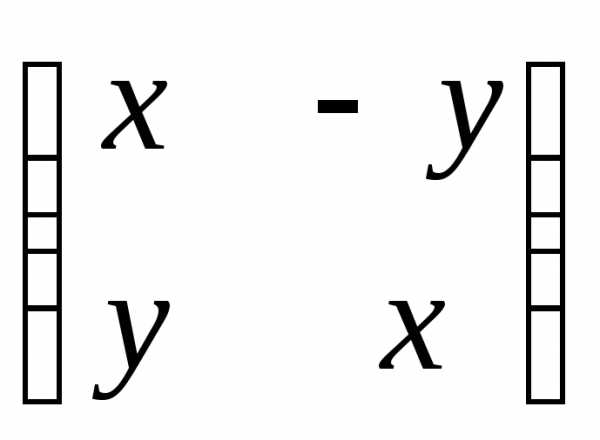 .
.
Каждое комплексное число можно представить в алгебраической и тригонометрической форме z = x + iy = r(cos + i sin). Если каждому такому числу
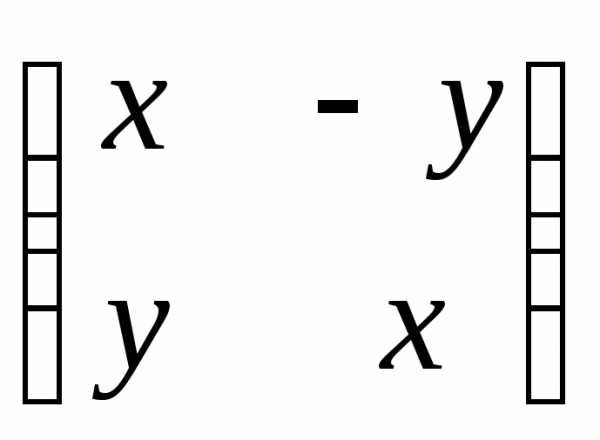 =
=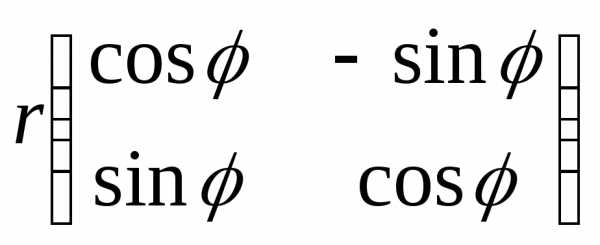 ,
то сумме, разности и произведению двух
любых комплексных чисел будет
соответствовать сумма, разность и
произведение соответствующих матриц.
Например, произведению чисел (x1 + iy1)
(x2 + iy2)
= (x1x2 – y1y2) + i(x1y2 + x2y1)
будет соответствовать матрица
,
то сумме, разности и произведению двух
любых комплексных чисел будет
соответствовать сумма, разность и
произведение соответствующих матриц.
Например, произведению чисел (x1 + iy1)
(x2 + iy2)
= (x1x2 – y1y2) + i(x1y2 + x2y1)
будет соответствовать матрица =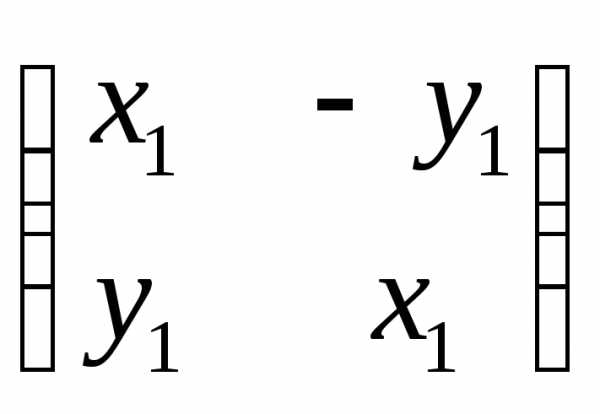
 .
.
Более
того, обратное для комплексного числа
(x + iy)–1 =
соответствует
матрице
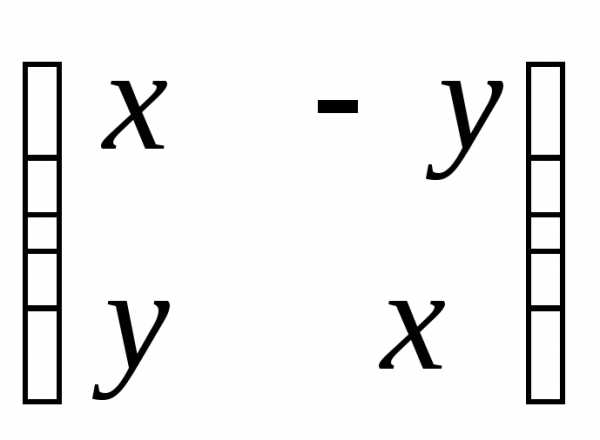 .
. Таким
образом, деление комплексных чисел
также сводимо к умножению матрицы
делимого на матрицу обратную к матрице
делителя. Поэтому данное множество
матриц вида 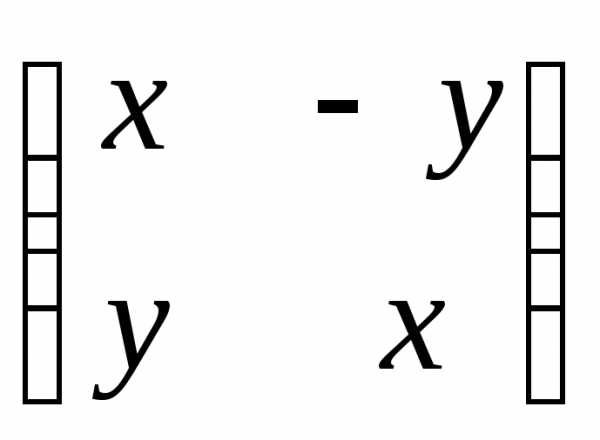 можно считать моделью поля комплексных
чисел. Тригонометрическое представление
матричной модели интересно ещё и тем,
что матрица
можно считать моделью поля комплексных
чисел. Тригонометрическое представление
матричной модели интересно ещё и тем,
что матрица задает
оператор поворота на угол,
что соответствует геометрическому
смыслу умножения на комплексное число
(при умножении происходит растяжение
в r
раз и поворот на угол, равный аргументу ).
задает
оператор поворота на угол,
что соответствует геометрическому
смыслу умножения на комплексное число
(при умножении происходит растяжение
в r
раз и поворот на угол, равный аргументу ).
Можно было ожидать, что при анализе уравнений более высоких степеней возникнет необходимость в дальнейшем обобщении понятия числа. Но в 1799 году К. Гаусс доказал так называемую Основную теорему алгебры.
Теорема. Всякое алгебраическое уравнение степени n с действительными или комплексными коэффициентами a0xn+ a1xn-1 + … + an-1 x + an= 0 в поле комплексных чисел имеет n корней (с учетом их кратностей).
Однако, получая возможность находить корни всех многочленов, мы теряем возможность сравнивать числа между собой.
Теорема. Поле комплексных чисел не является упорядоченным полем.
Доказательство: Действительно, любое упорядоченное поле должно являться расположенным кольцом, а значит для него справедливо свойство о том, что квадрат любого числа неотрицателен. В поле же комплексных чисел данное свойство не выполняется, так как i2 = –1 < 0.
Задания для самостоятельного решения
№3.4. . Вычислите:
a)
(7 – 3i)3; б) 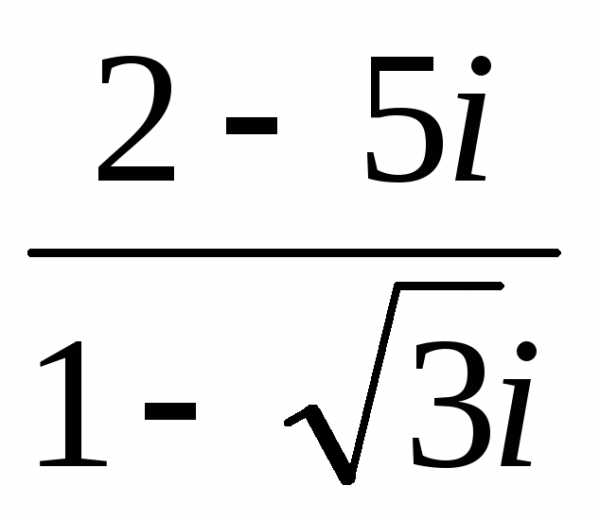 ;
в)
;
в)  ;
г) i5; д) i228; е) i137;
;
г) i5; д) i228; е) i137;
ж)
(2 + i)2; з) 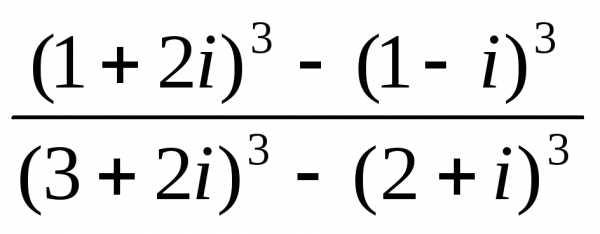 ; и)
; и) ;
к)
;
к) 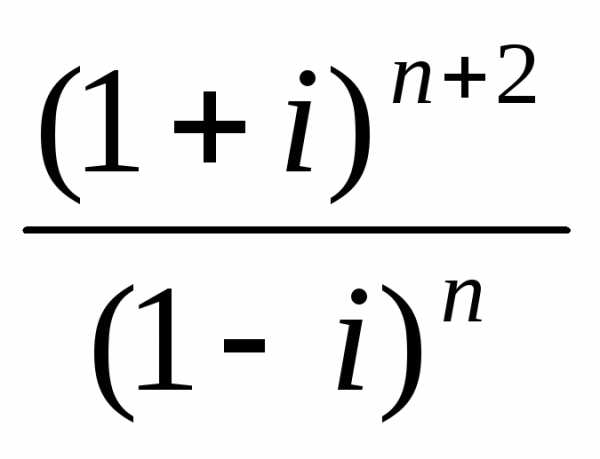 .
.
№ 3.5. Запишите числа комплексно-сопряжённые данным и на комплексной плоскости постройте векторы, изображающие данные числа и комплексно-сопряжённые с ними, запишите матричную форму данных чисел.
а) z = 3 + i; б) z = 3 – i; в) i; г) – 5i.
№ 3.6. На комплексной плоскости заштрихуйте все точки z, удовлетворяющие условиям
а)
|z
+ i | = 3; б) | z
– 1|2 + |z
+ 1|
в)
|z
– i | < |z
+ 2 – 3i|; г) 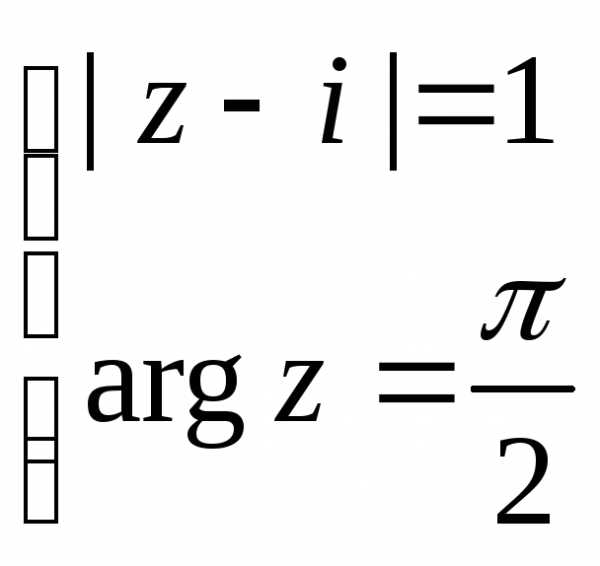
д) |z| < |z/2| + 1; е) |z – 1 + i| 2.
№ 3.7. Решите уравнения:
а) х2 – (4 + 3i)х + 1 + 5i = 0; б) .
studfiles.net
Часть 3. Комплексные числа
Предисловие
Третья часть учебно-методическогопособия посвящена комплексным числам. Это тема является традиционно трудной для студентов, и этому есть, на взгляд автора, ряд объективных причин.Во-первых,то обстоятельство, что комплексное число есть принципиально новый вид числа. Если действительные числа сопровождают человека повсюду в его обыденной жизни, то этого нельзя утверждать для комплексных чисел. От студента требуется определенный уровень даже не столько знаний, сколько способности абстрактного мышления.Во-вторых,геометрическая интерпретация комплексного числа, как точки плоскости, связана с совмещением двух принципиально различных систем координат на плоскости – прямоугольной декартовой и полярной, последняя из которых является новой для студентов. Кроме того, комплексное число изображается на плоскости с помощью вектора, поэтому от студента требуются устойчивые знания основ векторной алгебры. В- третьих, активно используется тригонометрия, которая сама по себе является «крепким орешком» для многих выпускников школ. И, наконец, принятая символика для обозначения корней из комплексных чисел остается прежней, как и для действительных чисел, а, по сути, обозначает принципиально иное, что часто вводит студентов в заблуждение. Освоить весь этот материал за короткий срок является весьма трудоемкой задачей. Помочь студенту справиться с этой задачей, получить устойчивые практические навыки при работе с комплексными числами – вот цели, которые автор ставил в этой части пособия.
3
СПИСОК ЗАДАЧ
Глава 20. Действия с комплексными числами
валгебраической форме записи
164.Найти сумму и разность двух комплексных чисел.
165.Найти произведение двух комплексных чисел.
166.Найти частное двух комплексных чисел.
167.Найти комплексное число, сопряженное данному.
Глава 21. Комплексная плоскость
и тригонометрическая форма комплексного числа
168.Построить комплексное число, заданное в алгебраической форме записи, на комплексной плоскости.
169.Построить комплексное число и сопряженное ему на комплексной плоскости.
170.Найти модуль и аргумент комплексного числа, заданного в алгебраической форме.
171.Записать тригонометрическую форму комплексного числа, заданного в алгебраической форме.
172.Найти модуль и аргумент комплексного числа, сопряженного данному.
173.Записать алгебраическую форму комплексного числа, заданного в тригонометрической форме.
174.Найти произведение двух комплексных чисел, заданных в тригонометрической форме.
175.Найти частное двух комплексных чисел, заданных в тригонометрической форме.
176.Найти целую степень комплексного числа, заданного в тригонометрической форме.
177.Найти расстояние между двумя точками на комплексной плоскости.
178.Изобразить все точки на комплексной плоскости, удаленные от данной на заданное расстояние.
4
studfiles.net
Универсальный калькулятор комплексных чисел онлайн
| Вы ввели следующее выражение |
| Окончательный результат выражения |
Описание
Обновление: На 12 сентября 2017 года, упрощен ввод данных. Теперь можно вводить выражение без знака умножения. Например 3(2+i)(-4+sin(i)). Если заметили неправильный расчет, просьба внизу страницы обозначить ошибку в виде комментария. Спасибо!
Позволяет высчитывать результат произвольного комплексного выражения с любым количеством скобок, любой длины и с любыми числами (как действительными, так и мнимыми)
Арифметическое выражение подразумевает собой выражение, которое использует 4 основных операции: умножение, деление, сложение и вычитание.
Напомним как производятся эти операции:
Сложение двух комплексных чисел
Вычитание двух комплексных чисел
Умножение двух комплексных чисел
Деление двух комплексных чисел
Данный бот еще может использовать пятую операцию — возведение в степень, а так же все основные тригонометрические функции (синус, косинус, тангенс), обратные тригонометрические функции, взятие логарифма и экспоненты.
Заметьте, эти функции могут использовать как действительные аргументы, так и комплексные, что открывает широкие возможности по вычислению выражений.
Возведение в степень осуществляется по известной формуле Муавра. Степень числа, может быть как действительным так и мнимым.
Калькулятор работает, исправен, и не допускает ошибки при корректном вводе выражения.
Как уже было сказано, выражение по сложности может быть неограниченным по размерам и иметь множество скобок.
Синтаксис
Если используете Jabber или любой другой XMPP клиент: calc_i <строка>
Если используете данный сайт: <строка>
Строкой может быть любое выражение без каких либо функций. Могут воспользоватся следующие операции:
+ сложение
— вычитание
* умножение
/ деление
^ возведение в степень
синус(sin)
косинус(cos)
натуральный логарифм(ln)
тангенс(tan)
артангенс(atan)
арксинус(asin)
арккосинус(acos)
гиперболический синус(sinh)
гиперболический косинус(cosh)
гиперболический тангенс(tanh)
Число в выражении может быть как действительным, которое записывается в привычном виде, так и комплексным числом которое обозначается символом i
Просьба по возможности оборачивать каждое комплексное число в круглые скобки, если первый символ в нём является минус (-)
Примеры
(-4-1i)/((-5-2i)+7-1.2i)
или в более наглядном виде
Получаем
Наш запрос выглядит так как мы его и сформировали в самом начале
calc_i (-4-1i)/((-5-2i)+7-1.2i)
Результат выражения
Действительная часть -0.33707865168539
Мнимая часть -1.0393258426966
i/(5-i)+(-4+2.7i)/(3-i)/0.2i
Получаем
Наш запрос выглядит так
calc_i (i/(5-i))^2+(-4+2.7i)/(3-i)/0.2i
Результат выражения
Действительная часть 2.0115384615385
Мнимая часть 7.5423076923077
Запрос calc_i i/((5-i)^2)+i
Результат выражения
Действительная часть -0.01479289940828
Мнимая часть 1.0355029585799
Запрос atan(i+2)-cos(1+i/(3-i))^(2*i^(1/2))
Результат выражения
Действительная часть 0.66468285388895
Мнимая часть 1.0051451851734
Как видите, сложность выражения может быть произвольной и включать в себя комплексные числа.
abakbot.ru
Приложение 03 — Комплексные числа
Приложение 3 72
Комплексные числа
Приложение 3
КОМПЛЕКСНЫЕ ЧИСЛА
Рассмотрим двумерное линейное пространство , изоморфное1) линейному пространству радиус-векторов на плоскости.
Каждый
элемент z пространства в
некотором базисе однозначно задается
двухкомпонентным столбцом  .
Если за базисные элементы пространства принять
и
.
Если за базисные элементы пространства принять
и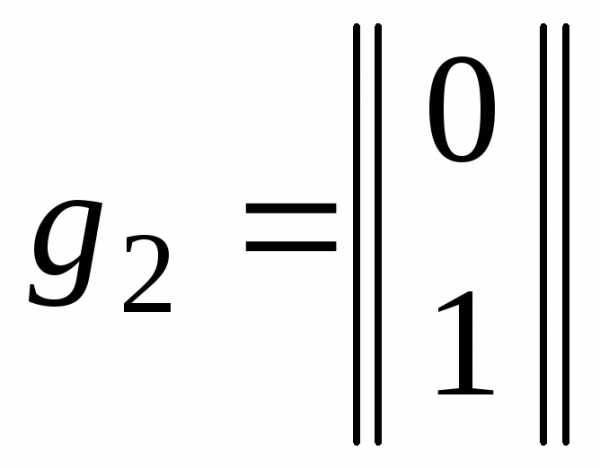 ,
то произвольный элемент
,
то произвольный элемент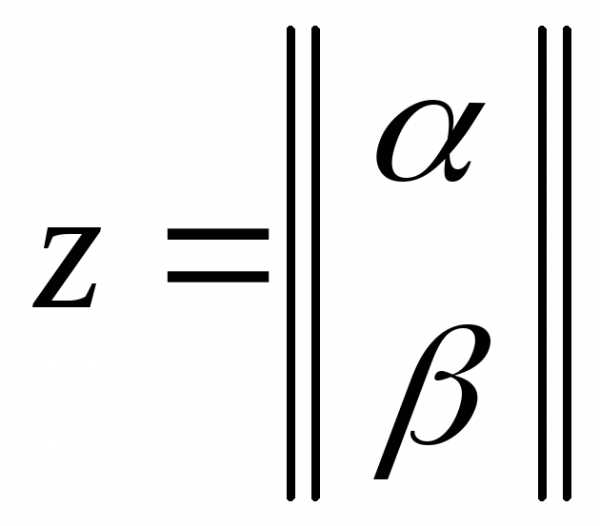 может быть представлен в виде.
может быть представлен в виде.
Введем операцию умножения элементов пространства по следующему правилу:
Определение Пр.3.0.1. | Результатом
операции умножения элементов |
Определение Пр.3.0.2. | Двумерное линейное пространство , с базисом {,}, в котором введена операция умножения элементов согласно определению Пр.3.0.1., называется множествомкомплексных чисел, а каждый элемент — комплексным числом. |
Замечания: 1. Операция умножения комплексных чисел коммутативна и обладает распределительным свойством относительно операции сложения, что следует непосредственно из ее определения.
2.
Операция умножения комплексных чисел
позволяет ввести операцию деления:
частным от деления комплексного числа 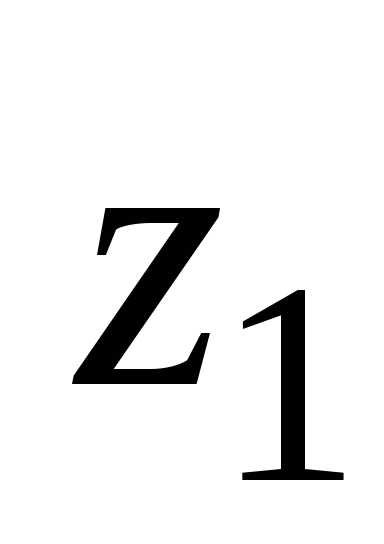 на ненулевое
на ненулевое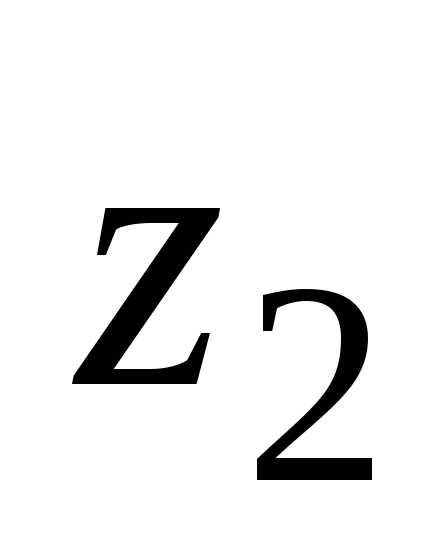 называется комплексное число
называется комплексное число такое, что
такое, что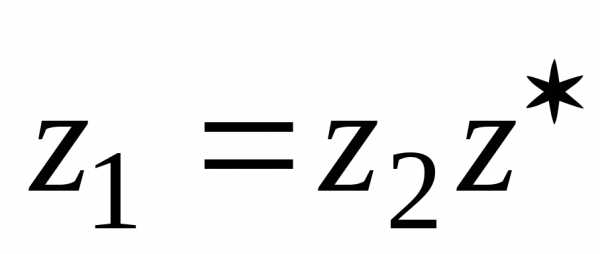 .
.
3.
Нетрудно убедиться, что подмножество
комплексных чисел вида  ,
где — произвольное вещественное число, в
силу определения Пр.3.0.2., обладает всеми
свойствами вещественных чисел, и потому
можно говорить, что вещественные числа
есть подмножество комплексных чисел.
,
где — произвольное вещественное число, в
силу определения Пр.3.0.2., обладает всеми
свойствами вещественных чисел, и потому
можно говорить, что вещественные числа
есть подмножество комплексных чисел.
На практике более употребительна специальная, упрощенная форма записи комплексных чисел: в представлении символопускается (как бы заменяется не записываемым явно множителем “единица”), а символ заменяется символомi (называемым иногда “мнимой единицей”). Тогда произвольное комплексное число z представимо как , а записи операций с комплексными числами принимают следующий вид:
Данная форма записи удобна тем, что с комплексными числами можно оперировать как с обычными алгебраическими двучленами, если принимать во внимание, что , поскольку
.
Тогда,
перемножая комплексные числа как
двучлены и заменяя повсюду 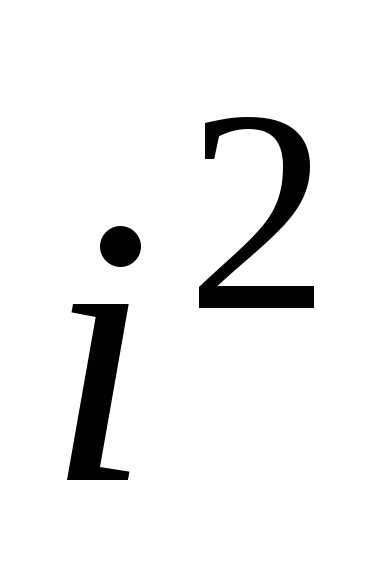 на число
на число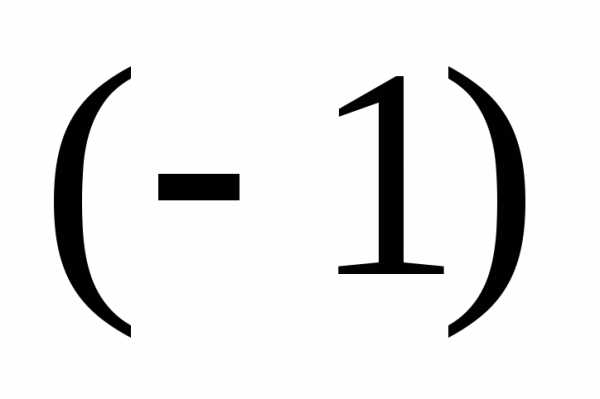 ,
мы формально приходим к соотношению
,
мы формально приходим к соотношению
,
которое согласуется с введенным выше определением Пр.3.0.1.
Достаточно просто может выполняться также и операция деления:
.
Определение Пр.3.0.3. | Для комплексного числа : 1.
Вещественное число называется вещественной
частью z и обозначается 2.
Вещественное число называется мнимой
частью z и обозначается 3. Вещественное число называется модулем z и обозначается . 4.
Вещественное число такое, что 5. Комплексное число называетсякомплексно сопряженным числу z и обозначается . |
Замечания: 1. Определения, аналогичные пунктам 1, 2 и 5, могут быть сделаны и для матриц, элементами которых являются комплексные числа.
2. Поскольку существует взаимно однозначное соответствие множества радиус-векторов на плоскости и множества комплексных чисел, то комплексные числа можно изображать точками на плоскости.
Свойства комплексного сопряжения
Имеют место следующие, легко проверяемые свойства для любых :
1.  ;
;
2. Число z будет вещественным тогда и только тогда, когда ;
3. Число всегда вещественное и неотрицательное;
4. ;
5.
Если 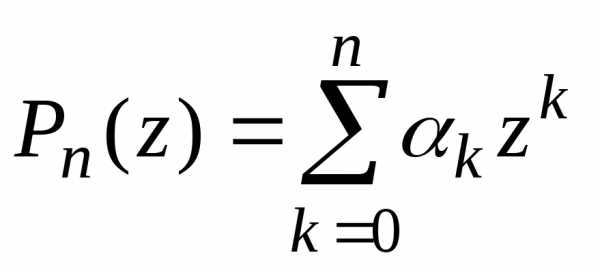 многочлен с вещественными коэффициентами,
имеющий корень,
то этот многочлен также будет иметь и
корень
многочлен с вещественными коэффициентами,
имеющий корень,
то этот многочлен также будет иметь и
корень  .
Действительно, пусть,
тогда
.
Действительно, пусть,
тогда
.
Замечание: если алгебраическое уравнение с вещественными коэффициентами имеет комплексные корни, то они попарно сопряжены, а алгебраическое уравнение с вещественными коэффициентами нечетной степени имеет, по крайней мере, один вещественный корень.
Задача На
множестве комплексных чисел решить
уравнение 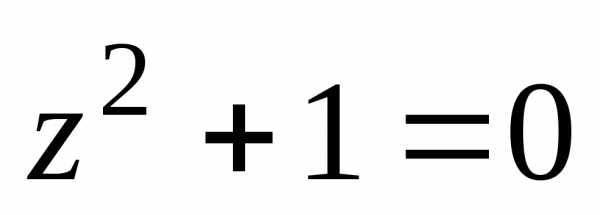 .
.
Пр.3.0.1.
Решение: Перепишем это уравнение, приняв, что , то есть. Заметим, что здесь мы воспользовались развернутыми представлениями чисели.
Выполнив
умножение и сложение в правой части
уравнения, приходим к равенству 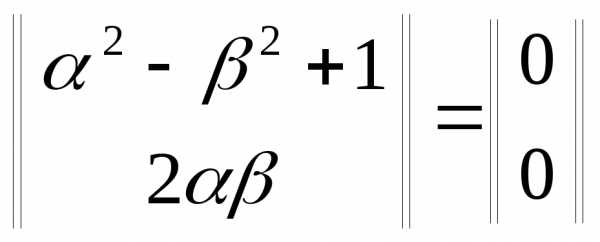 .
Но поскольку два комплексных числа
равны тогда и только тогда, когда
одновременно равны их вещественные и
мнимые части, то мы получаем следующую
систему нелинейных уравнений относительно
вещественных неизвестных и :
.
Но поскольку два комплексных числа
равны тогда и только тогда, когда
одновременно равны их вещественные и
мнимые части, то мы получаем следующую
систему нелинейных уравнений относительно
вещественных неизвестных и :
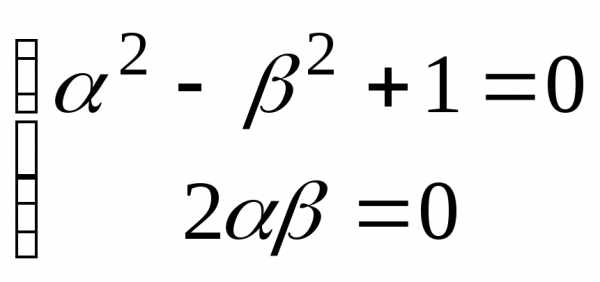 ,
,
которая,
как легко видеть, имеет два решения 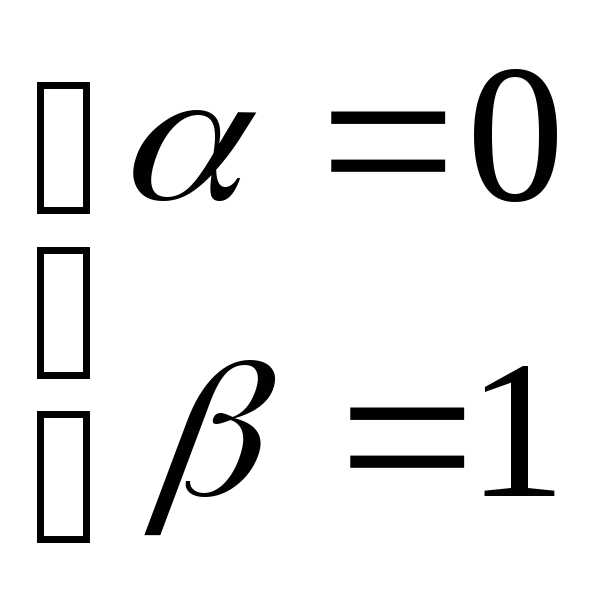 и
и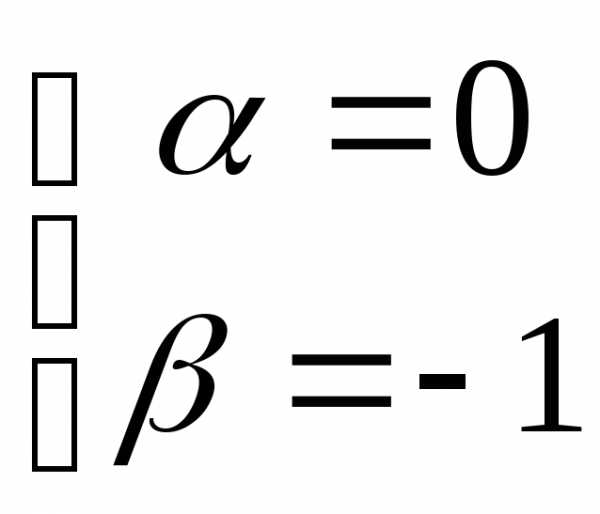 .
Поэтому исходное уравнение также имеет
два решения
.
Поэтому исходное уравнение также имеет
два решения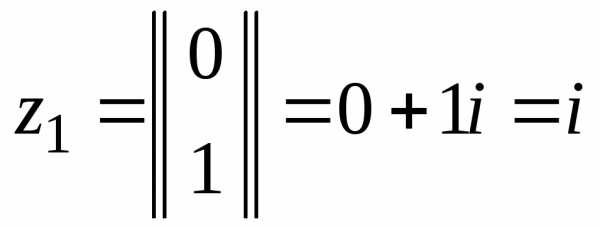 и.
и.
Тригонометрическая и экспоненциальная формы записи комплексных чисел
Исходя из определения Пр.3.0.3., можно получить специальную форму записи ненулевых комплексных чисел, называемую тригонометрической:
.
Тригонометрическая форма записи комплексных чисел соответствует заданию точки, изображающей комплексное число, в полярной системе координат.
Пусть — направляющим элементом полярной оси служит элемент , — значение модуля комплексного числа равно — расстоянию от начала координат до точки, изображающей данное число, — значение аргумента совпадает с величиной полярного угла, отсчитываемого против часовой стрелки, | z i 0
1 Рисунок Пр.3.0.1. |
тогда, согласно определению Пр.3.0.3., комплексное число представимо в тригонометрической форме
.
Другой часто используемой формой представления комплексных чисел, является их экспоненциальная форма, которая получается преобразованием тригонометрической формы по формуле Эйлера:
.
В этом случае из следует, что.
Использование экспоненциальной формы записи комплексных чисел может упростить решение некоторых задач, поскольку при перемножении комплексных чисел их модули перемножаются, а аргументы складываются1).
Например,
или
.
Задача Найти какое-либо вещественное решение уравнения .
Пр.3.0.2.
Решение: Из формулы Эйлера следует, что , поэтому данное уравнение можно записать в видеили, где.
Откуда находим, что , то естьили окончательно.
1) Изоморфизм (см §7.5.) в данном случае означает, что операции сложения и умножения на вещественное число выполняются в данном множестве так же, как и для векторов на плоскости.
1) Обоснование обобщения свойств экспоненциальной функции вещественного аргумента на комплексный случай приводится в курсе ТФКП.
studfiles.net
30.1. Комплексные числа и их изображение на плоскости
Комплексные числа возникли в связи с задачей решения квадратных уравнений. Оставаясь в множестве действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.
Комплексные числа необходимы в различных приложениях математики. В частности, теория функций комплексной переменной является действенным инструментом при использовании математических методов в различных областях науки.
Комплексным числом называется выражение вида где -действительные числа, -мнимая единица.
Итак, комплексным числом называется всякая упорядоченная пара действительных чисел иДействительное числоназывают абсциссой комплексного числадействительное числоего ординатой
или
Всякое комплексное число можно изобразить на плоскости в виде точки Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексного переменного
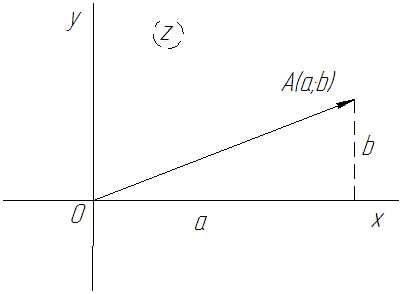
Рис. 62
Плоскость комплексного переменного
Действительные числа изображаются точками оси абсцисс, мнимые числа изображаются точками оси ординат. Поэтому ось называют действительной осью, а ось ординат мнимой осью.
Соединив точку с началом координат, получим векторВ некоторых случаях удобно считать геометрическим изображением комплексного числавекторПри этом действительная и мнимая части числа являются проекциями векторана действительную и мнимую оси.
Обозначим через и полярные координаты точкисчитая начало координат полюсом, а положительное направление осиполярной осью.
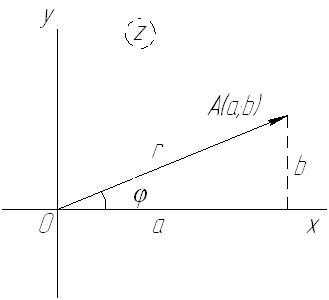
Рис. 63
Геометрическое изображение комплексного числа
Тогда имеют место следующие равенства
Следовательно, комплексное число можно представить в виде
– это есть тригонометрическая форма записи комплексного числа называется модулем комплексного числааргументом комплексного числа
30.2. Модуль и аргумент комплексного числа
Обозначение
определяется с точностью до слагаемого
Модуль и аргумент находятся следующим образом
так как
Так как
Пусть
найдем произведение этих чисел:
Произведение двух комплексных чисел есть такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент равен сумме аргументов сомножителей.
Найдем частное двух комплексных чисел
Модуль частного двух комплексных чисел равен частному модулей делимого и делителя, аргумент частного равен разности аргументов делимого и делителя.
Аргумент комплексного числа считается положительным, если он отсчитывается от положительного направления оси против часовой стрелки, и отрицательным, если он отсчитывается по часовой стрелке. Аргумент определяется неоднозначно, а с точностью до слагаемоголюбое целое число.
30.3. Различные формы записи комплексного числа. Формула Эйлера. Алгебраические действия над комплексными числами
Форма записи комплексного числа называетсяалгебраической формой комплексного числа Еслито числоназывается мнимым, еслито числобудет действительным.
Два комплексных числа отличающиеся только знаками мнимой части, называютсякомплексно сопряженными числами.
Комплексное число равно нулю тогда, и только тогда, когда его действительная и мнимая части равны нулю
Алгебраическая форма записи существенно облегчает выполнение арифметических операций над комплексными числами, как над обычными двучленами, учитывая, что
Пусть
Сложение чисел и:
Вычитание комплексных чисел и:
Умножение комплексных чисел и:
Произведение сопряженных комплексных чисел равно сумме квадратов их действительной и мнимой частей
Деление комплексных чисел и:
Рассмотрим пример. Представить комплексные числа в алгебраической форме и выполнить операции сложения, вычитания, умножения и деления
Показательная форма записи комплексного числа.
Пусть Определим показательную функцию комплексного переменного
Положим получим формулу Эйлера, выражающую показательную функцию с мнимым показателем через тригонометрические функции
Напомним, что комплексное число в тригонометрической форме имеет вид
тогда, применив к записи комплексного числа в показательной форме, получим
Арифметические действия над комплексными числами в показательной форме выполняются на основании свойств показательной функции.
Пусть
Произведение чисел и
Частное чисел и:
Возведение комплексного числа в степень:
Извлечение корня n-й степени из комплексного числа :
Контрольные вопросы
Какие числа называют комплексными?
Записать различные формы комплексного числа.
В каком случае применяют формулу Эйлера?
Перечислить алгебраические действия над комплексными числами.
Лекция №31. Дифференциальные уравнения
31.1. Задачи, приводящие к составлению и решению дифференциальных уравнений.
31.2. Дифференциальные уравнения первого порядка. Теорема Коши. Понятие об общем и частном решении дифференциального уравнения. Дифференциальные уравнения с разделяющими переменными.
studfiles.net
Универсальный калькулятор комплексных чисел онлайн
| Вы ввели следующее выражение |
| Окончательный результат выражения |
Описание
Обновление: На 12 сентября 2017 года, упрощен ввод данных. Теперь можно вводить выражение без знака умножения. Например 3(2+i)(-4+sin(i)). Если заметили неправильный расчет, просьба внизу страницы обозначить ошибку в виде комментария. Спасибо!
Позволяет высчитывать результат произвольного комплексного выражения с любым количеством скобок, любой длины и с любыми числами (как действительными, так и мнимыми)
Арифметическое выражение подразумевает собой выражение, которое использует 4 основных операции: умножение, деление, сложение и вычитание.
Напомним как производятся эти операции:
Сложение двух комплексных чисел
Вычитание двух комплексных чисел
Умножение двух комплексных чисел
Деление двух комплексных чисел
Данный бот еще может использовать пятую операцию — возведение в степень, а так же все основные тригонометрические функции (синус, косинус, тангенс), обратные тригонометрические функции, взятие логарифма и экспоненты.
Заметьте, эти функции могут использовать как действительные аргументы, так и комплексные, что открывает широкие возможности по вычислению выражений.
Возведение в степень осуществляется по известной формуле Муавра. Степень числа, может быть как действительным так и мнимым.
Калькулятор работает, исправен, и не допускает ошибки при корректном вводе выражения.
Как уже было сказано, выражение по сложности может быть неограниченным по размерам и иметь множество скобок.
Синтаксис
Если используете Jabber или любой другой XMPP клиент: calc_i <строка>
Если используете данный сайт: <строка>
Строкой может быть любое выражение без каких либо функций. Могут воспользоватся следующие операции:
+ сложение
— вычитание
* умножение
/ деление
^ возведение в степень
синус(sin)
косинус(cos)
натуральный логарифм(ln)
тангенс(tan)
артангенс(atan)
арксинус(asin)
арккосинус(acos)
гиперболический синус(sinh)
гиперболический косинус(cosh)
гиперболический тангенс(tanh)
Число в выражении может быть как действительным, которое записывается в привычном виде, так и комплексным числом которое обозначается символом i
Просьба по возможности оборачивать каждое комплексное число в круглые скобки, если первый символ в нём является минус (-)
Примеры
(-4-1i)/((-5-2i)+7-1.2i)
или в более наглядном виде
Получаем
Наш запрос выглядит так как мы его и сформировали в самом начале
calc_i (-4-1i)/((-5-2i)+7-1.2i)
Результат выражения
Действительная часть -0.33707865168539
Мнимая часть -1.0393258426966
i/(5-i)+(-4+2.7i)/(3-i)/0.2i
Получаем
Наш запрос выглядит так
calc_i (i/(5-i))^2+(-4+2.7i)/(3-i)/0.2i
Результат выражения
Действительная часть 2.0115384615385
Мнимая часть 7.5423076923077
Запрос calc_i i/((5-i)^2)+i
Результат выражения
Действительная часть -0.01479289940828
Мнимая часть 1.0355029585799
Запрос atan(i+2)-cos(1+i/(3-i))^(2*i^(1/2))
Результат выражения
Действительная часть 0.66468285388895
Мнимая часть 1.0051451851734
Как видите, сложность выражения может быть произвольной и включать в себя комплексные числа.
- Факториальный многочлен >>
abakbot.ru
Комплексные числа
Комплексные числа
[S1] ИСТОРИЧЕСКАЯ СПРАВКА
Комплексные числа были введены в математику для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Это, однако, не является достаточным основанием для того, чтобы вводить в математику новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, уже не содержащему квадратный корень из отрицательного числа. В XVI в. Кардано нашел формулу для решения кубического уравнения. Оказалось, когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа. Поэтому квадратные корни из отрицательных чисел стали употреблять в математике и назвали их мнимыми числами – тем самым они как бы приобрели право на нелегальное существование. Полные гражданские права мнимым числам дал Гаусс, который назвал их комплексными числами, дал геометрическую интерпретацию и доказал основную теорему алгебры, утверждающую, что каждый многочлен имеет хотя бы один действительный корень.
1.ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА
Решение многих задач математики, физики сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов в математике. Стремление сделать уравнения разрешимыми – одна из главных причин расширения понятия числа.
Так для решимости уравнений вида X+A=B положительных чисел недостаточно. Например, уравнение X+5=2 не имеет положительных корней. Поэтому приходится вводить отрицательные числа и нуль.
На множестве рациональных чисел разрешимы алгебраические уравнения первой степени, т.е. уравнения вида A·X+B=0 (A
0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2 =2, X3 =5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Простейшее из них – уравнение X2 +1=0. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.
Выясним предварительно, какой вид должны иметь комплексные числа. Будем считать, что на множестве комплексных чисел уравнение X2 +1=0 имеет корень. Обозначим этот корень буквой i Таким образом, i – это комплексное число, такое, что i 2 = –1.
Как и для действительных чисел, нужно ввести операции сложения и умножения комплексных чисел так, чтобы сумма и произведение их были бы комплексными числами. Тогда, в частности, для любых действительных чисел A и B выражение A+B·i можно считать записью комплексного числа в общем виде. Название “комплексное” происходит от слова “составное”: по виду выражения A+B·i .
Комплексными числами называют выражения вида A+B·i , где A и B –действительные числа, а i – некоторый символ, такой что i 2 = –1, и обозначают буквой Z.
Число A называется действительной частью комплексного числа A+B·i , а число B – его мнимой частью. Число i называется мнимой единицей.
Например, действительная часть комплексного числа 2+3·i равна 2, а мнимая равна 3.
Для строгого определения комплексного числа нужно ввести для этих чисел понятие равенства.
Два комплексных числа A+B·i и C+D·i называются равными тогда и только тогда, когда A=C и B=D, т.е. когда равны их действительные и мнимые части.
2.ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОМПЛЕКСНОГО ЧИСЛА
Действительные числа геометрически изображаются точками числовой прямой. Комплексное число A+B·i можно рассматривать как пару действительных чисел(A;B). Поэтому естественно комплексное число изображать точками плоскости. В прямоугольной системе координат комплексное число Z=A+B·i изображается точкой плоскости с координатами (A;B), и эта точка обозначается той же буквой Z (рисунок 1). Очевидно, что получаемое при этом соответствие является взаимно однозначным. Оно дает возможность интерпретировать комплексные числа как точки плоскости на которой выбрана система координат. Такая координатная плоскость называется комплексной плоскостью . Ось абсцисс называется действительной осью , т.к. на ней расположены точки соответствующие действительным числам. Ось ординат называется мнимой осью – на ней лежат точки, соответствующие мнимым комплексным числам.
Не менее важной и удобной является интерпретация комплексного числа A+B·i как вектора, т.е. вектора с началом в точке
O(0;0) и с концом в точке М(A;B) (рисунок 2).
Соответствие установленное между множеством комплексных чисел, с одной стороны, и множествами точек или векторов плоскости, с другой, позволяет комплексные числа точками или векторами.
3.МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА
Пусть дано комплексное число Z=A+B·i . Сопряженным с Z называется комплексное число A – B·i , которое обозначается
, т.е. ==A – B·i .Отметим, что
= A+B·i , поэтому для любого комплексного числа Z имеет место равенство =Z.Модулем комплексного числа Z=A+B·i называется число
и обозначается , т.е. == (1)Из формулы (1) следует, что
для любого комплексного числа Z, причем =0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:4.СЛОЖЕНИЕ И УМНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Суммой двух комплексных чисел A+B·i и C+D·i называется комплексное число (A+C) + ( B+D)·i , т.е. ( A+B · i ) + ( C+D · i )=( A+C) + (B+D) · i
Произведением двух комплексных чисел A+B·i и C+D·i называется комплексное число (A·C – B·D)+(A·D+B·C) ·i , т.е.
( A + B · i ) · (C + D · i )=(A · C – B · D) + (A · D + B · C) · i
Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами, считая i 2 = –1. Операции сложения и умножения комплексных чисел обладают свойствами действительных чисел. Основные свойства:
Переместительное свойство :
Z1 +Z2 =Z2 +Z1 , Z1 ·Z2 =Z2 ·Z1
Сочетательное свойство :
(Z1 +Z2 )+Z3 =Z1 +(Z2 +Z3 ), (Z1 ·Z2 )·Z3 =Z1 ·(Z2 ·Z3 )
Распределительное свойство :
Z1 ·(Z2 +Z3 )=Z1 ·Z2 +Z1 ·Z3
Геометрическое изображение суммы комплексных чисел
Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых, мнимая часть суммы равна сумме мнимых частей слагаемых. Точно также определяются координаты суммы векторов:
Сумма двух векторов с координатами (A1 ;B1 ) и (A2 ;B2 ) есть вектор с координатами (A1 +A2 ;B1 +B2 ). Поэтому, чтобы найти вектор, соответствующий сумме комплексных чисел Z1 и Z2 нужно сложить векторы, соответствующие комплексным числам Z1 и Z2 .
Пример 1 : Найти сумму и произведение комплексных чисел Z1 =2 – 3×i и
1 Способ:
Z2 = –7 + 8× i .
Z1 + Z2 = 2 – 7 + (–3 + 8)× i = – 5 + 5× i
Z1 ×Z2 = (2 – 3× i )×(–7 + 8× i ) = –14 + 16× i + 21× i + 24 = 10 + 37× i
mirznanii.com

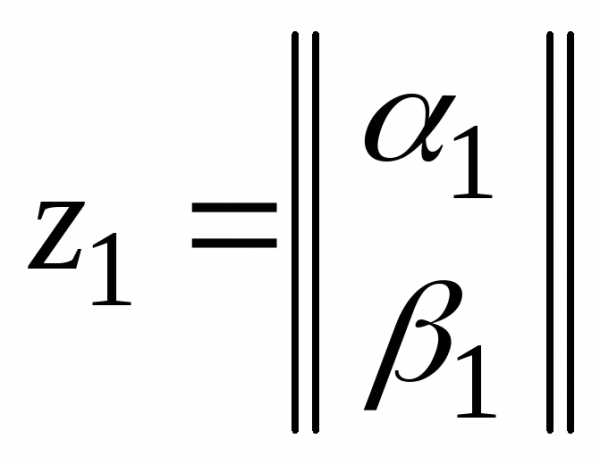 и
и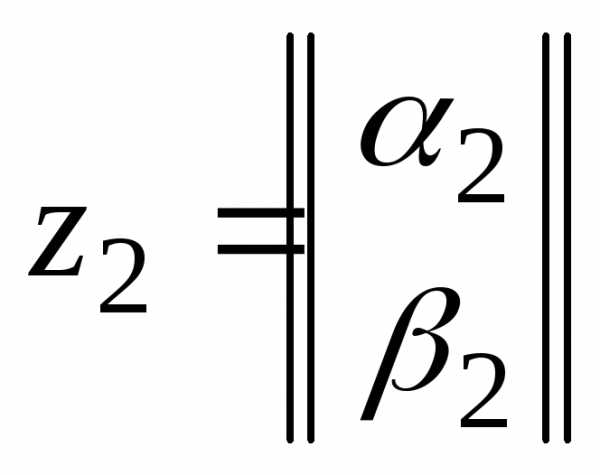 пространства является элемент также этого пространства
пространства является элемент также этого пространства 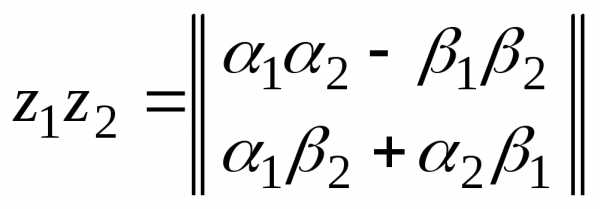 .
.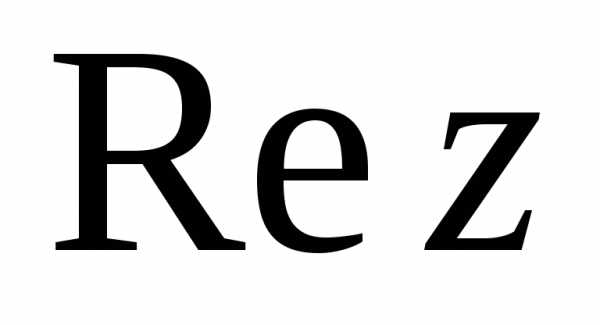 .
.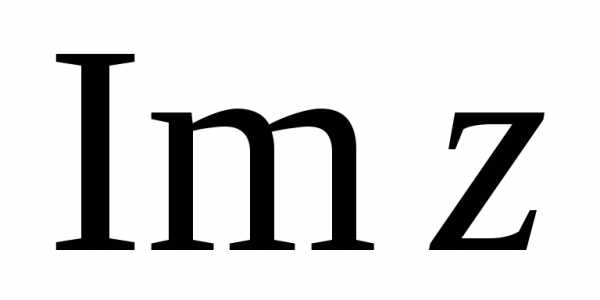 .
.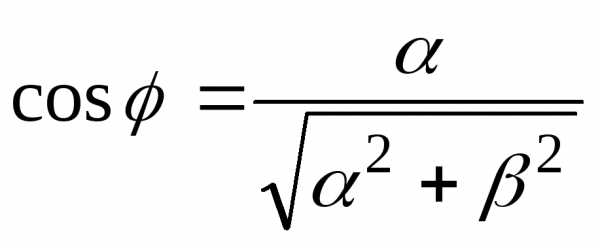 и
и  называется аргументом z и обозначается
называется аргументом z и обозначается 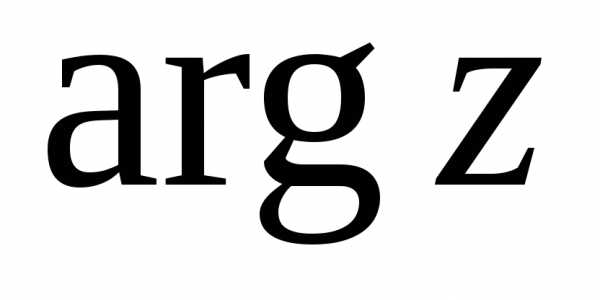 ,
при условии, что.
,
при условии, что.