Как решать интегралы для чайников, примеры решений
Как решать?
Процесс решения интегралов в науке под названием «математика» называется интегрированием. С помощью интегрирования можно находить некоторые физические величины: площадь, объем, массу тел и многое другое.
Интегралы бывают неопределенными и определенными. Рассмотрим вид определенного интеграла и попытаемся понять его физический смысл. Представляется он в таком виде: $$ \int ^a _b f(x) dx $$. Отличительная черта написание определенного интеграла от неопределенного в том, что есть пределы интегрирования a и b. Сейчас узнаем для чего они нужны, и что всё-таки значит определенный интеграл. В геометрическом смысле такой интеграл равен площади фигуры, ограниченной кривой f(x), линиями a и b, и осью Ох.
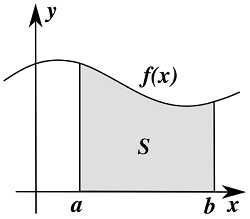
Из рис.1 видно, что определенный интеграл — это и есть та самая площадь, что закрашена серым цветом. Давайте, проверим это на простейшем примере. Найдем площадь фигуры на изображении представленном ниже с помощью интегрирования, а затем вычислим её обычным способом умножения длины на ширину.
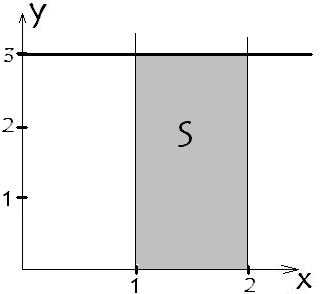
Из рис.2 видно, что $ y=f(x)=3 $, $ a=1, b=2 $. Теперь подставим их в определение интеграла, получаем, что $$ S=\int _a ^b f(x) dx = \int _1 ^2 3 dx = $$ $$ =(3x) \Big|_1 ^2=(3 \cdot 2)-(3 \cdot 1)=$$ $$=6-3=3 \text{ед}^2 $$ Сделаем проверку обычным способом. В нашем случае длина = 3, ширина фигуры = 1. $$ S = \text{длина} \cdot \text{ширина} = 3 \cdot 1 = 3 \text{ед}^2 $$ Как видим, всё отлично совпало.
Появляется вопрос: как решать интегралы неопределенные и какой у них смысл? Решение таких интегралов — это нахождение первообразных функций. Этот процесс противоположный нахождению производной. Для того, чтобы найти первообразную можно использовать нашу помощь в решении задач по математике или же необходимо самостоятельно безошибочно вызубрить свойства интегралов и таблицу интегрирования простейших элементарных функций. Нахождение выглядит так $$ \int f(x) dx = F(x) + C \text{где} F(x) $ — первообразная $ f(x), C = const $.
Для решения интеграла нужно интегрировать функцию $ f(x) $ по переменной. Если функция табличная, то записывается ответ в подходящем виде. Если же нет, то процесс сводится к получению табличной функции из функции $ f(x) $ путем хитрых математических преобразований. Для этого есть различные методы и свойства, которые рассмотрим далее.
Свойства интегралов
- Вынос константы из под знака интеграла: $$ $$ $$ \int Cg(x) dx = C\int g(x) dx $$
- Интеграл суммы/разности двух функций равен сумме/разности интегралов этих функций: $$ \int ( f(x) \pm g(x)) dx = \int f(x) dx \pm \int g(x) dx $$
- Изменение направления интегрирования: $$ \int _a ^b f(x) = -\int _b ^a f(x) dx $$
- Разбиение отрезка интегрирования: $$ \int_a^b f(x) dx = \int_a^c f(x) dx + \int_c^b f(x) dx $$ $$ c \in (a,b) $$
Итак, теперь составим алгоритм как решать интегралы для чайников?
Алгоритм вычисления интегралов
- Узнаем определенный интеграл или нет.
- Если неопределенный, то нужно найти первообразную функцию $ F(x) $ от подынтегральной $ f(x) $ с помощью математических преобразований приводящих к табличному виду функцию $ f(x) $.
- Если определенный, то нужно выполнить шаг 2, а затем подставить пределы $ а $ и $ b $ в первообразную функцию $ F(x) $. По какой формуле это сделать узнаете в статье «Формула Ньютона Лейбница».
Примеры решений
| Пример 1 |
| $$ \int x dx $$ |
| Решение |
$$ \int x dx = \frac{x^2}{2} + C, C=const $$ Данный интеграл содержит под своим знаком табличную функцию, а это значит, что можно сразу записать ответ взятый из таблицы. |
| Ответ |
| $$ \int x dx = \frac{x^2}{2} + C $$ |
| Пример 2 |
| $$ \int 3xdx $$ |
| Решение |
$$ \int 3xdx = 3\int xdx = \frac{3x^2}{2}+C $$ Замечаем, что под знаком интеграла есть постоянная 3. По первому свойству можно ее вынести за значок интеграла. Далее, видим, что подынтегральная функция является табличной и получаем из нее первообразную для f(x)=x. |
| Ответ |
| $$ \int 3xdx = \frac{3x^2}{2}+C $$ |
| Пример 3 |
| $$ \int (x^3+\frac{1}{2\sqrt{x}}) dx $$ |
| Решение |
$$ \int (x^3+\frac{1}{2\sqrt{x}}) dx =$$ $$ = \int x^3 dx + \int \frac{1}{2\sqrt{x}}dx =$$ $$ = \frac{x^4}{4}+\sqrt{x} + C, C=const $$ Проанализировав неопределенный интеграл заметили, что подынтегральные функции являются табличными. И дана их сумма. Можно воспользоваться свойством номер 2. Значит, производим операции над функцией $ f(x) $ и $ g(x) $ согласно указанным в табличке преобразованиям. Так как интеграл неопределенный, то получаем в ответе первообразную. |
| Ответ |
| $$ \int (x^3+\frac{1}{2\sqrt{x}}) dx = \frac{x^4}{4}+\sqrt{x} + C $$ |
Итак, вы узнали как решать интегралы для чайников, примеры решения интегралов разобрали по полочкам. Узнали физический и геометрический их смысл. О методах решения будет изложено в других статьях.
xn--24-6kcaa2awqnc8dd.xn--p1ai
Примеры решений неопределенных интегралов
- Попробуйте решить приведенные ниже неопределенные интегралы.
- Нажмите на изображение интеграла, и вы попадете на страницу с подробным решением.
Примеры на основные формулы и методы интегрирования
См раздел
Основные формулы и методы интегрирования > > >
Решение > > >
Решение > > >
Решение > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования рациональных функций (дробей)
См раздел
Интегрирование рациональных функций (дробей) > > >
> > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования иррациональных функций (корней)
См раздел
Методы интегрирования иррациональных функций (корней) > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования тригонометрических функций
См раздел
Методы интегрирования тригонометрических функций > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Определённый интеграл и методы его вычисления
Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F(b) — F(a)).
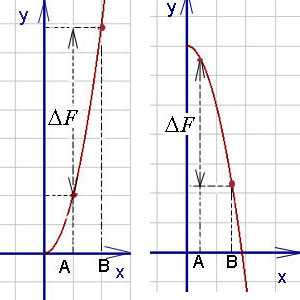
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
(38)
Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
Таким образом, для вычисления
определённого интеграла необходимо найти любую первообразную подынтегральной
функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С
из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела
При a = b по определению принимается
Пример 1. Вычислить определённый интеграл
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
получимТеорема 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.
Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.
(40)
Пусть F(x) – первообразная для f(x). Для f(t) первообразной служит та же функция F(t), в которой лишь иначе обозначена независимая переменная. Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если
то
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его, т.е.
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать, т.е.
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
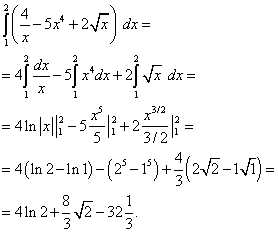
Пусть f(x) – непрерывная на отрезке [a, b] функция, а F(x) – её первообразная. Рассмотрим определённый интеграл
(47)
где
,
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х, которую обозначим через Ф(х), т.е.
(48)
Докажем, что функция Ф(х) является первообразной для f(x) = f(t). Действительно, дифференцируя Ф(х), получимтак как F(x) – первообразная для f(x), а F(a) – постояная величина.
Функция Ф(х) – одна из бесконечного множества первообразных для f(x), а именно та, которая при x = aобращается в нуль. Это утверждение получается, если в равенстве (48) положить x = aи воспользоваться теоремой 1 предыдущего параграфа.
При выводе формулы интегрирования по частям было получено равенство u dv = d (uv) – v du. Проинтегрировав его в пределах от a до b и учитывая теорему 4 параграфа этой статьи о свойствах определённого интеграла, получим
Как это следует из теоремы 2 параграфа о свойствах неопределённого интеграла, первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде
получаем формулу интегрирования по частям для вычисления определенного интеграла:
(49)
Пример 6. Вычислить определённый интеграл
Решение. Интегрируем по частям, полагая u = ln x, dv = dx; тогда du = (1/x)dx, v = x. По формуле (49) находим
Найти определённый интеграл по частям самостоятельно, а затем посмотреть решение
Перейдём к вычислению определённого интеграла методом замены переменной. Пусть
где, по определению, F(x) – первообразная для f(x). Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции, равна
Пусть α и β – значения переменной t , при которых функция
принимает соответственно значения aи b, т.е.
Тогда
Но, согласно формуле Ньютона-Лейбница, разность F(b) – F(a) есть
поскольку F(x) – первообразная для f(x).
Итак,
(50)
Это и есть формула перехода к новой переменной под знаком определённого интеграла. С её помощью определённый интеграл
после замены переменной
преобразуется в определённый интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются новыми пределами и . Чтобы найти новые пределы, нужно в уравнение
поставить значения x = aи x = b, т.е. решить уравнения
и
относительно и . После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.
При вычислении определённого интеграла методом замены переменной часто бывает удобно выражать не старую переменную как функцию новой, а, наоборот, новую – как функцию старой.
Пример 9. Вычислить определённый интеграл
Решение. Произведём замену переменной, полагая
Тогда dt = 2x dx, откуда x dx = (1/2) dt, и подынтегральное выражение преобразуется так:
Найдём новые пределы интегрирования. Подстановка значений x = 4 и x = 5 в уравнение
даёт
а
Используя теперь формулу (50), получим
После замены переменной мы не возвращались к старой переменной, а применили формулу Ньютона-Лейбница к полученной первообразной.
Найти определённый интеграл заменой переменной самостоятельно, а затем посмотреть решение
Начало темы «Интеграл»
Продолжение темы «Интеграл»
Поделиться с друзьями
function-x.ru
Методы решения интегралов, формулы и примеры
1. Непосредственное интегрирование
Непосредственное интегрирование – метод интегрирования, при котором подынтегральная функция путем тождественных преобразований и применения свойств интеграла приводится к одному или нескольким табличным интегралам.
Подробнее про непосредственное интегрирование читайте по ссылке.
2. Метод подведения под знак дифференциала
Метод подведения под знак дифференциала. Этот метод является эквивалентным методу подстановки. Если , то
Подробнее про метод подведения под знак дифференциала читайте по ссылке.
3. Метод замены переменной или метод подстановки
Метод замены переменной или метод подстановки. Этот метод заключается во введении новой переменной интегрирования (то есть делается подстановка). При этом заданный интеграл приводится к новому интегралу, который является табличным или с помощью преобразований его можно свести к табличному.
Пусть требуется вычислить интеграл . Сделаем подстановку . Тогда и интеграл принимает вид:
Подробнее про метод замены переменной/подстановки читайте по ссылке.
4. Метод интегрирования по частям
Метод интегрирования по частям. Этот метод основывается на следующей формуле:
или
При этом предполагается, что нахождение интеграла проще, чем исходного интеграла . В противном случае применение метода неоправданно.
Подробнее про метод интегрирования по частям читайте по ссылке.
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Неопределенный интеграл
Интегральное исчисление.
Первообразная функция.
Определение:ФункцияF(x) называетсяпервообразной функцией функцииf(x) на отрезке [a,b], если в любой точке этого отрезка верно равенство:
F(x) =f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) =F2(x) +C.
Неопределенный интеграл.
Определение:Неопределенным интегралом функцииf(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) +C.
Записывают:
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1.
2.
3.
4.
5. ,
6.
Пример:
Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.
Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.
Интеграл | Значение | Интеграл | Значение | ||
1 |
| -lncosx+C | 9 |
| ex + C |
2 |
| lnsinx+ C | 10 |
| sinx + C |
3 |
| | 11 |
| -cosx + C |
4 |
| | 12 |
| tgx + C |
5 |
|
| 13 |
| -ctgx + C |
6 |
| ln | 14 |
| arcsin |
7 |
|
| 15 |
|
|
8 |
| | 16 |
| |
Методы интегрирования.
Рассмотрим три основных метода интегрирования.
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Требуется найти
значение интеграла  .
На основе известной формулы дифференцирования
.
На основе известной формулы дифференцирования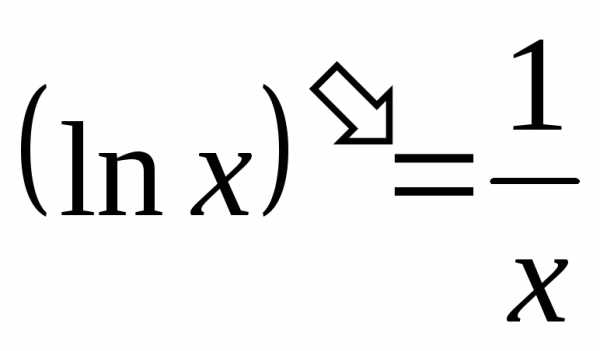 можно сделать вывод, что искомый интеграл
равен
можно сделать вывод, что искомый интеграл
равен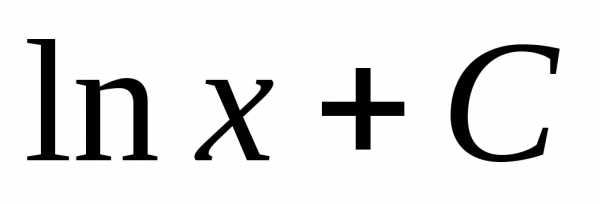 ,
где С – некоторое постоянное число.
Однако, с другой стороны.
Таким образом, окончательно можно
сделать вывод:
,
где С – некоторое постоянное число.
Однако, с другой стороны.
Таким образом, окончательно можно
сделать вывод:
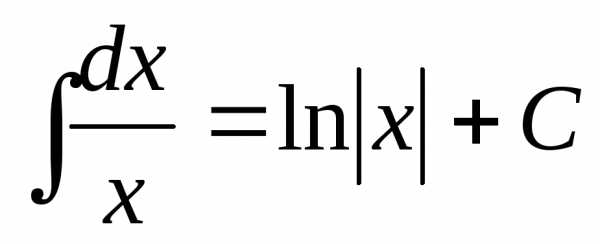
Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.
Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.
Способ подстановки (замены переменных).
Теорема:Если
требуется найти интеграл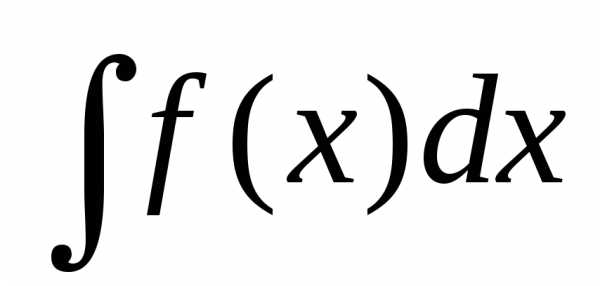 ,
но сложно отыскать первообразную, то с
помощью заменыx=(t)
иdx=(t)dtполучается:
,
но сложно отыскать первообразную, то с
помощью заменыx=(t)
иdx=(t)dtполучается:
Доказательство: Продифференцируем предлагаемое равенство:
По рассмотренному выше свойству №2 неопределенного интеграла:
f(x)dx = f[(t)](t)dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Пример.Найти неопределенный интеграл.
Сделаем замену t = sinx, dt = cosxdt.
Пример.
Замена Получаем:
Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)=uv+vu
где uиv– некоторые функции от х.
В дифференциальной форме: d(uv) =udv+vdu
Проинтегрировав, получаем: , а в соответствии с приведенными выше свойствами неопределенного интеграла:
или;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример.
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Пример.
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
Таким образом, интеграл найден вообще без применения таблиц интегралов.
Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.
Пример.
Пример.
Пример.
Пример.
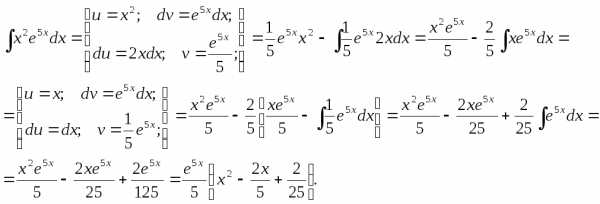
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Интегрирование элементарных дробей.
Определение:Элементарными называются дроби следующих четырех типов:
I. 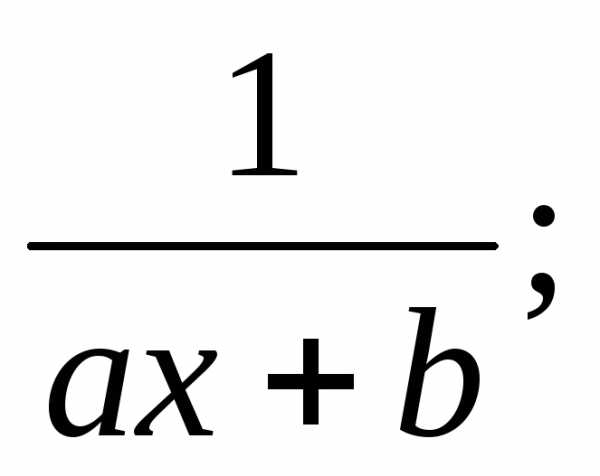 III.
III. 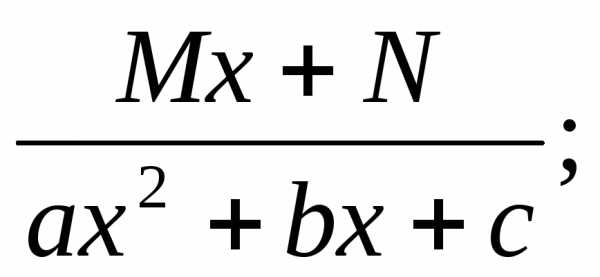
II.  IV.
IV. 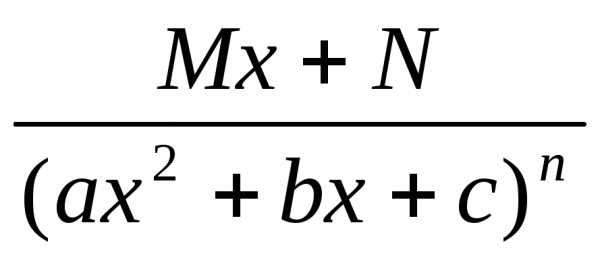
m,n– натуральные числа (m2,n2) иb2– 4ac<0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t=ax+b.
II.
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида IIIможет быть представлен в виде:
Здесь в общем виде показано приведение интеграла дроби вида IIIк двум табличным интегралам.
Рассмотрим применение указанной выше формулы на примерах.
Пример.
Вообще говоря, если у трехчлена ax2+bx+cвыражениеb2– 4ac>0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.
Пример.
Пример.
Рассмотрим теперь методы интегрирования простейших дробей IVтипа.
Сначала рассмотрим частный случай при М = 0, N= 1.
Тогда интеграл вида 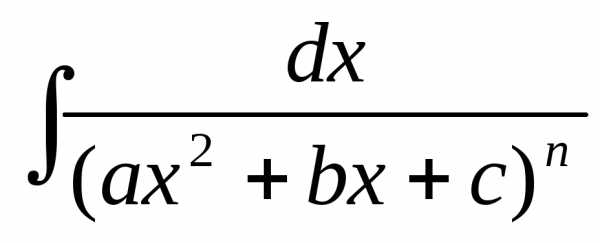 можно путем выделения в знаменателе
полного квадрата представить в виде
можно путем выделения в знаменателе
полного квадрата представить в виде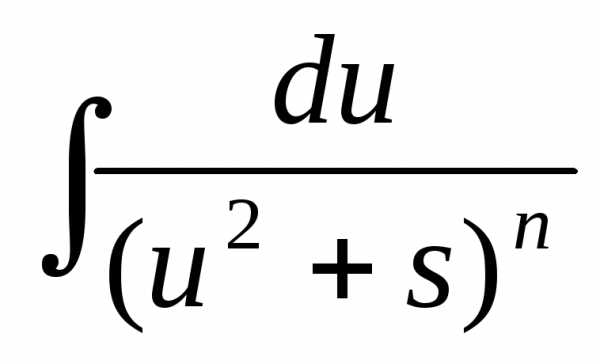 .
Сделаем следующее преобразование:
.
Сделаем следующее преобразование:
.
Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим: 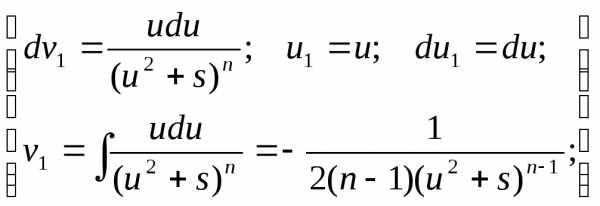
Для исходного интеграла получаем:
Полученная формула называетсярекуррентной.Если применить ееn-1
раз, то получится табличный интеграл .
.
Вернемся теперь к интегралу от элементарной дроби вида IVв общем случае.
В
полученном равенстве первый интеграл
с помощью подстановки t = u2 + sприводится к табличному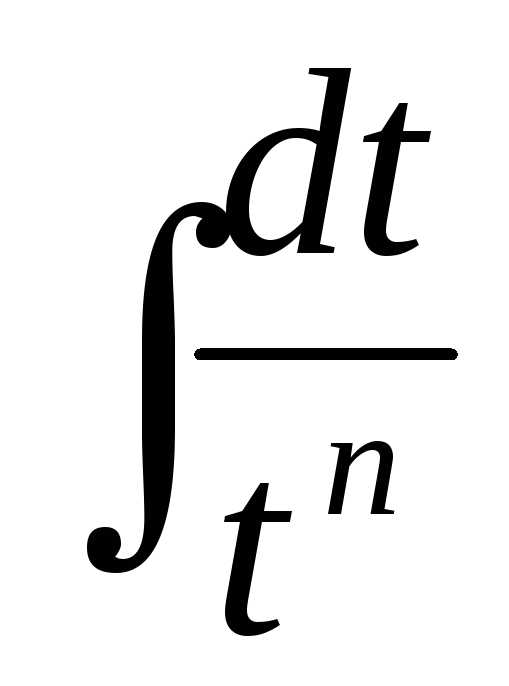 ,
а ко второму интегралу применяется
рассмотренная выше рекуррентная формула.
,
а ко второму интегралу применяется
рассмотренная выше рекуррентная формула.
Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степеньюn, а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.
Пример:
Интегрирование рациональных функций.
Интегрирование рациональных дробей.
Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
Теорема:Если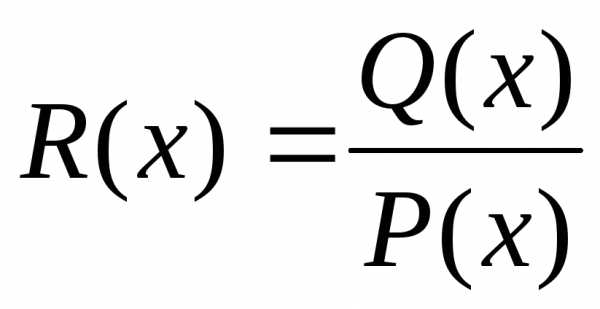 — правильная рациональная дробь,
знаменательP(x)
которой представлен в виде произведения
линейных и квадратичных множителей
(отметим, что любой многочлен с
действительными коэффициентами может
быть представлен в таком виде:P(x)
= (x — a)…(x — b)(x2 + px + q)…(x2 + rx + s)), то эта дробь может быть разложена
на элементарные по следующей схеме:
— правильная рациональная дробь,
знаменательP(x)
которой представлен в виде произведения
линейных и квадратичных множителей
(отметим, что любой многочлен с
действительными коэффициентами может
быть представлен в таком виде:P(x)
= (x — a)…(x — b)(x2 + px + q)…(x2 + rx + s)), то эта дробь может быть разложена
на элементарные по следующей схеме:
где Ai,Bi,Mi,Ni,Ri,Si– некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величинAi,Bi,Mi,Ni,Ri,Siприменяют так называемыйметод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Применение этого метода рассмотрим на конкретном примере.
Пример.
Т.к. (, то
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:

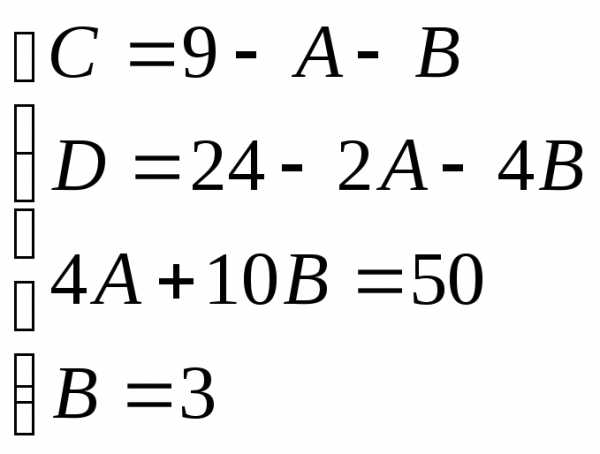
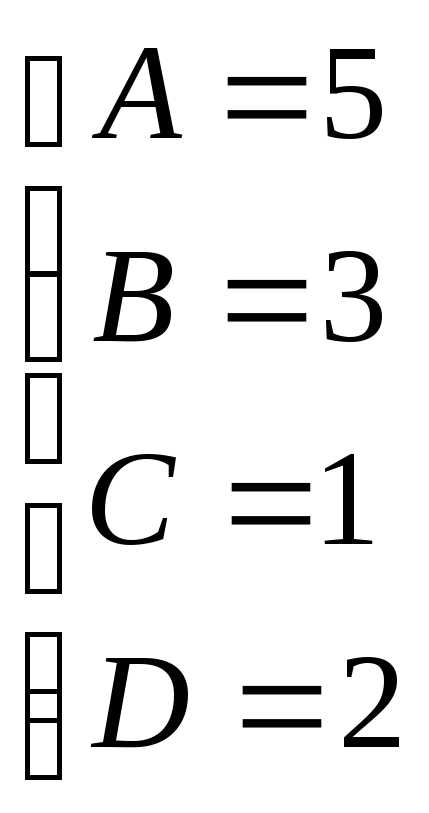
Итого:
Пример.
Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:
6x5– 8x4– 25x3+ 20x2– 76x– 7 3x3– 4x2– 17x+ 6
6x5– 8x4– 34x3+ 12x22x2+ 3
9x3 + 8x2 – 76x — 7
9x3 – 12x2 – 51x +18
20x2 – 25x – 25
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:
3x3– 4x2– 17x+ 6x- 3
3x3– 9x23x2+ 5x- 2
5x2– 17x
5x2– 15x
— 2x+ 6
-2x+ 6
0
Таким образом 3x3– 4x2– 17x+ 6 = (x– 3)(3x2+ 5x– 2) = (x– 3)(x+ 2 )(3x– 1). Тогда:
Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемыйметод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:
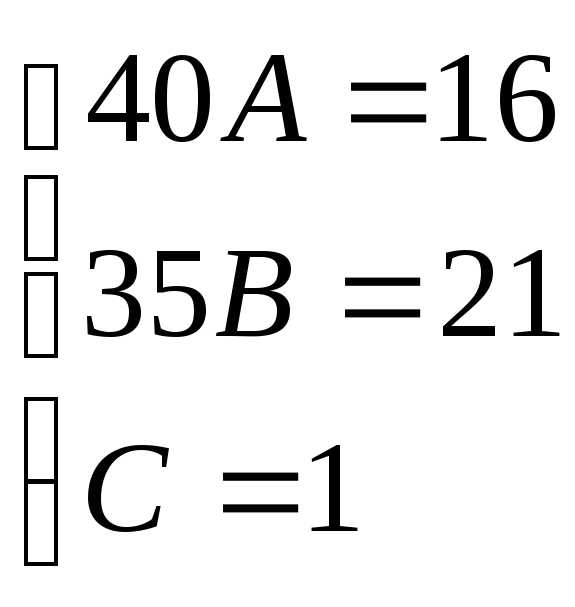
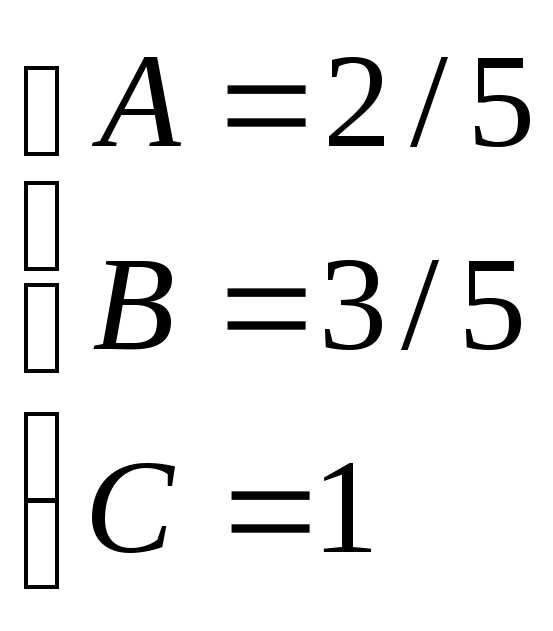
Окончательно получаем:
=
Пример.
Найдем неопределенные коэффициенты:
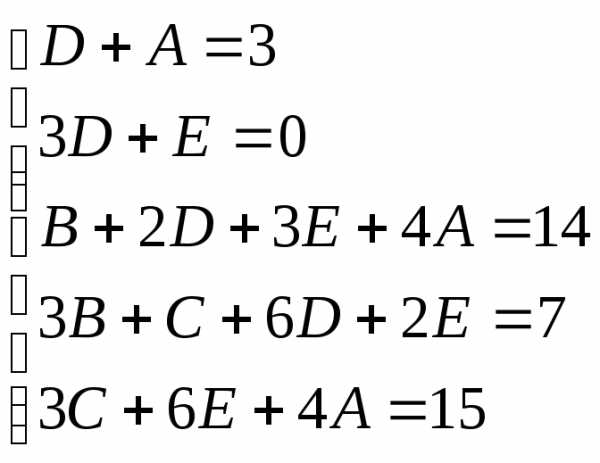
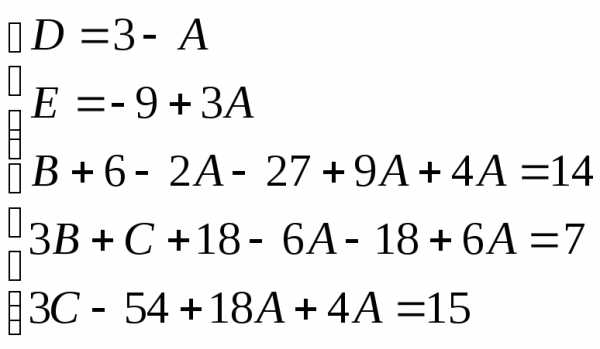
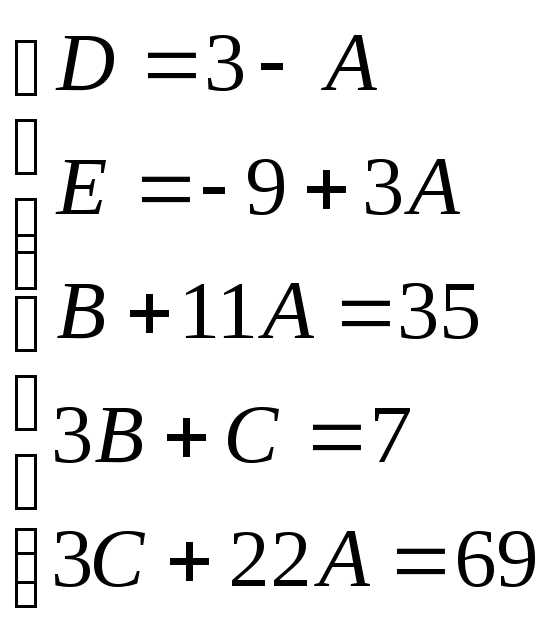


Тогда значение заданного интеграла:
Интегрирование некоторых тригонометрических
функций.
Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.
Интеграл вида .
Здесь R– обозначение некоторой рациональной функции от переменныхsinxиcosx.
Интегралы этого вида
вычисляются с помощью подстановки 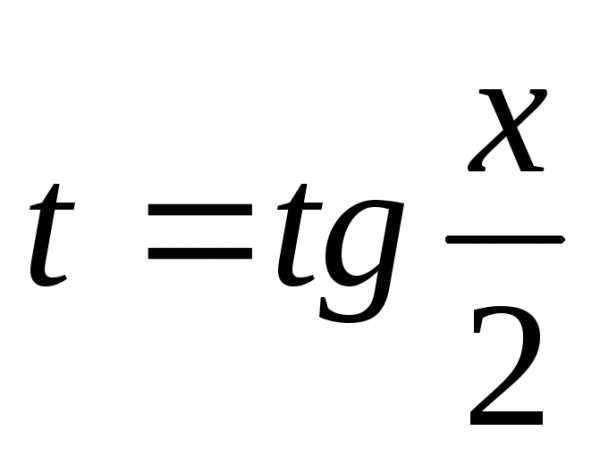 .
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
.
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
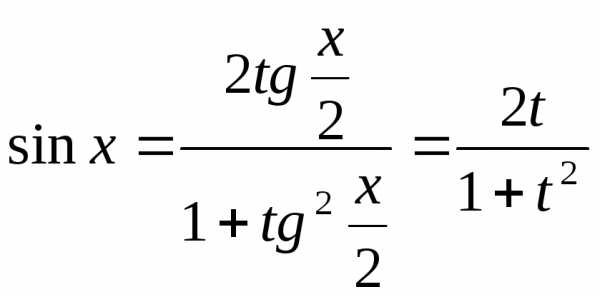 ,
,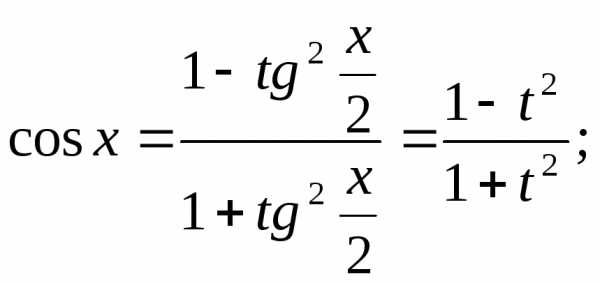
Тогда
Таким образом:
Описанное выше преобразование называетсяуниверсальной тригонометрической подстановкой.
Пример.
Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.
Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.
Пример.
Интеграл вида если
функция R является нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
Функция 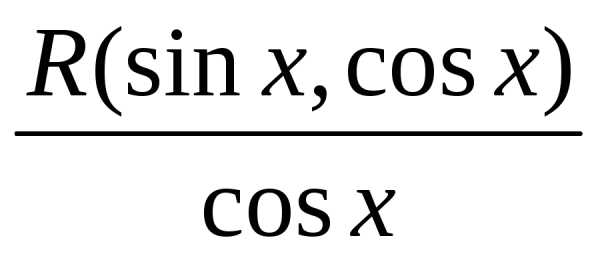 может содержатьcosxтолько
в четных степенях, а, следовательно,
может быть преобразована в рациональную
функцию относительноsinx.
может содержатьcosxтолько
в четных степенях, а, следовательно,
может быть преобразована в рациональную
функцию относительноsinx.
Пример.
Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.
Интеграл вида если
функция R является нечетной относительно sinx.
По аналогии с рассмотренным выше случаем делается подстановка t = cosx.
Тогда
Пример.
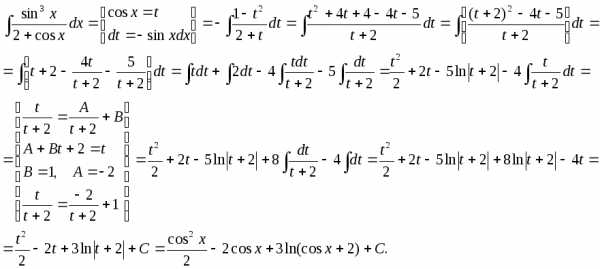
Интеграл вида
функция R четная относительно sinx и cosx.
Для преобразования функции Rв рациональную используется подстановка
t = tgx.
Тогда
Пример.
Интеграл произведения синусов и косинусов
различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
Пример.
Пример.
Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.
Пример.
Пример.
Иногда применяются некоторые нестандартные приемы.
Пример.
Итого
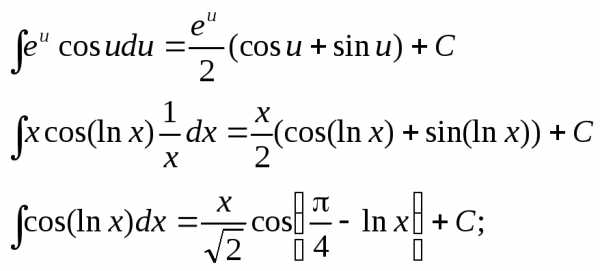
Интегрирование некоторых иррациональных функций.
Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.
Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.
Интеграл
вида 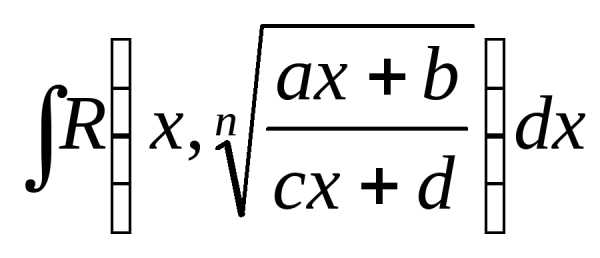 гдеn— натуральное
число.
гдеn— натуральное
число.
С помощью подстановки 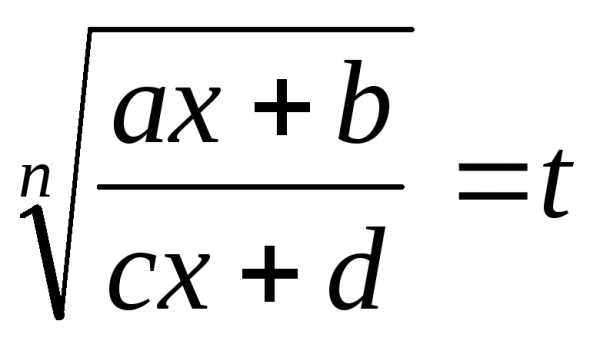 функция рационализируется.
функция рационализируется.
Тогда
Пример.
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
Проиллюстрируем это на примере.
Пример.
Интегрирование биноминальных дифференциалов.
Определение:Биноминальным дифференциалом называется выражение
xm(a + bxn)pdx
где m, n,иp– рациональные числа.
Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:
Если р– целое число, то интеграл рационализируется с помощью подстановки
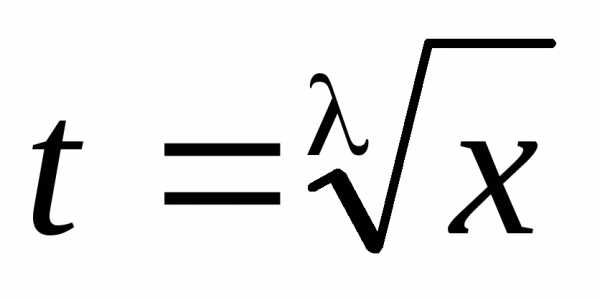 ,
где- общий знаменательmиn.
,
где- общий знаменательmиn.
Если
 — целое число, то интеграл рационализируется
подстановкой
— целое число, то интеграл рационализируется
подстановкой
studfiles.net
Взаимосвязь между интегрированием и дифференцированием
Производная неопределенного интеграла. Первая основная теорема математического анализа
Сейчас мы обсудим удивительную взаимосвязь, которая существует между интегрированием и дифференцированием. Связь между этими двумя действиями аналогична в какой-то мере связи между операциями возведения в квадрат и извлечения квадратного корня. Если мы возведем положительное число в квадрат и затем возьмем положительное значение квадратного корня, то в результате опять получим исходное число. Аналогичным образом, если мы возьмем неопределенный интеграл от некоторой непрерывной функции f, мы получим новую функцию, производная которой даст нам опять исходную функцию f.
Например,
если f(x) = x2, то неопределенный интеграл A(x) определяется следующим образом
$A(x)=\int\limits_c^x f(t) \ dt = \int\limits_c^x t^2 \ dt = \frac{x^3}{3} — \frac{c^3}{3},$
где c — константа интегрирования. Дифференцируя эту функцию, мы получаем A'(x) = x2 = f(x). Этот пример — хорошая иллюстрация важной теоремы, лежащей в основе математического анализа.
Она формулируется следующим образом:
Теорема о производной интеграла по верхнему пределу
Пусть функция f интегрируема на [a, x] для любого x на промежутке [a, b]. Пусть c удовлетворяет условию a ≤ c ≤ b . Определим новую функцию A следующим образом:
$A(x)=\int\limits_c^x f(t) \ dt, \qquad \qquad a \leq x \leq b$
Тогда A'(x) существует в каждой точке x из открытого интервала (a, b), где f непрерывна, и для таких x мы имеем
(5.1) A'(x) = f(x).
Сначала приведем геометрическую иллюстрацию истинности этой теоремы, а затем проведем строгое аналитическое доказательство.
Геометрическая иллюстрация. На рисунке 5.1 изображен график функции f на промежутке [a, b]. Здесь h положительно, и
$\int\limits_x^{x+h} f(t) \ dt = \int\limits_c^{x+h} f(t) \ dt — \int\limits_c^x f(t) \ dt = A(x+h) — A(x)$
Здесь функция непрерывна на интервале [x, x + h]. Следовательно, по теореме о среднем значении для интегралов, получим
A(x + h) — A(x) = hf(Z), где x ≤ z ≤ x + h.
Следовательно,
(5.2) [A(x + h) — A(x)]/h = f(z),
Поскольку x ≤ z ≤ x + h, получаем, что f(z) → f(x) когда h → 0 для всех положительных значений. Аналогичные рассуждения справедливы, если h → 0 для всех отрицательных значений. Следовательно, A'(x) существует и равно f (x).
Эти рассуждения предполагали, что функция
f непрерывна в некоторой окрестности точки x. Однако формулировка теоремы требует непрерывности только в точке x. Следовательно, для доказательства теоремы при этом, более слабом, условии, мы должны использовать иной метод.
Аналитическое доказательство. Пусть функция непрерывна в точке x. В этой точке определим следующее выражение
[A(x + h) — A(x)]/h
Для доказательства теоремы необходимо доказать, что это выражение стремится к пределу f(x), когда h → 0. Числитель этого выражения имеет вид:
$A(x+h) — A(x) = \int\limits_c^{x+h} f(t) \ dt — \int\limits_c^x f(t) \ dt = \int\limits_x^{x+h} f(t) \ dt.$
Если в последний интеграл подставить выражение f(t) =f(x) + [f(t) -f(x)] , получаем
откуда находим
(5.3)
$\frac{A(x+h) — A(x)}{h} = f(x) + \frac{1}{h} \int\limits_x^{x+h} [f(t) — f(x)] \ dt $
Следовательно, для завершения доказательства (5.1) нужно доказать, что
$\lim\limits_{h\rightarrow 0} \ \frac{1}{h} \int\limits_x^{x+h} [f(t) — f(x)] \ dt = 0$
Эта часть доказательства использует условие непрерывности в точке x.
Обозначим второе слагаемое в правой части (5.3) через G(h). Необходимо доказать, что G(h) -f 0 когда h —f 0. Используя определение предела, мы должны показать, что для дюбого ε > 0 существует δ > 0 такое, что
(5.4) |G(h)|
Из непрерывности функции f в точке x следует, что если дано ε, то существует положительное δ такое, что
(5.5) |f(t) -f(x)| когда (5.6) x — δ
Если h выбрано таким образом, что 0
$|\int \limits_x^{x+h} [f(t) — f(x)] \ dt | \leq \int \limits_x^{x+h} |f(t) — f(x)| \ dt \leq \int \limits_x^{x+h} \frac{1}{2} \epsilon \ dt = \frac{1}{2} h \epsilon
Разделив его на h, мы видим, что (5.4) справедливо для 0
www.math10.com
Что такое интеграл? Интегралы с подробным решением. Таблица интегралов :: SYL.ru
Слово «интеграл» происходит от латинского integralis – целостный. Это название предложил в 17 в. ученик великого Лейбница (и также выдающийся математик) И. Бернулли. А что такое интеграл в современном понимании? Ниже мы постараемся дать всесторонний ответ на этот вопрос.
Исторические предпосылки возникновения понятия интеграла
В начале 17 в. в рассмотрении ведущих ученых находилось большое число физических (прежде всего механических) задач, в которых нужно было исследовать зависимости одних величин от других. Самыми наглядными и насущными проблемами были определение мгновенной скорости неравномерного движения тела в любой момент времени и обратная этой задача нахождения величины пути, пройденного телом за определенный промежуток времени при таком движении. Сегодня мы уже знаем, что такое интеграл от скорости движения – это и есть пройденный путь. Но понимание того, как его вычислять, зная скорость в каждый момент времени, появилось не сразу.
Поначалу из рассмотрения таких зависимостей физических величин, например, пути от скорости, было сформировано математическое понятие функции y = f(x). Исследование свойств различных функций привело к зарождению математического анализа. Ученые активно искали способы изучения свойств различных функций.

Как возникло вычисление интегралов и производных?
После создания Декартом основ аналитической геометрии и появления возможности изображать функциональные зависимости графически в осях декартовой системы координат, перед исследователями встали две крупные новые задачи: как провести касательную к кривой линии в любой ее точке и как найти площадь фигуры, ограниченной сверху этой кривой и прямыми, параллельными осям координат. Неожиданным образом оказалось, что первая из них эквивалентна нахождению мгновенной скорости, а вторая – нахождению пройденного пути. Ведь он при неравномерном движении изображался в декартовых осях координат «расстояние» и «время» некоторой кривой линией.
Гением Лейбница и Ньютона в середине 17 в. были созданы методы, позволившие решать обе эти задачи. Оказалось, что для проведения касательной к кривой в точке нужно найти величину так называемой производной от функции, описывающей эту кривую, в рассматриваемой ее точке, и эта величина оказывается равной скорости изменения функции, т. е. применительно к зависимости «путь от скорости» собственно мгновенной скоростью тела.
Для нахождения же площади, ограниченной кривой линией, следовало вычислить определенный интеграл, который давал ее точную величину. Производная и интеграл – основные понятия дифференциального и интегрального исчисления, являющихся базисом современного матанализа – важнейшего раздела высшей математики.
Площадь под кривой линией
Итак, как же определить ее точную величину? Попробуем раскрыть процесс ее вычисления через интеграл подробно, с самых азов.
Пусть f является непрерывной на отрезке [ab] функцией. Рассмотрим кривую у = f(x), изображенную на рисунке ниже. Как найти площадь области, ограниченной кривой ), осью х, и линиями х = а и х = b? То есть площадь заштрихованной фигуры на рисунке.
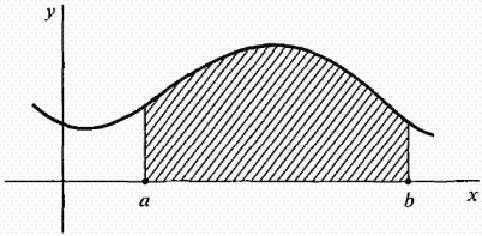
Самый простой случай, когда f является постоянной функцией; то есть, кривая есть горизонтальная линия f(X) = k, где k постоянная и k ≥ 0, как показано на рисунке ниже.
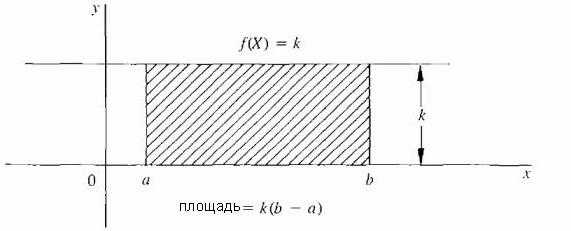 В этом случае область под кривой — всего лишь прямоугольник с высотой k и шириной (b – a), так что площадь определяется как: k · (b — а).
В этом случае область под кривой — всего лишь прямоугольник с высотой k и шириной (b – a), так что площадь определяется как: k · (b — а).Области некоторых других простых фигур, таких как треугольник, трапеция и полуокружность, даются формулами из планиметрии.
Площадь под любой непрерывной кривой у = f(х) дается определенным интегралом, который записывается так же, как обычный интеграл.
Риманова сумма
Прежде чем погрузиться в подробный ответ на вопрос, что такое интеграл, выделим некоторые основные идеи.
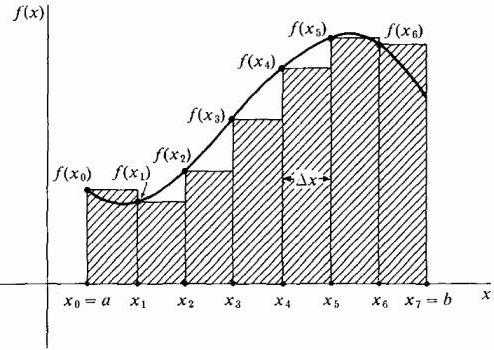
Во-первых, область под кривой делится на некоторое число n вертикальных полос достаточно малой ширины Δx. Далее каждая вертикальная полоса заменяется вертикальным прямоугольником высотой f(х), шириной Δx, и площадью f(х)dx. Следующим шагом является формирование суммы площадей всех этих прямоугольников, называемой Римановой суммой (смотрите рисунки ниже).
Рисуя наши прямоугольники шириной Δx, мы можем брать их высоту, равную значению функции на левом краю каждой полоски, т. е. на кривой будут лежать крайние левые точки их верхних коротких сторон шириной Δx. При этом на участке, где функция растет, и ее кривая является выпуклой, все прямоугольники оказываются ниже этой кривой, т. е. их сумма будет заведомо меньшей точной величины площади под кривой на этом участке (см. рисунок ниже). Такой способ аппроксимации называется левосторонним.
В принципе, можно нарисовать аппроксимирующие прямоугольники таким образом, чтобы на кривой лежали крайние правые точки их верхних коротких сторон шириной Δx. Тогда они будут выше кривой, и приближение площади на этом участке окажется больше ее точной величины, как показано на рисунке ниже. Этот способ носит название правостороннего.
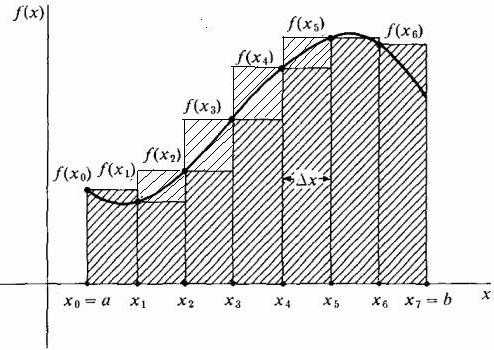
Но мы можем также взять высоту каждого из аппроксимирующих прямоугольников, равной просто некоторому значению функции в произвольной точке x*i внутри соответствующей полоски Δxi (смотри рис. ниже). При этом мы даже можем не брать одинаковую ширину всех полосок.
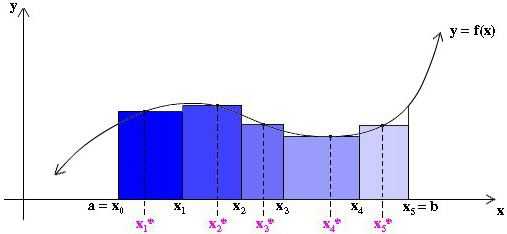
Составим Риманову сумму:
Переход от Римановой суммы к определенному интегралу
В высшей математике доказывается теорема, которая гласит, что если при неограниченном возрастании числа n аппроксимирующих прямоугольников наибольшая их ширина стремится к нулю, то Риманова сумма An стремится к некоторому пределу A. Число A – одно и то же при любом способе образования аппроксимирующих прямоугольников и при любом выборе точек x*i.
Наглядное пояснение теоремы дает рисунок ниже.
Из него видно, что, чем уже прямоугольники, тем ближе площадь ступенчатой фигуры к площади под кривой. При числе прямоугольников n→∞ их ширина Δxi→0, а предел A суммы An численно равен искомой площади. Этот предел и есть определенный интеграл функции f (х):
Символ интеграла, представляющий собой видоизмененную курсивную литеру S, был введен Лейбницем. Ставить сверху и снизу обозначения интеграла его пределы предложил Ж. Б. Фурье. При этом ясно указывается начальное и конечное значение x.
Геометрическое и механическое истолкование определенного интеграла
Попробуем дать развернутый ответ на вопрос о том, что такое интеграл? Рассмотрим интеграл на отрезке [a,b] от положительной внутри него функции f(х), причем считаем, что верхний предел больше нижнего a<b. Как мы уже видели выше, в этом случае площадь, находящаяся между графиком y= f(х) и осью абсцисс в пределах отрезка [a,b], численно равна интегралу от a до b.
Если ординаты функции f(х) отрицательны внутри [a,b], то абсолютное значение интеграла равно площади между осью абсцисс и графиком y=f(х), сам же интеграл отрицателен.
В случае же однократного или неоднократного пересечения графиком y=f(х) оси абсцисс на отрезке [a,b], как показано на рисунке ниже, для вычисления интеграла нужно определить разность, в которой уменьшаемое будет равно суммарной площади участков, находящихся над осью абсцисс, а вычитаемое – суммарной площади участков, находящихся под ней.
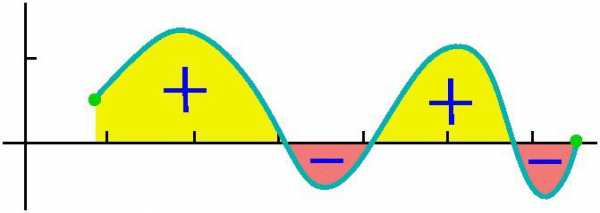 Так, для функции, показанной на рисунке выше, определенный интеграл от a до b будет равен (S1 + S3) – (S2+S4).
Так, для функции, показанной на рисунке выше, определенный интеграл от a до b будет равен (S1 + S3) – (S2+S4).Механическое истолкование определенного интеграла тесно связано с геометрическим. Вернемся к разделу «Риманова сумма» и представим, что приведенный на рисунках график выражает функцию скорости v=f(t) при неравномерном движении материальной точки (ось абсцисс является осью времени). Тогда площадь любого аппроксимирующего прямоугольника шириной Δt, который мы строили при формировании Римановой суммы, будет выражать приближенно путь точки за время Δt, а именно v(t*)Δt.
Полная сумма площадей прямоугольников на отрезке от t1=a до t2=b выразит приближенно путь s за время t2– t1 , а предел ее, т. е. интеграл (определенный) от a до b функции v = f(t) по dt даст точное значение пути s.
Дифференциал определенного интеграла
Если вернуться к его обозначению, то вполне можно предположить, что a = const, а b является конкретным значением некоторой независимой переменной x. Тогда определенный интеграл с верхним пределом x̃ из конкретного числа превращается в функцию от x̃. Такой интеграл равен площади фигуры под кривой, обозначенной точками aABb на рисунке ниже.
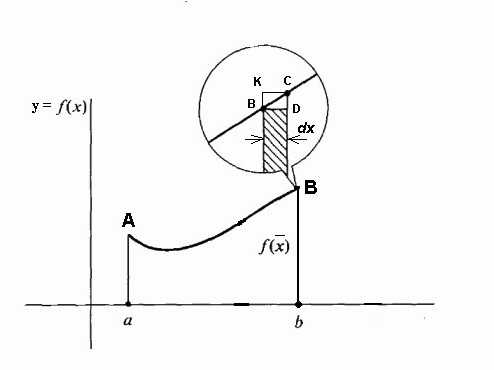 При неподвижной линии aA и подвижной Bb эта площадь становится функцией f(x̃), причем приращения Δx̃ по-прежнему откладываются вдоль оси х, а приращением функции f(x̃) являются приращения площади под кривой.
При неподвижной линии aA и подвижной Bb эта площадь становится функцией f(x̃), причем приращения Δx̃ по-прежнему откладываются вдоль оси х, а приращением функции f(x̃) являются приращения площади под кривой.Предположим, что мы дали переменной x̃ = b некоторое малое приращение Δx̃. Тогда приращение площади фигуры aABb складывается из площади прямоугольника (заштрихован на рисунке) Bb∙Δx̃ и площади фигуры BDC под кривой. Площадь прямоугольника равна Bb∙Δx̃ = f(x̃)Δx̃, т.е она является линейной функцией приращения независимой переменной. Площадь же фигуры BDC заведомо меньше, чем площадь прямоугольника BDCK = Δx̃∙Δy, и при стремлении Δx̃ →0 она уменьшается еще быстрее него. Значит, f(x̃)Δx̃ = f(x̃)dx̃ есть дифференциал переменной площади aABb, т. е. дифференциал определенного интеграла
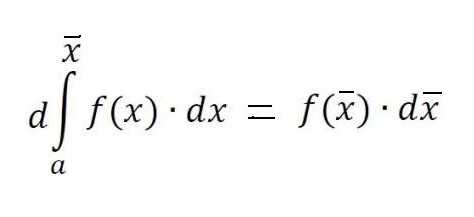
Отсюда можно заключить, что вычисление интегралов заключается в разыскании функций по заданным выражениям их дифференциалов. Интегральное исчисление как раз и представляет собой систему способов разыскания таких функций по известным их дифференциалам.
Фундаментальное соотношение интегрального исчисления
Оно связывает отношения между дифференцированием и интегрированием и показывает, что существует операция, обратная дифференцированию функции, — ее интегрирование. Оно также показывает, что если любая функция f(х) непрерывна, то применением к ней этой математической операции можно найти целый ансамбль (совокупность, множество) функций, первообразных для нее (или иначе, найти неопределенный интеграл от нее).
Пусть функция F(x) является обозначением результата интегрирования функции f(х). Соответствие между этими двумя функциями в результате интегрирования второй из них обозначается следующим образом:
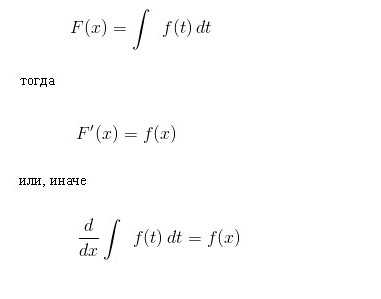
Как видно, при символе интеграла отсутствуют пределы интегрирования. Это означает, что из определенного он преобразован в неопределенный интеграл. Слово «неопределенный» означает, что результатом операции интегрирования в данном случае является не одна, а множество функций. Ведь, кроме собственно функции F(x), последним выражениям удовлетворяет и любая функция F(x)+С, где С = const. При этом подразумевается, что постоянный член в ансамбле первообразных можно задавать по произволу.
Следует подчеркнуть, что, если интеграл, определенный от функции, является числом, то неопределенный есть функция, точнее, их множество. Термин «интегрирование» применяется для определения операции разыскания обоих видов интегралов.
Основное правило интегрирования
Оно представляет собой полную противоположность соответствующему правилу для дифференцирования. Как же берутся неопределенные интегралы? Примеры этой процедуры мы рассмотрим на конкретных функциях.
Давайте посмотрим на степенную функцию общего вида:
f(х) = cxn
После того как мы сделали это с каждым слагаемым в выражении интегрируемой функции (если их несколько), мы добавляем постоянную в конце. Напомним, что взятие производной от постоянной величины уничтожает ее, поэтому взятие интеграла от любой функции даст нам восстановление этой постоянной. Мы обозначаем ее С, так как постоянная неизвестна — это может быть любое число! Поэтому мы можем иметь бесконечно много выражений для неопределенного интеграла.
Давайте рассмотрим простые неопределенные интегралы, примеры взятия которых показаны ниже.
Пусть нужно найти интеграл от функции:
f(х) = 4x2 + 2x – 3.
Начнем с первого слагаемого. Мы смотрим на показатель степени 2 и увеличиваем его на 1, затем делим первый член на результирующий показатель 3. Получаем: 4(x3) / 3.
Затем мы смотрим на следующий член и делаем то же самое. Так как он имеет показатель степени 1, то результирующий показатель будет 2. Таким образом, мы разделим это слагаемое на 2: 2(x2) / 2 = x2.
Последний член имеет множитель х, но мы просто не видим его. Мы можем представить себе последнее слагаемое как (-3x0). Это эквивалентно (-3)∙(1). Если мы используем правило интегрирования, мы добавим 1 к показателю, чтобы поднять его до первой степени, а затем разделим последний член на 1. Получим 3x.
Это правило интегрирования работает для всех значений n, кроме n = – 1 (потому что мы не можем разделить на 0).

Мы рассмотрели самые простой пример нахождения интеграла. Вообще же решение интегралов является делом непростым, и в нем хорошим подспорьем является уже накопленный в математике опыт.
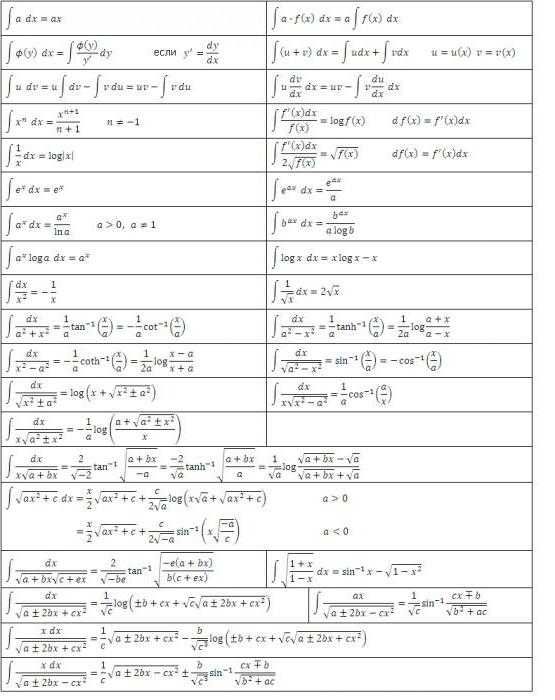
Таблицы интегралов
В разделе выше мы видели, что из каждой формулы дифференцирования получается соответствующая формула интегрирования. Поэтому все возможные их варианты уже давно получены и сведены в соответствующие таблицы. Нижеприведенная таблица интегралов содержит формулы интегрирования основных алгебраических функций. Эти формулы нужно знать на память, заучивая их постепенно, по мере их закрепления упражнениями.
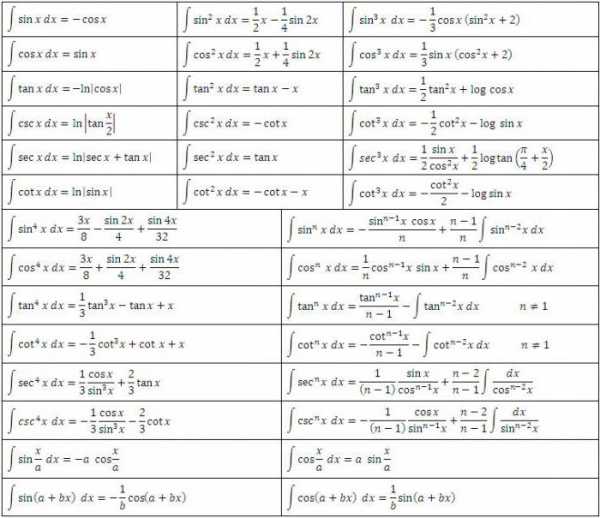
Еще одна таблица интегралов содержит основные тригонометрические функции:
Как же вычислить определенный интеграл
Оказывается, сделать это, умея интегрировать, т. е. находить неопределенные интегралы, очень просто. И помогает в этом формула основателей интегро-дифференциального исчисления Ньютона и Лейбница
Согласно ей, вычисление искомого интеграла состоит на первом этапе в нахождении неопределенного, последующем вычислении значения найденной первообразной F(x) при подстановке x, равного сначала верхнему пределу, затем нижнему и, наконец, в определении разности этих значений. При этом константу С можно не записывать. т.к. она пропадает при выполнении вычитания.
Рассмотрим некоторые интегралы с подробным решением.
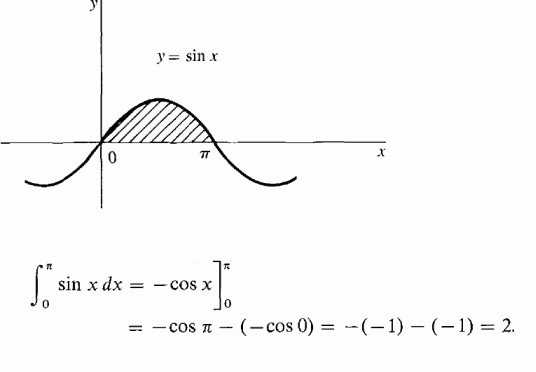
Найдем площадь участка под одной полуволной синусоидой.
 Вычислим заштрихованную площадь под гиперболой.
Вычислим заштрихованную площадь под гиперболой.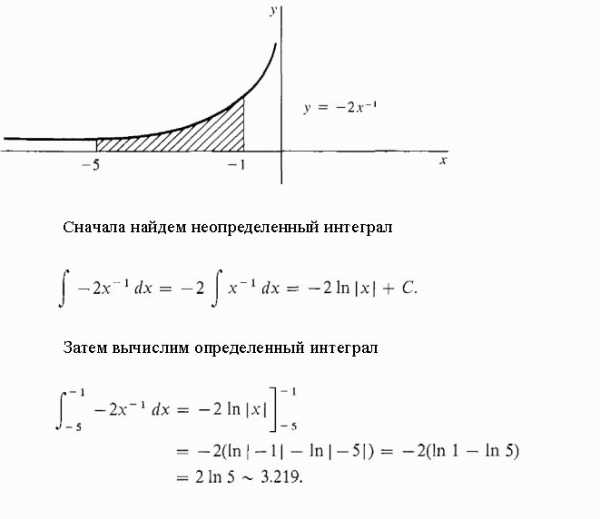
Рассмотрим теперь интегралы с подробным решением, использующим в первом примере свойство аддитивности, а во втором — подстановку промежуточной переменной интегрирования. Вычислим определенный интеграл от дробно-рациональной функции:
y=(1+t)/t3 от t=1 до t=2.
Теперь покажем, как можно упростить взятие интеграла введением промежуточной переменной. Пусть нужно вычислить интеграл от (x+1)2.
О несобственных интегралах
Мы говорили об определенном интеграле для конечного промежутка [a,b] от непрерывной на нем функции f(х). Но ряд конкретных задач приводит к необходимости расширить понятие интеграла на случай, когда пределы (один или оба) равны бесконечности, или при разрывной функции. Например, при вычислении площадей под кривыми, асимптотически приближающимися к осям координат. Для распространения понятия интеграла на этот случай, кроме предельного перехода при вычислении Римановой суммы аппроксимирующих прямоугольников, выполняется еще один. При таком двукратном переходе к пределу получается несобственный интеграл. В противоположность ему все интегралы, о которых говорилось выше, называются собственными.
www.syl.ru

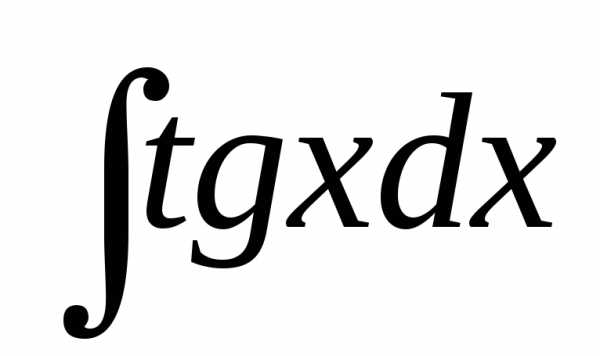
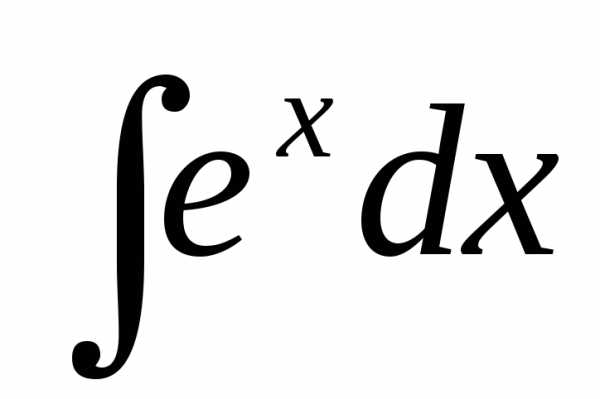
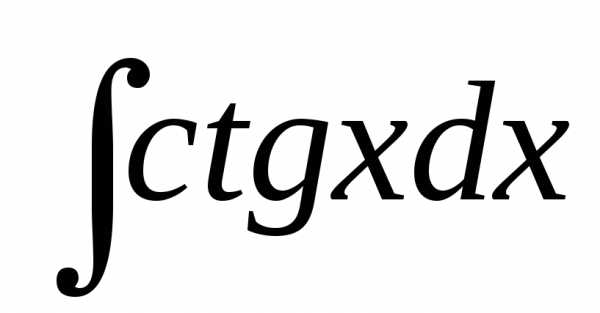
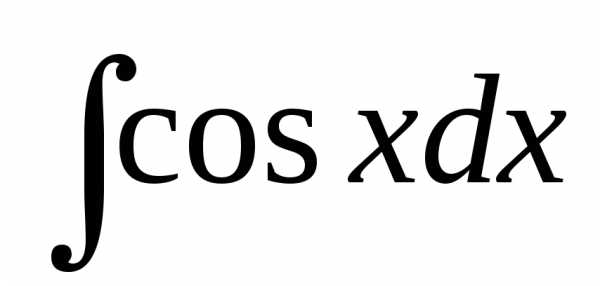

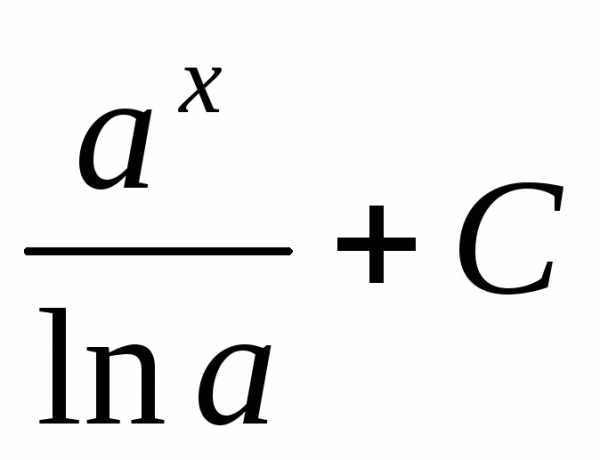
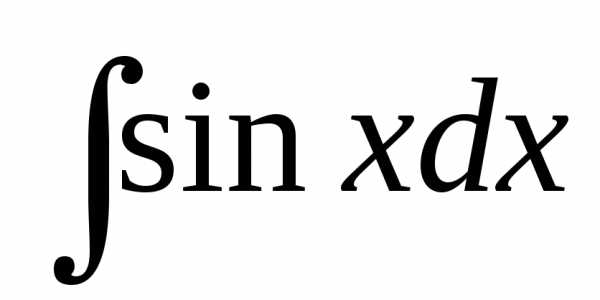
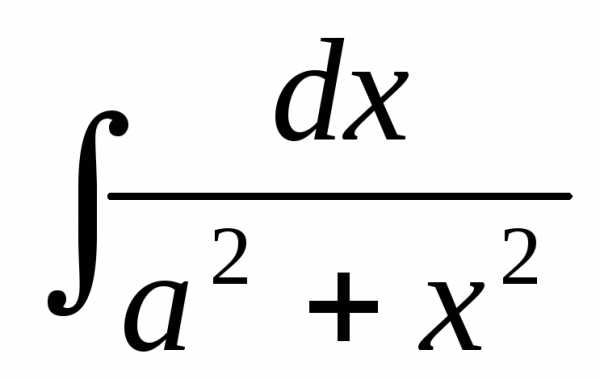
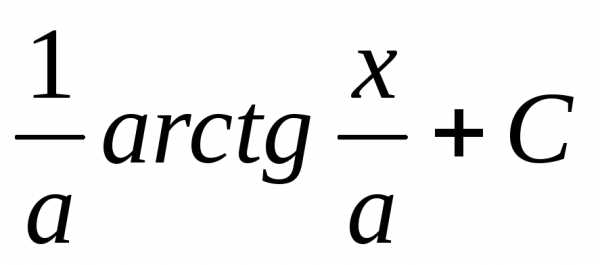
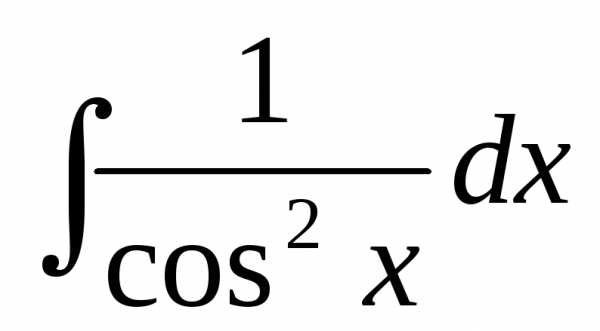
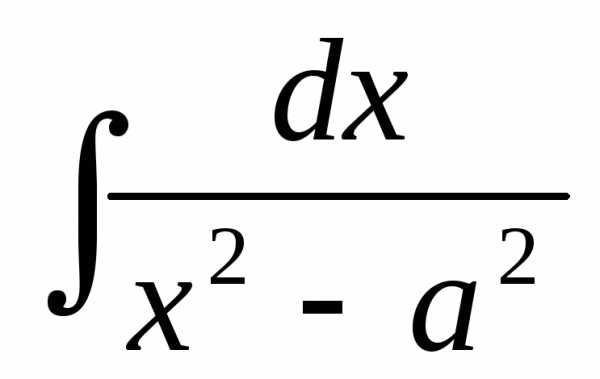
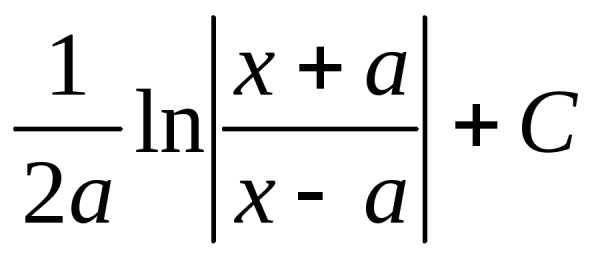
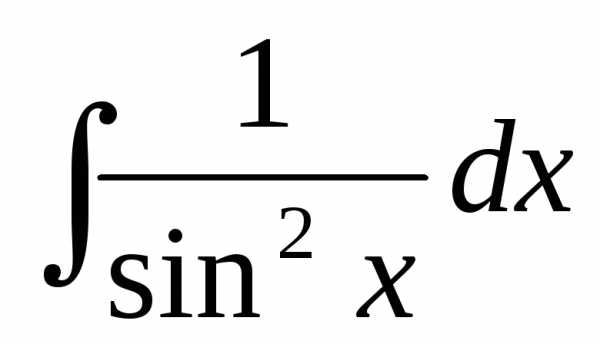
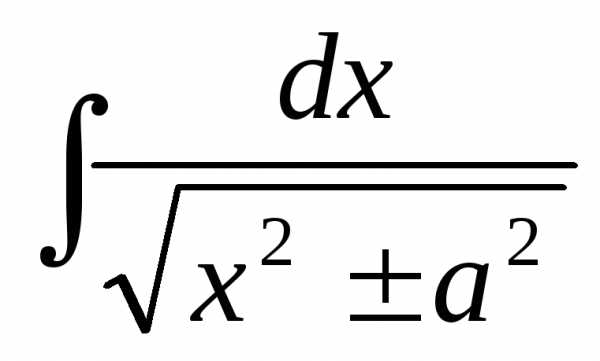
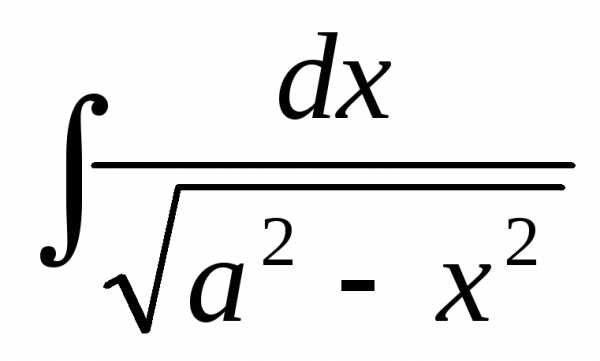
 + C
+ C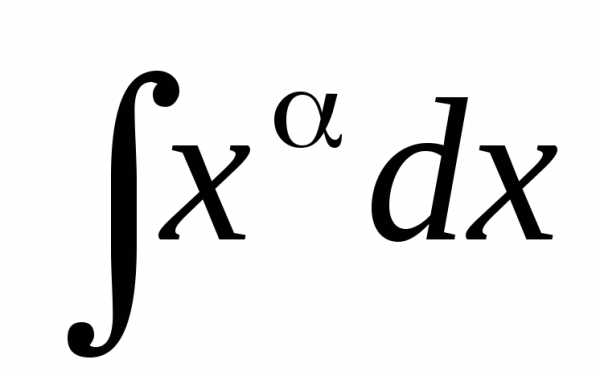

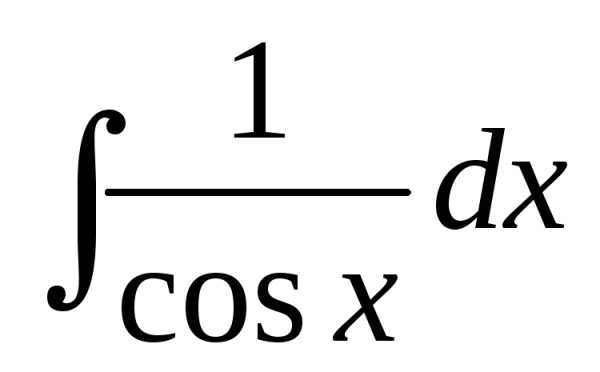


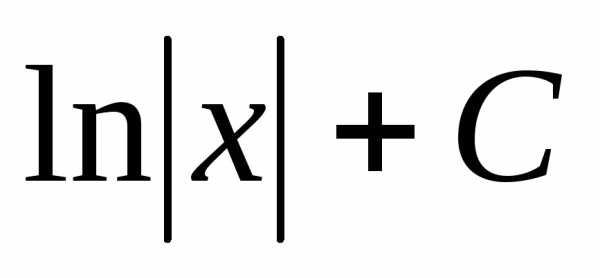
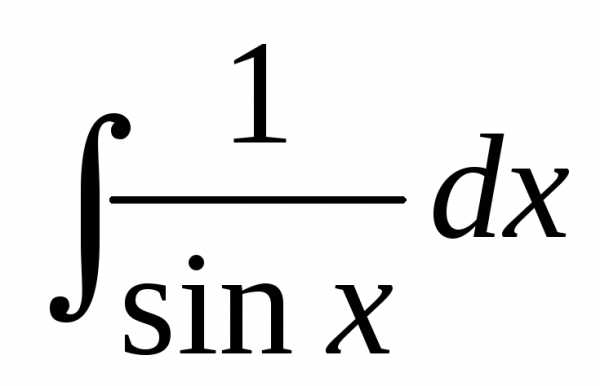

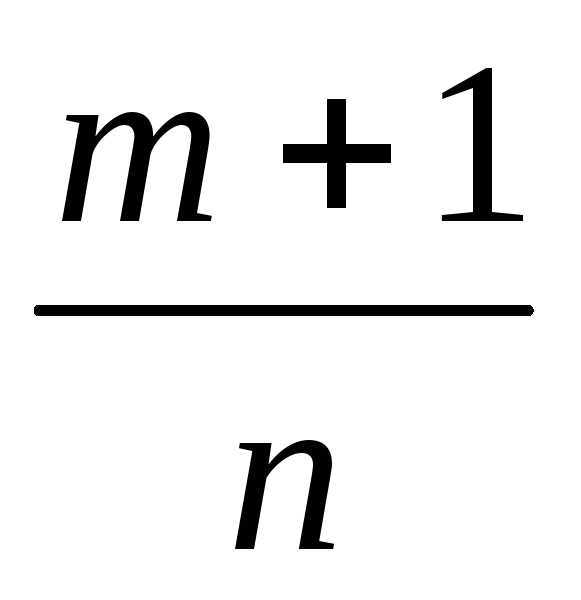 — целое число, то интеграл рационализируется
подстановкой
— целое число, то интеграл рационализируется
подстановкой