Конспект урока по алгебре «Применение производной к исследованию функций и построению графика функции», 10 класс
План-конспект урока «Применение производной к исследованию функций и построению графика функции»
Образовательные цели:-Научить применять производную к исследованию функции
— Научить строить график функции на основе проведённого исследования.
— систематизировать и совершенствовать знания, умения и навыки учащихся при решении задач;
2. Развивающие цели:
— формирование активного, самостоятельного творческого мышления;
— наблюдательности, сообразительности, инициативы;
— умения анализировать, сравнивать и обобщать;
— учить проводить рассуждения, используя математическую речь;
3. Воспитательные цели:
— формирование нравственных качеств личности: аккуратности, дисциплинированности, трудолюбия, ответственности, креативности, требовательности к себе, любознательности.
Оборудование: компьютер, презентация, интерактивная доска, программа
Ход урока:
I этап: Организационный
II этап: Подготовительный
Устная работа
1. Найдите производную функции: (Слайд 1, 2):
а) sin x
б) tg х
в) х2 + 2
г) х4
д)
е) ех+2
III этап: Решение задач
Тема нашего занятия – «Исследование функции и построение графиков с помощью производной».
Цель урока – научиться строить график функции, применяя производную для исследования функции.
-Одним из важнейших этапов построения графика функции является определение экстремумов функции и как вы знаете это удобно делать с помощью производной.
Задание1: исследовать на наличие экстремумов функцию f(x)=
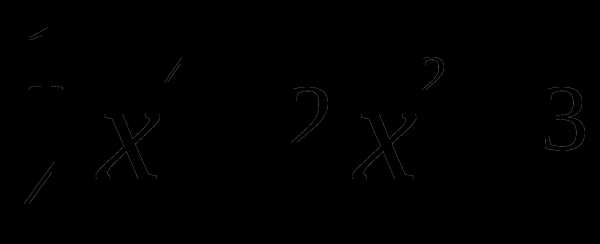и построить эскиз её графика.
1. 
.
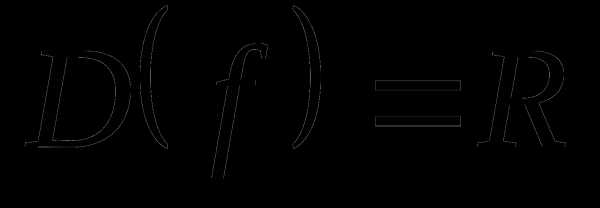2.
3.
4. 
при х=0, х=2, х=-2
5. Точки пересечения с осями координат (-3;0), (3;0)
Наносим полученные точки на координатную плоскость. Возникает проблема: какой линией соединить имеющиеся точки графика, чтобы она более точно передавала свойства заданной функции? Предлагаем 4 варианта соединения точек. Какой из них верный? (Слайд 4) Ответить на вопрос, можно вспомнив, что во всех найденных точках экстремумов производная равна нулю. Значит, касательные к графику функции в этих точках должны быть параллельны осиЗадание2. Глядя на данную таблицу, постройте схематично график функции (слайд 5).
Задание3. По графику самостоятельно заполнить таблицу (слайд 6)
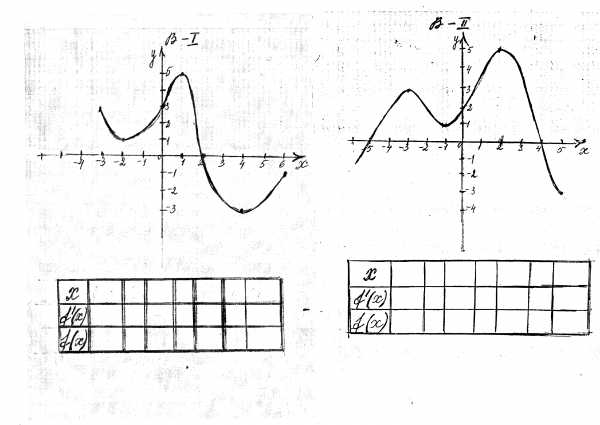
Задание4. Построить графики функций на компьютере и определить по графику их точки экстремума
( слайд 7)
а) ;
б)
При определении точек экстремума возникла проблема: для функции б) найти точки экстремума с помощью построения графика на компьютере можно точно, а для функции а) – лишь приближённо. а) ;
б)
Разрешить проблему можно, применяя аналитический метод. Найдем точки экстремума предложенных функций, используя производную (учащиеся приводят аналитическое решение проблемы)
а) ;
б)
Вывод: аналитический способ нахождения точек экстремума более совершенный по сравнению с графическим.
IV этап: Итог урока.
Какие выводы мы сделали сегодня на уроке:
аналитический способ нахождения точек экстремума более совершенный по сравнению с графическим
при построении графика при помощи исследования функции с помощью производной нужно использовать всю аналитически найденную информацию
Проведём блиц-тест (на компьютере)
VI этап: Домашнее задание.
Исследуйте функции, на основе проведённого исследования постройте графики этой функции в тетради, а на следующем занятии проверьте построение графика с помощью компьютера.
infourok.ru
Методическая разработка по математике (10 класс) на тему: Урок по теме: «Исследование функций и построение графиков с помощью производной».
По теме: методические разработки, презентации и конспекты
Исследование функции и построение графиков с применением производнойЦел Цель урока: Выявить уровень овладения учащимися комплексом знаний и умений по исследованию функции и ликвидировать пробелы в знаниях в соответствии с…
Административный контроль Алгебра 9 класс Тема: «Исследование функции и построение графика функции»Пояснительная записка Данная проверочная работа предназначена для подготовки выпускников 9-ых классов МБОУ СОШ № 35 г.о. Самара к экзаменационной работе по математике в новой ф…
Открытый урок по теме:»Линейная функция и её график.График функции у=IхI.Открытый урок по теме:»Линейная функция и её график.График функции у=IхI.»содержит следующие материалы:1)Описание открытого урока.2)Презентацию №1 для 1 этапа урока,созданную учителем,3)Презентацию №2…
Открытый урок по теме:»Линейная функция и её график.График функции у=IхI.Открытый урок по теме:»Линейная функция и её график.График функции у=IхI.»содержит следующие материалы:1)Описание открытого урока.2)Презентацию №1 для 1 этапа урока,созданную учителем,3)Презентацию №2…
Исследование функций и построение графиков является завершение изучения раздела «Дифференциальное исчисление» и включает в себя комплекс изученных понятий….
Индивидуальные задания по алгебре для 10 класса на тему «Исследование функции и построение графика»Задания на исследование функций и построение их графиков…
Методическая разработка по теме: Исследование функции и построение графика функции.Методическая разработка — конспект урока по теме: Исследование функции с помощью производной и построение графика функции. Урок построен в форме игры., в ходе которой проверяются знания по …
nsportal.ru
Исследование функции, ее график, сопутствующие задачи на примере функции f(x)=3×5-5×3+2. Задача с параметром
Тема: Производная
Урок: Исследование функций; сопутствующие задачи
На этом занятии будет продолжена тема исследование функции с помощью производной. На предыдущем уроке была подробно рассмотрена функция . Выяснили, что эта функция допускает подробное исследование с помощью производной. Была найдена производная, интервалы знакопостоянства, промежутки монотонности функции, точки экстремума.
Найти множество значений функции.
.
В связи с этим – типовая задача.
1. Дано: . При каких значениях параметра , данное уравнение имеет хотя бы одно решение?
Методика решения подобных задач.
Построить график функции из левой части ( построили на предыдущем уроке). Поскольку множество значений функции любое действительное число. Это означает, что при любом , хотя бы один корень есть.
Ответ: при уравнение имеет хотя бы одно решение.
Найти , при которых нет решений у данного уравнения.
Ответ : нет таких .
2. Дано: . Найти число корней уравнения, в зависимости от параметра .
Решение.
Мы не можем точно найти корень, даже если . Методика решения состоит в следующем.
1) Построить график функции (см. рис.1).
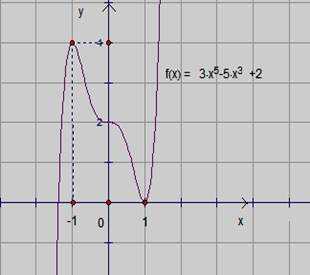
Рис. 1. График функции .
2) Рассечь график функции семейством прямых (см. рис.2).
3) Найти точки пересечения (их число) и выписать ответ.
Рис. 2. График функции и прямые .
Ответ:
1) при любом , уравнение имеет одно решение. Можем охарактеризовать, где лежит это решение: .
2) При — уравнение имеет два решения.
3) При — уравнение имеет три различных корня.
4) Если , то уравнение имеет два решения.
5) При любом — уравнение имеет единственное решение.
1. Найти наибольшее значение параметра , при которых уравнение имеет два различных решения.
Два различных решения имеем при и при .
Ответ: таким образом, наибольшее значение параметра при котором уравнение имеет два различных решения .
2. Найти число значений параметра , при каждом из которых уравнение имеет ровно два различных решения.
Решение.
Таких параметров – два. При и при уравнение имеет два решения .
Ответ: 2.
3. Найти все значения параметра , при которых уравнение имеет ровно три различных решения.
Решение.
В общей задаче, где мы перебрали все и для каждого дали ответ, есть ответ на поставленную задачу. Три решения есть, когда меняется от нуля до четырех.
Ответ: .
4. Найти натуральные значения параметра , при которых уравнение имеет три различных решения.
Эта задача отличается от предыдущей тем, что среди промежутка выбрать натуральные значения . Итак, при , при и при — натуральных числах, уравнение имеет три различных корня.
Ответ: , , .
Итак, на уроке была рассмотрена методика построения графика функции пятой степени с помощью производной. Были найдены промежутки монотонности функции, точки максимума и точки минимума функции. Также были рассмотрены сопутствующие задачи. Наиболее сложная из них такова: дано уравнение , найти число решений уравнения с параметром . На уроке сформулирована методика решения такой задачи. Главным в такой задаче – построение графика функции с помощью производной. Потом этот график нужно рассекать семейством прямых , при разных , и считывать ответ.
Список рекомендованной литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.
8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics.ru (Источник).
2. Портал Естественных Наук (Источник).
3. Интернет-портал Exponenta.ru (Источник).
Сделай дома
№45.11 (б), 45.12 (б) ( Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
interneturok.ru
10 класс. Алгебра. Производная. Применение производной к исследованию функции. — Исследование функции и построение графика
Комментарии преподавателя
Построение графика произвольной функции может быть как отдельной задачей, так и вспомогательной — например, при решении уравнений графическим способом, или при решении задач с параметрами.
Алгоритм исследования функции и построения ее графика таков:
1. Находим область определения (D(f)) функции .
2. Если область определения функции симметрична относительно нуля (то есть для любого значения из D(f) значение также принадлежит области определения, то проверяем функцию на четность.
Если , то функция четная. (Примером четной функции является функция )
Для нас важно, что график четной функции симметричен относительно оси OY.
Если , то функция нечетная. (Примером нечетной функции является функция )
График нечетной функции симметричен относительно начала координат.
Если функция является четной или нечетной, то мы можем построить часть ее графика для , а затем соответствующим образом отразить ее.
3. Находим точки пересечения графика с осями координат.
Находим нули функции — это точки пересечения графика функции с осью абсцисс (OX).
Для этого мы решаем уравнение .
Корни этого уравнения являются абсциссами точек пересечения графика функции с осью ОХ.
Находим точку пересечения графика функции с осью ординат (OY). Для этого ищем значение функции при .
4. Находим промежутки знакопостоянства функции, то есть промежутки, на которых функция сохраняет знак. Это нам потребуется для контроля правильности построения графика.
Чтобы найти промежутки знакопостоянства функции , нам нужно решить неравенства и .
5. Находим асимптоты графика функции.
6. Если функция периодическая, то находим период функции.
7. Исследуем функцию с помощью производной: находим промежутки возрастания и убывания функции, а также точки максимума и минимума.
Для этого мы следуем привычному алгоритму.
а) Находим производную
б) Приравниваем производную к нулю и находим корни уравнения — это стационарные точки.
в) Находим промежутки знакопостоянства производной. Промежутки, на которыхпроизводная положительна, являются промежутками возрастания функции.
Промежутки, на которых производная отрицательна, являются промежутками убыванияфункции.
Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.
Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.
8. И последний номер наше программы — точки перегибы и промежутки выпуклости и вогнутости.
Подробнее о том, как находить точки перегиба и промежутки выпуклости и вогнутости читайте здесь.
Итак, давайте, для примера, исследуем функцию и построим ее график.
1. Найдем D(y).
Сразу отметим, что при знаменатель дроби равен нулю, следовательно, прямые и являются вертикальными асимптотами графика функции .
2. Исследуем функцию на четность. Область определения функции симметрична относительна нуля (мы выкололи две симметричные точки: и )
Получили, что , следовательно, функция — нечетная, и график функции симметричен относительно начала координат.
3. Найдем точки пересечения с осями координат.
а) Точки пересечения с осью ОХ (y=0)
б) Точка пересечения с осью ОY (x=0)
www.kursoteka.ru
Презентация на тему Исследование функции и построение графика (10 класс)
Презентацию на тему Исследование функции и построение графика (10 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет презентации : Математика. Красочные слайды и илюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого презентации воспользуйтесь плеером, или если вы хотите скачать презентацию — нажмите на соответствующий текст под плеером. Презентация содержит 40 слайдов.
Слайд 1Исследование функции и построение графика.
Урок алгебры в 10 классе
Слайд 2ЕГЭ — 2014 Ответ: 3
Слайд 3Ответ: -0,25
Слайд 4Ответ: 7
Слайд 5Ответ: 2
Слайд 6
Слайд 7Ответ: 9
Слайд 8Ответ: 0
Слайд 9Ответ: -2
Слайд 10Ответ: 5
Слайд 11Ответ: 4
Слайд 12Ответ: -3
Слайд 13
Слайд 14Ответ: -12
Слайд 15
Слайд 16Исследование функции
Слайд 171. Область определения функции
Слайд 182. Четность и нечетность функции Условие четности: f(-x)=f(x) Условие нечетности: f(-x)=-f(x)
Слайд 19Четные и нечетные функции
Слайд 203. Асимптоты
Слайд 21
Слайд 22Асимптоты
Слайд 234. Найдем: Стационарные и критические точки. Промежутки монотонности. Экстремумы функции Значения функции в точках экстремума
Слайд 245. Точки пересечения с осями координат.
Слайд 256. Дополнительные точки.
Слайд 267. Построение графика функции
Слайд 27исследование функции
Область определения Чётность и нечётность функции Асимптоты Производная Стационарные точки Критические точки Промежутки монотонности Экстремумы функции Значения функции в точках экстремумов Точки пересечения с осями координат Дополнительные точки Построение графика функции.
Слайд 28Закрепление:
В классе: §35, №895(в)
Слайд 29Домашнее задание: §35, №927
Слайд 30
Слайд 31
Слайд 321. Найдите область определения функции
Слайд 332. Исследуйте на четность и нечетность
Слайд 34
Слайд 35
Слайд 363. Исследуйте на асимптоты
Слайд 37
Слайд 38Найдите точки пересечения с осями координат
Слайд 39В классе: §35, №893(Г) Дополнительно: №897(в)
Слайд 40§35, №893(а), Дополнительно: №897(а)
prezentacii.org