Онлайн найти экстремумы функции двух переменных – Экстремумы функции онлайн

5. Экстремумы функции двух переменных Основные определения

Определение 1. Точка М(x₀; у₀) называется точкой максимума (минимума) функции z = f(x; y), если существует окрестность точки М, такая, что для всех точек (x; y) из этой окрестности выполняется неравенство:

f(x₀; y₀)  f(x; y), .

Теорема 1 (необходимое условие существования экстремума). Если дифференцируемая функция z = f(x; y) достигает экстремума в точке М(x₀; y₀), то ее частные производные первого порядка в этой точке равны нулю, т.е. ;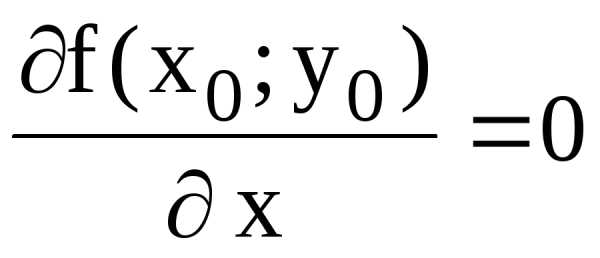

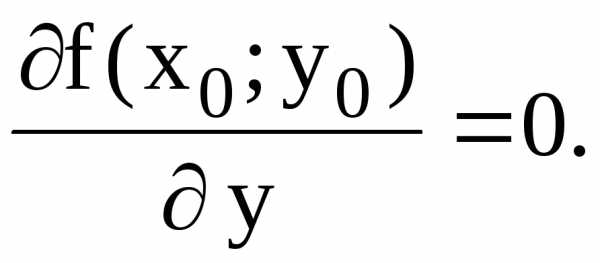
Точки, в которых частные производные равны нулю, называются

стационарными или критическими точками.

Теорема 2 (достаточное условие существования экстремума)

Пусть функция z = f(x; y):

а) определена в некоторой окрестности точки (x₀; y₀), в которо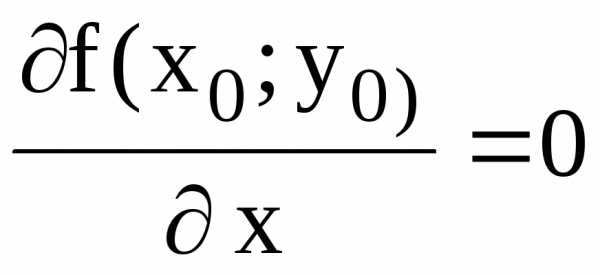й и;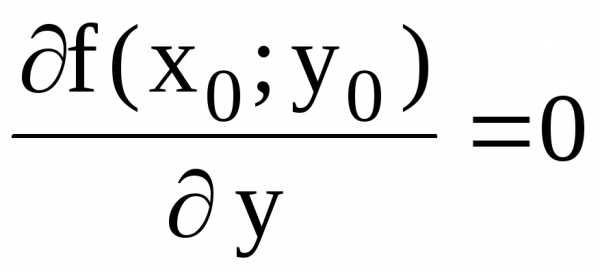

б) имеет в этой точке непрерывные частные производные второго порядка

;

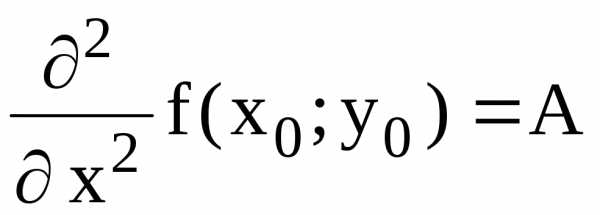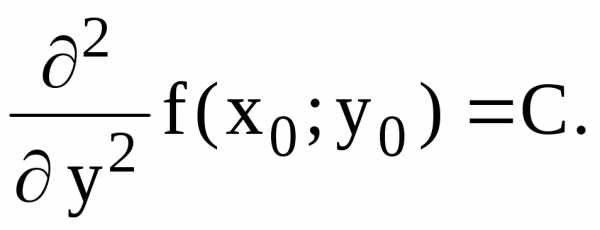
Тогда, если  = АС  B² > 0, то в точке (x₀; y₀) функция z = f(x; y) имеет экстремум, причем, если А < 0 (или С < 0) – максимум, если А > 0 (или С > 0) – минимум. В случае  = АС  В

2 < 0, функция z = f(x; y) экстремума не имеет. Если  = AC  B² = 0, то требуется дальнейшее исследование (сомнительный случай).

Пример 1. Найти экстремум функции z = x² + xy + y²  3x  6y.

Решение. Найдем частные производные первого порядка:

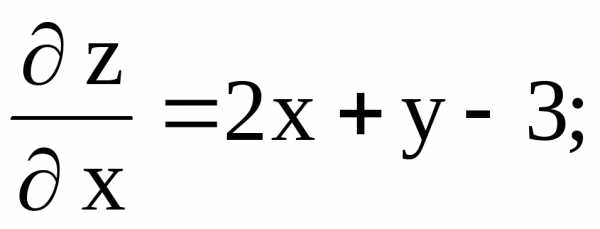
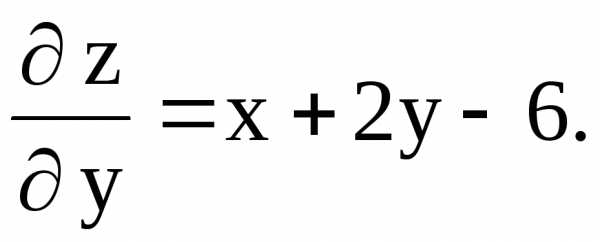
Воспользуемся необходимым условием существования экстремума:

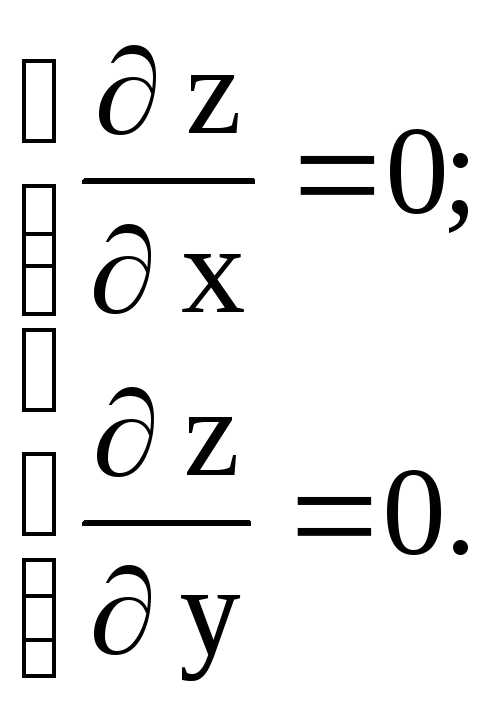
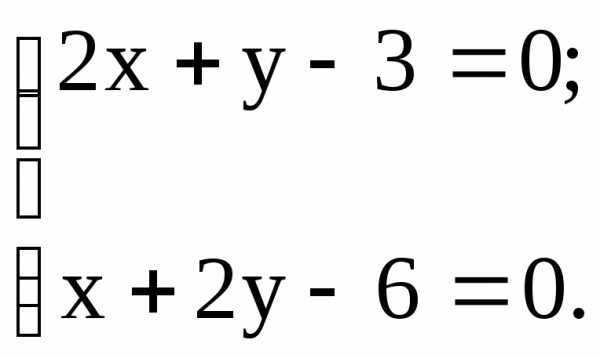
Решая систему уравнений, находим координаты x и y стационарных точек: x = 0; y = 3, т. е. М(0; 3).

Вычислим частные производные второго порядка и найдем их значения в точке М.

А = 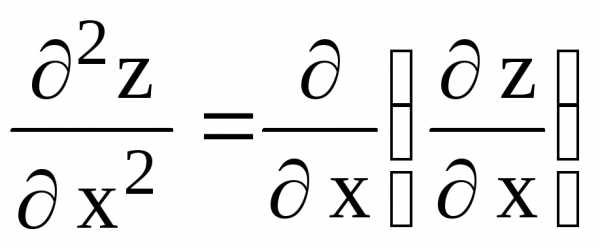= 2; С =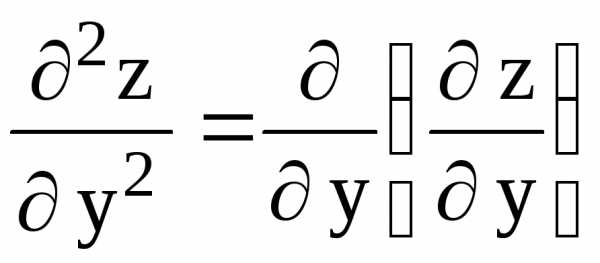= 2;

В = .

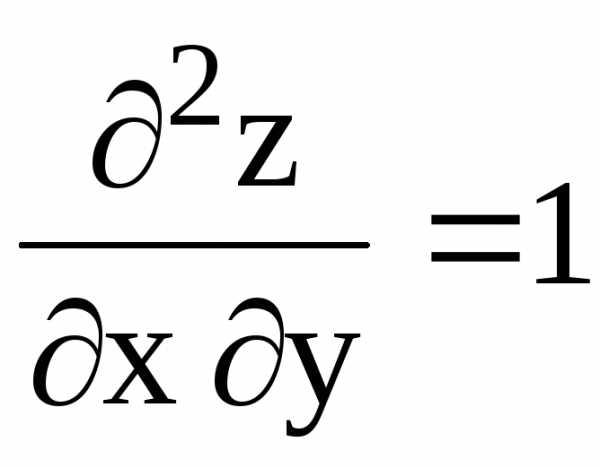Составим дискриминант  = АС  В² = 2  2  1 > 0, A = 2 > 0. Следовательно, в точке М(0; 3) заданная функция имеет минимум. Значение функции в этой точке z_min = 9.

Найти экстремумы функций

322. z = x² + y² + xy  4x  5y 323. z = y³  x³  3xy

324. z = x²  2xy + 4y³

325. z =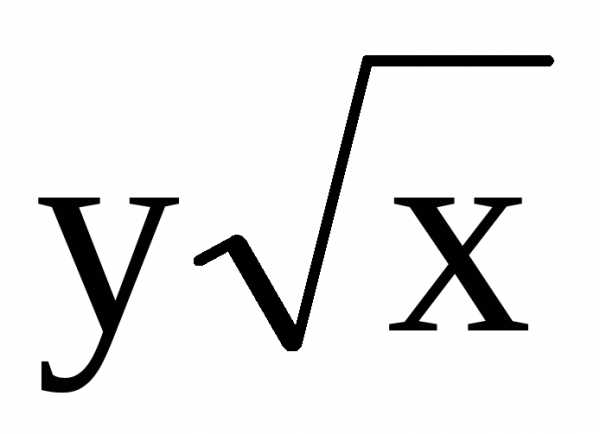  y²  x + 6y

326. z = x y (1  x  y) 327. z = 2xy  4x  2y

328. z = e^x/2(x + y²) 329. z = x³ + 8y³  6xy + 1

330. z = 3x²y  x³  y⁴ 331. z = 3x + 6y  x²  xy + y²

Наибольшее и наименьшее значения функции двух переменных в замкнутой области

Для того, чтобы найти наибольшее и наименьшее значения функции в замкнутой области, надо:

1) найти критические точки, расположенные в данной области, и вычислить значения функции в этих точках;

2) найти критические точки на границе области и вычислить наибольшее и наименьшее значения функций в них;

3) из всех найденных значений выбрать наибольшее и наименьшее.

Пример 2. Найти наибольшее и наименьшее значения функции z = 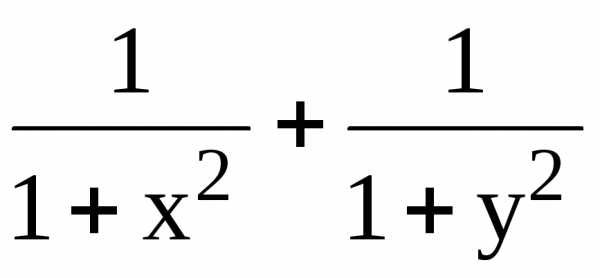в круге x² + y²  1.

Решение. Найдем координаты критических точек, расположенных внутри рассматриваемой области, для чего вычислим частные производные первого порядка функции z и приравняем их к нулю.

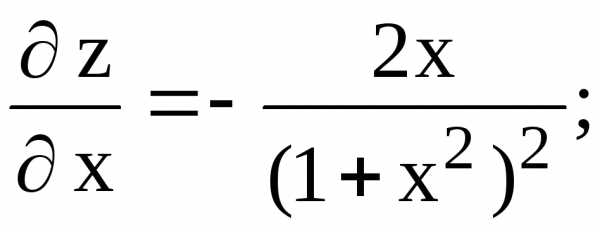
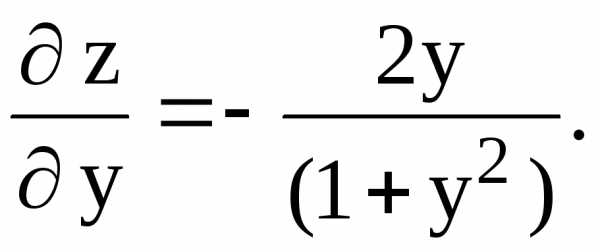
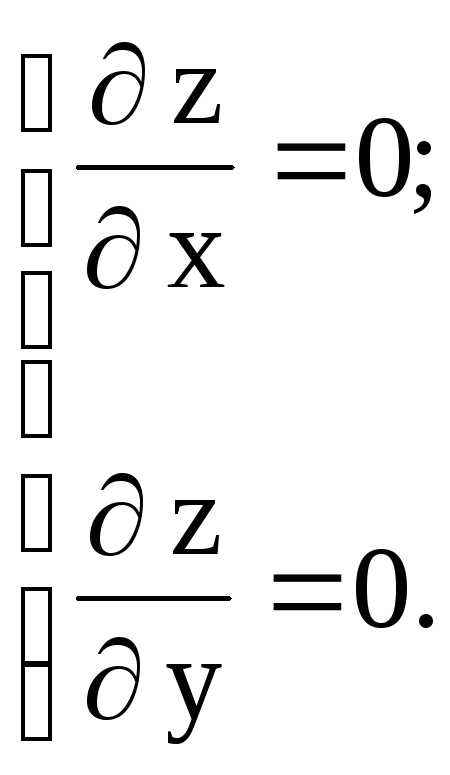
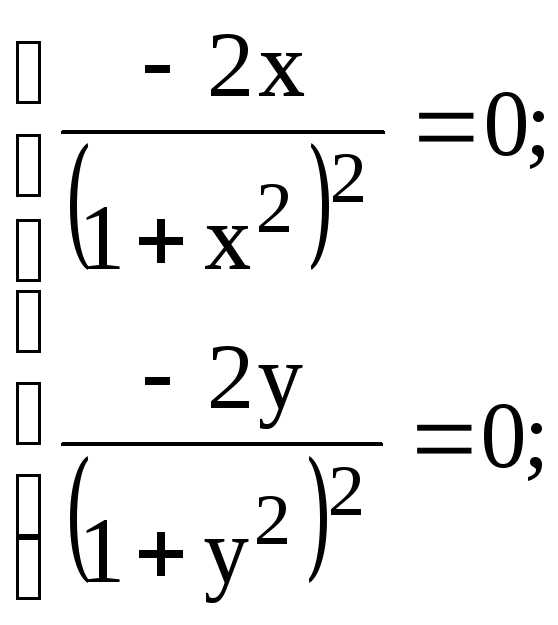
откуда x = 0, y = 0 и, следовательно, М(0; 0) – критическая точка.

Вычислим значение функции z в точке М(0; 0): z(0; 0) = 2.

Найдем критические точки на границе области  окружности, заданной уравнением x² + y² = 1. Подставляя у² = 1  x² в функцию z = z(x; y), получим функцию одной переменной

z = ;

причем x[1; 1].

Вычислив производную 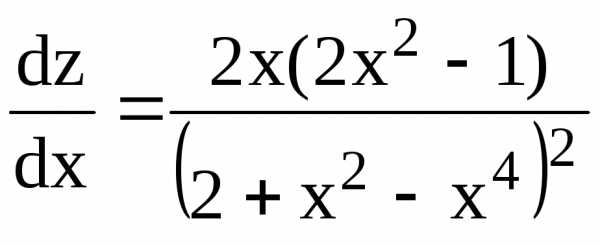и приравняв ее нулю, получим критические точки на границе области x₁ = 0, x₂ =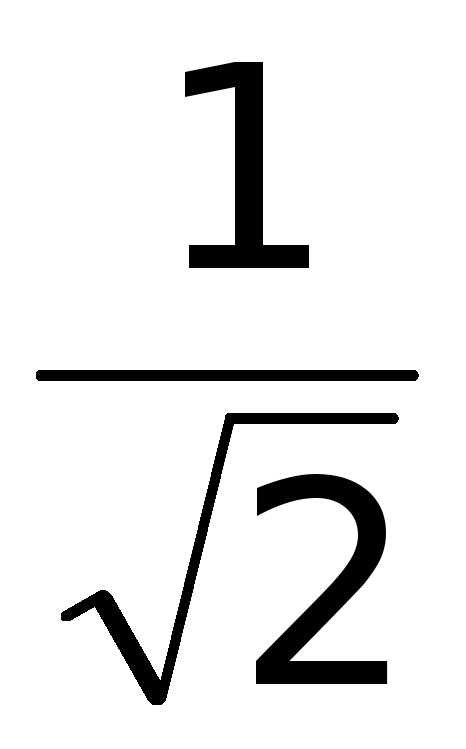, x₃ =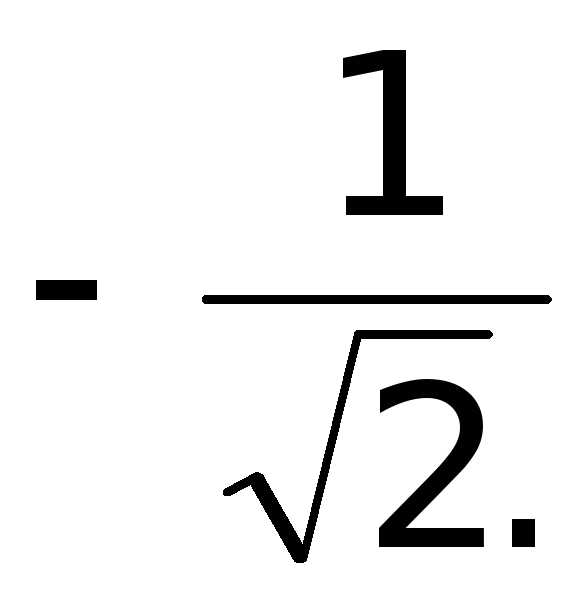

Найдем значение функции z(x) = 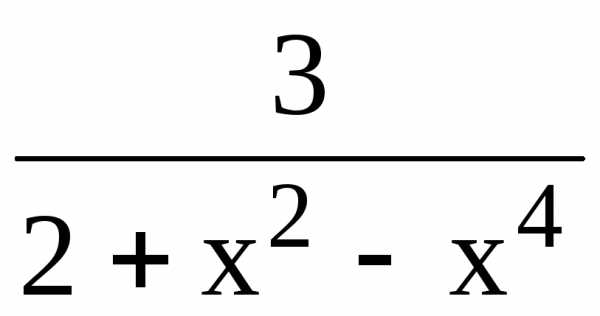в критических точках и на концах отрезка [1; 1]: z(0) =

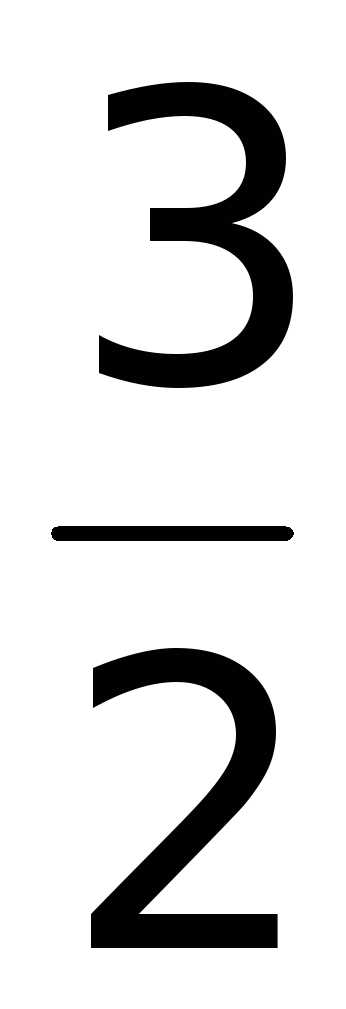
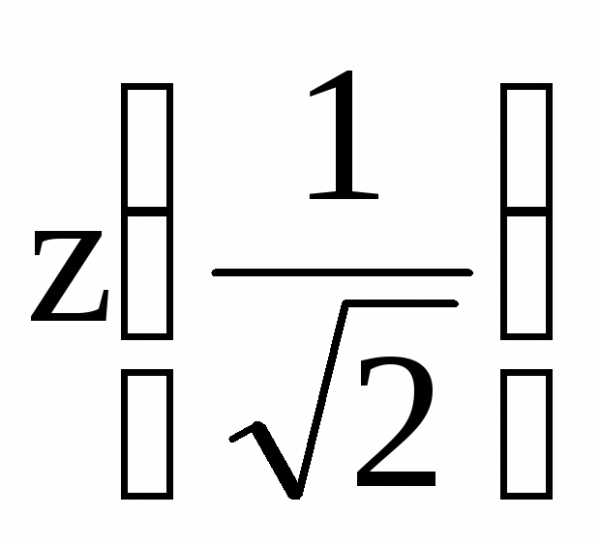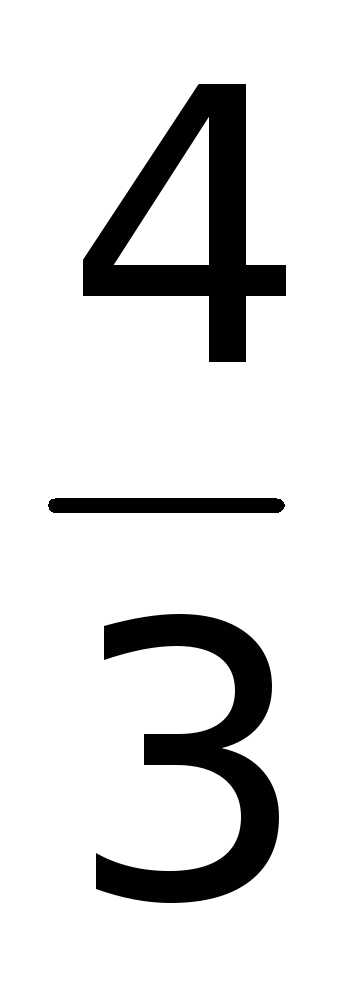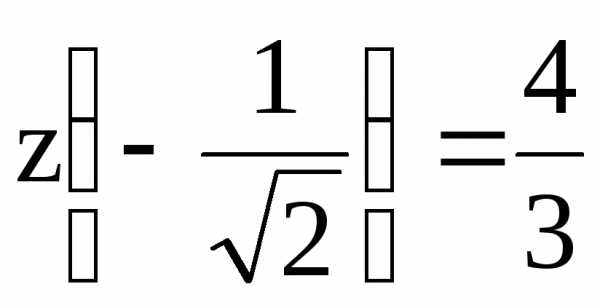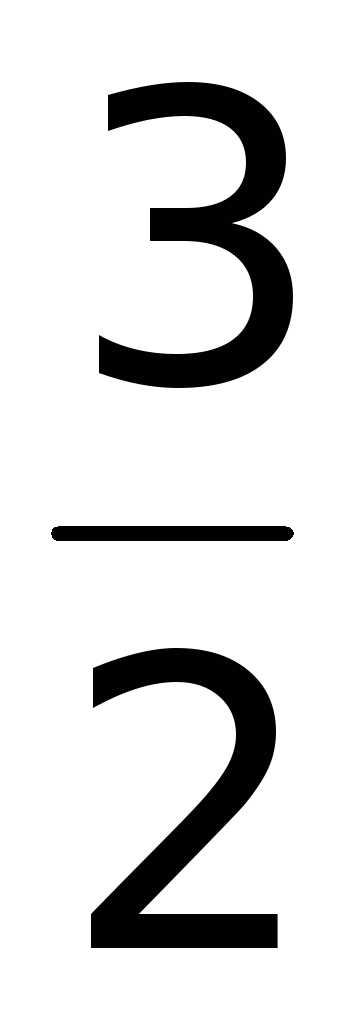;=;; z(1) = ; z(1) =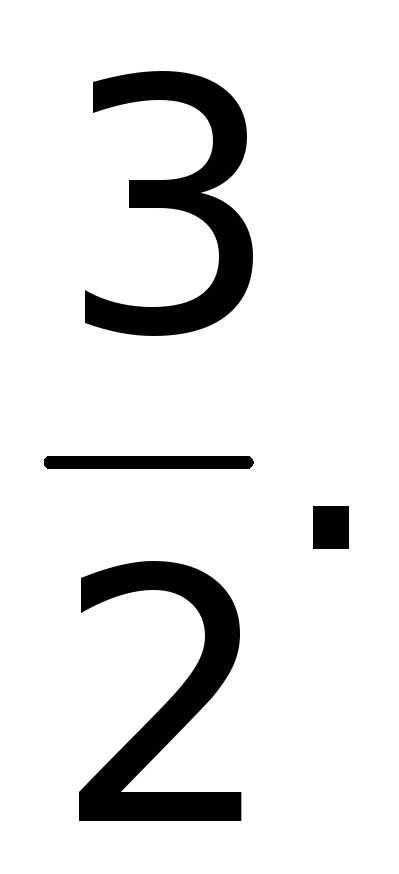

Выберем наибольшее и наименьшее среди значений функции z в критических точках, расположенных внутри и на границе круга.

Итак, z_наиб. = z(0; 0) = 2

и

z_наим. = z

studfiles.net

Функция \(z=f(x,y)\) имеет максимум (минимум) в точке \(M_0(x_0;y_0)\) , если значение функции в этой точке больше (меньше), чем ее значение в лююой другой точке \(M(x;y)\) некоторой окресности точки \(M_0\) т.е. \(f(x_0;y_0)>f(x,y)\) для всех точек \(M(x;y)\) , удовлетворящих условию \(\left|M_0M \right|

Максимум или минимум функции называется ее экстремумом. Точка \(M_0\), в которой функция имеет экстремум, называется точкой экстремума.

Если дифференцируемая функция \(z=f(x,y)\) достигает экстремума в точке \(M_0(x_0;y_0)\) то ее частные производные первого порядка в этой точке равны нулю, т.е.

$$\frac{\partial f(x_0,y_0)}{\partial x}=0;\frac{\partial f(x_0,y_0)}{\partial y}=0$$

необходимые условия экстремума.

Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.

Пример 1. Найти экстремум функции \(z=x^2+xy+y^2-3x-6y.\)

Находим частные производные первого порядка :

$$\frac{\partial z}{\partial x}=2x+y-3,\frac{\partial z}{\partial y}=x+2y-6.$$

Воспользовавшись необходимыми условиями экстремума, находим стационарные точки :

$$\begin{cases} & \text{ } 2x+y-3= 0 \\ & \text{ } x+2y-6=0 \end{cases}$$

Откуда \(x=0,y=3; M(0;3).\)

Находим значения частных производных второго порядка в точке \(M\) :

$$\frac{\partial ^2z}{\partial x^2}=2,\frac{\partial ^2z}{\partial y^2}=2,\frac{\partial ^2z}{\partial x\partial y}=1$$

и составляем дискриминант

$$\triangle=AC-B^2=2\cdot 2-1=3>0;A>0.$$

Следовательно, в точке \(M(0;3)\) заданная функция имеет минимум. Значение в этой точки \(z_{min}=-9.\)

Пример 2. Найти экстремум функции

$$z=\frac{1}{2}xy+(47-x-y)\left(\frac{x}{3}+\frac{y}{4} \right).$$

Находим частные производные первого порядка :

$$\frac{\partial z}{\partial x}=-\frac{1}{12}y-\frac{2}{3}x+\frac{47}{3},\frac{\partial z}{\partial y}=-\frac{1}{2}y-\frac{1}{12}x+\frac{47}{4}.$$

Воспользовавшись необходимыми условиями экстремума, находим стационарыне точки:

$$\begin{cases} & \text{ }-\frac{1}{12}y-\frac{2}{3}x+\frac{47}{3}=0 \\ & \text{ }-\frac{1}{2}y-\frac{1}{12}x+\frac{47}{4}= 0 \end{cases}$$

или

$$\begin{cases} & \text{ }8x+y=188 \\ & \text{ }x+6y= 141. \end{cases}$$

Отсюда \(x=21,y=20;\) стационарная точка \(M(21;20)\).

Найдем значения вторых производных в точке \(M :\)

$$\frac{\partial ^2z}{\partial x^2}=-\frac{2}{3},\frac{\partial ^2z}{\partial y^2}=-\frac{1}{2},\frac{\partial ^2z}{\partial x\partial y}=-\frac{1}{12}.$$

Тогда

$$\triangle=AC-B^2=(-2/3)(-1/2)-(-1/12)^2=1/3-1/144>0.$$

Так как \(A

Условный экстремум. Наибольшее и наименьшее значения функции в замкнутой области

Условный экстремум функции \(z=f(x,y)\) называется экстремум этой функции, достигнутый при условии, что переменные \(x\) и \(y\) связаны уравнением \(\varphi (x,y)=0\) (уравнение связи).

Отыскание условного экстремума можно свести к исследованию на обычный экстремум так называемой функции Лагранжа \(u=f(x,y)+\lambda \varphi (x,y)\) , где \(\lambda\) — неопределенный постоянный множитель.

Необходимые условия экстремума функции Лагранжа имеют вид

$$\frac{\partial u}{\partial x}\equiv \frac{\partial f}{\partial x}+\lambda\frac{\partial \varphi }{\partial x}=0,$$

$$\frac{\partial u}{\partial y}\equiv \frac{\partial f}{\partial y}+\lambda\frac{\partial \varphi }{\partial y}=0,$$

$$\varphi (x,y)=0.$$

Из этих трьех уравнений можно найти неизвестные \(x,y,\lambda\).

Для того что бы найти наибольшее и наименьшее значения функции в замкнутой области, надо :

1) найти стационарные точки, расположенные в данной области, и вычислить значения функции в этих точках;

2) найти наибольшее и наименьшее значения функции на линиях, образующих границу области;

3) из всех найденных значений выбрать наибольшее и наименьшее.

Пример 1. Найти экстремум функции \(z=xy\) при условии, что \(x\) и \(y\) связаны уравнением \(2x+3y-5=0.\)

Рассмотрим функцию Лагранжа \(u=xy+\lambda(2x+3y-5)=0.\) Имеем

$$\frac{\partial u}{\partial x}=y+2\lambda, \frac{\partial u}{\partial y}=x+3\lambda.$$

Из системы уравнений (необходимые условия экстремума)

$$\begin{cases} & \text{ } y+2\lambda =0, \\ & \text{ } x+3\lambda =0, \\ & \text{ } 2x+3y-5= 0 \end{cases}$$

находим \(\lambda=-5/12, x=5/4, y=5/6.\) Нетрудно видеть, что в точке \((5/4;5/6)\) функция \(z=xy\) достигает наибольшего значения \(z_{max}=25/24.\)

---

2012-12-15 • Просмотров [ 17197 ]

primat.org

Экстремумы функций двух переменных

Задачи для самостоятельного решения

	№		Задание		Варианты ответов
	п/п
		Вычислить полный дифференциал функции			1.	-0.1
	1.	z = arctg( y/ x) в точке x= 2,		y = 2 при	2.	0.1
		x = 0.1,	y = 0.1		3.	0
					4.	0.2
					1.	1.01
	2.	Найти приближенное значение		1.01 0.99	2.	0.99
					3.	1
					4.	1.02

Если для функции z = f(x, y) в некоторой окрестности точки М0(х0, у0), принадлежащей области определения, верно неравенствоf (x0 , y0 ) > f (x, y) ,

то точка М0 называется точкой локального максимума.

Если для функции z = f(x, y) в некоторой окрестности точки М0(х0, у0), принадлежащей области определения, верно неравенство

f (x0 , y0 ) < f (x, y) то точка М0 называется точкой локального минимума.

Функция многих переменных может иметь максимум или минимум (экстремум) только в точках, лежащих внутри области определения функции, в которой все ее частные производные первого порядка равны нулю или не существует хотя бы одна из них. Такие точки называются критическими.

Названные условия являются необходимыми условиями экстремума, но не достаточными (т.е. эти условия могут выполняться и в точках, где нет экстремума). Чтобы проверить является ли критическая точка точкой экстремума, используютдостаточные условия экстремума.

Сформулируем достаточные условия экcтремума для функции двух переменных. Пусть точка Mo(xo, yo) — критическая точка функции z = f(x, y), в которойfx′(x0 ,y0 ) = 0, fy′(x0 ,y0 ) = 0 , и кроме того функция z = f(x, y)

имеет непрерывные вторые частные производные в некоторой окрестности

точки	Mo(xo,	yo).	Обозначим	z′′x x (x0 , y0 )= A, z′′x y (x0 , y0 )= B,
z′′y y (x0 , y0 )= C,		= AC- B2 . Тогда:

1)если > 0, то функцияz имеет экстремум в точке Mo: максимум при A

<0, минимум при A > 0;

2)если < 0, то экстремума в точке Mo нет;

3)если = 0, то требуется дополнительное исследование.

Пример. Исследовать функцию z = y4 — 2xy2 + x2 + 2y + y2 на экстремум.Решение. Находим частные производные:z′x = — 2y2 + 2x,z′y = 4y3 — 4xy

+2 +2y. Для отыскания критических точек решим систему уравнений:

studfiles.net

Экстремумы функции двух переменных | Высшая математика | Студенту | Статьи и обсуждение вопросов образования в Казахстане | Образовательный сайт Казахстана

Пусть функция z=f(x,y) определена в некоторой области D, точка N₀(x₀;y₀)D. Точка N₀(x₀;y₀) называется точкой максимума функции z=f(x,y), если существует δ — окрестность точки N₀(x₀;y₀), что для каждой точки (x,y), отличной от N₀(x₀;y₀), из этой окрестности выполняется неравенство f(x,y)₀;y₀). Аналогично определяется точка минимума функции, т.е. если выполняется неравенство f(x,y)>f(x₀;y₀), то N₀(x₀;y₀) — точка минимума.

Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумом.

Теорема 1 (необходимые условия экстремума). Если в точке N₀(x₀;y₀) дифференцируемая функция z=f(x,y) имеет экстремум, то ее частные производные в этой точке равны нулю: f’_x(x₀;y₀)=0, f’_y=(x₀;y₀)=0.

Точка в которой частные производные первого порядка функции z=f(x,y) равны нулю, т.е. f’_x=0, f’_y=0, называется стационарной точкой функции z (или точкой возможного экстремума). Стационарные точки и точки, в которых хотя бы одна частная производная не существует называется критическими точками. В критических точках функция может иметь экстремума, а может не иметь. Равенство нулю частных производных является необходимым, но недостаточным условием существования экстремума. Для нахождения экстремумов функции в данной области необходимо критическую точку функции подвергнуть дополнительному исследованию.

Теорема 2 (достаточные условия экстремума). Пусть в стационарной точке N₀(x₀;y₀) и некоторой ее окрестности функция f(x,y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке N₀(x₀;y₀) значения A=f’_x‘_x(x₀;y₀), B=f’_x‘_y(x₀;y₀), C=f’_y‘_y(x₀;y₀)Обозначим . Тогда:

1. Если Δ>0, то функция f(x,y) в точке N₀(x₀;y₀) имеет экстремум: максимум, если A<0: минимум, если A>0.
2. Если Δ<0, то функция f(x,y) в точке N₀(x₀;y₀) экстремума не имеет.
3. В случае Δ=0 экстремум в точке N₀(x₀;y₀) может быть, может не быть. Необходимо дополнительные исследования.

Пример 1. Найти экстремум функции z=3x²y-x³-y⁴

Имеем z’_x=6xy-3x², z’_y=3x²-4y³. Точки, в которых частные производные не существуют, отсутствуют. Найдем стационарные точки, решая систему уравнений:

отсюда получаем точки M₁(6;3) и M₂(0;0).
Находим частные производные второго порядка данной функции:
z’_x‘_x=6y-6x, z’_x‘_y=6x, z’_y‘_y=-12y²

В точке M₁(6;3) имеем: A=-18, B=36, C=-108 отсюда
AC-B²=-18•(-108)•-36²=648, т.е. Δ>0

Так как A<0, то в точке M₁(6;3) функция имеет локальный максимум: z_max=z(6;3)-3•36•3-6³-3⁴=27.

В точке M₂(0;0): A=0, B=0, C=0 и значит, Δ=0. Проведем дополнительное исследование. Значение функции z в точке M₂ равно нулю: z(0;0)=0. Можно заметить, что z=-y⁴<0 при x=0, y≠0: z=-x³>0 при x≠0, y=0. Значит, в окрестности точки M₂(0;0) функция z принимает как отрицательные, так и положительные значения. Следовательно, в точке M₂ функция экстремума не имеет.

(x>

Порядок вывода комментариев: По умолчаниюСначала новыеСначала старые

testent.ru