экстремум функции двух переменных — 22 Июля 2014 — Примеры решений задач
Ключевые слова: калькулятор экстремумов, найти экстремум функции двух переменных, частные производные первого и второго порядков, стационарные точки, калькулятор частных производных.
Пример 1. Исследовать на экстремум функцию:
Алгоритм решения следующий:
1) находим частные производные первого порядка:
Примечание: найти частные производные онлайн (первого и второго порядка) можно с помощью калькулятора.
2). Решаем систему уравнений:
и таким образом находим стационарные точки функции.
Точки, в которых значение производной функции равно нулю, называются стационарными точками.
Для данного примера получаем систему уравнений:
стационарная точка: (-1;1)
3) Находим вторые частные производные
Вычисляем значения этих частных производных второго порядка в каждой из найденных в п.2 стационарных точках M(x
Для данного примера, получаем
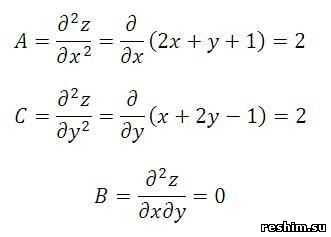
4) Делаем вывод о наличии экстремумов:
а) если AC – B2 > 0 и A < 0 , то в точке M имеется максимум;
б) если AC – B2 > 0 и A > 0 , то в точке M имеется минимум;
в) если AC – B2 < 0, то экстремума нет;
г) если AC – B2 = 0, то вопрос о наличии экстремума остается открытым;
Тогда в точке x=-1, y=1
Следовательно в точке x=-1, y=1 функция имеет локальный минимум
Ответ: min{z}=0
Проверить правильность решения можно с помощью калькулятора «экстремум функции».
www.reshim.su
Экстремумы функции двух переменных
Определение. Точками экстремума функции двух переменных называются точки минимума и максимума этой функции. Значения самой функции в точках экстремума называются экстремумами функции двух переменных.
Определение. Точка P(x0, y0) называется точкой максимума функции двух переменных z = z(x, y), если значение функции в этой точке больше, чем в точках её окрестности. Значение функции в точке максимума называется максимумом функции двух переменных.
Определение. Точка P(x0, y0) называется точкой максимума функции двух переменных z = z(x, y
Теорема (необходимый признак экстремума функции двух переменных). Если точка P(x0, y0) — точка экстремума функции двух переменных z = z(x, y), то первые частные производные функции (по «иксу» и по «игреку») в этой точке равны нулю или не существуют:
и
.
Определение. Точки, в которой первые частные производные функции двух переменных равны нулю, называются стационарными точками.
Определение. Точки, в которой первые частные производные функции двух переменных равны нулю или не существуют, называются критическими точками.
Как и в случае с функцией одной переменной, необходимое условие существования экстремума функции двух переменных не является достаточным. Встречаются немало функций, в случаях которых первая частная производная функции равна нулю или не существует, но экстремумов в соответствующих точках нет. Каждая точка экстремума является критической точкой, но не каждая критическая точка является экстремумом.
Достаточный признак существования экстремума функции двух переменных. В точке P существует экстремум функции двух переменных, если в окрестности этой точки полное приращение функции не меняет знак. Так как в критической точке первый полный дифференциал равен нулю, то приращение функции определяет второй полный дифференциал
.
Локальный характер экстремумов функции двух переменных. Максимум функции двух переменных на каком-либо участке области определения функции не обязательно является максимумом во всей области определения, так же как и минимум на каком-либо участке не является минимумом во всей области определения. Пусть мы рассматриваем высоту волн на участке прибрежной области моря (участок меньше области). Тогда на этом участке мы можем зафиксировать (по-крайней мере, зрительно) наибольшую высоту волны. Но на другом участке, на котором ветер вызывает бОльшую высоту волн, мы фиксируем минимальную высоту волны. Это к тому, что максимум высоты волны на первом участке может оказаться меньше, чем минимум высоты волны на втором участке. Поэтому, как и в случае экстремума функции одной переменной, необходимо уточнить это понятие и говорить об экстремумах как о локальных экстремумах функции двух переменных.
Наибольший интерес представляет алгоритм нахождения экстремумов функции двух переменных, так как он, во-первых, отличается от алгоритма нахождения экстремумов функции одной переменных, а во-вторых, по аналогии с ним можно составить алгоритм нахождения функции трёх переменных. В частности, потребуется вычислять определители.
Итак, алгоритм нахождения экстремумов функции двух переменных.
Дана функция двух переменных .
Шаг 2. Составляем систему уравнений из равенств этих производных нулю (их равенство нулю и есть необходимый признак существования экстремума):
Решения этой системы уравнений являются точками возможного экстремума — критическими точками.
Шаг 3. Пусть является критической точкой, найденной на шаге 2. Чтобы убедиться, что в ней существует экстремум функции двух переменных, находим частные производные второго порядка
как частные производные от частных производных первого порядка, найденных на шаге 1.
Шаг 4. Присваиваем частным производным второго порядка, найденным на шаге 3, буквенные обозначения:
Находим определитель и проверяем достаточный признак существования экстремума.
Если , то экстремума в найденной критической точке нет,
если , то экстремум в найденной критической точке есть,
если , то требуются дополнительные исследования.
Если экстремум в найденной точке есть и если , то в этой точке существует минимум функции двух переменных, если , то максимум.
Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значение экстремума функции двух переменных (минимума или максимума).
Примеры начнём с более сложного, в котором составленная система уравнений имеет несколько решений, а, значит, найдено несколько критических точек.
Пример 1. Найти экстремумы функции двух переменных .
Решение. Следуем изложенному выше алгоритму.
Шаг 1. Находим частные производные:
.
Шаг 2. Составляем систему уравнений из равенств этих производных нулю:
Делим первое уравнение системы на 3, а второе на 6 и получаем
Умножаем это уравнение на и получаем
.
Производим замену переменной: и получаем
.
Решаем полученное квадратное уравнение: .
Так как и , то
Таким образом, получили четыре критических точки — точки возможного экстремума.
Шаг 3. Находим частные производные второго порядка
Шаг 4. Находим определитель :
, т. е. экстремума в найденной критической точке нет,
, т. е. экстремума в найденной критической точке нет,
и , т. е. в найденной критической точке есть минимум функции двух переменных,
и , т. е. в найденной критической точке есть максимум функции двух переменных.Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значения экстремума функции двух переменных:
,
Найти экстремумы функции двух переменных самостоятельно, а затем посмотреть решение
Третий пример — на десерт, так как в нём только одна критическая точка.
Пример 3. Найти экстремумы функции двух переменных .
Шаг 1. Находим частные производные:
.
Шаг 2. Составляем систему уравнений из равенств этих производных нулю:
Решаем систему уравнений:
Таким образом, получили критическую точку — точку возможного экстремума.
Шаг 3. Находим частные производные второго порядка
Шаг 4. Находим определитель , т. е. в найденной критической точке есть экстремум, причём так как , то это минимум.
Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значение экстремума функции двух переменных:
.
Найти экстремумы ещё одной функции двух переменных самостоятельно, а затем посмотреть решение
Функции нескольких переменных
function-x.ru
Как найти условные экстремумы функции двух и более переменных
В задачах оптимизации возникает необходимость найти экстремумы функции двух и более переменных при условии, что существует связь между переменными этой связи, заданная уравнением . В этом случае говорят, что требуется найти условный экстремум.
Для того чтобы найти условный экстремум требуется находить частные производные и решать системы уравнений Существует алгоритм нахождения условного экстремума из трёх шагов, который сейчас и разберём на примере, и геометрический смысл условного экстремума, который должен дойти до каждого при разборе этого самого примера.
Итак, алгоритм, который разберём на примере самой распространённой задачи — нахождение условного экстремума функции двух переменных..
Шаг 1. Вводится функция Лагранжа
,
где первое слагаемое — сама исходная функция, а второе слагаемое со знаком минус — левая часть уравнения условия связи, умноженная на (лямбда) — множитель Лагранжа.
Пример 1. Найти условные экстремумы функции двух переменных , выражающей площадь прямоугольника через его стороны x и y при условии , означающем, что существует верёвка, которой можно ограничить этот прямоугольник, и длина этой верёвки равна 100.
Шаг 1. Решение. Приведём уравнение условия связи к требуемому виду с нулём в правой части:
.
Составим функцию Лагранжа:
.
Шаг 2. Составляем систему уравнений из равенств частных производных нулю и уравения условия связи (необходимый признак существования условного экстремума):
Решения этой системы уравнений являются точками возможного условного экстремума — стационарными точками или, как ещё говорят, критическими точками.
Пример 1. Шаг 2.
Решение. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:
Из первого и второго уравнений выразим соответственно x и y:
Подставим эти выражения в третье уравнение и найдём значение множителя Лагранжа:
Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции:
Получили и . Эти значения являются также координатами стационарной точки. Таким образом, получили стационарную точку .
Шаг 3. Пусть является стационарной точкой, найденной на шаге 2. Чтобы определить, является ли условный экстремум минимумом или максимумом, нужно найти второй дифференциал функции Лагранжа
и в полученном выражении подставить вместо «лямбды» её значения (значения множителя Лагранжа), найденные на шаге 2.
Если значение второго дифференциала функции Лагранжа меньше нуля (), то стационарная точка является точкой максимума, если больше нуля (), то стационарная точка является точкой минимума. Если значение второго дифференциала функции Лагранжа равно нулю, то требуются дополнительные исследования, но такие случаи практически не попадаются в задачах, задаваемых студентам.
Координаты стационарных точек подставляются в исходную точку и, таким образом, мы окончательно находим условные экстремумы (или минимум и максимум или что-то одно из этих экстремумом).
Пример 1. Шаг 3.
Решение. Найдём второй дифференциал функции Лагранжа:
В нашем случае, так как первое и третье составляющие равны нулю, нам не придётся подставлять в них значения множителя Лагранжа. Зато нужно найти отношения между дифференциалами dx и dy:
Так как полученные значения — противоположные по знаку, то получаем, что в любом случае .
Теперь можем найти значение условного экстремума исходной функции, являющееся максимумом:
.
Это заданная исходной функцией максимальная площадь прямоугольника, который можно ограничить верёвкой, длина которой равна 100.
Пример 2. Найти условные экстремумы функции двух переменных при условии .
Решение.
Шаг 1. Составим функцию Лагранжа:
.
Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:
Из первого и второго уравнений выразим соответственно x и y:
Подставим эти выражения в третье уравнение и найдём значения множителя Лагранжа:
Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции при двух значениях множителя Лагранжа:
Эти значения икса и игрека являются координатами двух стационарных точек. Таким образом, получили стационарные точки .
Шаг 3. Найдём частные производные второго порядка функции Лагранжа:
:
Найдём второй дифференциал функции Лагранжа по формуле
:
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :
Получили значение, меньшее нуля, следовательно, точка — точка условного максимума:
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :
Получили значение, большее нуля, следовательно, точка — точка условного минимума:
.
Таким образом, условные экстремумы заданной функции найдены.
Пример 3. Найти условные экстремумы функции двух переменных при условии .
Решение.
Шаг 1. Составим функцию Лагранжа:
.
Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:
Из первого и второго уравнений выразим соответственно x и y:
Получаем, что , однако подстановка этих значений переменных в третье уравнение системы не даёт верного равенства. Поэтому считаем, что на самом деле второй сомножитель равенства равен нулю: . Отсюда получаем
Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что . Из третьего уравнения системы получаем:
Получили две стационарные точки:
Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что .
На основании вычислений двух первых стационарных точек получилаем ещё две стационарные точки:
Шаг 3. Найдём частные производные второго порядка функции Лагранжа:
:
Найдём второй дифференциал функции Лагранжа по формуле
:
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :
Получили значение, меньшее нуля, следовательно, точки — точки условного максимума:
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :
Получили значение, большее нуля, следовательно, точки — точки условного минимума:
.
Таким образом, условные экстремумы заданной функции найдены.
Аналогичным образом можно находить условные экстремумы функций трёх и более переменных.
Функции нескольких переменных
function-x.ru
Калькулятор для нахождения экстремума функции. Замечание. Данный калькулятор находит производную функции, решает уравнение f ‘ (x)=0, и выдает точки подозрительные на экстремум (необходимое условие экстремума). Данные точки будут экстремумами, если также будет выполнятся достаточное условие экстремума: Если f ‘(x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет. Пример. Найти экстремумы функции
Проверим достаточное условие экстремумов: Из рисунка видно, что экстремум функции находится в точке x=6, и называется локальным минимумом, а также получаем интервалы монотонности функции: (-∞ ;2) и (6;+∞) — функция возрастает, (-2;6) — функция убывает
Второе достаточное условие. Пусть функция f(x) имеет производную Если f ‘ (xо) = 0, f «(x0)>0 (f «(x0)<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же f «(x0)=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные, см. калькулятор высших производных. Решенные примеры: Полное исследование функции |
www.reshim.su
Нахождение точек локального экстремума функции онлайн
| Функция: | |
Локальный экстремум
Определение 1. Пусть существует число такое, что функция определена в -окрестности точки то есть на множестве и пусть для всех выполняется неравенство
Тогда говорят, что функция имеет в точке локальный минимум.
Аналогично, если существует число такое, что для всех выполняется неравенство
то говорят, что функция имеет в точке локальный максимум.
Определение 2. Если точка является точкой локального минимума или локального максимума функции то говорят, что — точка локального экстремума функции
Теорема Ферма
Теорема (Ферма). Если функция имеет локальный экстремум в точке и дифференцируема в этой точке, то
Этой теоремой пользуются для нахождения точек локального экстремума.
umath.ru
Экстремум функции 3 переменных. Контрольные онлайн
Экстремум функции трех переменных
Найти точки экстремума функции и определить их характер.Решение
Найдем стационарные точки заданной функции, то есть точки, в которых выполняется необходимое условие существования экстремума. Для функции трех переменных стационарные точки (координаты точек) находятся из системы
Для заданной функции , ,
и система примет вид
Решениями системы являются и
Получили две стационарные точки и .
Для проверки достаточных условий экстремума в стационарной точке необходимо определить знаки определителей ,
и в этой точке.
Найдем , , , , , .
Для точки ,
,
.
Так как , , , то в точке функция имеет максимум, при этом
.
Для точки ,
,
.
Так как , , , то в точке функция не имеет экстремума.
www.matem96.ru
Экстремум функции двух переменных
Экстремум функции двух переменных
Экстремум функции двух переменных
Говорят, что функция имеет максимум в точке , т.е. при , если для всех точек , достаточно близких к точке и отличных от неё.
Говорят, что функция
имеет минимум в точке ,
т.е. при ,
если
для всех точек ,
достаточно близких к точке
и отличных от неё.
Максимум и минимум функции называются экстремумами функции.
Теорема (необходимое условие экстремума функции двух переменных). Если
функция
достигает экстремума при ,
то каждая частная производная первого порядка от
или обращается в нуль при этих значениях аргументов, или не существует.
Теорема (достаточное условие экстремума функции двух переменных). Пусть
в некоторой области, содержащей точку
функция
имеет непрерывные частные производные до третьего порядка включительно. Пусть,
кроме того, точка
является критической точкой функции ,
т.е.
,
тогда при :
1)
имеет максимум, если дискриминант
и ,
где ;
2)
имеет минимум, если дискриминант
и ;
3)
не имеет ни минимума, ни максимума, если дискриминант ;
4) если
, то экстремум может быть, а может и не быть (требуется дополнительное исследование).
Примеры решения задач
Пример 1. Исследовать на экстремум функцию .
Решение.
На первом шаге, в соответствие с достаточным условием экстремума функции двух переменных, найдем точки, удовлетворяющие условию:
Частные производные первого порядка от функции
равны:
Приравняем их к нулю и решим систему уравнений:
Выпишем отдельно первое уравнение системы и найдем его корни:
Подставим найденные значения переменной
во второе уравнение системы:
и
Таким образом, получили две точки и , в которых будет продолжено исследование функции на экстремум.
На втором шаге найдем все вторые частные производные от функции :
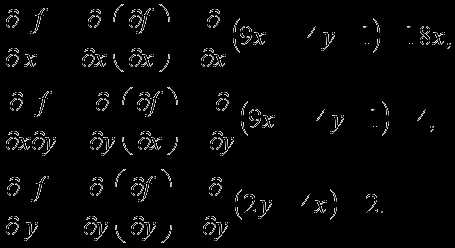
На третьем шаге для каждой из точек и установим наличие экстремума функции (для этого вычислим значения вторых производных и найдем знак дискриминанта в указанных точках).
1) Для точки :
Так как дискриминант больше нуля и ,
то функция
имеет минимум в точке :
.
2) Для точки :
Так как дискриминант меньше нуля, то функция не имеет в точке ни минимума, ни максимума.
Ответ: в точке функция имеет минимум.
pgsksaa07.narod.ru
