2. Уравнения касательной и нормали к кривой
Пусть
дано уравнение (1) F(x;y)=0,
и для функцииF(x;y)
в окрестности точки (х0;y0)
выполнены условия теоремы 1. Тогда в
окрестности точких0V(х0)
уравнение (1) задает функциюу=f(х),
определенную, непрерывную и дифференцируемую
в некоторой окрестности точких0иf(х0)=y0.
Графиком этой функции является некоторая
кривая. Так как существует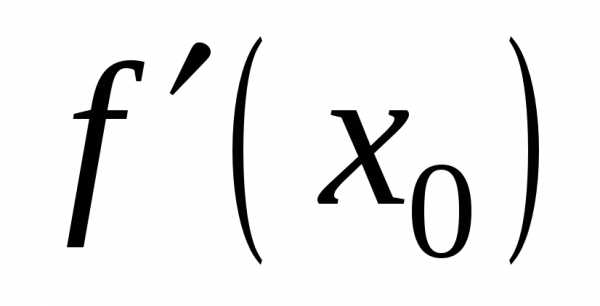 ,
то существует касательная и нормаль к
кривой (1).
,
то существует касательная и нормаль к
кривой (1).
Для функции y=f(x) уравнение касательной точкех0имеет вид:
, (10)
Из
теоремы 1 следует  . (12)
. (12)
Подставляя (12) в (10), (11), получим
– уравнение касательной;
или
– уравнение нормали.
3. Неявные функции нескольких переменных
Пусть дано уравнение . (13)
— функция (n+1)-й переменной. Если в каждой точкесуществует единственное значениеy, которое совместно сxудовлетворяет уравнению (13), то уравнение (13) на множествеGопределяет функциюnпеременных, (14)
и имеет место тождество наG.
Теорема
2 (достаточное
условие существования и дифференцируемости
неявной функцииnпеременных). Пусть функцияFи ее частные производные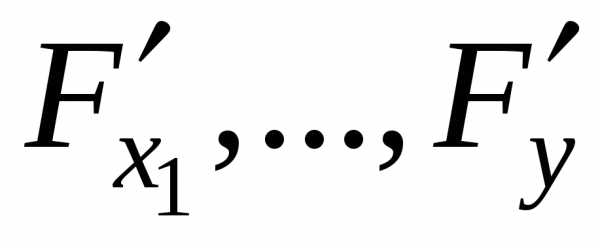 непрерывны в некоторой окрестности
точки,
и пусть,
а.
Тогда уравнение (13) определяет функциюопределенную, непрерывную и дифференцируемую
в некоторой окрестности точки
непрерывны в некоторой окрестности
точки,
и пусть,
а.
Тогда уравнение (13) определяет функциюопределенную, непрерывную и дифференцируемую
в некоторой окрестности точки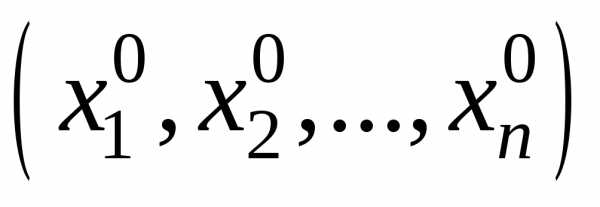
 находятся по формулам:
находятся по формулам: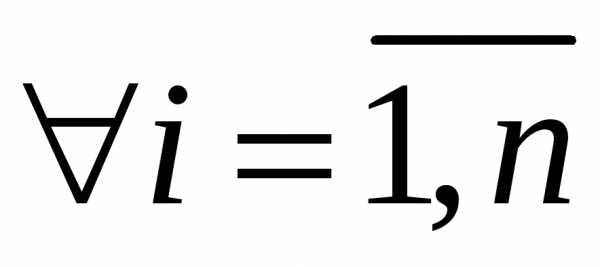 .
.
Рассмотрим
частный случай. Пусть на  дано уравнение
дано уравнение
F(x;y;z)=0. (15)
Пусть
это уравнение определяет неявную функцию z=f(x;y),
дифференцируемую на ,
т.е. справедливо тождество (16)F(x
,
т.е. справедливо тождество (16)F(x
 0.
Правая часть (16) – сложная функция отхиу.
В силу условий теоремы (2) (существуют
непрерывные
0.
Правая часть (16) – сложная функция отхиу.
В силу условий теоремы (2) (существуют
непрерывные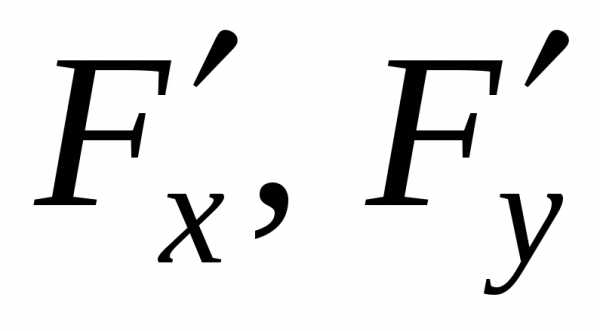 )
эта функция дифференцируема наD.
Дифференцируя (16) поx,
получим:
)
эта функция дифференцируема наD.
Дифференцируя (16) поx,
получим:.
Отсюда 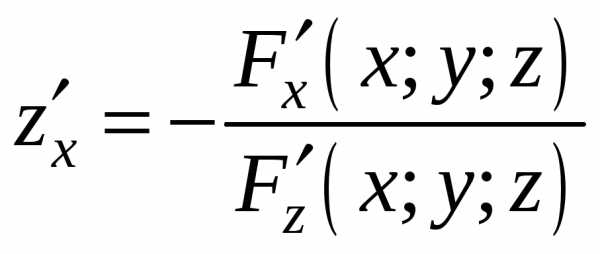 . (17)
. (17)
Дифференцируя (16) по y, получим:
.
Отсюда 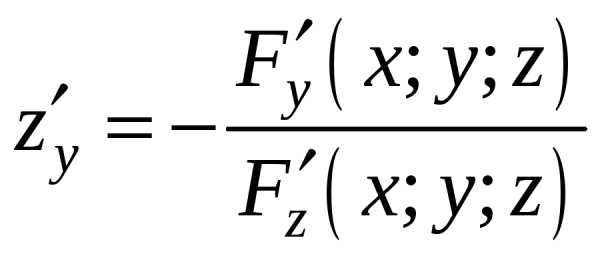 . (18)
. (18)
Пример
2.Пусть
уравнение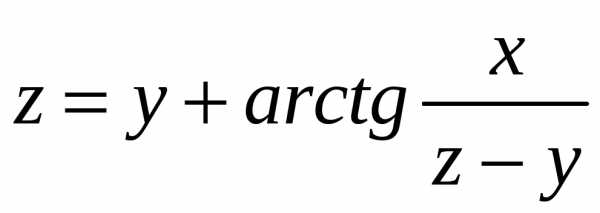 определяет функциюz=f(x;y).
Найти
определяет функциюz=f(x;y).
Найти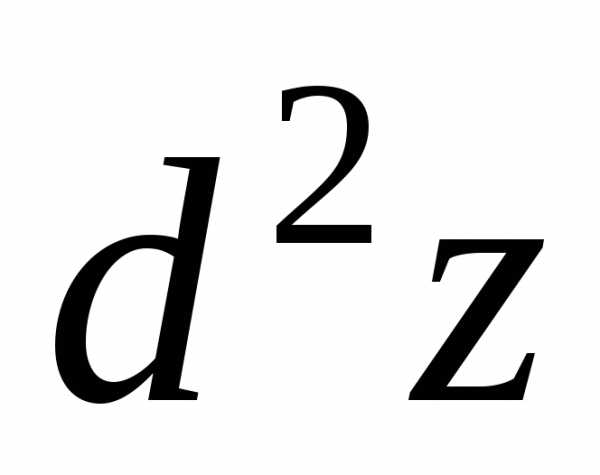
.
По формулам (17), (18):
,
,
.
Подставляя
сюда выражение для 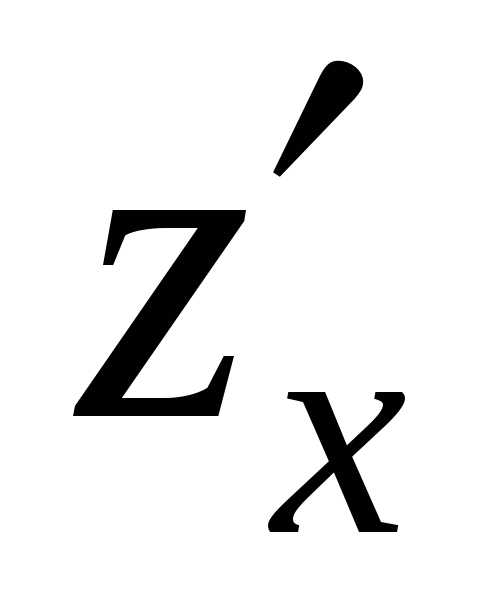 и
заменяяzнаf(x;y),
найдем
и
заменяяzнаf(x;y),
найдем .
.
Тогда .
4. Уравнения касательной плоскости и нормали к поверхности
Пусть уравнение (15) F(x;y;z)=0 определяет поверхность. Тогда (15) называется уравнением поверхности.
Пусть в окрестности (x0;y0;z0) выполняется условия теоремы 2. Тогда в окрестности точки (x0;y0) определена функцияz=f(x;
– уравнение касательной плоскости,
– уравнение нормали.
Так как , то
–
уравнение касательной плоскости,
– уравнение нормали.
Неявные функции могут определяться системой функциональных уравнений.
§ 9. Экстремум функции двух переменных
1. Понятие экстремума, необходимое и достаточное условия
Пусть функция z=f(x;y) задана в некоторой окрестности точкиM0(x0;y0)V(M0).
Определение
1.Функцияz=f(x;y)
имеет в точкеM0(x0;y0)строгий
максимум(строгий
минимум),
если
Определение
2.Функцияz=f(x;y)
имеет в точкеM0(x0;y0)максимум(минимум),
если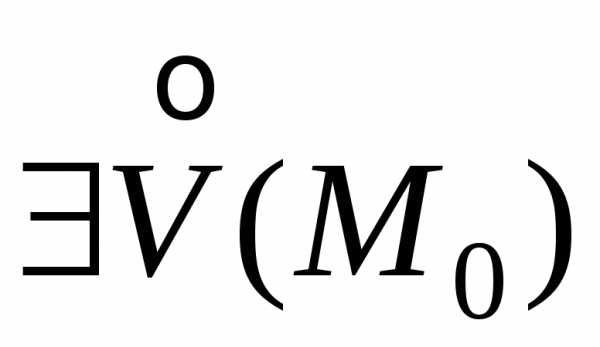 ,
такая, чтовыполнено неравенствоf(x;y)f(х0;y0)
(f(x;y)f(х0;y0)).
,
такая, чтовыполнено неравенствоf(x;y)f(х0;y0)
(f(x;y)f(х0;y0)).
Определение 3.Функцияz=f(x;y) имеет в точкеM0(x0;y0) (строгий)экстремум, если она имеет в этой точке (строгий) максимум или (строгий) минимум.
Точку М0называют точкой (строгого) экстремума, а значение функции в ней, т.е.f(M0) – (строгим) экстремумом.
Теорема
1(необходимое условие экстремума). Пусть
функцияz=f(x;y)
достигает экстремума в точке M0(x0;y0).
Если в этой точке существуют частные
производные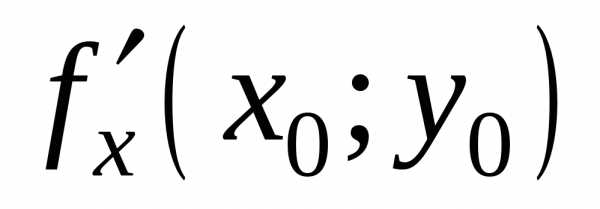 и
и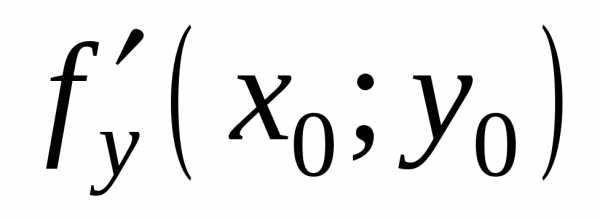 ,
то они в этой точке равны нулю, то есть
,
то они в этой точке равны нулю, то есть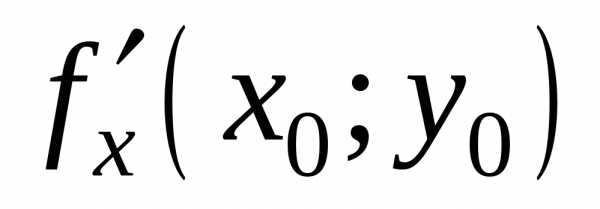 =0
и
=0
и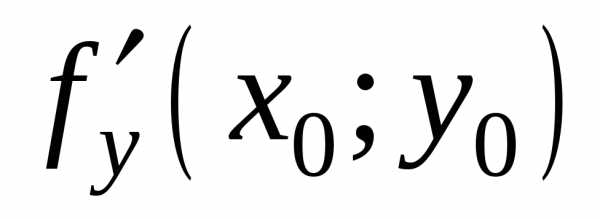 =0.
=0.
Доказательство.

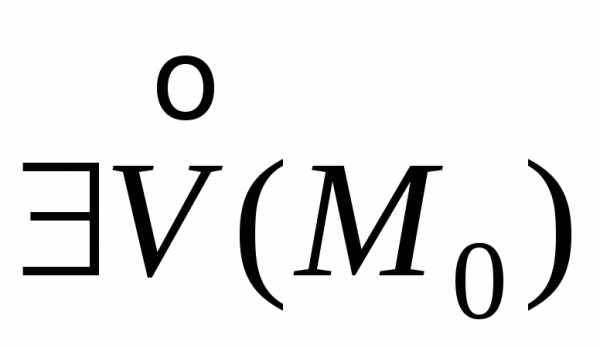 ,
такая, чтовыполнено
,
такая, чтовыполненоf(x;y)f(х0;y0). (1)
Рассмотрим
точки окрестности V(M0),
для которыхy=y0.
На этом множестве точек, т.е. на,
функцияf(x;y)
превращается в функциюf(x;y0)
одной
переменнойх.
Из (1) следует, чтоf(x;y0)f(х0;y0).
Это означает, что функция одной
переменнойf(x;y0)
имеет в точкех0максимум. По условию.
Она совпадает с
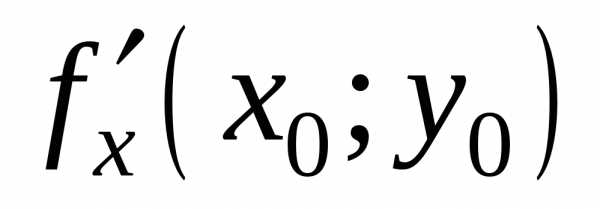 =
=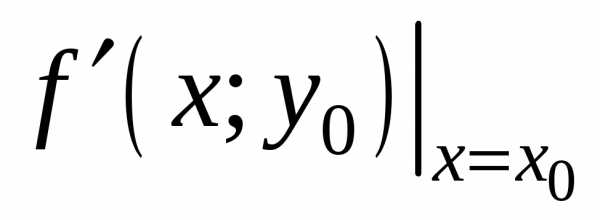 .
На основании необходимого условия
экстремума функции одной переменной
.
На основании необходимого условия
экстремума функции одной переменной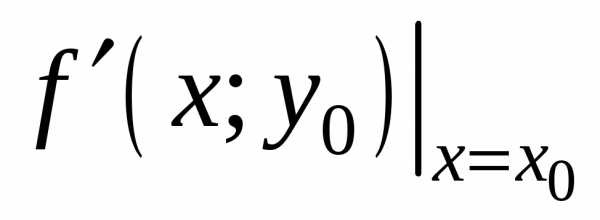 =0.
Следовательно,
=0.
Следовательно,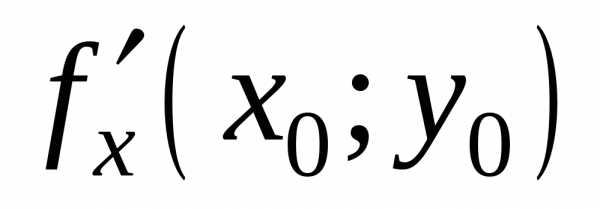 =0.
=0. Аналогично,
рассмотрим точки окрестности V(M0),
для которыхх=х0.
На этом множестве точек, функцияf(x;y)
становится функциейf(x0;y)
одной
переменнойу.
Из (1) следует, чтоf(x0;y)f(х0;y0).
Значит, функция одной
переменнойf(x0; y)
имеет в точкеу0максимум. По необходимому условию
экстремума функции одной переменной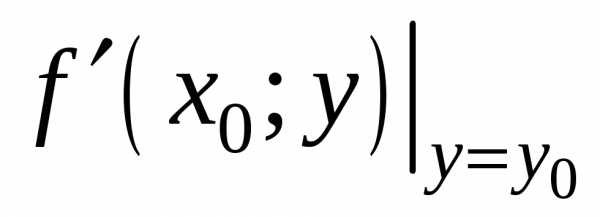 =0.
Следовательно,
=0.
Следовательно,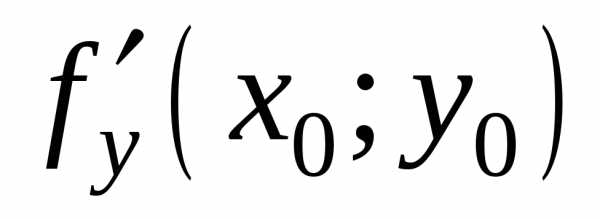 =0.
=0.
Замечание.Если функцияz=f(x;y)
дифференцируема в точке (х0;y0),
то условие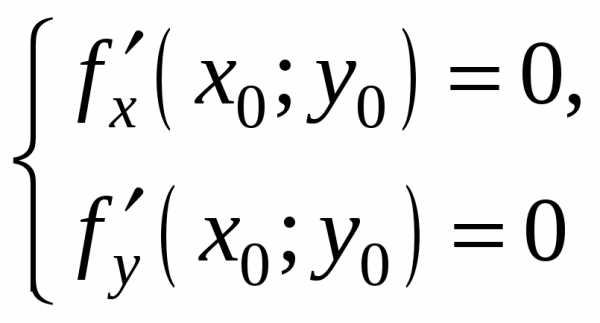 равносильно условиюdf(х0;y0)=0.
равносильно условиюdf(х0;y0)=0.
Следствие.Если функцияz=f(x;y) имеет экстремум в точке (х0;y0) и дифференцируема этой точке, тоdf(х0;y0)=0.
Определение 3.Точки, в которых частные производные равны нулю, называютсястационарными точкамифункцииz=f(x;y).
Определение 4.Точки, в которых частные производные равны нулю (или не существуют) называютсякритическими точкамифункцииz=f(x;y).
Из теоремы 1 и определения 3 следует, что если функция дифференцируема, то точки экстремума являются стационарными точками. Обратное неверно. Не всякая стационарная точка является точкой экстремума.
Пример. Рассмотрим функциюz=f(x;y)=x2—y2,f(0;0)=0.
,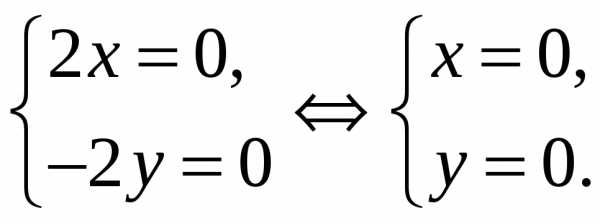
(0;0) – стационарная точка.
(0;0) – стационарная точка.
Рассмотрим 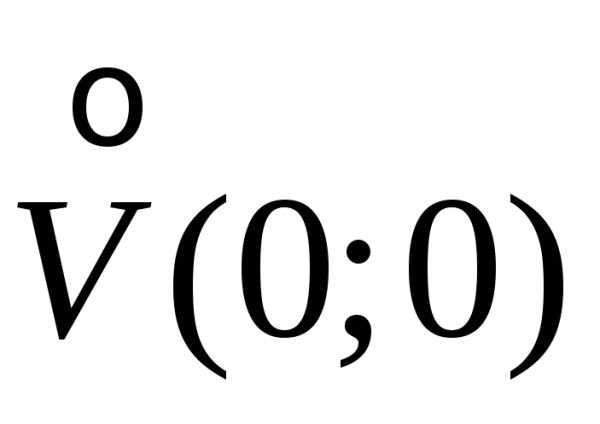 .
На оси Охf(x;0)=x2>0,
на оси Оуf(0;y)=—y2<0.
Следовательно, в любой окрестности
.
На оси Охf(x;0)=x2>0,
на оси Оуf(0;y)=—y2<0.
Следовательно, в любой окрестности есть значения функции, как большиеf(0;0)=0,
так и меньшиеf(0;0)=0.
Значит, точка (0;0) не может быть точкой
экстремума.
есть значения функции, как большиеf(0;0)=0,
так и меньшиеf(0;0)=0.
Значит, точка (0;0) не может быть точкой
экстремума.
Теорема 2 (достаточное условие экстремума).
Пусть функция z=f(x;y) определена и имеет непрерывные частные производные до второго порядка включительно в некоторой окрестности точкиМ0(x0;y0)V(x0;y0). ПустьМ0(x0;y0) — стационарная точка, то естьи. Обозначим
.
Тогда
1) если то z=f(x;y) имеет в точкеМ0(x0;y0) экстремум, причем приA<0(C<0)- локальный максимум, при — локальный минимум;
2) если , то точка М0(x0;y0) не является точкой экстремума;
3) если , то никакого заключения о характере стационарной точки сделать нельзя, требуются дополнительные исследования.
Доказательство.
 Т.к.
по условию функция имеет непрерывные
частные производные второго порядка,
то можем записать для нее формулу Тейлора
с остаточным членом в форме Лагранжа,
ограничиваясь двумя членами:
Т.к.
по условию функция имеет непрерывные
частные производные второго порядка,
то можем записать для нее формулу Тейлора
с остаточным членом в форме Лагранжа,
ограничиваясь двумя членами:
(0<<1).
Т.к. М0(x0;y0) — стационарная точка, тоdf(x0;y0)=0, следовательно,
,
где х=х-х0, у=y—y0.
Положим
, где,
, где,
, где.
Т.к. частные производные второго порядка непрерывны, то. Полное приращение функции запишется в виде:
.
Положим , где.
Тогда
.(2)
1) Пусть .
В этом случае АС>0, следовательно,А0, и первый трехчлен в скобках в формуле (2) можно записать следующим образом:
. (3)
Очевидно, что при выражение в квадратных скобках положительно. Следовательно, первый трехчлен формулы (2) сохраняет знак коэффициентаА. Модуль этого трехчлена – непрерывная на [0;2] функция оти, значит, достигает на [0;2] своего наименьшего значенияm:
.
Теперь рассмотрим второй трехчлен в (2). Если выбрать достаточно малым (а, значит, и х, умалы), то, поскольку,,0 при х,у0, будем иметь
.
Но тогда все выражение в скобках в (2) будет сохранять тот же знак, что и первый трехчлен, то есть знак коэффициента А.
Итак, если A>0, то и f(x0;y0)>0. Следовательно,f(x;y)>f(x0;y0). Т.е. в точке (x0;y0) функция имеет строгий минимум. А еслиA<0, то и f(x0;y0)<0. Следовательно,f(x;y)<f(x0;y0). Значит, в точке (x0;y0) функция имеет строгий максимум.
2) Предположим теперь, что .
а) Пусть А0. Тогда можно использовать преобразование (3).
Если =1=0, то из (3) следует, что выражение в квадратных скобках равно.
Если =2 определить так, чтоAcos2+Bsin2=0 (ясно, что при этом sin20, т. к. иначе будетА=0), то выражение в квадратных скобках равно.
Если достаточно мало, то второй трехчлен в скобках в (2) будет сколь угодно мал. Следовательно, знак fопределяется знаком первого трехчлена.
Из (3) следует:
при A>0 и=1он положителен,
=2он отрицателен,
при A<0 и=1он отрицателен,
=2он положителен.
Итак, в любой окрестности точки (х0;y0) fбудет иметь значения противоположных знаков на лучах=1и=2. Следовательно, точка (х0;y0) не может быть точкой экстремума.
б) Пусть А=0. Тогда первый трехчлен в (2) равен
.
Если А=0,
то из условияследует, чтоВ0.
Тогда можно взять уголнастолько малым, чтобы выражение
2Bcos+Csinбыло близко к 2Ви, значит, сохраняло знак. Тогда при=1 и=-1первый трехчлен в (2) будет иметь
противоположные знаки. Следовательно,
и в этом случае точка (х0;y0)
не может быть точкой экстремума.
Теорема 2 равносильна следующей теореме.
Теорема 3. Пустьdf(х0;y0)=0. Еслиd2f(х;y) сохраняет знак в некоторой достаточно малой окрестности точки (х0;y0), то в этой точке функция имеет строгий экстремум, причем, еслиd2f(х0;y0)<0, то строгий максимум, а если d2f(х0;y0)>0, то строгий минимум.
В таком виде достаточное условие экстремума переносится на случай функций любого числа переменных.
Пример.Исследовать функциюf(x;y)=xy(a—x—y),a>0 на экстремум.
 .
.
Найдем стационарные точки.
fx=y(a-x-y)-xy=y(a-2x-y),fy=x(a-x-y)-xy=x(a-x-2y)
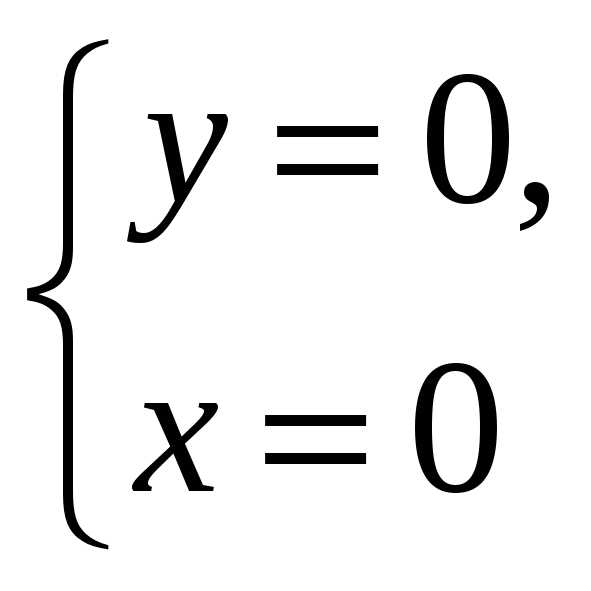
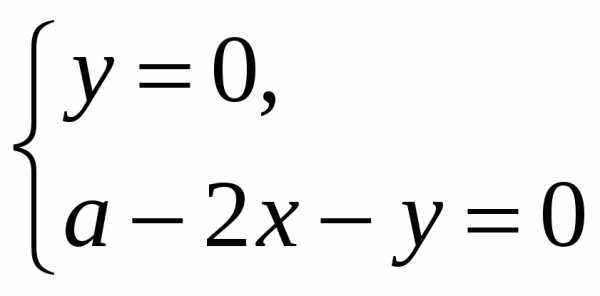
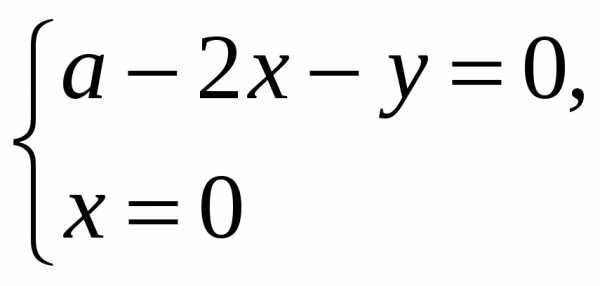
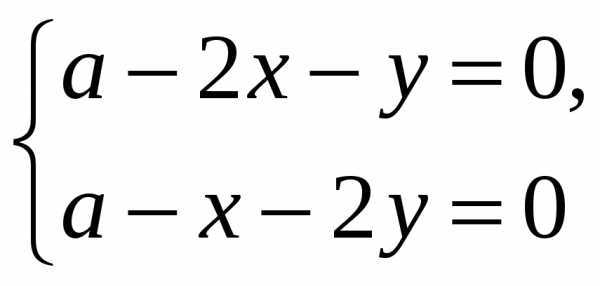
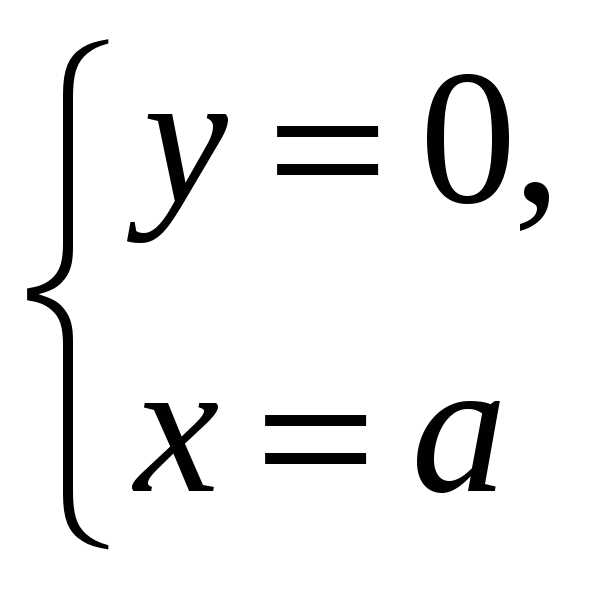
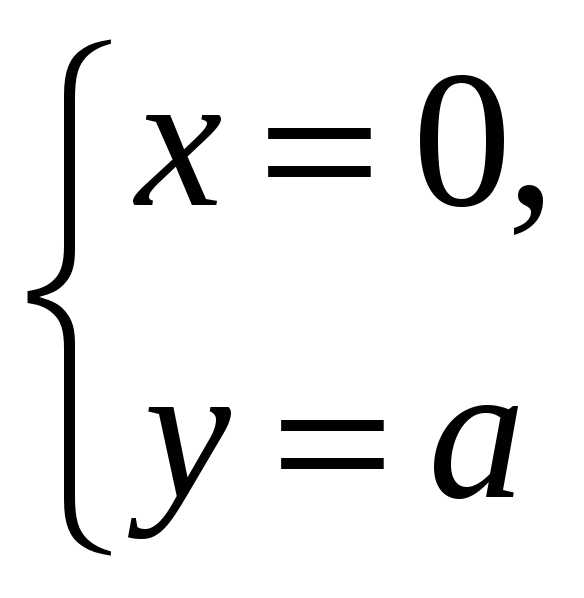
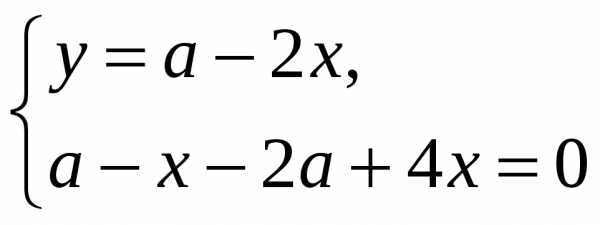
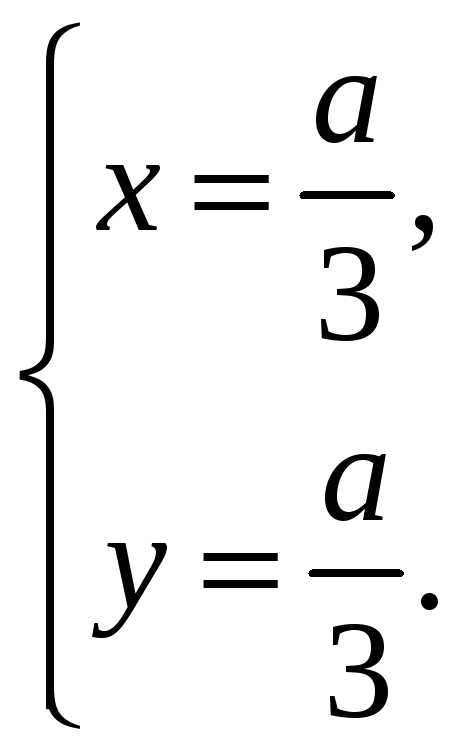
Стационарные
точки: О(0;0),М(а;0),N(0;a),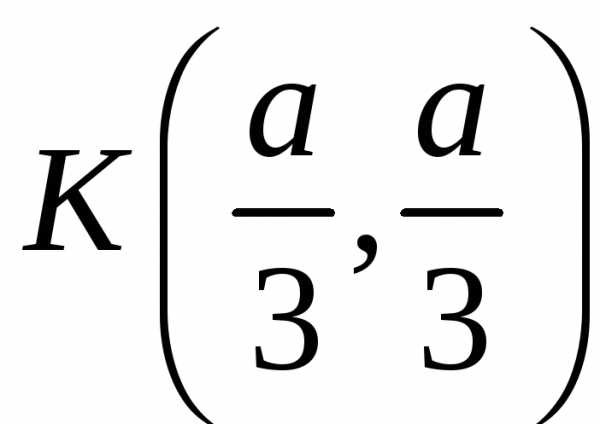 .
.
Проверим, являются ли они точками экстремума.
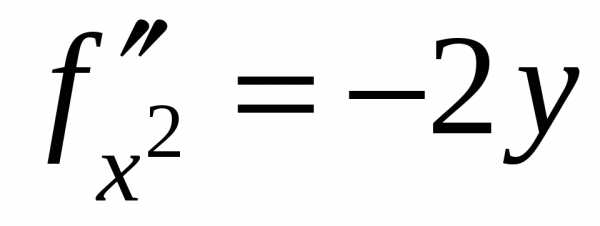 ,,
,,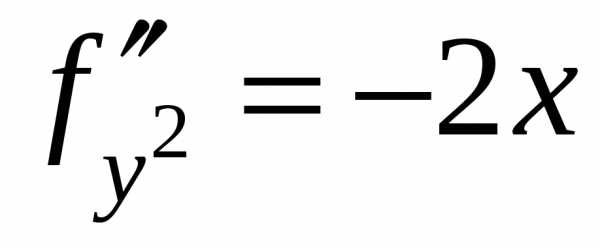 .
.
О(0;0):А=0,В=а,С=0,АС-В2=0-а2<0 экстремума нет;
М(а;0):А=0,В=-а,С=—2а,АС-В2=0-а2<0 экстремума нет;
N(0;a):А=-2a,В=-а,С=0,АС-В2=0-а2<0 экстремума нет;
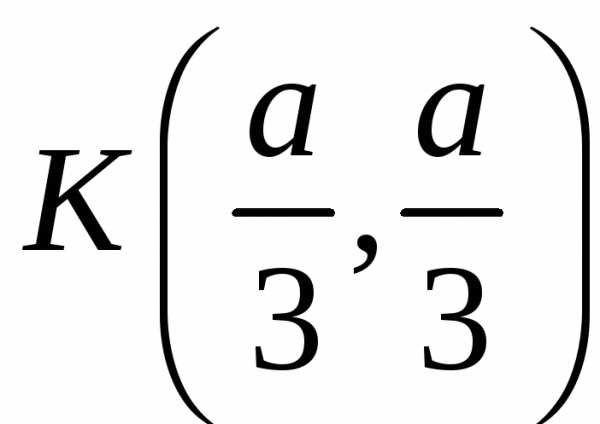 :
: ,,
,, ,
,
К– точка экстремума, т.к.A<0,
то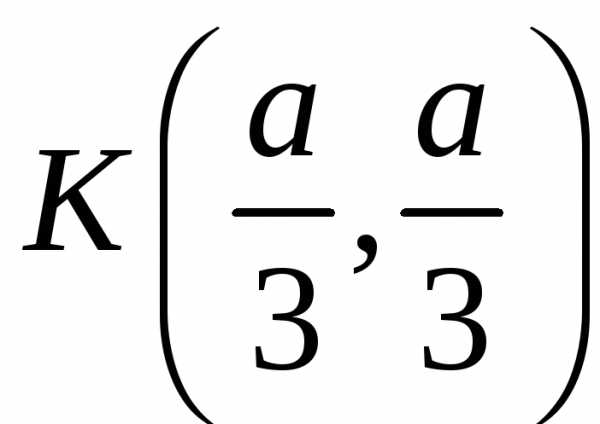 — точка максимума.
— точка максимума.
studfiles.net
Экстремум функции нескольких переменных. Условный экстремум — КиберПедия
Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0(х0, у0) верно неравенство , то точка М0 называется точкой максимума.
Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0(х0, у0) верно неравенство , то точка М0называется точкой минимума.
Теорема (необходимые условия экстремума).
Если функция f(x,y) в точке (х0, у0) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю , либо хотя бы одна из них не существует.
Эту точку (х0, у0) будем называть критической точкой.
Теорема (достаточные условия экстремума).
Пусть в окрестности критической точки (х0, у0) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение: , где , , .
1) Если D(x0, y0) > 0, то в точке (х0, у0) функция f(x, y) имеет экстремум, если — максимум, если — минимум.
2) Если D(x0, y0) < 0, то в точке (х0, у0) функция f(x, y) не имеет экстремума.
3) Если D = 0, вывод о наличии экстремума сделать нельзя, необходимы дополнительные исследования.
Пример 19. Найти точки экстремума функции .
Решение. Находим частные производные первого порядка М(1; 2) – критическая точка.
Найдём значения вторых производных в точке М(1; 2):
, , .Тогда . Так как , то в точке М(1; 2) функция имеет минимум .
Пример 20.Исследовать на экстремум функцию , заданную неявно.
Решение. Схема исследований та же, только все параметры задачи надо определить по методам функций, заданных неявно.
1. Найдём критические точки.
Пусть , тогда
В третьей системе присоединяем данное уравнение. Решением системы являются точки , , . Если , то , следовательно, уравнение в этой точке не определяет однозначную функцию и эта точка не подлежит исследованию.
2. Для проверки достаточных условий найдём вторые частные производные по правилам дифференцирования неявных функций:
, , .
При : , , . , т.к. в точке — минимум.
При : , , . в точке — экстремума нет.
Условный экстремум находится, когда переменные х и у, входящие в функцию u = f(x, y), не являются независимыми, т.е. существует некоторое соотношение j(х, у) = 0, которое называется уравнением связи. Отыскание условного экстремума можно свести к исследованию на обычный экстремум так называемой функцией Лагранжа[11] u = f(x, y) + lj(x,y), где l — неопределённый постоянный множитель. Необходимые условия экстремума функции Лагранжа имеют вид
Замечание. Если вторые частные производные не содержат , то процесс нахождения условного экстремума вырождается в процесс нахождения локального (абсолютного) экстремума функции − что не приемлемо. Тогда для исследования на экстремум в полученных критических точках вычисляем значение .
Если , то функция в точке имеет условный минимум; если — то условный максимум.
Пример 21. Найти экстремум функции f(x, y) = xy, если уравнение связи:
2x + 3y – 5 = 0.
Решение.Составим функцию Лагранжа .
Найдем частные производные и составляем необходимые условия экстремума для функции Лагранжа:
М0 — стационарная точка. Для исследования на экстремум в полученных критических точках вычисляем значения и составляем определитель = -12.
Т.к в точке М0функция f(x, y) = xy имеет условный максимум.
Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.
Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.
cyberpedia.su
2. Экстремум неявно заданной функции
Пусть уравнение F(x;y;z)=0 задает неявно функцию z=f(x;y). Пусть функция дважды непрерывно дифференцируема в . Если (х0;у0) – стационарная точка, то в ней выполнены равенства:
, ,
, .
Очевидно, верно и обратное утверждение. Следовательно, стационарные точки неявной функции могут быть найдены из системы:
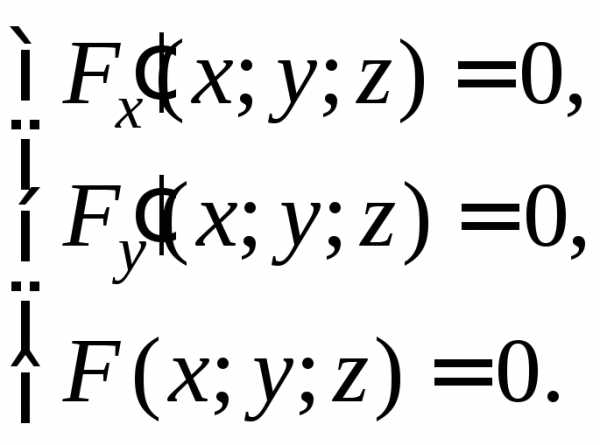
Достаточное условие формулируется так же, как в случае явного задания функции.
3. Нахождение наибольших и наименьших значений
Пусть функция z=f(x;y) определена и дифференцируема на ограниченной замкнутой области G. Тогда она на имеет наибольшее и наименьшее значения. Если наибольшее (наименьшее) значение функция f принимает во внутренней точке области , то эта точка является точкой максимума (минимума). Т.о., подозрительными точками внутри области являются стационарные точки. Но функция f может принимать наибольшее (наименьшее) значения и на границе области G.
План нахождения наибольшего и наименьшего значений функции
Найти стационарные точки внутри области и значения функции в них.
Найти наибольшее и наименьшее значения на границе области и значения функции в них. Для этого границу области следует задать либо одним уравнением, либо параметрически. Тогда на границе исходная функция будет функцией одного переменного.
Если в области существуют точки, в которых функция не дифференцируема, то надо вычислить в них значения функции.
Из полученных чисел выбрать наибольшее и наименьшее.
Пример 2. Найти наибольшее и наименьшее значения функции z=f(x;y)=2x2—2y2 в круге х2+у29.
1)
, 
(0;0) – стационарная точка.
(0;0) – стационарная точка.
z1=f(0;0)=0.
2) Граница области задана уравнением х2+у2=9. Отсюда у2=9-х2. Тогда на границе получаем функцию одной переменной: z=2x2—2(9-х2), z=4х2-18, x[-3;3].
z=8x, z=0 при х=0. Тогда у=3. Значения функции в стационарных точках границы: z2=f(0;3)=-18, z3=f(0;-3)=-18.
Значения функции на концах отрезка [-3;3]: z4=f(3;0)=18, z5=f(-3;0)=18.
3) zнаиб.=f(3;0)=f(-3;0)=18, zнаим.=f(0;3)=f(0;-3)=-18.
34
studfiles.net
Локальные экстремумы функции двух переменных
Определение. Точканазывается точкой локального максимума
(минимума) функции,
если существует -окрестность
этой точки, такая, что для всех точек
-окрестность
этой точки, такая, что для всех точек (принадлежащих
(принадлежащих -окрестности
этой точки), отличных от точки,
выполняется неравенство().
-окрестности
этой точки), отличных от точки,
выполняется неравенство().
Значение называют локальным максимумом (минимумом) функции и пишут
().
Точки максимума и минимума функции называют точками экстремума функции, а максимумы и минимумы функции — экстремумами функции.
Пример.Функцияимеет локальный максимум в точке (1;
1):
(1;
1): (1,
1) = 1.
(1,
1) = 1.
Действительно, существует окрестность
точки  (1;
1), в которой выполняется условие
(1;
1), в которой выполняется условие (1;
1) >
(1;
1) > для.
Графиком этой функции является поверхность
— параболоид вращения, представленный
на рисунке.
для.
Графиком этой функции является поверхность
— параболоид вращения, представленный
на рисунке.
Отметим, что если функция имеет в точкелокальный экстремум, то:
в случае локального максимума,
в случае локального минимума.
Из сказанного выше следует, что полное
приращение функции не меняет знака в  .
Однако для всех точек
.
Однако для всех точек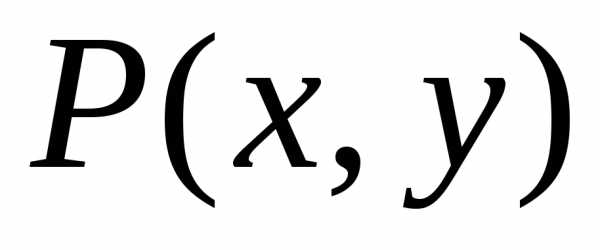
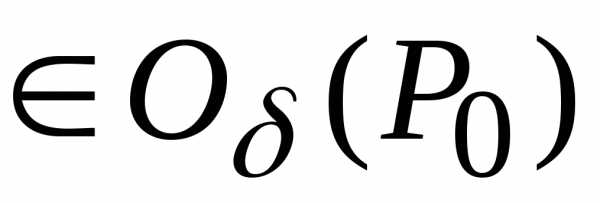 определить знак приращения
определить знак приращения практически невозможно, поэтому надо
искать другие условия, по которым можно
судить о наличии и характере экстремума
функции в данной точке.
практически невозможно, поэтому надо
искать другие условия, по которым можно
судить о наличии и характере экстремума
функции в данной точке.
Теорема (необходимые условия существования локального экстремума). Если в точкедифференцируемая функцияимеет локальный экстремум, то ее частные производные в этой точке равны нулю:
и,
или, по крайней мере, одна из них не существует.
Доказательство. Докажем только первое утверждение теоремы.
Рассмотрим в  лишь те точки, для которых
лишь те точки, для которых .
Получим функциюодной переменной
.
Получим функциюодной переменной .
Эта функция имеет в точке
.
Эта функция имеет в точке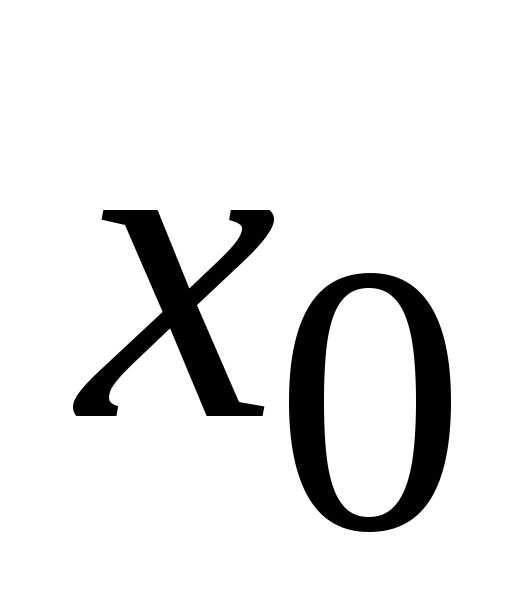 экстремум, следовательно,.
экстремум, следовательно,.
Аналогично доказывается, что .
Теорема доказана.
Проиллюстрируем примером второе утверждение теоремы .
Функция
имеет максимум в точке О(0; 0; 0), так как
для любой точки (О)
выполняется условие
(О)
выполняется условие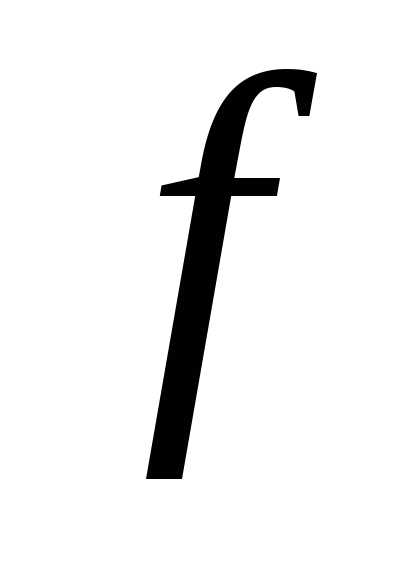 (0;
0) >
(0;
0) >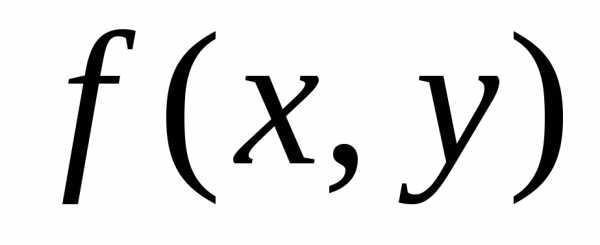 .
Частные производные
.
Частные производные
 ,
,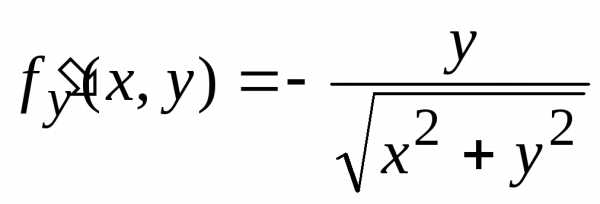
в точке О(0; 0) не существуют для . Графиком этой функции является конус, представленный на рисунке.
Следствие.Если функцияимеет в точкелокальный экстремум, то ее дифференциал в этой точке равен нулю или не существует.
Точка , в которой частные производные равны нулю, или хотя бы одна из них не существует, называется точкой возможного экстремума. Такие точки называются также стационарными или критическими.
Равенство нулю частных производных первого порядка не является достаточным условием существования экстремума функции в точке.
Действительно, возьмем, например, функцию 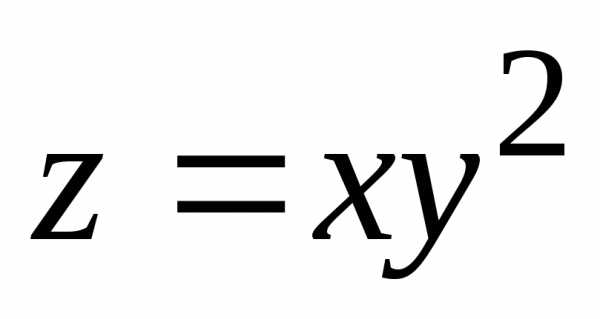 .
Она задана на всей числовой плоскостиR2. Точка О(0; 0) будет
критической, поскольку частные производные
в ней равны нулю. Так как функция равна
нулю в точке О, а в любой сколь угодно
малой окрестности
.
Она задана на всей числовой плоскостиR2. Точка О(0; 0) будет
критической, поскольку частные производные
в ней равны нулю. Так как функция равна
нулю в точке О, а в любой сколь угодно
малой окрестности (О)
она принимает как положительные, так и
отрицательные значения, то функция
(О)
она принимает как положительные, так и
отрицательные значения, то функция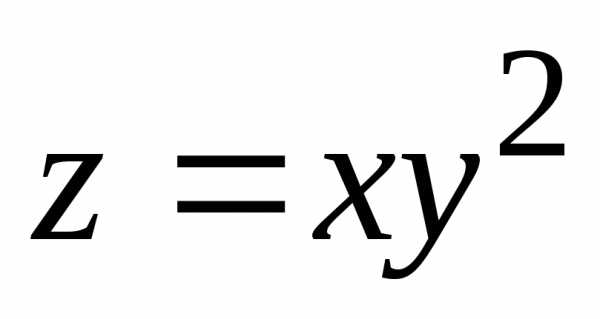 не имеет в точке О экстремума.
не имеет в точке О экстремума.
Теорема (достаточные условия
существования локального экстремума). Пусть— стационарная точка трижды дифференцируемой
в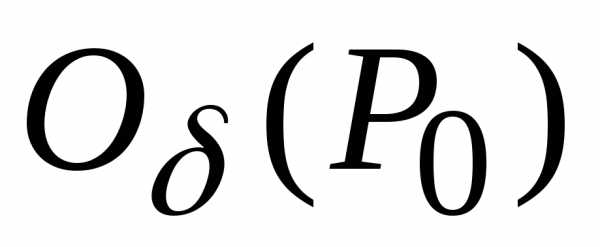 функциии пусть
функциии пусть
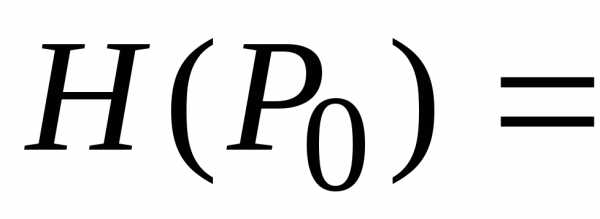 .
.
Тогда стационарная точка является:
1) точкой локального максимума, если и;
2) точкой локального минимума, если и;
3) если , то стационарная точкане является точкой локального экстремума функции.
Замечание.Если,
то нельзя определенно ответить на вопрос
о существовании экстремума в точке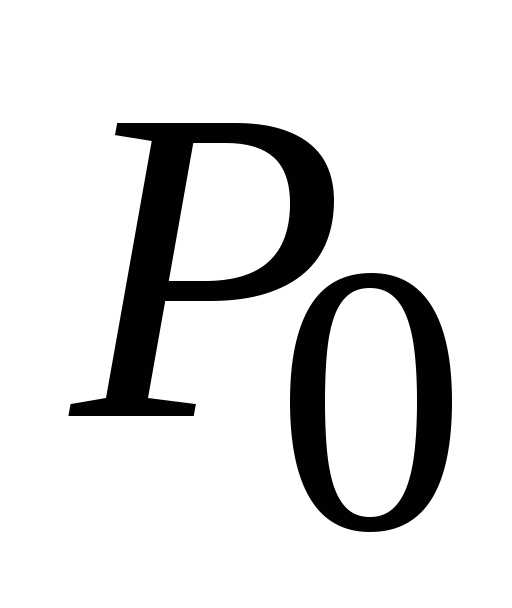 .
В этом случае необходимо произвести
дополнительные исследования знака
функциив
.
В этом случае необходимо произвести
дополнительные исследования знака
функциив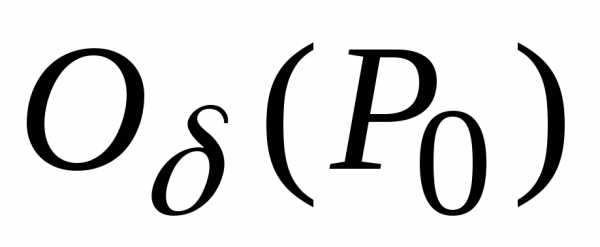 .
.
Приращения 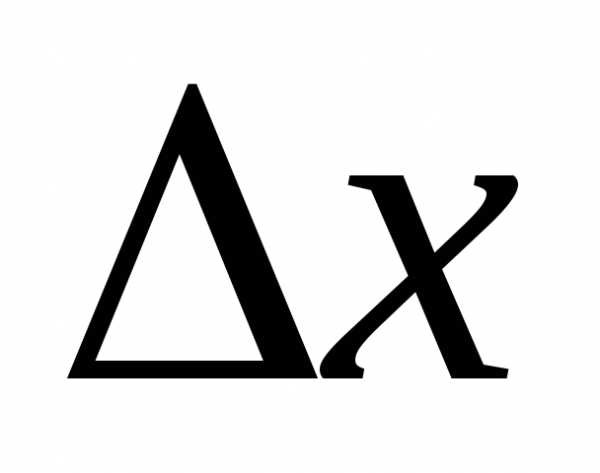 и
и не могут равняться нулю одновременно,
поскольку в подобном случае точкасовпала бы с точкойи функцияне получила бы никакого приращения.
не могут равняться нулю одновременно,
поскольку в подобном случае точкасовпала бы с точкойи функцияне получила бы никакого приращения.
Пример. Исследовать на экстремум функцию.
Решение.Вычислим частные производные первого порядка данной функции:
,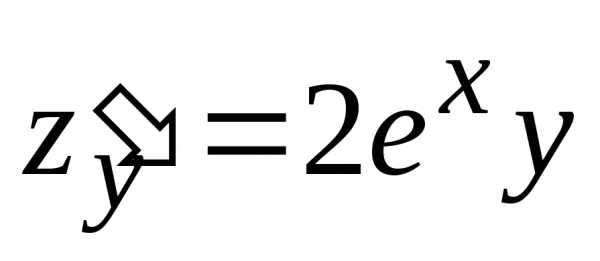 .
.
Находим точки возможного экстремума. Для этого решим систему уравнений:
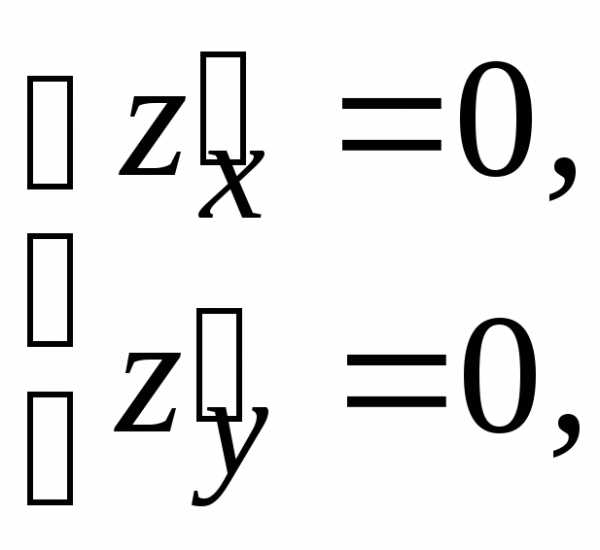

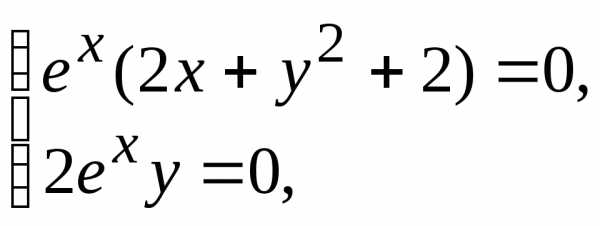
 (т. к.
(т. к.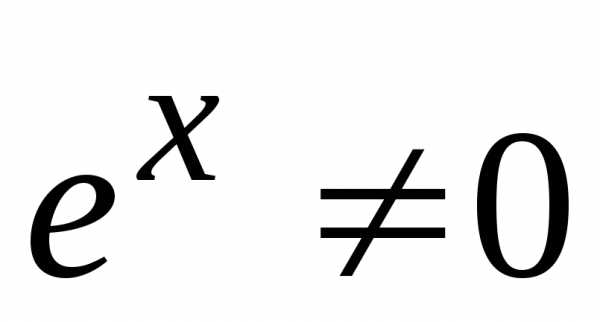 для
для R)
R)

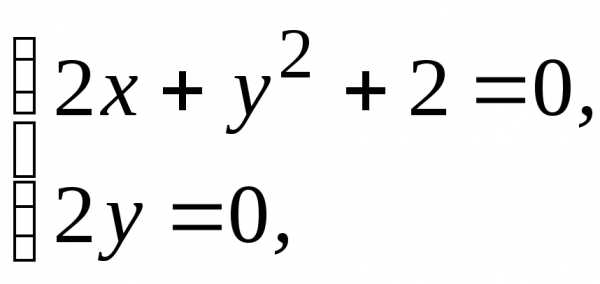


Таким образом, существует только одна
стационарная точка 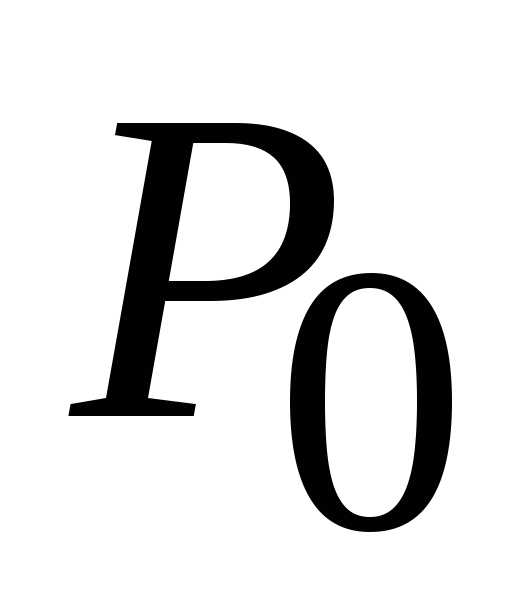 (1; 0), в которой
функция
(1; 0), в которой
функция может достигать экстремума.
может достигать экстремума.
Воспользуемся теоремой о достаточных условиях существования локального экстремума.
Для этого найдем частные производные второго порядка функции z:
,,.
Вычислим значения частных производных
второго порядка для стационарной точки 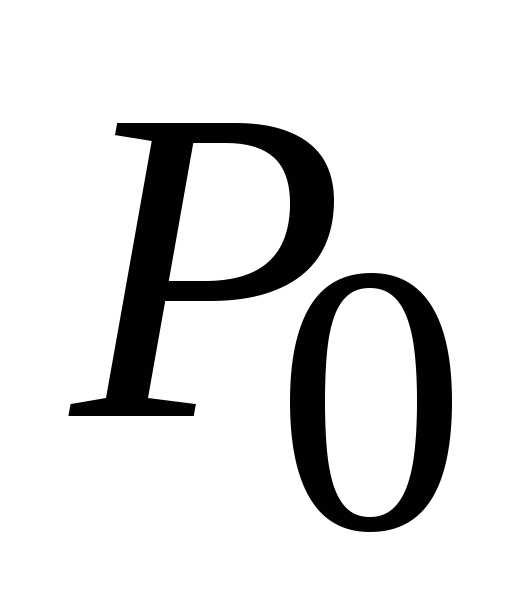 :
:
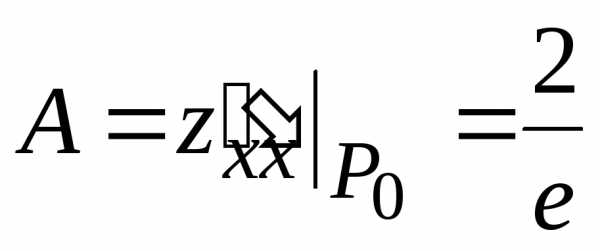 ,
,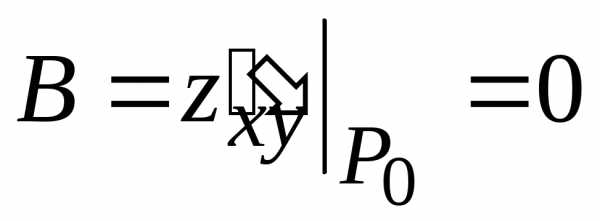 ,
,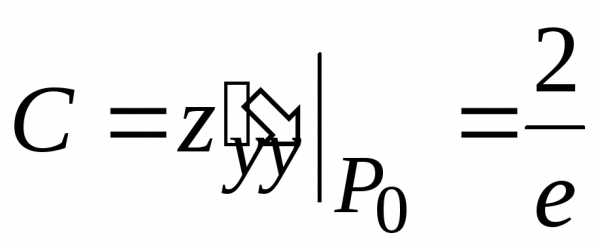 .
.
Так как  (1;
0),
(1;
0),
то по теореме о достаточных условиях
существования локального экстремума
точка  (1; 0) является
точкой локального экстремума, а т. к. А
> 0, то точка
(1; 0) является
точкой локального экстремума, а т. к. А
> 0, то точка (1; 0) является
точкой локального минимума, при этом
(1; 0) является
точкой локального минимума, при этом
.
Пример. Исследовать на экстремум функцию.
Решение.Вычислим частные производные первого порядка данной функции:,.
Для определения точек возможного экстремума решим систему уравнений:
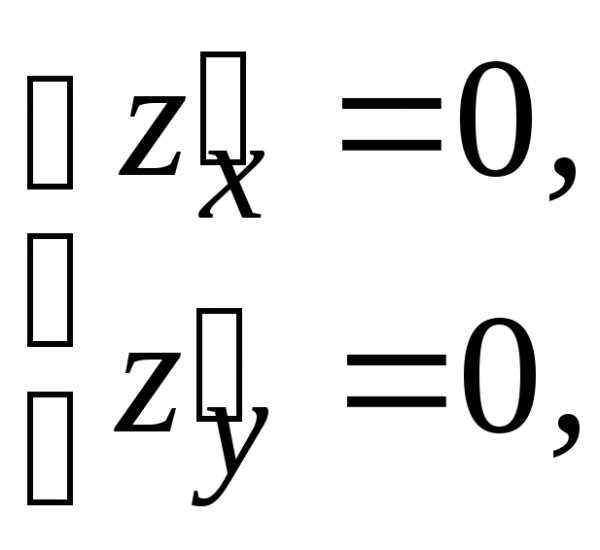

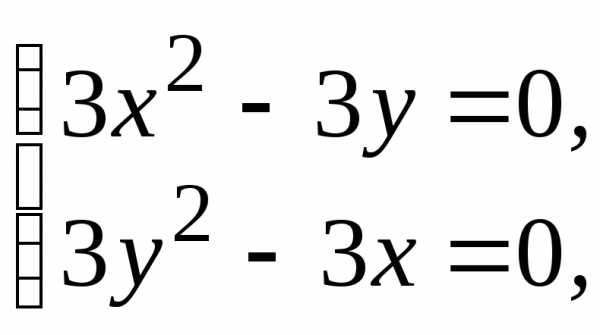


Данная система имеет два решения
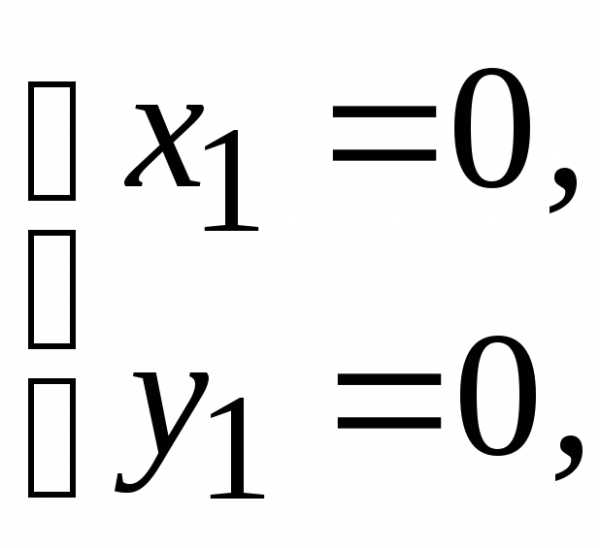 и
и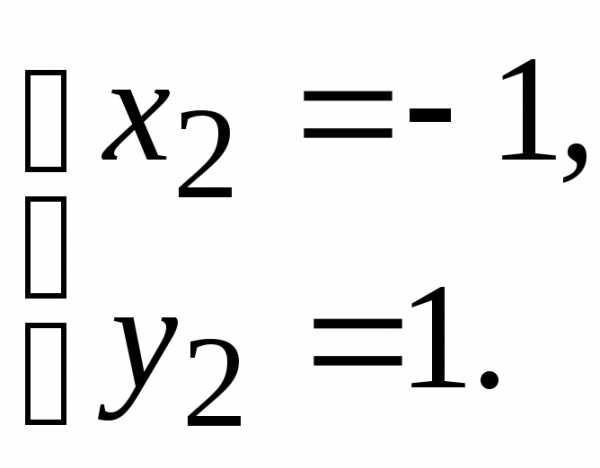
Следовательно, функция имеет две
стационарные точки  (0;
0) и
(0;
0) и (1,
1). Вычислим частные производные второго
порядка функции
(1,
1). Вычислим частные производные второго
порядка функции :
:
,,.
.
Вычислим  для точки
для точки (0;
0). Так как
(0;
0). Так как (0;
0),
то в точке
(0;
0),
то в точке (0;
0) нет экстремума.
(0;
0) нет экстремума.
Вычислим  для точки
для точки (1,
1). Т. к.
(1,
1). Т. к. (1;
1),
то точка
(1;
1),
то точка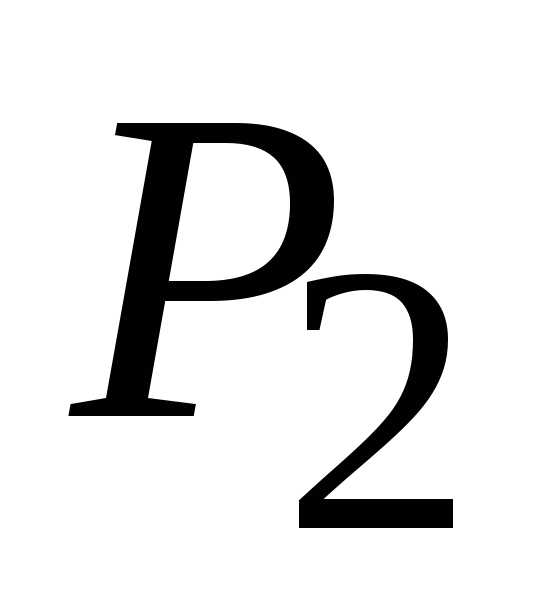 (1,
1) является точкой локального экстремума,
а т. к.
,
то точка
(1,
1) является точкой локального экстремума,
а т. к.
,
то точка (1,
1) является точкой локального максимума,
при этом
(1,
1) является точкой локального максимума,
при этом
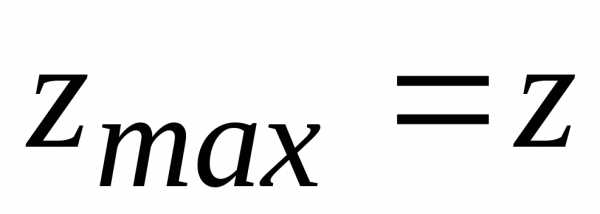 (1;
1)=9.
(1;
1)=9.
Пример. Исследовать на экстремум
функцию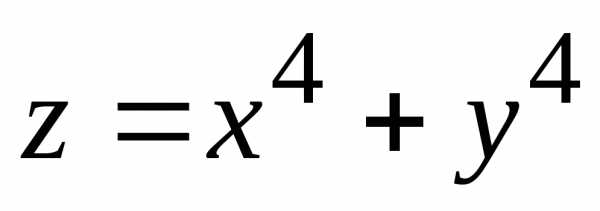 .
.
Решение.Вычислим частные
производные первого порядка функции :
:

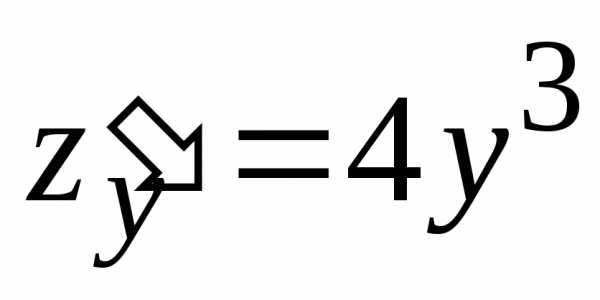 .
.
Решая систему уравнений:


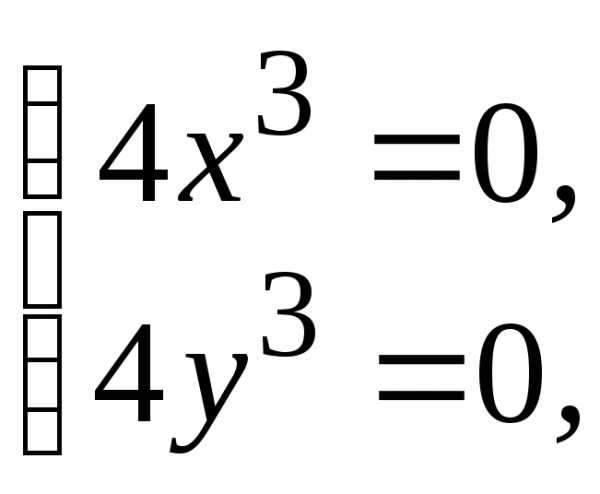

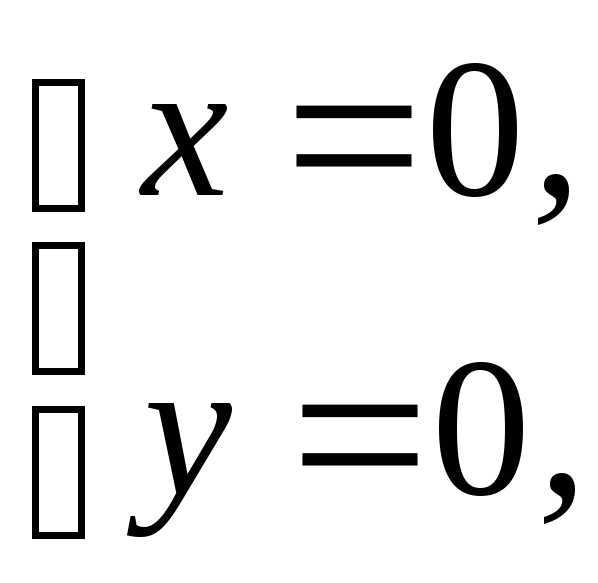
находим единственную стационарную
точку 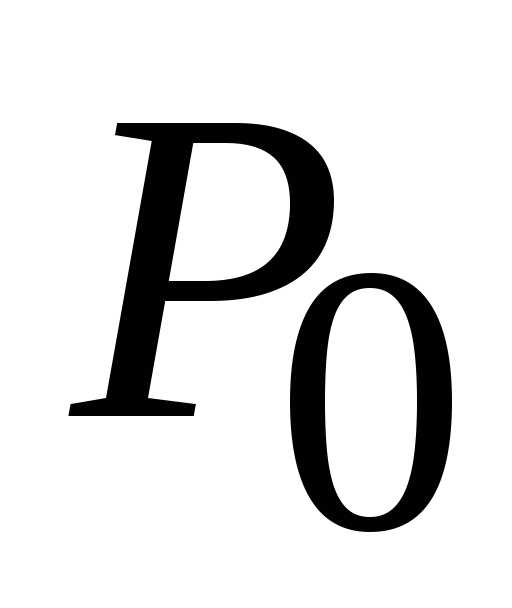 (0; 0) данной функции.
(0; 0) данной функции.
Найдем частные производные второго
порядка функции  :
:
,,
Для стационарной точки 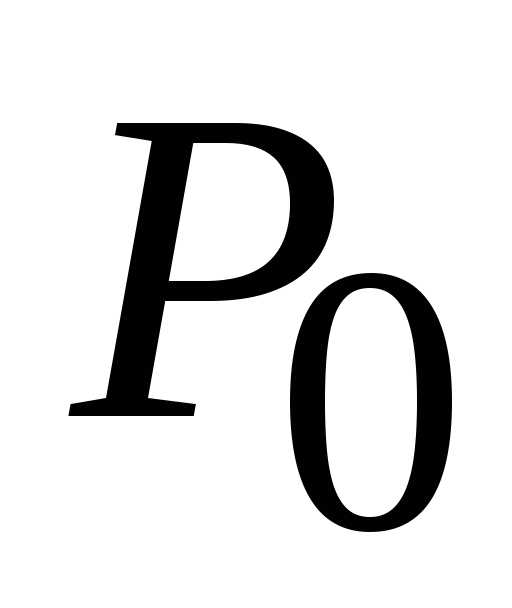 (0; 0)
(0; 0)
,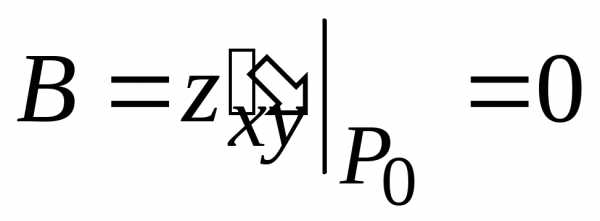 ,
,

 .
.
Следовательно, по теореме о достаточных
условиях существования локального
экстремума нельзя определенно ответить
на вопрос о существовании экстремума
в точке 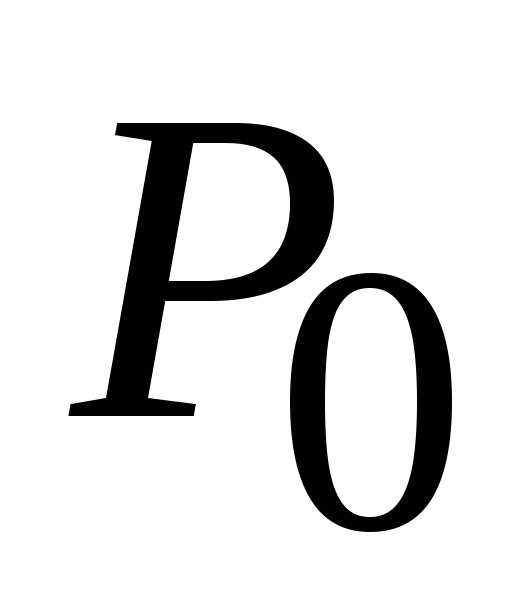 (0; 0). В данном случае стационарная
точка
(0; 0). В данном случае стационарная
точка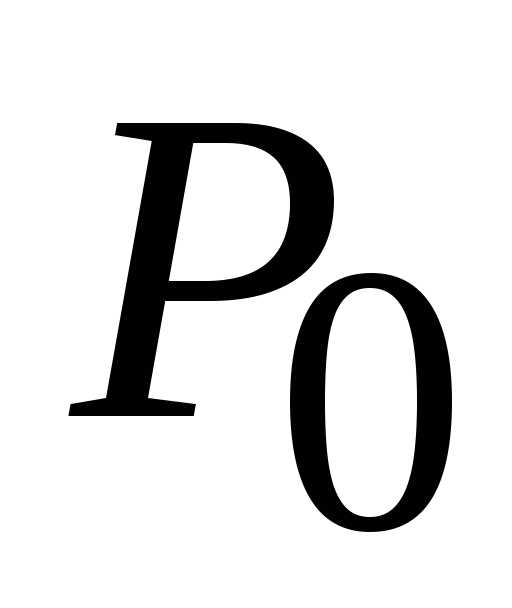 (0; 0) является точкой локального
минимума, поскольку,
(0; 0) является точкой локального
минимума, поскольку,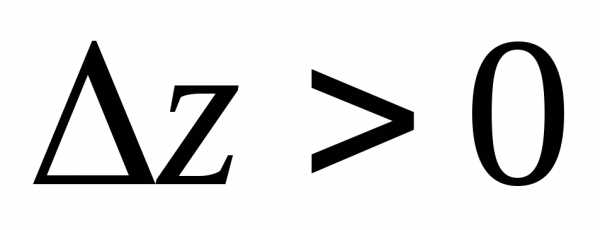 для
для
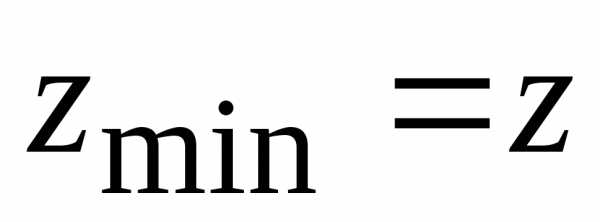 (0;
0)=0.
(0;
0)=0.
studfiles.net
21. Условный экстремум.
Задачи об отыскании экстремумов ф-ции, аргументы которой удовлетворяют дополнительным условиям связи-экстремумы такого рода будем наз-ть условными.
Пусть тр-ся
найти экс-мум ф-ции u=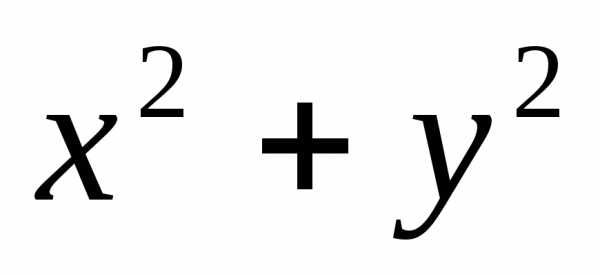 при
условии, что аргументы этой ф-ции
уовлетворяют условию связи х+у-1=0. Таким
образом, экстремумы ф-цииu=
при
условии, что аргументы этой ф-ции
уовлетворяют условию связи х+у-1=0. Таким
образом, экстремумы ф-цииu=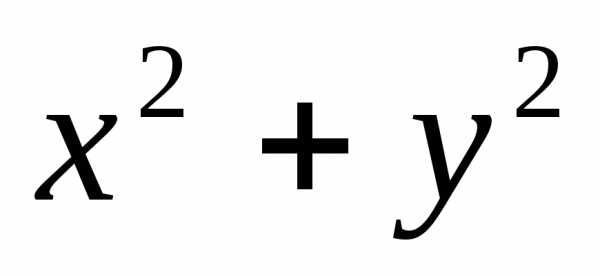 ищутся не на всей плоскости Оху, а лишь
на прямой х+у-1=0. Для решения подставим
в ур-ие ф-ции u=
ищутся не на всей плоскости Оху, а лишь
на прямой х+у-1=0. Для решения подставим
в ур-ие ф-ции u=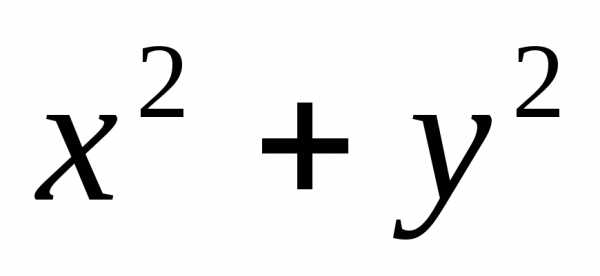 зн-ие у, определяемое из условия связи
х+у-1=0. Таким путём мы сведём поставленную
задачу к задаче об отыскании безусловного
экстремума ф-цииu=2
зн-ие у, определяемое из условия связи
х+у-1=0. Таким путём мы сведём поставленную
задачу к задаче об отыскании безусловного
экстремума ф-цииu=2
Последний экстремум
нах-ся без труда : так как
то
ф-ияu=2с условием связи х+у-1=0 имеет условный
минимумu=1/2
в точке (1/2,1/2). Отметим, что безусловный
минимум ф-ции u= достигается в точке (0;0) и равенu=0.
(графиком явл парабалоид вращения) на
всей плоскости с ее минимумом на прямой
х+у-1=0.
достигается в точке (0;0) и равенu=0.
(графиком явл парабалоид вращения) на
всей плоскости с ее минимумом на прямой
х+у-1=0.
Прейдем к общей постановке задачи об отыскании условного экстремума. Пусть треб-ся найти экстремум ф-ции m+n переменных
U=f((40)
При наличии m условий связи
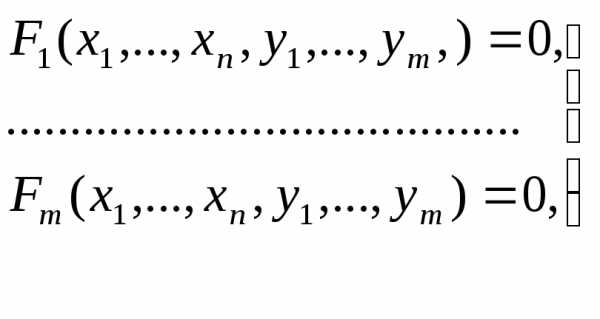 (41)
(41)
Функция при наличии
связей (41) имеет условный максимум
(минимум ) в точке ),
координаты которой удовлетворяют
условиям связи (41), если найдётся такая
окр-ть точки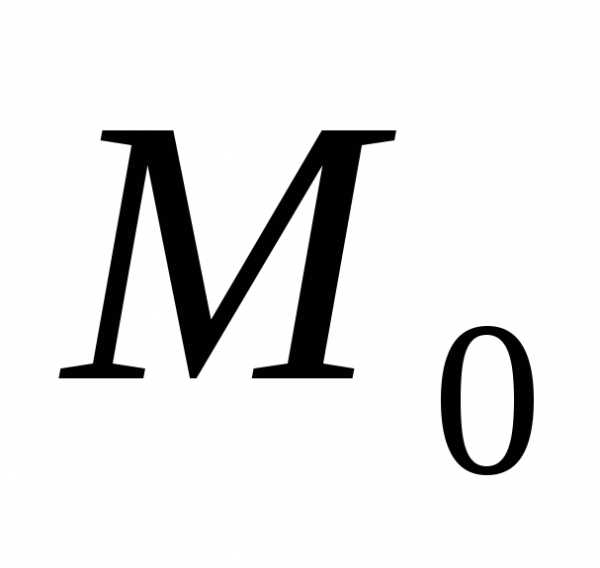 ,
в пределах которой зн-ие ф-ции (40) в точке
,
в пределах которой зн-ие ф-ции (40) в точке явл. наибольшим (наименьшим ) среди ее
зн-ий во всех точках, координаты которых
удовлетворяю условиям связи (41).
явл. наибольшим (наименьшим ) среди ее
зн-ий во всех точках, координаты которых
удовлетворяю условиям связи (41).
22. Неявные функции, теорема о неявной функции. Производная неявной функции.
Часто переменная u, явл. по смыслу задачи функцией аргументов x,y,…,задается посредством функционального ур-я F(u,x,y,…)=0 (15.1)
В этом сл. гов., что
u
как функция аргументов x,y,.. задана неявна . Например,
функ. U=-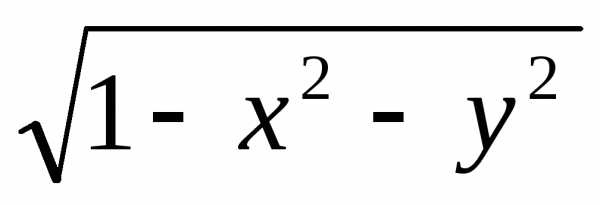 ,рассматривая
в круге
,
м/б неявно задана с пом. функцион-го Ур-я
,рассматривая
в круге
,
м/б неявно задана с пом. функцион-го Ур-я
F(u,x,y,…)=(15.2)
Возникает вопрос: при каких усл. Ур-е (15.1) однозначно разрешимо отн-но u, т.е однозначно определяет явную функцию u=и при каких усл. Эта функция явл.Непрерывной и дифференцируемой.
(Обозначения: через R б/т пространство переменных (u,x,y,…), а пр-во переменных (x,y,…) символом R’)
Теорема о существовании и диф-ти неявной функции.
Пусть функция
F(u,x,y)
диф-ма в некоторой окрестности точки 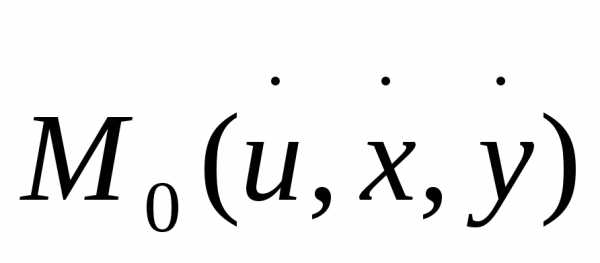 пр-ваR,
причём частная производная dF/du
непрерывна в точке
пр-ваR,
причём частная производная dF/du
непрерывна в точке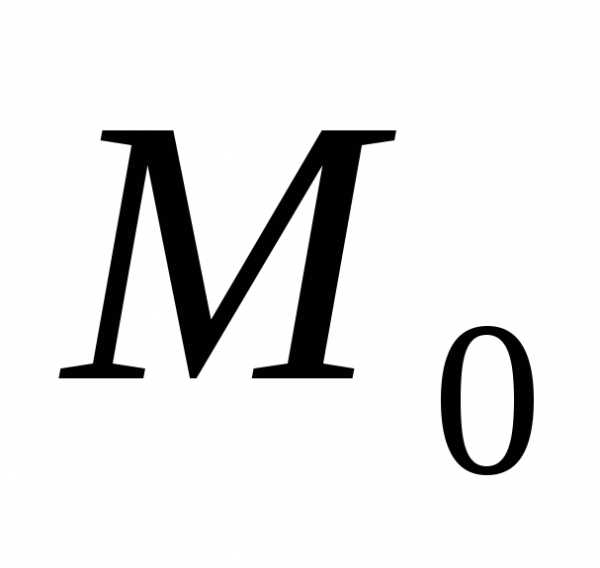 . Тогда если в точке
. Тогда если в точке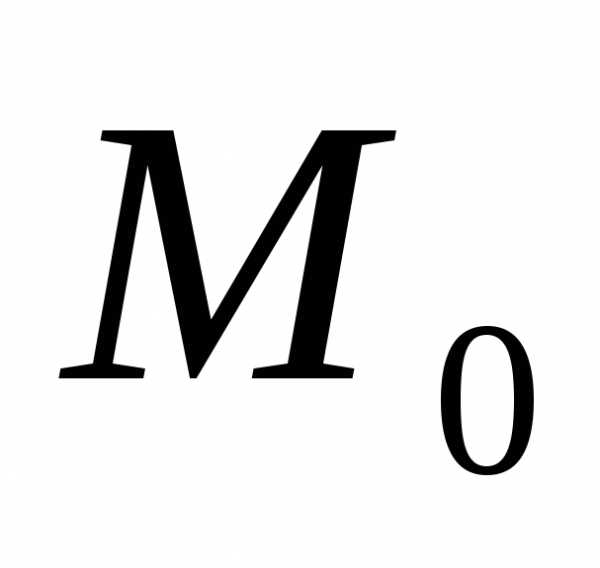 функцияFобращается
в нуль, а частная производная dF/du
не обращается в нуль, то для любого
достаточно малого положительного числа
функцияFобращается
в нуль, а частная производная dF/du
не обращается в нуль, то для любого
достаточно малого положительного числа  найдется такая окр-ть точки
найдется такая окр-ть точки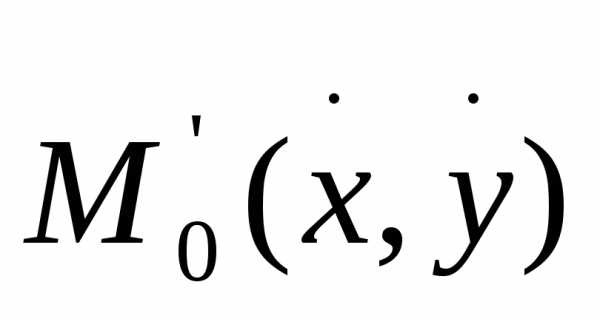 пр-ваR’
, что в пределах этой окр-ти сущ-ет
единственная ф-ия
которая
удовл-ет усл.
пр-ваR’
, что в пределах этой окр-ти сущ-ет
единственная ф-ия
которая
удовл-ет усл.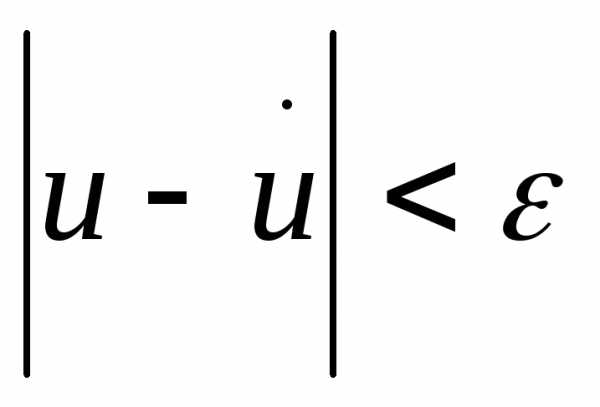 и явл. решением ур-я
и явл. решением ур-я
F(u,x,y,…)=0 (15.3)
Причём эта функциянепрерывна и диф-ма в указанной окр-ти
точки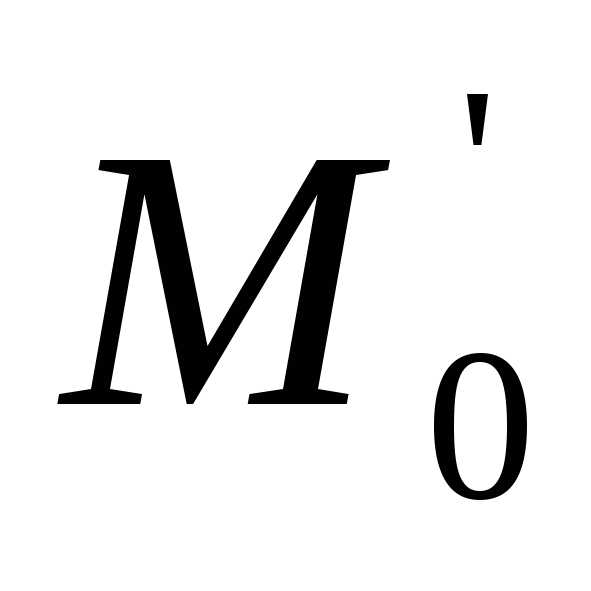 .
.
Замечание.В
усл. Теоремы можно опустить требование
непрерывности частной производной
dF/du
в точке 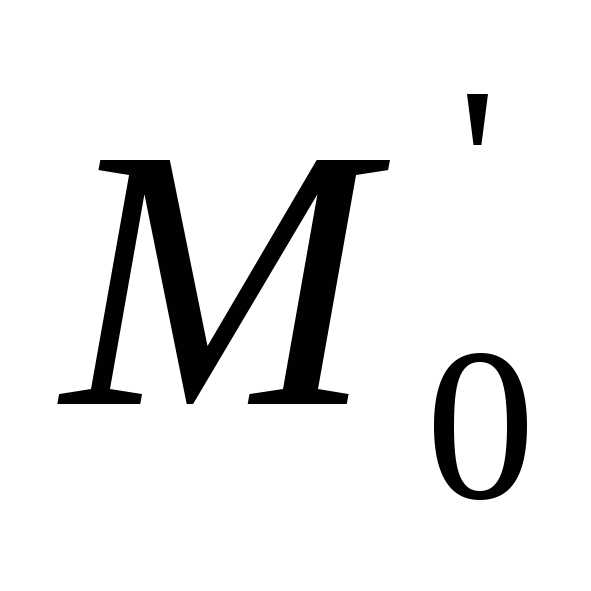 ,
но тогда придётся потребовать, чтобы
эта производная не обращалась к нулю
не только в самой точке
,
но тогда придётся потребовать, чтобы
эта производная не обращалась к нулю
не только в самой точке ,
но и в некоторой окр-ти этой самой точки
и сохраняла определенный знак в этой
окр-ти.
,
но и в некоторой окр-ти этой самой точки
и сохраняла определенный знак в этой
окр-ти.
Вычисление частных производных неявно заданной ф-ции.
F(u,x,y,…)=0, пусть выполнены все усл. Теоремы , частные производные ф-ции определяются ф-ми
Du/dx=-(dF/dx)/(dF/du), du/dy=-(dF/dy)/(dF/du). (15.11)
(а если не от 2, а
от более аргументов, то du/d =
=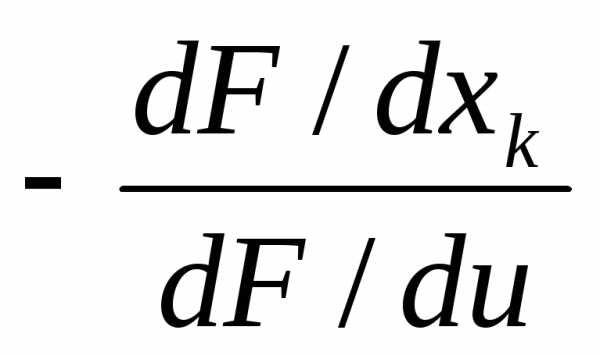 )
(k=1,2,…….м)
)
(k=1,2,…….м)
Если нужно найти частне произв. 2-го порядка, то нужно добавить усл. дифференц-ти дважды.
Пример. Вфчислить
частную произв. 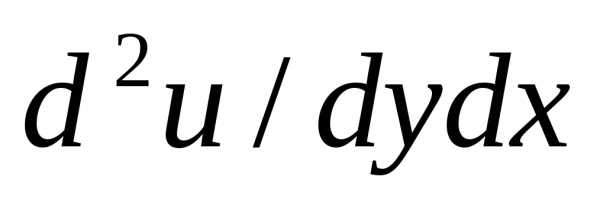 ф-ции ,заданной
использую ф-лу (15.11), получим du/dx=-(x/u),
du/dy=-(y/u).
ф-ции ,заданной
использую ф-лу (15.11), получим du/dx=-(x/u),
du/dy=-(y/u).
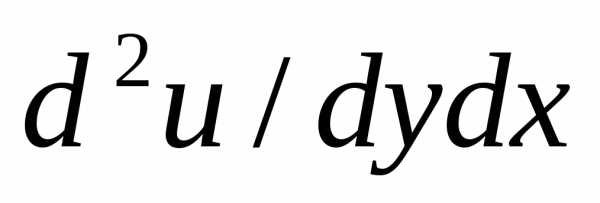 =D(du/dx)|Dy=D(-(x/u))/Dy=x
* du/dy|
=D(du/dx)|Dy=D(-(x/u))/Dy=x
* du/dy|  =-(xy)/
=-(xy)/ 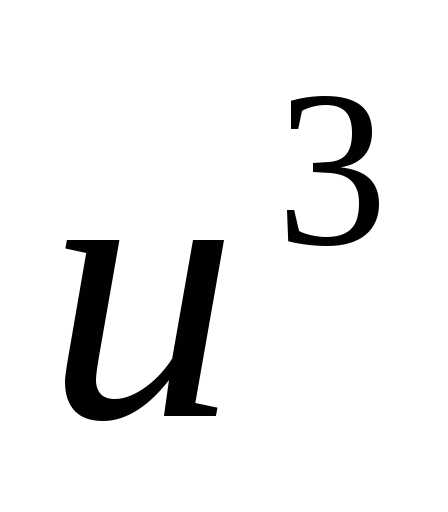
Условия, обеспечивающие сущ-ие для ф-ции y=f(x) обратной ф-ции.
Применим теорему
для выяснения условий, при выполнении
которых y=f(x)
имеет в некоторой окр-ти точки x0
обратную ф-ю x=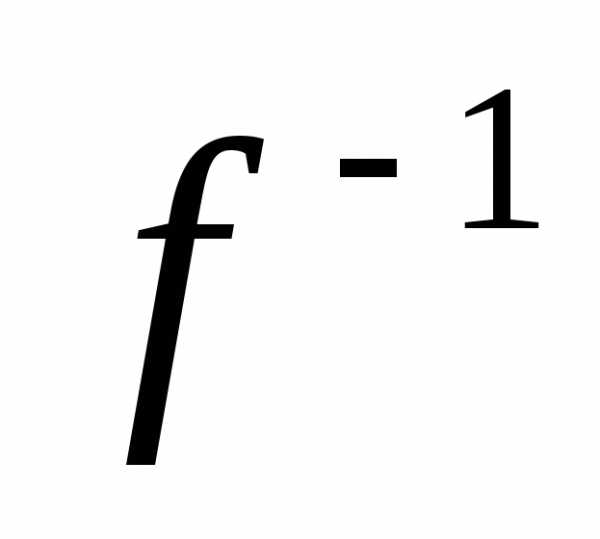 (y),
определенную в некоторойокр-ти точки
y0,
где y0=f(x0).
Будем рассматривать y=f(x)
как ф-ю, определяемую уравнением вида
F(x,y)=f(x)-y=0.
То вопрос о сущ-ии обр. ф-ии совпадает с
вопросом о разрешимости относительно
х указанного функционального уравнения. Если ф-ция y=f(x)
имеет отличную от нуля производную в
некоторой окр-ти точки х0, то для этой
ф-ции в окр-ти х0 существует обратная
ф-я x=
(y),
определенную в некоторойокр-ти точки
y0,
где y0=f(x0).
Будем рассматривать y=f(x)
как ф-ю, определяемую уравнением вида
F(x,y)=f(x)-y=0.
То вопрос о сущ-ии обр. ф-ии совпадает с
вопросом о разрешимости относительно
х указанного функционального уравнения. Если ф-ция y=f(x)
имеет отличную от нуля производную в
некоторой окр-ти точки х0, то для этой
ф-ции в окр-ти х0 существует обратная
ф-я x=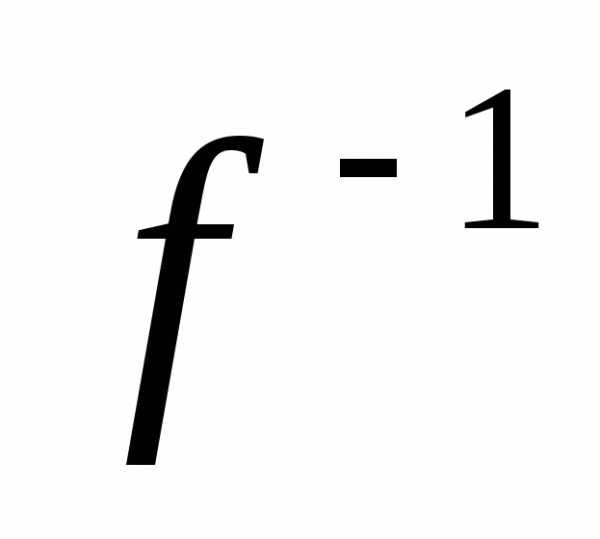 (y),
определенная и дифференцируемая в
некоторой окр-ти точки у0, где у0=f(x0).
Производная указанной обр. ф-ции в точке
у0 в силу второй из формул (15.11) равна
1/f’(x0).
(y),
определенная и дифференцируемая в
некоторой окр-ти точки у0, где у0=f(x0).
Производная указанной обр. ф-ции в точке
у0 в силу второй из формул (15.11) равна
1/f’(x0).
Неявные ф-ции, определяемые системой функциональных Ур-ий.
Предположим, что m-функций
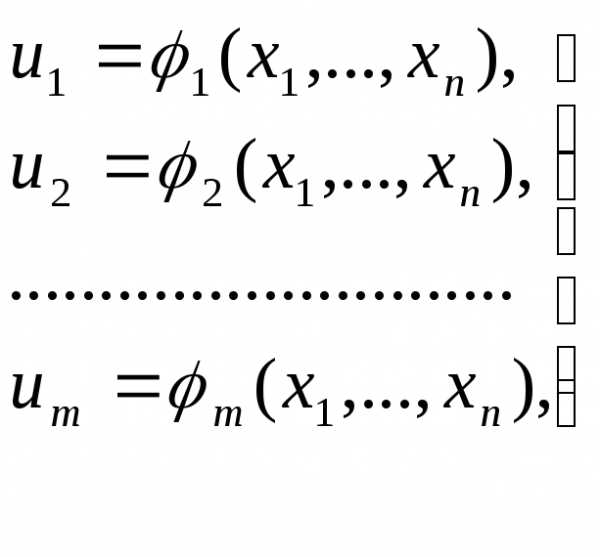 (13)
(13)
ищутся как решение системы m функциональных Ур-ий
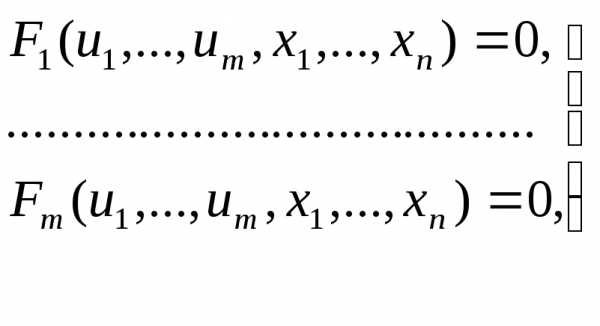 (14)
(14)
Это решение будем
наз-ть непрерывным и дифференцируемым
в некоторой области D
изменения переменных 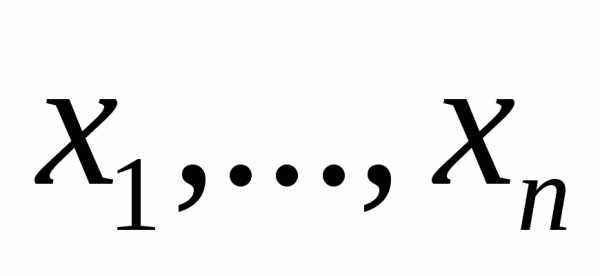 ,
если каждая из ф-ций (13) непрерывна и
диф-ма в областиD.
(символом R
будет пространство (m+n)
переменных
,
а сисмволомR’
пространство n
переменных
,
если каждая из ф-ций (13) непрерывна и
диф-ма в областиD.
(символом R
будет пространство (m+n)
переменных
,
а сисмволомR’
пространство n
переменных  )
)
Рассмотрим
m
функций 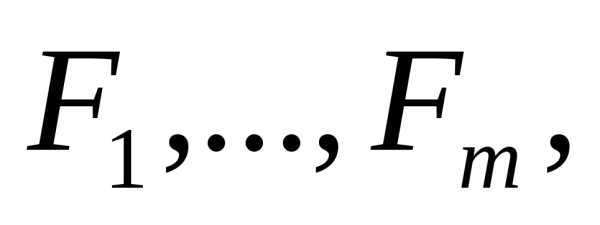 стоящих в левых частях системы (14), и
составим из частных производных этих
ф-ий следующий определитель:
стоящих в левых частях системы (14), и
составим из частных производных этих
ф-ий следующий определитель:
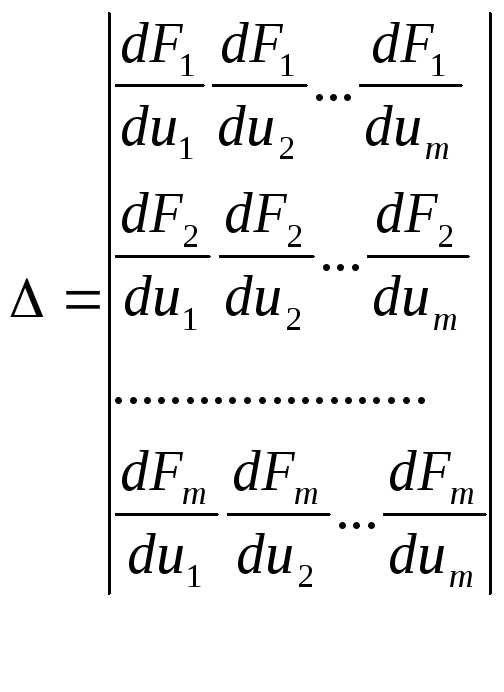 (15)(15)-
определитель Якоби. (или якобианом )
ф-ции
(15)(15)-
определитель Якоби. (или якобианом )
ф-ции 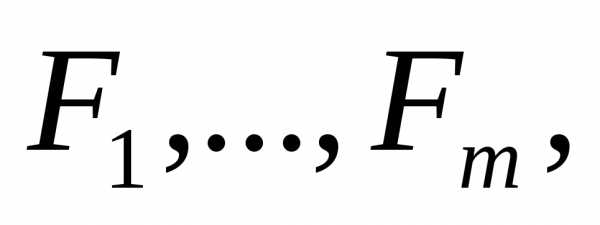 по переменным
по переменным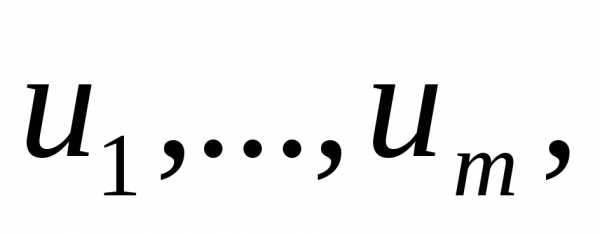 и кратко обозначать символом
и кратко обозначать символом
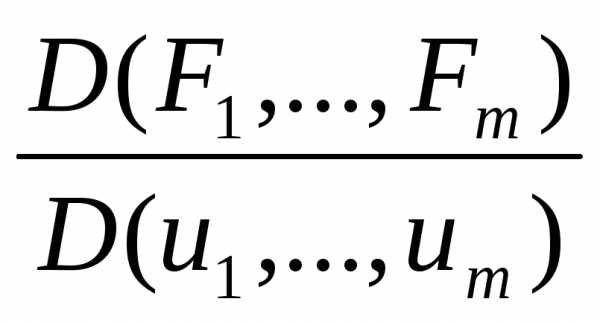 .
.
Теорема Пусть m функций 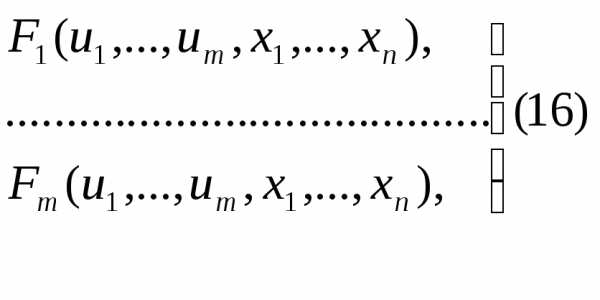 дифференцируемы в некоторой окр-ти
точки)
пространстваR,
причем частные производные этих ф-ий
по перевменным
дифференцируемы в некоторой окр-ти
точки)
пространстваR,
причем частные производные этих ф-ий
по перевменным 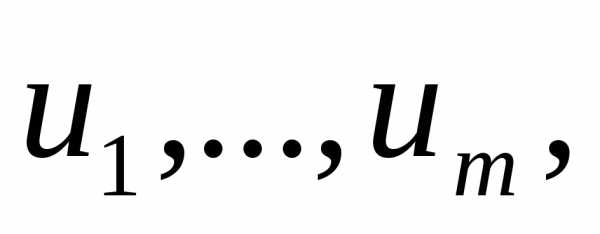 непрерывны в точке
непрерывны в точке  .
Тогда, если в точке
.
Тогда, если в точке все ф-ции (16) обращаются в нуль, а якобиан
все ф-ции (16) обращаются в нуль, а якобиан 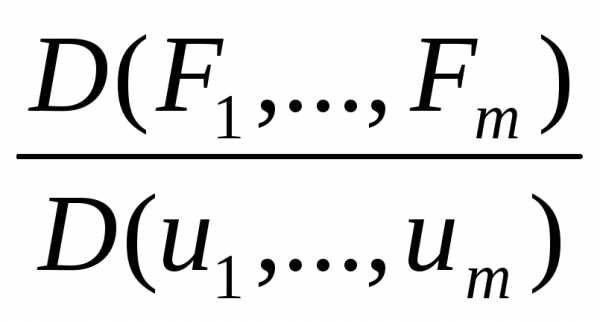 отличен от нуля, то для достаточно малых
положительных чисел
отличен от нуля, то для достаточно малых
положительных чисел найдется такая окр-ть точки
найдется такая окр-ть точки  пространстваR’,
что в пределах этой окр-ти сущ-ют
единственные m функций (13), которые удовлетворяют
условиям
и явл-ся решением системы Ур-ий (14), причём
это решение непрерывно и дифференцируемо
в указанной окр-ти точки
пространстваR’,
что в пределах этой окр-ти сущ-ют
единственные m функций (13), которые удовлетворяют
условиям
и явл-ся решением системы Ур-ий (14), причём
это решение непрерывно и дифференцируемо
в указанной окр-ти точки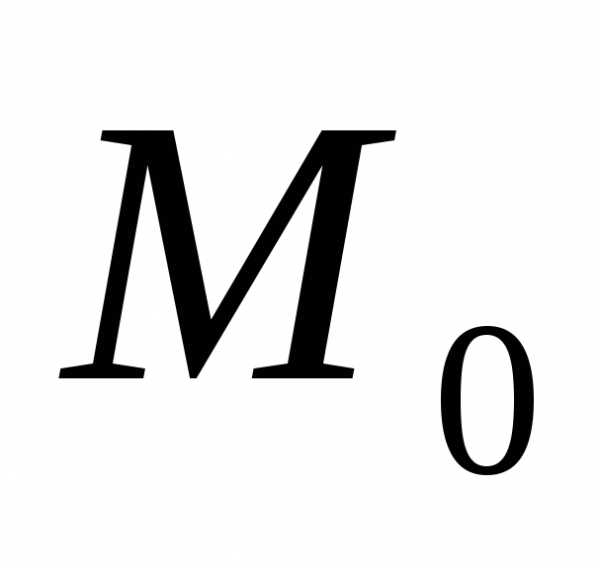 ’.
’.
Зависимость ф-ий. Пусть m функций от одних и тех же n переменных
 (28) Определены и
диф-мы в некоторой открытой n-мерной
области D.
(28) Определены и
диф-мы в некоторой открытой n-мерной
области D.
Одна из этих ф-ий,
например,  ,
зависит в областиD
от остальных ф-ций, если сразу для всех
точек
,
зависит в областиD
от остальных ф-ций, если сразу для всех
точек  в областиD (29), где Ф-некоторая ф-ия, определенная
и диф-ая в соответствующей области
изменения своих аргументов. Ф-ции
в областиD (29), где Ф-некоторая ф-ия, определенная
и диф-ая в соответствующей области
изменения своих аргументов. Ф-ции 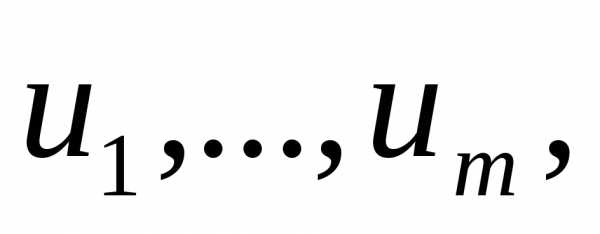 будем наз-ть зависимыми в областиD,
если одна из этих функций зависит в
области D
, еслиодна из этих ф-ций зависит в области
D
от остальных.
будем наз-ть зависимыми в областиD,
если одна из этих функций зависит в
области D
, еслиодна из этих ф-ций зависит в области
D
от остальных.
Пример
Зависимы в любой
области D
четырехмерного пр-ва, ибо для всех точек
( )
этой области
)
этой области
Теорема Пусть mфункций
от n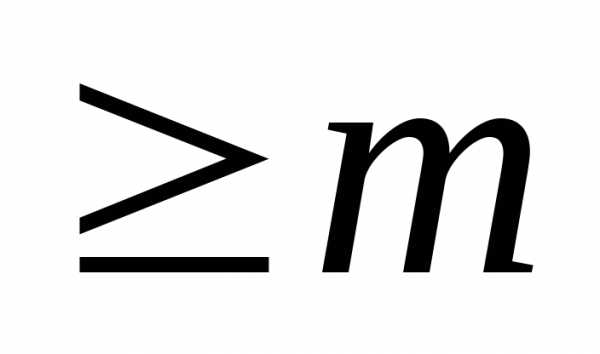 переменных
переменных
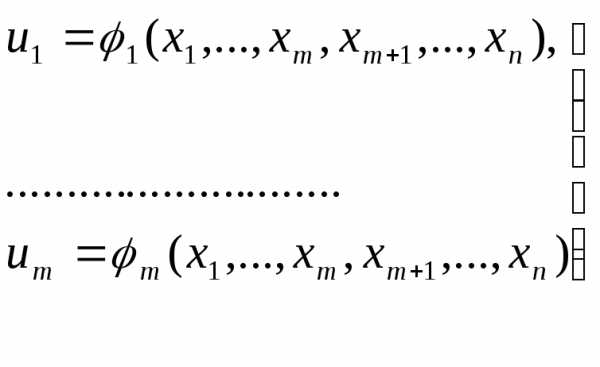
Определены и
дифференцируемы в окр-ти точки ).
Тогда если якобиан из этих ф-ций по
каим-ибоm переменным отличен от нуля в точке  ,
то эти ф-ции независимы в некоторой
окр-ти точки
,
то эти ф-ции независимы в некоторой
окр-ти точки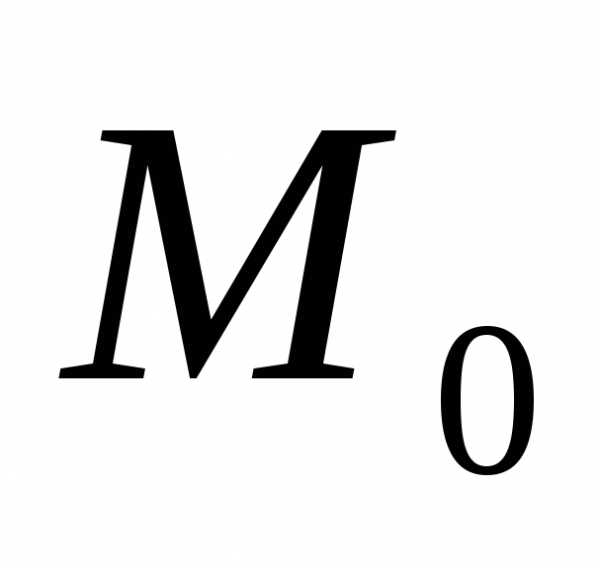 .
.
Пример.Две ф-ции
независимы в окр-ти любой точки М(х,у)
так как якобиан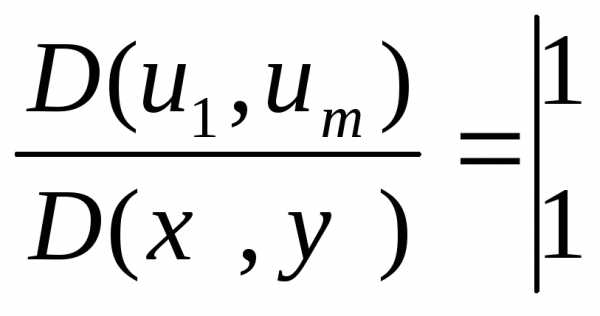
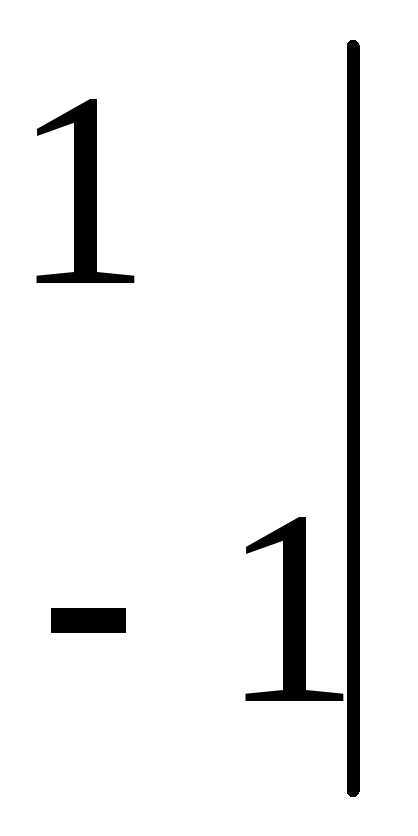 =-2не
равен нулю всюду.
=-2не
равен нулю всюду.
studfiles.net
Условный экстремум функций нескольких переменных. Глобальный экстремум
Задача
отыскания экстремума в случае функции
многих переменных может быть поставлена
как задача об условном экстремуме
функции
с ограничениями вида,,
…,,
которые называютсяуравнениями
связи. Разумеется, функциидолжны быть определены, непрерывны и
непрерывно дифференцируемы в области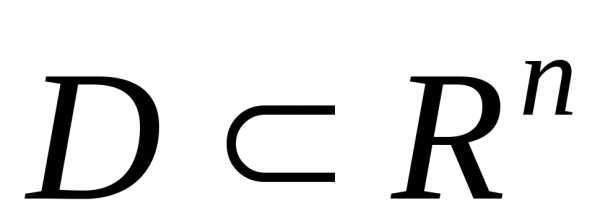 .
Таким образом, ведется поиск экстремума
не на всей области определения, а лишь
на множестве точек, удовлетворяющих
уравнениям связи. Такой экстремум
называетсяусловным.
.
Таким образом, ведется поиск экстремума
не на всей области определения, а лишь
на множестве точек, удовлетворяющих
уравнениям связи. Такой экстремум
называетсяусловным.
Наиболее
простым способом нахождения условного
экстремума функции двух переменных
является сведение задачи к отысканию
экстремума функции одной переменной.
Допустим, требуется найти экстремум
функции
при условии, что.
Для этого из уравнениявыражают одну из переменных через
другую, например,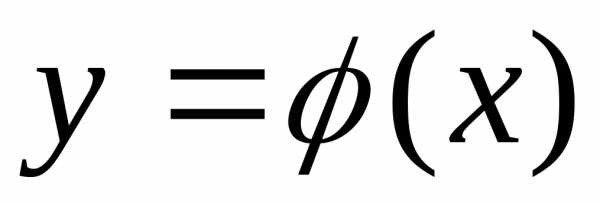 .
Подставив это выражение в,
получают– функцию одной переменной, которую
исследуют на обычный экстремум. Однако,
в большинстве более сложных случаев
решить этим способом задачу отыскания
экстремума не удается.
.
Подставив это выражение в,
получают– функцию одной переменной, которую
исследуют на обычный экстремум. Однако,
в большинстве более сложных случаев
решить этим способом задачу отыскания
экстремума не удается.
Для отыскания условного экстремума в общем случае применяется метод множителей Лагранжа. Для этого вводится вспомогательная функция Лагранжа:
.
Эта функция зависит от и значений множителей Лагранжа.
Теорема.Если точка  является точкой условного экстремума
функциипри условиях,,…,,
то существует такое,
что точка
является точкой условного экстремума
функциипри условиях,,…,,
то существует такое,
что точка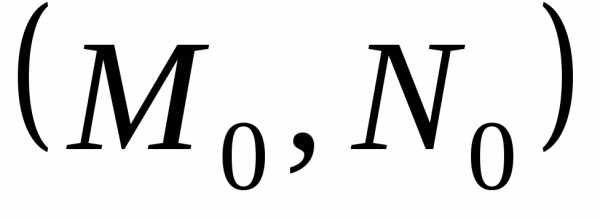 является точкой экстремума функции.
является точкой экстремума функции.
В качестве необходимых условий существования экстремума формируется система уравнений, решения которой и требуется найти:
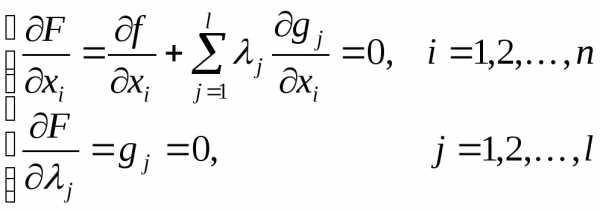
Решения
системы уравнений образуют множество
критических точек с переменными
;.
В каждой указанной точке должно
выполняться условие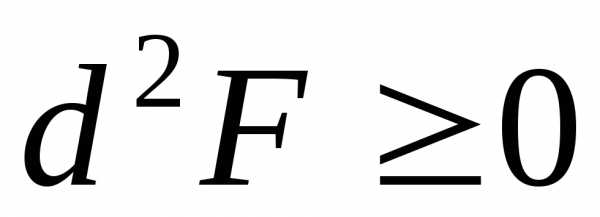 или
или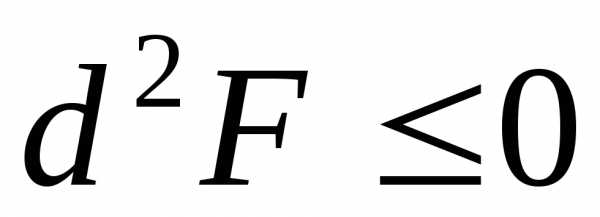 .
.
На практике в большинстве случаев ставится задача исследования функции , определенной на множестве точек, удовлетворяющих системе ограничений. Такое множество точек образует область, границами которой являются уравнения связи,, …,.
Наибольшее или наименьшее значение функции в данной области называется абсолютным или глобальным экстремумом функции (соответственно абсолютным максимумом или абсолютным минимумом) в этой области.
Согласно теореме Вейерштрасса функция непрерывная в ограниченной и замкнутой области, достигает в этой области своего наибольшего и своего наименьшего значений.
Теорема.Абсолютный (глобальный) экстремум функции в данной области достигается либо в критической точке функции, принадлежащей этой области, либо в граничной точке области.
Метод наименьших квадратов
При
определении вида эмпирической функции 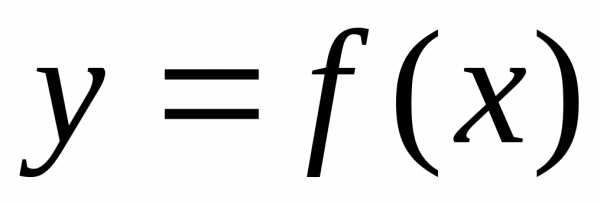 обычно предполагается, что это наиболее
гладкая кривая, согласованная с
экспериментальными данными. Кроме того,
для выбора этой функции привлекаются
дополнительные соображения, как правило,
не математического характера (теоретические
модели, опыт предшествующих исследований,
и т.п.).
обычно предполагается, что это наиболее
гладкая кривая, согласованная с
экспериментальными данными. Кроме того,
для выбора этой функции привлекаются
дополнительные соображения, как правило,
не математического характера (теоретические
модели, опыт предшествующих исследований,
и т.п.).
Эта
задача может быть решена в ходе
регрессионного анализа, который изучается
в курсе теории вероятностей, но решить
ее можно и математическими методами.
Согласно наиболее распространенному
и теоретически обоснованному методу
наименьших квадратов в качестве
неизвестных параметров функции 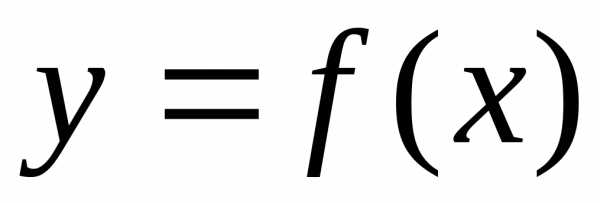 выбираются такие значения, которые
соответствуют минимальному значению
суммы квадратов отклонений эмпирических
значений
выбираются такие значения, которые
соответствуют минимальному значению
суммы квадратов отклонений эмпирических
значений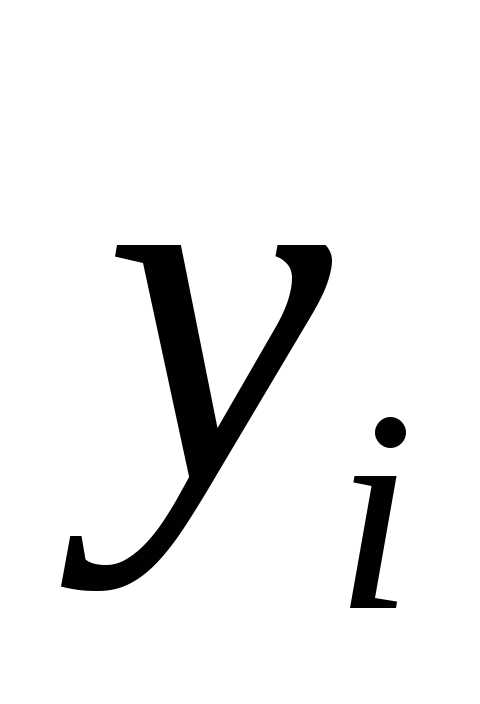 от значений функции
от значений функции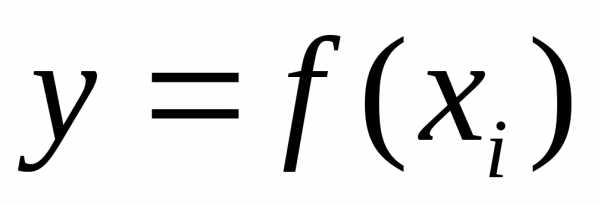 вычисленных по соответствующим им
значениям аргументов
вычисленных по соответствующим им
значениям аргументов ,
т.е.:
,
т.е.:
.
Разность называетсяневязкой. В качестве критерия согласия или величины отклонения можно было взять обычную сумму невязок или их абсолютных величин, но делать это нецелесообразно, поскольку в первом случае сумма невязок может быть малой или, даже, равняться нулю при значительном разбросе экспериментальных данных из-за того, что положительные отклонения будут скомпенсированы отрицательными. Сумма абсолютных величин невязок лишена этого недостатка, но она имеет другой – она не является дифференцируемой, что существенно затрудняет решение задачи.
В
ходе решения задачи отыскания оптимальных
параметров аппроксимационной функции 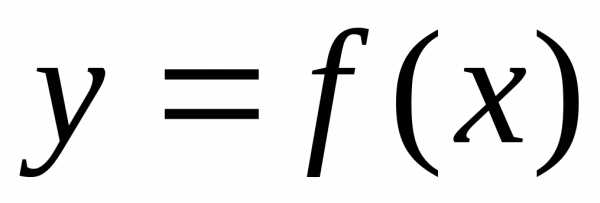 возникает необходимость поиска экстремума
функции нескольких переменных, поэтому
прежде чем решать эту задачу для
конкретных эмпирических функций,
необходимо рассмотреть свойства функций
нескольких переменных.
возникает необходимость поиска экстремума
функции нескольких переменных, поэтому
прежде чем решать эту задачу для
конкретных эмпирических функций,
необходимо рассмотреть свойства функций
нескольких переменных.
Предположим,
что функция  – линейная, т.е..
Если это выражение приближенно описывает
зависимость между
– линейная, т.е..
Если это выражение приближенно описывает
зависимость между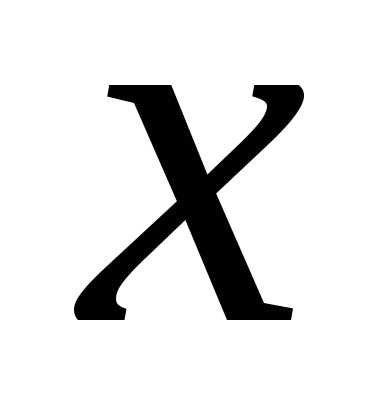 и
и ,
то сумма квадратов невязок должна быть
минимальной, т.е. значения параметров
,
то сумма квадратов невязок должна быть
минимальной, т.е. значения параметров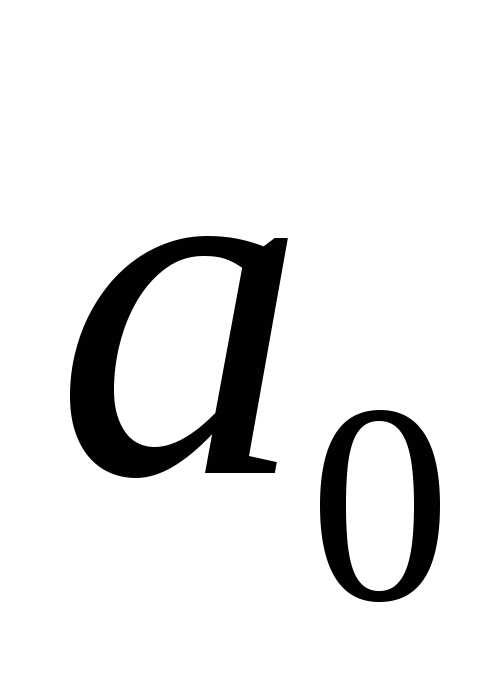 и
и должны соответствовать минимуму
величины:
должны соответствовать минимуму
величины:
.
Это
функция двух переменных 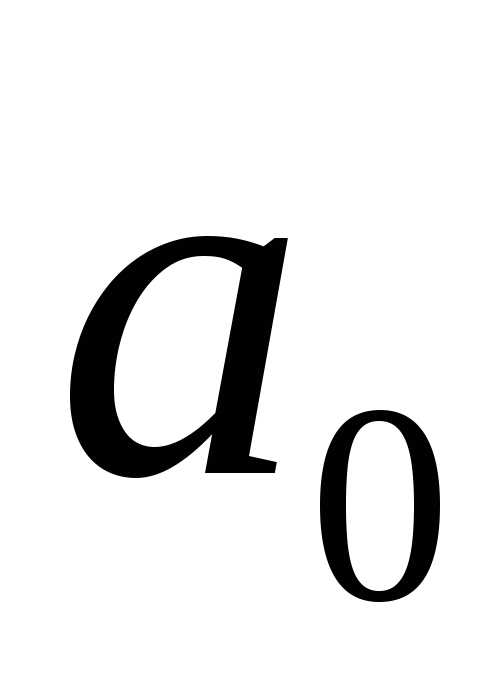 и
и ,
она непрерывна, дифференцируема,
неотрицательна и ограничена снизу. Для
того чтобы найти ее наименьшее значение,
необходимо ее частные производные
приравнять к нулю:
,
она непрерывна, дифференцируема,
неотрицательна и ограничена снизу. Для
того чтобы найти ее наименьшее значение,
необходимо ее частные производные
приравнять к нулю:
Таким
образом, для нахождения параметров 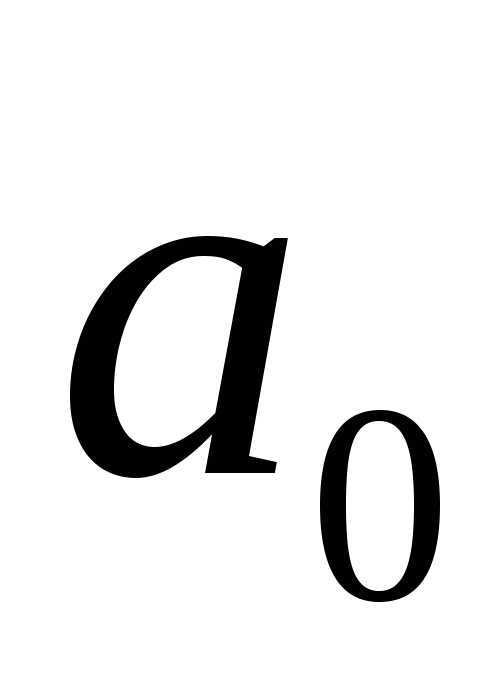 и
и необходимо решить систему уравнений:
необходимо решить систему уравнений:
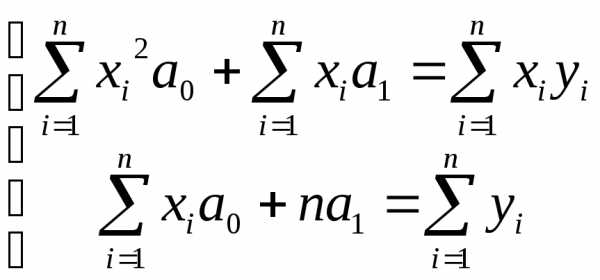
Эта линейная система уравнений имеет единственное решение, поскольку ее определитель:
не равен нулю.
Вторые
производные функции  равны:
равны:
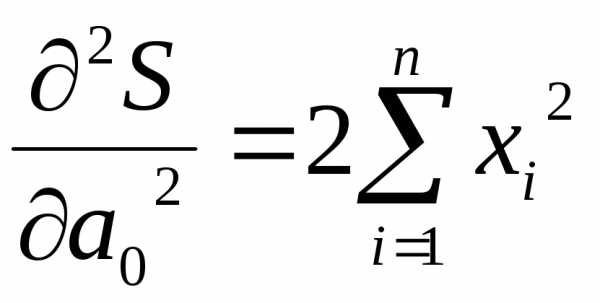 ;
; 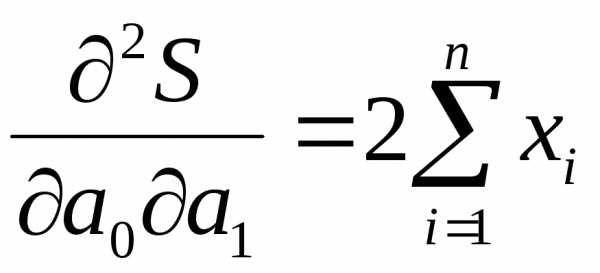 ;
;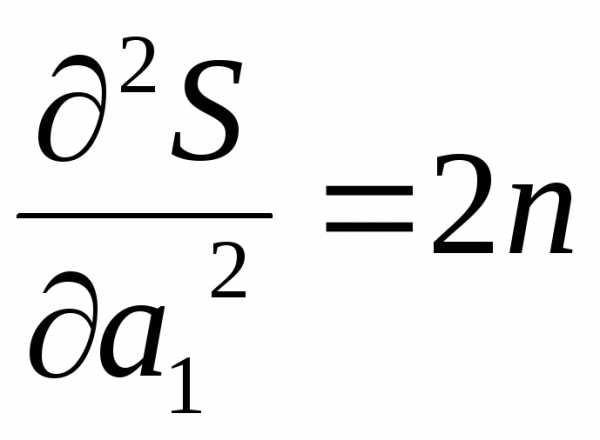 .
.
Главные
миноры матрицы квадратичной формы
положительны, т.е. 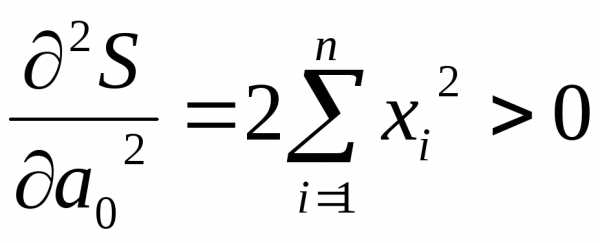 ;
;
.
Таким
образом, значения 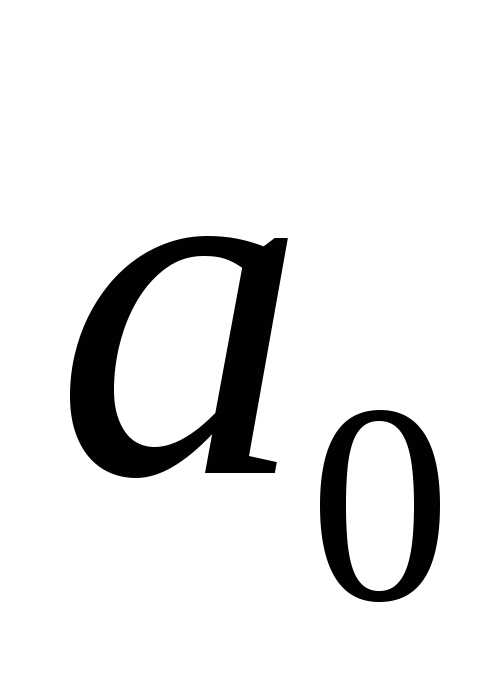 и
и ,
найденные при решении системы уравнений,
соответствуют минимуму функции
,
найденные при решении системы уравнений,
соответствуют минимуму функции .
.
Поскольку система невырождена, то решение можно найти по правилу Крамера:
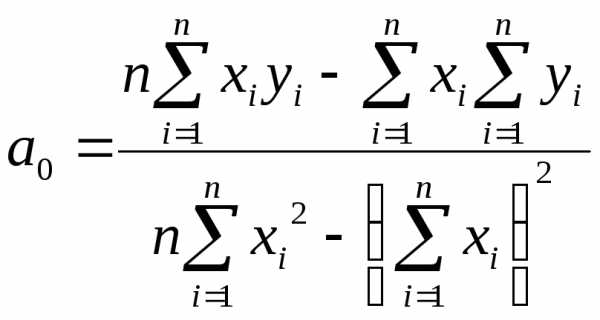 ,
,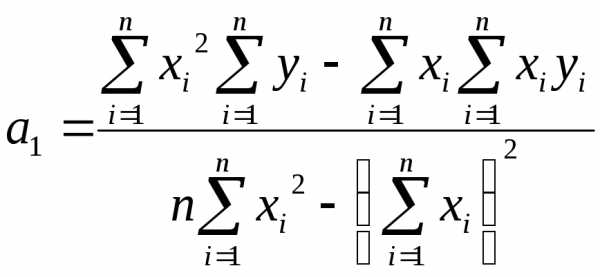 .
.
studfiles.net
Локальные экстремумы функции двух переменных
Определение. Точканазывается точкой локального максимума
(минимума) функции,
если существует -окрестность
этой точки, такая, что для всех точек
-окрестность
этой точки, такая, что для всех точек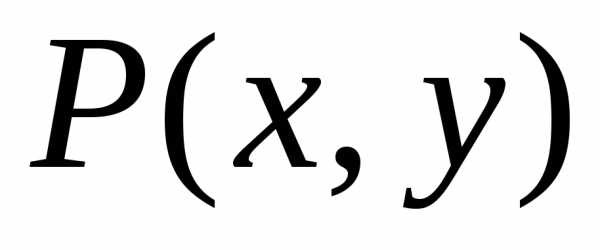
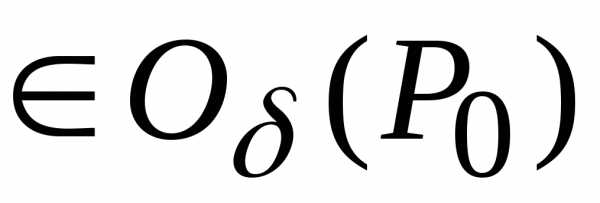 (принадлежащих
(принадлежащих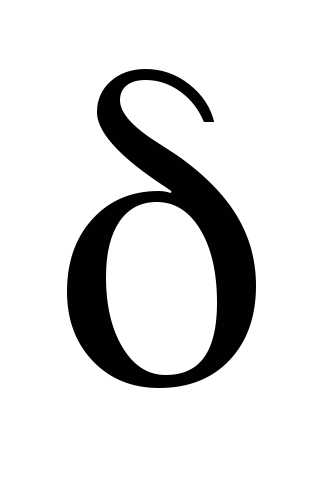 -окрестности
этой точки), отличных от точки,
выполняется неравенство().
-окрестности
этой точки), отличных от точки,
выполняется неравенство().
Значение называют локальным максимумом (минимумом) функции и пишут
().
Точки максимума и минимума функции называют точками экстремума функции, а максимумы и минимумы функции — экстремумами функции.
Пример.Функцияимеет локальный максимум в точке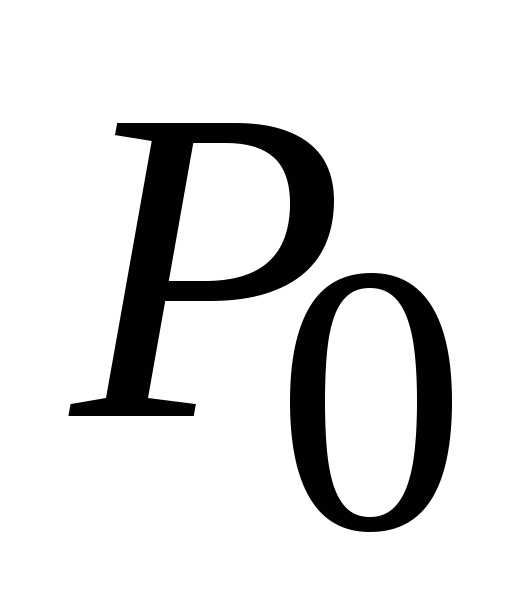 (1;
1):
(1;
1):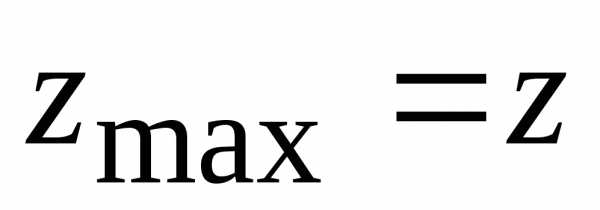 (1,
1) = 1.
(1,
1) = 1.
Действительно, существует окрестность
точки 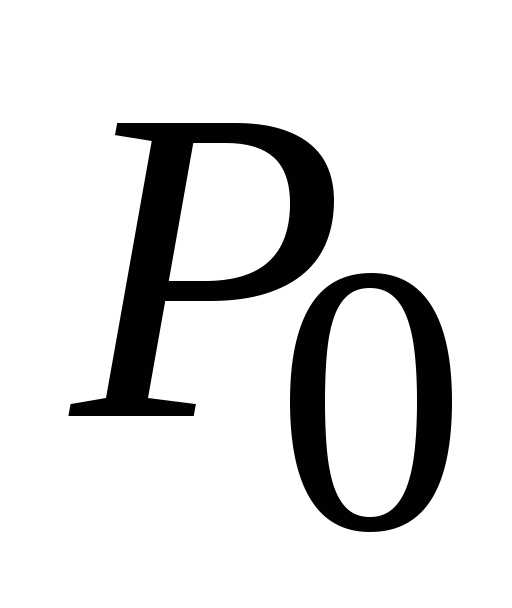 (1;
1), в которой выполняется условие
(1;
1), в которой выполняется условие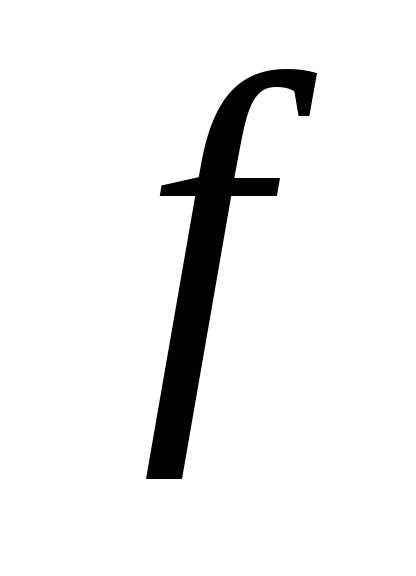 (1;
1) >
(1;
1) >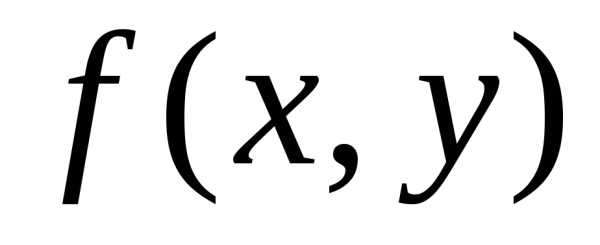 для.
Графиком этой функции является поверхность
— параболоид вращения, представленный
на рисунке.
для.
Графиком этой функции является поверхность
— параболоид вращения, представленный
на рисунке.
Отметим, что если функция имеет в точкелокальный экстремум, то:
в случае локального максимума,
в случае локального минимума.
Из сказанного выше следует, что полное
приращение функции не меняет знака в  .
Однако для всех точек
.
Однако для всех точек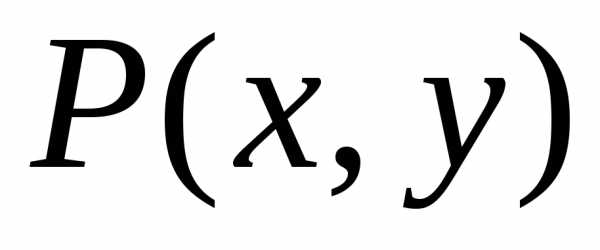
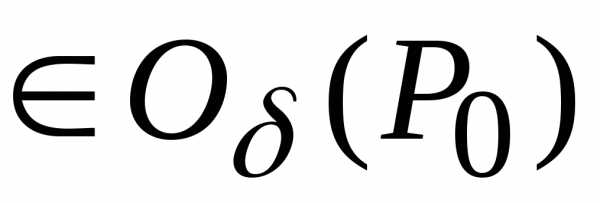 определить знак приращения
определить знак приращения практически невозможно, поэтому надо
искать другие условия, по которым можно
судить о наличии и характере экстремума
функции в данной точке.
практически невозможно, поэтому надо
искать другие условия, по которым можно
судить о наличии и характере экстремума
функции в данной точке.
Теорема (необходимые условия существования локального экстремума). Если в точкедифференцируемая функцияимеет локальный экстремум, то ее частные производные в этой точке равны нулю:
и,
или, по крайней мере, одна из них не существует.
Доказательство. Докажем только первое утверждение теоремы.
Рассмотрим в  лишь те точки, для которых
лишь те точки, для которых .
Получим функциюодной переменной
.
Получим функциюодной переменной .
Эта функция имеет в точке
.
Эта функция имеет в точке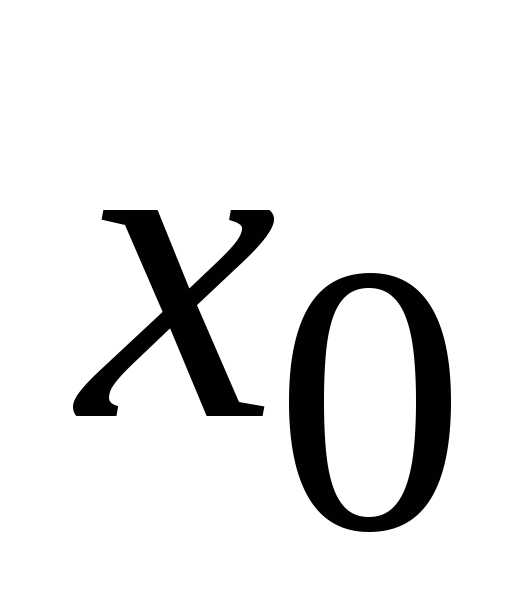 экстремум, следовательно,.
экстремум, следовательно,.
Аналогично доказывается, что .
Теорема доказана.
Проиллюстрируем примером второе утверждение теоремы .
Функция
имеет максимум в точке О(0; 0; 0), так как
для любой точки (О)
выполняется условие
(О)
выполняется условие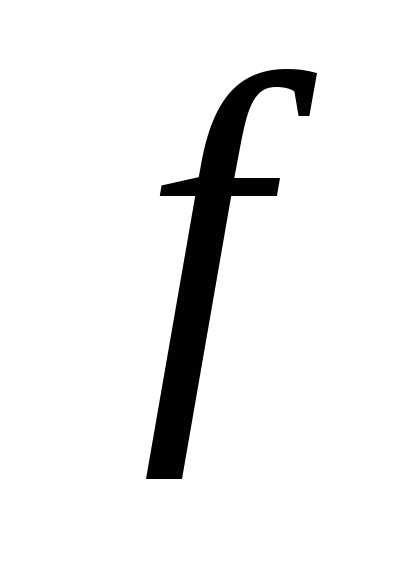 (0;
0) >
(0;
0) >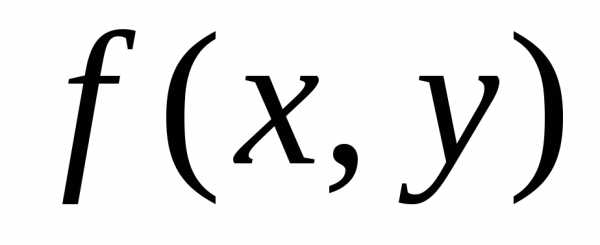 .
Частные производные
.
Частные производные
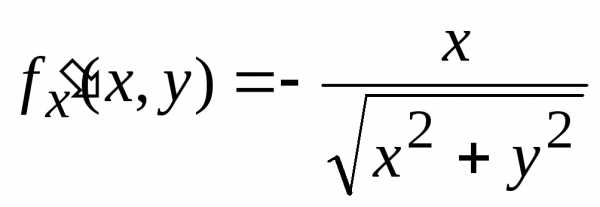 ,
,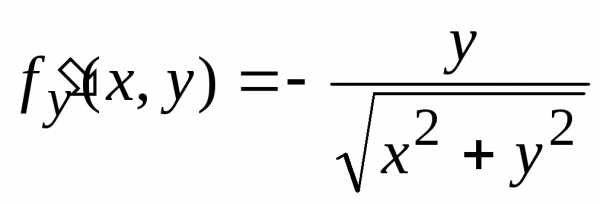
в точке О(0; 0) не существуют для . Графиком этой функции является конус, представленный на рисунке.
Следствие.Если функцияимеет в точкелокальный экстремум, то ее дифференциал в этой точке равен нулю или не существует.
Точка , в которой частные производные равны нулю, или хотя бы одна из них не существует, называется точкой возможного экстремума. Такие точки называются также стационарными или критическими.
Равенство нулю частных производных первого порядка не является достаточным условием существования экстремума функции в точке.
Действительно, возьмем, например, функцию 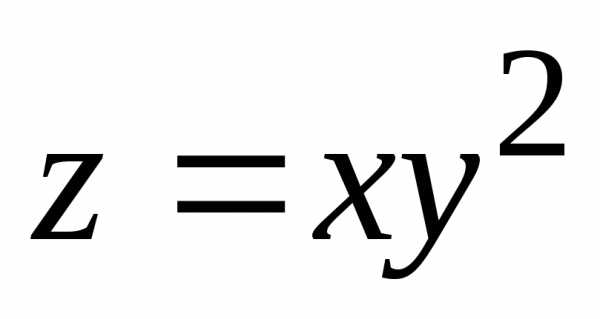 .
Она задана на всей числовой плоскостиR2. Точка О(0; 0) будет
критической, поскольку частные производные
в ней равны нулю. Так как функция равна
нулю в точке О, а в любой сколь угодно
малой окрестности
.
Она задана на всей числовой плоскостиR2. Точка О(0; 0) будет
критической, поскольку частные производные
в ней равны нулю. Так как функция равна
нулю в точке О, а в любой сколь угодно
малой окрестности (О)
она принимает как положительные, так и
отрицательные значения, то функция
(О)
она принимает как положительные, так и
отрицательные значения, то функция не имеет в точке О экстремума.
не имеет в точке О экстремума.
Теорема (достаточные условия
существования локального экстремума). Пусть— стационарная точка трижды дифференцируемой
в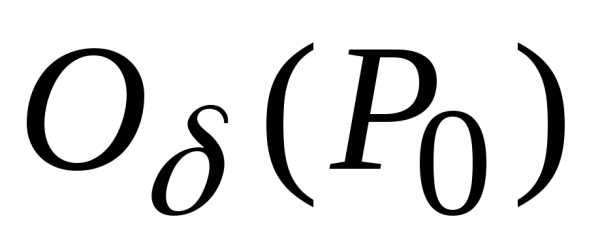 функциии пусть
функциии пусть
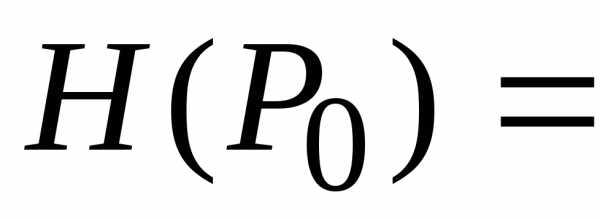 .
.
Тогда стационарная точка является:
1) точкой локального максимума, если и;
2) точкой локального минимума, если и;
3) если , то стационарная точкане является точкой локального экстремума функции.
Замечание.Если,
то нельзя определенно ответить на вопрос
о существовании экстремума в точке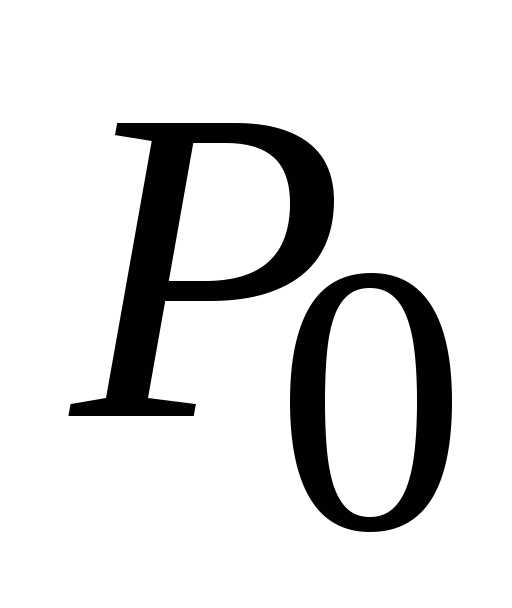 .
В этом случае необходимо произвести
дополнительные исследования знака
функциив
.
В этом случае необходимо произвести
дополнительные исследования знака
функциив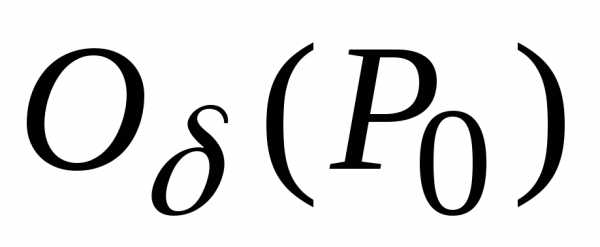 .
.
Приращения 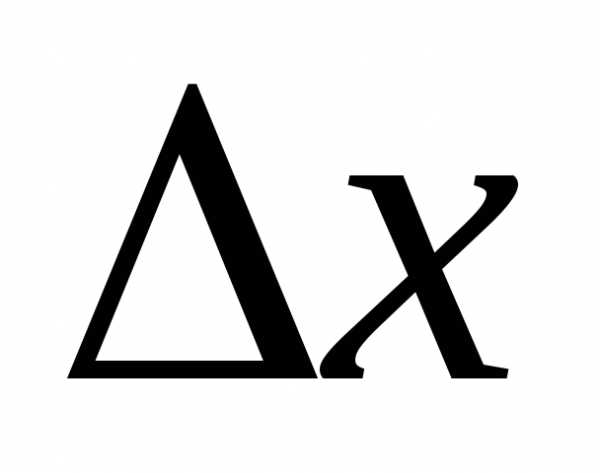 и
и не могут равняться нулю одновременно,
поскольку в подобном случае точкасовпала бы с точкойи функцияне получила бы никакого приращения.
не могут равняться нулю одновременно,
поскольку в подобном случае точкасовпала бы с точкойи функцияне получила бы никакого приращения.
Пример. Исследовать на экстремум функцию.
Решение.Вычислим частные производные первого порядка данной функции:
,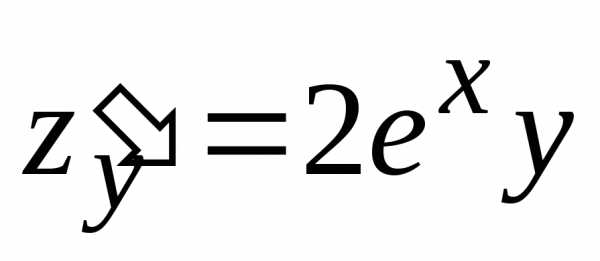 .
.
Находим точки возможного экстремума. Для этого решим систему уравнений:
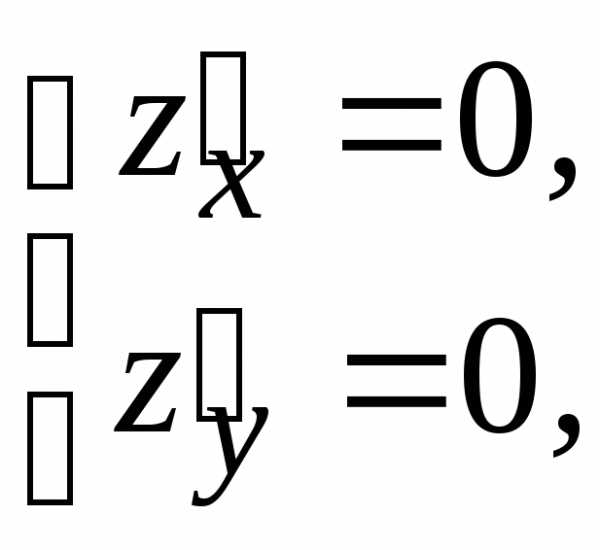

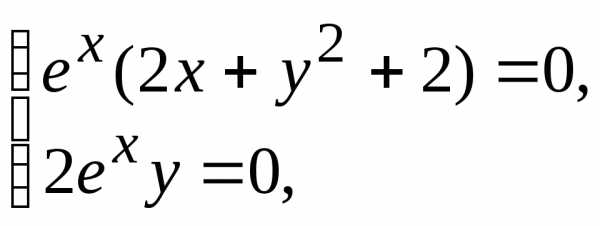
 (т. к.
(т. к.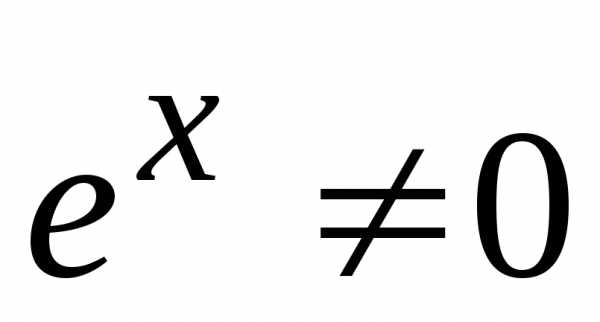 для
для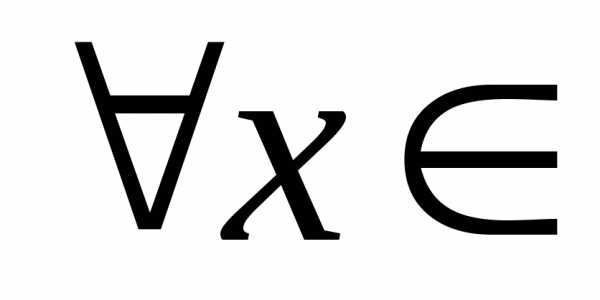 R)
R)
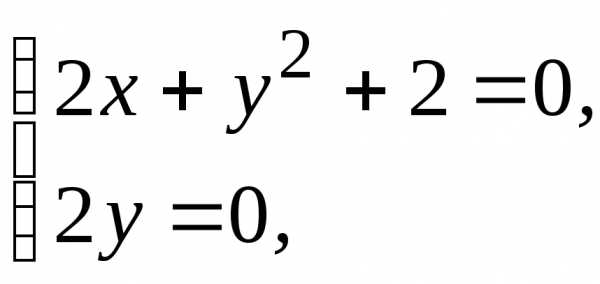

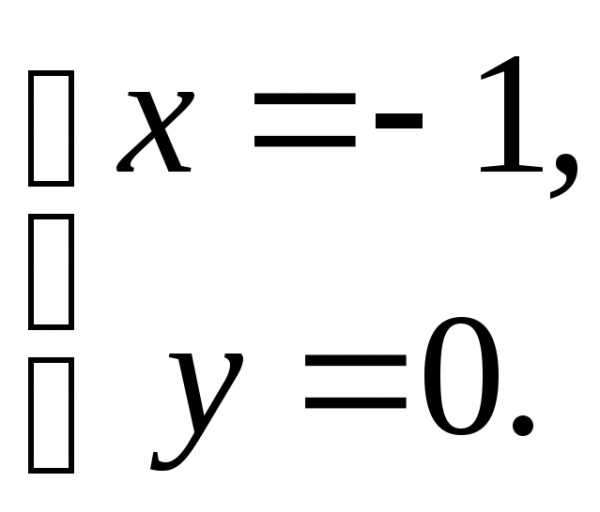
Таким образом, существует только одна
стационарная точка 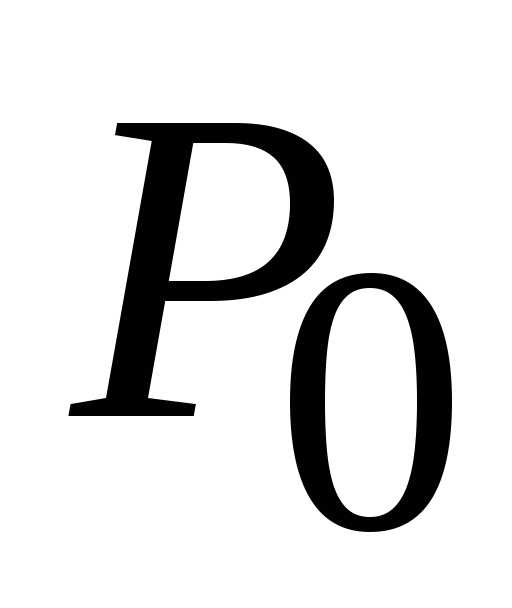 (1; 0), в которой
функция
(1; 0), в которой
функция может достигать экстремума.
может достигать экстремума.
Воспользуемся теоремой о достаточных условиях существования локального экстремума.
Для этого найдем частные производные второго порядка функции z:
,,.
Вычислим значения частных производных
второго порядка для стационарной точки 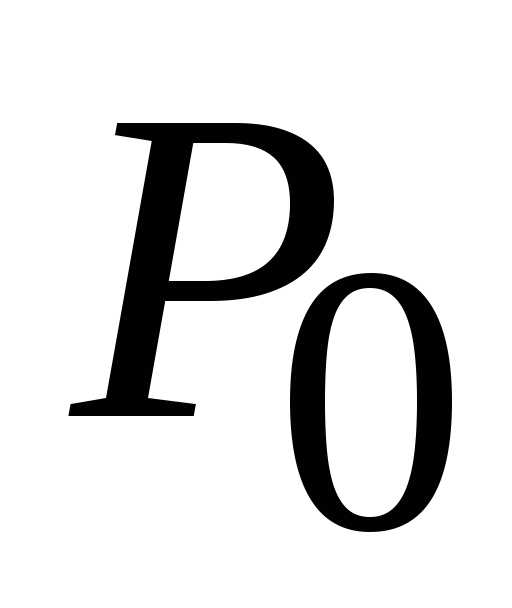 :
:
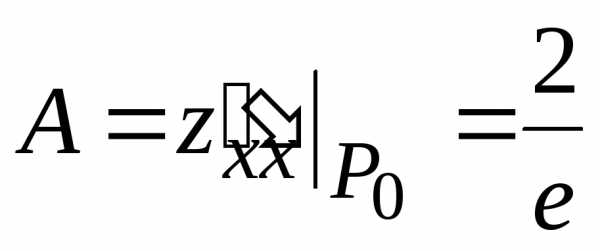 ,
,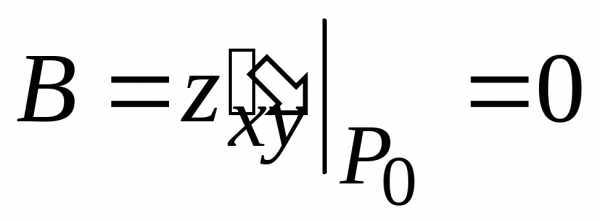 ,
,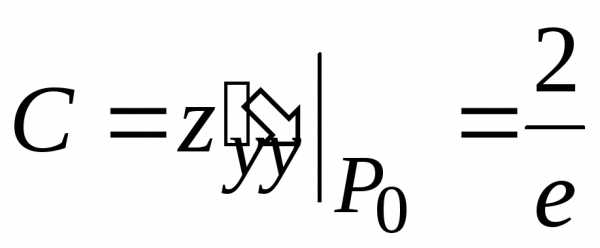 .
.
Так как  (1;
0),
(1;
0),
то по теореме о достаточных условиях
существования локального экстремума
точка 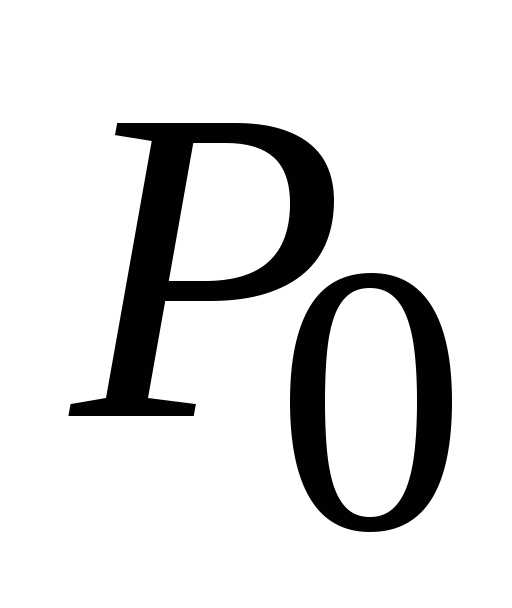 (1; 0) является
точкой локального экстремума, а т. к. А
> 0, то точка
(1; 0) является
точкой локального экстремума, а т. к. А
> 0, то точка (1; 0) является
точкой локального минимума, при этом
(1; 0) является
точкой локального минимума, при этом
.
Пример. Исследовать на экстремум функцию.
Решение.Вычислим частные производные первого порядка данной функции:,.
Для определения точек возможного экстремума решим систему уравнений:


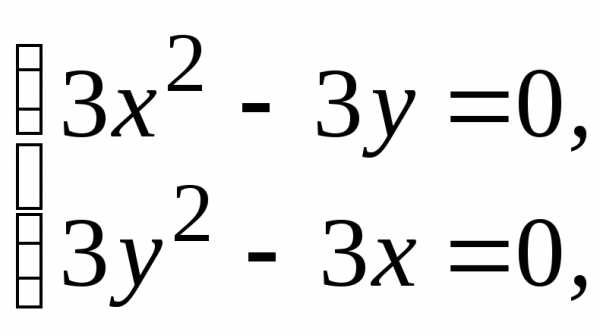

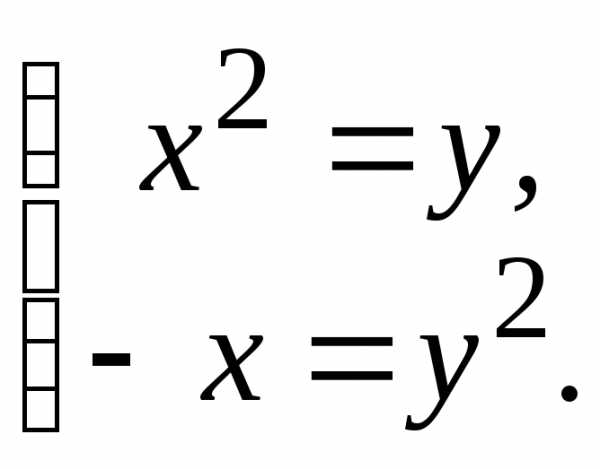
Данная система имеет два решения
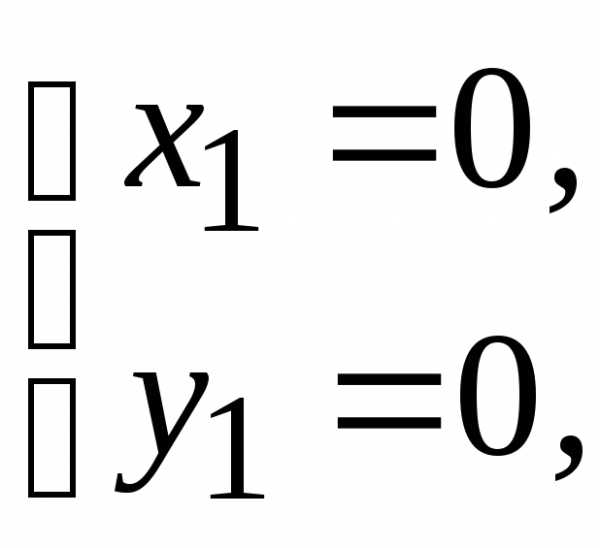 и
и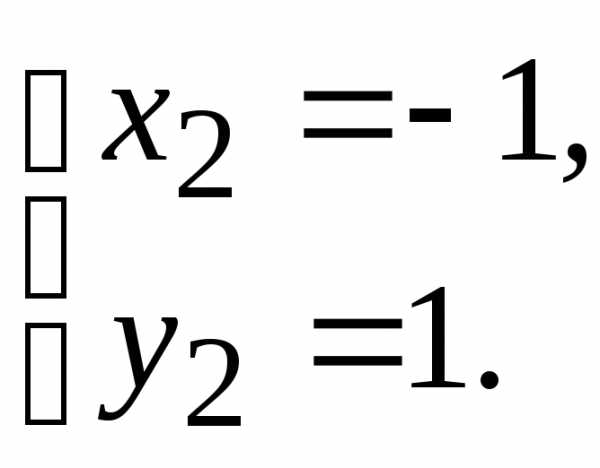
Следовательно, функция имеет две
стационарные точки  (0;
0) и
(0;
0) и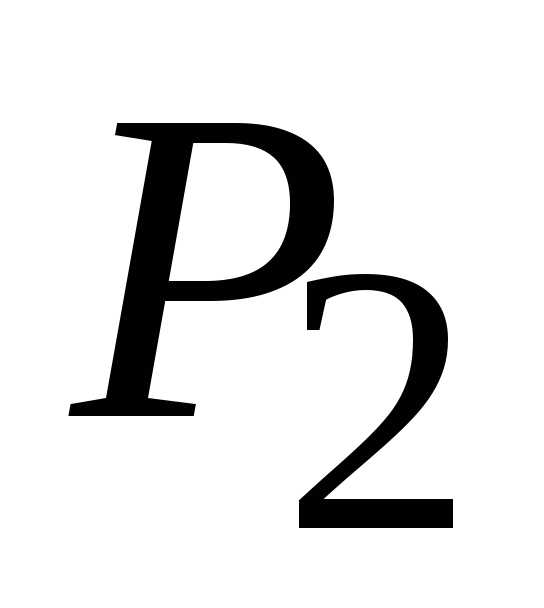 (1,
1). Вычислим частные производные второго
порядка функции
(1,
1). Вычислим частные производные второго
порядка функции :
:
,,.
.
Вычислим  для точки
для точки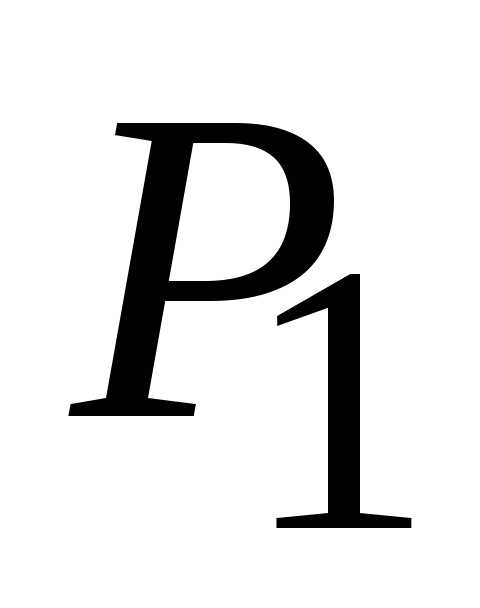 (0;
0). Так как
(0;
0). Так как (0;
0),
то в точке
(0;
0),
то в точке (0;
0) нет экстремума.
(0;
0) нет экстремума.
Вычислим  для точки
для точки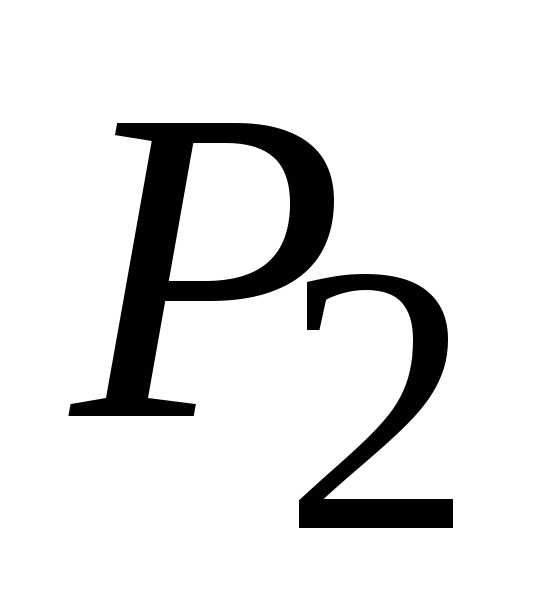 (1,
1). Т. к.
(1,
1). Т. к. (1;
1),
то точка
(1;
1),
то точка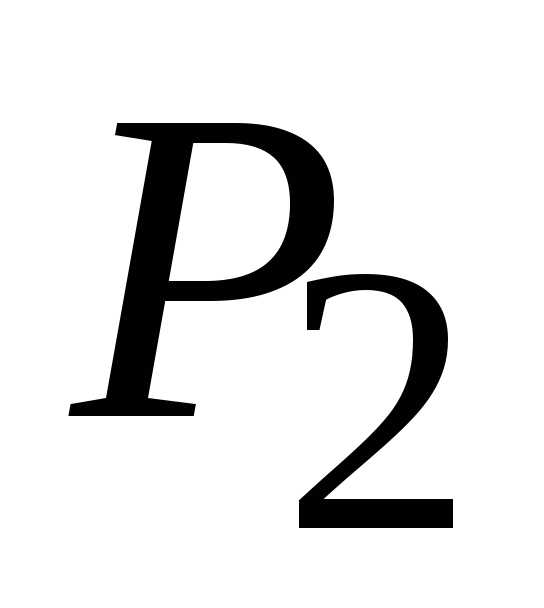 (1,
1) является точкой локального экстремума,
а т. к.
,
то точка
(1,
1) является точкой локального экстремума,
а т. к.
,
то точка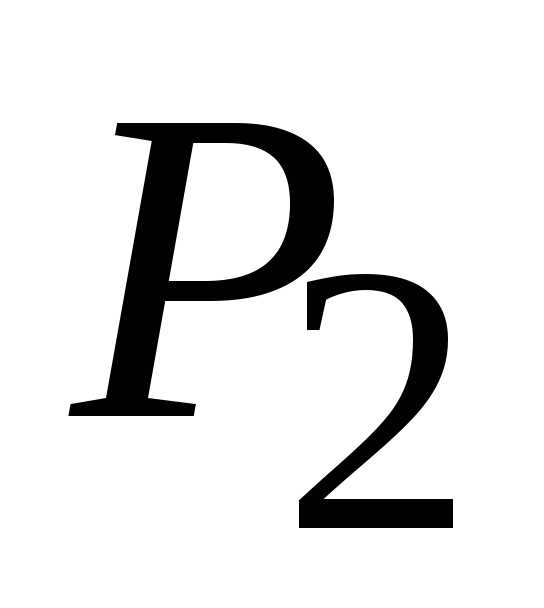 (1,
1) является точкой локального максимума,
при этом
(1,
1) является точкой локального максимума,
при этом
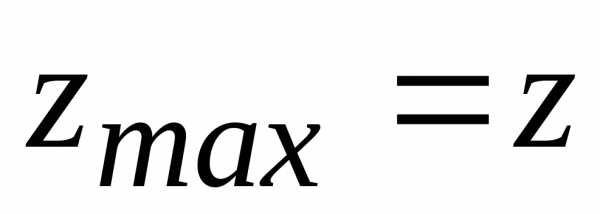 (1;
1)=9.
(1;
1)=9.
Пример. Исследовать на экстремум
функцию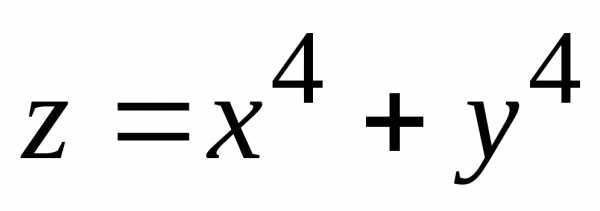 .
.
Решение.Вычислим частные
производные первого порядка функции :
:

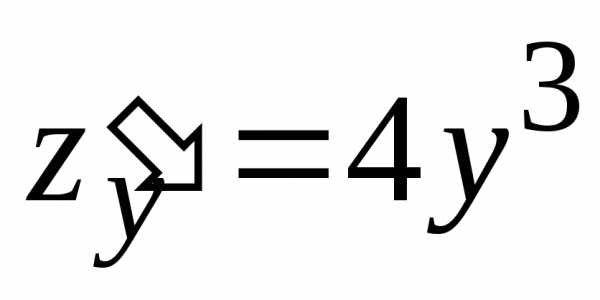 .
.
Решая систему уравнений:
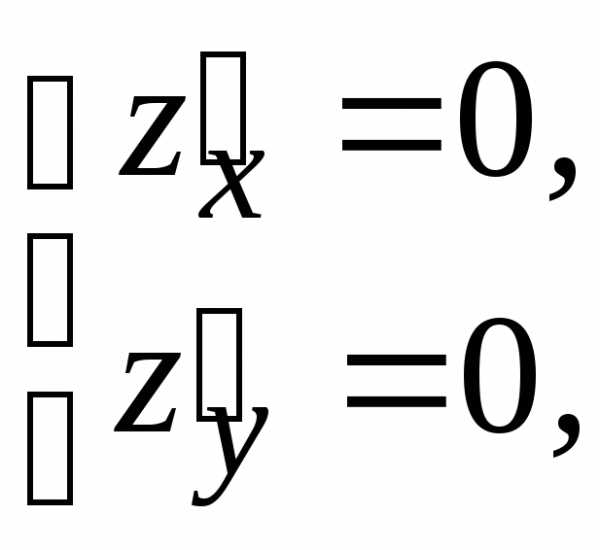

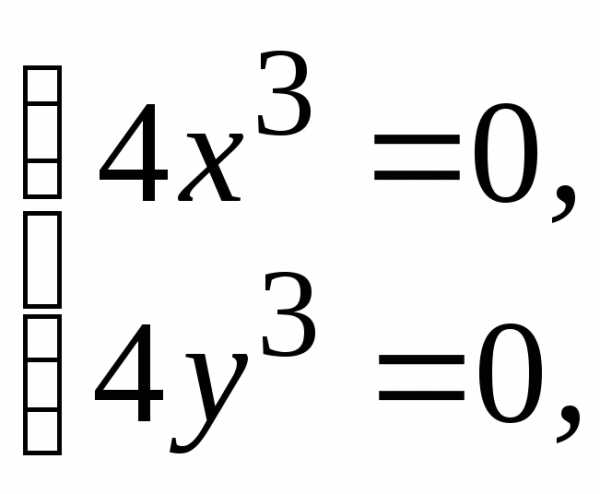

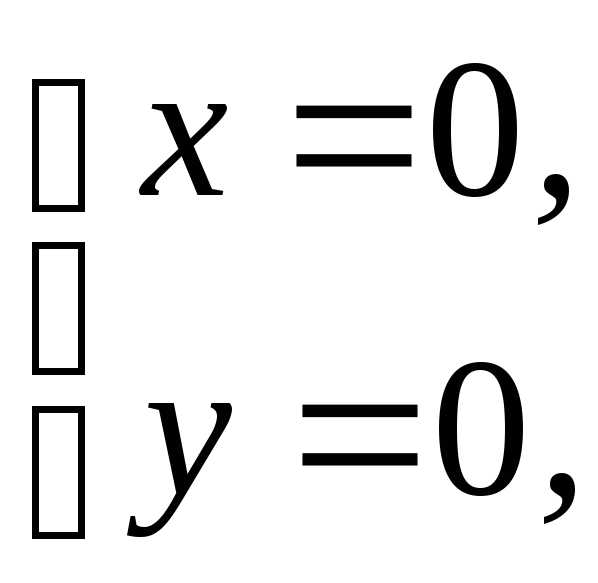
находим единственную стационарную
точку 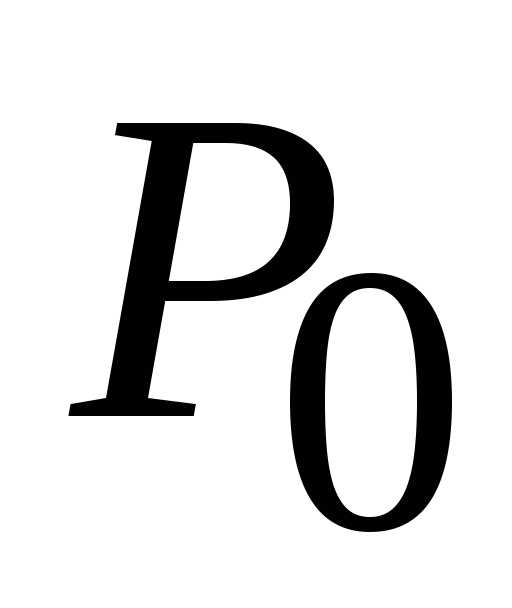 (0; 0) данной функции.
(0; 0) данной функции.
Найдем частные производные второго
порядка функции  :
:
,,
Для стационарной точки 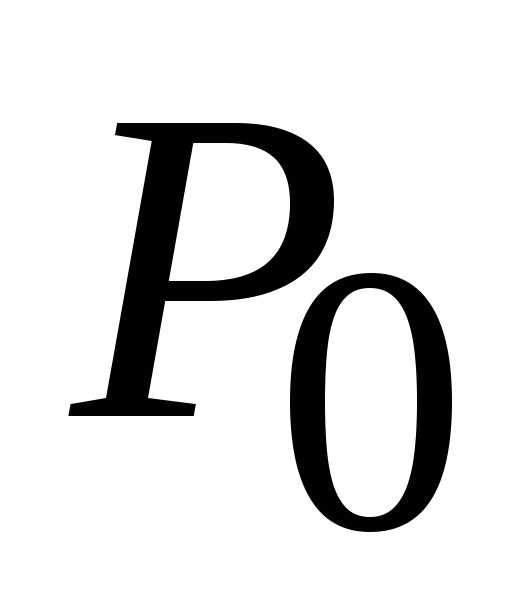 (0; 0)
(0; 0)
,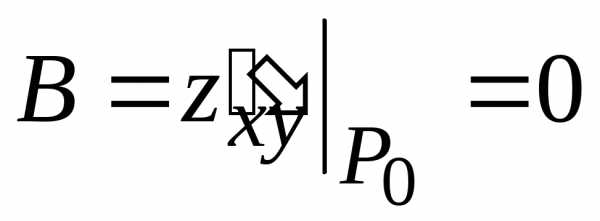 ,
,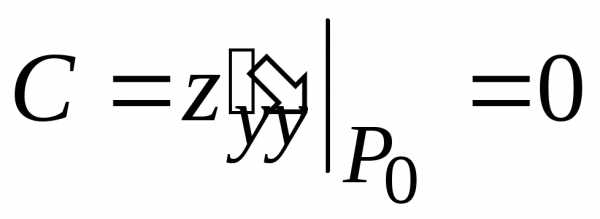

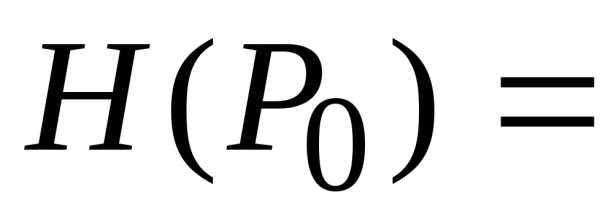 .
.
Следовательно, по теореме о достаточных
условиях существования локального
экстремума нельзя определенно ответить
на вопрос о существовании экстремума
в точке 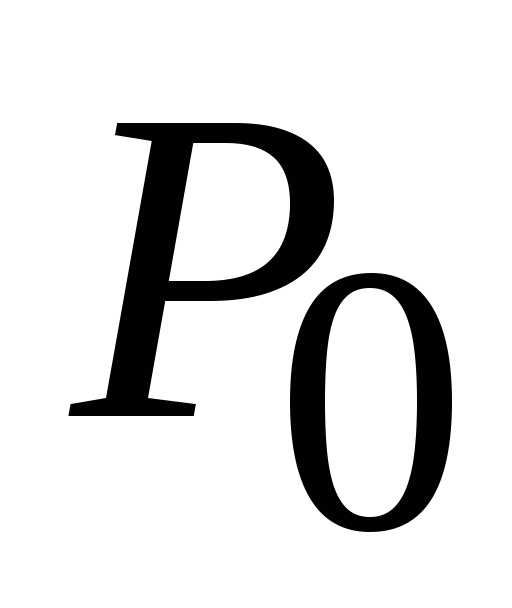 (0; 0). В данном случае стационарная
точка
(0; 0). В данном случае стационарная
точка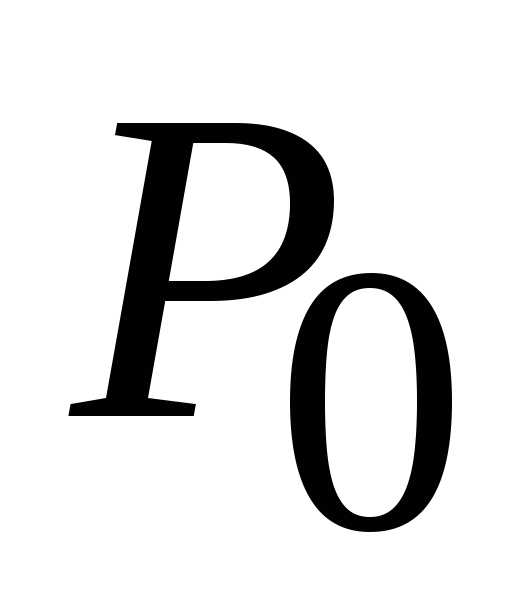 (0; 0) является точкой локального
минимума, поскольку,
(0; 0) является точкой локального
минимума, поскольку,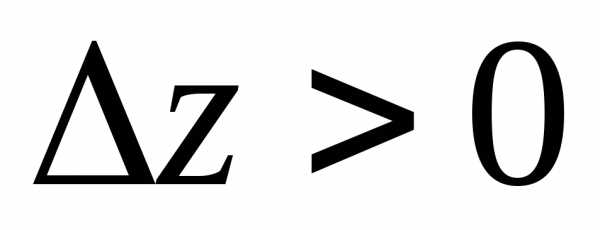 для
для
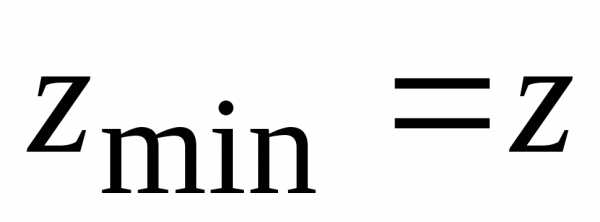 (0;
0)=0.
(0;
0)=0.
studfiles.net
