Построить график функции y=f(x). Исследование функции онлайн.
Введите график функции
Построим (исследуем) график функции y=f(x), для этого задайте функцию f(x)
Важно: a должно быть меньше b, иначе график не сможет построиться. Cледите за масштабом — если графика на рисунке нету, значит стоит поварьировать значения a и b
Примеры
С применением степени
(квадрат и куб) и дроби
(x^2 - 1)/(x^3 + 1)
Квадратный корень
sqrt(x)/(x + 1)
Кубический корень
cbrt(x)/(3*x + 2)
С применением синуса и косинуса
2*sin(x)*cos(x)
Арксинус
x*arcsin(x)
Арккосинус
x*arccos(x)
Применение логарифма
x*log(x, 10)
Натуральный логарифм
ln(x)/x
Экспонента
exp(x)*x
Тангенс
tg(x)*sin(x)
Котангенс
ctg(x)*cos(x)
Иррациональне дроби
(sqrt(x) - 1)/sqrt(x^2 - x - 1)
Арктангенс
x*arctg(x)
Арккотангенс
x*arсctg(x)
Гиберболические синус и косинус
2*sh(x)*ch(x)
Гиберболические тангенс и котангенс
ctgh(x)/tgh(x)
Гиберболические арксинус и арккосинус
x^2*arcsinh(x)*arccosh(x)
Гиберболические арктангенс и арккотангенс
x^2*arctgh(x)*arcctgh(x)
Исследование графика функции
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число — «Пи», которое примерно равно 3.14
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
www.kontrolnaya-rabota.ru
Оператор |
Описание |
Простейшие математические операции |
|
+ — * / () |
Сложение, вычитание, умножение, деление и группирующие символы: + — * / () . Знак умножения * — необязателен: выражение 2sin(3x) эквивалентно 2*sin(3*x). Cкобки используются для группирования выражений. |
0.5 |
Десятичные дроби записываются через точку:
|
Элементарные функции |
|
xn |
Возведение в степень: x^n, например, для ввода x2 используется x^2 |
√x |
Квадратный корень: \sqrt(x) или x^(1/2) |
3√x |
Кубический корень: x^(1/3) |
n√x |
Корень n-той степени из x: x^(1/n) |
ln(x) |
Натуральный логарифм (логарифм c основанием e): log(x) |
logax |
Логарифм от x по основанию a: log(x)/log(a) |
lg(x) |
Десятичный логарифм (логарифм по основанию 10): log(x)/log(10) |
ex |
Экспоненциальная функция: exp(x) |
Тригонометрические функции |
|
sin(x) |
Синус от x: sin(x) |
cos(x) |
Косинус от x: cos(x) |
tg(x) |
Тангенс от x: tan(x) |
ctg(x) |
Котангенс от x: 1/tan(x) |
arcsin(x) |
Арксинус от x: arcsin(x) |
arccos(x) |
Арккосинус от x: arccos(x) |
arctan(x) |
Арктангенс от x: arctan(x) |
arcctg(x) |
Арккотангенс от x: \pi/2 — arctan(x) |
Некоторые константы |
|
e |
Число Эйлера e: \e |
π |
Число π: \pi |
ru.onlinemschool.com
| Обозначение | Описание |
| + | Сложение |
| — | Вычитание |
| * | Умножение |
| / | Деление |
| ( ) | Группирующие символ |
| x^n или p(x,n) | Возведение x в степень n |
| exp(x) | Экспоненциальная функция, т.е. возведение e в степень x |
| root(x,n) | Корень n-степени из x |
| sqr(x) или sqrt(x) | Квадратный корень из x |
| cbr(x) или cbrt(x) | Кубический корень из x |
| logn(x,a) | Логарифм x по основанию a |
| ln(x) | Натуральный логарифм x, т.е. логарифм x по основанию e |
| lb(x) | Логарифм x по основанию 2 |
| lg(x) | Логарифм x по основанию 10 |
| sin(x) | Синус от x |
| cos(x) | Косинус от x |
| tan(x) | Тангенс от x |
| cotan(x) | Котангенс от x |
| sec(x) | Секанс от x |
| csc(x) | Косеканс от x |
| asin(x) | Арксинус от x |
| acos(x) | Арккосинус от x |
| atan(x) | Арктангенс от x |
| acot(x) | Арккотангенс от x |
| asec(x) | Арксеканс от x |
| acsc(x) | Арккосеканс от x |
| sinh(x) | Гиперболический синус от x |
| cosh(x) | Гиперболический косинус от x |
| tanh(x) | Гиперболический тангенс от x |
| coth(x) | Гиперболический котангенс от x |
| sech(x) | Гиперболический секанс от x |
| csch(x) | Гиперболический косеканс от x |
| asinh(x) | Гиперболический арксинус от x |
| acosh(x) | Гиперболический арккосинус от x |
| atanh(x) | Гиперболический арктангенс от x |
| acoth(x) | Гиперболический арккотангенс от x |
| asech(x) | Гиперболический арксеканс от x |
| acsch(x) | Гиперболический арккосеканс от x |
| Нормальное распределение (распределение Гаусса) со средним значением m и стандартным отклонением n | |
| min(n1,n2) | Возвращает наименьшее из двух значений |
| max(n1,n2) | Возвращает наибольшее из двух значений |
| round(x) | Классическое округление x до целого числа |
| floor(n1,n2) | Округление x вниз до ближайшего целого числа |
| ceil(n1,n2) | Округление x вверх до ближайшего целого числа |
| abs(x) | Модуль x |
| rand | Случайное число от 0 до 1 |
| sgn(x) | Сигнум x. Возвращает 1, если x>0 Возвращает 0, если x=0 Возвращает -1, если x<0 |
| e | Число Эйлера: 2.7182818284… |
| Phi | Золотое отношение: 1.6180339887… |
| pi | Число Пи: 3.1415926535… |
allcalc.ru
| Обозначение | Описание |
| + | Сложение |
| — | Вычитание |
| * | Умножение |
| / | Деление |
| () | Группирующие символ |
| x^n | Возведение x в степень n |
| p(x,n) | Возведение x в степень n |
| exp(x) | Экспоненциальная функция, т.е. возведение e в степень x |
| root(x,n) | Корень n-степени из x |
| sqr(x) | Квадратный корень из x |
| sqrt(x) | Квадратный корень из x |
| cbr(x) | Кубический корень из x |
| cbrt(x) | Кубический корень из x |
| logn(x,a) | Логарифм x по основанию a |
| ln(x) | Натуральный логарифм x, т.е. логарифм x по основанию e |
| lb(x) | Логарифм x по основанию 2 |
| lg(x) | Логарифм x по основанию 10 |
| sin(x) | Синус от x |
| cos(x) | Косинус от x |
| tan(x) | Тангенс от x |
| cotan(x) | Котангенс от x |
| sec(x) | Секанс от x |
| csc(x) | Косеканс от x |
| asin(x) | Арксинус от x |
| acos(x) | Арккосинус от x |
| atan(x) | Арктангенс от x |
| acot(x) | Арккотангенс от x |
| asec(x) | Арксеканс от x |
| acsc(x) | Арккосеканс от x |
| sinh(x) | Гиперболический синус от x |
| cosh(x) | Гиперболический косинус от x |
| tanh(x) | Гиперболический тангенс от x |
| coth(x) | Гиперболический котангенс от x |
| sech(x) | Гиперболический секанс от x |
| csch(x) | Гиперболический косеканс от x |
| asinh(x) | Гиперболический арксинус от x |
| acosh(x) | Гиперболический арккосинус от x |
| atanh(x) | Гиперболический арктангенс от x |
| acoth(x) | Гиперболический арккотангенс от x |
| asech(x) | Гиперболический арксеканс от x |
| acsch(x) | Гиперболический арккосеканс от x |
| gaussd(x,m,n) | Нормальное распределение (распределение Гаусса) со средним значением m и стандартным отклонением n |
| min(n1,n2) | Возвращает наименьшее из двух значений |
| max(n1,n2) | Возвращает наибольшее из двух значений |
| round(x) | Классическое округление x до целого числа |
| floor(n1,n2) | Округление x вниз до ближайшего целого числа |
| ceil(n1,n2) | Округление x вверх до ближайшего целого числа |
| abs(x) | Модуль x |
| rand | Случайное число от 0 до 1 |
| sgn(x) | Сигнум x. Возвращает 1, если x>0 Возвращает 0, если x=0 Возвращает -1, если x<0 |
| e | Число Эйлера: 2.7182818284… |
| Phi | Золотое отношение: 1.6180339887… |
| pi | Число Пи: 3.1415926535… |
www.aiportal.ru
Окружность. Как построить окружность? Формула окружности.
Как построить окружность?
Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соединяющей точку окружности с ее центром.
Чтобы построить окружность необходимо знать уравнение окружности:
(х – а)2 + (у – b)2 = R 2
Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:
Пример №1:
(х – 1)2 + (у – 2)2 = 42
Найдем центр окружности:
х – 1=0
x=1
у – 2=0
y=2
Центр окружности будет находится в точке (1;2)
Найдем радиус окружности:
R 2=4
R 2=22
R=2
Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.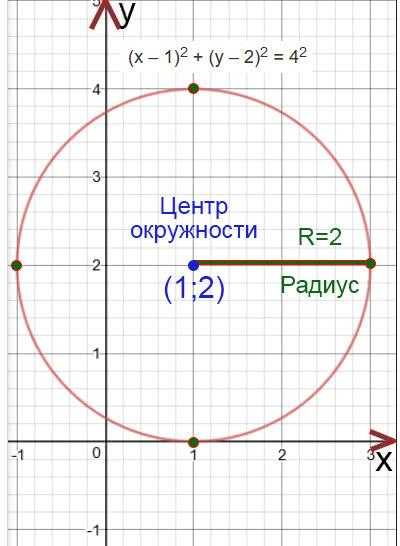
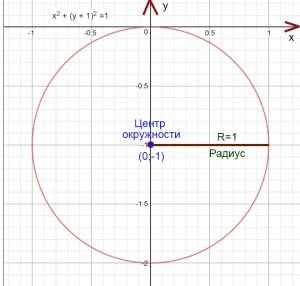
Пример №2:
х2 + (у + 1)2 =1
Можно представить уравнение окружности ввиде:
(х-0)2 + (у + 1)2 =12
Найдем центр окружности:
х=0
у + 1=0
y=–1
Центр окружности будет находится в точке (0;–1)
Найдем радиус окружности:
R 2=1
R 2=12
R=1
Построим окружность.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
tutomath.ru
ОНЛАЙН ДИАГРАММЫ | создавайте Ваши собственные диаграммы онлайн
Диаграммы — великолепное изобретение для визуализации информации. На сайте OnlineCharts.ru Вы сможете создавать и публиковать Ваши собственные онлайн диаграммы абсолютно бесплатно.
Наша система поддерживает множество типов диаграмм, включая такие, как: столбчатые диаграммы, круговые диаграммы, линейные диаграммы, пузырьковые диаграммы и радиальные диаграммы.
Создайте Вашу диаграмму »
Столбчатая
Линейная
С областями
Круговая
XY график
Радиальная
Точечная
Пузырьковая
Полярные бульки
Спидометр
Столбчатая/Линейная
Пирамида
Примеры диаграмм
Car Sales 1967-2007 (NL)
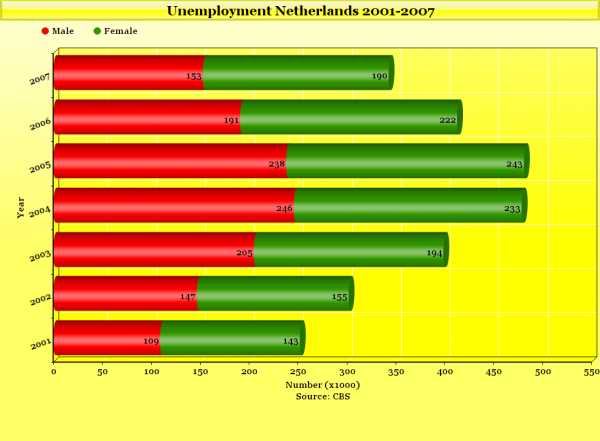
Unemployment 2001-2007 (NL)
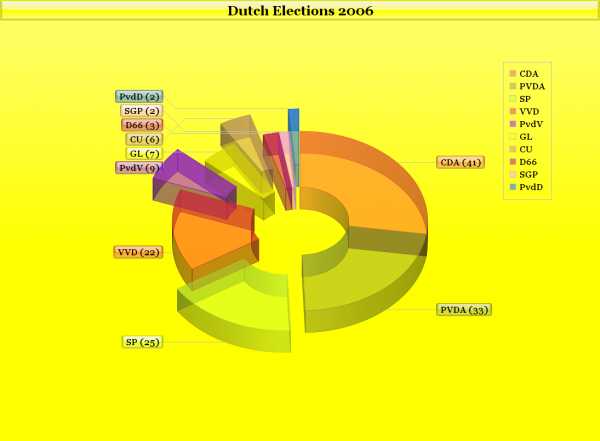
Dutch Elections 2006
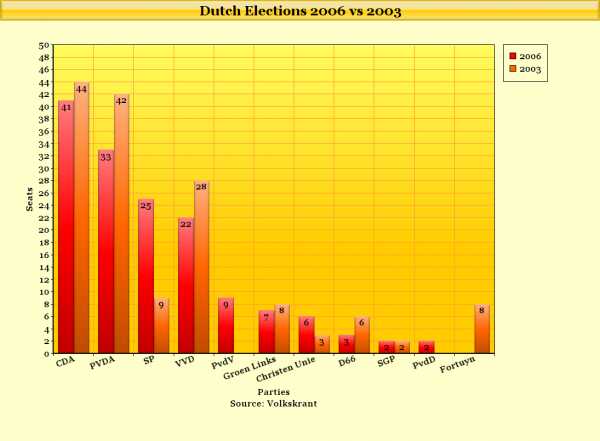
Dutch Elections 2006 vs 2003
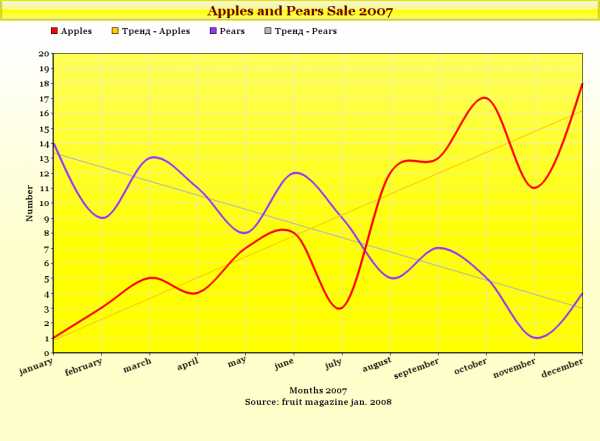
Apples and Pears Sale 2007
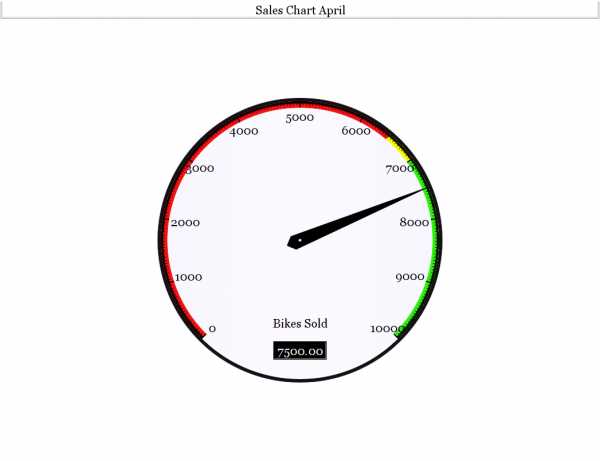
Sales Chart April
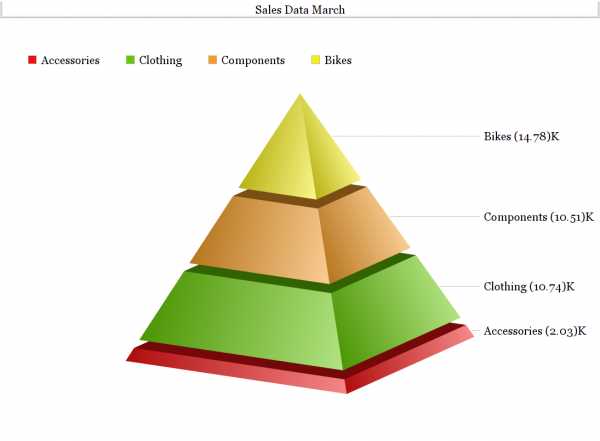
Sales Data March
www.onlinecharts.ru
Уравнения, радиуса и центра окружности по трем точкам
Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.
Уравнение окружности
r2 = (x — h)2 + (y — k)2
где,
- h,k — координаты центра Окружности
- x,y — координаты точки окружности
- r — радиус
Пример
Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)
Решение :
Шаг:1
Подставляем координаты точек в формулу
- (2 — h)2 + (2 — k)2 = r2
- (2 — h)2 + (4 — k)2 = r
- (5 — h)2 + (5 — k)2 = r2
Шаг :2
Найдем значение k упрощая 1 и 2 уравнения
- (2 — h)2 + (2 — k)2 = (2 — h)2 + (4 — k)2
- 4 — 4h + h2+ 4 — 4k + k2 = 4 — 4h + h2+16 — 8k + k2
- 8 — 4k = 20 — 8k
- k=3
Шаг :3
Найдем значение h упрощая уравнения 2 и 3
- (2 — h)2 + (2 — k)2 = (5 — h)2 + (5 — k)2
- 4 — 4h + h2+ 4 — 4k + k2 = 25 — 10h + h2+ 25 — 10k + k2
- 8 — 4k — 4h = 50 — 10h — 10k
- 6k + 6h = 42
Подставив значение k=3 в уравнение
Получаем координаты точки центра (h,k) = (4,3)
Шаг :4
Подставим значения h,k в формулу
- r2 = (x — h)2 + (y — k)2
- r2 = (2 — 4)2 + (2 — 3)2
- r2 = (-2)2 + (-1)2
- r2 = 5
- r = 2.24
Шаг :5
Подставим значения h, k в уравнение окружности
(x — h)2 + (y — k)2
Уравнение окружности = (x — 4)2 + (y — 3)2
Ответ :
- Координаты точки центра окружности c(h,k) = c(4,3)
- Радиус окружности r = 2.24
- Уравнение окружности = (x — 4)2 + (y — 3)2 = (2.24)2
wpcalc.com
