Два вектора перпендикулярны если – .

Перпендикулярные векторы и условие перпендикулярности

ОПРЕДЕЛЕНИЕ Два вектора и называются ортогональными (перпендикулярными), если угол между ними прямой.

Перпендикулярные векторы и условие перпендикулярности

Условие ортогональности векторов. Векторы и будут ортогональными тогда и только тогда, когда их скалярное произведение равно нулю:

   

Если векторы заданы своими координатами: и , то условие ортогональности запишется в виде:

   

Примеры решения задач

ПРИМЕР

Задание	Исследовать векторы и на ортогональность.
Решение	Согласно условию ортогональности, два вектора перпендикулярны, если их скалярное произведение равно нулю. Вычислим скалярное произведение заданных векторов, оно равно сумме произведений соответствующих координат:     Поскольку в результате получили ненулевое значение, то делаем вывод, что векторы не являются ортогональными.
Ответ	Векторы и не ортогональны.

ПРИМЕР

Задание	При каком значении параметра векторы и будут ортогональными?
Решение	Два вектора ортогональны, если их скалярное произведение равно нулю:         Таким образом, заданные векторы ортогональны при .
Ответ

ru.solverbook.com

Ортогональность векторов.

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = {a_x; a_y} и b = {b_x; b_y}, условие ортогональности запишется следующим образом:

a · b = a_x · b_x + a_y · b

y = 0

Пример 1. Доказать что вектора a = {1; 2} и b = {2; -1} ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 2. Проверить являются ли вектора a = {3; -1} и b = {7; 5} ортогональными.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Пример 3. Найти значение числа n при котором вектора a = {2; 4} и b = {n; 1} будут ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2n + 4
2n + 4 = 0
2n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = {a_x

; a_y; a_z} и b = {b_x; b_y; b_z}, условие ортогональности запишется следующим образом:

a · b = a_x · b_x + a_y · b_y + a_z · b_z = 0

Пример 4. Доказать что вектора a = {1; 2; 0} и b = {2; -1; 10} ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 5. Проверить являются ли вектора a = {2; 3; 1} и b = {3; 1; -9} ортогональными.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 6. Найти значение числа n при котором вектора a = {2; 4; 1} и b = {n; 1; -8} будут ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 — 8 = 2n — 4
2n — 4 = 0
2n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

ru.onlinemschool.com

Как найти вектор перпендикулярный вектору

Рассмотрим формулы и примеры, с помощью которых станет проще понять как найти вектор перпендикулярный вектору.
Для перпендикулярности двух векторов необходимо выполнение одного условия: скалярное произведение данных векторов должно быть равным нулю.
Сразу же рассмотрим два случая:

1-й случай. Векторы заданы на плоскости. В таком случае они будут заданы двумя координатами х и у и условие перпендикулярности этих векторов будет:

   

2-й случай. Векторы заданы в пространстве. В таком случае они будут заданы тремя координатами х, у и z и условие перпендикулярности этих векторов:

   

Рассмотрим на примере как найти вектор перпендикулярный другому вектору.

Пример 1.
Заданы два вектора и . Найдем значение d, при котором данные векторы будут перпендикулярными.

Решение.
Для перпендикулярности векторов, заданных на плоскости, необходимо, чтобы выполнялось условие равности их скалярного произведения нулю, то есть для нашего случая условие первое:

   

Подставим в него известные координаты векторов и вычислим неизвестное d:

   

   

   

   

Ответ. Векторы и будут перпендикулярными при .

На самом деле ничего сложно нет, нужно только определить на плоскости или в пространстве заданы векторы, взять нужную формулу, подставить в нее координаты и посчитать результат.

ru.solverbook.com

РГР 2

Вопросы к защите РГР №2 по математике за 1 семестр.

Вектор — это направленный отрезок, который имеет начало и конец.

Длиной ненулевого вектора  называется длина отрезка AB.

Нулевой вектор — вектор, начало которого совпадает с его концом.

Орты – единичный вектор.

Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.

Векторы называются компланарными, если существует плоскость, которой они параллельны.

Чтобы сложить два вектора, нужно от конца одного из них отложить второй вектор; тогда сумма – это вектор с началом в начале первого вектора и концом в конце второго вектора: .

Разностью двух векторов  и называется такой третий вектор , который равен сумме векторов и .

Проекцией вектора  на ось l называется длина его составляющей  по этой оси, взятая со знаком «+», если   сонаправлен с l, и со знаком «-»,если  не сонаправлен с l.

Два вектора называются равными, если они сонаправленные и имеют равные модули.

a={a_x; a_y; a_z} и b={b_x; b_y; b_z} коллинеарны если

Радиус-вектор точки — называется вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Для перпендикулярности двух ненулевых векторов инеобходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство.

Необходимое и достаточное условие перпендикулярности двух векторов в координатах имеет вид .

Векторным произведением вектора на вектор называется третий вектор который обладает следующими свойствами:

1. Его длина равна  =

2. Вектор перпендикулярен к плоскости, в которой лежат вектора и 

3. Вектор направлен так, что поворот от вектора к вектору осуществляется против часовой стрелки, если смотреть из конца вектора (в этом случае, говорят, что тройка векторов и – правая).

Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.

Смешанное произведение векторов a, b, c — скалярное произведение вектора a на векторное произведение векторов b и c.

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами a, b, c.

 Ax + By + Cz + D = 0

Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.

1) By + Cz + D = 0 — параллельна оси Ox;

2) Ax + Cz + D = 0 — параллельна оси Oy;

3) Ax + By + D = 0 — параллельна оси Oz;

4) Cz + D = 0 — параллельна оси Oxy;

5) By + D = 0 — параллельна оси Oxz;

6) Ax + D = 0 — параллельна оси Oyz;

7) Ax + By + Cz = 0 — проходит через начало координат;

8) By + Cz = 0 — проходит через ось Ox;

9) Ax + Cz = 0 — проходит через ось Oy;

10) Ax + By = 0 — проходит через ось Oz;

11) z = 0 — плоскость Oxy;

12) y = 0 — плоскость Oxz;

13) x = 0 — плоскость Oyz.

Две плоскости параллельны тогда и только тогда, когда их нормальные векторы параллельны, а значит .

Две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а значит .

m, n, p – направляющий вектор прямой

Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны. 

Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю (скалярное произведение).

Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.

Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

1. Привести уравнение прямой к параметрическому виду: ;  ;

2. Подставить эти выражения в уравнение плоскости.

3. Из полученного найти t, а потом  x,y и z.

studfiles.net

Если ненулевые векторы перпендикулярные, то их скалярное произведение равно

Если ненулевые векторы перпендикулярные, то их скалярное произведение равно

+а) 0

б) 1

в) -1

г) 10

д) -10

9. Скалярное произведение векторов равно-…

ОТВЕТ:1

10. Определитель равен

+а) -1

б) 7

в) 1

г) -4

д) -7

11. Порядок определителя 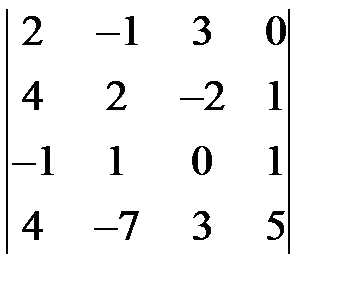равен-…

ОТВЕТ:4

Числовая матрица – это

+а) таблица

б) число

в) вектор

г) скаляр

д) линия

13.Если , то значение равно

+а)

б)

в)

г)

д)

14.Если , то значение равно

+а)

б)

в)

г)

д)

15. — это обозначение матрицы

+а) транспонированной

б) симметрической

в) косоугольной

г) треугольной

д) диагональной

16.Матрица является вырожденной при равном-…

ОТВЕТ:6

СЛАУ, имеющая решение, называется

+а) совместной

б) определённой

в) регулярной

г) несовместной

д) неопределённой

18. Угловой коэффициент прямой, проходящей через точки A(1;1) и B(2;3), равен-…

ОТВЕТ:2

19.Расстояние между точками A(-1;2;6) и B(-3;-4;3) равно-…

+а) 7

б) 6

в) 5

г) 4

д) 3

20.Предел равен

+а) 1

б) 2

в) 1/3

г) 1/2

д) ∞

21.Производная функции равна

+а)

б)

в)

г)

д)

22. . равна

+а)

б)

в)

г)

д)

23.Минимум функции равен-…

ОТВЕТ:-3

24.Функция имеет минимум в точке , равной

+а) 2

б) 0

в) -2

г) 1

д) -1

25.Производная на интервале. Тогда функция на этом интервале

+а) возрастает

б) убывает

в) постоянна

г) ограничена

д) выпуклая

26.Интеграл равен

+а)

б)

в)

г)

д)

27.Интеграл равен

а)

б)

в)

+г)

д)

28.Пять судей распределяют в пять различных районных судов. Количество различных вариантов равно-…

ОТВЕТ:120

29.Для проверки отбирают три банка из семи. Количество различных вариантов выбора равно-…

ОТВЕТ:35

В партии 7 стандартных и три нестандартных изделия. Вероятность того, что наудачу выбранное изделие стандартное, равна

+а) 0.7

б) 0.3

в) 0.5

г) 0.1

д) 1

В партии 7 стандартных и три нестандартных изделия. Вероятность того, что наудачу выбранное изделие нестандартное, равна

+а) 0.3

б) 0.7

в) 0.6

г) 0.4

д) 0

32. Вероятность достоверного события равна-…

ОТВЕТ:1

33.Случайные величины изучают в дисциплине

+а) теория вероятностей

б) алгебра и геометрия

в) математич. анализ

г) программирование

д) история цивилизаций

Дискретная случайная величина задана законом распределения

	-2
	0.1	0.3	?	0.4

Пропущенное значение вероятности равно

+а) 0.2

б) 0.1

в) 0.3

г) 0.4

д) 0

Случайная величина принимает значения 3, 5, 8, 8, 11. Мода величины равна

+а) 8

б) 3

в) 11

г) 5

д) 0

36.Определитель 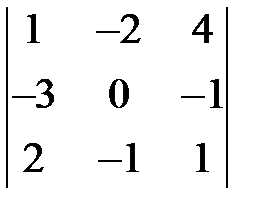равен-…

ОТВЕТ:9

37.Если — решение системы уравнений , то равно-…

ОТВЕТ:3

38.Если — решение системы уравнений , то равно

+а) 1

б) 5

в) 4

г) -1

д) -3

39.Если — решение системы уравнений , то равно

+а) 2

б) 5

в) 3

г) -1

д) -4

40.Матрица 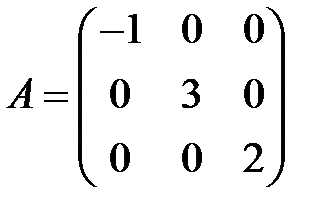является

+а) диагональной

б) вырожденной

в) единичной

г) размера

д) нулевой

41. Длина вектора равна-…

ОТВЕТ:7

42. . Тогда равно

+а)

б)

в)

г)

д)

43.Если векторы перпендикулярные, то их скалярное произведение равно

+а) 0

б) 1

в) -1

г) 10

д) -10

44. Скалярное произведение векторов равно-…

ОТВЕТ:1

45. Определитель равен

+а) 10

б) 17

в) -11

г) -3

д) -7

46. Порядок матрицы 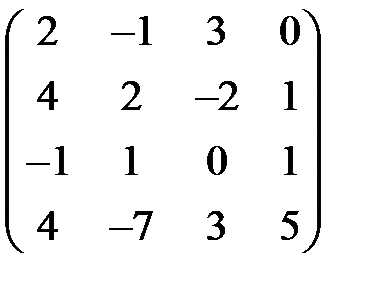равен-…

ОТВЕТ:4

Определитель – это

+а) число

б) таблица

в) вектор

г) скаляр

д) кривая

48.Если , то значение равно

+а)

б)

в)

г)

д)

49.Если , то значение равно

+а)

б)

в)

г)

д)

50. — это обозначение матрицы

+а) единичной

б) симметричной

в) косоугольной

г) треугольной

д) диагональной

51.Матрица является вырожденной при равном-…

ОТВЕТ:6

В урне 7 белых и три чёрных шара. Вероятность того, что наудачу выбранный шар белый, равна

+а) 0.7

б) 0.3

в) 0.5

г) 0.1

д) 1

Дискретная случайная величина задана законом распределения

	-2
	0.1	?	0.2	0.4

Матрица – это

+а) таблица

б) число

в) вектор

г) скаляр

д) линия

83.Если , то значение равно

+а)

б)

в)

г)

д)

84.Если , то значение равно

+а)

б)

в)

г)

д)

85. — это обозначение матрицы

+а) транспонированной

б) симметрической

в) косоугольной

г) треугольной

д) диагональной

86.Матрица является вырожденной при равном-…

ОТВЕТ:9

Диагональная матрица – это

+а) таблица

б) число

в) вектор

г) скаляр

д) кривая

118.Дано: . Тогда значение равно

+а)

б)

в)

г)

д)

119.Дано: . Тогда значение равно

+а)

б)

в)

г)

д)

120. — это обозначение матрицы

+а) обратной

б) симметричной

в) единичной

г) треугольной

д) диагональной

121.Матрица является вырожденной при равном-…

ОТВЕТ:6

Если ненулевые векторы перпендикулярные, то их скалярное произведение равно

+а) 0

б) 1

в) -1

г) 10

д) -10

9. Скалярное произведение векторов равно-…

ОТВЕТ:1

10. Определитель равен

+а) -1

б) 7

в) 1

г) -4

д) -7

11. Порядок определителя 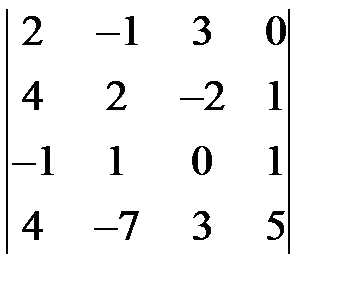равен-…

ОТВЕТ:4

Числовая матрица – это

+а) таблица

б) число

в) вектор

г) скаляр

д) линия

13.Если , то значение равно

+а)

б)

в)

г)

д)

14.Если , то значение равно

+а)

б)

в)

г)

д)

15. — это обозначение матрицы

+а) транспонированной

б) симметрической

в) косоугольной

г) треугольной

д) диагональной

16.Матрица является вырожденной при равном-…

ОТВЕТ:6

cyberpedia.su

Условие перпендикулярности векторов

Векторы на плоскости

1. Координаты вектора

Чтобы найти координаты вектора, нужно из координат

конца вычесть соответственные координаты начала.

Абсолютная величина вектора (модуль вектора, длина вектора)

Длина вектора равна корню квадратному из суммы квадратов его координат.

Равные вектора

Векторы равны, если равны их соответственные координаты, и наоборот.

Одинаково направленные (сонаправленные) и противоположно направленные векторы

Коллинеарные векторы

а) определение

 

 

Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

б) Условие коллинеарности векторов

Если два вектора коллинеарны, то их соответственные координаты пропорциональны и наоборот.

Действия с векторами

1.Сложение векторов

Чтобы сложить два вектора, нужно сложить их соответственные координаты.

2. Правила сложения векторов

а) Правило треугольника

Чтобы сложить векторы по правилу треугольника, нужно отложить их последовательно друг за другом. Вектор, равный их сумме, направлен от начала первого к концу второго.

б) Правило параллелограмма

 

 

Чтобы сложить векторы по правилу параллелограмма, нужно отложить их из общего начала, достроить параллелограмм на этих векторах как на сторонах. Их суммой является вектор, выходящий из общего начала и являющийся диагональю параллелограмма.

 

в) Правило многоугольника

 

 

Чтобы сложить векторы по правилу многоугольника, нужно отложить их последовательно друг за другом. Их суммой является вектор, выходящий из начала первого к концу второго.

3. Вычитание векторов

Чтобы вычесть векторы, нужно вычесть их соответственные координаты.

4. Правило вычитания векторов

 

 

Чтобы вычесть векторы, нужно отложить их из общего начала и соединить их концы. Направить вектор к уменьшаемому.

5. Умножение вектора на число

Чтобы умножить число на вектор, нужно умножить каждую координату вектора на это число.

1.

2.

 

 

Скалярное произведение векторов

а) Определение скалярного произведения

Скалярным произведением называется число, равное сумме произведений соответственных координат.

б) Теорема о скалярном произведении

Скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними.

Условие перпендикулярности векторов

Два вектора перпендикулярны, если их скалярное произведение равно нулю, и наоборот.

Скалярный квадрат

Скалярный квадрат вектора равен квадрату модуля этого вектора.

9. Свойство вектора

studopedya.ru