МА. Равномерная сходимость функциональных последовательностей и рядов
Теоретический минимум (окончание)Продолжим с функциональными рядами. Функциональный ряд сходится, если сходится последовательность его частичных сумм. Если эта сходимость
равномерная, то и ряд называется равномерно сходящимся. Следовательно, непосредственный способ установить, сходится ли ряд равномерно —
исследовать функциональную последовательность его частичных сумм, как показано выше. Однако этот способ может быть тяжело реализуемым.
Фактически он предполагает суммирование функционального ряда — а это более сложная задача. Поэтому существует набор теорем, позволяющих
ответить на вопрос о равномерной сходимости ряда без проведения его суммирования. Перед тем как обратиться к этим теоремам, укажем, что не может
равномерно сходиться ряд, последовательность членов которого не сходится равномерно к нулю. Обратное неверно: из того, что последовательность
общих членов ряда равномерно сходится к нулю, не следует равномерная сходимость ряда.
Одна из часто используемых теорем — мажорантный признак Вейерштрасса. Рассмотрим ряд . Если ,
а ряд сходится, то ряд равномерно сходится на множестве .
Этот признак очень удобен в использовании.
Приведём ещё два признака равномерной сходимости: Абеля и Дирихле.
Признак Абеля заключается в следующем. Если общий член ряда можно представить в виде , причём
последовательность монотонна и ограничена:
, а ряд равномерно сходится на множестве , то ряд равномерно сходится на множестве .
Признак Дирихле основан тоже на представлении общего члена ряда в виде произведения .
Теперь последовательность предполагается монотонной и равномерно сходящейся к тождественно равной нулю функции.
Частичные суммы ряда предполагаются равномерно ограниченными, т.е. любая частичная сумма для любого значения по модулю
не превышает одного и того же числа. В этом случае ряд равномерно сходится на множестве .
Наконец, существует ещё критерий Коши равномерной сходимости ряда. Этот признак формализован несколько сложнее, так как формулируется
.
Почему так интересна равномерная сходимость ряда? Ответ заключается в том, что качество сходимости ряда лучше, если он сходится равномерно.
Этот ответ, конечно, ни на какую строгость не претендует, но отражает общую идею, чему способствуют и графические интерпретации. Вернитесь
ещё раз к самому первому графику темы и сравните, как сходятся две функциональные последовательности. Особенно обратите внимание на поведение
в окрестности правого конца отрезка элементов последовательности с ростом их номера. Несложно видеть, что в пределе поведение функции в этой
области становится «плохим»: резкий скачок вверх, а потом вниз. Другое дело, что в пределе этот скачок исчезает. Однако представьте себе, что
это последовательность частичных сумм некоторого функционального ряда. Такое поведение частичных сумм не может не сказаться на аналитических
На почленном дифференцировании ряда хотелось бы остановиться немного подробнее. Интересно то, что для того чтобы ряд можно было почленно
дифференцировать не требуется его равномерная сходимость. Требуется, однако, равномерная сходимость ряда, составленного из производных
от членов исходного ряда. В этом случае если сам ряд сходится к некоторой функции , то ряд производных сходится к функции .
Строго говоря, ещё требуется непрерывная дифференцируемость членов исходного ряда.
Примеры
Пример 1. Исследование на основе определения равномерной сходимости.
Исследовать на равномерную сходимость на отрезке ряд .
В данном случае можно не прибегать к специальным признакам равномерной сходимости, так как легко найти частичные суммы ряда:
.
Следовательно,
Применим критерий равномерной сходимости функциональной последовательности:
Значит, последовательность не является равномерно сходящейся. Поэтому и ряд не сходится равномерно.
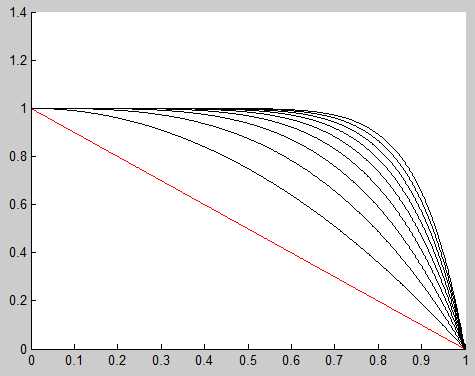
Ниже изображены графики нескольких первых частичных сумм (первая отмечена красным цветом). Отсутствие равномерной сходимости можно
увидеть непосредственно.
Пример 2. Использование критерия Коши.
Исследовать на равномерную сходимость на отрезке ряд .
Здесь применим критерий Коши, для чего оценим сумму членов ряда, начиная с -го, заканчивая -м:
.
Таким образом, при выборе критерий Коши будет выполнен. Ряд сходится равномерно.
На графике ниже изображены кривые для нескольких первых значений (первая кривая красная, последняя —
зелёная). Видно, что последовательность частичных сумм сходится равномерно.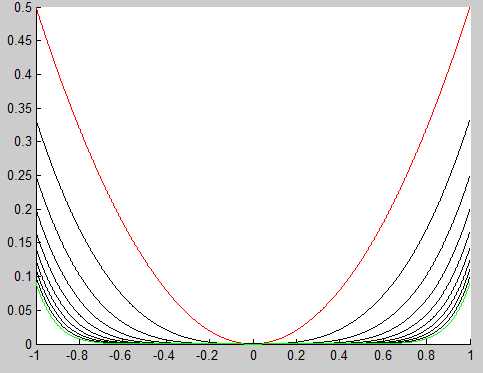
Пример 3. Использование признака Вейерштрасса.
Исследовать на равномерную сходимость на интервале ряд .
Здесь удобно применить признак Вейерштрасса, так как несложно подобрать мажоранту для ряда. Найдём максимум общего члена ряда:
.
Следовательно,
.
Мажорирующий ряд сходится. Поэтому исходный ряд сходится равномерно.
Пример 4. Использование признака Дирихле.
Исследовать на равномерную сходимость на интервале ряд .
Применим признак Дирихле. Представим общий член ряда в виде произведения
.
Последовательность , монотонно убывая, стремится к нулю. Рассмотрим далее частичные суммы :
.
Следовательно,
.
Здесь сыграло свою роль то обстоятельство, что концы заданного в условии промежутка не входят в рассмотрение, а потому знаменатель
последней дроби в нуль не обращается. Итак, исходный ряд сходится равномерно по признаку Дирихле.
Пример 5. Использование критерия Коши.
Как должно быть уже понятно, на данном отрезке исследовать ряд тем же методом, что и в предыдущем примере, не получится:
частичные суммы вспомогательного ряда не будут ограничены. Более того, мы сейчас с помощью критерия Коши покажем, что ряд на данном
промежутке не сходится равномерно. Для этого сначала запишем отрицание критерия Коши:
.
Выберем , тогда
.
Итак, для ряда выполнилось отрицание критерия Коши, следовательно, он не сходится равномерно.
Пример 6. Почленное дифференцирование ряда.
Докажем, что ряд можно почленно дифференцировать.
Непрерывная дифференцируемость членов ряда очевидна. Составим ряд производных:
.
Оценим общий член этого ряда:
.
Таким образом, подобран мажорирующий ряд , который сходится. Поэтому по признаку
Вейерштрасса ряд производных сходится равномерно. Следовательно, исходный ряд можно почленно дифференцировать.
Равномерная сходимость функционального ряда.
Определим вначале понятие равномерной сходимости числовой последовательности.
Определение 4.4. Функциональная
последовательностьfn(x) называетсяравномерно сходящейся
к функции f на
множестве Х, если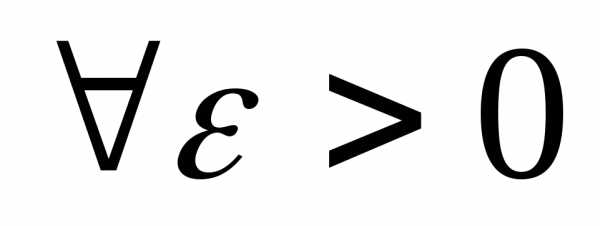 и
и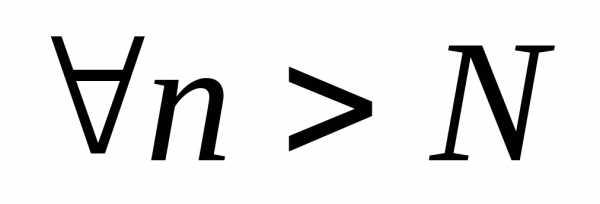
.
Замечание 1. Будем обозначать обычную сходимость функциональной последователь-ности а равномерную сходимость -.
Замечание 2. Отметим еще раз принципиальное
отличие равномерной сходимости от
обычной: в случае обычной сходимости
при выбранном значении ε для каждого 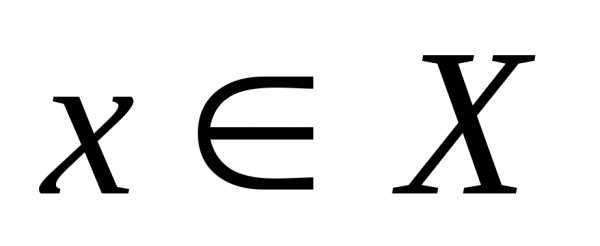 существуетсвой номерN, для
которого приn > Nвыполняется неравенство:
существуетсвой номерN, для
которого приn > Nвыполняется неравенство:
. При этом может оказаться, что подобрать для данного ε общий номерN,обеспечивающий выполнение этого неравенства для любогох, невозможно. В случае же равномерной сходимости такой номерN,общий для всех х, существует.
Определим теперь понятие равномерной сходимости функционального ряда. Посколь-ку каждому ряду соответствует последовательность его частичных сумм, равномерная сходимость ряда определяется через равномерную сходимость этой последовательно-
сти:
Определение 4.5. Функциональный ряд называетсяравномерно сходящимся на
множествеХ, если наХравномерно
сходится последовательность его
частичных сумм.
называетсяравномерно сходящимся на
множествеХ, если наХравномерно
сходится последовательность его
частичных сумм.
Признак Вейерштрасса.
Теорема 4.1. Если числовой ряд сходится и для всех
сходится и для всех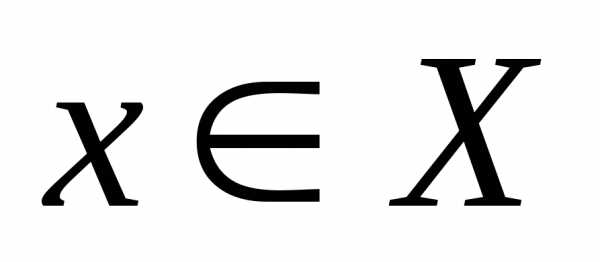 и для всехп =1, 2,… выполняется
неравенството ряд
и для всехп =1, 2,… выполняется
неравенството ряд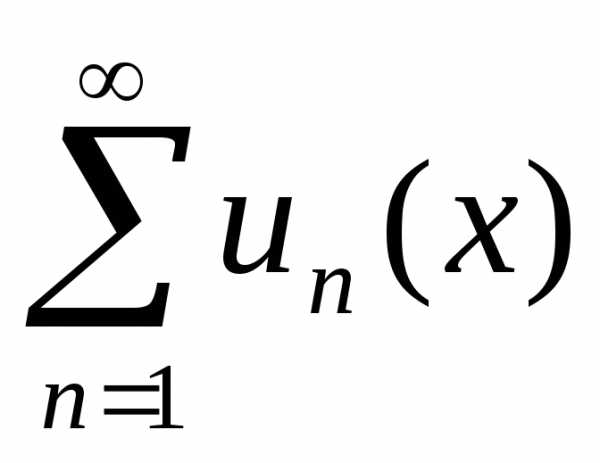 сходится абсолютно и равномерно на
множествеХ.
сходится абсолютно и равномерно на
множествеХ.
Доказательство.
Для любого ε> 0cуществует
такой номерN, что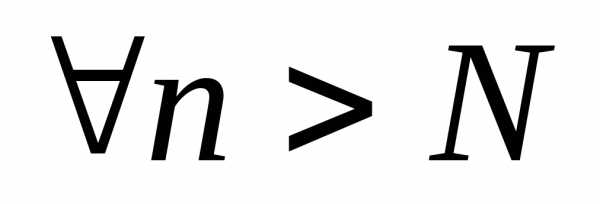

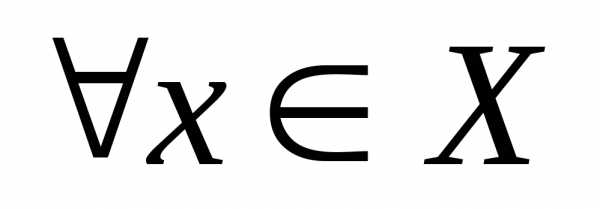 и
и  для остатковrn ряда
для остатковrn ряда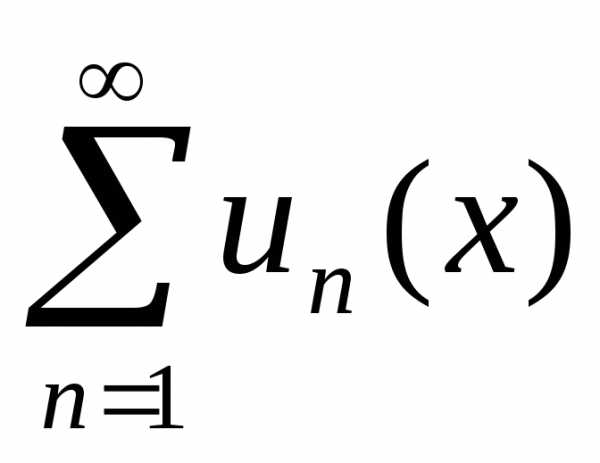 справедлива оценка
справедлива оценка
Следовательно, поэтому ряд
поэтому ряд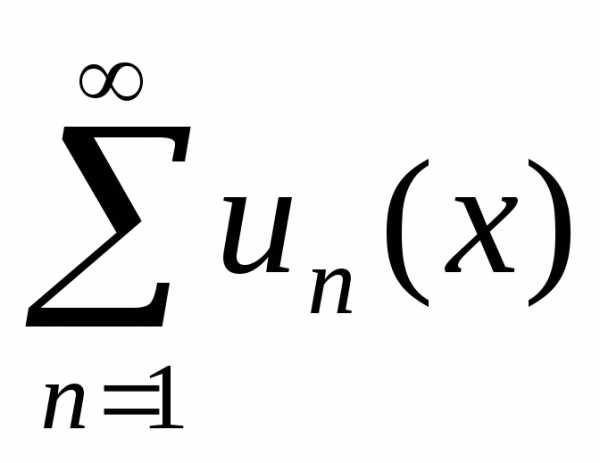 равномерно сходится.
равномерно сходится.
Замечание. Процедура подбора числового ряда, отвечающего условиям теоремы 4.1, обычно называется мажорированием, а сам этот ряд –мажорантой для данного функционального ряда.
Пример. Для функционального ряда 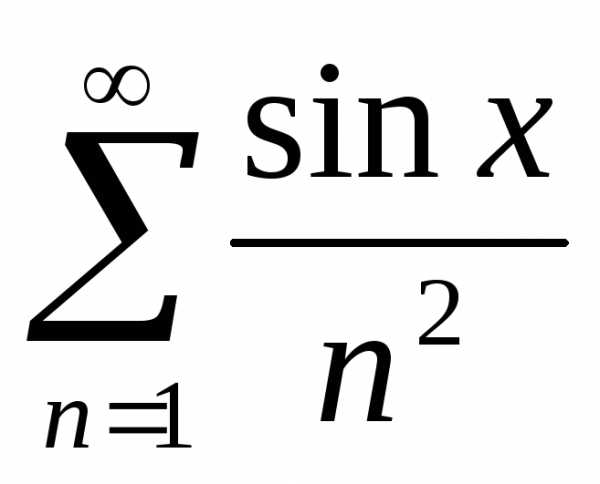 мажорантой при любом значениихявляется сходящийся знакоположительный
ряд
мажорантой при любом значениихявляется сходящийся знакоположительный
ряд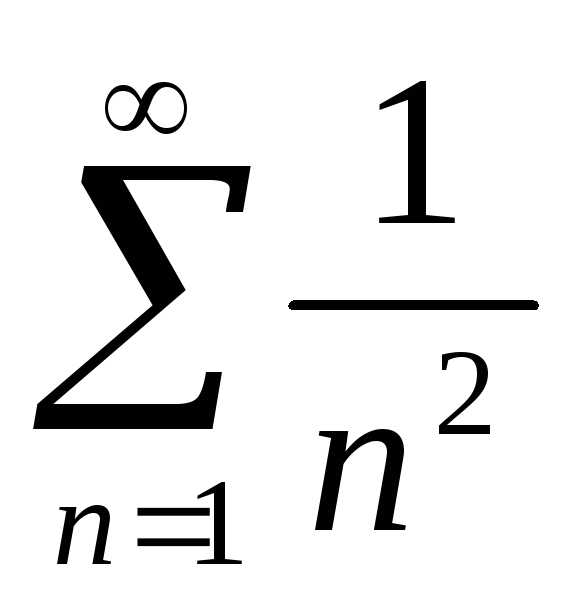
Свойства равномерно сходящихся рядов.
Теорема 4.2. Если функцииun(x) непрерывны прии
ряд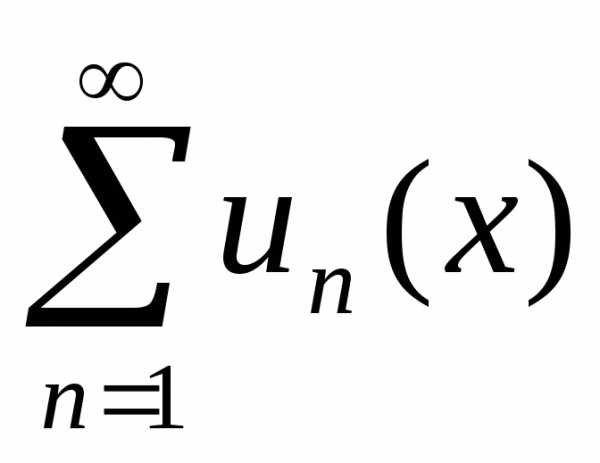 равномерно сходится наХ, то его
суммаs(x)тоже непрерывна в точкех0 .
равномерно сходится наХ, то его
суммаs(x)тоже непрерывна в точкех0 .
Доказательство.
Выберем ε > 0. Тогда , поэтому существует такой номерп0 , что
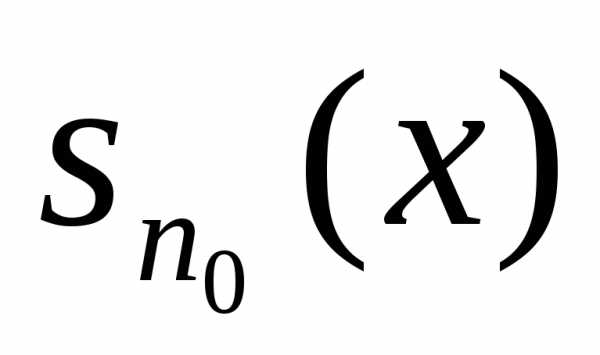 — сумма конечного числа непрерывных
функций, поэтому
— сумма конечного числа непрерывных
функций, поэтому 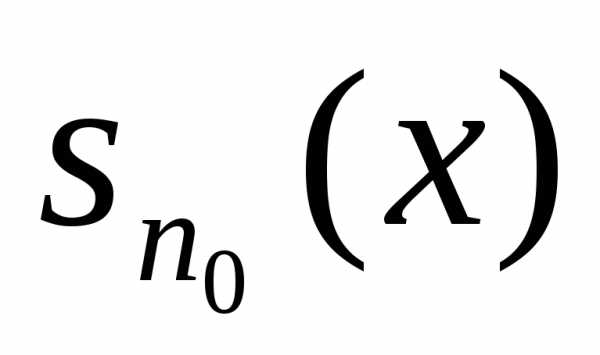 непрерывна в точкех0 .Поэтому существует такое δ > 0, что Тогда получаем:
непрерывна в точкех0 .Поэтому существует такое δ > 0, что Тогда получаем:
то есть функцияs(x) непрерывна прих = х0 .
Теорема 4.3. Пусть функцииun(x) непрерывны на отрезке [a, b] и ряд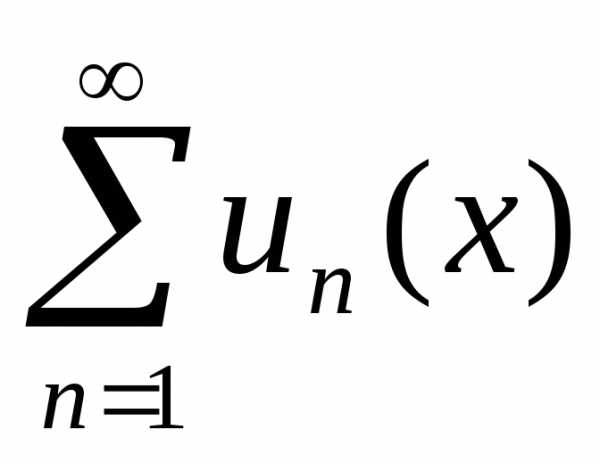 равно-мерно сходится на этом отрезке.
Тогдаряд
равно-мерно сходится на этом отрезке.
Тогдаряд тоже равномерно сходится на [a, b] и
тоже равномерно сходится на [a, b] и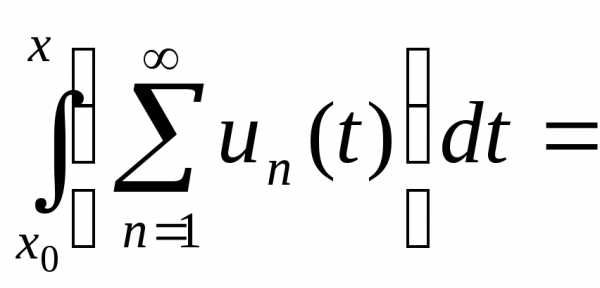
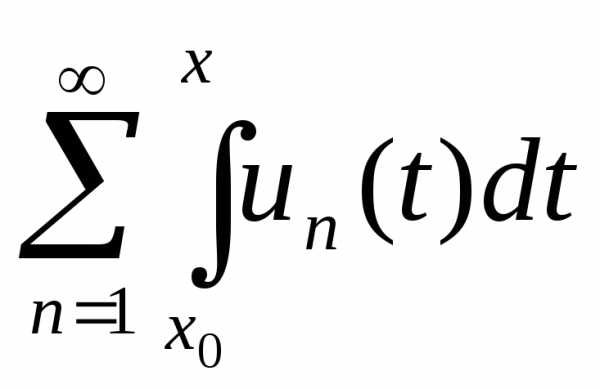 (4.2)
(4.2)
(то есть в условиях теоремы ряд можно почленно интегрировать).
Доказательство.
По теореме 4.2 функция s(x)
=  непрерывна на [a, b]
и, следовательно, интегрируема на нем,
то есть интеграл, стоящий в левой части
равенства (4.2), существует. Покажем, что
ряд
непрерывна на [a, b]
и, следовательно, интегрируема на нем,
то есть интеграл, стоящий в левой части
равенства (4.2), существует. Покажем, что
ряд равномерно сходится к функции
равномерно сходится к функции
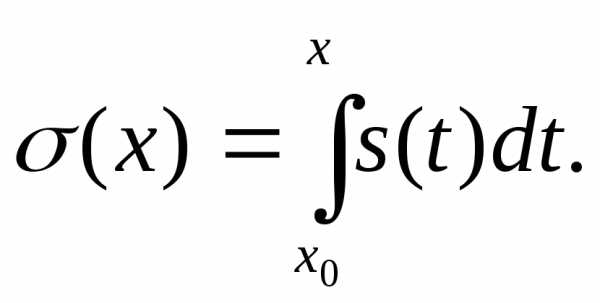 Обозначим
Обозначим
Тогда для любого ε найдется такой номерN, что приn > N
Значит,
ряд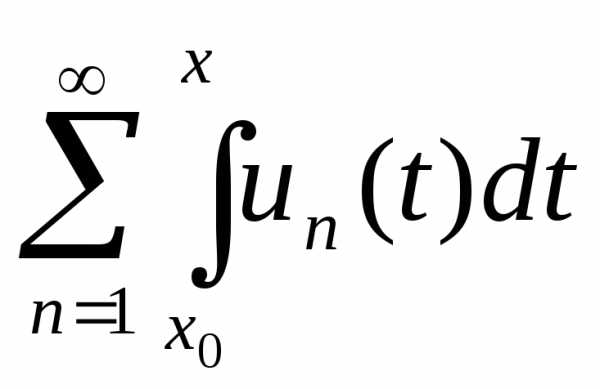 равномерно сходится, и его сумма равна
σ (х) =
равномерно сходится, и его сумма равна
σ (х) =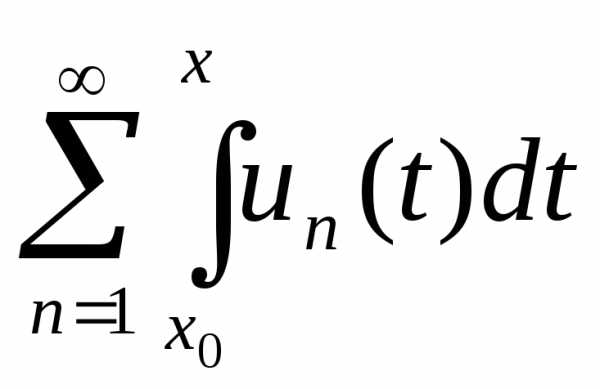 .
.
Теорема доказана.
Теорема 4.4. Пусть функцииun(x) непрерывно дифференцируемы на отрезке [a, b] и ряд, составленный из их производных:
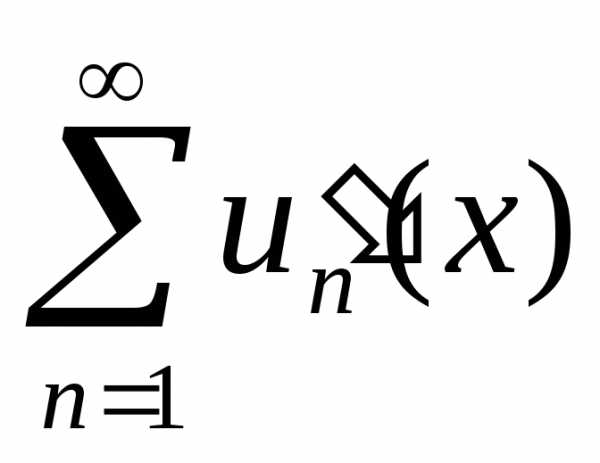 (4.3)
(4.3)
равномерно сходится на [a, b]. Тогда, если ряд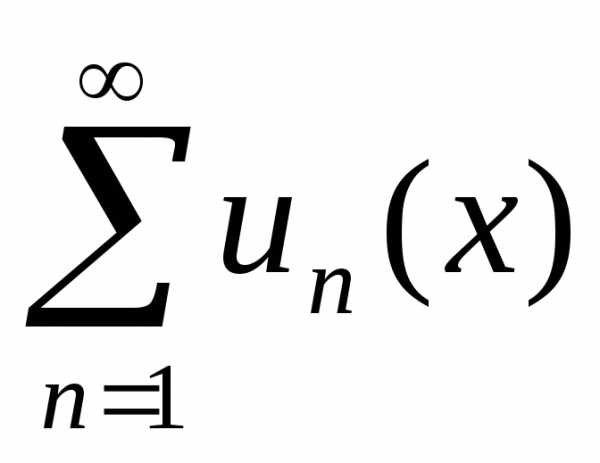 сходится хотя бы в одной точке
сходится хотя бы в одной точке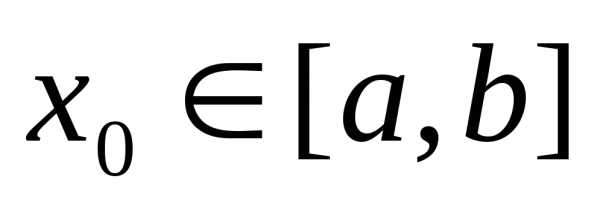 ,
то он сходится равномерно на всем [a, b], его суммаs(x)=
,
то он сходится равномерно на всем [a, b], его суммаs(x)=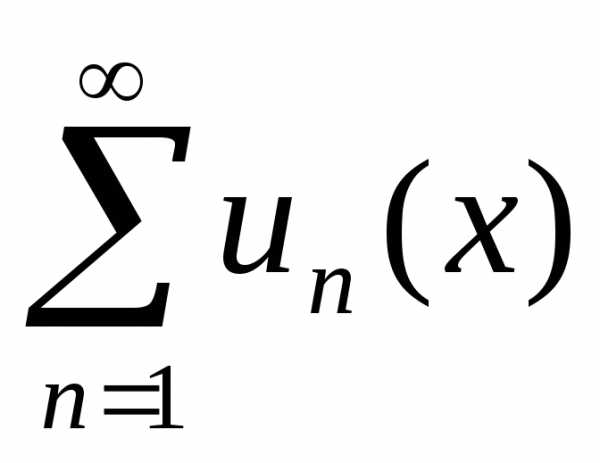 является непрерывно дифференцируемой
функцией и
является непрерывно дифференцируемой
функцией и
(ряд  можно почленно дифференцировать).
можно почленно дифференцировать).
Доказательство.
Определим функцию σ(х) как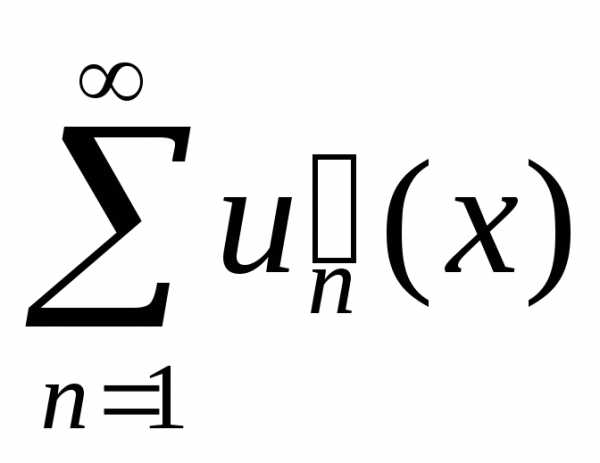 .
По теореме 4.3 ряд (4.3) можно почленно
интегрировать:
.
По теореме 4.3 ряд (4.3) можно почленно
интегрировать:
.
Ряд, стоящий в правой части этого
равенства, равномерно сходится на [a, b] по теореме 4.3. Но
числовой ряд по условию теоремы сходится, следовательно,
равномерно сходится и ряд
по условию теоремы сходится, следовательно,
равномерно сходится и ряд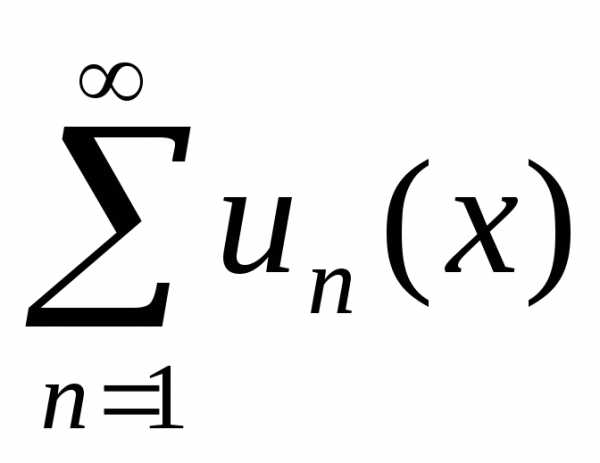 .
Тогда
.
Тогда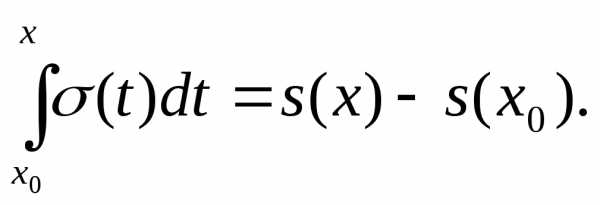 Функция σ(t) является
суммой равномерно сходящегося ряда
непрерывных функций на [a, b] и поэтому сама
непрерывна. Тогда функция
Функция σ(t) является
суммой равномерно сходящегося ряда
непрерывных функций на [a, b] и поэтому сама
непрерывна. Тогда функция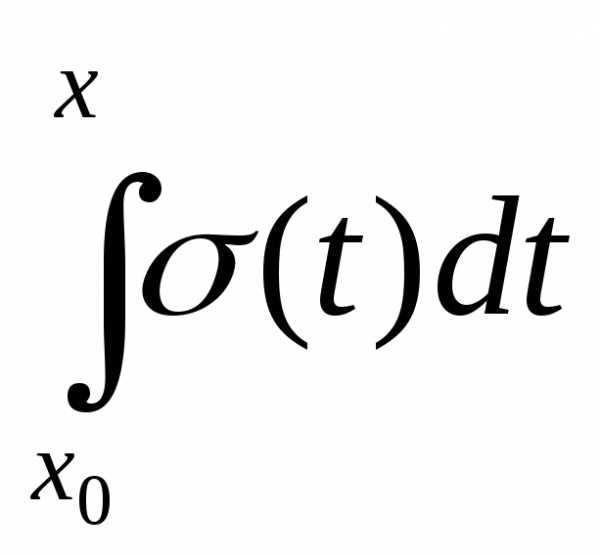 непрерывно дифференцируема на [a, b], и,
что и требовалось доказать.
непрерывно дифференцируема на [a, b], и,
что и требовалось доказать.
Лекция 5.
Степенные ряды. Теорема Абеля. Область сходимости степенного ряда. Радиус сходимости. Основные свойства степенных рядов: равномерная сходимость, непрерывность и бесконечная дифференцируемость суммы. Почленное интегрирование и дифференцирование степенных рядов.
Определение 5.1. Степенным рядомназывается функциональный ряд вида
(5.1)
Замечание. С помощью замены х – х0 = tряд (5.1) можно
привести к виду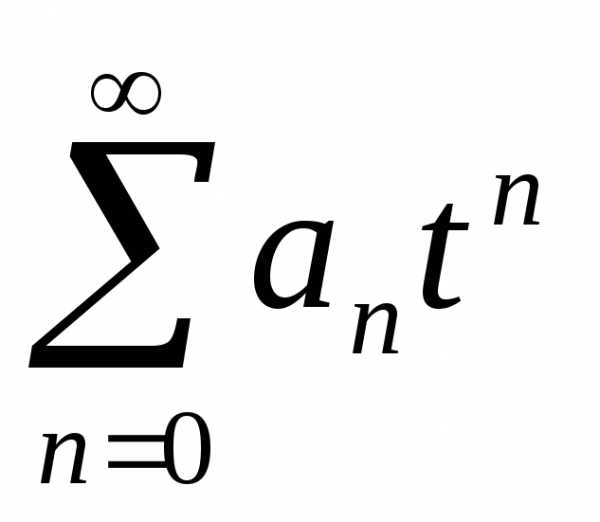 ,
поэтому все свойства степенных рядов
достаточно доказать для рядов вида
,
поэтому все свойства степенных рядов
достаточно доказать для рядов вида
 (5.2)
(5.2)
Теорема 5.1 (1-я теорема Абеля). Если степенной ряд (5.2) сходится прих = х0 ,то при любомx: |x| < |x0|ряд (5.2) сходится абсолютно. Если же ряд (5.2) расходится прих = х0 ,то он расходится при любомx: |x| > |x0|.
Доказательство.
Если ряд 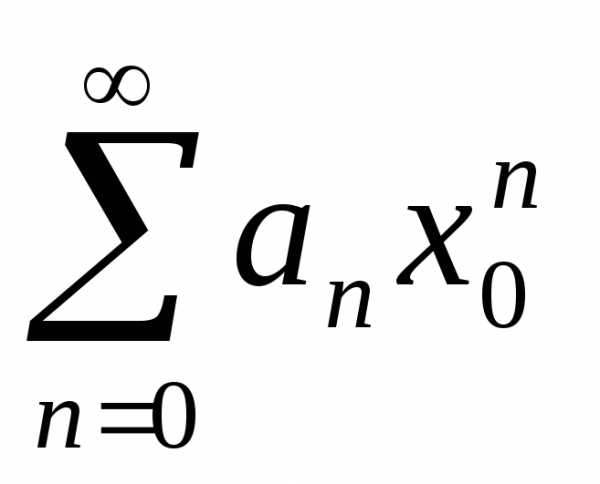 сходится, то
сходится, то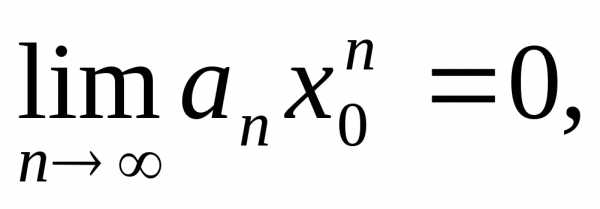 поэтому существует константас > 0:
поэтому существует константас > 0:
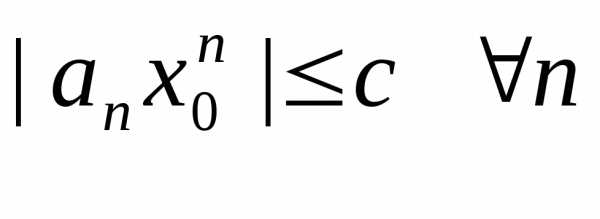 .
Следовательно,,
а рядпри |x|<|x0|
сходится, так как является суммой
бесконечно убывающей геометрической
прогрессии. Значит, ряд
.
Следовательно,,
а рядпри |x|<|x0|
сходится, так как является суммой
бесконечно убывающей геометрической
прогрессии. Значит, ряд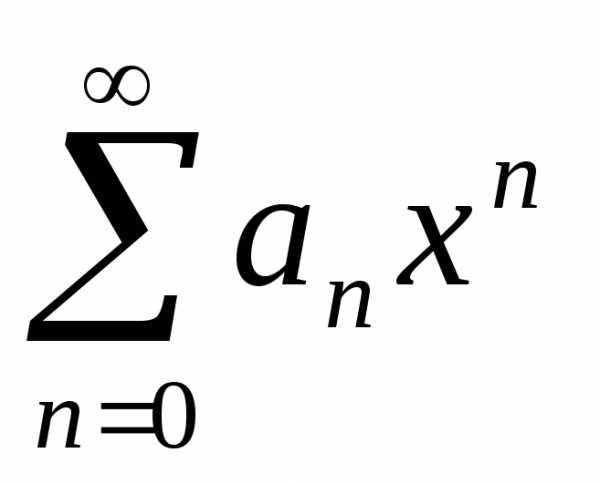 при |x|<|x0|
абсолютно сходится.
при |x|<|x0|
абсолютно сходится.
Если известно, что ряд (5.2) расходится при х = х0, то он не может сходиться при |x| > |x0| ,так как из ранее доказанного при этом следовало бы, что он сходится и в точкех0 .
Таким образом, если найти наибольшее из чисел х0> 0 таких, что (5.2) сходится прих = х0 , то областью сходимости данного ряда, как следует из теоремы Абеля, будет интервал (- х0 , х0 ), возможно, включающий одну или обе границы.
Определение 5.2. ЧислоR ≥ 0 называетсярадиусом сходимости степенного ряда (5.2), еслиэтот ряд сходится, арасходится. Интервал (—R , R ) называ-етсяинтервалом сходимости ряда (5.2).
Примеры.
Для исследования абсолютной сходимости ряда
 применим
признак Далам-бера:.
Следовательно, ряд сходится только прих= 0, и радиус его сходимости равен
0:R= 0.
применим
признак Далам-бера:.
Следовательно, ряд сходится только прих= 0, и радиус его сходимости равен
0:R= 0.Используя тот же признак Даламбера, можно показать, что ряд
 сходится при любомх, то есть
сходится при любомх, то есть
Для ряда
 по признаку Даламбера получим:
по признаку Даламбера получим:
Следовательно, при –1 <x< 1 ряд сходится, при
x< -1 иx> 1 расходится. Прих= 1 получаем
гармонический ряд, который, как извест-но,
расходится, а прих= -1 ряд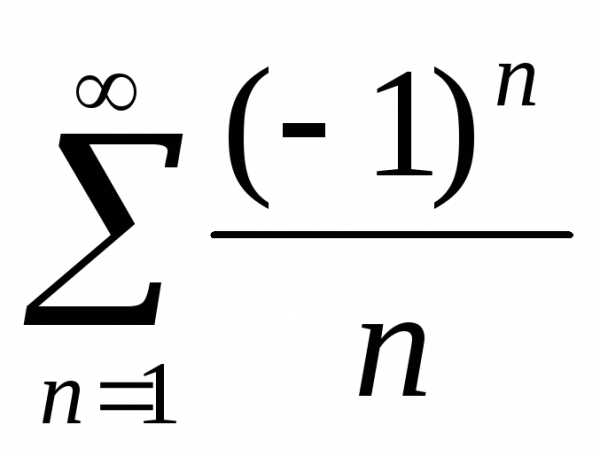 сходится условно по признаку Лейбница.
Таким образом, радиус сходимости
рассматриваемого рядаR= 1, а интервал сходи-мости – [-1, 1).
сходится условно по признаку Лейбница.
Таким образом, радиус сходимости
рассматриваемого рядаR= 1, а интервал сходи-мости – [-1, 1).
Формулы для определения радиуса сходимости степенного ряда.
Формула Даламбера.
Рассмотрим степенной ряд  и
применим к нему признак Даламбера: для
сходимости ряда необходимо, чтобы.Если
существует
и
применим к нему признак Даламбера: для
сходимости ряда необходимо, чтобы.Если
существует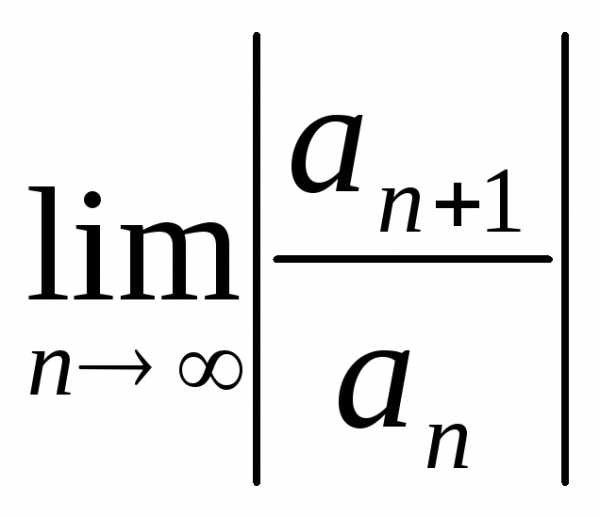 ,
то область сходимости определяется
неравенством
,
то область сходимости определяется
неравенством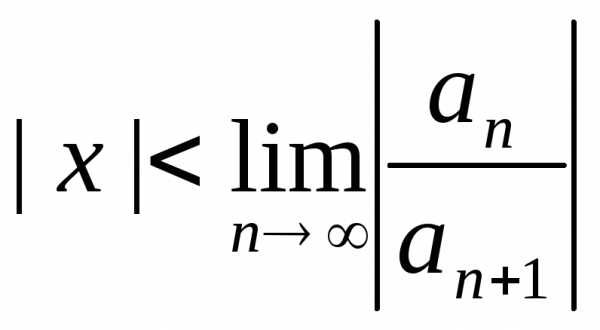 ,
то есть
,
то есть
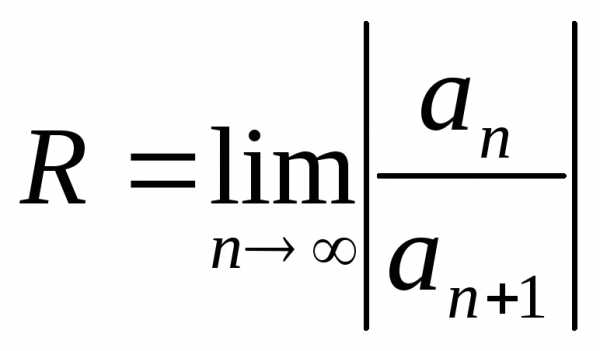 —
(5.3)
—
(5.3)
Формула Коши-Адамара.
Используя радикальный признак Коши и
рассуждая аналогичным образом, получим,
что можно задать область сходимости
степенного ряда как множество решений
неравенства  при условии существования этого предела,
и, соответствен-но, найти еще одну формулу
для радиуса сходимости:
при условии существования этого предела,
и, соответствен-но, найти еще одну формулу
для радиуса сходимости:
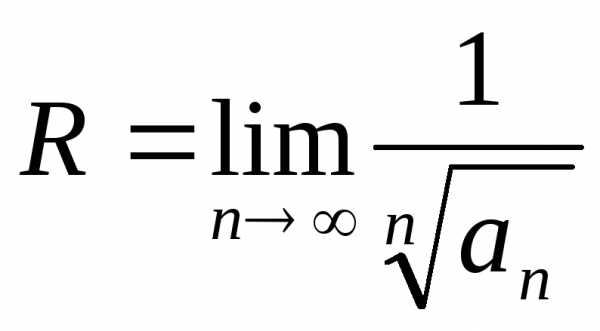 (5.4)
(5.4)
studfiles.net
Равномерная сходимость последовательностей и рядов — ПриМат
Равномерная сходимость функциональных последовательностей
Равномерная сходимость функциональных рядов
Теорема
Если функциональный ряд равномерно сходится на множестве , то последовательность его членов равномерно стремится к нулю на множестве .
Доказательство
Обозначим частичные суммы ряда как , а сумму ряда (предельную функцию последовательности частичных сумм) как . Согласно определению равномерной сходимости ряда
$$\forall \varepsilon >0 \quad \exists n_{ \varepsilon }\in \mathbb{N}: \forall n \ge n_\varepsilon \ \forall x \in E \Rightarrow \left|S_n(x)-S(x) \right| < \frac{\varepsilon}{2} ,$$
поэтому для справедливо также неравенство
$$\left| u_{ n+1 }(x) \right| =\left| S_{ n+1 }(x)-S_{ n }(x) \right| =\left| \left[ S_{n+1}(x)-S(x) \right] + \left[S(x) — S_n(x) \right] \right| < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon .$$
А это и означает равномерную сходимость к нулю последовательности .
Равномерная сходимость последовательностей и рядов
Лимит времени: 0
Информация
После прочтения статьи, для закрепления материала, рекомендуется пройти тест по данной теме
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Таблица лучших: Равномерная сходимость последовательностей и рядов
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Поделиться ссылкой:
Похожее
ib.mazurok.com
06. Равномерная сходимость функциональной последовательности, ряда. П
Пусть задана последовательность функций , определенных на множестве .
Определение. Поточечно сходится к на , если , т. е. .
Пример. Пусть , . Тогда при имеем: . При и . Таким образом, последовательность поточечно сходится к функции .
Если рассматривать функциональный ряд , составленный из определенных на множестве функций, то под его Поточечной сходимостью понимается поточечная сходимость последовательности его частичных сумм.
Выше мы видим, что поточечный предел последовательности непрерывных функций может оказаться разрывной функцией.
Чтобы избежать подобных неприятностей, рассмотрим более сильное понятие равномерной сходимости.
Определение. Последовательность Равномерно сходится к при на множестве , если . Это обозначается так: на при .
Равномерная сходимость функционального ряда – это равномерная сходимость последовательности его частичных сумм к сумме ряда на . Это равносильно тому, что на при , т. е. тому, что на .
Теорема. (Критерий Коши равномерной сходимости последовательности ). на множестве .
Без доказательства.
Из этой теоремы сразу следует Критерий Коши равномерной сходимости функционального ряда: равномерно сходится на .
Следствие. (Необходимый признак сходимости ряда). Положим в критерий Коши . Тогда получаем: , т. е. .
Теорема. (Признак Вейерштрасса). Пусть выполняется неравенство . Пусть, кроме того, ряд сходится. Тогда ряд сходится на множестве абсолютно и равномерно.
Доказательство. Достаточно проверить справедливость критерия Коши, т. е. доказать, что . Но последнее неравенство следует из того, что , а для ряда выполняется критерий Коши, т. е. .
Примеры использования теоремы.
Пример 1. Ряд равномерно (и абсолютно) сходится на . Действительно, при выполнена оценка , а ряд сходится.
Пример 2. равномерно и абсолютно сходится на всей числовой прямой, т. к. для всех , а — сходится.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Глава 12. Функциональные ряды
56
12.1. Сходимость функциональных последовательностей и рядов
Пусть последовательность функций, каждая из которых определена на некотором подмножестве. В этом случае говорят, что на множествезаданафункциональная последовательность . Например:
,
.
Аналогично, если задан ряд , каждый член которого является функцией, определенной на множестве, то говорят, что на множествезаданфункциональный ряд. Например, ,.
Определение 1. Функциональная последовательность называетсясхдящейся на множестве к функции , еслипоследовательностьсходится к, т.е.такое, что выполняетсядля.
Обозначается . Эта сходимость называется монотонной, т.е. сходимостью в каждой точке множества.
Определение 2. Функциональный ряд называетсясходящимся намножестве к функции , если последовательность его частных суммсходится к функциина множестве, которое называетсяобластью сходимости ряда.
, .
Функция называетсясуммой функционального ряда.
Один из основных вопросов, рассматриваемых в теории функциональных рядов – нахождение области сходимости функционального ряда.
Пример 1. Найти область сходимости следующих рядов:
а) ; б); в)
Решение. а)– бесконечная геометрическая про- грессия. На множествеX=(-1,1) ряд сходится, причем .
б) По признаку Даламбера ряд сходится для. Следовательно, исходный ряд сходится абсолютно для.
в) По признаку Коши = Откуда следует, что х>4. Областью сходимости является множество X=(4,+).
Кроме поточечной сходимости , есть также другой тип сходисти, которая называется равномерной сходимостью на множестве.
Определение 3. Последовательность называетсяравномерно сходящейся на множестве к функции , еслитакое, чтоивыполняется. Обозначается.
Определение 4. Функциональный ряд называетсяравномерно сходящимся на множестве к функции, если последовательность его частичных суммсходится равномерно нак.
Сравним между собой оба типа сходимости. Пусть ряд сходит- ся для. Это означает, что каждомубудет соответствовать свой числовой ряд, для сходимости которого, определенное в каждой точке. В общем случае значениебудет меняться от точки к точке, т.е.. При равномерной сходимости требуется, чтобы для выбранногочислоне зависело оти было одним и тем же для.
Отсюда следует важный вывод: если последовательность (ряд) равномер но сходится на , то последовательность (ряд) просто сходятся на. Обратное утверждение неверно.
Пример 2. Проверить сходимость последовательности ,.
Решение. Понятно, что , т.е. последовательность сходится. Однако эта сходимость будет неравномерной. Действительно, возьмем. Найдется литакое, что дляивыполняется неравенство? Выполнение этого неравенства для всех точекневозможно, так как прих близких к 1 , потому что. Таким образом, последовательность сходится, но неравномерно.
Пример 3. Рассмотрим ряд . Он сходится на. Покажем, что он сходится неравномерно.
Решение. Последовательность частичных сумм сходится кпри. Поэтому длятакое, чтодля. Однако дляэто невозможно, так как прифункцияпринимает любое, как угодно большое значение. Ряд сходится, но неравномерно.
Теорема 1. (критерий Коши). а) Для того, чтобы последовательность равномерно сходилась на множественеобходимо и достаточно, чтобы длятаких, что дляивыполнялось
; (1)
б) Для того, чтобы функциональный ряд равномерно сходился на множестве, необходимо и достаточно, чтобы длятаких, что дляивыполнялось, или, если обозначить, то
, (2)
Доказательство выполним для последовательностей.
Необходимость. Пусть равномерно сходится кна. Зададим, тогда, чтои.
Возьмем , тогда дляимеем
, т.е. выполняется (1).
Достаточность. Пусть выполняется условие теоремы а), т.е. для такие, что дляивыполняется. Это означает, что длячисловая последовательностьфундаментальная, а, следовательно, она сходится. Положим. Перейдем к пределу в неравенствепри. Тогда получим, что длявыполняется неравенство, т.е. сходится равномерно кна, при.
Пример 4. Исследовать сходимость ряда на интервале.
Решение. Неравенство ,, показывает, что последовательность сходится к нулю равномерно на, но в тоже время для любого значениярядрасходится.
Теорема 2. (Признак Вейерштрасса). Пусть для ивыполняются неравенстваи числовой рядсходится. Тогда функциональный рядсходится абсолютно и равномерно на множестве.
Так как числовой ряд сходится, то для него выполняется критерий Коши, т.е., что выполняетсядля
Возьмем и, тогда дляимеем
, ,
т.е. выполняется критерий Коши (2). Ряд сходится равномерно и абсолютно по признаку сравнения. ■
Замечание. Ряд в теореме 2 называетсямажорантой для ряда , а саму теорему 2 часто называютмажорантным признаком сходимости.
Пример 5. Доказать сходимость ряда .
Решение. Рассмотрим ряд . Этот ряд сходится абсолютно, т.к. по признаку сравнения. Поэтому исходный ряд абсолютно и равномерно сходится.
Пример 6. Исследовать сходимость ряда на отрезке.
Решение. Первое слагаемое в сумме принимает наибольшее значение в точке, второе в точке. Следовательно, для всехимеем, что, и в силу признака Вейерштрасса получаем, что данный ряд сходится равномерно на.
Признак Вейерштрасса дает только достаточное условие. Непосредственно из определения вытекает необходимый и достаточный признак равномерной сходимости, которым удобно пользоваться на практике.
Теорема 3. Для того чтобы функциональная последовательность равномерно сходилась на множествек предельной функциинеобходимо и достаточно, чтобы
, (3)
где ,.
Необходимость. Пусть при. Так как по определениюнеравенствовыполняется дляи при, то при такихбудет справедливо. Отсюда следует, чтопри.
Достаточность. Пусть при. Это означает, что дляпри достаточно большихбудет выполняться, тогда тем более для всехибудет выполняться. А это означает равномерную сходимость.
Теперь, пользуясь этой теоремой и определением равномерно сходящегося функционального ряда, можно сформулировать необходимое и достаточное условия равномерной сходимости ряда: для того, чтобы функциональный ряд сходился кнанеобходимо и достаточно, чтобы функциональная последовательностьравномерно сходилась к нулю, т.е..
Пример 7. Исследовать сходимость .
Решение. Ранее было показано, что сходимость есть, но она неравномерная. Это же самое получается более просто по теореме 3:
.
При этом не стремится к 0 при, поэтому сходимость неравномерная.
Пример 8. Сходится ли равномерно последовательность ,.
Решение. Сначала проверим существование предельной функции .
при ,.
Таким образом, . Рассмотрим
,
где .
Найдем , т.е. наибольшее значениена. Вычислим значенияна концах интервала
и
и в критических точках. Продифференцируем :
.
при , откуда.
При этом берем только . Тогда. Поэтомупри. Следовательно,прина. Последовательностьравномерно сходится на.
Пример 9. Проверить сходимость ряда ,.
Решение. Прежде всего, отметим, что в указанном промежутке ряд сходится по признаку сравнения, так как он знакоположительный, и существует сходящийся ряд для, так что выполняется условие.
Рассмотрим остаток и найдем его сумму. Так как, тот-я частичная сумма остатка будет
, при .
Т.е. . Тогдапри. Таким образом, наряд сходится неравномерно. На любом промежутке, где сходимость равномерная, т.к.
при .
Пример 10. Исследовать на равномерную сходимость ряд на.
Решение. Так как ,, то оценкане дает сходящегося мажорантного ряда. Найдем. Поскольку, то, следовательно,,и в силу признака Вейерштрасса ряд сходится равномерно на.
studfiles.net
Равномерная сходимость функционального ряда.
Определим вначале понятие равномерной сходимости числовой последовательности.
Определение 4.4. Функциональная
последовательностьfn(x) называетсяравномерно сходящейся
к функции f на
множестве Х, если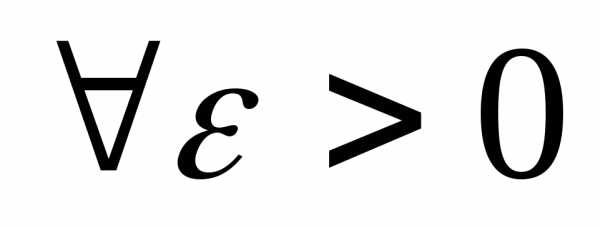 и
и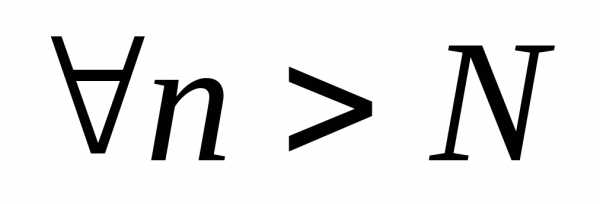
.
Замечание 1. Будем обозначать обычную сходимость функциональной последователь-ности а равномерную сходимость -.
Замечание 2. Отметим еще раз принципиальное
отличие равномерной сходимости от
обычной: в случае обычной сходимости
при выбранном значении ε для каждого  существуетсвой номерN, для
которого приn > Nвыполняется неравенство:
существуетсвой номерN, для
которого приn > Nвыполняется неравенство:
. При этом может оказаться, что подобрать для данного ε общий номерN,обеспечивающий выполнение этого неравенства для любогох, невозможно. В случае же равномерной сходимости такой номерN,общий для всех х, существует.
Определим теперь понятие равномерной сходимости функционального ряда. Посколь-ку каждому ряду соответствует последовательность его частичных сумм, равномерная сходимость ряда определяется через равномерную сходимость этой последовательно-
сти:
Определение 4.5. Функциональный ряд называетсяравномерно сходящимся на
множествеХ, если наХравномерно
сходится последовательность его
частичных сумм.
называетсяравномерно сходящимся на
множествеХ, если наХравномерно
сходится последовательность его
частичных сумм.
Признак Вейерштрасса.
Теорема 4.1. Если числовой ряд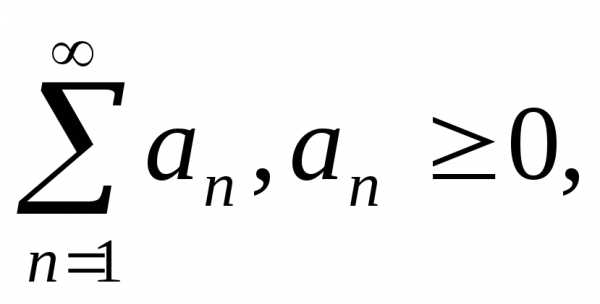 сходится и для всех
сходится и для всех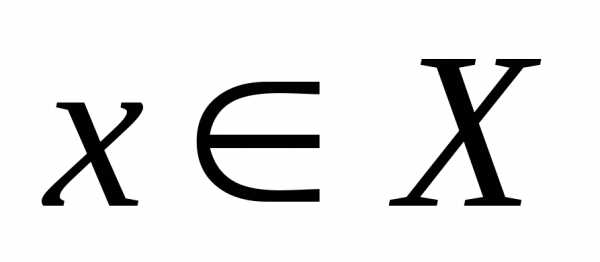 и для всехп =1, 2,… выполняется
неравенството ряд
и для всехп =1, 2,… выполняется
неравенството ряд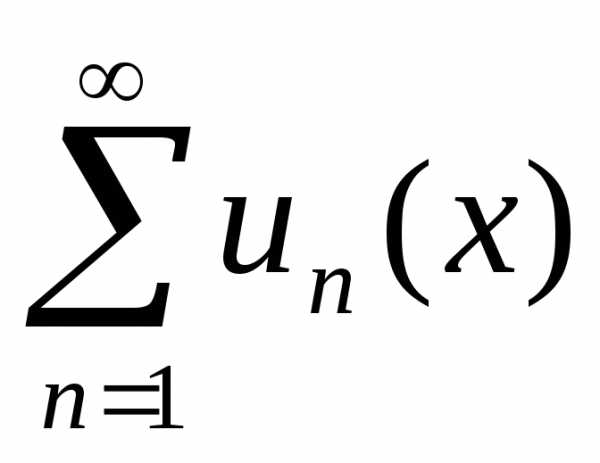 сходится абсолютно и равномерно на
множествеХ.
сходится абсолютно и равномерно на
множествеХ.
Доказательство.
Для любого ε> 0cуществует
такой номерN, что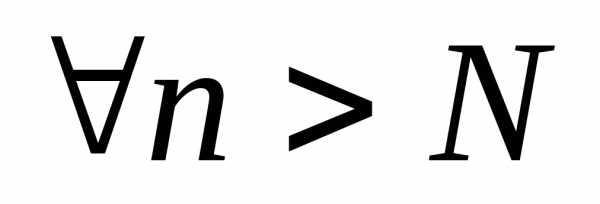
 поэтому
поэтому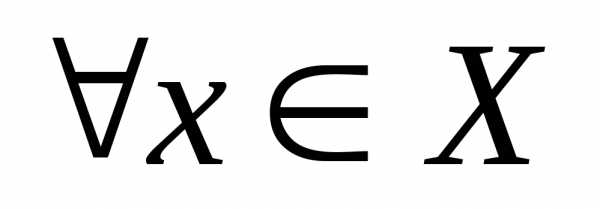 и
и
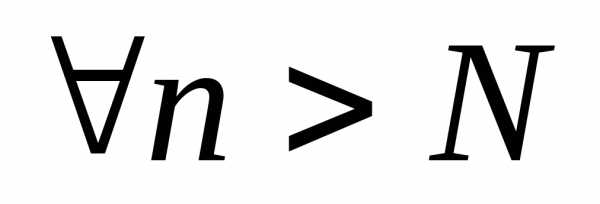 для остатковrn ряда
для остатковrn ряда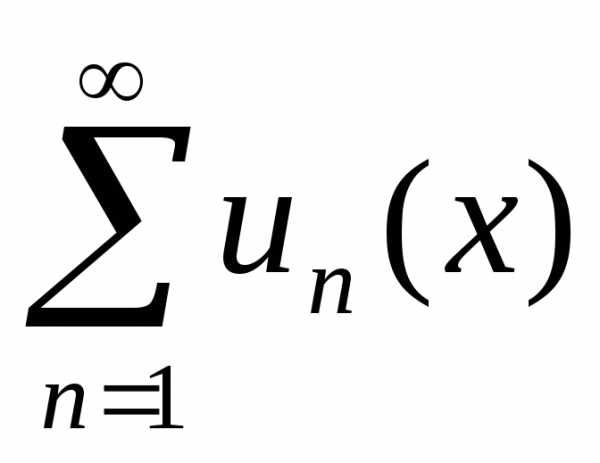 справедлива оценка
справедлива оценка
Следовательно, поэтому ряд
поэтому ряд равномерно сходится.
равномерно сходится.
Замечание. Процедура подбора числового ряда, отвечающего условиям теоремы 4.1, обычно называется мажорированием, а сам этот ряд –мажорантой для данного функционального ряда.
Пример. Для функционального ряда  мажорантой при любом значениихявляется сходящийся знакоположительный
ряд
мажорантой при любом значениихявляется сходящийся знакоположительный
ряд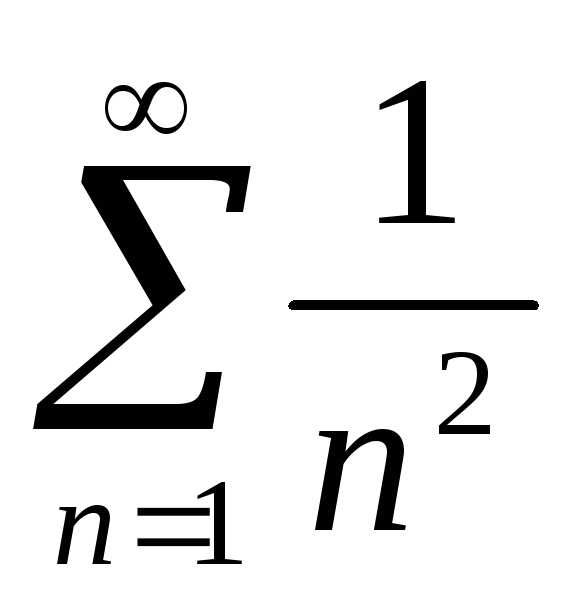 .
Поэтому исходный ряд равно-мерно сходится
на (-∞, +∞).
.
Поэтому исходный ряд равно-мерно сходится
на (-∞, +∞).
Свойства равномерно сходящихся рядов.
Теорема 4.2. Если функцииun(x) непрерывны прии
ряд равномерно сходится наХ, то его
суммаs(x)тоже непрерывна в точкех0 .
равномерно сходится наХ, то его
суммаs(x)тоже непрерывна в точкех0 .
Доказательство.
Выберем ε > 0. Тогда , поэтому существует такой номерп0 , что
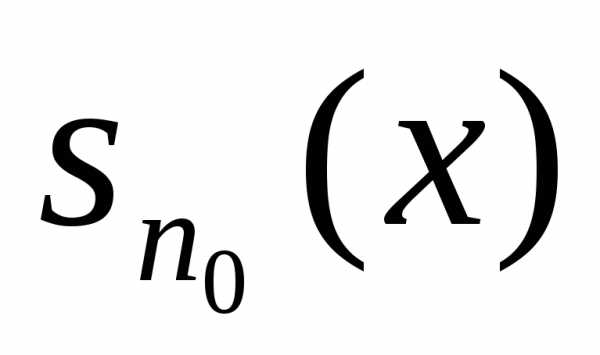 — сумма конечного числа непрерывных
функций, поэтому
— сумма конечного числа непрерывных
функций, поэтому 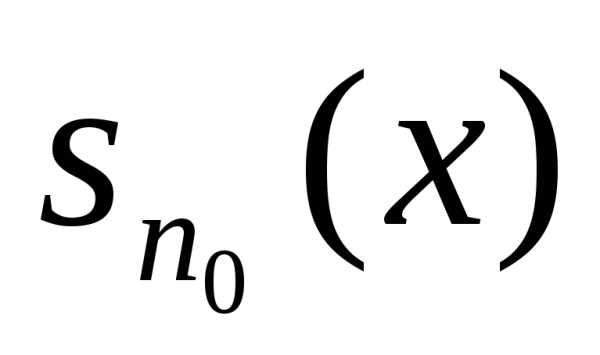 непрерывна в точкех0 .Поэтому существует такое δ > 0, что Тогда получаем:
непрерывна в точкех0 .Поэтому существует такое δ > 0, что Тогда получаем:
то есть функцияs(x) непрерывна прих = х0 .
Теорема 4.3. Пусть функцииun(x) непрерывны на отрезке [a, b] и ряд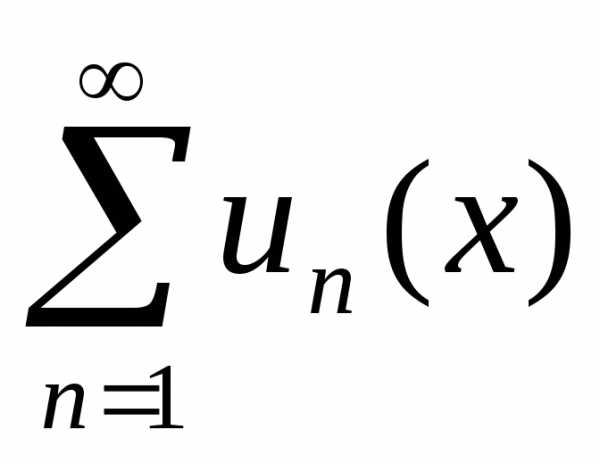 равно-мерно сходится на этом отрезке.
Тогдаряд
равно-мерно сходится на этом отрезке.
Тогдаряд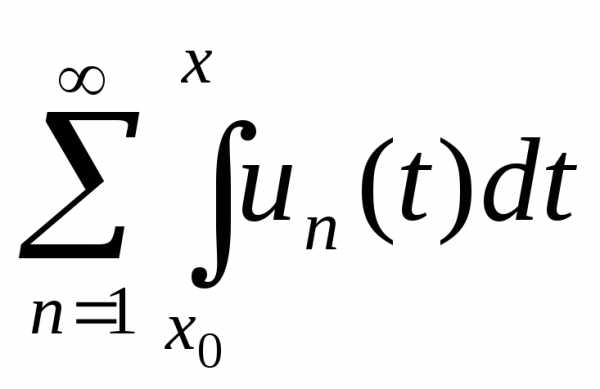 тоже равномерно сходится на [a, b] и
тоже равномерно сходится на [a, b] и
 (4.2)
(4.2)
(то есть в условиях теоремы ряд можно почленно интегрировать).
Доказательство.
По теореме 4.2 функция s(x)
=  непрерывна на [a, b]
и, следовательно, интегрируема на нем,
то есть интеграл, стоящий в левой части
равенства (4.2), существует. Покажем, что
ряд
непрерывна на [a, b]
и, следовательно, интегрируема на нем,
то есть интеграл, стоящий в левой части
равенства (4.2), существует. Покажем, что
ряд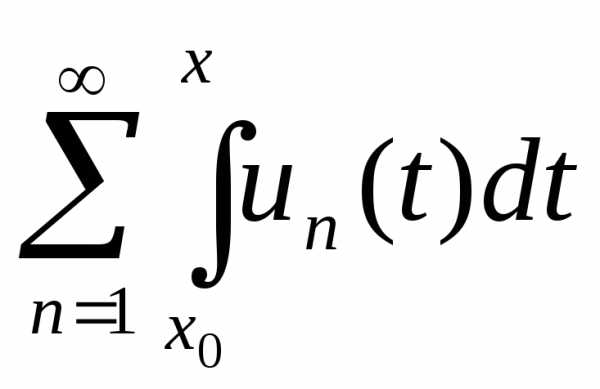 равномерно сходится к функции
равномерно сходится к функции
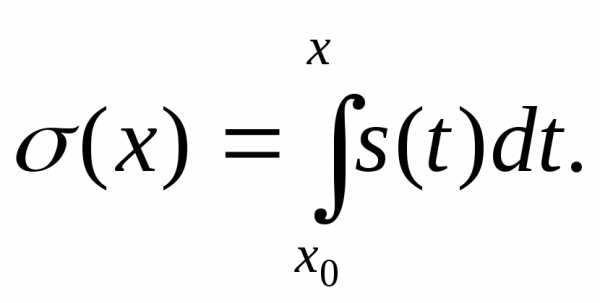 Обозначим
Обозначим
Тогда для любого ε найдется такой номерN, что приn > N
Значит,
ряд равномерно сходится, и его сумма равна
σ (х) =
равномерно сходится, и его сумма равна
σ (х) = .
.
Теорема доказана.
Теорема 4.4. Пусть функцииun(x) непрерывно дифференцируемы на отрезке [a, b] и ряд, составленный из их производных:
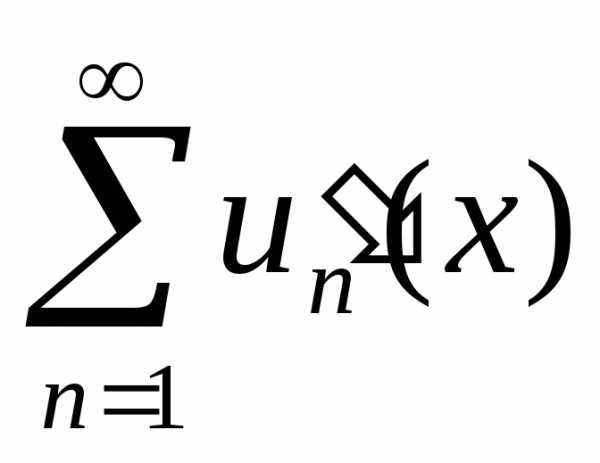 (4.3)
(4.3)
равномерно сходится на [a, b]. Тогда, если ряд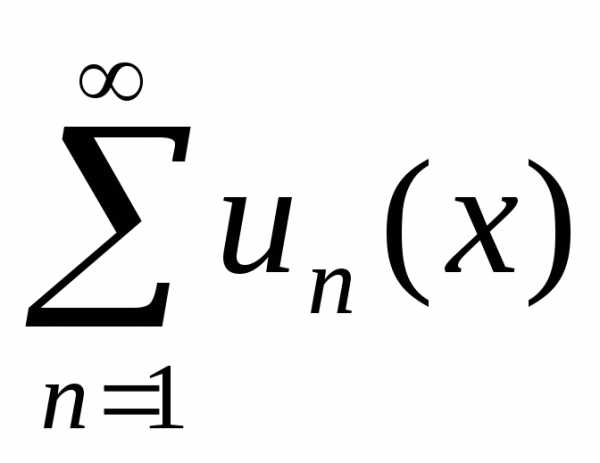 сходится хотя бы в одной точке
сходится хотя бы в одной точке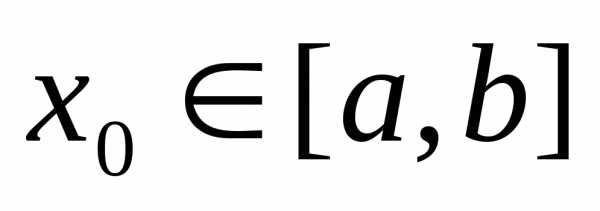 ,
то он сходится равномерно на всем [a, b], его суммаs(x)=
,
то он сходится равномерно на всем [a, b], его суммаs(x)=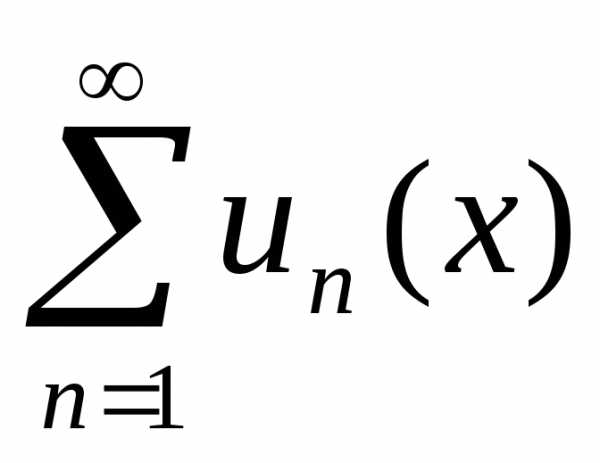 является непрерывно дифференцируемой
функцией и
является непрерывно дифференцируемой
функцией и
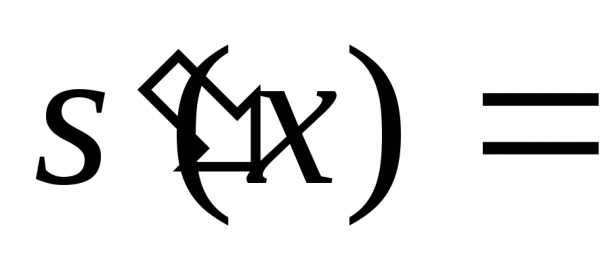
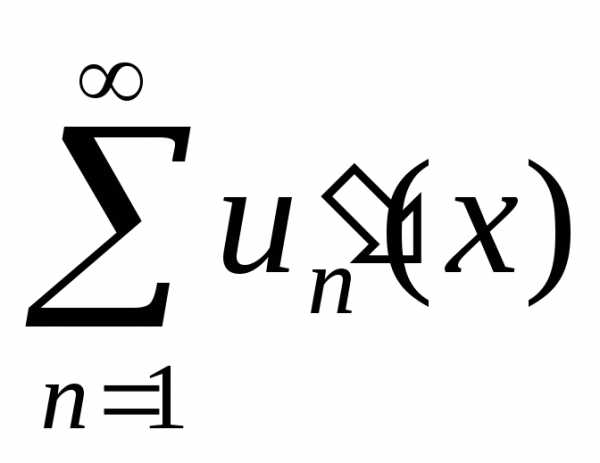
(ряд 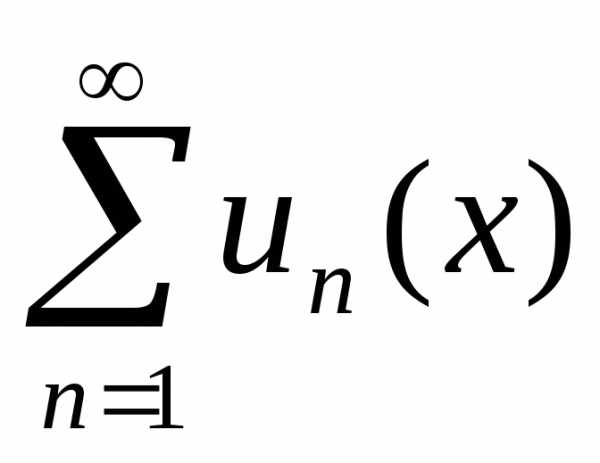 можно почленно дифференцировать).
можно почленно дифференцировать).
Доказательство.
Определим функцию σ(х) как .
По теореме 4.3 ряд (4.3) можно почленно
интегрировать:
.
По теореме 4.3 ряд (4.3) можно почленно
интегрировать:
.
Ряд, стоящий в правой части этого
равенства, равномерно сходится на [a, b] по теореме 4.3. Но
числовой ряд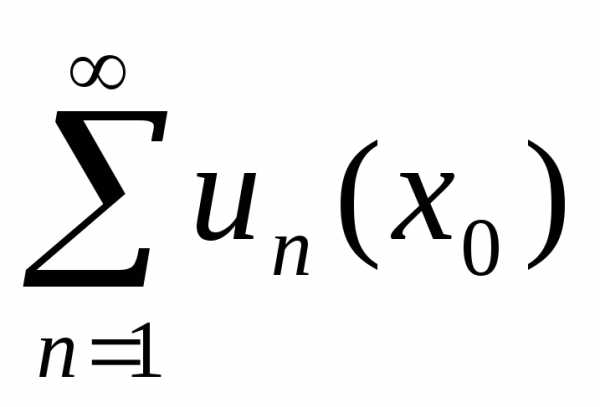 по условию теоремы сходится, следовательно,
равномерно сходится и ряд
по условию теоремы сходится, следовательно,
равномерно сходится и ряд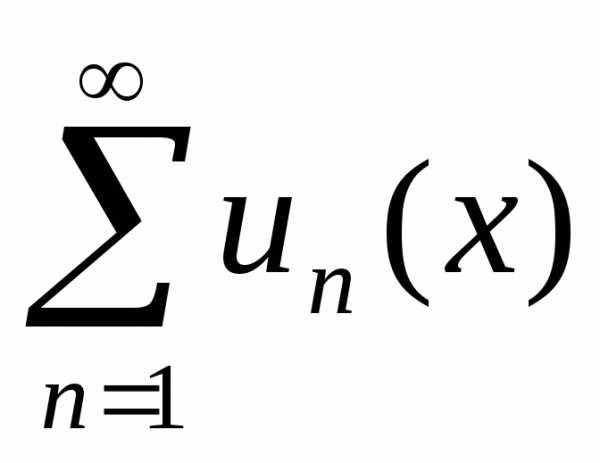 .
Тогда
.
Тогда Функция σ(t) является
суммой равномерно сходящегося ряда
непрерывных функций на [a, b] и поэтому сама
непрерывна. Тогда функция
Функция σ(t) является
суммой равномерно сходящегося ряда
непрерывных функций на [a, b] и поэтому сама
непрерывна. Тогда функция непрерывно дифференцируема на [a, b], и,
что и требовалось доказать.
непрерывно дифференцируема на [a, b], и,
что и требовалось доказать.
Лекция 5.
Степенные ряды. Теорема Абеля. Область сходимости степенного ряда. Радиус сходимости. Основные свойства степенных рядов: равномерная сходимость, непрерывность и бесконечная дифференцируемость суммы. Почленное интегрирование и дифференцирование степенных рядов.
Определение 5.1. Степенным рядомназывается функциональный ряд вида
(5.1)
Замечание. С помощью замены х – х0 = tряд (5.1) можно
привести к виду ,
поэтому все свойства степенных рядов
достаточно доказать для рядов вида
,
поэтому все свойства степенных рядов
достаточно доказать для рядов вида
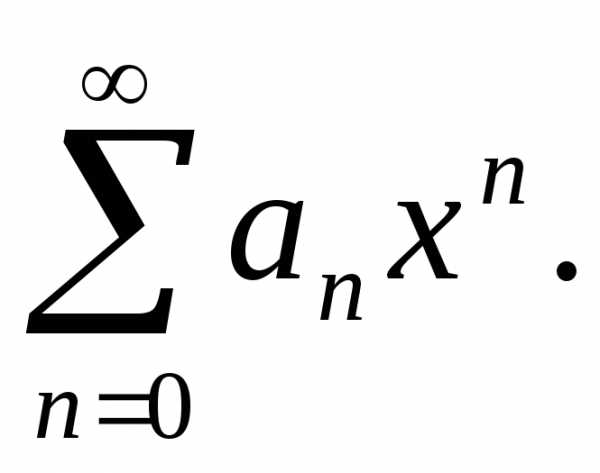 (5.2)
(5.2)
Теорема 5.1 (1-я теорема Абеля). Если степенной ряд (5.2) сходится прих = х0 ,то при любомx: |x| < |x0|ряд (5.2) сходится абсолютно. Если же ряд (5.2) расходится прих = х0 ,то он расходится при любомx: |x| > |x0|.
Доказательство.
Если ряд 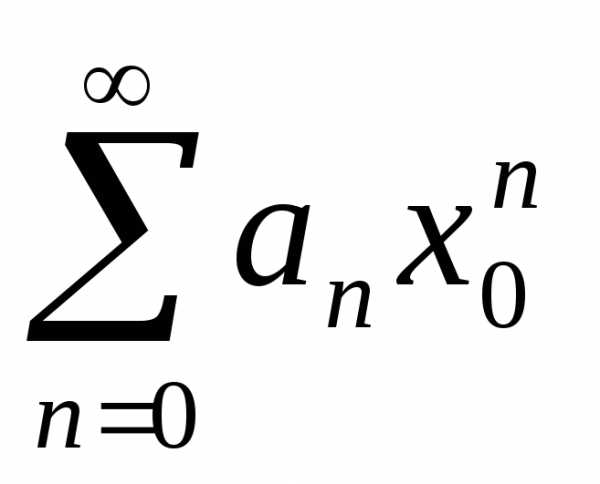 сходится, то
сходится, то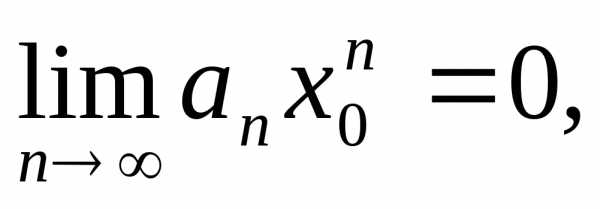 поэтому существует константас > 0:
поэтому существует константас > 0:
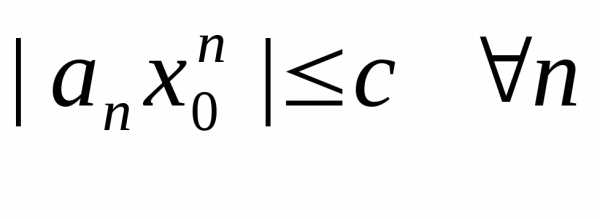 .
Следовательно,,
а ряд
.
Следовательно,,
а ряд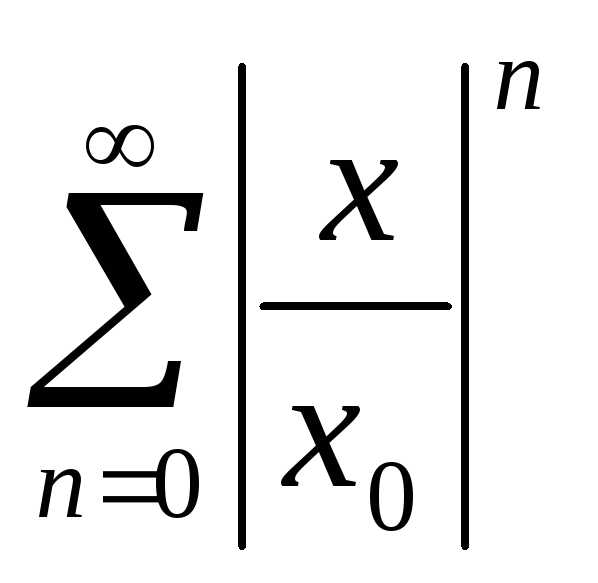 при |x|<|x0|
сходится, так как является суммой
бесконечно убывающей геометрической
прогрессии. Значит, ряд
при |x|<|x0|
сходится, так как является суммой
бесконечно убывающей геометрической
прогрессии. Значит, ряд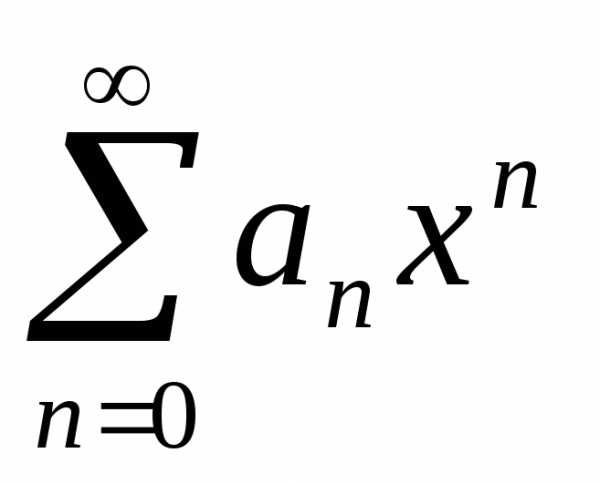 при |x|<|x0|
абсолютно сходится.
при |x|<|x0|
абсолютно сходится.
Если известно, что ряд (5.2) расходится при х = х0, то он не может сходиться при |x| > |x0| ,так как из ранее доказанного при этом следовало бы, что он сходится и в точкех0 .
Таким образом, если найти наибольшее из чисел х0> 0 таких, что (5.2) сходится прих = х0 , то областью сходимости данного ряда, как следует из теоремы Абеля, будет интервал (- х0 , х0 ), возможно, включающий одну или обе границы.
Определение 5.2. ЧислоR ≥ 0 называетсярадиусом сходимости степенного ряда (5.2), еслиэтот ряд сходится, арасходится. Интервал (—R , R ) называ-етсяинтервалом сходимости ряда (5.2).
Примеры.
Для исследования абсолютной сходимости ряда
 применим
признак Далам-бера:.
Следовательно, ряд сходится только прих= 0, и радиус его сходимости равен
0:R= 0.
применим
признак Далам-бера:.
Следовательно, ряд сходится только прих= 0, и радиус его сходимости равен
0:R= 0.Используя тот же признак Даламбера, можно показать, что ряд
 сходится при любомх, то есть
сходится при любомх, то есть
Для ряда
 по признаку Даламбера получим:
по признаку Даламбера получим:
Следовательно, при –1 <x< 1 ряд сходится, при
x< -1 иx> 1 расходится. Прих= 1 получаем
гармонический ряд, который, как извест-но,
расходится, а прих= -1 ряд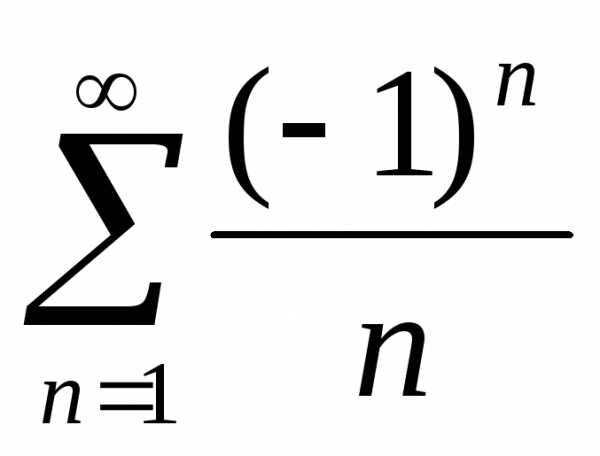 сходится условно по признаку Лейбница.
Таким образом, радиус сходимости
рассматриваемого рядаR= 1, а интервал сходи-мости – [-1, 1).
сходится условно по признаку Лейбница.
Таким образом, радиус сходимости
рассматриваемого рядаR= 1, а интервал сходи-мости – [-1, 1).
Формулы для определения радиуса сходимости степенного ряда.
Формула Даламбера.
Рассмотрим степенной ряд 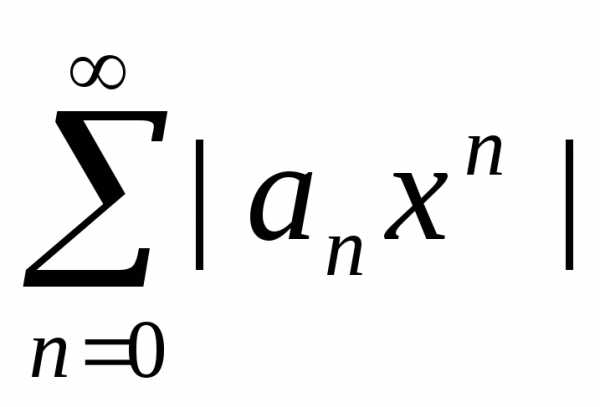 и
применим к нему признак Даламбера: для
сходимости ряда необходимо, чтобы.Если
существует
и
применим к нему признак Даламбера: для
сходимости ряда необходимо, чтобы.Если
существует ,
то область сходимости определяется
неравенством
,
то область сходимости определяется
неравенством ,
то есть
,
то есть
 —
(5.3)
—
(5.3)
Формула Коши-Адамара.
Используя радикальный признак Коши и
рассуждая аналогичным образом, получим,
что можно задать область сходимости
степенного ряда как множество решений
неравенства 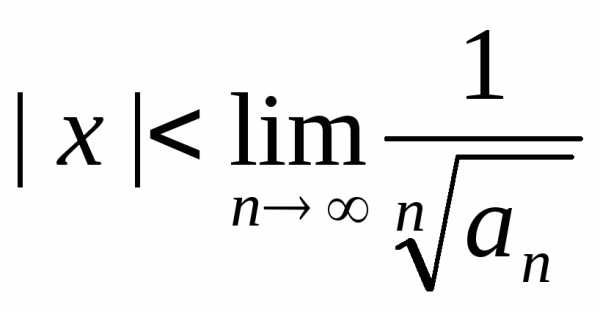 при условии существования этого предела,
и, соответствен-но, найти еще одну формулу
для радиуса сходимости:
при условии существования этого предела,
и, соответствен-но, найти еще одну формулу
для радиуса сходимости:
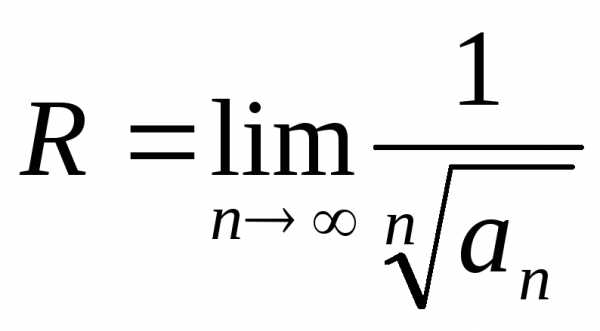 (5.4)
(5.4)
studfiles.net
РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
Основным вопросом функциональных рядов является вопрос о свойствах суммы ряда в зависимости от свойств членов этого ряда. Возникают вопросы:
1) если члены ряда – непрерывные функции, то будет ли тоже непрерывной функцией?
2) если члены ряда интегрируемые (дифференцируемые) функции, то будет ли сумма ряда интегрируемой (дифференцируемой) функцией?
Пример 18. Найдите сумму ряда , .
Решение. Очевидно, что . Пусть . Ряд в этом случае представляет собой сумму бесконечно убывающей геометрической прогрессии со знаменателем и сходится.
Сумма прогрессии равна , .
Окончательно сумма ряда имеет вид:
.
Хотя все члены ряда являются непрерывными на отрезке функциями, сумма ряда оказалась разрывной функцией. Т.о. в общем случае сумма функционального рядя не всегда наследует свойства членов ряда.
Определение 8. Ряд называется равномерно сходящимся в области к сумме , если (номер, зависящий от и не зависящий от x), такой, что выполняется неравенство , (или ).
На рисунке 1 приведена геометрическая иллюстрация равномерной сходимости функционального ряда:
Рис.1 Иллюстрация равномерной сходимости.
Пример 18. Докажите равномерную сходимость функционального ряда на отрезке [0,1].
Решение. Оценим остаток ряда: .
Выражение под знаком модуля при каждом фиксированном является знакочередующимся рядом, который сходится по признаку
Лейбница и его сумма не превосходит первого члена:
.
Решая неравенство , находим .
Таким образом, существует номер , не зависящий от x, такой
что , , . Следовательно, по определению функциональный ряд сходится равномерно при .
Ответ:ряд сходится равномерно при .
Теорема 17. (признак Вейерштрасса равномерной сходимости).
Если члены ряда , удовлетворяют неравенству , и числовой знакоположительный ряд сходится, то сходится равномерно в области .
Пример 19. Исследуйте на равномерную сходимость ряд .
Решение. При любых выполняется неравенство:
.
Обобщённый гармонический ряд сходится ( ). Следовательно, по признаку Вейерштрасса функциональный ряд сходится равномерно при любом действительном .
Ответ:ряд сходится равномерно при .
СВОЙСТВА РАВНОМЕРНО СХОДЯЩИХСЯ РЯДОВ
Теорема 18 (о непрерывности суммы ряда). Пусть в области :
1) все члены ряда являются непрерывными функциями;
2) ряд сходится равномерно к сумме .
Тогда сумма ряда есть непрерывная функция в области .
Теорема 19 (о почленном интегрировании ряда). Пусть в области :
1) все члены ряда являются непрерывными функциями,
2) ряд сходится равномерно к сумме .
Тогда его можно почленно интегрировать на любом отрезке
и справедлива формула
Теорема 20 (о почленном дифференцировании ряда). Пусть в области :
1) все члены ряда являются непрерывно-дифференцируемыми функциями;
2) ряд сходится к сумме ,
3) ряд, составленный из производных , сходится равномерно.
Тогда в области ряд сходится равномерно,
его сумма является непрерывно-дифференцируемой функцией,
ряд можно почленно дифференцировать:
.
Пример 20. Докажите равномерную сходимость функционального ряда , .
Решение. Составим ряд из производных и докажем его равномерную сходимость. Заметим, что . Обобщённый гармонический ряд сходится ( ). Следовательно, по признаку Вейерштрасса функциональный ряд сходится равномерно при любом действительном . Тогда по теореме о
почленном дифференцировании исходный ряд сходится равномерно при , причём .
Ответ: ряд сходится равномерно при .
СТЕПЕННЫЕ РЯДЫ
Определение 9.Функциональные ряды вида или , составленные из степенных функций, называются степенными.
Действительные числа называются коэффициентами степенного ряда.
Степенной ряд сходится по крайней мере в одной точке , а ряд – в точке .
Так как заменой ряд сводится к ряду ,
то в дальнейшем будем рассматриваются ряды вида .
Теорема 21 (Абеля). Пусть степенной ряд сходится в некоторой точке . Тогда он сходится абсолютно в любой точке , удовлетворяющей неравенству , и сходится равномерно в области . Пусть ряд расходится в некоторой точке . Тогда он расходится и во всех точках , таких, что .
На рисунке 2 приведена геометрическая иллюстрация теоремы Абеля.
| Рис.2. Иллюстрация теоремы Абеля. |
Таким образом, областью сходимости степенного ряда всегда является конечный или бесконечный интервал с центром в точке или единственная точка .
Пример 21. Найдите область сходимости степенного ряда .
Решение. Зафиксируем x. Получим числовой ряд, который в общем случае является знакочередующимся. Поэтому составим ряд из модулей и применим к нему признак Даламбера:
.
Ряд будет сходиться, если , т.е. .
При получим числовой знакоположительный ряд . Применим к нему предельный признак сравнения. Возьмём в качестве ряда сравнения который сходится как ряд Дирихле ( ). Найдём предел . Следовательно, ряды и сходятся одновременно. Таким образом, ряд сходится на правом конце интервала сходимости .
При получаем числовой знакочередующийся ряд , который сходится абсолютно, т.к. сходится ряд из модулей . На левом конце интервала сходимости ряд также сходится.
Ответ: областью сходимости степенного ряда является отрезок .
Пример 22. Найдите область сходимости степенного ряда .
Решение. Зафиксируем x. Получим числовой ряд, который является знакоположительным для любых x. Применим признак Даламбера:
По признаку Даламбера степенной ряд будет сходиться, если , т.е. при . Подставляя и в исходный степенной ряд, получим расходящийся гармонический ряд . Таким образом, на концах интервала сходимости степенной ряд расходится.
Ответ: областью сходимости степенного ряда является интервал .
Следствиями теоремы Абеля являются следующие теоремы.
Теорема 22. Сумма степенного ряда есть функция, непрерывная на любом отрезке из интервала сходимости.
Теорема 23. Степенной ряд можно почленно интегрировать на любом отрезке, целиком принадлежащем интервалу сходимости ряда. Степенной ряд можно почленно дифференцировать в интервале сходимости любое число раз. При этом ряды, полученные почленным интегрированием или дифференцированием степенного ряда, имеют тот же радиус сходимости, что и исходный ряд.
Пример 23. Найдите сумму ряда .
Решение. Интервалом сходимости данного степенного ряда является . Составим ряд из производных: . Члены этого ряда образуют бесконечно убывающую геометрическую прогрессию со знаменателем сумма прогрессии равна .
Проинтегрируем последнее равенство в пределах от 0 до x , где :
;
.
Ответ: , .
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru

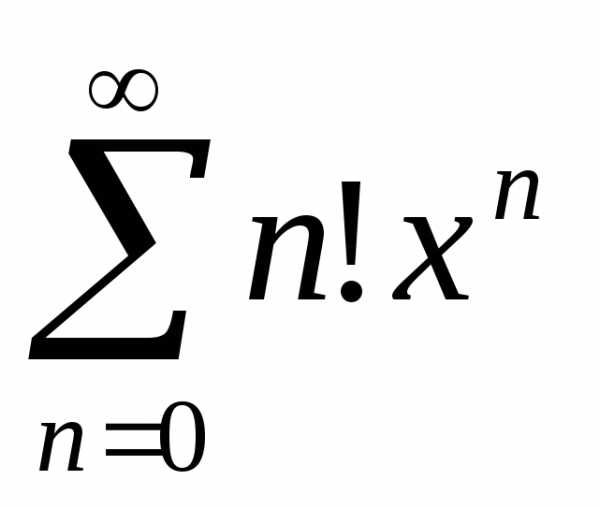 применим
признак Далам-бера:.
Следовательно, ряд сходится только прих= 0, и радиус его сходимости равен
0:R= 0.
применим
признак Далам-бера:.
Следовательно, ряд сходится только прих= 0, и радиус его сходимости равен
0:R= 0. сходится при любомх, то есть
сходится при любомх, то есть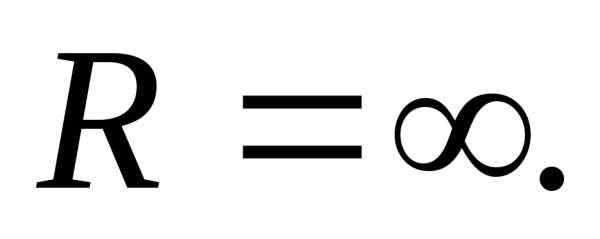
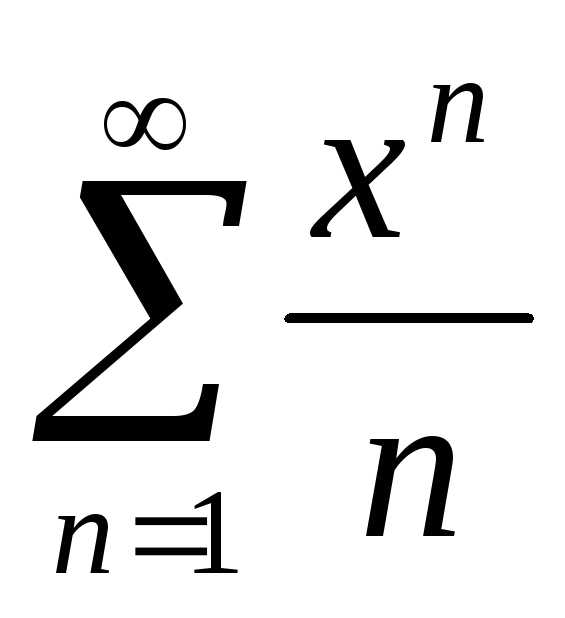 по признаку Даламбера получим:
по признаку Даламбера получим: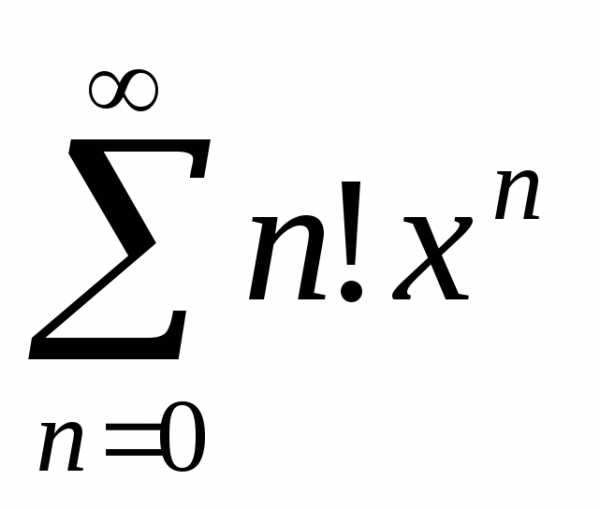 применим
признак Далам-бера:.
Следовательно, ряд сходится только прих= 0, и радиус его сходимости равен
0:R= 0.
применим
признак Далам-бера:.
Следовательно, ряд сходится только прих= 0, и радиус его сходимости равен
0:R= 0.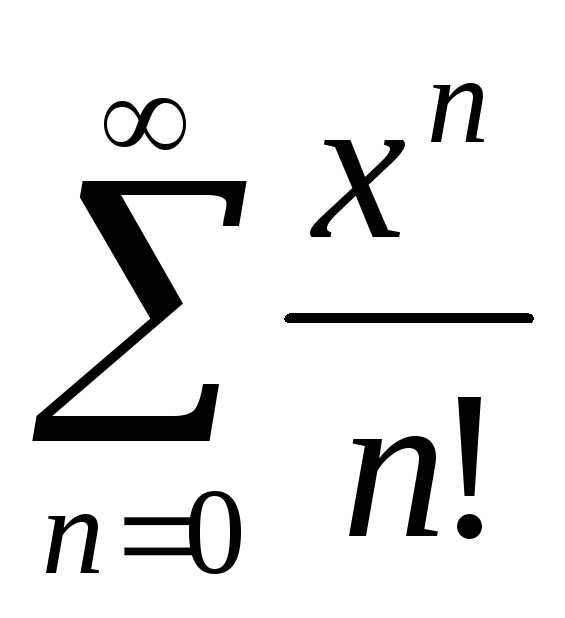 сходится при любомх, то есть
сходится при любомх, то есть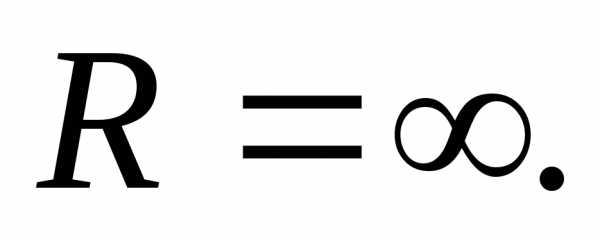
 по признаку Даламбера получим:
по признаку Даламбера получим: