Как решать систему неравенств с квадратным уравнением?
Поиск ЛекцийРешение квадратных неравенств методом параболы
Задания 4, 8, 21. Уравнения, неравенства и их системы
Пропорция
Отношение – это частное двух чисел.
Пропорция– равенство двух отношений.
Основное свойство пропорции:
Произведение крайних членов пропорции равно произведению ее средних членов.
Пример: Найти неизвестный член пропорции х : 20 = 2 : 5.
Решение: х и 5 — крайние члены пропорции, а 20 и 2 — средние.
5·х = 20·2—применяем основное свойство пропорции;
х = 40:5 — произведение средних членов делим на известный крайний член;
х = 8— получили искомый крайний член пропорции.
Уравнения
Уравнение– это буквенное равенство, которое справедливо только при некоторых значениях входящих в него букв.
Эти буквы называются неизвестными (переменными), а их значения, при которых данное уравнение обращается в верное равенство – корнями уравнения.
Решить уравнение– значит найти все его корни или доказать, что корней нет.
Равносильные уравнения – уравнения, у которых одинаковое решение
Основные тождественные преобразования (свойства уравнений)
Перенос слагаемых из одной части уравнения в другую со сменой знака.
12x – 4=15x – 10
12х – 15х = – 10 +4
Умножение или деление обеих частей уравнения на одно и то же число (выражение), отличное от нуля.
· 2
5х – 6 = 2х
3. Замена одного выражения другим, тождественно равным ему.
(3x+ 2)2 = 15x+10
9×2 + 12x + 4 = 15x + 10
Линейное уравнение с одной переменной
Общий вид линейного уравнения: ax + b = 0 , где а и b – любые числа.
Решение линейных уравненийпредполагает использование тождественных преобразований уравнений.
Пример: 3(х – 2) = 10 – (х – 5) — раскроем скобки
3х – 6 = 10 – х + 5 — перенесем слагаемые с х в одну часть, без х в другую
3х + х = 15 + 6 — приведем подобные слагаемые
4х = 21 — обе части уравнения разделим на 4
х = 5,25
Квадратное уравнение
Общий вид квадратного уравнения: + bx + c = 0, гдеa, b, c – числа, x – переменная. Если a = 0, то уравнение становится линейным. Поэтому, говоря о квадратных уравнениях, предполагается, что a 0.
Если коэффициент а = 1, то квадратное уравнение называют приведенным.
Квадратные уравнения
Полные(a 0, b 0, c 0) Неполные
+ bx + c = 0
+ bx = 0 (с = 0) + с = 0 (b = 0) = 0 (b = 0, с = 0)
Решение квадратных уравнений
1. В общем случае корни находятся через дискриминант D = b2 – 4ac.
® Если D> 0, то уравнение имеет 2 корня:
® Если D = 0, то уравнение имеет 1 корень:
® Если D< 0, то уравнение не имеет корней.
2. Если коэффициент b четный, то можно найти =.
Тогда корни находятся по формуле: .
3. Если уравнение приведенное, то можно использовать т. Виета:
Сумма корней приведенного квадратного уравнения + bx + c = 0 равна коэффициенту перед х, взятому с противоположным знаком, а произведение равно свободному члену.
+ = – b
· = c
4. Неполные квадратные уравнения принято решать не через дискриминант.
Дробно-рациональные уравнения
Квадратные неравенства.
Найти общий знаменатель дробей;
2. Умножить обе части уравнения на общий знаменатель;
3. Решить получившееся целое уравнение;
4. Найти область допустимых значений (ОДЗ), исключив числа, при которых знаменатель обращается в 0.
5. В ответ записываются все корни, кроме тех, которые не удовлетворяют ОДЗ.
Пример: x(x-5) — умножим дроби на общий знаменатель
x(x-3) + x – 5 = x + 5 ОДЗ: х(х-5) 0
х2 – 3x – 10 = 0 x 0 и х – 5 0
x1 = -2; x2 = 5 х 5
Ответ: -2
Решение неравенств
Решить неравенство – значит найти границы, внутри которых должны находиться переменные, так чтобы неравенство было верным.
Линейные неравенства
Общий вид линейного неравенства:
Линейные неравенства решаются с опорой на свойства, аналогично линейным уравнениям.Помним, если было произведено умножение или деление обеих частей неравенства на отрицательное число, то знак неравенства меняется на противоположный. В отличии от уравнений в ответ выписывается не конкретный набор чисел, а числовой промежуток.
Пример:
Ответ: х (- )
Квадратные неравенства
Общий вид квадратного неравенства: ах2 + bх + с < 0(знак неравенства может быть другим), где a, bи с– числа, х – неизвестная.
Для решения квадратных неравенств, есть 2 подхода (метод параболы и метод интервалов).
Решение квадратных неравенств методом параболы
Алгоритм:
ах2 + bх + с < 0 (ах2 + bх + с > 0)
1. Найти корни квадратного трехчлена ах2 + bх + с, для этого решаем квадратное уравнение ах2 + bх + с = 0.
2. Определить, куда направлены ветви параболы
3. Отметить найденные корни на оси х (если неравенство строгое, то точки выколоты).
4. Схематично изобразить график.
5. Определить, для каких х ординаты графика отрицательны (положительны).
Другими словами: для каких х график функции находится ниже (выше) оси х.
6. Выписать промежуток в ответ.
Пример: х2 + х – 6 0
х2 + х – 6 = 0
х1 = -3, х2 = 2
у = х2 + х – 6
коэффициент а=1 > 0 => ветви вверх
находим часть параболы, которая выше оси х
Ответ: ( ]
Алгоритм:
1) Преобразовать неравенство таким образом, чтобы в правой части остался 0.
2) Разложить выражение в левой части на множители.
3) Приравнять это выражение к 0 и решить получившееся уравнение.
Замечание: если уравнение дробно-рациональное, не забываем найти ОДЗ.
4) Полученные корни отметить на координатной прямой (если знак неравенства строгий – точки выколоты, если нестрогий – закрашены).
Замечание: если уравнение дробно-рациональное, то точки, не вошедшие в ОДЗ выкалываем на координатной прямой.
5) Отмеченные точки разбивают координатную прямую на промежутки.
Берем любое число из каждого промежутка, подставляем вместо х в разложенное на множители выражение (п.2) и определяем знак этого выражения.
Над каждым промежутком подписываем этот знак.
6) В ответ берутся те промежутки, которые соответствуют знаку неравенства («+» соответствует >0, «–» соответствует <0)
Пример 1: (х + 3)(х – 2) 0
(х + 3)(х – 2) = 0
х = -3, х = 2
Ответ: ( )
| — перенесем 2 в левую часть неравенства— приведем к общему знаменателю— вычтем дроби— разложим на множители выражение слева (в числителе применяем формулу «квадрат разности»)— находим нули числителя и знаменателя— отмечаем на координатной прямой точку 1 (закрашена) и точку 0 (выколота)— получилось 3 промежутка, берем из каждого любое число и подставляем в выражение (х-1)2, везде получается знак + |
Пример 2:
х = 1
Знак неравенства , это значит, что в ответ пойдут промежутки со знаком «–» и точки, отмеченные на оси. Видим, что промежутков со знаком «–» нет и есть всего одна закрашенная точка на оси. Она и идет в ответ.
Ответ: 1
Системы уравнений
Пару чисел (х; у), которая одновременно является решением и первого, и второго уравнения системы, называют решением системы уравнений.
Решить систему – значит найти все ее решения или установить, что решений нет.
©2015-2018 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Нарушение авторских прав и Нарушение персональных данных
Квадратные неравенства — это неравенства, содержащие квадратный трехчлен ax2 + bx + c, где a ≠ 0.
Решить квадратное неравенство (как и любое другое) — это значит, найти область значений переменной (x), при которых неравенство становится верным.
Квадратное неравенство можно решить графическим методом (методом изображения параболы) и методом интервалов. Хотя метод интервалов также можно считать графическим, если эти интервалы изображаются на прямой.
Как известно, графиком функции y = ax2 + bx + c является парабола. Ее ветви направлены вверх, если a > 0, и вниз, если a < 0. Ось x парабола пересекает тогда, когда y = 0. То есть, решив уравнение ax2 + bx + c = 0, мы найдем те координаты x, в которых парабола пересекает ось x. Та часть (или части) параболы, которая лежит выше оси x, — это положительные значения функции. Ниже оси x — отрицательные. В зависимости от знака квадратного неравенства указываются числовые промежутки, где функция y = ax2 + bx + c принимает положительные или отрицательные значения.
Парабола может и не пересекать ось x. При этом соответствующее такой функции квадратное уравнение корней не имеет. Если же говорить о соответствующем неравенстве, то его решение зависит от знака неравенства и того, выше или ниже оси x расположена парабола. Когда знак неравенства > (, т. е. больше нуля), то вся парабола (любые значения x) является его решением, если она расположена выше оси x. Если знак
Для того, чтобы схематично изобразить или вообразить параболу на числовой оси, надо найти корни уравнения ax2 + bx + c = 0 (или обнаружить их отсутствие).
Пусть дано квадратное неравенство 4×2 – 5x + 1 < 0. Найдем корни уравнения 4×2 – 5x + 1 = 0:
D = (–5)2 – 4 * 4 * 1 = 25 – 16 = 9
x1 = (–(–5) + 3) / (2 * 4) = 1; x2 = (–(–5) – 3) / (2 * 4) = 0,25
Значит, парабола пересекает ось x в двух точках: 0,25 и 1. Так как коэффициент a данного уравнения положительный, то ветви параболы направлены вверх. Так как знак соответствующего уравнению неравенства < (требуется найти области значения x, при которых квадратный трехчлен меньше нуля), то область значений параболы, удовлетворяющих неравенству, находится в промежутке от 0,25 до 1 (чтобы понять это надо нарисовать или представить параболу). Так как знак неравенства не строгий, то сами эти числа в область значений не входят.
Таким образом, решением квадратного неравенства 4×2 – 5x + 1 < 0 является числовой промежуток, где x ∈ (0,25; 1).
Решение квадратных неравенств методом интервалов заключается в следующем:
- Определяются корни соответствующего трехчлену уравнения.
- Квадратных трехчлен раскладывается на множители по формуле ax2 + bx + c = a(x – x1)(x – x2), где x1 и x2 корни квадратного уравнения.
- Выясняется, при каких значениях x (на каких интервалах) разложенный на множители трехчлен положителен или отрицателен.
- В зависимости от знака квадратного неравенства определяется область значений, являющаяся его решением.
Пусть дано рассмотренное выше неравенство. Так как его корни 0,25 и 1, то получим неравенство:
4(x – 0,25)(x – 1) < 0
При каких значениях x данное произведение будет отрицательно?
- Если x > 1, то все множители (и x – 0,25, и x – 1, и 4) положительны и, следовательно, произведение положительно. Значит область значений x > 1 не может быть решением неравенства.
Алгебра – 9 класс. Системы неравенств
- Если 0,25 < x < 1, то множитель x – 0,25 > 0, а вот x – 1 < 0. Следовательно, произведение множителей отрицательно, а неравенство верно. Значит промежуток (0,25; 1) является решением неравенства.
- Если x < 0,25, то x – 0,25 < 0 и x – 1 < 0. Произведение двух отрицательных множителей и одного положительного (4) даст положительное число. Таким образом область значений x меньше 0,25 не является решением неравенства.
Делается вывод, что решением является лишь один интервал, где x ∈ (0,25; 1). При этом для наглядности на числовой прямой обозначают интервалы, где x принимает положительные или отрицательные значения.
Поиск ЛекцийРешение квадратных неравенств методом параболы
Задания 4, 8, 21.
Математика
Уравнения, неравенства и их системы
Пропорция
Отношение – это частное двух чисел.
Пропорция– равенство двух отношений.
Основное свойство пропорции:
Произведение крайних членов пропорции равно произведению ее средних членов.
Пример: Найти неизвестный член пропорции х : 20 = 2 : 5.
Решение: х и 5 — крайние члены пропорции, а 20 и 2 — средние.
5·х = 20·2—применяем основное свойство пропорции;
х = 40:5 — произведение средних членов делим на известный крайний член;
х = 8— получили искомый крайний член пропорции.
Уравнения
Уравнение– это буквенное равенство, которое справедливо только при некоторых значениях входящих в него букв.
Эти буквы называются неизвестными (переменными), а их значения, при которых данное уравнение обращается в верное равенство – корнями уравнения.
Решить уравнение– значит найти все его корни или доказать, что корней нет.
Равносильные уравнения – уравнения, у которых одинаковое решение
Основные тождественные преобразования (свойства уравнений)
Перенос слагаемых из одной части уравнения в другую со сменой знака.
12x – 4=15x – 10
12х – 15х = – 10 +4
Умножение или деление обеих частей уравнения на одно и то же число (выражение), отличное от нуля.
· 2
5х – 6 = 2х
3. Замена одного выражения другим, тождественно равным ему.
(3x+ 2)2 = 15x+10
9×2 + 12x + 4 = 15x + 10
Линейное уравнение с одной переменной
Общий вид линейного уравнения: ax + b = 0 , где а и b – любые числа.
Решение линейных уравненийпредполагает использование тождественных преобразований уравнений.
Пример: 3(х – 2) = 10 – (х – 5) — раскроем скобки
3х – 6 = 10 – х + 5 — перенесем слагаемые с х в одну часть, без х в другую
3х + х = 15 + 6 — приведем подобные слагаемые
4х = 21 — обе части уравнения разделим на 4
х = 5,25
Квадратное уравнение
Общий вид квадратного уравнения: + bx + c = 0, гдеa, b, c – числа, x – переменная. Если a = 0, то уравнение становится линейным. Поэтому, говоря о квадратных уравнениях, предполагается, что a 0.
Если коэффициент а = 1, то квадратное уравнение называют приведенным.
Квадратные уравнения
Полные(a 0, b 0, c 0) Неполные
+ bx + c = 0
+ bx = 0 (с = 0) + с = 0 (b = 0) = 0 (b = 0, с = 0)
Решение квадратных уравнений
1. В общем случае корни находятся через дискриминант D = b2 – 4ac.
® Если D> 0, то уравнение имеет 2 корня:
® Если D = 0, то уравнение имеет 1 корень:
® Если D< 0, то уравнение не имеет корней.
2. Если коэффициент b четный, то можно найти =.
Тогда корни находятся по формуле: .
3. Если уравнение приведенное, то можно использовать т. Виета:
Сумма корней приведенного квадратного уравнения + bx + c = 0 равна коэффициенту перед х, взятому с противоположным знаком, а произведение равно свободному члену.
+ = – b
· = c
4. Неполные квадратные уравнения принято решать не через дискриминант.
Дробно-рациональные уравнения
1. Найти общий знаменатель дробей;
2. Умножить обе части уравнения на общий знаменатель;
3. Решить получившееся целое уравнение;
4. Найти область допустимых значений (ОДЗ), исключив числа, при которых знаменатель обращается в 0.
5. В ответ записываются все корни, кроме тех, которые не удовлетворяют ОДЗ.
Пример: x(x-5) — умножим дроби на общий знаменатель
x(x-3) + x – 5 = x + 5 ОДЗ: х(х-5) 0
х2 – 3x – 10 = 0 x 0 и х – 5 0
x1 = -2; x2 = 5 х 5
Ответ: -2
Решение неравенств
Решить неравенство – значит найти границы, внутри которых должны находиться переменные, так чтобы неравенство было верным.
Линейные неравенства
Общий вид линейного неравенства: aх + b < 0 (знак неравенства может быть другим), где aи b – числа, х – неизвестная.
Линейные неравенства решаются с опорой на свойства, аналогично линейным уравнениям.Помним, если было произведено умножение или деление обеих частей неравенства на отрицательное число, то знак неравенства меняется на противоположный. В отличии от уравнений в ответ выписывается не конкретный набор чисел, а числовой промежуток.
Пример:
Ответ: х (- )
Квадратные неравенства
Общий вид квадратного неравенства: ах2 + bх + с < 0(знак неравенства может быть другим), где a, bи с– числа, х – неизвестная.
Для решения квадратных неравенств, есть 2 подхода (метод параболы и метод интервалов).
Решение квадратных неравенств методом параболы
Алгоритм:
ах2 + bх + с < 0 (ах2 + bх + с > 0)
1. Найти корни квадратного трехчлена ах2 + bх + с, для этого решаем квадратное уравнение ах2 + bх + с = 0.
2. Определить, куда направлены ветви параболы
3. Отметить найденные корни на оси х (если неравенство строгое, то точки выколоты).
4. Схематично изобразить график.
5. Определить, для каких х ординаты графика отрицательны (положительны).
Другими словами: для каких х график функции находится ниже (выше) оси х.
6. Выписать промежуток в ответ.
Пример: х2 + х – 6 0
х2 + х – 6 = 0
х1 = -3, х2 = 2
у = х2 + х – 6
коэффициент а=1 > 0 => ветви вверх
находим часть параболы, которая выше оси х
Ответ: ( ]
Решение квадратных неравенств методом интервалов.
Алгоритм:
1) Преобразовать неравенство таким образом, чтобы в правой части остался 0.
2) Разложить выражение в левой части на множители.
3) Приравнять это выражение к 0 и решить получившееся уравнение.
Замечание: если уравнение дробно-рациональное, не забываем найти ОДЗ.
4) Полученные корни отметить на координатной прямой (если знак неравенства строгий – точки выколоты, если нестрогий – закрашены).
Замечание: если уравнение дробно-рациональное, то точки, не вошедшие в ОДЗ выкалываем на координатной прямой.
5) Отмеченные точки разбивают координатную прямую на промежутки.
Берем любое число из каждого промежутка, подставляем вместо х в разложенное на множители выражение (п.2) и определяем знак этого выражения.
Над каждым промежутком подписываем этот знак.
6) В ответ берутся те промежутки, которые соответствуют знаку неравенства («+» соответствует >0, «–» соответствует <0)
Пример 1: (х + 3)(х – 2) 0
(х + 3)(х – 2) = 0
х = -3, х = 2
Ответ: ( )
| — перенесем 2 в левую часть неравенства— приведем к общему знаменателю— вычтем дроби— разложим на множители выражение слева (в числителе применяем формулу «квадрат разности»)— находим нули числителя и знаменателя— отмечаем на координатной прямой точку 1 (закрашена) и точку 0 (выколота)— получилось 3 промежутка, берем из каждого любое число и подставляем в выражение (х-1)2, везде получается знак + |
Пример 2:
х = 1
Знак неравенства , это значит, что в ответ пойдут промежутки со знаком «–» и точки, отмеченные на оси. Видим, что промежутков со знаком «–» нет и есть всего одна закрашенная точка на оси. Она и идет в ответ.
Ответ: 1
Системы уравнений
Пару чисел (х; у), которая одновременно является решением и первого, и второго уравнения системы, называют решением системы уравнений.
Решить систему – значит найти все ее решения или установить, что решений нет.
©2015-2018 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Нарушение авторских прав и Нарушение персональных данных
Примеры решения квадратных неравенств
Рассмотрим различные примеры решения квадратных неравенств.
1) 2x2 + x + 3 > 0
D = 1 – 4 × 2 × 3 < 0, корней нет, знак решаемого неравенства совпадает со знаком старшего коэффициента.
Ответ: R.
2) –x2 + 2x + 3 ³ 0
d = D = 1 + 3 = 4 > 0
Находим корни: x2 – 2x – 3 = 0, x1 = –1, x2 = 2.
Мысленно представляем себе график и сопоставляем его с заданным неравенством.
Ответ: .
Можно, конечно, сначала преобразовать данное неравенство, добившись того, чтобы старший коэффициент стал положительным: x2 – 2x – 3 £ 0.
3) 3x2 – 4x + 2 < 0
d = 22 – 2 × 3 < 0, корней нет. Левая часть всегда положительна.
Ответ: Æ (решений нет).
4) 4x2 – 12x + 9 £ 0
d = 62 – 4 × 9 = 0, корень (левая часть является полным квадратом
(2x – 3)2). Левая часть во всех остальных точках положительна.
Ответ: .
5) 2x2 + 5x – 7 > 0
Дискриминант можно не считать – надо сразу видеть, что трехчлен имеет два корня. Один угадывается (x = 1), второй находится по теореме Виета x1 = –, x2 = 1.
Старший коэффициент положителен. Записываем ответ.
Ответ: .
Ответы можно записывать и в виде неравенств x < –, x > 1.
6) (x – 3)(2x + 3) ³ 0
Разумеется, не нужно перемножать скобки.
Решение неравенств
Вся информация о поведении квадратичной функции в левой части очевидна.
Корни: x1 = –, x2 = 3 (не забывайте сначала писать меньший корень).
Знак старшего коэффициента: +.
Представляем мысленно график и записываем ответ, не забыв включить в него корни.
Ответ: .
7) x2 + (x + 1)2 > 0
Никаких преобразований делать не надо. В левой части стоит сумма двух квадратов, которая, конечно, неотрицательна. В нуль она обратиться не может, так как это могло быть только в случае, когда каждый из квадратов равен нулю, что одновременно невозможно.
Ответ: R.
8) –x2 + 4x – 4 < 0
Неравенство лучше преобразовать:
x2 – 4x + 4 > 0
(x – 2)2 > 0
Ответ: x¹2, или (–¥ ; 2) È (2; +¥ ).
Если у Вас остались вопросы по теме «Решение квадратных неравенств» и Вы хотите подготовиться к ГИА по математике, то рекомендуем Вам обратиться за помощью к онлайн репетитору по алгебре.
pasmr21.ru
Решение квадратных уравнений и неравенств с помощью ЭВМ
Разделы: Математика, Информатика
Подготовка к уроку:
- Создание слайдов презентации.
- Создание программы решения квадратных уравнений на языке программирования Basic (на предыдущем уроке).
План урока:
- Повторение формул корней квадратного уравнения и основных операторов языка Basic.
- Самостоятельная работа по вариантам.
- Решение уравнений, приводимых к квадратным заменой переменной.
- Решение биквадратных уравнений.
- Решение дробно-рациональных уравнений.
- Решение неравенств.
- Задание на дом.
- Подведение итогов.
Цели урока:
- Образовательная: повторение формул корней квадратных уравнений, повторение решения уравнений и неравенств, приводимых к квадратным, повторение основных операторов языка программирования Basic составление программы для решения биквадратных уравнений.
- Воспитательная: развитие познавательного интереса, развитие внимания, расширение кругозора учащихся.
- Развивающая: развитие коммуникативных, информационных компетенций, развитие памяти, преодоление трудностей, умение работать в команде, повышение интереса к математике и информатике.
Ход урока
Учитель информатики: Здравствуйте, позвольте как хозяйке кабинета приветствовать Вас здесь. Урок у нас сегодня необычный: мы будем заниматься математикой, а её инструментов будет служить информатика.
Учитель математики: Целями сегодняшнего урока будут: повторение формул корней квадратного уравнения, повторение решения уравнений и неравенств, приводимых к квадратным, то есть подготовка к экзамену.
Учитель информатики: цель нашей части урока – повторить основные операторы языка программирования Basic и написание программы для решения биквадратных уравнений. Итак, начнем! (Приложение).
Учитель математики: Необходимо выйти к доске и написать общий вид квадратного уравнения. Что нужно найти, чтобы определить количество корней у уравнения? Правильно, дискриминант. Слово «Дискриминант» переводится как «различитель». Если дискриминант больше нуля, то уравнение имеет два корня, если равен нулю, то один корень, и если дискриминант меньше нуля, то уравнение не имеет корней.
Учитель информатики: А теперь давайте перечислим основные операторы языка программирования Basic: Print – вывод, Input – ввод с клавиатуры, Cls – очистка экрана, Let – оператор присвоения, If Then – оператор условия. Молодцы! А сейчас, чтобы вы ещё раз хорошенько для себя уяснили все формулы и операторы, проведем самостоятельную работу. Для этого поделимся на математиков и информатиков. Каждый выполняет свой вариант, после выполнения задания вы меняетесь листочками и проверяете друг у друга, выставляя оценки, математики проверяют у информатиков и наоборот.
На эту работу отводится 7 минут.
Самостоятельная работа для математиков:
Решить уравнения.
- 2х2 + 3х – 14 = 0
- 2х2 – х – 3 = 0
Самостоятельная работа для информатиков:
Вставить пропущенные слова.
- Оператор … очищает экран.
- Блок действия в схеме алгоритма обозначается …
- Оператор … позволяет ввести данные с клавиатуры.
- Для того, чтобы напечатать результат работы программы на экране, нужно воспользоваться оператором …
- Чтобы вычислить квадратный корень на языке Basic, нужен оператор …
Учитель информатики: Итак, переходим к основной части нашего урока. Для решения квадратных уравнений необходимо знать несколько формул. А что нужно сделать для того, чтобы эти уравнения решать с помощью ЭВМ?
- Составить алгоритм решения и написать программу.
- Правильно! Составим алгоритм решения квадратного уравнения на доске (один ученик идет к доске, остальные работают в тетрадях).
А теперь по этому алгоритму составим программу на языке программирования Basic: (один ученик к доске, остальные работают за компьютерами).
10 Csl
20 Input a,b,c
30 D= b^2 – 4*a*c
40 If D>=0 then goto 50 else goto 90
50 X1 = (-b+sqr(D))/(2*a)
60 X2 = (-b-sqr(D))/(2*a)
70 Print «X1=»; X1
80 Print «X2=»;X2
85 GOTO 100
90 Print «корней нет»
100 End
Учитель математики: Давайте попробуем решить квадратное уравнение с помощью ЭВМ.
100х² -160 +63 = 0
Вводим коэффициенты: 100, -160, 63
Получаем ответ: х1=0,9 х1 = 0,7
Таким образом, имея программу можно решать любые квадратные уравнения. Но оказывается не только их.
Попробуем решить уравнение методом замены переменной (приложение).
1) (х+2)² – 2(х+2) – 3= 0
х + 2 = t
t² – 2t – 3 =0
С помощью нашей программы получаем корни этого уравнения:
t1 = 3 |
|
|
|
t2 = — 1 |
х +2 = 3 |
|
|
|
х + 2 = — 1 |
х = 1 |
|
|
|
х = — 3 |
Ответ: х1 = 1, х2 = -3
2) (х² – 5х +4)(х² – 5х +6) = 120
х² – 5х = у
(у + 4)(у + 6) = 120
у² + 10у – 96 = 0
у1 = -16 |
|
|
|
у2 = 6 |
х² – 5х = -16 |
|
|
|
х² – 5х = 6 |
корней нет |
|
|
|
х1 = -1, х2 = 6 |
Ответ: х1 = -1, х2 = 6
Учитель информатики: Скажите, пожалуйста, эта программа подходит для решения биквадратного уравнения?
Подходит, но она не вычисляет окончательные корни такого уравнения.
Давайте переделаем программу.
(Один ученик у доски, остальные на местах).
10 Csl
20 Input a,b,c
30 D= b^2 – 4*a*c
40 If D>=0 then goto 50 else goto 90
50 t1 = (-b+sqr(D))/(2*a)
60 t2 = (-b-sqr(D))/(2*a)
70 If t1 >= 0 then 72 else goto 90
72 x1 = sqr (t1)
73 x2 = — sqr(t1)
74 If t2 >= 0 then 74 else goto 90
75 x3 = sqr (t2)
76 x4 = — sqr(t2)
77 Print x1,x2,x3,x4
78 goto 100
85 GOTO 100
90 Print «корней нет»
100 End
Учитель информатики: Давайте посмотрим насколько быстро решаются биквадратные уравнения с помощью ЭВМ.
1) х4 – 17х² + 4 = 0
х² = t
t² – 17t +4 = 0
Ответ: x1 = 2, x2 = — 2, x3 = 0,5, x4 = — 0,5
2) 4х4 – 5х² + 1 = 0
Ответ: х1 = 1, х2 = — 1, х3 = 0,5, х4 = — 0,5
Физкультминутка.
Учитель математики: А теперь возвращаемся к нашей первоначальной программе и с её помощью будем решать дробно-рациональные уравнения.
1) (2х² – 3х – 14)/(х +2) = 0
х1 = 3,5 € ОДЗ
х2 = -2 не € ОДЗ
Ответ: х = 3,5
2) (2х² – 5х – 7)/(х +1) = 0
х1 = 3,5 € ОДЗ
х2 = -1 не € ОДЗ
Ответ: х = 3,5
Учитель математики: Следующее задание: определить область допустимых значений.
у = √ 5х² – 6х + 1
5х² – 6х + 1 ≥ 0
х1 = 1
х2 = 0,2
С помощью числовой прямой определяем, что х € (-∞; 0,2] U [1;+∞).
Учитель математики: Теперь попробуем решить квадратное неравенство 2х² + 15х < 8 и найти все решения, принадлежащие промежутку [-1; 2].
2х² + 15х < 8
2х² + 15х – 8 = 0
х1 = 0,5 х2 = -8
Ответ: х € [-1;0,5)
Учитель информатики: посмотрите на ваше домашнее задание (приложение). Мы задали вам задание и по математике и по информатике, выполняете на те дни, когда у нас следующие уроки. Задание по математике со звездочкой для более сильных учеников.
Домашнее задание по математике:
- Решить уравнения:
а) (х2 – х)2 – 14(х2 – х) + 24 = 0
б) (х2 + 4х)(х2 + 4х – 17) + 60 = 0
* в) х6 – 5х5 + 6х4 – х2 + 5х – 6 = 0 - Решить неравенство:
а) 3х2 – 14х + 15 ≥ 0
б) х2 – 10х + 21 < 0
Домашнее задание по информатике: Повторить основные операторы языка Basic и условные обозначения блок-схем алгоритма.
Учитель информатики: А сейчас подведём итоги урока. Тех целей, что мы ставили на начало урока, мы достигли. Мы с вами повторили решение квадратных уравнений и неравенств, повторили основные операторы языка программирования Basic и создали программу, которая будет помогать нам при решении квадратных уравнений и неравенств. Спасибо за урок!
18.06.2009
xn--i1abbnckbmcl9fb.xn--p1ai
Практическая работа «Решение квадратных уравнений и неравенств»
Курс – 1
Семестр – 1
Дисциплина – «МАТЕМАТИКА»
Практическая работа № 5 по теме:
«Решение квадратных уравнений и неравенств»
Вариант 1.
Решите квадратное уравнение:
а) ; б) ;
в)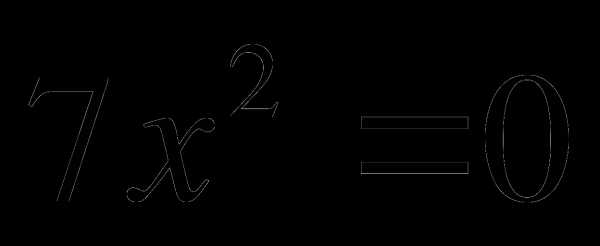 
; г) .
Решите квадратное уравнение с использованием теоремы Виета:
а) ; б) .
Составьте квадратное уравнение по его корням:
а) ; б) 
.
Сократите дробь:
.
.5. Решите неравенство графически:
а) ; б) .
6. Не решая уравнение , вычислите 
.
7. Решите задачу:
В треугольнике основание на 4 см меньше высоты, а площадь равна
96 см2. Найти основание и высоту этого треугольника.
Курс – 1
Семестр – 1
Дисциплина – «МАТЕМАТИКА»
Практическая работа № 5 по теме:
«Решение квадратных уравнений и неравенств»
Вариант 2.
Решите квадратное уравнение:
а) ; б) ;
в) 
; г) .
Решите квадратное уравнение с использованием теоремы Виета:
а) ; б) .
Составьте квадратное уравнение по его корням:
а) ; б) 
.
Сократите дробь:
.
.Решите неравенство графически:
а) ; б) .
При каком соотношении между коэффициентами в уравнении , сумма корней его равна их произведению?
Решите задачу:
В прямоугольнике одна сторона на 8 см больше другой, а его площадь равна 9 см2. Найти периметр этого прямоугольника.
infourok.ru
Решение квадратных неравенств с помощью квадратичной функции
Вопросы занятия:
· повторить, какие неравенства называются квадратичными;
· подробно рассмотреть такой способ решения квадратных неравенств как графический;
· вспомнить алгоритм решения таких неравенств.
Материал урока
Напомним, что квадратным неравенством называется неравенство вида:
Для решения такого рода неравенств как правило используют два основных метода решения: графический и аналитический метод или по-другому, метод интервалов. В любом случае, чтобы решить квадратное неравенство сначала надо решить соответствующее квадратное уравнение.
Сегодня мы с вами повторим графический метод решения квадратных неравенств.
Для того, чтобы применить этот способ, давайте вспомним, что графиком квадратичной функции является парабола.
Мы знаем, что если рассматривать не неравенство, а квадратное уравнение, то, в зависимости от знака дискриминанта у уравнения может не быть корней, быть один или два корня.
Графически решениями уравнения будут абсциссы точек пересечения параболы и оси Ох.
То есть можно составить таблицу, в которой графически будут изображены все случаи, пересечения параболы и оси Ох.
Найдя корни соответствующего квадратного уравнения, решить квадратное неравенство нетрудно.
Рассмотрим несколько примеров.
Пример.
Для того, чтобы не заучивать таблицу, которую мы заполняли выше, давайте вспомним алгоритм решения квадратного неравенства.
1. Определить направление ветвей параболы.
2. Найти корни соответствующего квадратного уравнения или установить, что это уравнение не имеет корней.
3. Схематично изобразить график квадратичной функции, отмечая абсциссы точек пересечения графика с осью Ох.
4. По графику определить промежутки, которые будут решениями неравенства.
Рассмотрим пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Итоги урока
Сегодня на уроке мы вспомнили какие неравенства называются квадратными, подробнее рассмотрели такой способ решения квадратных неравенств как графический. Вспомнили алгоритм решения таких неравенств.
videouroki.net
Как решить квадратное неравенство 🚩 квадратичное неравенство 🚩 Математика
Автор КакПросто!
Решение квадратных неравенств и уравнений – основная часть школьного курса алгебры. На умение решать квадратные неравенства рассчитано множество задач. Не стоит забывать и о том, что решение квадратных неравенств пригодится учащимся как при сдаче Единого Государственного Экзамена по математике и поступлении в ВУЗ. Разобраться же в их решении довольно просто. Существуют различные алгоритмы. Один из наиболее простых: решение неравенств методов интервалов. Он состоит из простых шагов, последовательное выполнение которых гарантировано приводит учащегося к решению неравенства.
Статьи по теме:
Вам понадобится
- Умение решать квадратные уравнения
Инструкция
Для того, чтобы решить квадратное неравенство методом интервалов, сперва нужно решить соответствующее квадратное уравнение. Переносим все члены уравнения с переменной и свободный член в левую часть, в правой части остается ноль. Корни квадратного уравнения, соответствующего неравенству (в нем знак «больше» или«меньше» заменен на «равно») можно найти по известным формулам через дискриминант.
На втором этапе мы записываем неравенство в виде произведения двух скобок (x-x1)(x-x2)<>0.
Отмечаем найденные корни на числовой оси. Далее мы смотрим на знак неравенства. Если неравенство строгое («больше» и «меньше»), то точки, которыми отмечаем корни на координатной оси пустые, в противном случае («больше или равно»).
Берем число, левее первого (правого на числовой оси корня). Если при подстановке этого числа в неравенство, оно оказывается правильным, то интервал от «минус бесконечности» до самого малого корня является одним из решений уравнения, наравне с интервалом от второго корня до «плюс бесконечности». Иначе решением будет интервал между корнями.
Видео по теме
Обратите внимание
Не ошибитесь при решении соответствующего квадратного уравнения — в данном случае вы неправильно решите неравенство.
Полезный совет
Не забывайте о том, строгое или нестрогое неравенство решаете. Если неравенство строгое, то ставим круглые скобки (то есть не берем в интервал корень уравнения), иначе берем его в промежуток (ставим квадратные скобки).
Источники:
- Дорофеев Г. В. Учебник по алгебре для 7-ого класса
- как решить неравенство с корнем
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Решение квадратных неравенств методом параболы
Поиск ЛекцийЗадания 4, 8, 21. Уравнения, неравенства и их системы
Пропорция
Отношение – это частное двух чисел.
Пропорция– равенство двух отношений.
Основное свойство пропорции:
Произведение крайних членов пропорции равно произведению ее средних членов.
Пример: Найти неизвестный член пропорции х : 20 = 2 : 5.
Решение: х и 5 — крайние члены пропорции, а 20 и 2 — средние.
5·х = 20·2—применяем основное свойство пропорции;
х = 40:5 — произведение средних членов делим на известный крайний член;
х = 8— получили искомый крайний член пропорции.
Уравнения
Уравнение– это буквенное равенство, которое справедливо только при некоторых значениях входящих в него букв.
Эти буквы называются неизвестными (переменными), а их значения, при которых данное уравнение обращается в верное равенство – корнями уравнения.
Решить уравнение– значит найти все его корни или доказать, что корней нет.
Равносильные уравнения – уравнения, у которых одинаковое решение
Основные тождественные преобразования (свойства уравнений)
Перенос слагаемых из одной части уравнения в другую со сменой знака.
12x – 4=15x – 10
12х – 15х = – 10 +4
Умножение или деление обеих частей уравнения на одно и то же число (выражение), отличное от нуля.
· 2
5х – 6 = 2х
3. Замена одного выражения другим, тождественно равным ему.
(3x+ 2)2 = 15x+10
9x2 + 12x + 4 = 15x + 10
Линейное уравнение с одной переменной
Общий вид линейного уравнения: ax + b = 0 , где а и b – любые числа.
Решение линейных уравненийпредполагает использование тождественных преобразований уравнений.
Пример: 3(х – 2) = 10 – (х – 5) — раскроем скобки
3х – 6 = 10 – х + 5 — перенесем слагаемые с х в одну часть, без х в другую
3х + х = 15 + 6 — приведем подобные слагаемые
4х = 21 — обе части уравнения разделим на 4
х = 5,25
Квадратное уравнение
Общий вид квадратного уравнения: + bx + c = 0, гдеa, b, c – числа, x – переменная. Если a = 0, то уравнение становится линейным. Поэтому, говоря о квадратных уравнениях, предполагается, что a ≠ 0.
Если коэффициент а = 1, то квадратное уравнение называют приведенным.
Квадратные уравнения
Полные(a ≠ 0, b ≠ 0, c ≠ 0) Неполные
+ bx + c = 0
+ bx = 0 (с = 0) + с = 0 (b = 0) = 0 (b = 0, с = 0)
Решение квадратных уравнений
1. В общем случае корни находятся через дискриминант D = b2 – 4ac.
® Если D> 0, то уравнение имеет 2 корня:
® Если D = 0, то уравнение имеет 1 корень:
® Если D< 0, то уравнение не имеет корней.
2. Если коэффициент b четный, то можно найти = .
Тогда корни находятся по формуле: .
3. Если уравнение приведенное, то можно использовать т. Виета:
Сумма корней приведенного квадратного уравнения + bx + c = 0 равна коэффициенту перед х, взятому с противоположным знаком, а произведение равно свободному члену.
+ = – b
· = c
4. Неполные квадратные уравнения принято решать не через дискриминант.
| + bx = 0(с = 0) | + с = 0(b = 0) | = 0(b = 0, с = 0) |
| х2 – 2х = 0 х(х – 2) = 0 х = 0 или х – 2 = 0 х = 2 | х2 – 4 = 0 х2 = 4 х = ± 2 | 4х2 = 0 : 4 х2 = 0 х = 0 |
Дробно-рациональные уравнения
1. Найти общий знаменатель дробей;
2. Умножить обе части уравнения на общий знаменатель;
3. Решить получившееся целое уравнение;
4. Найти область допустимых значений (ОДЗ), исключив числа, при которых знаменатель обращается в 0.
5. В ответ записываются все корни, кроме тех, которые не удовлетворяют ОДЗ.
Пример: ∙x(x-5) — умножим дроби на общий знаменатель
x(x-3) + x – 5 = x + 5 ОДЗ: х(х-5) ≠ 0
х2 – 3x – 10 = 0 x≠ 0 и х – 5 ≠ 0
x1 = -2; x2 = 5 х ≠ 5
Ответ: -2
Решение неравенств
Решить неравенство – значит найти границы, внутри которых должны находиться переменные, так чтобы неравенство было верным.
Линейные неравенства
Общий вид линейного неравенства: aх + b < 0 (знак неравенства может быть другим), где aи b – числа, х – неизвестная.
Линейные неравенства решаются с опорой на свойства, аналогично линейным уравнениям.Помним, если было произведено умножение или деление обеих частей неравенства на отрицательное число, то знак неравенства меняется на противоположный. В отличии от уравнений в ответ выписывается не конкретный набор чисел, а числовой промежуток.
Пример:
Ответ: х (- )
Квадратные неравенства
Общий вид квадратного неравенства: ах2 + bх + с < 0(знак неравенства может быть другим), где a, bи с– числа, х – неизвестная.
Для решения квадратных неравенств, есть 2 подхода (метод параболы и метод интервалов).
Решение квадратных неравенств методом параболы
Алгоритм:
ах2 + bх + с < 0 (ах2 + bх + с > 0)
1. Найти корни квадратного трехчлена ах2 + bх + с, для этого решаем квадратное уравнение ах2 + bх + с = 0.
2. Определить, куда направлены ветви параболы
3. Отметить найденные корни на оси х (если неравенство строгое, то точки выколоты).
4. Схематично изобразить график.
5. Определить, для каких х ординаты графика отрицательны (положительны).
Другими словами: для каких х график функции находится ниже (выше) оси х.
6. Выписать промежуток в ответ.
Пример: х2 + х – 6 ≥ 0
▫ х2 + х – 6 = 0
х1 = -3, х2 = 2
▫ у = х2 + х – 6
коэффициент а=1 > 0 => ветви вверх
находим часть параболы, которая выше оси х
Ответ: ( ]
Решение квадратных неравенств методом интервалов.
Алгоритм:
1) Преобразовать неравенство таким образом, чтобы в правой части остался 0.
2) Разложить выражение в левой части на множители.
3) Приравнять это выражение к 0 и решить получившееся уравнение.
Замечание: если уравнение дробно-рациональное, не забываем найти ОДЗ.
4) Полученные корни отметить на координатной прямой (если знак неравенства строгий – точки выколоты, если нестрогий – закрашены).
Замечание: если уравнение дробно-рациональное, то точки, не вошедшие в ОДЗ выкалываем на координатной прямой.
5) Отмеченные точки разбивают координатную прямую на промежутки.
Берем любое число из каждого промежутка, подставляем вместо х в разложенное на множители выражение (п.2) и определяем знак этого выражения.
Над каждым промежутком подписываем этот знак.
6) В ответ берутся те промежутки, которые соответствуют знаку неравенства («+» соответствует >0, «–» соответствует <0)
Пример 1: (х + 3)(х – 2) ≥ 0
(х + 3)(х – 2) = 0х = -3, х = 2
Ответ: ( )
|
х = 1
Знак неравенства , это значит, что в ответ пойдут промежутки со знаком «–» и точки, отмеченные на оси. Видим, что промежутков со знаком «–» нет и есть всего одна закрашенная точка на оси. Она и идет в ответ.
Ответ: 1
Системы уравнений
Пару чисел (х; у), которая одновременно является решением и первого, и второго уравнения системы, называют решением системы уравнений.
Решить систему – значит найти все ее решения или установить, что решений нет.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Решение квадратных неравенств. Поурочные планы
Дополнительные сочиненияНа этом уроке мы рассмотрим квадратные неравенства. Вначале вспомним свойства квадратичных функций и решение квадратных уравнений: дискриминант, теорему Виета, разложение на множители. Решим несколько примеров на рассмотренные темы.
Тема: Рациональные неравенства и их системы
Урок: Решение квадратных неравенств
1. Определение квадратного неравенства
Определение: Квадратное неравенство – это неравенство вида
В случае если a=0, мы получаем линейное неравенство.
Вспомним терминологию.
x — независимая переменная. Необходимо найти множество всех x, при которых неравенство выполняется.
a, b,c – конкретные числа, параметры;
квадратный трехчлен;
квадратичная функция.
Решение квадратного неравенства целиком основано на свойствах квадратичной функции.
Вспомним и изучим эти свойства на примерах.
2. Решение квадратного неравенства, когда трехчлен не имеет корней
Решить неравенства:
a.
Рассмотрим функцию Построим и прочтем ее график.
Графиком квадратичной функции является парабола, шаблон — парабола сдвинутая относительно начала координат.
Определим координаты вершины.
Схематически изобразим график функции. Ветви параболы направлены вверх, т. к. .
Теперь прочтем полученный график.
Функция определена при . Основное свойство данной функции заключается в том, что при всех Более того,
Ответ:
Мы рассмотрели случай, когда график функции не пересекает ось ox.
3. Решение квадратного неравенства, когда трехчлен имеет один корень
b.
Рассмотрим функцию
Найдем корни квадратного трехчлена
D=8-8=0, значит
Схематически построим график функции
Корень x=1;
графиком является парабола, значит ветви направлены вверх.
Прочитаем график.
На промежутке функция положительна. На промежутке функция также положительна. При
Ответ:
Мы рассмотрели случай, когда кривая касается оси ox в одной точке.
4. Решение квадратного неравенства, когда трехчлен имеет два корня
c.
Найдем корни квадратного трехчлена Воспользуемся теоремой Виета.
Схематически изобразим график функции
Это парабола, ветви направлены вверх, т. к.
Прочитаем график. На промежутке функция положительна.
На промежутке функция отрицательна.
В точках пересечения с осью ox функция равна нулю.
Ответ:
5. Свойство квадратичной функции с двумя корнями
Мы продемонстрировали методику решения квадратных неравенств для трех случаев:
1. Соответствующий квадратный трехчлен не имеет корней.
2. Квадратный трехчлен имеет один корень.
3. Квадратный трехчлен имеет два корня.
Сформулируем важнейшее свойство квадратичной функции для случая, когда соответствующий квадратный трехчлен имеет два корня.
Функция сохраняет свой знак вне интервала корней трехчлена. Функция сохраняет свой знак внутри интервала корней трехчлена. Функция меняет свой знак при переходе аргумента через корень.
Эти простейшие свойства, которые мы повторили, лежат в основе решения квадратных неравенств.
6. Решение задач
Продолжим решение неравенств.
1.
Рассмотрим функцию
Найдем корни трехчлена Один из корней легко определить методом подбора. Возьмем Проверяем: корень подходит.
Второй корень найдем по теореме Виета.
Построим эскиз графика функции. Графиком является парабола, ветви направлены вверх.
Отметим знаки на интервалах знакопостоянства и выберем интервалы, удовлетворяющие нашим условиям.
Ответ:
Мы продемонстрировали на примере применение методики решения квадратных неравенств. Один из корней мы нашли методом подбора, рассмотрим еще один подобный пример.
2.
Рассмотрим уравнение Можно ли угадать корень такого уравнения? Очевидно, что один из корней Второй корень найдем по теореме Виета.
Графиком функции является парабола, ветви направлены вверх. Построим эскиз графика.
Вне интервала корней функция положительна, внутри интервала – отрицательна. Нашему условию удовлетворяет промежуток внутри интервала корней.
Ответ:
Рассмотрим сопутствующую задачу: найти все целочисленные решения неравенства.
Точки пересечения графика с осью ox выколотые, не являются решениями. В рассматриваемом интервале только одно целочисленное решение,
Ответ:
Бывают неполные квадратные неравенства, вот одно из них:
3.
Рассмотрим функцию
Построим график, ветви параболы направлены вверх.
Нашему условию удовлетворяет интервал вне корней.
Ответ:
7. Заключение
Мы рассмотрели квадратные неравенства, методику их решения, и проиллюстрировали ее на конкретных примерах.
Список рекомендованной литературы
1. Мордкович А. Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А. Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш. А., Колягин Ю. М., Сидоров Ю. В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Портал Естественных Наук .
2. Центр образования «Технология обучения» .
3. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку .
4. Виртуальный репетитор .
5. Раздел College. ru по математике .
Рекомендованное домашнее задание
1. Мордкович А. Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.№№ 5; 6; 7.
dp-adilet.kz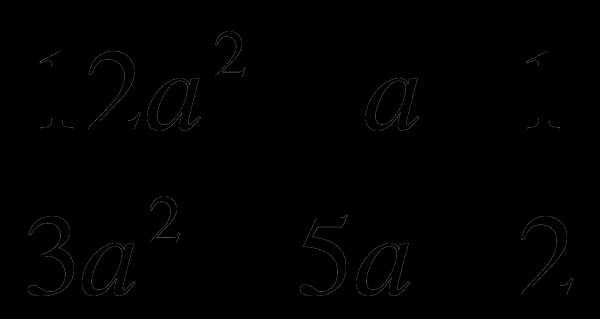