Примеры вертикальных углов – Свойства вертикальных углов, с примерами

Содержание

Смежные и вертикальные углы

Начальные сведения об углах

Пусть нам даны два произвольных луча. Наложим их начала друг на друга. Тогда

Определение 1

Углом будем называть два луча, которые имеют одно и тоже начало.

Определение 2

Точка, которая является началом лучей в рамках определения 3, называется вершиной этого угла.

Угол будем обозначать следующими тремя её точками: вершиной, точкой на одном из лучей и точкой на другом луче, причем вершина угла записывается в середине его обозначения (рис. 1).

Определим теперь, что такое величина угла.

Для этого необходимо выбрать какой-то «эталонный» угол, который мы будем принимать за единицу. Чаще всего таким углом является угол, который равен $\frac{1}{180}$ части развернутого угла. Такую величину называют градусом. После выбора такого угла мы проводим с ним сравнение углов, величину которого нужно найти.

Существуют 4 вида углов:

Определение 3

Угол называется острым, если он меньше $90^0$.

Определение 4

Угол называется тупым, если он больше $90^0$.

Определение 5

Угол называется развернутым, если он равен $180^0$.

Определение 6

Угол называется прямым, если он равен $90^0$.

Помимо таких видов углов, которые описаны выше, можно выделять виды углов по отношению их друг к другу, а именно вертикальные и смежные углы.

Смежные углы

Рассмотрим развернутый угол $COB$. Из его вершины проведем луч $OA$. Этот луч разделит первоначальный на два угла. Тогда

Определение 7

Два угла будем называть смежными, если одна пара их сторон является развернутым углом, а другая пара совпадает (рис. 2).

В данном случае углы $COA$ и $BOA$ являются смежными.

Теорема 1

Сумма смежных углов равняется $180^0$.

Доказательство.

Рассмотрим рисунок 2.

По определению 7, в нем угол $COB$ будет равняться $180^0$. Так как вторая пара сторон смежных углов совпадает, то луч $OA$ будет разделять развернутый угол на 2, следовательно

$∠COA+∠BOA=180^0$

Теорема доказана.

Рассмотрим решение задачи с помощью данного понятия.

Пример 1

Найти угол $C$ из рисунка ниже

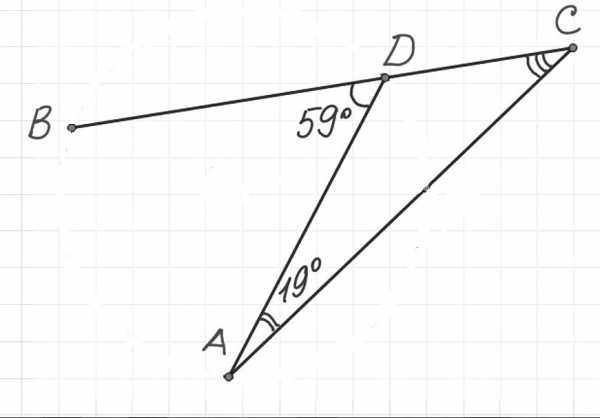
Решение.

По определению 7 получаем, что углы $BDA$ и $ADC$ являются смежными. Следовательно, по теореме 1, получим

$∠BDA+∠ADC=180^0$

$∠ADC=180^0-∠BDA=180〗0-59^0=121^0$

По теореме о сумме углов в треугольнике, будем иметь

$∠A+∠ADC+∠C=180^0$

$∠C=180^0-∠A-∠ADC=180^0-19^0-121^0=40^0$

Ответ: $40^0$.

Вертикальные углы

Рассмотрим развернутые углы $AOB$ и $MOC$. Совместим их вершины между собой (то есть наложим точку $O’$ на точку $O$) так, чтобы никакие стороны этих углов не совпали. Тогда

Определение 8

Два угла будем называть вертикальными, если пары их сторон являются развернутыми углами, а их величины совпадают (рис. 3).

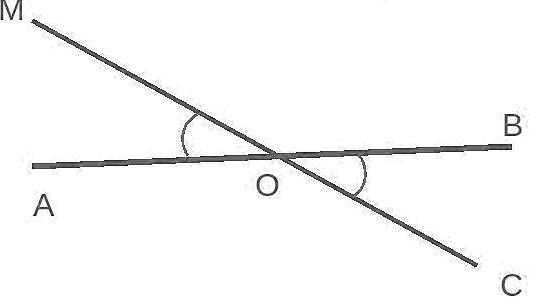
В данном случае углы $MOA$ и $BOC$ являются вертикальными и углы $MOB$ и $AOC$ также вертикальные.

Теорема 2

Вертикальные углы равняются между собой.

Доказательство.

Рассмотрим рисунок 3. Докажем, к примеру, что угол $MOA$ равняется углу $BOC$.

По определению 7, видим, что углы $AOM$ и $MOB$, а также углы $COB$ и $MOB$ будет являться смежными. Обозначим угол $MOB$ через $β$. По теореме 1, получим

$∠AOM+β=180^0$

$∠AOM=180^0-β$

С другой стороны

$∠COB+β=180^0$

$∠COB=180^0-β$

Получаем, что

$∠AOM=∠COB$

Теорема доказана.

Рассмотрим решение задачи с помощью данного понятия.

Пример 2

Найти угол $COB$ из рисунка ниже

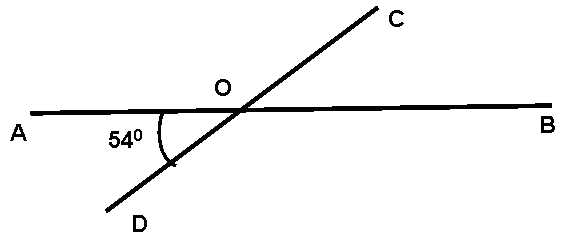
Решение.

По определению 8 получаем, что углы $AOD$ и $COB$ являются вертикальными. Следовательно, по теореме 2, получим

$∠COB=∠AOD=54^0$

Ответ: $54^0$.

Пример смешанной задачи

Пример 3

Найти угол $COB$ из рисунка ниже

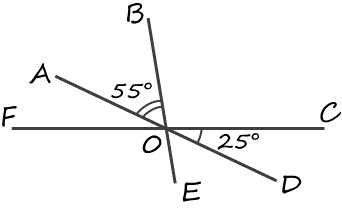
Решение. По определению 8 получаем, что углы $FAO$ и $COD$ являются вертикальными. Следовательно, по теореме 2, получим

$∠FAO=∠COD=25^0$

По определению 7 получаем, что углы $BOF$ и $BOC$ являются смежными. Следовательно, по теореме 1, получим

$∠BOF+∠BOC=180^0$

$∠BOC=180^0-∠BOF=180^0-55^0-25^0=100^0$

Ответ: $100^0$.

spravochnick.ru

Что такое вертикальные углы

Чтобы понять, что такое вертикальные углы, представьте себе две пересекающиеся прямые.
При пересечении этих двух прямых образуется 4 угла. Углы, которые располагаются друг против друга и будут вертикальными. Таких углов при двух пересекающихся прямы две пары.
Рассмотрим определение вертикальных углов.
Углы, которые имеют общую вершину и стороны, которые продолжают одна другую, называют вертикальными.
Существует теорема о вертикальных углах, которая звучит следующим образом:
Вертикальные углы между собой равны.

Пример 1.
Задан угол QOK, который образовался при пересечении прямых FK и MQ, равный . Найдем углы FOM и FOQ?

Решение.
Так как углы QOK и FOM вертикальные, следовательно, они равны, а значит:

Углы FOM и FOQ являются смежными, тогда согласно теореме про смежные углы получим, что их сумма равна 180 градусов:

Таким образом, имеем:

Ответ. , .

Пример 2.
Два вертикальных угла в сумме составляют . Найдем величину всех четырех углов, которые образовались при пересечении двух прямых.

Решение.
Обозначим заданные вертикальные углы и . Тогда
— по условию.
Так как вертикальные углы равны, то:

Пусть смежным к углу будет , а к углу — . Сумма смежных углов равна 180 градусов, поэтому:

Углы и вертикальные, значит

Ответ. , 57, , .

ru.solverbook.com

Доказательства и свойства вертикальных углов :: SYL.ru

Две пересекающиеся в одной точке линии встречаются не только в математике, но и в повседневной жизни. Мы можем наблюдать их, смотря на ножницы, на две скрещенные прямые веточки деревьев. Мы регулярно встречаем их в архитектурных объектах, машиностроении, в различных механизмах и других предметах. Примеров может быть масса. Образованные углы при пересечении составляют основу геометрии и изучаются детьми в средних классах.

Определение вертикальных углов в математике

Вертикальные углы — это два угла, образованных путем пересечения двух прямых линий в одной точке. Стороны одного угла в таком случае всегда являются продолжением другого. Таким образом, вертикальные углы находятся напротив друг друга в пересекающихся прямых с общей точкой пересечения.

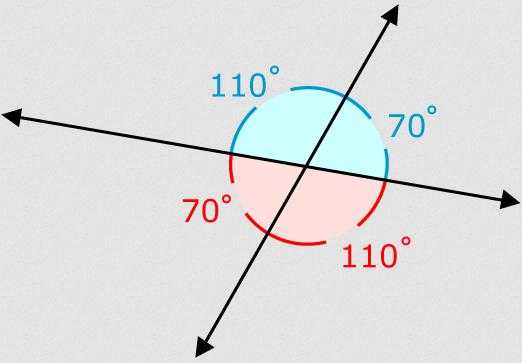
Свойства вертикальных углов

Решая различные задачи по геометрии, ребенку первоначально необходимо определить, с чем он имеет дело. То есть, перво-наперво он изучает форму фигуры, с которой начинает работу. Для этого он опирается на свойства всех ему известных фигур. Свойства вертикальных углов помогают легко составить в голове алгоритм для решения задачи:

Две прямые, пересекаясь между собой в одной точке, образуют две пары углов.
Образованные друг напротив друга вертикальные углы равны.
Сумма всех углов при пересечении двух прямых в одной точке равно 360°.
Смежные углы составляют половину вертикальных углов.

При построении прямых линий с одной точкой пересечения образуется два вертикальных угла и четыре смежных. Одно из доказательств равности вертикальных углов — это равность суммы градусов 1 + 2 угла и 3 + 4. Как в смежных, так и в вертикальных углах, если известен один из углов, то второй можно вычислить нехитрым способом. Зная, какими свойствами вертикальные углы наделены, можно быстро определить второй угол. Если из 180° вычесть известный угол, то мы узнаем величину второго.

www.syl.ru

Вертикальные углы — что это такое? :: SYL.ru

Геометрия — древняя и удивительная наука. Точки, плоскости, прямые, углы, объемные тела и плоские фигуры — вот все то, что изучает эта учебная дисциплина. Теоремы, гипотезы и доказательства строятся на простых, элементарных свойствах и законах. Углы — неотъемлемая составляющая геометрии. Они есть в фигурах и пространственных телах. А какие же углы называют вертикальными?

Вертикальные углы — что это такое? Определение

Плоские углы, которые получаются пересечением двух прямых линий, называются вертикальными — это определение вертикальных углов. Можно рассмотреть их на примере треугольника. Если взять любой угол этой фигуры, продолжить прямые, которыми он образован, то получатся вертикальные углы. Их можно получить также при наложении на две параллельные прямые секущей линии. В данном случае формируются четыре пары вертикальных углов.

Теоремы и свойства

Основное свойство и теорема о вертикальных углах состоит в том, что они равны.
Когда две прямые линии пересекаются, получается две пары вертикальных и четыре пары смежных углов, их сумма составляет 360 градусов.
Если задана градусная мера одного из вертикальных углов, то несложно найти величину и трех оставшихся. Один из углов будет равен данному. Два других, которые также равны между собой, можно найти, если вычесть из 360 градусов сумму известных, а затем получившееся значение разделить пополам.

Теорема о вертикальных углах, пожалуй, одна из основных в геометрии наряду с «пифагоровыми штанами» и с суммой углов треугольника. Такие углы встречаются повсюду. Даже буква Х является своеобразным вертикальным углом. Знание основополагающих геометрических теорем и свойств поможет с легкостью разобраться с более сложными и запутанными задачами. Нужно просто включать логику и воображение, и тогда самая замысловатая, мудреная задача и вопросы со звездочками будут казаться элементарными.

www.syl.ru

какие углы называются вертикальные? каким свойством обладают вертикальные углы?

Вертикальные углы — два угла, которые образуются при пересечении двух прямых, эти углы не имеют общих сторон. Другими словами — два угла называют вертикальными, если стороны одного угла являются продолжениями сторон другого. Два вертикальных угла равны.

Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого . Вертикальные углы равны. Дополнительные углы в сумме составляют 90°, а смежные углы в сумме дают 180°

Вертикальные углы — два угла, у которых стороны одного являются продолжениями сторон другого. Вертикальные углы равны.

Вертикальные углы — два угла, у которых стороны одного являются продолжениями сторон другого. Вертикальные углы равны

два угла, у которых стороны одного являются продолжениями сторон другого. Вертикальные углы равны.

Сами делайте!!!

два угла, у которых стороны одного являются продолжениями сторон другого. Вертикальные углы равны.

Если углы вертикальные то они не равны

два угла, отличные от развёрнутого, называют вертикальными, если стороны одного угла являются дополнительными лучами сторон другого.

два угла называються вертиальными если стороны одного угла яв продолж сторон другово

touch.otvet.mail.ru

Доказать свойство вертикальных углов

Если продолжить стороны угла дальше его вершины, то полученные углы будут вертикальными.

Определение.
Углы называют вертикальными, если стороны одного угла — это продолжения сторон другого угла.

Свойство вертикальных углов состоит в том, что они равны между собой.

Убедимся в справедливости свойства.

Для этого недостаточно проверки отдельных числовых примеров, так как выводы, которые можно сделать на основе отдельных примеров, могут оказаться ошибочными.

Докажем это свойство.

Доказательство.

Рассмотрим две пары смежных углов , и , . Их сумма равна \textit{2d. }При этом углы и — вертикальные:

Из равности правых частей уравнений выплывает равенство их левых частей:

В этом равенстве в обеих его частях присутствует один и тот же . Таким образом, можно от обеих частей данного равенства можно отнять , при этом равенство останется правильным. Получим:

Полученный результат говорит о том, что вертикальные углы равны между собой.

Свойство доказано.

Утверждение (суждение), справедливость которого требует доказательства, называют теоремой.

Таким образом мы доказали теорему о свойстве вертикальных углов.

ru.solverbook.com

Вертикальные углы — это… Что такое Вертикальные углы?

Вертикальные углы

пары углов с общей вершиной, образуемые при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. На рис. — две пары В. у.

Рис. к ст. Вертикальные углы.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

Вертикальные профсоюзы
Вертикальный дренаж

Смотреть что такое «Вертикальные углы» в других словарях:

ВЕРТИКАЛЬНЫЕ УГЛЫ — см. Угол … Большой Энциклопедический словарь
вертикальные углы — см. Угол. * * * ВЕРТИКАЛЬНЫЕ УГЛЫ ВЕРТИКАЛЬНЫЕ УГЛЫ, см. Угол (см. УГОЛ) … Энциклопедический словарь
Вертикальные углы — Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая из C и D. В геометрии, два угла называются вертикальными, если они созданы пересечением двух … Википедия
ВЕРТИКАЛЬНЫЕ УГЛЫ — см. Угол … Естествознание. Энциклопедический словарь
углы геометрической видимости — Углы, определяющие зону минимального телесного угла, в которой должна быть видна видимая поверхность огня. Эта зона определяется сегментами сферы, центр которой совпадает с исходным центром огня, а экватор параллелен грунту. Эти сегменты… … Справочник технического переводчика
углы геометрической видимости — 2.12 углы геометрической видимости: Углы, определяющие зону минимального телесного угла, в которой должна быть видна видимая поверхность огня. Эта зона определяется сегментами сферы, центр которой совпадает с исходным центром огня, а экватор… … Словарь-справочник терминов нормативно-технической документации
Инсоляционные углы светопроема — горизонтальные и вертикальные углы, в пределах которых на плоскости светопроема возможно поступление прямых солнечных лучей. При расчете инсоляционных углов глубина световых проемов принимается равной расстоянию от наружной плоскости стены до… … Официальная терминология
ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Угол — У этого термина существуют и другие значения, см. Угол (значения). Угол ∠ Размерность ° Единицы измерения СИ Радиан … Википедия
ГОСТ Р ИСО 12509-2010: Машины землеройные. Осветительные, сигнальные и габаритные огни и светоотражатели — Терминология ГОСТ Р ИСО 12509 2010: Машины землеройные. Осветительные, сигнальные и габаритные огни и светоотражатели оригинал документа: 3.1.5 габаритная ширина (overall width): Расстояние между двумя вертикальными плоскостями объемного… … Словарь-справочник терминов нормативно-технической документации

Книги

Геометрия. 7 класс. Комплексная тетрадь для контроля знаний, И. С. Маркова, С. П. Бабенко, В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия… Издатель: Наша школа, АРКТИ, Подробнее Купить за 164 руб
Геометрия. 8 класс. Комплексная тетрадь для контроля знаний, И. С. Маркова, С. П. Бабенко, В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 8 класса. Содержание пособия… Издатель: АРКТИ, Наша школа, Подробнее Купить за 157 руб
Комплексная тетрадь для контроля знаний. Геометрия. 7 класс. ФГОС, Бабенко Светлана Павловна, Маркова Ирина Сергеевна, В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия… Серия: Комплексная тетрадь для контроля знаний Издатель: Наша школа, Производитель: Наша школа, Подробнее Купить за 144 грн (только Украина)

Другие книги по запросу «Вертикальные углы» >>

dic.academic.ru