Открытое образование — Высшая математика. 1 семестр
- 11 недель
- от 10 до 14 часов в неделю
- 4 зачётных единицы
Курс высшей математики для общетехнических специальностей. Включает программу 1 семестра, соответствующую ГОС.
О курсе
Данный курс предназначен для студентов и слушателей, желающих изучить основы высшей математики. Курс соответствует государственным образовательным стандартам.
В первом семестре изучаются 4 раздела: элементы линейной алгебры, векторная алгебра, аналитическая геометрия и начала математического анализа.
Рекомендуется к использованию для студентов-заочников общетехнических направлений и в качестве дополнения к основному курсу высшей математики высших технических учебных заведений.
Формат
Курс включает видеолекции, в которых разобраны основные понятия: определения и теоремы, некоторые из которых доказываются, а также разбираются практические задачи и примеры. Более полное изложение курса содержится в приведенной литературе. Кроме того, по каждой теме предлагается небольшой online тест на проверку полученных знаний. В конце курса – итоговый тест, по результатам которого выдается сертификат о прохождении курса высшей математики за 1 семестр.
Программа курса
Раздел 1. Линейная алгебра: определители, матрицы, системы линейных уравнений
- Определители и системы линейных уравнений
- Матрицы и действия с ними
- Общая теория линейных систем
Раздел 2. Векторная алгебра
- Линейные операции над векторами
- Операции умножения векторов
Раздел 3. Аналитическая геометрия на плоскости и в пространстве
- Прямая на плоскости
- Плоскость и прямая в пространстве
- Кривые и поверхности второго порядка
Раздел 4. Начала математического анализа: предел числовой последовательности, предел и непрерывность функции
- Множества и функции
- Предел числовой последовательности
- Предел и непрерывность функции
Результаты обучения
Студент должен освоить программу высшей математики за первый семестр. Научиться решать произвольные линейные системы, освоить векторную алгебру, аналитическую геометрию на плоскости и в пространстве. Также студент должен изучить основы математического анализа, научиться вычислять пределы и исследовать функцию на непрерывность.
Формируемые компетенции
- Рассматривает возможные варианты решения задачи, оценивая их достоинства и недостатки
- Анализирует задачу, выделяя ее базисные составляющие, осуществляет декомпозицию задачи
openedu.ru
Открытое образование — Высшая математика. Математический анализ
- 16 недель
- 3 зачётных единицы
О курсе
Этот курс логически является первой частью двойного авторского курса Алексея Савватеева «Высшая математика для всех». Здесь излагаются основные понятия математического анализа: предел и его различные применения (сумма ряда, предел последовательности, производная, интеграл), непрерывность, построение графиков функций, функциональные последовательности и ряды (в частности, степенные). Курс в первую очередь ориентирован на слушателей, начинающих изучение этих тем или знакомых с ними поверхностно и желающих разобраться глубже. В отличие от классических курсов высшей математики, лектор не стремится к строгому формальному изложению материала и систематическому покрытию всех тем. Изложение строится вокруг ряда математических сюжетов, которые обсуждаются сначала неформально и на примерах, и только потом − с использованием строгих формулировок. Главной сюжетной линией является построение экспоненты как функции сначала вещественной, а потом и комплексной переменной (а в последующей второй части курса, посвящённой линейной алгебре, будет строиться экспонента от оператора). В связи с этой задачей оказываются задействованными основные инструменты математического анализа и типичные приёмы математических рассуждений, вокруг чего и строится материал лекций и семинаров.
Формат
Курс включает 13 недель лекционных и семинарских занятий. На лекциях излагаются основные идеи, примеры, сюжеты, теория. На семинарах − более технические вопросы и задачи, иллюстрирующие использование методов. В конце каждой недели слушателям предлагаются контрольные задачи, а по окончании всех недель − проверочный экзамен. В основном задачи ориентированы на проверку понимания материалов лекций и семинаров, но есть и более сложные задания, требующие самостоятельной работы.
Логическим продолжением этого курса является вторая часть двойного курса «Высшая математика для всех» − «Линейная алгебра и элементы топологии». По замыслу автора эти две части − математический анализ и линейная алгебра − должны восприниматься слушателями как единое целое. Перед изучением второй части курса очень желательно быть знакомым с первой частью.
Требования
Курс не требует предварительных знаний и умений, выходящих за рамки школьной программы.Программа курса
- Мотивирующие примеры: как далеко видно с горы, приближенные вычисления, последовательность вложенных треугольников.
- Примеры сходящихся и расходящихся рядов. Полнота множества вещественных чисел. Признаки сходимости рядов: интегральный, Даламбера и Коши.
- Последовательности, интуитивное представление о сходимости. Сходимость без указания предела (фундаментальные последовательности). Предел последовательности, его связь с суммой ряда. Примеры пределов последовательностей. Рекуррентные последовательности.
- Общее понятие предела, основанное на системе окрестностей. Использование пределов в математическом анализе: производная, задание и вычисление вещественных чисел, интеграл, асимптотика.
- Многочлены и их графики. Корни многочлена и теорема Безу. Локальные экстремумы и производная. Старшие производные.
- Экспонента: введение. Возникновение экспоненты и числа e в различных задачах.
- Экспонента: алгебраический подход. Теорема о промежуточном значении и неизменность знака экспоненты. Построение экспоненты «по непрерывности».
- Степенные ряды. Экспонента как степенной ряд. Число e − основание степени в экспоненте. «Замечательный предел» для числа e и экспоненты. Продолжение экспоненты на комплексную плоскость. Раскрытие скобок в произведении рядов. Абсолютная сходимость ряда и перестановка слагаемых. Условно сходящиеся ряды.
- Функциональные последовательности и ряды. Равномерная сходимость функциональных последовательностей. Мажорируемая сходимость. Радиус сходимости степенного ряда.
- Комплексная экспонента. Комплексные тригонометрические функции.
openedu.ru
Высшая математика (краткий курс лекций)
113
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ГЛАВА 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И МАТЕМАТИЧЕСКОЙ ЛОГИКИ.
§1. Понятие множества. Некоторые сведения о математической логике.
§2. Числовые множества. Множество действительных чисел.
§3. Числовые промежутки.
§4. Модуль действительного числа.
ГЛАВА 2. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.
§1. Понятие функции и способы ее задания.
§2. Основные характеристики функций.
§3. Элементарные функции.
§4. Приложение функций в экономике.
ГЛАВА 3. ПРЕДЕЛЫ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ
§1. Числовая последовательность и ее предел.
Понятие предела является фундаментальным в математическом анализе. Начальные сведения о пределах встречаются еще в школьном курсе. Например, в алгебре с понятием предела связан вопрос о сумме членов бесконечной убывающей прогрессии, в геометрии – вопрос о вычислении длины окружности, площадей плоских фигур и поверхностей, объемов тел вращения.
В курсе математического анализа с помощью предела вводятся понятия производной, определенного интеграла.
Ознакомимся с понятием числовой последовательности и ее предела.
Определение.Если каждому натуральному числуnпоставлено в соответствие числохn, то говорят, что заданапоследовательность
x1, х2, …, хn = {xn} (1.1)
Общий элемент последовательности является функцией отn.
xn = f(n)
Таким образом, последовательность может рассматриваться как функция порядкового номера элемента.
Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.
Примеры.
10) {xn} = {3n} или {xn} = 3; 6; 9; 12; …
20)
{xn} =
{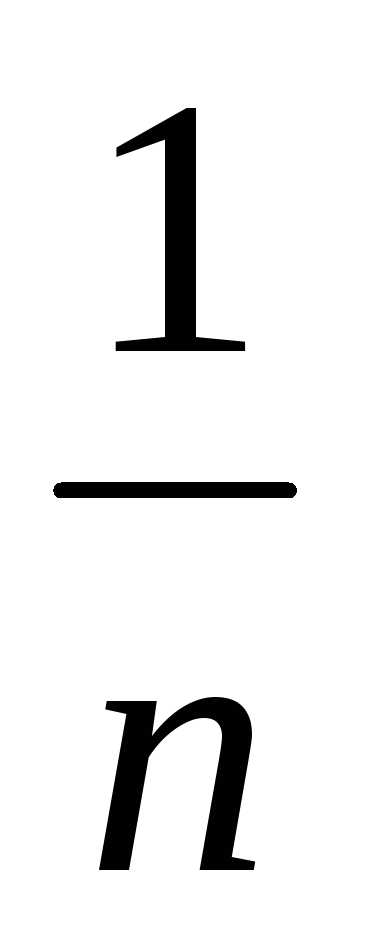 }
или {xn}
= 1;
}
или {xn}
= 1;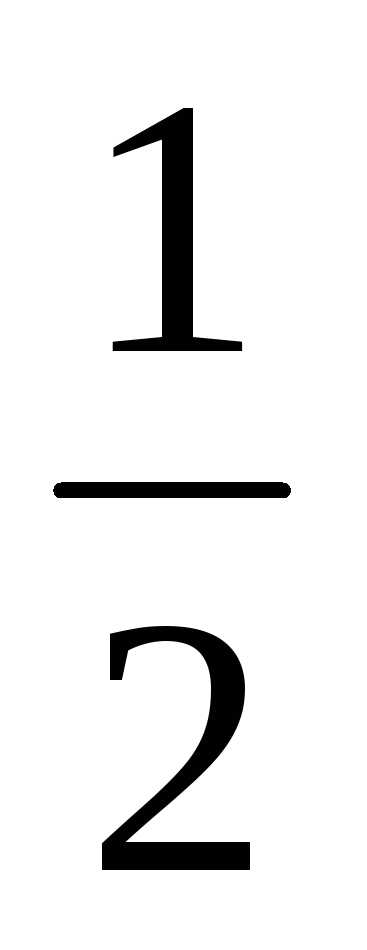 ;
;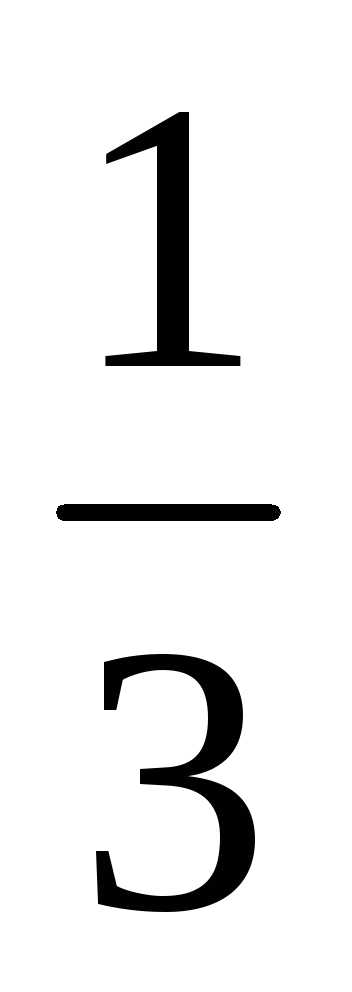 ;
;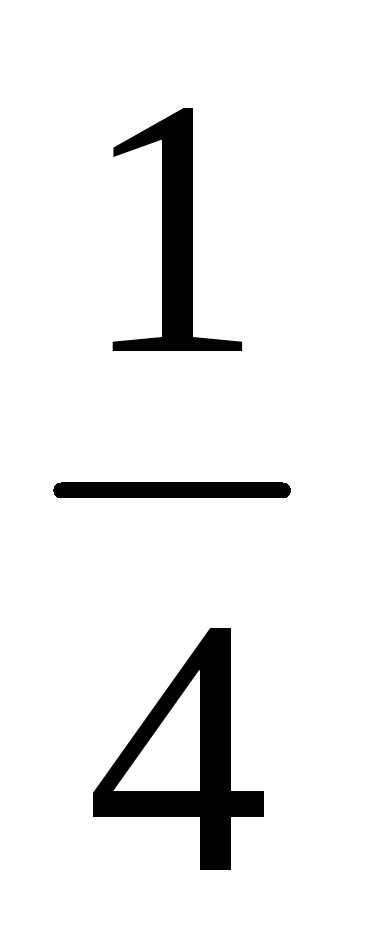
30) {xn} = {(-1)n} или {xn} = -1; 1; -1; 1; …
40) {xn} = {sinpn/2} или {xn} = 1; 0; -1; 0; …
50) {xn} = {6} или {xn} = 6; 6; 6; 6; …
Для последовательностей можно определить следующие операции:
Умножение последовательности на число m:m{xn} = {mxn}, т.е.mx1,mx2, …
Сложение (вычитание) последовательностей: {xn}±{yn} = {xn±yn}.
Произведение последовательностей: {xn}×{yn} = {xn×yn}.
Частное последовательностей:
 при{yn}
¹
0.
при{yn}
¹
0.
Замечание.Если переменнаяxn принимает значенияx1, х2, …, хn,…, то говорят, что эта переменная «пробегает» числовую последовательность{xn}. Такую переменную называют «упорядоченной». Часто упорядоченную переменную отождествляют с числовой последовательностью, которую она «пробегает» и обозначаютxn. Переменнаяxn не является непрерывной, она –дискретная.
Заметим, что n(номер) можно увеличивать неограниченно, пишутn→∞и последовательность (1.1) являетсябесконечнойчисловой последовательностью.
Вернемся к рассмотренному примеру 10): {xn} = {3n} или {xn} = 3; 6; 9; 12; … На данном примере можно заметить, что приn→∞переменная величинаxnтоже неограниченно возрастает. Такие величины называют бесконечно большими.
Определение.Переменная величинаxnназывается бесконечно большой, если для любого (сколь угодно большого) М>0 можно найти такой номерn=N,начиная с которого все последующие значения переменной будут удовлетворять неравенству:
|xn|³M
Рассматривая
пример 20), можно заметить, что
величинаxn=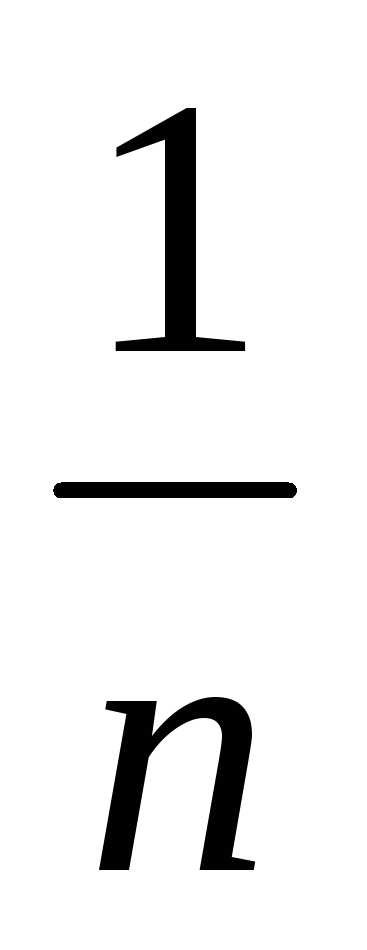 → 0 приn → ∞. Такие величины называютсябесконечно малыми.
→ 0 приn → ∞. Такие величины называютсябесконечно малыми.
Рассмотрим
еще один пример: {xn}
= {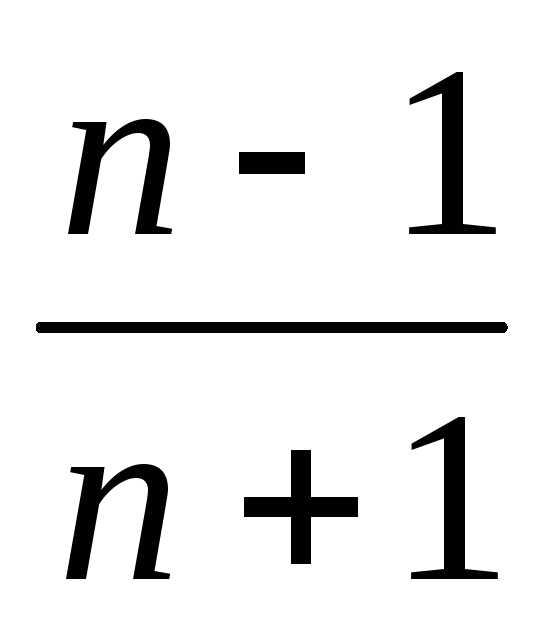 }
или {xn}
= 0;
}
или {xn}
= 0;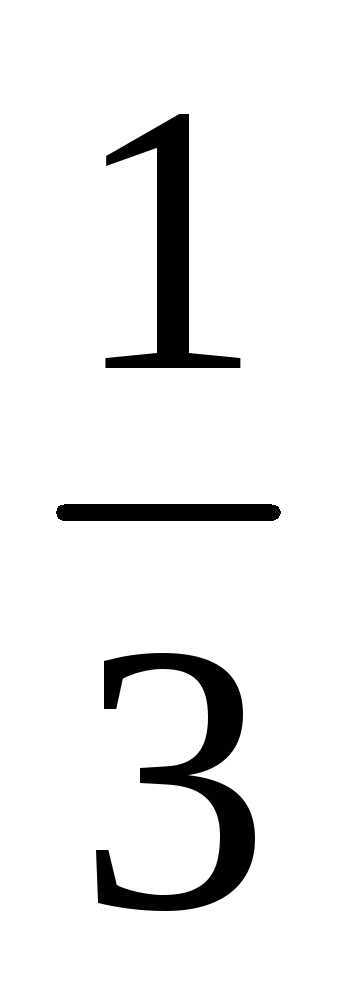 ;
;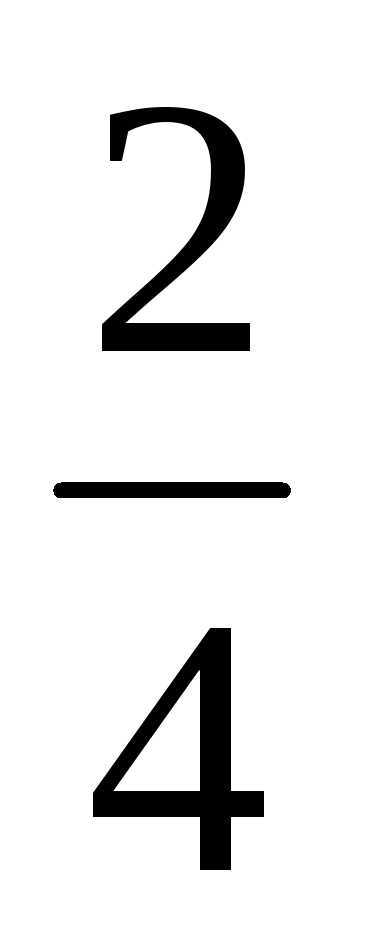 ;
;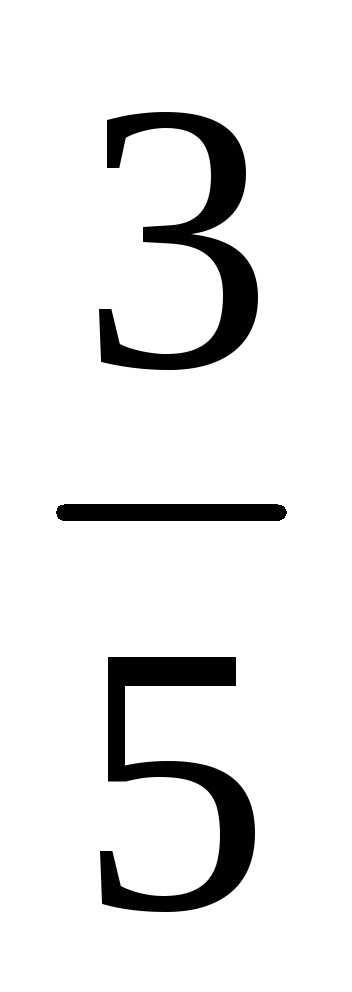 …
…
По мере возрастания номера nчлены числовой последовательности
приближаются к числу 1. Говорят, что 1 –
предел этой числовой последовательности.
Точно так же в примере 20) 0 – предел
этой последовательности. Кратко это
записывается так 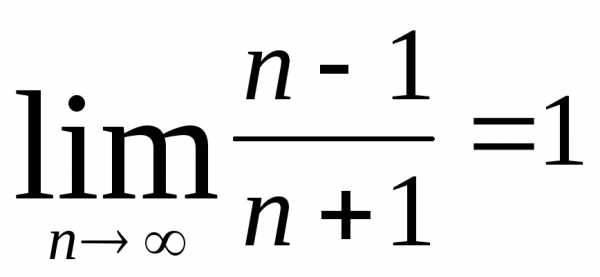 .
.
Определение. Окрестностью точкианазывается любой интервал (α, β), содержащий точкуа. В частности, симметричный интервал (а — ε;а+ ε), где ε > 0, называется ε-окрестностью точкиа.
Замечание.х  (а — ε;а+ ε)
(а — ε;а+ ε)
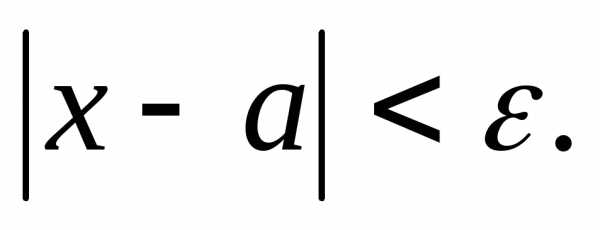
В общем случае, если последовательность
{xn}имеет
своим пределом числоа, то это
записывают так 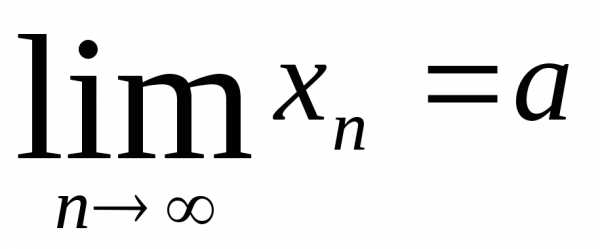 .
.
Геометрически это означает, что начиная с некоторого номера n=N,N+1,N+2, …все члены последовательности попадают в ε-окрестность точкиа. (ε – достаточно малое положительное число) или
Последовательности 30),40) не имеют предела (расходятся). Последовательность, которая имеет предел – сходится.
Определение.Числоаназываетсяпределомпоследовательности {xn}, если для любого положительногоe>0 существует такой номерN, что для всехn>Nвыполняется условие:
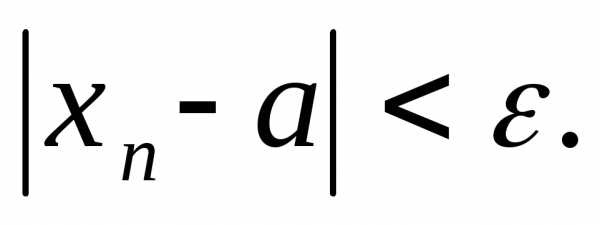
Это записывается: 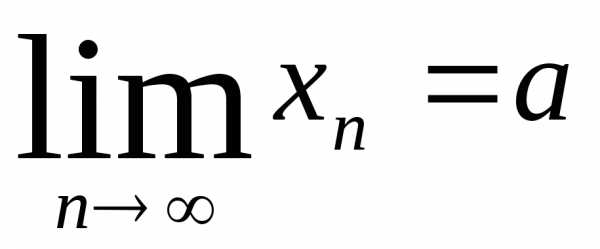
В этом случае говорят, что последовательность {xn} сходитсяка приn®¥.
Свойство:Если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.
Пример.Доказать, что предел последовательностиlim 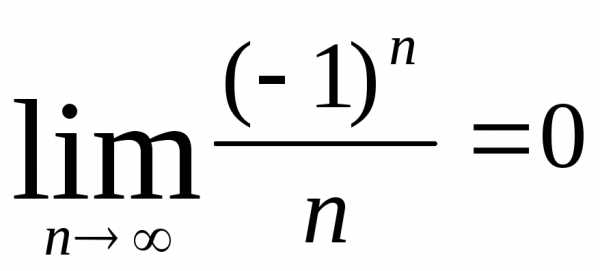 .
.
Пусть при n>Nверно 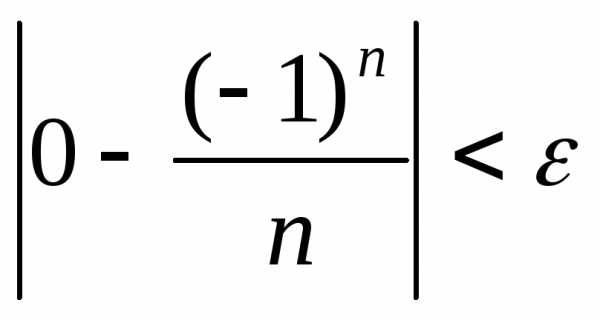 ,
т.е.
,
т.е.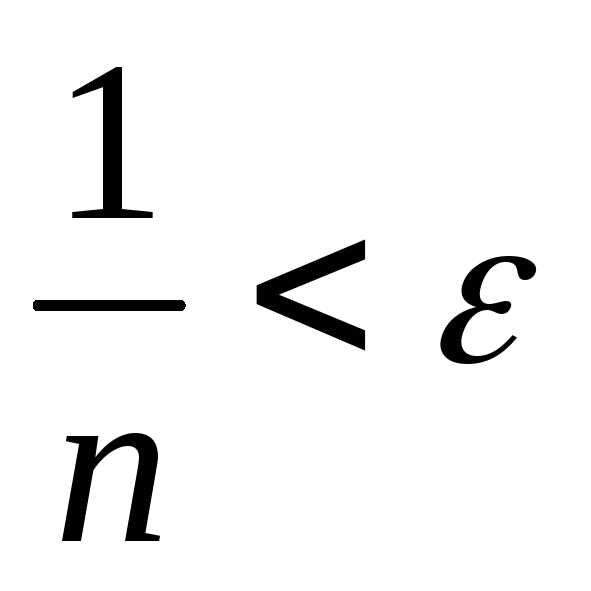 .
Это верно при
.
Это верно при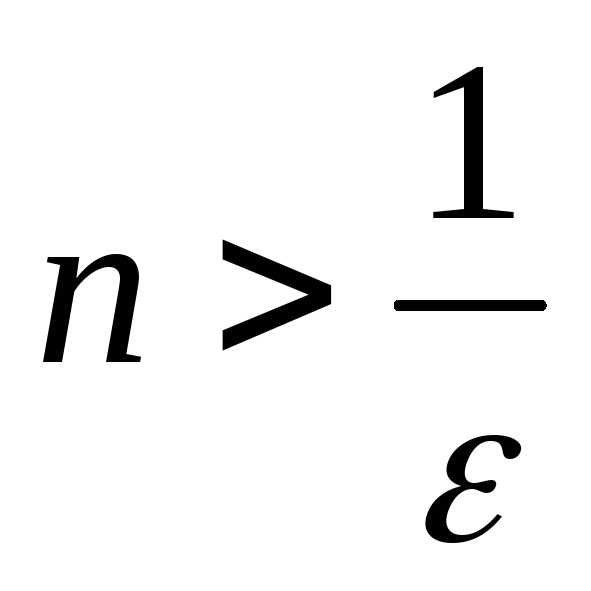 ,
таким образом, если заNвзять целую часть от
,
таким образом, если заNвзять целую часть от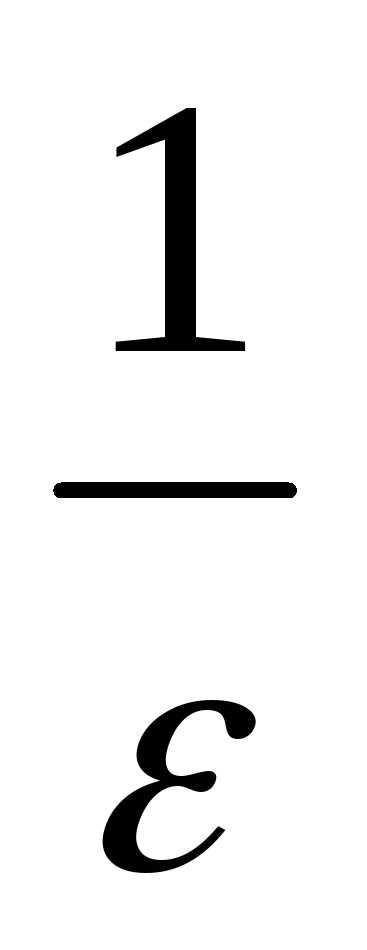 ,
то утверждение, приведенное выше,
выполняется.
,
то утверждение, приведенное выше,
выполняется.
Пример.Показать, что приn®¥последовательность 3, имеет пределом число 2.
Итого: {xn}= 2 + 1/n; 1/n=xn– 2
Очевидно, что
существует такое число n,
что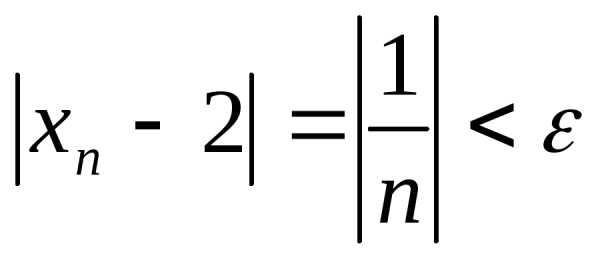 ,
т.е.lim {xn}= 2.
,
т.е.lim {xn}= 2.
Теорема.Последовательность не может иметь более одного предела.
Доказательство.Предположим, что последовательность {xn}имеет два пределаa иb, не равные друг другу, т.еxn ® a; xn ® b; a ¹ b.
Тогда по определению существует такое число e>0, что
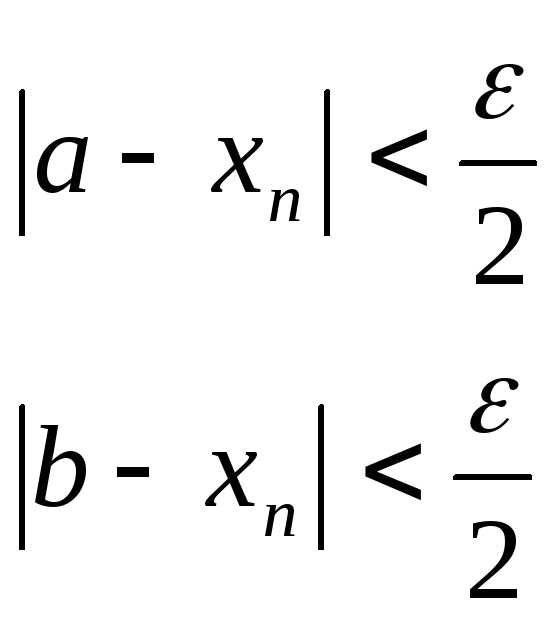
Запишем выражение:
А т.к. e-любое число, то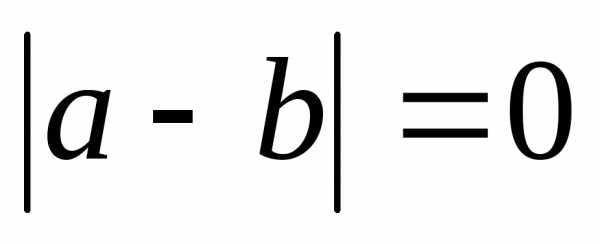 ,
т.е.a=b.
Теорема доказана.
,
т.е.a=b.
Теорема доказана.
Замечание.Говорят, чтонепрерывнаяпеременнаях→а, если эту переменную можно представить как бесконечное число числовых последовательностей, каждая из которых имеет пределом числоа.
Переменная хстремится каслева (справа), если все члены последовательностей, имеющих пределом числоа,
х→а-0
х→а+0
Переменная х→ +∞, если для любого сколь угодно большого М>0 найдетсях, начиная с которого все следующие значенияхбудут больше М :х> М их→ —∞, если для любого сколь угодно большого М>0 найдетсях, начиная с которого все следующие значенияхбудут меньше — М :х<- М. В этих случаях переменнаяхназывается бесконечно большой.
studfiles.net

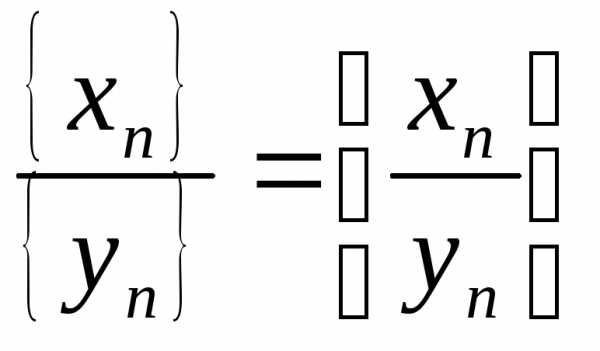 при{yn}
¹
0.
при{yn}
¹
0.