Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
2015-06-04 Действительная и мнимая ось
Аргумент комплексного числа
Главный аргумент комплексного числа
Тригонометрическая форма комплексного числа
Задание комплексного числа $z = a+bi$ равносильно заданию двух действительных чисел $a,b$ — действительной и мнимой частей данного комплексного числа. Но упорядоченная пара чисел $(a,b)$ изображается в декартовой прямоугольной системе координат точкой с координатами $(a, b)$. Таким образом, эта точка может служить изображением и для комплексного числа $z$: между комплексными числами и точками координатной плоскости устанавливается взаимно однозначное соответствие.
При использовании координатной плоскости для изображения комплексных чисел ось $Ox$ обычно называют действительной осью (так как действительная часть числа принимается за абсциссу точки), а ось $Oy$ — мнимой осью (так как мнимая часть числа принимается за ординату точки).
Комплексное число $z$, изображаемое точкой $M(a,b)$, называется аффиксом этой точки. При этом действительные числа изображаются точками, лежащими на действительной оси, а все чисто мнимые числа $bi$(при $a = 0$) — точками, лежащими на мнимой оси. Число нуль изображается точкой O.
Рис.1
На рис. 1 построены изображения чисел $z_{1} = 2 + 3i, z_{2}=1 =1,z_{3} = 4i, z_{4} = -4 + i, z_{5} = -2, z_{6} = — 3 – 2i, z_{7} = -5i, z_{8} = 2 – 3i$.
Два комплексно сопряженных числа изображаются точками, симметричными относительно оси $Ox$ (точки $z_{1}$ и $z_{8}$ на рис. 1).
Рис. 2
Часто с комплексным числом $z$ связывают не только точку $M$, изображающую это число, но и вектор $\vec{OM}$, ведущий из $O$ в $M$; изображение числа $z$ вектором удобно с точки зрения геометрического истолкования действия сложения и вычитания комплексных чисел. На рис. 2, а показано, что вектор, изображающий сумму комплексных чисел $z_{1}, z_{2}$, получается как диагональ параллелограмма, построенного на векторах $\vec{OM_{1}}, \vec{OM_{2}}$, изображающих слагаемые. Это правило сложения векторов известно как правило параллелограмма (например, для сложения сил или скоростей в курсе физики). Вычитание может быть сведено к сложению с противоположным вектором (рис. 2, б).
Рис. 3
Как известно, положение точки на плоскости можно задавать также ее полярными координатами $r, \phi$. Тем самым и комплексное число — аффикс точки также определится заданием $r$ и $\phi$. Из рис. 3 ясно, что $r = OM = \sqrt{x^{2} + y^{2}}$ является в то же время модулем комплексного числа $z$: полярный радиус точки, изображающей число $z$, равен модулю этого числа.
Полярный угол точки $M$ называют аргументом числа $z$, изображаемого этой точкой.
Аргумент комплексного числа (как и полярный угол точки) определен неоднозначно; если $\phi_{0}$ -одно из его значений, то все его значения выражаются формулой
$\phi = \phi_{0} + 2k \pi (k = 0, \pm 1, \pm 2, \cdots)$
Все значения аргумента в совокупности обозначаются символом $Arg \: z$.
Итак, всякому комплексному числу может быть поставлена в соответствие пара действительных чисел: модуль и аргумент данного числа, причем аргумент определяется неоднозначно. Напротив, заданным модулю $|z| = r$ и аргументу $\phi$ отвечает единственное число $z$, имеющее данные модуль и аргумент. Особыми свойствами обладает число нуль: его модуль равен нулю, аргументу не приписывается никакого определенного значения.
Для достижения однозначности в определении аргумента комплексного числа можно условиться одно из значений аргумента называть главным. Его обозначают символом $arg \: z$. Обычно в качестве главного значения аргумента выбирается значение, удовлетворяющее неравенствам
$0 \leq arg \: z (в других случаях неравенствам $- \pi
Обратим еще внимание на значения аргумента действительных и чисто мнимых чисел:
$arg \: a = \begin{cases} 0, & \text{если} a>0, \\
\pi, & \text{если} a $arg \: bi = \begin{cases} \frac{\pi}{2}, & \text{если} b > 0, \\
\frac{3 \pi}{2}, & \text{если} b
Действительная и мнимая части комплексного числа (как декартовы координаты точки) выражаются через его модуль и аргумент (полярные координаты точки) по формулам:
$a = r \cos \phi, b = r \sin \phi$, (1)
и комплексное число может быть записано в следующей тригонометрической форме:
$z = r( \cos \phi \phi + i \sin \phi)$ (2)
(запись числа в виде $z = a + bi$ будем называть записью в алгебраической форме).
Условие равенства двух чисел, заданных в тригонометрической форме, таково: два числа $z_{1}$ и $z_{2}$ равны тогда и только тогда, когда их модули равны, а аргументы равны или отличаются на целое число периодов $2 \pi$.
Переход от записи числа в алгебраической форме к его записи в тригонометрической форме и обратно совершается по формулам (4):
$r = \sqrt{a^{2} + b^{2}}, \cos \phi = \frac{a}{r}= \frac{a}{\sqrt{a^{2} + b^{2}}}, \sin \phi = \frac{b}{r} = \frac{b}{\sqrt{a^{2} + b^{2}}}, tg \phi = \frac{b}{a}$ (3)
и формулам (1). При определении аргумента (его главного значения) можно пользоваться значением одной из тригонометрических функций $\cos \phi$ или $\sin \phi$ и учитывать знак второй.
Пример. Записать в тригонометрической форме следующие числа:
а)$6 + 6i$; б) $3i$; в) $—10$.
Решение, а) Имеем
$r = \sqrt{6^{2} + (-6)^{2}} = 6 \sqrt{2}$,
$\cos \phi = \frac{6}{6 \sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$,
$\sin \phi = — \frac{6}{6 \sqrt{2}} = — \frac{1}{\sqrt{2}} = — \frac{\sqrt{2}}{2}$,
откуда $\phi = \frac{7 \pi}{4}$, и, следовательно,
$6-6i = 6 \sqrt{2} \left ( \cos \frac{7 \pi}{4} + i \sin \frac{7 \pi}{4} \right )$;
б) $r = 3, \cos \phi = 0, \sin \phi = 1, \phi = \pi /2$;
$3i = 3 \left ( \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \right )$
в) $r = 10, \cos \phi = —1, \sin \phi = 0, \phi = \pi$;
$-10 = 10 (\cos \pi + i \sin \pi)$
earthz.ru
1.1.4 Геометрическое изображение комплексных чисел. Комплексная плоскость.
Если для изображения действительных чисел используются точки числовой прямой, то изображениями комплексных чисел служат точки координатной плоскости.
Введем на плоскости прямоугольную
декартову систему координат с осями х иу. Тогда каждому комплексному
числубудет отвечать точка с координатами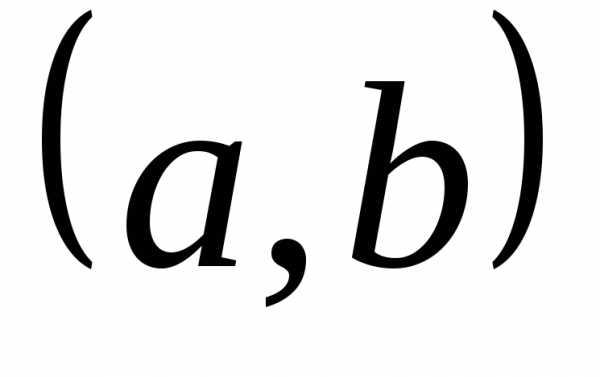 .
Эту точку чаще всего обозначают той же
буквой
.
Эту точку чаще всего обозначают той же
буквой ,
что и само число.
,
что и само число.
При таком способе изображения комплексных
чисел любому действительному числу,
т.е. числу вида 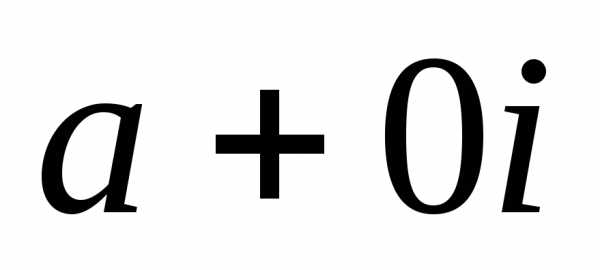 ,
отвечает точка
,
отвечает точка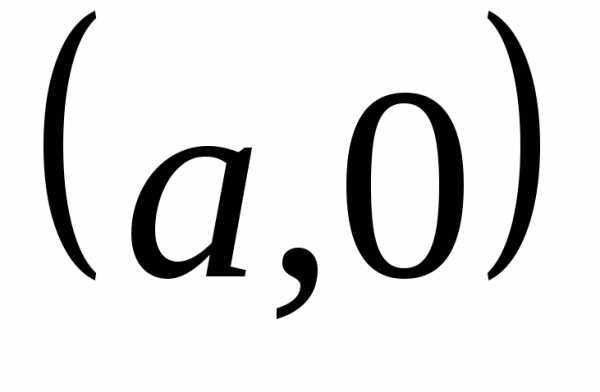 ,
лежащая на осих. Таким образом,
приходим к уже известному способу
изображения действительных чисел
точками числовой прямойх. В связи
с этим осьхназываютдействительной
осью. Комплексным же числам вида
,
лежащая на осих. Таким образом,
приходим к уже известному способу
изображения действительных чисел
точками числовой прямойх. В связи
с этим осьхназываютдействительной
осью. Комплексным же числам вида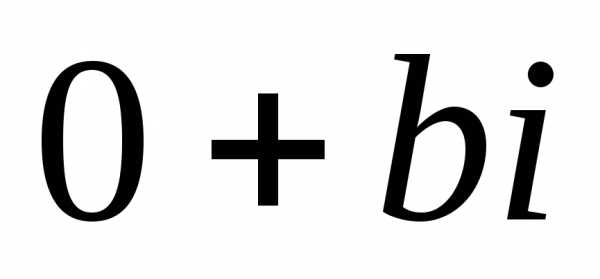 отвечают точки
отвечают точки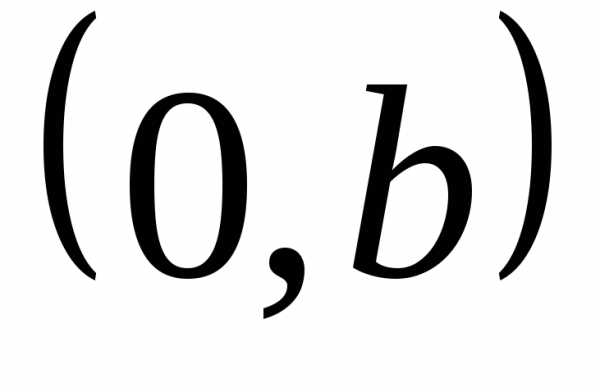 осиу; по этой причине осьуназываютмнимой осью. На рис. 1 указаны
изображения некоторых комплексных
чисел.
осиу; по этой причине осьуназываютмнимой осью. На рис. 1 указаны
изображения некоторых комплексных
чисел.
Наряду
с изображением комплексных чисел точками
плоскости применяется и другой способ
изображения – с помощью векторов
плоскости. Числу 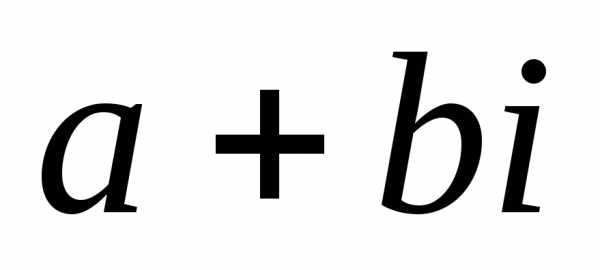 сопоставляется радиус-вектор точки
сопоставляется радиус-вектор точки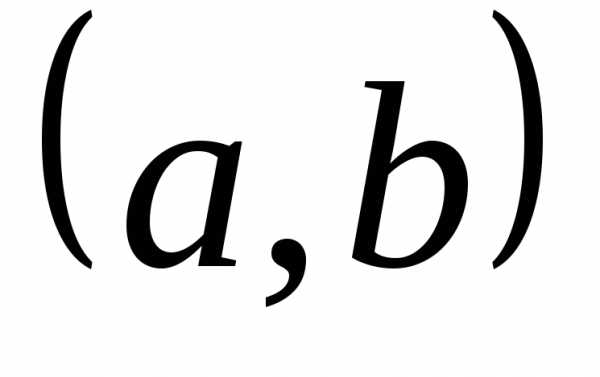 (Рис.2). «Точечный» и «векторный» способы
изображения комплексных чисел применяются
одинаково часто.
(Рис.2). «Точечный» и «векторный» способы
изображения комплексных чисел применяются
одинаково часто.
Изображение комплексных чисел с помощью
векторов имеет то преимущество, что оно
хорошо «увязано» с операцией сложения
комплексных чисел. Пусть числам
,соответствуют векторы,.
Тогда числусоответствует вектор с координатами,
т.е. вектор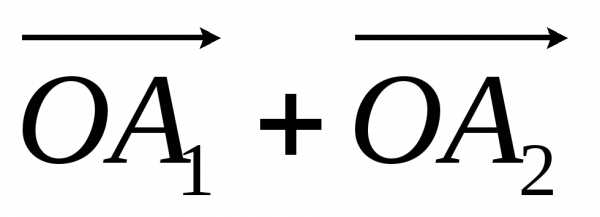
у
х
Рис. 3 Рис. 4
Поскольку
сложение комплексных чисел сводится к
сложению векторов, это же должно быть
верно и по отношению к вычитанию. Если
вектор 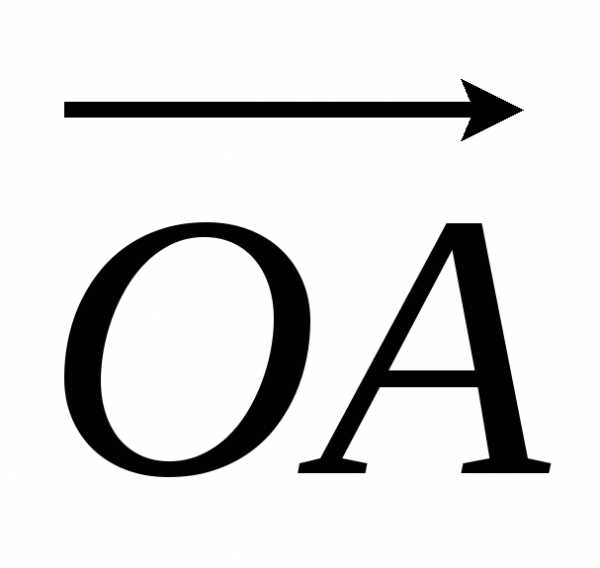 изображает комплексное число
изображает комплексное число ,
а вектор
,
а вектор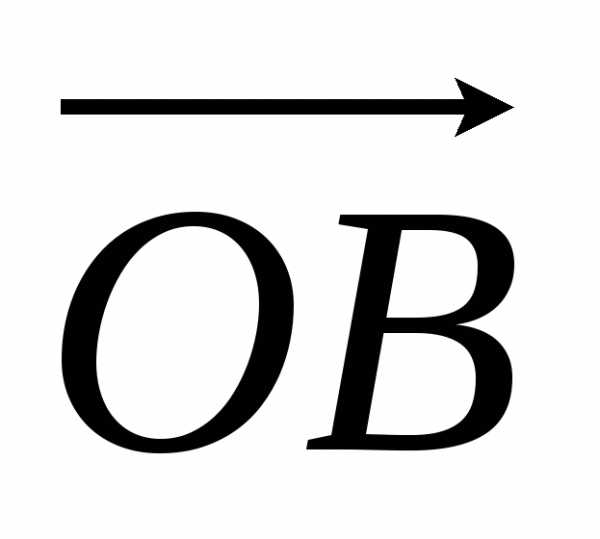
 ,
то векторявляется изображением числа
,
то векторявляется изображением числа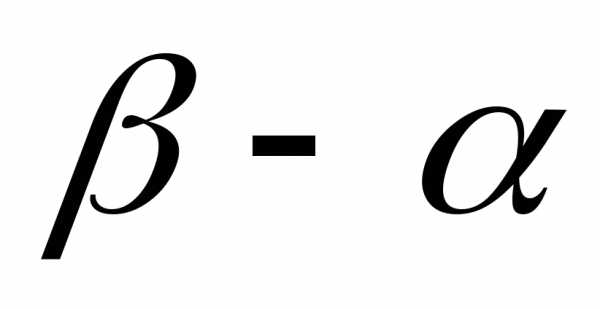 .
Разумеется, чтобы получить точку,
изображающую число
.
Разумеется, чтобы получить точку,
изображающую число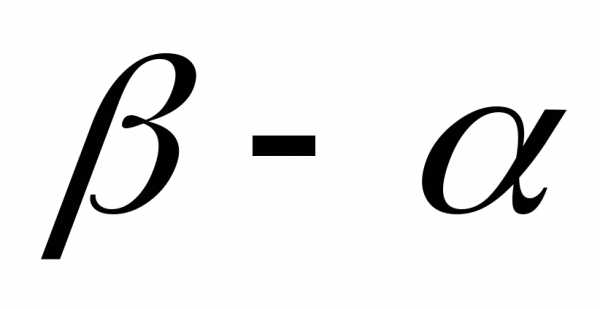 ,
этот вектор нужно отложить от начала
координат (точка С на рис. 4).
,
этот вектор нужно отложить от начала
координат (точка С на рис. 4).1.2 Тригонометрическая форма комплексного числа и
ее применение.
1.2.1. Модуль и аргумент комплексного числа.
Комплексное число
в прямоугольной декартовой системе
координатхОуизображается либо
точкойАс абсциссойаи ординатойb, либо радиус-вектором
этой точки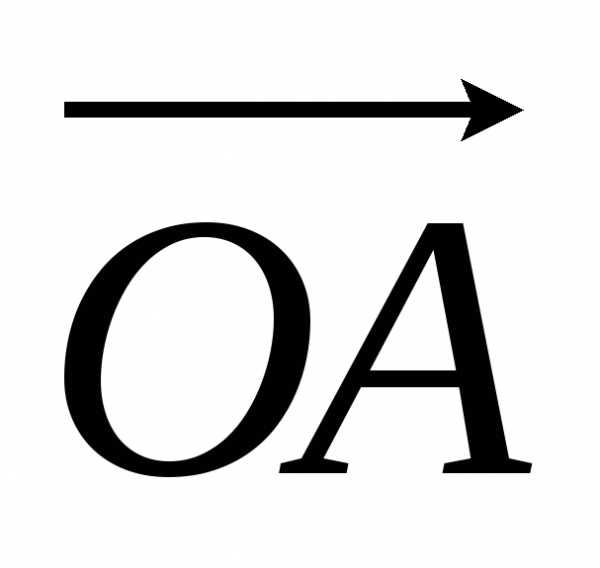 .
Длина вектора
.
Длина вектора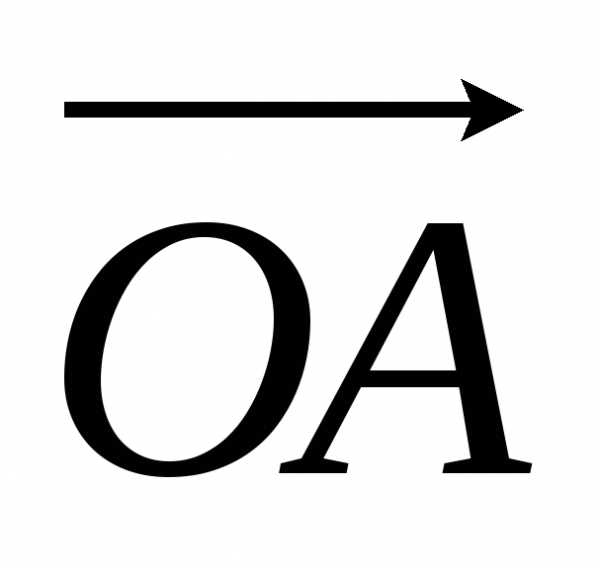 называетсямодулем
называетсямодулем
 :
:(1)
Угол , образованный
вектором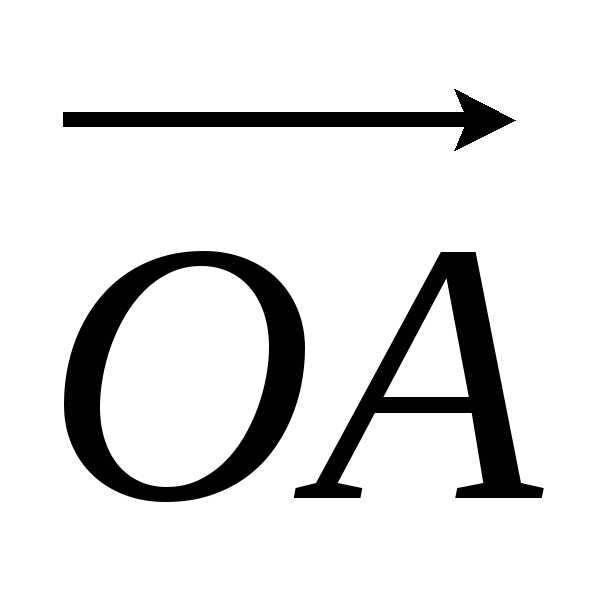 с положительным направлением осиОх,
называетсяаргументомчислаи обозначается.
Связь между аргументом комплексного
числа и его действительной и мнимой
частями выражается формулами
с положительным направлением осиОх,
называетсяаргументомчислаи обозначается.
Связь между аргументом комплексного
числа и его действительной и мнимой
частями выражается формулами
(2)
или 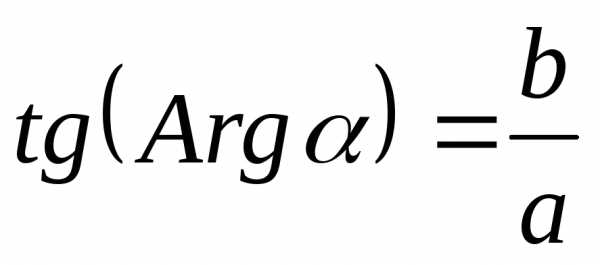 .
(3)
.
(3)
Формулы
(2) и (3) позволяют для заданного комплексного
числа
находить модуль и аргумент. Обратно,
если заданы модуль
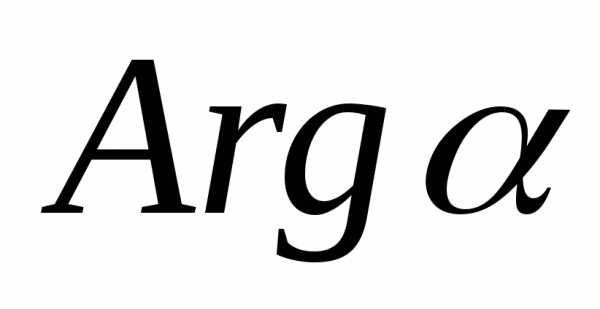 комплексного числа,
то числонаходится с помощью равенств:
комплексного числа,
то числонаходится с помощью равенств:. (4)
Аргумент комплексного числа определяется
неоднозначно: если - аргумент числа,
то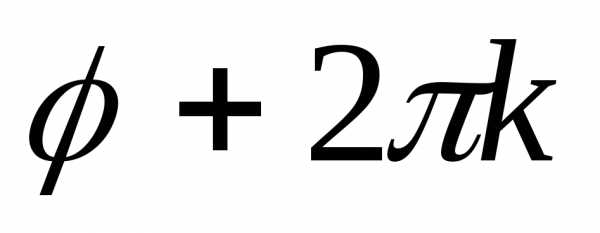 ,
где
,
где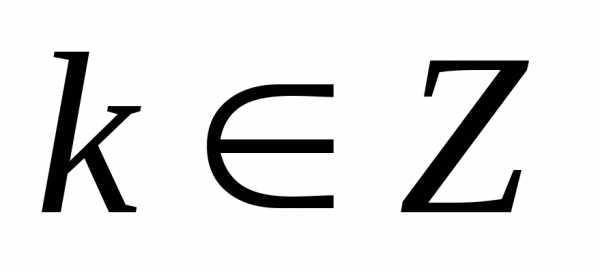 ,
— также аргумент этого числа. Для
однозначности определения аргумента
его выбирают в промежутке
,
— также аргумент этого числа. Для
однозначности определения аргумента
его выбирают в промежутке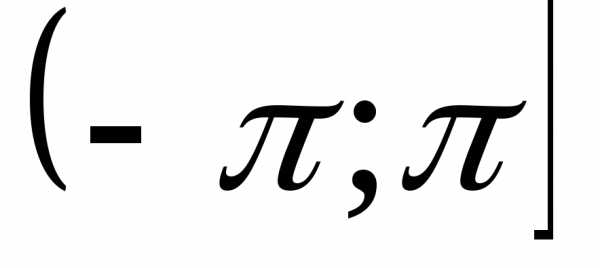 и называютглавным
значением аргумента.Главное значение аргумента обозначают
и называютглавным
значением аргумента.Главное значение аргумента обозначают 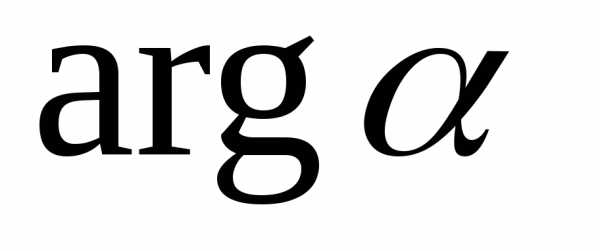 .
.
Так как , то аргументможно представить в виде
.
Используя формулу (1), находим модуль данного числа:
.
Далее, согласно формуле (2), получим
Так как
точка, изображающая данное число, лежит
во IIчетверти, то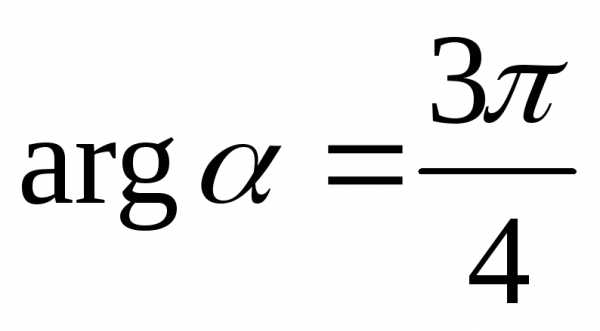 и, следовательно,.
и, следовательно,.
Для главного значения аргумента справедливы соотношения:
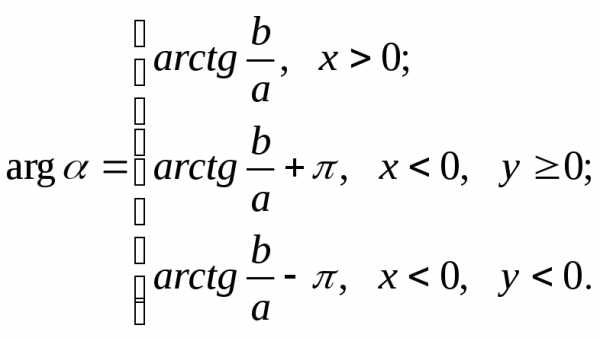
В самом
деле, так как главное значение 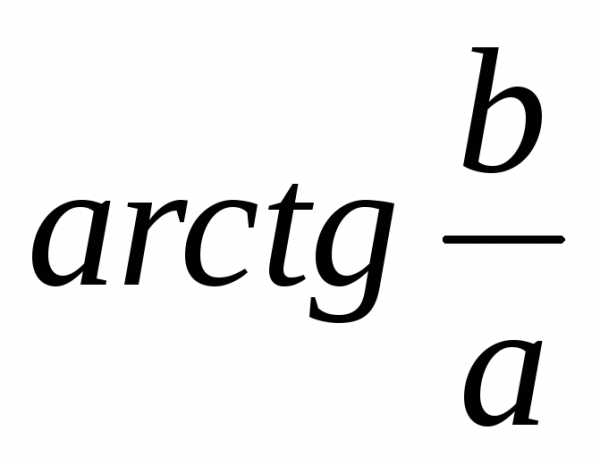 лежит между
лежит между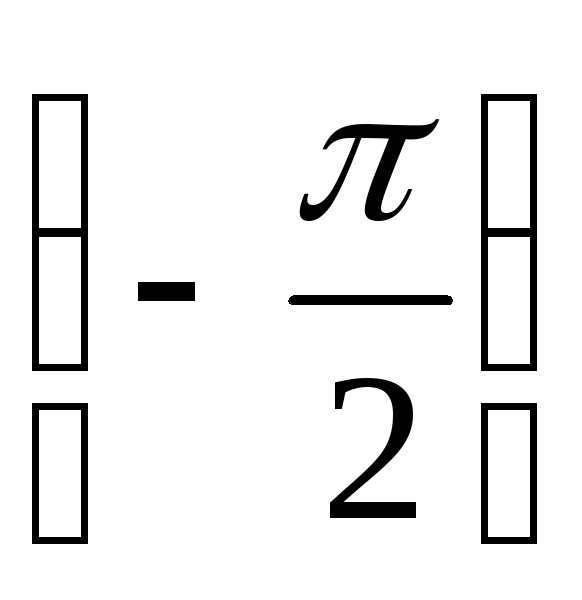 и
и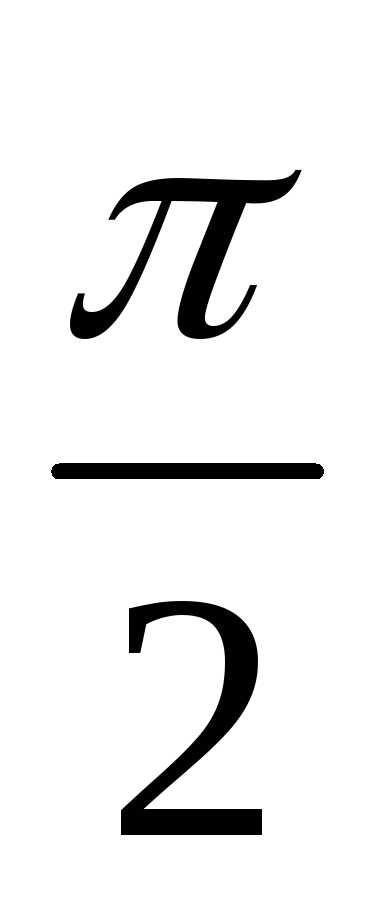 ,
то:
,
то:
если точкалежит вIилиIVчетверти
 ,
то и
,
то и ;
;
если точкалежит вIIчетверти, то и;
3) если точкалежит вIIIчетверти, то и;
Пример 2.Найти модуль и аргумент комплексного числа.
Решение.Вычислим модуль:.
Так как  ,
, ,
то числолежит вIIIчетверти, поэтому.
,
то числолежит вIIIчетверти, поэтому.
Следовательно,
,
где .
.
2. Геометрическое изображение комплексного числа. Понятие о модуле и аргументе
Всякому комплексному
числу
однозначно можно сопоставить точку плоскости
плоскости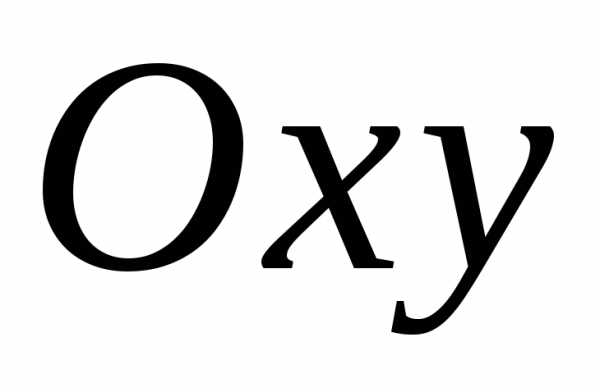 ,
абсцисса которой совпадает с вещественной
частью числа
,
абсцисса которой совпадает с вещественной
частью числа ,
а ордината – мнимой частью:
,
а ордината – мнимой частью: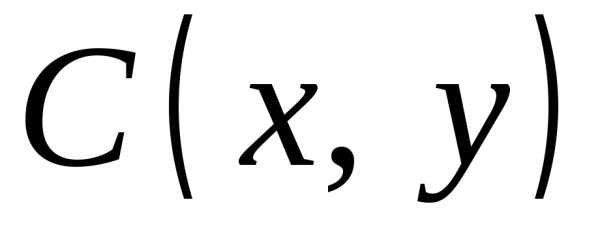 (рис. 1):
(рис. 1):
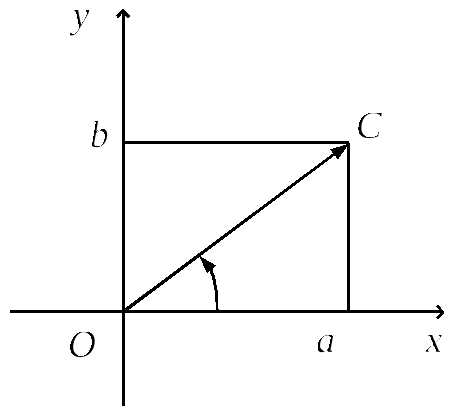
Рис. 1
В дальнейшем
точку, которой соответствует комплексное
число
,
будем обозначать соответствующей
заглавной буквой.
Плоскость
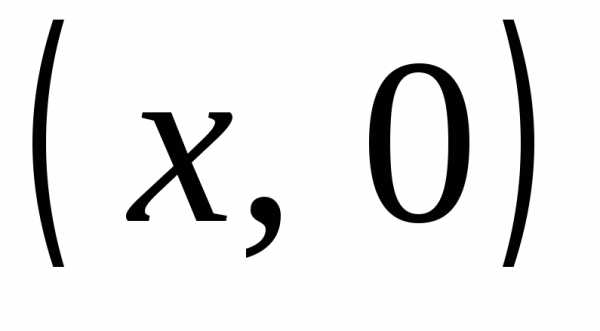 и им соответствуют действительные числа
и им соответствуют действительные числа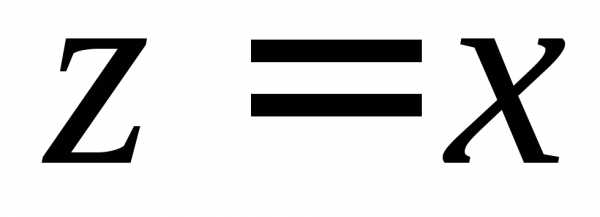 .
Точки, лежащие на оси ординат, имеют
координаты
.
Точки, лежащие на оси ординат, имеют
координаты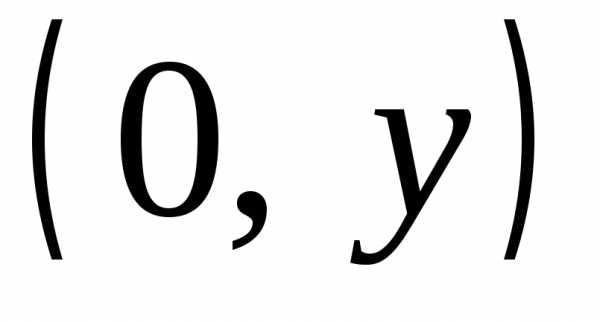 и им соответствуют чисто мнимые числа
и им соответствуют чисто мнимые числа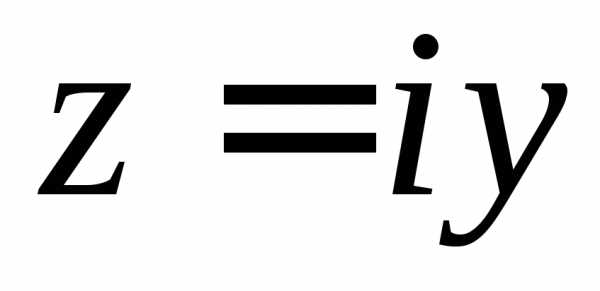 .
Остальным точкам плоскости соответствуют
комплексные числа, не являющиеся ни
вещественными и ни чисто мнимыми.
Поэтому, ось абсцисс называетсявещественной
осью, а ось
ординат – мнимой
осью.
.
Остальным точкам плоскости соответствуют
комплексные числа, не являющиеся ни
вещественными и ни чисто мнимыми.
Поэтому, ось абсцисс называетсявещественной
осью, а ось
ординат – мнимой
осью. Расстояние 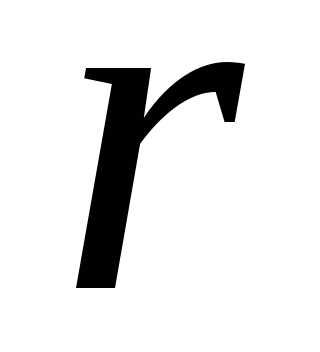
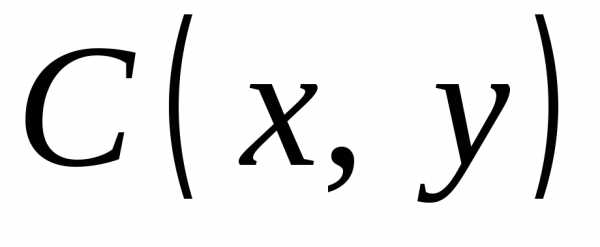 ,
соответствующей комплексному числу,
до нулевой точки – начала координат
называетсямодулем этого комплексного числа и обозначается
,
соответствующей комплексному числу,
до нулевой точки – начала координат
называетсямодулем этого комплексного числа и обозначается  или
или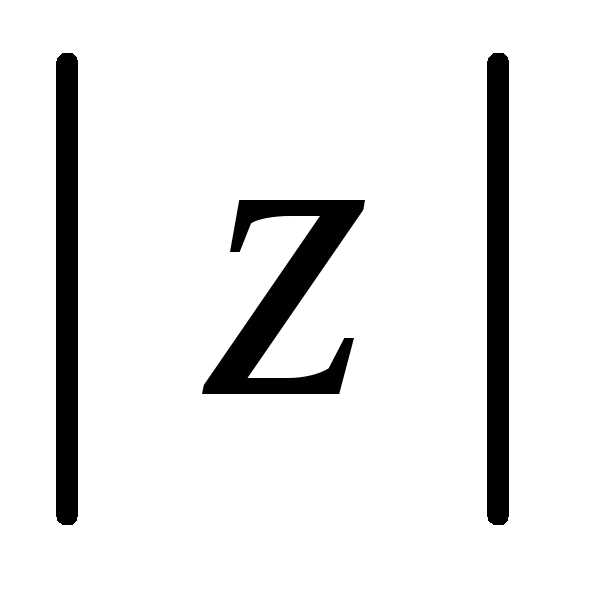 .
Так как треугольник
.
Так как треугольник – прямоугольный и
– прямоугольный и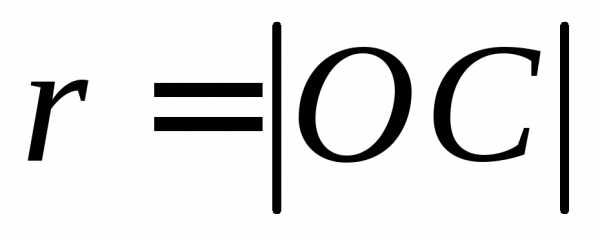 – гипотенуза этого треугольника, то по
теореме Пифагора, имеем
– гипотенуза этого треугольника, то по
теореме Пифагора, имеемили
. (2.1)
Числа, имеющие
один и тот же модуль  ,
изображаются точками окружности радиуса
,
изображаются точками окружности радиуса с центром в начале координат. Нулевое
число является единственной точкой
комплексной плоскости модуль которого
равен нулю.
с центром в начале координат. Нулевое
число является единственной точкой
комплексной плоскости модуль которого
равен нулю.
Отметим некоторые свойства модуля комплексного числа.
Свойство
1. Для любого
комплексного числа  справедливо неравенство
справедливо неравенство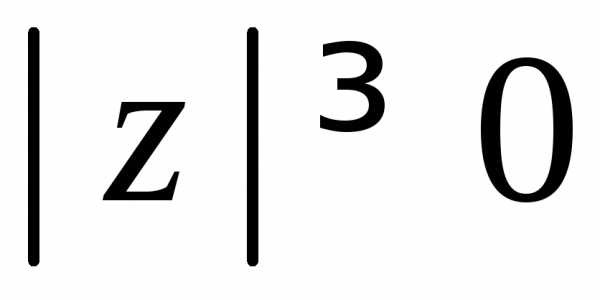 ,
причем равенство
,
причем равенство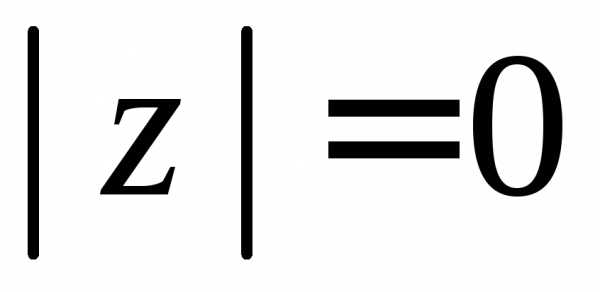 имеет место тогда и только тогда, когда
имеет место тогда и только тогда, когда .
.
Свойство
2. Для любого
комплексного числа
справедливо равенство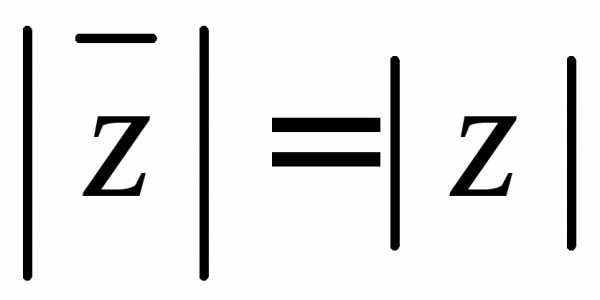 ,
то есть.
,
то есть.
Свойство
3. Для любого
комплексного числа  справедливы равенства.
справедливы равенства.
Угол  между вектором
между вектором и положительным направлением оси
и положительным направлением оси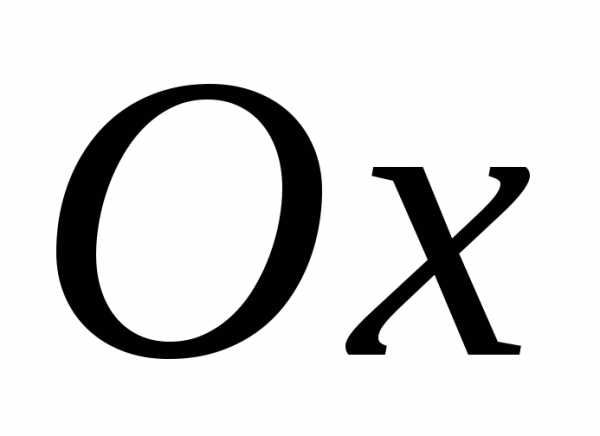 называется аргументом комплексного
числа
называется аргументом комплексного
числа и обозначается
и обозначается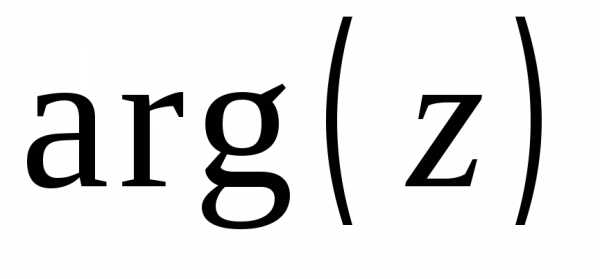 :.
Величина этого угла определяется двумя
способами.
:.
Величина этого угла определяется двумя
способами.
а) Пусть осуществляется
кратчайший поворот положительного
направления оси 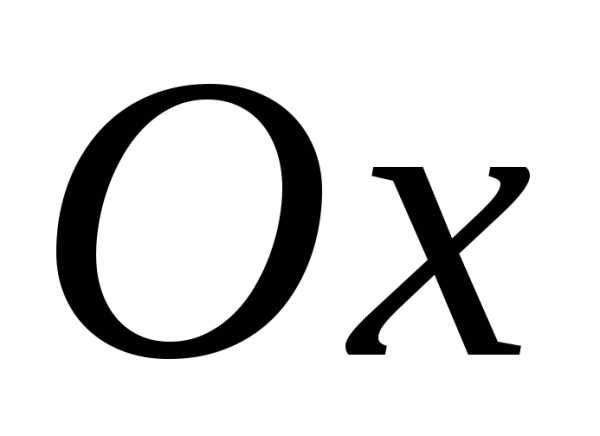 вокруг начала координат до совмещения
с направлением вектора
вокруг начала координат до совмещения
с направлением вектора .
Полученное значение угла называетсяглавным
значением аргумента. Если поворот был осуществлен против
хода часовой стрелки, то угол считается
положительным; если же поворот был
осуществлен по ходу часовой стрелки –
отрицательным. Главное значение аргумента
произвольного комплексного числа
.
Полученное значение угла называетсяглавным
значением аргумента. Если поворот был осуществлен против
хода часовой стрелки, то угол считается
положительным; если же поворот был
осуществлен по ходу часовой стрелки –
отрицательным. Главное значение аргумента
произвольного комплексного числа  удовлетворяет условию
удовлетворяет условию
.
Например,
, 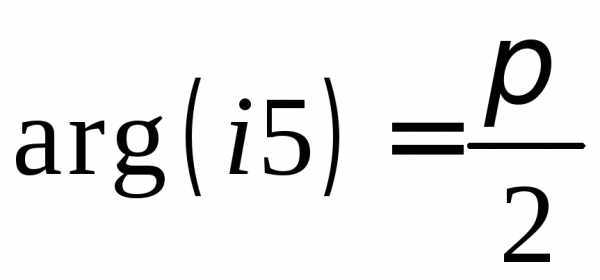 ,,
,,
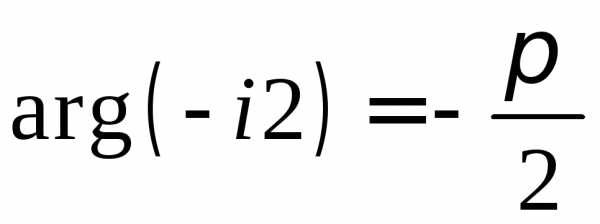 ,
, 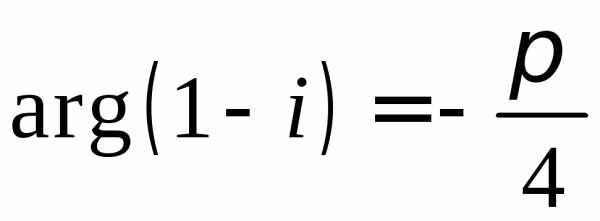 ,.
,.
б) Пусть поворот
положительного направления оси 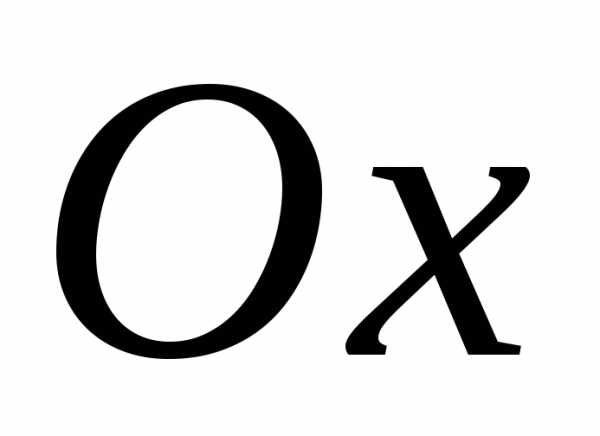 вокруг начала координат осуществляется
против хода часовой стрелки до совмещения
направлением вектора
вокруг начала координат осуществляется
против хода часовой стрелки до совмещения
направлением вектора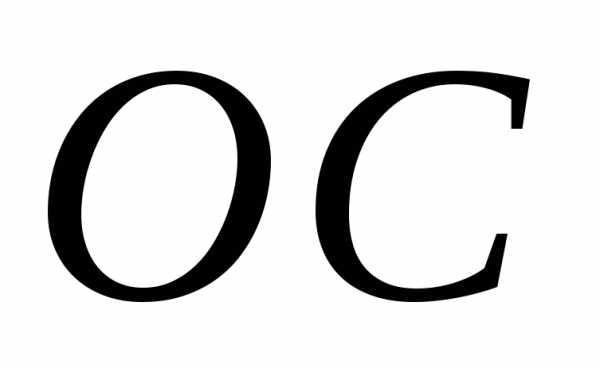 .
Полученное значение угла называетсястандартным
значением аргумента. Стандартное значение аргумента
произвольного комплексного числа
.
Полученное значение угла называетсястандартным
значением аргумента. Стандартное значение аргумента
произвольного комплексного числа  удовлетворяет условию
удовлетворяет условию
.
Например,
, 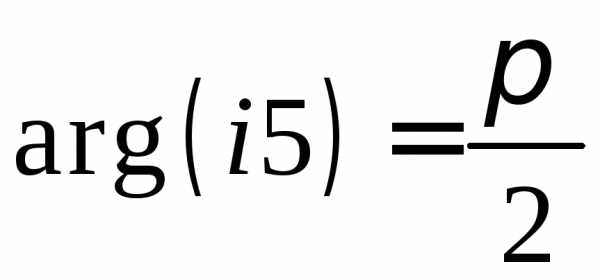 ,,
,,
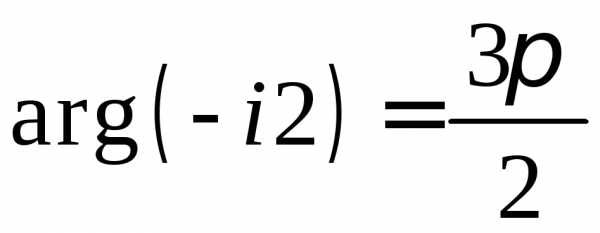 ,
, 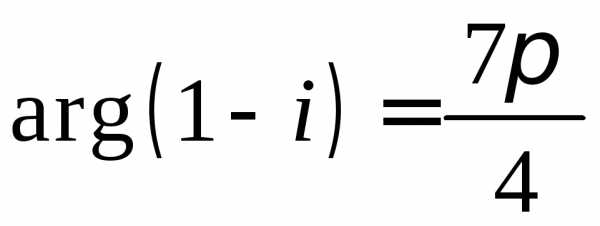 ,.
,.
Связь между главным
значением  и стандартным значением
и стандартным значением комплексного числа
комплексного числа устанавливается с помощью равенств:
устанавливается с помощью равенств: ,
если;,
если.
Эта связь показывает, что если известно
одно из значений (главное или стандартное)
аргумента, то легко можно получить и
другое значение. Поэтому, если не
оговорено особо, то в качестве значения
аргумента комплексного числа будет
рассматриваться его стандартное
значение.
,
если;,
если.
Эта связь показывает, что если известно
одно из значений (главное или стандартное)
аргумента, то легко можно получить и
другое значение. Поэтому, если не
оговорено особо, то в качестве значения
аргумента комплексного числа будет
рассматриваться его стандартное
значение.
Пусть дано
комплексное число
.
Если это число является чисто вещественным
или чисто мнимым, то аргумент определяется
просто. В противном случае комплексное
число принадлежит одной из четырех
четвертей. Запись будет обозначать, что комплексное число
принадлежит первой четверти. Аналогично,
записи
будет обозначать, что комплексное число
принадлежит первой четверти. Аналогично,
записи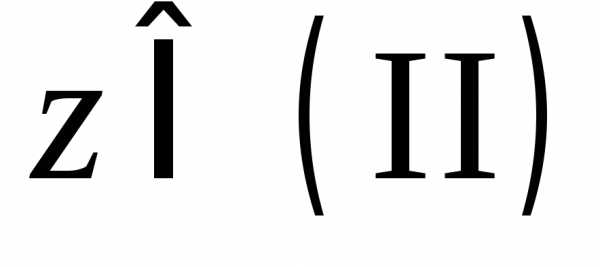 ,
,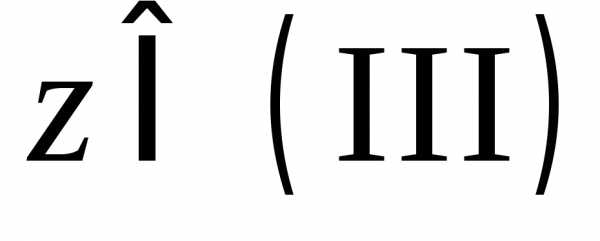 ,
,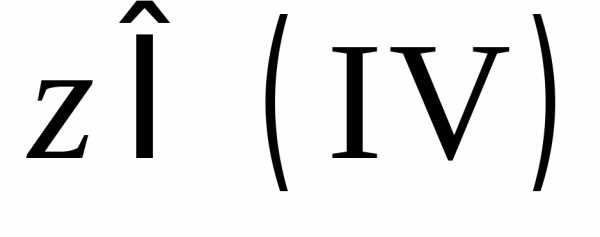 будут обозначать, что комплексное число
принадлежит второй, третьей или четвертой
четверти, соответственно.
будут обозначать, что комплексное число
принадлежит второй, третьей или четвертой
четверти, соответственно.
Для нахождения
аргумента вначале находим вспомогательный
угол  :
:
 .
(2.2)
.
(2.2)
Затем по формуле
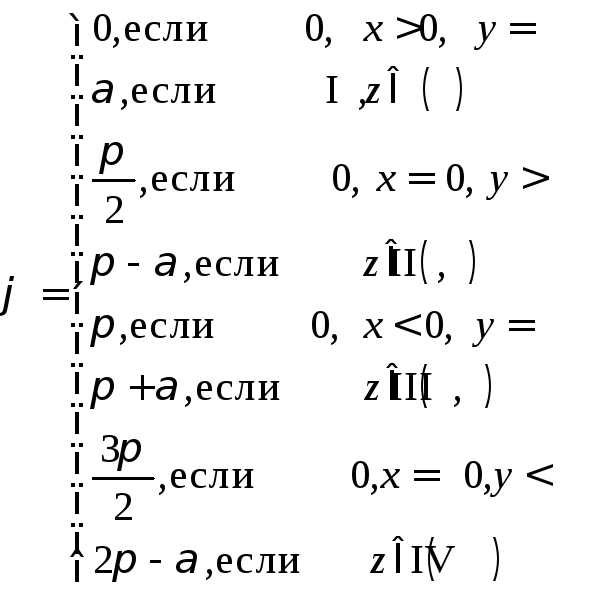 (2.3)
(2.3)
определим значение аргумента комплексного числа.
Пусть 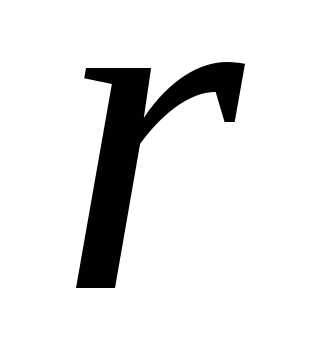 – модуль, а
– модуль, а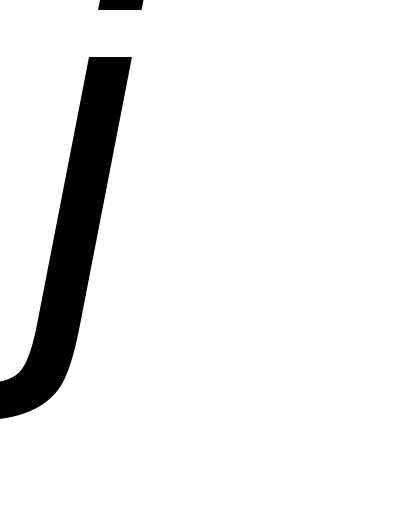 – аргумент комплексного числа.
Из треугольника
– аргумент комплексного числа.
Из треугольника (рис. 1) будем иметь
(рис. 1) будем иметь
. (2.4)
Следовательно, комплексное число
(2.5)
можно представить в виде
. (2.6)
Представление комплексного числа в виде (2.6), называется тригонометрической формой комплексного числа.
Имеется еще одна форма записи комплексного числа. Она основана на равенстве
. (2.7)
Равенство (2.7) называется формулой Эйлера. Представление (2.6) с учетом (2.7) можно переписать в виде
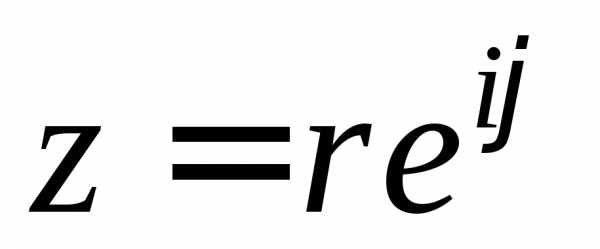 .
(2.8)
.
(2.8)
Представление комплексного числа в виде (2.8), называется показательной формой комплексного числа.
Запись комплексного числа в виде (2.5) называется алгебраической формой комплексного числа.
studfiles.net
4.2. Геометрическое изображение комплексных чисел. Тригонометрическая и показательная формы записи комплексного числа
Поскольку комплексное
число мы определили как упорядоченную
пару действительных чисел, то вполне
естественно изобразить комплексное
число 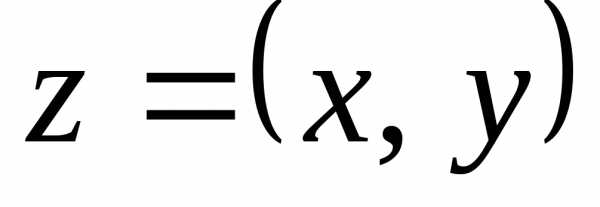 точкой плоскости с декартовыми
координатами
точкой плоскости с декартовыми
координатами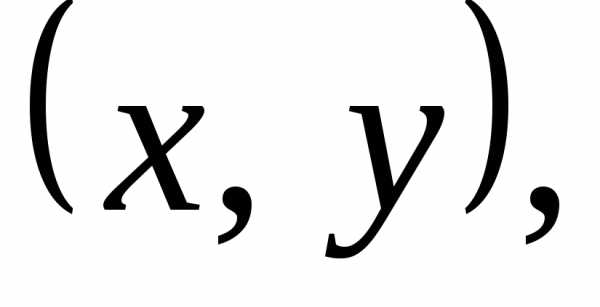 либо вектором, идущим из начала координат
в эту точку (рис. 1).
либо вектором, идущим из начала координат
в эту точку (рис. 1).
Рис. 1.
На оси Ох расположены
все действительные числа, а на оси Оу – чисто мнимые, т.е. комплексные числа
вида  .
.
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью (её также обозначают C). Ось абсцисс называется действительной осью, а ось ординат – мнимой.
Длина вектора  ,
изображающего комплексное число
,
изображающего комплексное число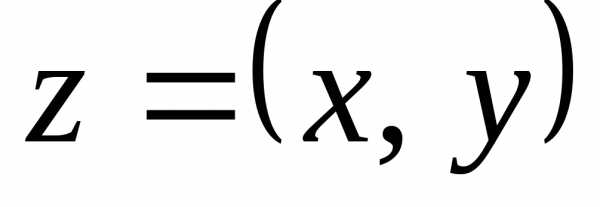 ,
естьмодуль
комплексного числа:
,
естьмодуль
комплексного числа:
,
а угол  ,
который образует этот вектор с осьюОх,
называется аргументом
комплексного числа
,
который образует этот вектор с осьюОх,
называется аргументом
комплексного числа 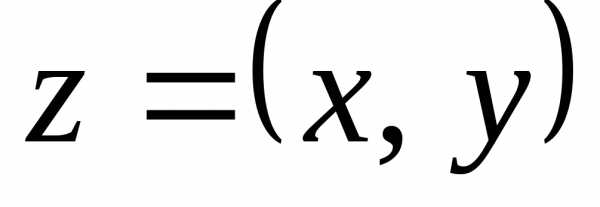 .
.
Очевидно, что угол  определён с точностью до.
определён с точностью до.
Условимся называть
главным значением аргумента – значение
угла  в интервале.
Символически главное значение аргумента
комплексного числа обозначают:
в интервале.
Символически главное значение аргумента
комплексного числа обозначают:
Тогда всю совокупность
значений аргумента  обозначают символом:
обозначают символом:
Очевидны формулы:
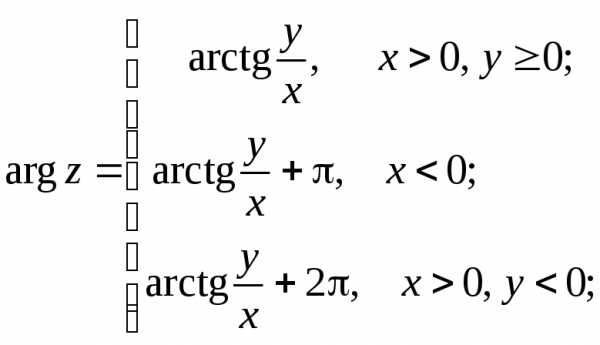
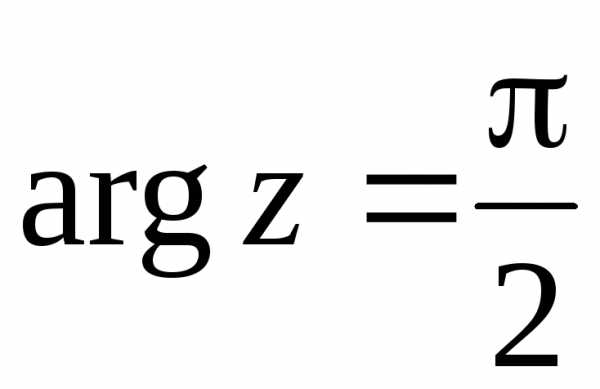 при
при
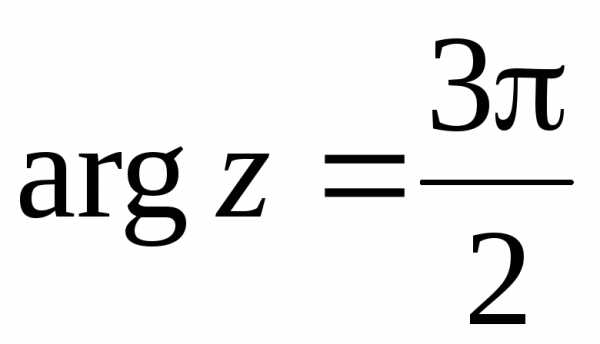 при
при
Из рис. 1 легко получить соотношения: , тогда
.
Определение. Представление комплексного числа 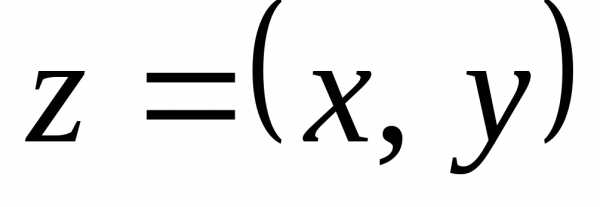 в виденазываетсятригонометрической
формой записи комплексного числа.
в виденазываетсятригонометрической
формой записи комплексного числа.
Для сокращения записи комплексных чисел в тригонометрической форме удобно использовать формулу Эйлера:
.
Тогда комплексное число можно записать в виде:
.
Определение. Представление комплексного числа 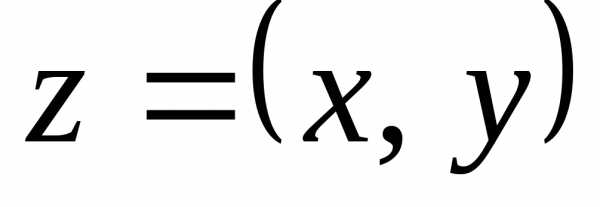 в виде
в виде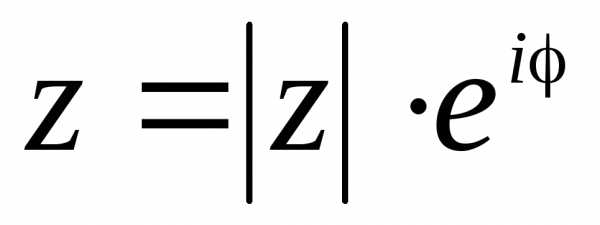 называетсяпоказательной
формой записи комплексного числа.
называетсяпоказательной
формой записи комплексного числа.
Таким образом,
комплексное число 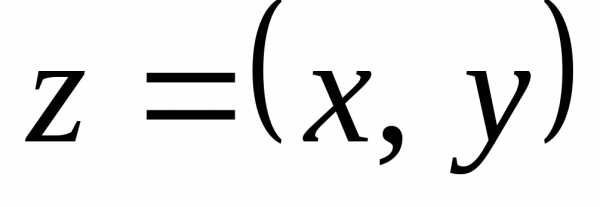 может быть записано в трёх равноправных
формах:
может быть записано в трёх равноправных
формах:
–алгебраическая форма записи комплексного числа;
–тригонометрическая форма записи комплексного числа;
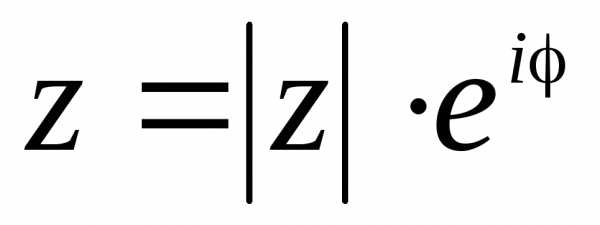 –показательная
форма записи комплексного числа,
–показательная
форма записи комплексного числа,
где ,
Пример 3. Записать комплексные числа в трёх формах записи:
а)
;
б);
б)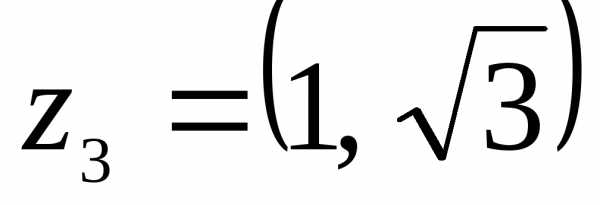 и изобразить их векторами на плоскости.
и изобразить их векторами на плоскости.
Решение. а) – алгебраическая форма записи комплексного числа. Находим модуль и аргумент комплексного числа.
Здесь ,
Значит,
–тригонометрическая форма записи комплексного числа ;
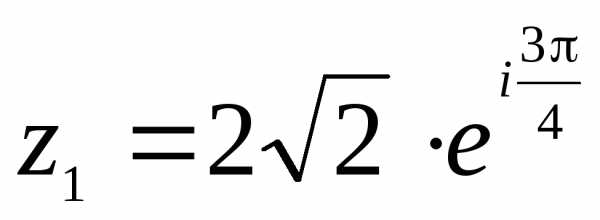 –показательная
форма записи комплексного числа
.
–показательная
форма записи комплексного числа
.
б) 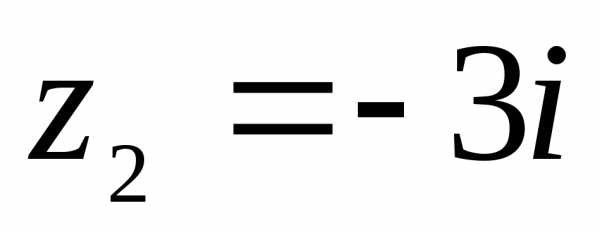 – алгебраическая форма записи комплексного
числа.
Находим модуль и аргумент комплексного
числа
– алгебраическая форма записи комплексного
числа.
Находим модуль и аргумент комплексного
числа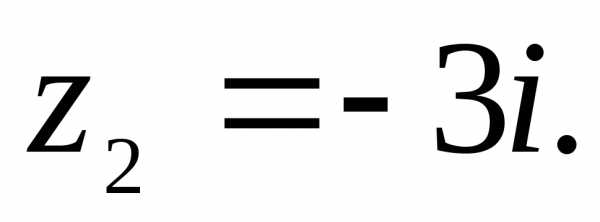 ЗдесьЗначит,
ЗдесьЗначит,
–тригонометрическая форма записи комплексного числа ;
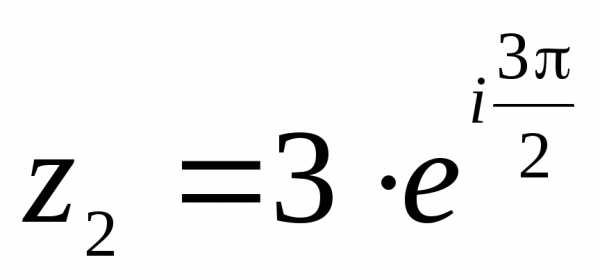 –показательная
форма записи комплексного числа
.
–показательная
форма записи комплексного числа
.
в)
– алгебраическая форма записи комплексного
числа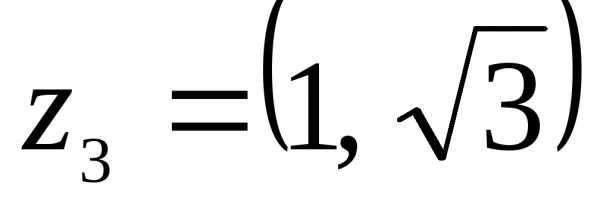 .
Находим модуль и аргумент комплексного
числаЗдесь
.
Находим модуль и аргумент комплексного
числаЗдесь
Значит,
–тригонометрическая
форма записи комплексного числа 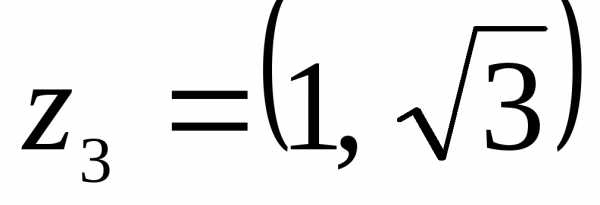 ;
;
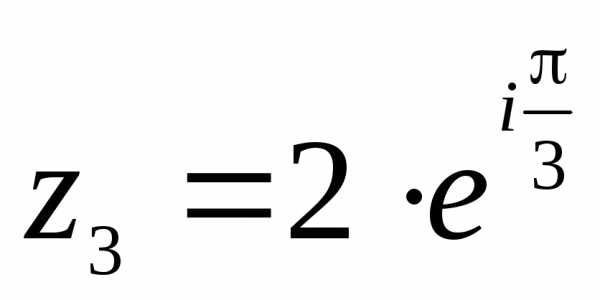 –показательная
форма записи комплексного числа
–показательная
форма записи комплексного числа 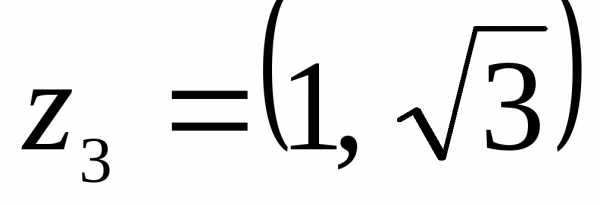 .
.
Рис. 2.
Изображения комплексных чисел представлены на рис. 2.
studfiles.net
Геометрическое изображение комплексных чисел. Тригонометрическая и показательная формы записи комплексного числа
Поиск ЛекцийПоскольку комплексное число мы определили как упорядоченную пару действительных чисел, то вполне естественно изобразить комплексное число точкой плоскости с декартовыми координатами либо вектором, идущим из начала координат в эту точку (рис. 1).
Рис. 1.
На оси Ох расположены все действительные числа, а на оси Оу – чисто мнимые, т.е. комплексные числа вида .
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью (её также обозначают C). Ось абсцисс называется действительной осью, а ось ординат – мнимой.
Длина вектора , изображающего комплексное число , есть модуль комплексного числа:
,
а угол , который образует этот вектор с осью Ох, называется аргументом комплексного числа .
Очевидно, что угол определён с точностью до .
Условимся называть главным значением аргумента – значение угла в интервале . Символически главное значение аргумента комплексного числа обозначают:
Тогда всю совокупность значений аргумента обозначают символом:
Очевидны формулы:
при
при
Из рис. 1 легко получить соотношения: , тогда
.
Определение. Представление комплексного числа в виде называется тригонометрической формой записи комплексного числа.
Для сокращения записи комплексных чисел в тригонометрической форме удобно использовать формулу Эйлера:
.
Тогда комплексное число можно записать в виде:
.
Определение. Представление комплексного числа в виде называется показательной формой записи комплексного числа.
Таким образом, комплексное число может быть записано в трёх равноправных формах:
– алгебраическая форма записи комплексного числа;
– тригонометрическая форма записи комплексного числа;
– показательная форма записи комплексного числа,
где ,
Пример 3.Записать комплексные числа в трёх формах записи:
а) ; б) ; б) и изобразить их векторами на плоскости.
Решение.а) – алгебраическая форма записи комплексного числа . Находим модуль и аргумент комплексного числа .
Здесь ,
Значит,
– тригонометрическая форма записи комплексного числа ;
– показательная форма записи комплексного числа .
б) – алгебраическая форма записи комплексного числа . Находим модуль и аргумент комплексного числа Здесь Значит,
– тригонометрическая форма записи комплексного числа ;
– показательная форма записи комплексного числа .
в) – алгебраическая форма записи комплексного числа . Находим модуль и аргумент комплексного числа Здесь
Значит,
– тригонометрическая форма записи комплексного числа ;
– показательная форма записи комплексного числа .
Рис. 2.
Изображения комплексных чисел представлены на рис. 2.
4.3. Формула Муавра и извлечение корня п-ой степени из комплексного числа
Вычислив произведение комплексных чисел, записанных в тригонометрической форме, можно убедиться, что модуль и аргумент комплексного числа обладают следующими свойствами:
. Модуль произведения комплексных чисел равен произведению модулей этих чисел: .
. Аргумент произведения комплексных чисел равен сумме аргументов этих чисел: .
Используя эти свойства, легко можно получить формулу возведения комплексного числа в целую положительную степень, а именно:
если , то
– формула Муавра,
или в показательной форме записи:
.
Определение.Корнем п-ой степени из комплексного числа называется такое комплексное число , которое, будучи возведено в степень п даст число .
Из определения и формулы Муавра ясно, что модуль искомого корня будет , а аргумент
Таким образом,
(1)
Придавать значения, большие , не имеет смысла, так как будем получать уже имеющиеся значения аргумента (с точностью до ).
Следовательно, корень п-ой степени из комплексного числа имеет п различных значений, модули которых одинаковы ( ), т.е. все значения корня лежат на окружности с центром в начале координат радиуса , а аргументы последовательных значений отличаются на угол .
Пример 4.Используя формулу Муавра, вычислить:
а) ; б)
Решение.а) Представим число в тригонометрической форме. Имеем:
. Значит,
– тригонометрическая форма записи комплексного числа .
Применяя формулу Муавра, получим:
б) Представим число в тригонометрической форме. Имеем: . Поэтому
– тригонометрическая форма записи комплексного числа .
Применяя формулу Муавра, получим:
Пример 5.Найти все значения корня: .
Решение.Представим комплексное число в тригонометрической форме. Здесь Поэтому
.
По формуле (1) находим:
где
Полагая , получим:
Найденным корням соответствуют вершины правильного пятиугольника, вписанного в окружность радиуса с центром в начале координат (рис. 3).
Рис. 3.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Тригонометрическая форма записи комплексных чисел
Р ассмотрим
другую важную форму представления
комплексных чисел [1, с. 187-188]:,
где
ассмотрим
другую важную форму представления
комплексных чисел [1, с. 187-188]:,
где – модуль комплексного числа, а
– модуль комплексного числа, а – его аргумент.
– его аргумент.
Связь между алгебраической и тригонометрической формами записи можно получить из равенства: . Тогда, откуда
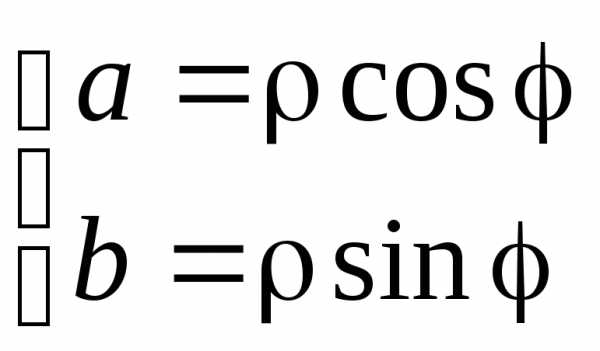 .
Возведя оба равенства в квадрат и сложив
их, получим.
А угол
.
Возведя оба равенства в квадрат и сложив
их, получим.
А угол определяется с точностью до,
из системы:
определяется с точностью до,
из системы:
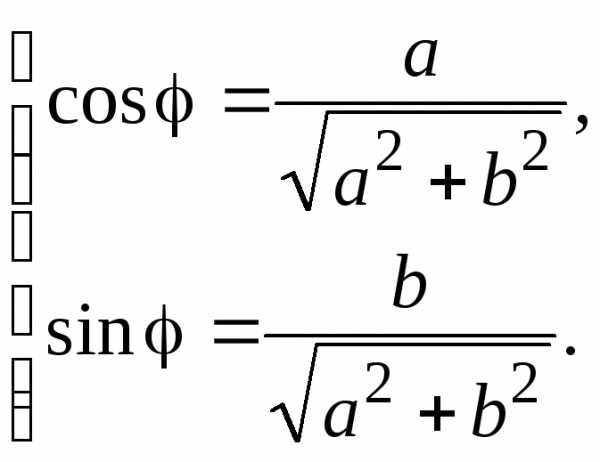 (1.1)
(1.1)
Для однозначного соответствия между комплексным числом и его аргументом выделим его главное значение argz , для которого принимаем:. В дальнейшем будем придерживаться ограничений:. Для числаz = 0 аргумент не определяется.
Геометрический
смысл 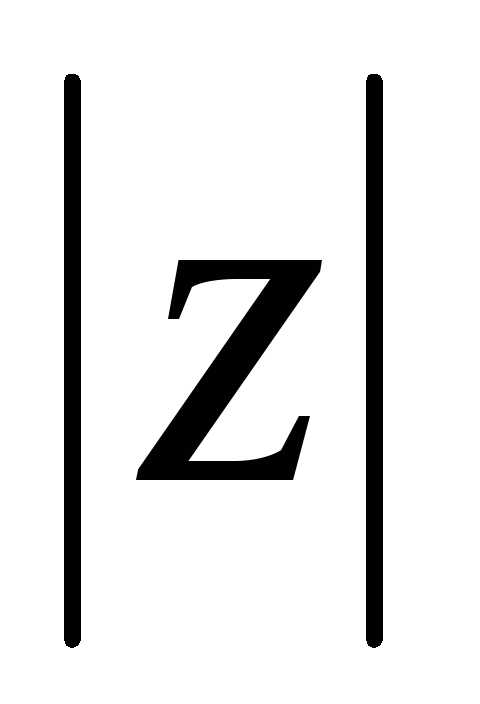 иargz ясен из рис 1.2:
иargz ясен из рис 1.2: есть расстояние от точки до начала
координат, аargz – угол, на который необходимо повернуть
вещественную осьRez до совпадения с числомz.
есть расстояние от точки до начала
координат, аargz – угол, на который необходимо повернуть
вещественную осьRez до совпадения с числомz.
Пример 14 Представить в тригонометрической форме числоz = 1.
Для числа z = 1a = 1,b = 0. Следовательно,и по формуле (1.1) находим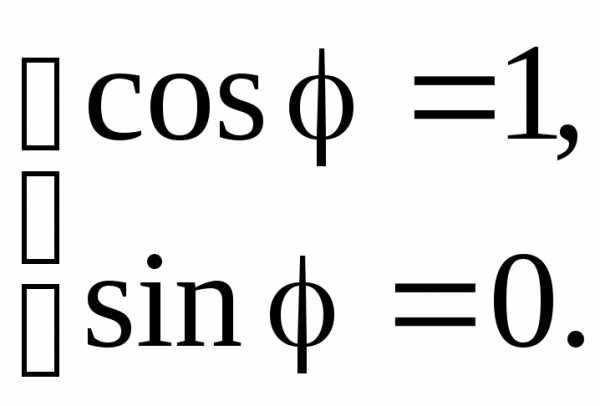 Эта система имеет решение:
Эта система имеет решение: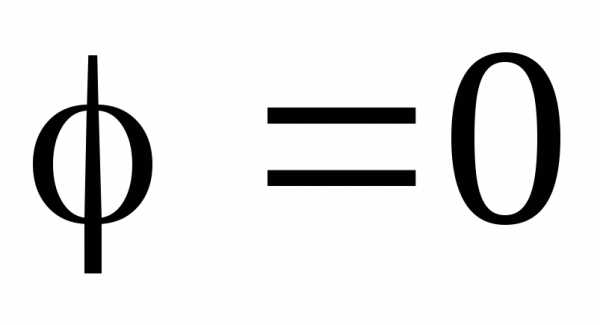 .
В итоге: .
.
В итоге: .
Пример 15 Представить в тригонометрической форме числоz = –i. Для негоa = 0, b = –1. Следовательно,и система (1.1) имеет вид:. Отсюда .
Пример 16 Представить в тригонометрической
форме числоz =
–1.
Для числаz =
–1a = –1,b = 0. Следовательно,и система (1.1) имеет вид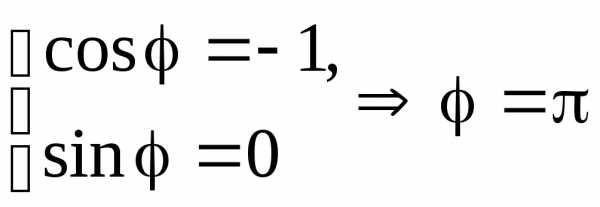 .
Получаем .
.
Получаем .
Пример 17 Представить в тригонометрической
форме числоz = 1
+ i.Для негоa = 1,b = 1. Следовательно,и по системе (1.1)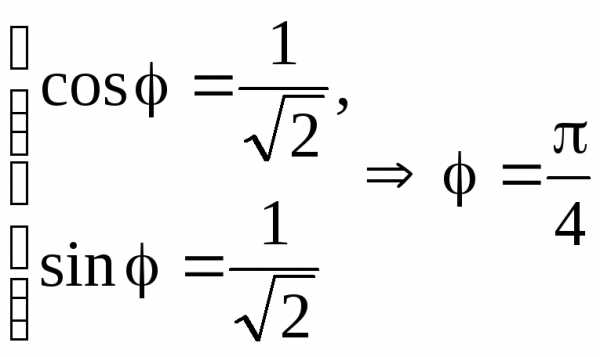 .
Значит, .
.
Значит, .
Пример 18 Представить в тригонометрической форме числоz = –5 + 7i.
Для него a = –5,b = 7.
Следовательно,и система (1.1) принимает вид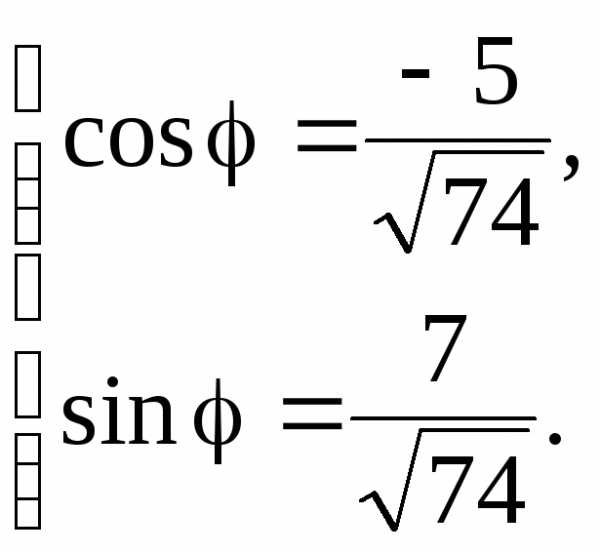 Решением этой системы будет
Решением этой системы будет
. Тогда
.
Умножение и деление комплексных чисел. Формула Муавра
Пусть . Тогда верны формулы:
,
, (1.2)
. (1.3)
Последняя формула называется формулой Муавра [1, с. 190]. Она верна для любого натурального n.
Пример 19 Вычислить: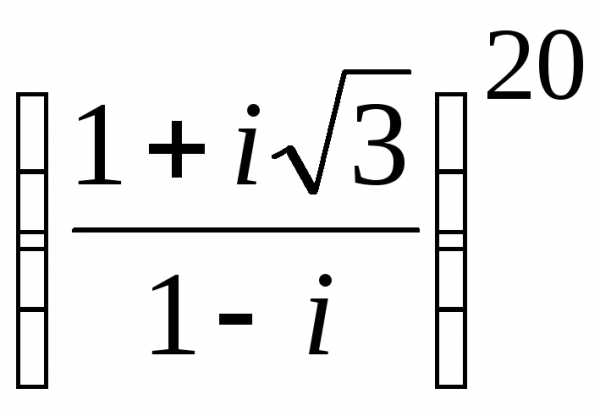 .
.
Решение.Переведем числитель и знаменатель дроби из алгебраической формы в тригонометрическую.
Для числа
, .
.
Для числа 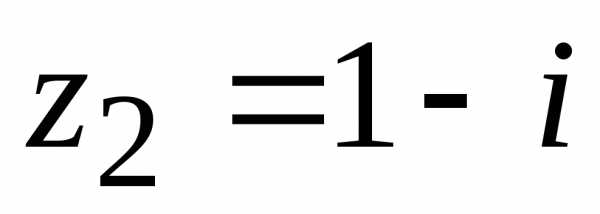 ,.
Таким образом,
,.
Таким образом,
В итоге:
Задачи на построение областей на комплексной плоскости
Пример 20 Изобразить на комплексной
плоскости числа, модуль которых равен
1, т. е.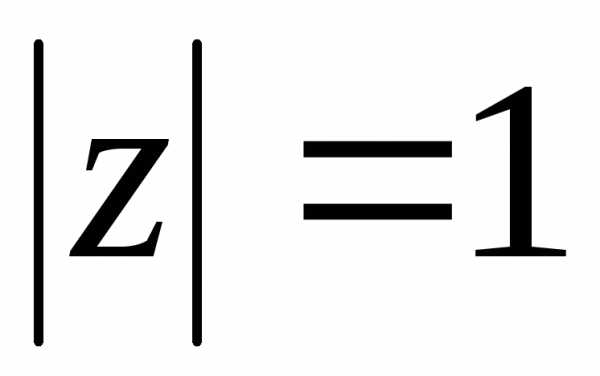 .
.
Решение. Запишем комплексное число
в алгебраической форме.
По условию задачи интерес представляют
те числа, модуль которых равен 1, т. е.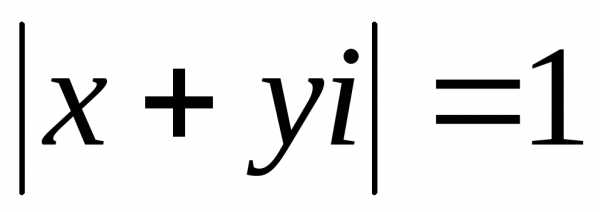 .
По определению модуля комплексного
числа.
Возведя обе части равенства в квадрат,
получим
.
По определению модуля комплексного
числа.
Возведя обе части равенства в квадрат,
получим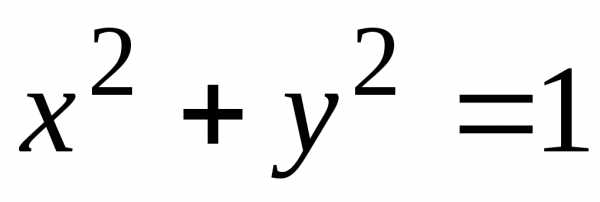 .
Данное уравнение определяет на плоскостиокружность с центром в точке с
координатами (0; 0) и радиусом, равным 1.
.
Данное уравнение определяет на плоскостиокружность с центром в точке с
координатами (0; 0) и радиусом, равным 1.
Пример 21 Найти геометрическое место
точек, изображающих числаz,
удовлетворяющие неравенству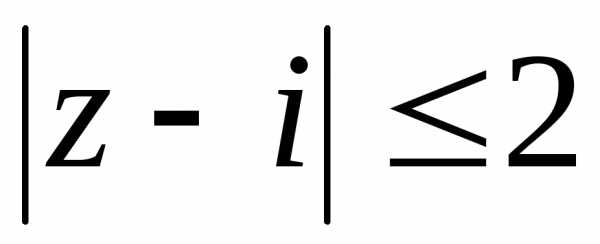 .
.
Запишем комплексное число в общем виде
.
По условию задачи, интерес представляют
те числа, модуль которых меньше или
равен 2, т. е..
Сгруппируем под знаком модуля слагаемые,
содержащие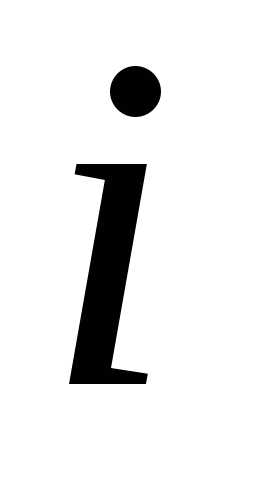 :
.
По определению модуля комплексного
числа:.
:
.
По определению модуля комплексного
числа:.
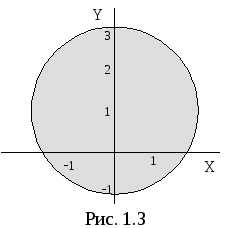
Данное уравнение определяет на плоскости круг с центром в точке с координатами (0; 1) и радиусом равным 2 (рис. 1.3).
Пример 22 Найти геометрическое место
точек, изображающих числаz,
удовлетворяющие неравенству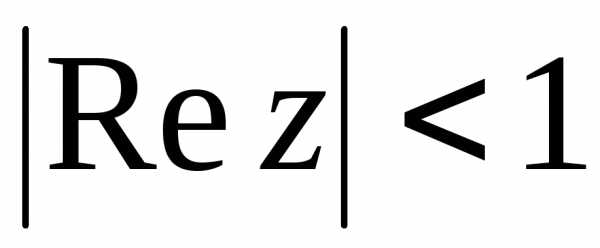 .
.
Rez–
действительная часть числаz,  неравенство можно записать как
неравенство можно записать как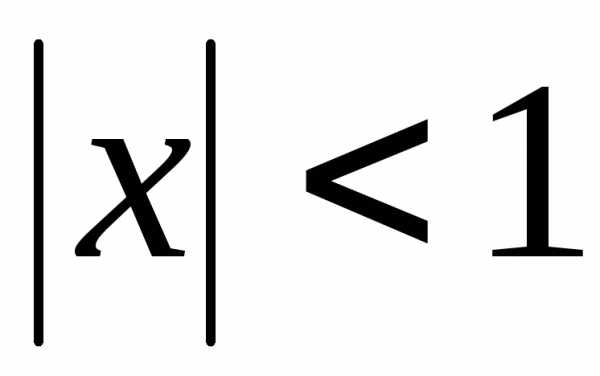 ,
или
,
или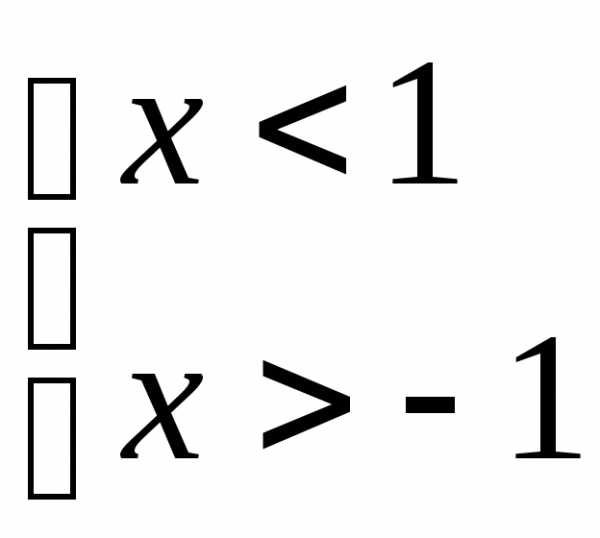 или.
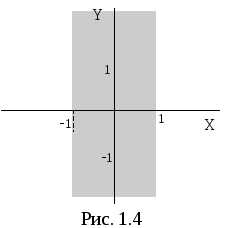
Эта система определяет на плоскостиполосу, ограниченную прямыми x = 1 и x = ‑1.
Причем, обе прямые нарисованы на
штрихами, так как сами прямые в искомую
область не входят из-за строгого знака
неравенства (рис. 1.4).
или.
Эта система определяет на плоскостиполосу, ограниченную прямыми x = 1 и x = ‑1.
Причем, обе прямые нарисованы на
штрихами, так как сами прямые в искомую
область не входят из-за строгого знака
неравенства (рис. 1.4).
Пример 23 Найти геометрическое место
точек, изображающих числаz,
удовлетворяющие системе неравенств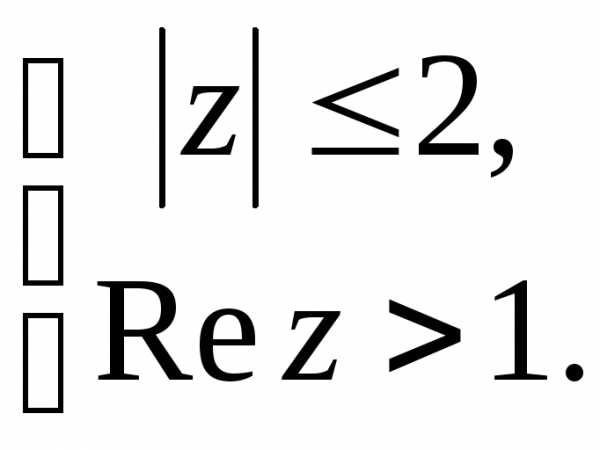
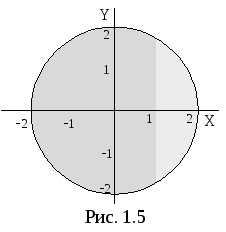
Как показано в примерах 20 и 21, неравенство 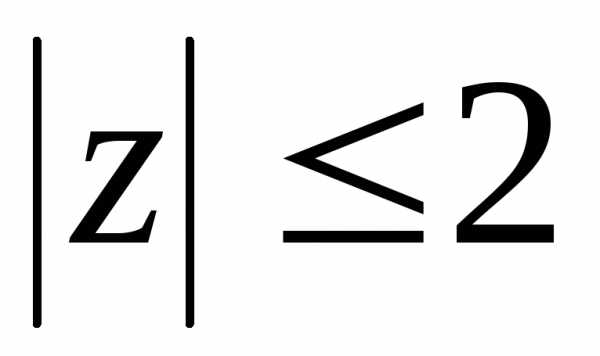 определяет на плоскости круг с центром
в точке (0; 0) и радиусом, равным 2.
Неравенство,
согласно примеру 22, определяет
полуплоскость, ограниченную прямойx = 1 и находящуюся от нее справа. Так
как неравенствострогое, то сама прямаяx = 1 в область не входит и штрихами
определяет на плоскости круг с центром
в точке (0; 0) и радиусом, равным 2.
Неравенство,
согласно примеру 22, определяет
полуплоскость, ограниченную прямойx = 1 и находящуюся от нее справа. Так
как неравенствострогое, то сама прямаяx = 1 в область не входит и штрихами
пунктиром. Обе эти области изображены на рис. 1.5. Искомая область представляет собой пересечение двух данных областей (рис. 1.6).
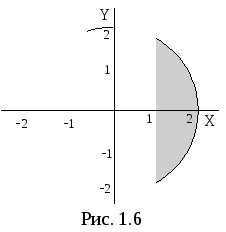
П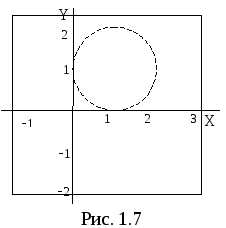 ример
24Найти геометрическое место точек,
изображающих числаz,
удовлетворяющие системе неравенств
ример
24Найти геометрическое место точек,
изображающих числаz,
удовлетворяющие системе неравенств
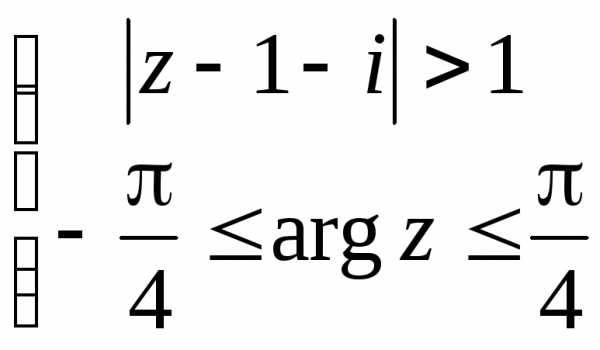 .
.
Неравенство определяет область вне круга с центром в точке (1; 1) и радиусом 1. Так как неравенство строгое, то сама окружность в область не входит и изображена штрихами (рис. 1.7).
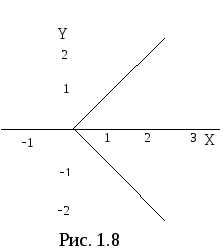
Двойное неравенство 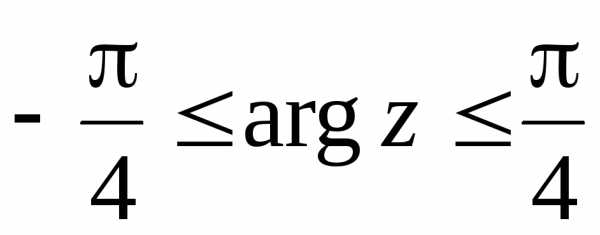 определяет на плоскости область, в
которую входят комплексные числа с
аргументами в интервале от
определяет на плоскости область, в
которую входят комплексные числа с
аргументами в интервале от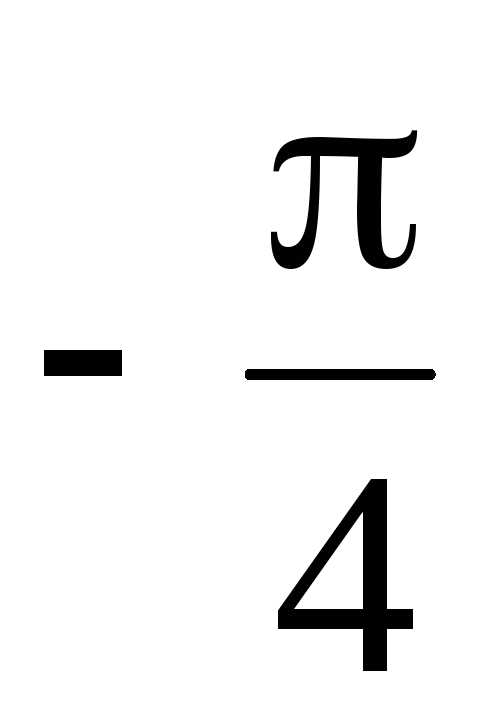 до
до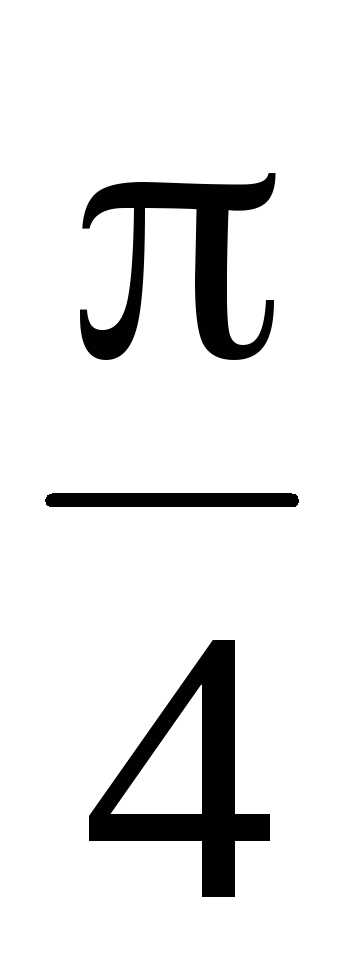 .
Эта область представляет собой угол
(рис. 1.8).
.
Эта область представляет собой угол
(рис. 1.8).
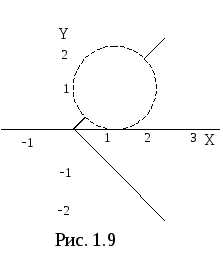
Искомая область представляет собой пересечение двух данных областей (рис. 1.9).
studfiles.net
Комплексная плоскость | Математика
Комплексная плоскость — это плоскость с прямоугольной декартовой системой координат xOy.
Комплексные числа на этой плоскости изображаются в виде точек либо в виде векторов.
I. Геометрическая интерпретация комплексных чисел в виде точек на комплексной плоскости
Каждому комплексному числу z=a+bi на комплексной плоскости соответствует точка z(a;b).
И наоборот, каждую точку z(a;b) плоскости можно считать изображением комплексного числа z=a+bi.
Таким образом, геометрическое изображение комплексных чисел в виде точек координатной плоскости устанавливает взаимно однозначное соответствие между комплексными числами и точками плоскости.
Действительные числа z=a+0i на комплексной плоскости изображаются точками с координатами (a;0) (лежащими на оси Ox), чисто мнимые числа z=0+bi — точками с координатами (0;b) (на оси Oy).
Поэтому ось абсцисс Ox называют действительной осью, а ось ординат Oy — мнимой осью.
Комплексно-сопряженные числа на плоскости изображаются точками, симметричными относительно оси Ox; противоположные комплексные числа — точками, симметричными относительно точки O (начала координат).
Например,
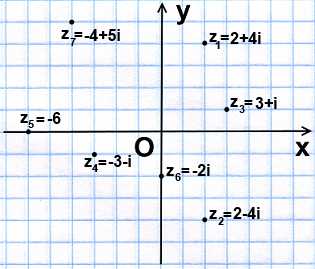
Комплексную плоскость называют также плоскостью Гаусса.
Геометрическая интерпретация комплексных чисел в виде радиус-векторов
Комплексные числа изображаются также векторами с началом в точке O и концом в точке z(a:b) (радиус-векторами).
Соответствие между комплексными числами и радиус-векторами также является взаимно однозначным.
Например,
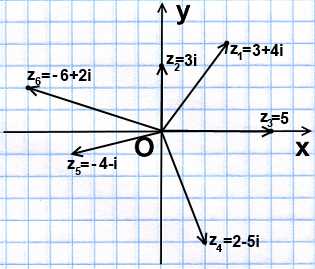
Геометрически сумма комплексных чисел в виде радиус-векторов строятся по правилу параллелограмма сложения векторов.
Геометрически комплексные числа также можно вычитать, как векторы.
На комплексной плоскости удобно изображать различные множества комплексных чисел, удовлетворяющие заданным условиям.
www.matematika.uznateshe.ru

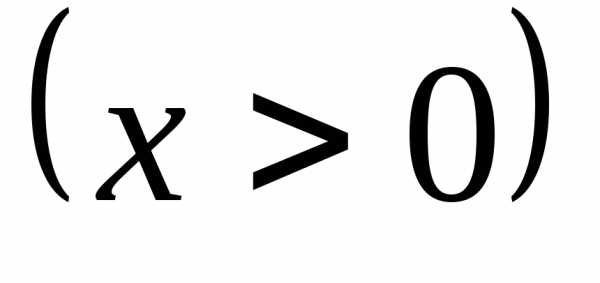 ,
то и
,
то и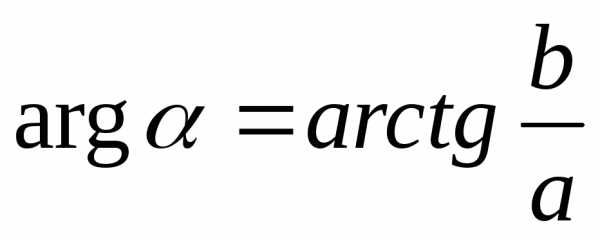 ;
;