Как из кнф получить днф – 11.2.4 Преобразование кнф в днф и днф в кнф

ДНФ, СДНФ, КНФ, СКНФ

2. Свойства конъюнкции, дизъюнкции и отрицания

Особая роль двух функций (из этих трех) определяется тем обстоятельством, что определение этих функций легко может быть перенесено на любое число переменных:

Конъюнкцией n переменных f (x₁, x₂, …, x_n) = x₁ x₂…x_n называется функция, которая принимает значение 1, если и только если все переменные равны 1 (и, значит, равна 0, если хотя бы одна из этих переменных равна 0).

Дизъюнкцией

n переменных f (x₁, x₂, …, x_n) = x_1Ú x_2Ú … Ú x_n называется такая функция, которая равна 0 если и только если все переменные равны 0 (и, значит, равна 1 тогда и только тогда, когда хотя бы одна переменная равна 1).

Из этих определений видно, что конъюнкция и дизъюнкция коммутативны, т. е. обе функции не зависят от порядка переменных.

Будем обозначать через (x₁,x₂,… ,x_n) новую функцию, которая на наборе переменныхx₁,x₂, …,x_n принимает значение, противоположноеf(x₁,x₂, …,x

_n).

Заметим, что в перечисленных далее свойствах в роли x, y, z может выступатьлюбая логическая функция. Все свойства легко могут быть доказаны из приведенных выше определений этих функций.

1. Универсальные границы:

x1 = 1; x0 =х;х1 =х;х0 = 0.

2. Ассоциативность конъюнкции и дизъюнкции:

x(yz) = (xy)z;x (y z) = (x y)z.

Это свойство означает, что в конъюнкции или дизъюнкции нескольких переменных можно как угодно расставлять скобки (а значит, можно вообще их не ставить).

3. Поглощение (“целое поглощает часть”):

х ху=х(1у) =х.

4. Два распределительных закона:

х (y z) =x y  x z;х (y z) = (x

y)(x z),

оба свойства могут быть доказаны простым рассуждением (например, если х = 0, тогда по свойству 1 справа выражение равно 0 и слева тоже 0, еслих = 1, то справа стоитy z и слева будет то же самое).

5. Правила де Моргана:

оба эти правила обобщаются на любое число переменных:

6.Правило Блейка:

Пусть К₁ иК₂ –какие-то логические функции, тогда

что легко доказывается справаналево:

Следствием правила Блейка являются два правила обобщенного поглощения:

Заметим, что правила Блейка и следствия из него часто используются для упрощения дизъюнкции (см. разд. 5)

Замечание.Конъюнкция, дизъюнкция, отрицание были определены для объектов, принимающих лишь два значения0и1. Однако бывают случаи, когда можно ввести такие операции для некоторых других объектов (эти операции также называют иногда конъюнкцией, дизъюнкцией и отрицанием), для которых также выполнены свойства 1–6. В этом случае говорят, что на этих объектах введена

булева алгебра.

Например, пусть– некоторое множество точек (или элементарных событий в теории вероятности),– множество подмножеств из. ЕслиA,Bпринадлежат, то можно ввестисумму множеств (дизъюнкцию)A+B=AB(равную объединению точек изАиВ), произведение множеств (конъюнкцию)АВ=А В(равное набору точек, входящих и вА, и вBодновременно) и дополнение(отрицаниеА), т. е.– множество точек из, не входящих вА. Тогда для этих операций (и это легко проверить) будут выполнены свойства 1–6. Таким образом, множество всех подмножеств изявляетсябулевой алгеброй.

3. ДНФ, СДНФ, КНФ, СКНФ

Простойконъюнкциейназываетсяконъюнкцияоднойилинесколькихпеременных,приэтомкаждаяпеременнаявстречаетсянеболееодногораза(либосама,либоееотрицание).

Например,  является простой конъюнкцией,

Дизъюнктивнойнормальнойформой(ДНФ)называетсядизъюнкцияпростыхконъюнкций.

Например, выражение     является ДНФ.

Совершеннойдизъюнктивнойнормальнойформой(СДНФ)называетсятакаядизъюнктивнаянормальнаяформа,укоторойвкаждуюконъюнкциювходятвсепеременныеданногосписка(либосами,либоихотрицания),причемводномитомжепорядке.

Например, выражение    является ДНФ, но не СДНФ. Выражениеявляется СДНФ.

Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.

Простойдизъюнкциейназываетсядизъюнкцияоднойилинесколькихпеременных,приэтомкаждаяпеременнаявходитнеболееодногораза(либосама,либоееотрицание).Например, выражение– простая дизъюнкция,

Конъюнктивнойнормальнойформой(КНФ)называетсяконъюнкцияпростыхдизъюнкций(например выражение– КНФ).

Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.

Например, выражение      является СКНФ.

Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:

а) переход от ДНФ к КНФ

Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:

Заметим, что КНФ можно получить и из первоначального выражения, если вынести уза скобки;

б) переход от КНФ к ДНФ

Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)

Таким образом, получили ДНФ.

Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется

сокращеннойДНФ;

в) сокращение ДНФ (или СДНФ) по правилуБлейка

Применение этого правила состоит из двух частей:

— если среди дизъюнктных слагаемых в ДНФ имеются слагаемые    , то ко всей дизъюнкции добавляем слагаемоеК₁К₂. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;

— если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,

или

Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ    , после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):

в) переход от ДНФ к СДНФ

Если в какой-то простой конъюнкции недостает переменной, например,

z, вставляем в нее выражение,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:

       

г) переход от КНФ к СКНФ

Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение(это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):

Таким образом, из КНФ получена СКНФ.

Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.

studfiles.net

9.Днф и кнф

1)ДНФ назыв. дизъюнкция элементар. коньюкций

2)КНФ назыв. коньюкция элементар. дизъюнкций

Формула вида (краткая запись), где– конъюнкцииназывается дизъюнктивной нормальной формой (ДНФ). Для любой формулы алгебры логики существует равносильная ей дизъюнктивная нормальная форма.

Форма вида (краткая запись), где- дизъюнкцииназывается конъюнктивной нормальной формой (КНФ).

Такими являются, например, выражения:

, . Для любой формулы алгебры логики существует равносильная ей конъюнктивная нормальная форма.

10.Алгебра Жегалкина. Полином Жегалкина

Множество булевых функций, рассматриваемое вместе с операциями конъюнкции и сложения (по модулю два), будем называть алгеброй Жегалкина.

Непосредственно проверкой (с помощью таблиц истинности) устанавливаются следующие законы:

– закон коммутативности; – закон ассоциативности;

– закон дистрибутивности; ;.

В алгебре Жегалкина роль совершенных нормальных форм булевой алгебры играют полиномы Жегалкина.

Полиномом Жегалкина называется полином вида

причем в каждом наборе все координаты различны, а суммирование ведется по некоторому множеству таких не совпадающих наборов, а – константа 0 или 1.

Например, выражение является полиномом Жегалкина, а выраженияи– нет, так как в первом выражении имеется конъюнкция, содержащая две переменные y, а второе выражение содержит два одинаковых слагаемыхи.

Каждая булева функция может быть единственным образом выражена при помощи полинома Жегалкина.

11.Теоремы о разложении.

1 Всякая булева функция f(x1,x2,…,xn) может быть представлена в следующей форме:

,

где 1 ≤ k ≤ n, в дизъюнкции берется по всем наборам значений переменных.

Разложение по переменной Xn:

(3.2)

Если булева функция не есть константа 0, то справедливо разложение

Разложение по всем переменным:

, (3.3)

где дизъюнкция берется по всем наборам , при которых значение функцииравно 1.

Теорема 2 Всякая булева функция может быть представлена в следующей форме:

(3.4)

где 1≤k≤n, а конъюнкция берется по всем 2k наборам значений переменных.

Теорема3.Для любой формулы алгебры логики существует равносильная ей дизъюнктивная нормальная форма.

Теорема 4 Для любой формулы алгебры логики существует равносильная ей конъюнктивная нормальная форма.

Теорема 4 Формула алгебры логики тогда и только тогда является тождественно истинной, когда каждая дизъюнкция в ее конъюнктивной нормальной форме содержит некоторую переменную вместе с ее отрицанием.

Теорема 5 Формула алгебры логики тогда и только тогда является тождественно ложной, когда каждая конъюнкция в ее дизъюнктивной форме содержит некоторую переменную вместе с ее отрицанием.

12.Сднф и скнф. Алгоритмы их нахождения.

,

называется совершенной дизъюнктивной нормальной формой (сокращенная запись СДНФ) функции.

Разложение (3.3) дает способ построения СДНФ. Для этого в таблице истинности отмечаем все строки , в которых. Для каждой такой строки образуем конъюнкциюи затем все полученные конъюнкции соединяем знаком дизъюнкции.

Таким образом, существует взаимно однозначное соответствие между таблицей истинности функции и ее СДНФ. А это значит, что СДНФ для булевой функции единственна.

Единая булева функция, не имеющая СДНФ, есть константа 0.

,

разложение носит название совершенной конъюнктивной нормальной формы (СКНФ). Разложение (3.6) дает способ построения СКНФ. Для этого в таблице истинности отмечаем все строки , в которых. Для каждой такой строки образуем дизъюнкциюи затем все полученные конъюнкции соединяем знаком конъюнкции. Таким образом, существует взаимно

однозначное соответствие между таблицей истинности функции и ее СКНФ. А это значит, что СКНФ для булевой функции единственна.

Единственная булева функция, не имеющая СКНФ, есть константа 1

studfiles.net

Контрольное задание №2. Получить сднф, скнф, используя таблицу истинности. Построить днф, кнф, упростив выражение.

((х  у)  (х  z))y

Методические указания

Всякая логическая функция n переменных может быть задана таблицей, в левой части которой перечислены все 2ⁿ наборов значений переменных (т.е. двоичных векторов длины n), а в правой части — значения функции на этих наборах. В этой таблице (таблица истинности) наборы расположены в лексикографическом порядке, который совпадает с порядком возрастания значений наборов, рассматриваемых как двоичные числа.

Характеристическое множество логической переменной функции – это множество М₁ двоичных наборов, на котором функция принимает значение 1. Логическая функция может быть задана с помощью своего характеристического множества М₁ или с помощью множества М₀ наборов, на котором она равна 0.

В табл. 2 приведены все булевы функции f_i (х₁, х₂) от двух аргументов. В левом столбце показаны их выражения в терминах нескольких функций, принятых за основные, а в следующих столбцах значения, принимаемые данными функциями на каждом из четырех наборов значений аргументов х₁ и х₂ (приведенных в верхней части таблицы).

Таблица 2

Булевы функции от двух аргументов

х1	0	0		1		1
х2	0		1		0		1
f0 = 0– константа 0	0		0		0		0
f1 = х1  х2– конъюнкция	0		0		0		1
f2– отрицание импликации	0		0		1		0
f3 = х1	0		0		1		1
f4– отрицание обратной импликации	0		1		0		0
f5 = х2	0		1		0		1
f6 = х1  х2– сложение по модулю 2	0		1		1		0
f7 = х1  х2— дизъюнкция	0		1		1		1
f8 = х1 х2– стрелка Пирса	1		0		0		0
f9 = х1  х2– эквиваленция	1		0		0		1
f10 =х2	1		0		1		0
f11 = х2  х1– обратная импликация	1		0		1		1
f12 =х1	1		1		0		0
f13 = х1  х2– импликация	1		1		0		1
f14 = х1  х2– штрих Шеффера	1		1		1		0
f15 = 1 – константа 1	1		1		1		1

Для установления порядка выполнения операций в формулах используются скобки. При отсутствии скобок порядок устанавливается согласно приоритетам операций. Первым приоритетом обладает операция отрицания, затем выполняется . Третьим приоритетом обладают операции  и , четвертым приоритетом – операции ~ и . Для упрощения написания формул иногда символ конъюнкции опускается.

Все операции алгебры логики можно выразить через булевы операции. Справедливость формул (1)-(3) можно доказать простой подстановкой значений из табл. 2:

х  у = xy x y; (1)

х ~ у =xy  x y; (2)

х  у =x  y. (3)

Всякая дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).

Всякая конъюнкция элементарных дизъюнкция называется конъюнктивной нормальной формой (КНФ).

Любую логическую функцию, не равную тождественно единице, можно представить в ДНФ. Любую логическую функцию, не равную тождественно нулю, можно представить в КНФ.

Дизъюнктивная нормальная форма логической функции называется совершенной (СДНФ), если все её составляющие есть конституенты единицы.

Всякую, не равную тождественно нулю, логическую функцию можно представить в виде СДНФ.

Конъюнктивная нормальная форма называется совершенной (СКНФ), если все её составляющие есть конституенты нуля.

Всякую, не равную тождественно единице, логическую функцию можно представить в виде СКНФ.

Алгоритм построения СДНФ по таблице истинности функции состоит из трех шагов.

1. В таблице истинности выбираются наборы, на которых функция принимает значение 1 (единицы).

2. Для наборов, выбранных на первом шаге, составляются конституенты единицы, в которые переменная входит с инверсией, если в соответствующем наборе она принимает значение 0 (ноль), и без инверсии, если в соответствующем наборе она принимает значение 1 (единицы).

3. Составляется дизъюнкция построенных на втором шаге конституент единицы.

Алгоритм построения СКНФ по таблице истинности логической функции содержит три шага.

1. В таблице истинности функции выбираются наборы, на которых функция принимает значение 0 (нуля).

2. Для этих наборов составляются конституенты нуля, в которые переменная входит с инверсией, если в наборе она принимает значение единицы, и без инверсии, если в наборе она принимает значение нуля.

3. Составляется конъюнкция построенных на предыдущем шаге конституент нуля.

Приведение формулы к ДНФ сводится к раскрытию скобок в соответствии с первым дистрибутивным законом в булевой формуле функции, содержащей знаки инверсии на самих переменных, с последующим исключением тождественных нулей и объединением равных членов.

Приведение формулы к КНФ сводится к раскрытию скобок в соответствии со вторым дистрибутивным законом в булевой формуле, содержащей знаки инверсии на самих переменных, с последующим исключение тождественных единиц и объединением равных членов.

Решение.

Построим истинностную таблицу сложного высказывания, заданного формулой S = ((х  у)  (х  z))

Очевидно, истинностная таблица будет содержать 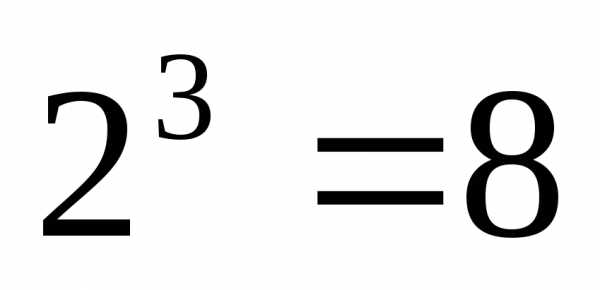строк.Построим таблицу (табл. 3).

Таблица 3

Истинностная таблица

x	y	z		х  у	х  z	((х  у)  (х  z))	S
0	0	0	1	1	0	1	1
0	0	1	1	1	1	1	1
0	1	0	0	1	0	1	0
0	1	1	0	1	1	1	0
1	0	0	1	0	1	1	1
1	0	1	1	0	0	0	0
1	1	0	0	1	1	1	0
1	1	1	0	1	0	1	0

Согласно алгоритмам построения СДНФ и СКНФ по таблице истинности получим следующие результаты

СДНФ =

СКНФ =

Пользуясь формулами (1) и (3), построим булево выражение, эквивалентное формуле ((х  у)  (х  z))y и найдем ДНФ и КНФ

((х  у)  (х  z))y = (x  y  xz x z)y = (x  y z)y =xy yz,

откуда ДНФ = xy yz, КНФ = (x  z)y .

studfiles.net