Таблица хи квадрат распределения – —

Хи квадрат-распределение. Распределение Пирсона. Квантили хи-квадрат распределения

-распределение. Распределение Пирсона. В таблице приведены значения квантилей Χ21-α(m) в зависимости от числа степеней свободы m и вероятности α m/α 0,99 0,98 0,95 0,90 0,80 0,20 0,10 0,05 0,02 0,01 0,001 1 0,00016 0,00063 0,00393 0,0158 0,0642 1,642 2,706 3,841 5,412 6,635 10,827 2 0,0201 0,0404 0,103 0,211 0,446 3,219 4,605 5,991 7,824 9,210 13,815 3 0,115 0,185 0,352 0,584 1,005 4,642 6,251 7,815 9,837 11,341 16,268 4 0,297 0,429 0,711 1,064 1,649 5,989 7,779 9,488 11,668 13,277 18,465 5 0,554 0,752 1,145 1,610 2,343 7,289 9,236 11,070 13,388 15,086 20,517 6 0,872 1,134 1,635 2,204 3,070 8,558 10,645 12,592 15,033 16,812 22,457 7 1,239 1,564 2,167 2,833 3,822 9,803 12,017 14,067 16,622 18,475 24,322 8 1,646 2,032 2,733 3,490 4,594 11,030 13,362 15,507 18,679 20,090 26,125 9 2,088 2,532 3,325 4,168 5,380 12,242 14,684 16,919 19,679 21,666 27,877 10 2,588 3,059 3,940 4,865 6,179 13,442 15,987 18,307 21,161 23,209 29,588 11 3,053 3,609 4,575 5,578 6,989 14,631 17,275 19,675 22,618 24,725 31,264 12 3,571 4,178 5,226 6,304 7,807 15,812 18,549 21,026 24,054 26,217 32,909 13 4,107 4,765 5,892 7,042 8,634 16,985 19,812 22,362 25,472 27,688 34,528 14 4,660 5,368 6,571 7,790 9,467 18,151 21,064 23,685 26,873 29,141 36,123 15 5,229 5,985 7,262 8,547 10,307 19,311 22,307 24,996 28,259 30,578 37,697 16 5,812 6,614 7,962 9,312 11,152 20,465 23,542 26,296 29,633 32,000 39,252 17 6,408 7,255 8,672 10,085 12,002 21,615 24,769 27,587 30,995 33,409 40,790 18 7,015 7,906 9,390 10,865 12,857 22,760 25,989 28,869 32,346 34,805 42,312 19 7,633 8,567 10,117 11,651 13,716 23,900 27,204 30,144 33,687 36,191 43,820 20 8,260 9,237 10,851 12,443 14,578 25,038 28,412 31,410 35,020 37,566 45,315 21 8,897 9,915 11,591 13,240 15,445 26,171 29,615 32,671 36,343 38,932 46,797 22 9,542 10,600 12,338 14,041 16,314 27,301 30,813 33,924 37,659 40,289 48,268 23 10,196 11,298 13,091 14,848 17,187 28,429 32,007 35,172 38,968 41,638 49,728 24 10,856 11,992 13,848 15,659 18,062 29,553 33,196 36,415 40,270 42,980 51,179 25 11,542 12,697 14,611 16,473 18,940 30,675 34,382 37,652 41,566 44,314 52,620 26 12,198 13,409 15,379 17,292 19,820 31,795 35,563 38,885 42,856 45,642 54,052 27 12,879 14,125 16,151 18,114 20,703 32,912 86,741 40,113 44,140 46,963 55,476 28 13,565 14,847 16,928 18,939 21,588 34,027 37,916 41,337 45,419 48,278 56,893 29 14,256 15,574 17,708 19,768 22,475 35,139 39,087 42,557 46,693 49,588 58,302 30 14,953 16,306 18,493 20,599 23,364 36,250 40,256 43,773 47,962 50,892 59,703

tehtab.ru

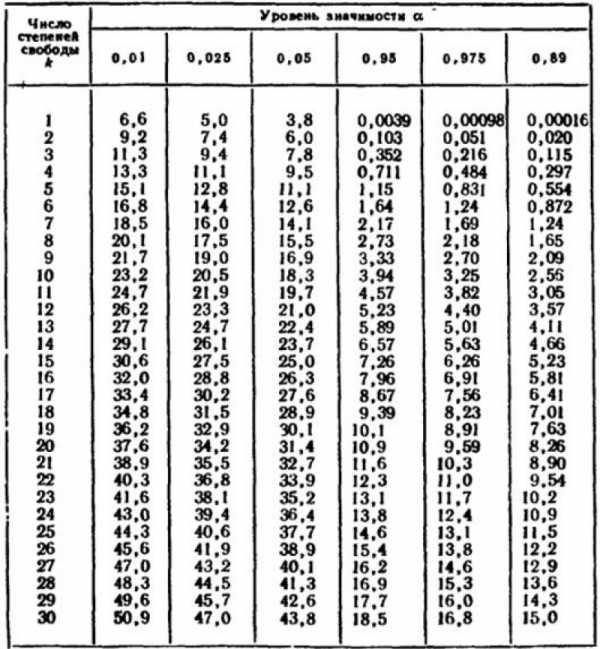
Таблица критических точек распределения χ2 (хи-квадрат) критерия Пирсона

Ниже представлена таблица значений критических точек распределения χ2 (хи-квадрат) критерия Пирсона, широко используемые в задачах математической статистики, таких как построение доверительных интервалов, проверка статистических гипотез и непараметрическое оценивание.

Число степеней свободы k	Уровень значимости α
	0,01	0,025	0,05	0,95	0,975	0,99
1	6,6	5	3,8	0,0039	0,00098	0,00016
2	9,2	7,4	6	0,103	0,051	0,02
3	11,3	9,4	7,8	0,352	0,216	0,115
4	13,3	11,1	9,5	0,711	0,484	0,297
5	15,1	12,8	11,1	1,15	0,831	0,554
6	16,8	14,4	12,6	1,64	1,24	0,872
7	18,5	16	14,1	2,17	1,69	1,24
8	20,1	17,5	15,5	2,73	2,18	1,65
9	21,7	19	16,9	3,33	2,7	2,09
10	23,2	20,5	18,3	3,94	3,25	2,56
11	24,7	21,9	19,7	4,57	3,82	3,05
12	26,2	23,3	21 ,0	5,23	4,4	3,57
13	27,7	24,7	22,4	5,89	5,01	4,11
14	29,1	26,1	23,7	6,57	5,63	4,66
15	30,6	27,5	25	7,26	6,26	5,23
16	32	28,8	26,3	7,96	6,91	5,81
17	33,4	30,2	27,6	8,67	7,56	6,41
18	34,8	31,5	28,9	9,39	8,23	7,01
19	36,2	32,9	30,1	10,1	8,91	7,63
20	37,6	34,2	31,4	10,9	9,59	8,26
21	38,9	35,5	32,7	11,6	10,3	8,9
22	40,3	36,8	33,9	12,3	11	9,54
23	41,6	38,1	35,2	13,1	11,7	10,2
24	43	39,4	36,4	13,8	12,4	10,9
25	44,3	40,6	37,7	14,6	13,1	11,5
26	45,6	41,9	38,9	15,4	13,8	12,2
27	47	43,2	40,1	16,2	14,6	12,9
28	48,3	44,5	41,3	16,9	15,3	13,6
29	49,6	45,7	42,6	17,7	16	14,3
30	50,9	47	43,8	18,5	16,8	15

Задача

Имеется три независимых реализации нормальной случайной величины: 0.6, 3.4, 2.0.

Проверить гипотезу : дисперсия равна 10.0.

Используются таблицы распределения хи-квадрат.

Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение или онлайн-помощь на зачете/экзамене 〉〉

Решение

Вычислим среднее и исправленную дисперсию:

Для того, чтобы при заданном уровне значимости  проверить нулевую гипотезу  о равенстве неизвестной генеральной дисперсии гипотетическому значению  при конкурирующей гипотезе  вычисляем наблюдаемое значение критерия:

При уровне значимости  находим:

 — нет оснований отвергнуть нулевую гипотезу

К оглавлению решебника по теории вероятностей и математической статистике 〉

100task.ru

Решим задачи, контрольные, курсовые… — Таблица критических точек распределения Пирсона (хи-квадрат).

k /α	0,01	0,025	0,05	0,95	0,975	0,99
1	6,63	5,02	3,84	0,00	0,00	0,00
2	9,21	7,38	5,99	0,10	0,05	0,02
3	11,34	9,35	7,81	0,35	0,22	0,11
4	13,28	11,14	9,49	0,71	0,48	0,30
5	15,09	12,83	11,07	1,15	0,83	0,55
6	16,81	14,45	12,59	1,64	1,24	0,87
7	18,48	16,01	14,07	2,17	1,69	1,24
8	20,09	17,53	15,51	2,73	2,18	1,65
9	21,67	19,02	16,92	3,33	2,70	2,09
10	23,21	20,48	18,31	3,94	3,25	2,56
11	24,72	21,92	19,68	4,57	3,82	3,05
12	26,22	23,34	21,03	5,23	4,40	3,57
13	27,69	24,74	22,36	5,89	5,01	4,11
14	29,14	26,12	23,68	6,57	5,63	4,66
15	30,58	27,49	25,00	7,26	6,26	5,23
16	32,00	28,85	26,30	7,96	6,91	5,81
17	33,41	30,19	27,59	8,67	7,56	6,41
18	34,81	31,53	28,87	9,39	8,23	7,01
19	36,19	32,85	30,14	10,12	8,91	7,63
20	37,57	34,17	31,41	10,85	9,59	8,26
21	38,93	35,48	32,67	11,59	10,28	8,90
22	40,29	36,78	33,92	12,34	10,98	9,54
23	41,64	38,08	35,17	13,09	11,69	10,20
24	42,98	39,36	36,42	13,85	12,40	10,86
25	44,31	40,65	37,65	14,61	13,12	11,52
26	45,64	41,92	38,89	15,38	13,84	12,20
27	46,96	43,19	40,11	16,15	14,57	12,88
28	48,28	44,46	41,34	16,93	15,31	13,56
29	49,59	45,72	42,56	17,71	16,05	14,26
30	50,89	46,98	43,77	18,49	16,79	14,95
31	52,19	48,23	44,99	19,28	17,54	15,66
32	53,49	49,48	46,19	20,07	18,29	16,36
33	54,78	50,73	47,40	20,87	19,05	17,07
34	56,06	51,97	48,60	21,66	19,81	17,79
35	57,34	53,20	49,80	22,47	20,57	18,51
36	58,62	54,44	51,00	23,27	21,34	19,23
37	59,89	55,67	52,19	24,07	22,11	19,96
38	61,16	56,90	53,38	24,88	22,88	20,69
39	62,43	58,12	54,57	25,70	23,65	21,43
40	63,69	59,34	55,76	26,51	24,43	22,16
41	64,95	60,56	56,94	27,33	25,21	22,91
42	66,21	61,78	58,12	28,14	26,00	23,65
43	67,46	62,99	59,30	28,96	26,79	24,40
44	68,71	64,20	60,48	29,79	27,57	25,15
45	69,96	65,41	61,66	30,61	28,37	25,90
46	71,20	66,62	62,83	31,44	29,16	26,66
47	72,44	67,82	64,00	32,27	29,96	27,42
48	73,68	69,02	65,17	33,10	30,75	28,18
49	74,92	70,22	66,34	33,93	31,55	28,94
50	76,15	71,42	67,50	34,76	32,36	29,71

 

О распределении Пирсона а Excel

Критические точки распределения Пирсона (хи-квадрат) можно вычислить в Excel по формуле =ХИ2ОБР(α; k)
где α — уровень значимости, k — число степеней свободы
Допустим, вам нужно вычислить значение при α = 0,1, k = 15. Забиваем в ячейку формулу
=ХИ2ОБР(0,1; 15). Получаем результат 22,307.

 

 

www.reshim.su

Квантили распределения хи-квадрат

Кванти́ли распределе́ния хи-квадра́т — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов, проверка статистических гипотез и непараметрическое оценивание

Квантиль хи-квадрат — это число величина хи-квадрат, при котором функция распределения хи-квадрат равна заданной затребованной вероятности а

Равенство функции распределения хи-квадрат вероятности а означает, что с вероятностью а будут наблюдаться значения хи-квадрат, не большие, чем найденный определенный согласно функции распределения квантиль хи-квадрат Таким образом, найти квантиль означает разграничить распределения хи-квадрат согласно заданной вероятности а

Содержание

• 1 Определение
• 2 Замечания
• 3 Аппроксимация квантилей
• 4 Таблица квантилей
• 5 См также
• 6 Примечания

Определение

Пусть F n }  — функция распределения хи-квадрат χ 2 n n} с n степенями свободы, и α ∈ [ 0 , 1 ] Тогда α -квантилем этого распределения называется число χ α , n 2 ^} такое, что

F n χ α , n 2 = α \left\chi _^\right=\alpha }

Замечания

• Прямо из определения следует, что случайная величина, имеющая распределение хи-квадрат с n степенями свободы, не превышает значение χ α , n 2 ^} с вероятностью α и превышает его с вероятностью 1 − α
• Функция F n } строго возрастает для любого n ∈ N } Следовательно, определена её обратная функция F n − 1 ^} , и

F n − 1 α = χ α , n 2 ^\alpha =\chi _^}

• Функция F n − 1 ^} не имеет простого представления Однако, возможно вычислить её значения численно

Аппроксимация квантилей

Для получения приближенных значений квантилей распределения хи-квадрат χ α , n 2 ^} существуют аппроксимации

• Аппроксимация Корниша-Фишера

χ α , n 2 = n + A n + B + C n + D n + E n n ^=n+A}+B+}}+}+}}}} ,

где:

A = d 2 }} ,

B = 2 3 d 2 − 1 }\left^}-1\right}

C = d ⋅ d 2 − 7 9 2 ^}-7}}}}}

D = − 6 d 4 + 14 d 2 − 32 405 ^}+14^}-32}}}

E = d ⋅ 9 d 4 + 256 d 2 − 433 4860 2 ^}+256^}-433}}}}}

d = 20637 ⋅ ln ⁡ 1 1 − α − 016 04274 − 15774 }-016\right}^}-15774} при 05 ≤ α ≤ 0999

d = − 20637 ⋅ ln ⁡ 1 α − 016 04274 + 15774 }-016\right}^}+15774} при 0001 ≤ α < 05

• Аппроксимация Голдштейна

χ α , n 2 = n ⋅ [ ∑ i = 0 6 n − i 2 ⋅ d i ⋅ a i + b i n + c i n 2 ] 3 ^=n\cdot ^^}}}\cdot ^}\cdot \left_}+_}}+_}^}}\right}\right]}^}} ,

где d определяется аналогично, а коэффициенты a, b,c приведены в таблице

a	b	c
10000886	-02237368	-001513904
04713941	002607083	-0008986007
00001348028	001128186	002277679
-0008553069	-001153761	-001323293
000312558	0005169654	-0006950356
-00008426812	000253001	0001060438
000009780499	-0001450117	0001565326

Таблица квантилей

Нижеприведённая таблица получена с помощью функции chi2inv пакета MATLAB

Также квантили можно получить с помощью других программных средств:

• пакет LibreOffice, электронная таблица Calc, функция CHIINV
• библиотека scipy для языка python, функция scipystatsdistributionschi2ppf
• встроенная функция в электронной таблице Excel : ХИ2ОБР или ХИ2ОБР
• библиотека MathNet для Net и Mono, метод MathNetNumericsDistributionsChiSquaredInvCDFn,a
• встроенная функция языка R: qchisqp, df

Чтобы получить значение χ α , n 2 ^} , необходимо найти строку, соответствующую нужному n , и колонку, соответствующую нужному α Искомое число находится в таблице на их пересечении
Например:

χ 0025 , 10 2 = 20483 ^=20483} ; χ 0975 , 10 2 = 3247 ^=3247} Квантили χ α , n 2 ^}

	0,01	0,025	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95	0,975	0,99
1	6,6349	5,0239	3,8415	2,7055	1,6424	1,0742	0,7083	0,4549	0,275	0,1485	0,0642	0,0158	0,0039	0,001	0,0002
2	9,2103	7,3778	5,9915	4,6052	3,2189	2,4079	1,8326	1,3863	1,0217	0,7133	0,4463	0,2107	0,1026	0,0506	0,0201
3	11,345	9,3484	7,8147	6,2514	4,6416	3,6649	2,9462	2,366	1,8692	1,4237	1,0052	0,5844	0,3518	0,2158	0,1148
4	13,277	11,143	9,4877	7,7794	5,9886	4,8784	4,0446	3,3567	2,7528	2,1947	1,6488	1,0636	0,7107	0,4844	0,2971
5	15,086	12,833	11,07	9,2364	7,2893	6,0644	5,1319	4,3515	3,6555	2,9999	2,3425	1,6103	1,1455	0,8312	0,5543
6	16,812	14,449	12,592	10,645	8,5581	7,2311	6,2108	5,3481	4,5702	3,8276	3,0701	2,2041	1,6354	1,2373	0,8721
7	18,475	16,013	14,067	12,017	9,8032	8,3834	7,2832	6,3458	5,4932	4,6713	3,8223	2,8331	2,1673	1,6899	1,239
8	20,09	17,535	15,507	13,362	11,03	9,5245	8,3505	7,3441	6,4226	5,5274	4,5936	3,4895	2,7326	2,1797	1,6465
9	21,666	19,023	16,919	14,684	12,242	10,656	9,4136	8,3428	7,357	6,3933	5,3801	4,1682	3,3251	2,7004	2,0879
10	23,209	20,483	18,307	15,987	13,442	11,781	10,473	9,3418	8,2955	7,2672	6,1791	4,8652	3,9403	3,247	2,5582
11	24,725	21,92	19,675	17,275	14,631	12,899	11,53	10,341	9,2373	8,1479	6,9887	5,5778	4,5748	3,8157	3,0535
12	26,217	23,337	21,026	18,549	15,812	14,011	12,584	11,34	10,182	9,0343	7,8073	6,3038	5,226	4,4038	3,5706
13	27,688	24,736	22,362	19,812	16,985	15,119	13,636	12,34	11,129	9,9257	8,6339	7,0415	5,8919	5,0088	4,1069
14	29,141	26,119	23,685	21,064	18,151	16,222	14,685	13,339	12,078	10,821	9,4673	7,7895	6,5706	5,6287	4,6604
15	30,578	27,488	24,996	22,307	19,311	17,322	15,733	14,339	13,03	11,721	10,307	8,5468	7,2609	6,2621	5,2293
16	32	28,845	26,296	23,542	20,465	18,418	16,78	15,338	13,983	12,624	11,152	9,3122	7,9616	6,9077	5,8122
17	33,409	30,191	27,587	24,769	21,615	19,511	17,824	16,338	14,937	13,531	12,002	10,085	8,6718	7,5642	6,4078
18	34,805	31,526	28,869	25,989	22,76	20,601	18,868	17,338	15,893	14,44	12,857	10,865	9,3905	8,2307	7,0149
19	36,191	32,852	30,144	27,204	23,9	21,689	19,91	18,338	16,85	15,352	13,716	11,651	10,117	8,9065	7,6327
20	37,566	34,17	31,41	28,412	25,038	22,775	20,951	19,337	17,809	16,266	14,578	12,443	10,851	9,5908	8,2604
21	38,932	35,479	32,671	29,615	26,171	23,858	21,991	20,337	18,768	17,182	15,445	13,24	11,591	10,283	8,8972
22	40,289	36,781	33,924	30,813	27,301	24,939	23,031	21,337	19,729	18,101	16,314	14,041	12,338	10,982	9,5425
23	41,638	38,076	35,172	32,007	28,429	26,018	24,069	22,337	20,69	19,021	17,187	14,848	13,091	11,689	10,196
24	42,98	39,364	36,415	33,196	29,553	27,096	25,106	23,337	21,652	19,943	18,062	15,659	13,848	12,401	10,856
25	44,314	40,646	37,652	34,382	30,675	28,172	26,143	24,337	22,616	20,867	18,94	16,473	14,611	13,12	11,524
26	45,642	41,923	38,885	35,563	31,795	29,246	27,179	25,336	23,579	21,792	19,82	17,292	15,379	13,844	12,198
27	46,963	43,195	40,113	36,741	32,912	30,319	28,214	26,336	24,544	22,719	20,703	18,114	16,151	14,573	12,879
28	48,278	44,461	41,337	37,916	34,027	31,391	29,249	27,336	25,509	23,647	21,588	18,939	16,928	15,308	13,565
29	49,588	45,722	42,557	39,087	35,139	32,461	30,283	28,336	26,475	24,577	22,475	19,768	17,708	16,047	14,256
30	50,892	46,979	43,773	40,256	36,25	33,53	31,316	29,336	27,442	25,508	23,364	20,599	18,493	16,791	14,953
31	52,191	48,232	44,985	41,422	37,359	34,598	32,349	30,336	28,409	26,44	24,255	21,434	19,281	17,539	15,655
32	53,486	49,48	46,194	42,585	38,466	35,665	33,381	31,336	29,376	27,373	25,148	22,271	20,072	18,291	16,362
33	54,776	50,725	47,4	43,745	39,572	36,731	34,413	32,336	30,344	28,307	26,042	23,11	20,867	19,047	17,074
34	56,061	51,966	48,602	44,903	40,676	37,795	35,444	33,336	31,313	29,242	26,938	23,952	21,664	19,806	17,789
35	57,342	53,203	49,802	46,059	41,778	38,859	36,475	34,336	32,282	30,178	27,836	24,797	22,465	20,569	18,509
36	58,619	54,437	50,998	47,212	42,879	39,922	37,505	35,336	33,252	31,115	28,735	25,643	23,269	21,336	19,233
37	59,893	55,668	52,192	48,363	43,978	40,984	38,535	36,336	34,222	32,053	29,635	26,492	24,075	22,106	19,96
38	61,162	56,896	53,384	49,513	45,076	42,045	39,564	37,335	35,192	32,992	30,537	27,343	24,884	22,878	20,691
39	62,428	58,12	54,572	50,66	46,173	43,105	40,593	38,335	36,163	33,932	31,441	28,196	25,695	23,654	21,426
40	63,691	59,342	55,758	51,805	47,269	44,165	41,622	39,335	37,134	34,872	32,345	29,051	26,509	24,433	22,164
41	64,95	60,561	56,942	52,949	48,363	45,224	42,651	40,335	38,105	35,813	33,251	29,907	27,326	25,215	22,906
42	66,206	61,777	58,124	54,09	49,456	46,282	43,679	41,335	39,077	36,755	34,157	30,765	28,144	25,999	23,65
43	67,459	62,99	59,304	55,23	50,548	47,339	44,706	42,335	40,05	37,698	35,065	31,625	28,965	26,785	24,398
44	68,71	64,201	60,481	56,369	51,639	48,396	45,734	43,335	41,022	38,641	35,974	32,487	29,787	27,575	25,148
45	69,957	65,41	61,656	57,505	52,729	49,452	46,761	44,335	41,995	39,585	36,884	33,35	30,612	28,366	25,901
46	71,201	66,617	62,83	58,641	53,818	50,507	47,787	45,335	42,968	40,529	37,795	34,215	31,439	29,16	26,657
47	72,443	67,821	64,001	59,774	54,906	51,562	48,814	46,335	43,942	41,474	38,708	35,081	32,268	29,956	27,416
48	73,683	69,023	65,171	60,907	55,993	52,616	49,84	47,335	44,915	42,42	39,621	35,949	33,098	30,755	28,177
49	74,919	70,222	66,339	62,038	57,079	53,67	50,866	48,335	45,889	43,366	40,534	36,818	33,93	31,555	28,941
50	76,154	71,42	67,505	63,167	58,164	54,723	51,892	49,335	46,864	44,313	41,449	37,689	34,764	32,357	29,707

См также

• Доверительный интервал для дисперсии нормальной выборки

Примечания

1. ↑ Goldberg H, Levine H Approximate formulas for the percentage points and normalization of t and χ 2 } // AMS 1945 V17 P 216—225
2. ↑ Goldstein RB Chi-square quantiles, Algorithm 451 // Commun Assoc Comp 1973 V 16 P 483—485

---

Квантили распределения хи-квадрат Информацию О

---

---

Квантили распределения хи-квадрат Комментарии

Квантили распределения хи-квадрат
Квантили распределения хи-квадрат
Квантили распределения хи-квадрат Вы просматриваете субъект

Квантили распределения хи-квадрат что, Квантили распределения хи-квадрат кто, Квантили распределения хи-квадрат описание

There are excerpts from wikipedia on this article and video

www.turkaramamotoru.com

Критерий согласия Пирсона χ2 (Хи-квадрат)

До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.

Так был изобретен критерий χ² (хи-квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ номинальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.

Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.

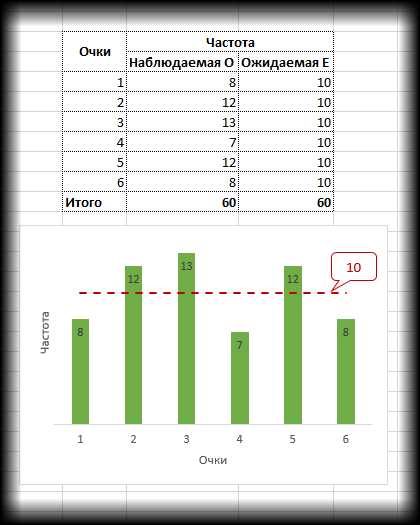
Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, то есть расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.

1. Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
2. Распределение этой меры при справедливости гипотезы о том, что различий нет.

Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.

Обратим внимание на следующие факты. В общем случае количество градаций, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной E_i будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение

будет иметь стандартное нормальное распределение.

Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой градации должна быть не менее 5. Только в этом случае величина, показанная выше, будет иметь стандартное нормальное распределение. Предположим, что это условие выполнено.

У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной градации. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.

Это и есть знамений критерий χ² Пирсона. Если частоты действительно соответствуют ожидаемым, то значение критерия будет относительно не большим (т.к. большинство отклонений находится около нуля). Но если критерий оказывается большим, то это свидетельствует в пользу существенных различий между частотами.

«Большим» критерий становится тогда, когда появление такого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение критерия при многократном повторении эксперимента, когда гипотеза о согласии частот верна.

Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем их больше, тем большее значение должно быть у критерия, ведь каждое слагаемое внесет свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ² – это целое семейство распределений.

И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество градаций номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.

По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам хи-квадрат).

Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.

Примерно также распределение статистического критерия может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей. Это чистая математика, никакой магии.

Таким образом, распределение χ² – это семейство распределений, каждое из которых зависит от параметра степеней свободы. А формальное определение критерия хи-квадрат следующее. Распределение χ² (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.

Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в специализированном ПО, которая есть даже в Excel.

Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.

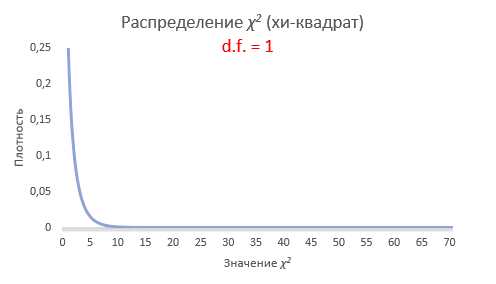
С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).

Проверка гипотезы по критерию хи-квадрат

{module 111}

Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по критерию хи-квадрат. Далее либо сам критерий сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т.е. вероятность получить такое или еще больше значение критерия при справедливости нулевой гипотезы.

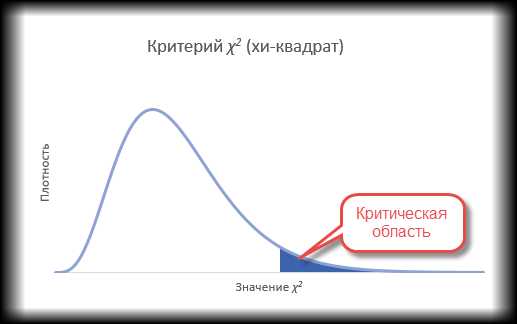
Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда критерий окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.

Вернемся к задаче с игральным кубиком. Рассчитаем по имеющимся данным значение критерия хи-квадрат.

Теперь найдем табличное значение критерия при 5-ти степенях свободы (k) и уровне значимости 0,05 (α).

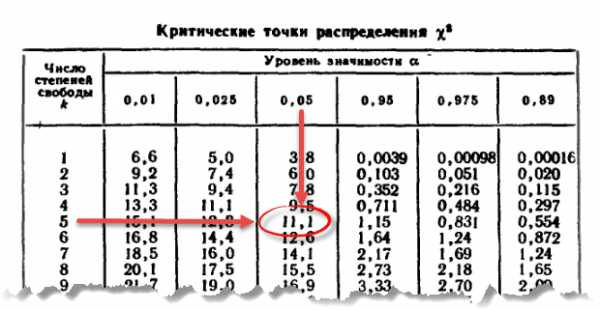
То есть χ²_{0,05; 5} = 11,1.

Сравним фактическое и табличное значение. 3,4 (χ²) < 11,1 (χ²_{0,05; 5}). Расчетный критерий оказался меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.

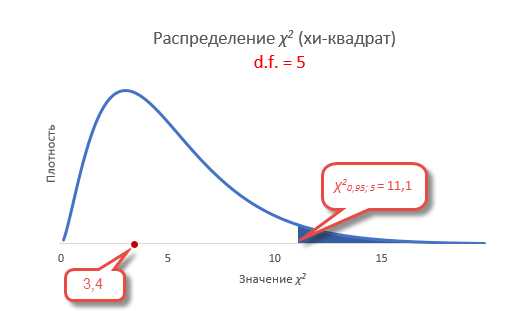
Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.

Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ПЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.

Ниже их краткое описание.

ХИ2.ОБР – критическое значение критерия при заданной вероятности слева (как в статистических таблицах)

ХИ2.ОБР.ПХ – критическое значение критерия при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.

ХИ2.РАСП – p-value слева (можно рассчитать плотность).

ХИ2.РАСП.ПХ – p-value справа.

ХИ2.ТЕСТ – по двум заданным диапазонам частот сразу проводит тест хи-квадрат. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.

Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:

=ХИ2.ОБР(0,95;5)

Или так

=ХИ2.ОБР.ПХ(0,05;5)

Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).

Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ² = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)

=ХИ2.РАСП.ПХ(3,4;5) = 0,63857

Значит, при 5-ти степенях свободы вероятность получить значение критерия χ² = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.

А теперь проверим гипотезу о согласии частот с помощью функции ХИ2.ТЕСТ.

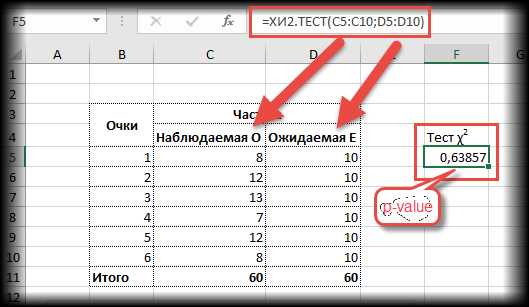Проверка гипотезы с помощью функции эксель ХИ2.ТЕСТ

Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.

Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).

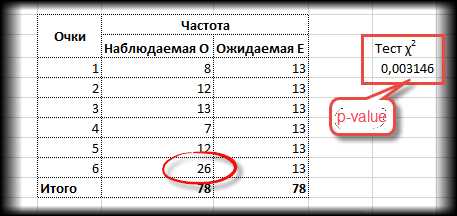
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.

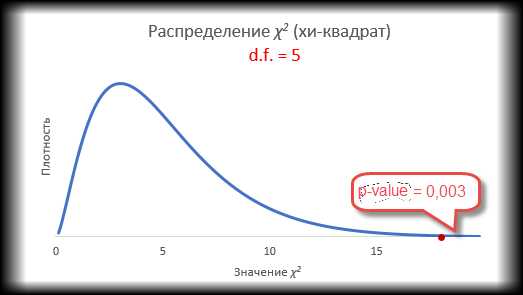
Сам критерий хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).

Надеюсь, мне удалось объяснить, что такое критерий согласия χ² (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.

Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой градации не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая часта превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.

Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.

Скачать файл с примером.

Поделиться в социальных сетях:

statanaliz.info

Таблица критических точек распределения Пирсона хи-квадрат

Таблица критических точек распределения Пирсона «хи-квадрат»)

k /α	0,01	0,025	0,05	0,95	0,975	0,99
1	6,63490	5,02389	3,84146	0,00393	0,00098	0,00016
2	9,21034	7,37776	5,99146	0,10259	0,05064	0,02010
3	11,34487	9,34840	7,81473	0,35185	0,21580	0,11483
4	13,2767	11,14329	9,48773	0,71072	0,48442	0,29711
5	15,08627	12,8325	11,0705	1,14548	0,83121	0,55430
6	16,81189	14,44938	12,59159	1,63538	1,23734	0,87209
7	18,47531	16,01276	14,06714	2,16735	1,68987	1,23904
8	20,09024	17,53455	15,50731	2,73264	2,17973	1,64650
9	21,66599	19,02277	16,91898	3,32511	2,70039	2,08790
10	23,20925	20,48318	18,30704	3,94030	3,24697	2,55821
11	24,72497	21,92005	19,67514	4,57481	3,81575	3,05348
12	26,21697	23,33666	21,02607	5,22603	4,40379	3,57057
13	27,68825	24,7356	22,36203	5,89186	5,00875	4,10692
14	29,14124	26,11895	23,68479	6,57063	5,62873	4,66043
15	30,57791	27,48839	24,99579	7,26094	6,26214	5,22935
16	31,99993	28,84535	26,29623	7,96165	6,90766	5,81221
17	33,40866	30,19101	27,58711	8,67176	7,56419	6,40776
18	34,80531	31,52638	28,86930	9,39046	8,23075	7,01491
19	36,19087	32,85233	30,14353	10,11701	8,90652	7,63273
20	37,56623	34,16961	31,41043	10,85081	9,59078	8,26040
21	38,93217	35,47888	32,67057	11,59131	10,2829	8,89720
22	40,28936	36,78071	33,92444	12,33801	10,98232	9,54249
23	41,63840	38,07563	35,17246	13,09051	11,68855	10,19572
24	42,97982	39,36408	36,41503	13,84843	12,40115	10,85636
25	44,31410	40,64647	37,65248	14,61141	13,11972	11,52398
26	45,64168	41,92317	38,88514	15,37916	13,84391	12,19815
27	46,96294	43,19451	40,11327	16,15140	14,57338	12,87850
28	48,27824	44,46079	41,33714	16,92788	15,30786	13,56471
29	49,58788	45,72229	42,55697	17,70837	16,04707	14,25645
30	50,89218	46,97924	43,77297	18,49266	16,79077	14,95346
31	52,19139	48,23189	44,98534	19,28057	17,53874	15,65546
32	53,48577	49,48044	46,19426	20,07191	18,29076	16,36222
33	54,77554	50,72508	47,39988	20,86653	19,04666	17,07351
34	56,06091	51,96600	48,60237	21,66428	19,80625	17,78915
35	57,34207	53,20335	49,80185	22,46502	20,56938	18,50893
36	58,61921	54,43729	50,99846	23,26861	21,33588	19,23268
37	59,89250	55,66797	52,19232	24,07494	22,10563	19,96023
38	61,16209	56,89552	53,38354	24,8839	22,87848	20,69144
39	62,42812	58,12006	54,57223	25,69539	23,65432	21,42616
40	63,69074	59,34171	55,75848	26,5093	24,43304	22,16426
41	64,95007	60,56057	56,94239	27,32555	25,21452	22,90561
42	66,20624	61,77676	58,12404	28,14405	25,99866	23,65009
43	67,45935	62,99036	59,30351	28,96472	26,78537	24,39760
44	68,70951	64,20146	60,48089	29,78748	27,57457	25,14803
45	69,95683	65,41016	61,65623	30,61226	28,36615	25,90127
46	71,20140	66,61653	62,82962	31,43900	29,16005	26,65724
47	72,44331	67,82065	64,00111	32,26762	29,95620	27,41585
48	73,68264	69,02259	65,17077	33,09808	30,75451	28,17701
49	74,91947	70,22241	66,33865	33,93031	31,55492	28,94065
50	76,15389	71,42020	67,50481	34,76425	32,35736	29,70668

Обычно такая точность (5 знаков после запятой) не требуется. Достаточно 1-2 знаков после запятой.

 

www.matem96.ru

Распределение «хи-квадрат» и его применение

Распределение вероятных значений случайной величины χ2 непрерывно и ассиметрично. Оно зависит от числа степеней свободы (n) и приближается к нормальному распределению по мере увеличения числа наблюдений. Поэтому применение критерия χ2 к оценке дискретных распределений сопряжено с некоторыми погрешностями, которые сказываются на его величине, особенно на малочисленных выборках. Для получения более точных оценок выборка, распределяемая в вариационный ряд, должна иметь не менее 50 вариантов. Правильное применение критерия χ2 требует также, чтобы частоты вариантов в крайних классах не были бы меньше 5; если их меньше 5, то они объединяются с частотами соседних классов, чтобы в сумме составляли величину большую или равную 5. Соответственно объединению частот уменьшается и число классов (N). Число степеней свободы устанавливается по вторичному числу классов с учетом числа ограничений свободы вариации.

Так как точность определения критерия χ2 в значительной степени зависит от точности расчета теоретических частот (Т), для получения разности между эмпирическими и вычисленными частотами следует использовать неокругленные теоретические частоты.

В качестве примера возьмем исследование, опубликованное на сайте, который посвящен применению статистических методов в гуманитарных науках.

Критерий «Хи-квадрат» позволяет сравнивать распределения частот вне зависимости от того, распределены они нормально или нет.

Под частотой понимается количество появлений какого-либо события. Обычно, с частотой появления события имеют дело, когда переменные измерены в шкале наименований и другой их характеристики, кроме частоты подобрать невозможно или проблематично. Другими словами, когда переменная имеет качественные характеристики. Так же многие исследователи склонны переводить баллы теста в уровни (высокий, средний, низкий) и строить таблицы распределений баллов, чтобы узнать количество человек по этим уровням. Чтобы доказать, что в одном из уровней (в одной из категорий) количество человек действительно больше (меньше) так же используется коэффициент Хи-квадрат.

Разберем самый простой пример.

Среди младших подростков был проведён тест для выявления самооценки. Баллы теста были переведены в три уровня: высокий, средний, низкий. Частоты распределились следующим образом:

Высокий (В) 27 чел.

Средний (С) 12 чел.

Низкий (Н) 11 чел.

Очевидно, что детей с высокой самооценкой большинство, однако это нужно доказать статистически. Для этого используем критерий Хи-квадрат.

Наша задача проверить, отличаются ли полученные эмпирические данные от теоретически равновероятных. Для этого необходимо найти теоретические частоты. В нашем случае, теоретические частоты – это равновероятные частоты, которые находятся путём сложения всех частот и деления на количество категорий.

В нашем случае:

(В + С + Н)/3 = (27+12+11)/3 = 16,6

Формула для расчета критерия хи-квадрат:

χ2 = ∑(Э — Т)² / Т

Для обработки полученных данных используем критерий хи-квадрат.

Для этого построим таблицу распределения эмпирических частот, т.е. тех частот, которые мы наблюдаем:

Теоретически, мы ожидаем, что частоты распределятся равновероятно, т.е. частота распределится пропорционально между мальчиками и девочками. Построим таблицу теоретических частот. Для этого умножим сумму по строке на сумму по столбцу и разделим получившееся число на общую сумму (s).

Итоговая таблица для вычислений будет выглядеть так:

χ2 = ∑(Э — Т)² / Т

n = (R — 1), где R – количество строк в таблице.

В нашем случае хи-квадрат = 4,21; n = 2.

По таблице критических значений критерия находим: при n = 2 и уровне ошибки 0,05 критическое значение χ2 = 5,99.

Полученное значение меньше критического, а значит принимается нулевая гипотеза.

Вывод: учителя не придают значение полу ребенка при написании ему характеристики.

Таблица 1

Студенты почти всех специальностей изучают в конце курса высшей математики раздел «теория вероятностей и математическая статистика», реально они знакомятся лишь с некоторыми основными понятиями и результатами, которых явно не достаточно для практической работы. С некоторыми математическими методами исследования студенты встречаются в специальных курсах (например, таких, как «Прогнозирование и технико-экономическое планирование», «Технико-экономический анализ», «Контроль качества продукции», «Маркетинг», «Контроллинг», «Математические методы прогнозирования», «Статистика» и др. – в случае студентов экономических специальностей), однако изложение в большинстве случаев носит весьма сокращенный и рецептурный характер. В результате знаний у специалистов по прикладной статистике недостаточно.

Поэтому большое значение имеет курс «Прикладная статистика» в технических вузах, а в экономических вузах – курса «Эконометрика», поскольку эконометрика – это, как известно, статистический анализ конкретных экономических данных.

1. Орлов А.И. Прикладная статистика. М.: Издательство «Экзамен», 2004.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1999. – 479с.

3. Айвозян С.А. Теория вероятностей и прикладная статистика, т.1. М.: Юнити, 2001. – 656с.

4. Хамитов Г.П., Ведерникова Т.И. Вероятности и статистика. Иркутск: БГУЭП, 2006 – 272с.

5. Ежова Л.Н. Эконометрика. Иркутск: БГУЭП, 2002. – 314с.

6. Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. М. : Наука, 1975. – 111с.

7. Мостеллер Ф. Вероятность. М. : Мир, 1969. – 428с.

8. Яглом А.М. Вероятность и информация. М. : Наука, 1973. – 511с.

9. Чистяков В.П. Курс теории вероятностей. М.: Наука, 1982. – 256с.

10. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ, 2000. – 543с.

11. Математическая энциклопедия, т.1. М.: Советская энциклопедия, 1976. – 655с.

12. http://psystat.at.ua/ — Статистика в психологии и педагогике. Статья Критерий Хи-квадрат. Автор: Попов О.А.

mirznanii.com