методы, примеры нахождения и определения
В данной статье пойдет речь о таком понятии, как ранг матрицы и необходимых дополнительных понятиях. Мы приведем примеры и доказательства нахождения ранга матрицы, а также расскажем, что такое минор матрицы, и почему он так важен.
Yandex.RTB R-A-339285-1Минор матрицы
Чтобы понять, что такое ранг матрицы, необходимо разобраться с таким понятием, как минор матрицы.
Определение 1Минор k-ого порядка матрицы — определитель квадратной матрицы порядка k×k, которая составлена из элементов матрицы А, находящихся в заранее выбранных k-строках и k-столбцах, при этом сохраняется положение элементов матрицы А.
Проще говоря, если в матрице А вычеркнуть (p-k) строк и (n-k) столбцов, а их тех элементов, которые остались, составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы и есть минор порядка k матрицы А.
Из примера следует, что миноры первого порядка матрицы А и есть сами элементы матрицы.
Можно привести несколько примеров миноров 2-ого порядка. Выберем две строки и два столбца. Например, 1-ая и 2 –ая строка, 3-ий и 4-ый столбец.
При таком выборе элементов минором второго порядка будет -1302=(-1)×2-3×0=-2
Другим минором 2-го порядка матрицы А является 0011=0
Предоставим иллюстрации построения миноров второго порядка матрицы А:
Минор 3-го порядка получается, если вычеркнуть третий столбец матрицы А:
003112-1-40=0×1×0+0×2×(-1)+3×1×(-4)-3×1×(-1)-0×1×0-0×2×(-4)=-9
Иллюстрация, как получается минор 3-го порядка матрицы А:
Для данной матрицы миноров выше 3-го порядка не существует, потому что
k≤min(p, n)=min (3, 4)=3
Сколько существует миноров k-ого порядка для матрицы А порядка p×n?
Число миноров вычисляют по следующей формуле:
Cpk×Cnk, где Сpk=p!k!(p-k)! и Cnk=n!k!(n-k)! — число сочетаний из p по k, из n по k соответственно.
После того, как мы определились, что такое миноры матрицы А, можно переходить к определению ранга матрицы А.
Ранг матрицы: методы нахождения
Определение 2Ранг матрицы — наивысший порядок матрицы, отличный от нуля.
Обозначение 1Rank (A), Rg (A), Rang (A).
Из определения ранга матрицы и минора матрицы становиться понятно, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы отличен от нуля.
Нахождение ранга матрицы по определению
Определение 3Метод перебора миноров — метод, основанный на определении ранга матрицы.
Алгоритм действий способом перебора миноров:
Необходимо найти ранг матрицы А порядка p×n. При наличии
zaochnik.com
Вычисление ранга матрицы методом окаймляющих миноров.
В данной теме нам понадобятся такие понятия как минор матрицы и окаймляющий минор. В теме «Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений» есть подробное пояснение этих понятий.
В предыдущей теме было рассмотрено понятие ранга матрицы, а также на примерах показано, как находить ранг по определению. Конечно, находить ранг матрицы таким образом несколько затруднительно, – в первую очередь из-за объёма вычислений. Однако количество вычисляемых миноров можно существенно уменьшить, если использовать так называемый метод окаймляющих миноров.
Суть метода окаймляющих миноров выражается парой пунктов простого алгоритма:
- Пусть некий минор $M$ k-го порядка не равен нулю.
- Если окаймляющие миноры для минора $M$ (это уже будут миноры (k+1)-го порядка), составить невозможно (т.е. матрица содержит k строк или k столбцов), то ранг равен k. Если окаймляющие миноры существуют и все равны нулю, то ранг равен k. Если среди окаймляющих миноров есть хотя бы один, отличный от нуля, то повторяем для него пункт №1, приняв k+1 вместо k.
Наглядно всё вышеизложенное можно выразить следующей схемой:

Поясню эту схему более подробно. Станем рассуждать с самого начала, т.е. с миноров первого порядка. Если все миноры первого порядка некоей матрицы $A$ (миноры первого порядка – это элементы матрицы) равны нулю, то $\rang A=0$. Если в матрице есть минор первого порядка $M_1\neq 0$, то $\rang A≥ 1$.
Проверяем окаймляющие миноры для минора $M_1$. Это уже будут миноры второго порядка. Если все миноры, окаймляющие $M_1$, равны нулю, то $\rang A=1$. Если среди миноров второго порядка, окаймляющих $M_1$, есть хоть один минор $M_2 \neq 0$, то $\rang A≥ 2$.
Проверяем окаймляющие миноры для минора $M_2$. Это будут миноры третьего порядка. Если все миноры третьего порядка, окаймляющие $M_2$, равны нулю, то $\rang A=2$. Если среди миноров третьего порядка, окаймляющих $M_2$, есть хоть один минор $M_3\neq 0$, то $\rang A≥ 3$.
Проверяем окаймляющие миноры для минора $M_3$. Если все миноры четвёртого порядка, окаймляющие $M_3$, равны нулю, то $\rang A=3$. Если среди миноров четвёртого порядка, окаймляющих $M_3$, есть хоть один минор $M_4\neq 0$, то $\rang A≥ 4$.
Проверяем все окаймляющие миноры для минора $M_4$, и так далее. В конце концов возможны два случая: либо на каком-то шаге окажется, что все окаймляющие миноры равны нулю, либо окаймляющий минор составить просто не получится, так как в матрице «закончатся» строки или столбцы. Порядок последнего составленного ненулевого минора и будет равен рангу матрицы.
Пример №1
Найти ранг матрицы $A=\left(\begin{array}{cccc} -1 & 2 & 1 & 3 \\ -3 & 0 & 5 & 4 \\ -5 & 4 & 7 & 10 \end{array} \right)$ методом окаймляющих миноров.
Решение
Можно, конечно, начать с миноров первого порядка, которые представляют собой просто элементы данной матрицы. Но лучше сразу выбрать какой-либо не равный нулю минор второго порядка, тем паче что такой выбор большой сложности не представляет. Например, на пересечении строк №1, №2 и столбцов №1, №2 расположены элементы минора $\left|\begin{array}{cc} -1 & 2 \\ -3 & 0 \end{array} \right|$, который несложно вычислить, используя формулу №1 из темы про вычисление определителей второго и третьего порядков:
$$ \left|\begin{array}{cc} -1 & 2 \\ -3 & 0 \end{array} \right|=-1\cdot 0-2\cdot (-3)=6. $$Итак, существует минор второго порядка, не равный нулю, из чего следует, что $\rang A≥ 2$. Рассмотрим миноры третьего порядка, окаймляющие данный минор второго порядка. Как составить окаймляющий минор? Для этого к набору строк и столбцов, на пересечении которых лежат элементы минора второго порядка, нужно добавить ещё одну строку и ещё один столбец. Вспоминаем, что элементы записанного нами минора второго порядка расположены на пересечении строк №1, №2 и столбцов №1, №2. Добавим к строкам ещё строку №3, а к столбцам – столбец №3. Мы получим минор третьего порядка, элементы которого (они показаны на рисунке синим цветом) лежат на пересечении строк №1, №2, №3 и столбцов №1, №2, №3.
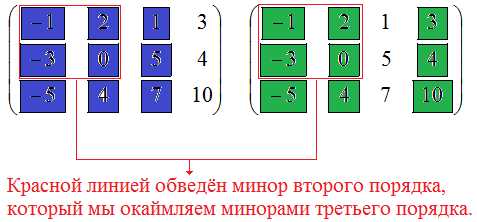
Найдём значение этого минора, используя формулу №2 из темы про вычисление определителей второго и третьего порядков:
$$ \left|\begin{array}{ccc} -1 & 2 & 1 \\ -3 & 0 & 5 \\ -5 & 4 & 7 \end{array} \right|=0. $$Окаймляющий минор равен нулю. О чём это говорит? Это говорит о том, что нам нужно продолжить нахождение окаймляющих миноров. Либо они все равны нулю (и тогда ранг будет равен 2), либо среди них найдётся хотя бы один, отличный от нуля.
Элементы второго окаймляющего минора лежат на пересечении строк №1, №2, №3 и столбцов №1, №2, №4. На рисунке выше элементы этого минора показаны зелёным цветом. Вычислим данный минор, используя всё ту же формулу №2 из темы про вычисление определителей второго и третьего порядков:
$$ \left|\begin{array}{ccc} -1 & 2 & 3 \\ -3 & 0 & 4 \\ -5 & 4 & 10 \end{array} \right|=0. $$И этот окаймляющий минор равен нулю. Иных окаймляющих миноров нет. Следовательно, все окаймляющие миноры равны нулю. Порядок последнего составленного ненулевого минора равен 2. Вывод: ранг равен 2, т.е. $\rang A=2$.
Ответ: $\rang A=2$.
Пример №2
Найти ранг матрицы $A=\left(\begin{array}{ccccc} 1 & 2 & 0 & 4 & 5\\ 3 & 6 & -2 & -1 & -3\\ -2 & -4 & 2 & 5 & 7\\ -1 & -2 & 2 & 9 & 11 \end{array} \right)$ методом окаймляющих миноров.
Решение
Вновь, как и в предыдущем примере, начнём решение с выбора минора второго порядка, не равного нулю. Например, на пересечении строк №1, №2 и столбцов №1, №2 расположены элементы минора $\left|\begin{array}{cc} 1 & 2 \\ 3 & 6 \end{array} \right|$, который несложно вычислить, используя формулу №1 из темы про вычисление определителей второго и третьего порядков:
Данный минор второго порядка равен нулю, т.е. выбор неудачен. Возьмём иной минор второго порядка. Например, тот, элементы которого расположены на пересечении строк №1, №2 и столбцов №2, №3:
$$ \left|\begin{array}{cc} 2 & 0 \\ 6 & -2 \end{array} \right|=-4. $$Итак, ненулевой минор второго порядка существует, поэтому $\rang A≥ 2$. Обозначим этот минор как $M_2$ и станем окаймлять его минорами третьего порядка. Например, добавим к строкам и столбцам, на которых расположены элементы $M_2$, ещё строку №3 и столбец №1. Т.е. найдём минор третьего порядка, элементы которого находятся на пересечении строк №1, №2, №3 и столбцов №1, №2, №3. Используем для этого формулу №2 из темы про вычисление определителей второго и третьего порядков. Подробные вычисления я приводить не стану, запишем лишь ответ:
$$ \left|\begin{array}{ccc} 1 & 2 & 0 \\ 3 & 6 & -2 \\ -2 & -4 & 2 \end{array} \right|=0. $$Этот минор равен нулю, значит нужно переходить к иному окаймляющему минору. Либо все миноры третьего порядка, окаймляющие $M_2$, равны нулю, либо среди них всё-таки найдётся хоть один, отличный от нуля.
Рассмотрим минор третьего порядка, элементы которого лежат на пересечении строк №1, №2, №3 и столбцов №2, №3, №4. Этот минор тоже окаймляет $M_2$:
$$ \left|\begin{array}{ccc} 2 & 0 & 4 \\ 6 & -2 & -1 \\ -4 & 2 & 5 \end{array} \right|=0. $$Итак, среди миноров третьего порядка, окаймляющих $M_2$, есть минор, не равный нулю, откуда следует $\rang A≥ 3$. Обозначим этот ненулевой минор как $M_3$. Элементы минора $M_3$ лежат на пересечении строк №1, №2, №3 и столбцов №2, №3, №5. Станем окаймлять минор $M_3$ минорами четвёртого порядка. Для начала возьмём минор четвёртого порядка, элементы которого лежат на пересечении строк №1, №2, №3, №4 и столбцов №1, №2, №3, №5. Этот минор окаймляет $M_3$. Его значение найти несложно, если использовать, например, разложение по строке или по столбцу:
$$ \left|\begin{array}{cccc} 1 & 2 & 0 & 5\\ 3 & 6 & -2 & -3\\ -2 & -4 & 2 & 7\\ -1 & -2 & 2 & 11 \end{array} \right|=0. $$Аналогично, рассматривая минор четвёртого порядка, элементы которого расположены на пересечении строк №1, №2, №3, №4 и столбцов №2, №3, №4, №5, получим:
$$ \left|\begin{array}{cccc} 2 & 0 & 4 & 5\\ 6 & -2 & -1 & -3\\ -4 & 2 & 5 & 7\\ -2 & 2 & 9 & 11 \end{array} \right|=0.$$Иных окаймляющих миноров для минора $M_3$ нет. Все миноры четвёртого порядка, окаймляющие $M_3$, равны нулю. Последний ненулевой минор, т.е. $M_3$, был третьего порядка. Вывод: ранг равен 3, т.е. $\rang A=3$.
Ответ: $\rang A=3$.
Пример №3
Найти ранг матрицы $A=\left(\begin{array}{ccccc} -1 & 3 & 2 & 4 & 1\\ 0 & -2 & 5 & 0 & -3\\ 1 & -5 & 3 & 7 & 6 \end{array} \right)$ методом окаймляющих миноров.
Решение
Снова начинаем решение с выбора минора второго порядка, не равного нулю. Например, на пересечении строк №1, №2 и столбцов №1, №2 расположены элементы минора $\left|\begin{array}{cc} -1 & 3 \\ 0 & -2 \end{array} \right|$, который вычисляем, используя формулу №1 из темы про вычисление определителей второго и третьего порядков:
$$ \left|\begin{array}{cc} -1 & 3 \\ 0 & -2 \end{array} \right|=2. $$Данный минор (обозначим его $M_2$) не равен нулю, посему именно его мы и станем окаймлять минорами третьего порядка. Например, добавим к строкам и столбцам, на которых расположены элементы $M_2$, ещё строку №3 и столбец №3. Т.е. найдём минор третьего порядка, элементы которого расположены на пересечении строк №1, №2, №3 и столбцов №1, №2, №3. Используем для этого формулу №2 из темы про вычисление определителей второго и третьего порядков:
$$ \left|\begin{array}{ccc} -1 & 3 & 2 \\ 0 & -2 & 5 \\ 1 & -5 & 3 \end{array} \right|=0. $$Этот минор равен нулю, значит нужно переходить к иному окаймляющему минору. Либо все миноры третьего порядка, окаймляющие $M_2$, равны нулю, либо среди них всё-таки найдётся хоть один, отличный от нуля.
Рассмотрим минор третьего порядка, элементы которого лежат на пересечении строк №1, №2, №3 и столбцов №1, №2, №4. Этот минор тоже окаймляет $M_2$:
$$ \left|\begin{array}{ccc} -1 & 3 & 4 \\ 0 & -2 & 0 \\ 1 & -5 & 7 \end{array} \right|=22. $$Итак, среди миноров третьего порядка, окаймляющих $M_2$, есть хоть один, не равный нулю. Миноры четвёртого порядка мы образовать уже не можем, так как для них потребуется 4 строки, а в матрице $A$ всего 3 строки. Посему, так как последний ненулевой минор был третьего порядка, то ранг равен 3, т.е. $\rang A=3$.
Ответ: $\rang A=3$.
math1.ru
Как найти обратную матрицу?
Поиск Лекций
Продолжаем разговор о действиях с матрицами. А именно – в ходе изучения данной лекции вы научитесь находить обратную матрицу. Научитесь. Даже, если с математикой туго.
Что такое обратная матрица? Здесь можно провести аналогию с обратными числами: рассмотрим, например, оптимистичное число 5 и обратное ему число . Произведение данных чисел равно единице: . С матрицами всё похоже! Произведение матрицы на обратную ей матрицу равно – единичной матрице, которая является матричным аналогом числовой единицы. Однако обо всём по порядку – сначала решим важный практический вопрос, а именно, научимся эту самую обратную матрицу находить.
Что необходимо знать и уметь для нахождения обратной матрицы? Вы должны уметь решать определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с ними.
Есть? Тогда поехали дальше. А хотя… ехать могут все, если что-то не знаете, я буду ставить нужную ссылку по ходу объяснений.
Существует два основных метода нахождения обратной матрицы:
с помощью алгебраических дополнений и с помощью элементарных преобразований.
Сегодня мы изучим первый, более простой способ.
Начнем с самого ужасного и непонятного. Рассмотрим квадратную матрицу . Обратную матрицу можно найти по следующей формуле:
, где – определитель матрицы , – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Обозначения: Как вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом
Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.
Пример:
Найти обратную матрицу для матрицы
Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
Если с пониманием сего действа плоховато, ознакомьтесь с материалом Как вычислить определитель?
Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось, , а значит, всё в порядке.
2) Находим матрицу миноров .
Для решения нашей задачи не обязательно знать, что такое минор, однако, желательно ознакомиться со статьей Как вычислить определитель.
Матрица миноров имеет такие же размеры, как и матрица , то есть в данном случае .
Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице
Сначала рассмотрим левый верхний элемент:
Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:
Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров:
Рассматриваем следующий элемент матрицы :
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент:
То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу:
Аналогично рассматриваем элементы второй строки и находим их миноры:
Готово.
– матрица миноров соответствующих элементов матрицы .
3) Находим матрицу алгебраических дополнений .
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:
Именно у этих чисел, которые я обвел в кружок!
– матрица алгебраических дополнений соответствующих элементов матрицы .
И всего-то лишь…
4) Находим транспонированную матрицу алгебраических дополнений .
Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
5) Ответ.
Вспоминаем нашу формулу
Всё найдено!
Таким образом, обратная матрица:
Ответ лучше оставить в таком виде. НЕ НУЖНО делить каждый элемент матрицы на 2, так как получатся дробные числа. Более подробно данный нюанс рассмотрен в той же статье Действия с матрицами.
Как проверить решение?
Необходимо выполнить матричное умножение либо
Проверка:
Получена уже упомянутая единичная матрица – это матрица с единицами на главной диагонали и нулями в остальных местах.
Таким образом, обратная матрица найдена правильно.
Если провести действие , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно, более подробную информацию можно найти в статье Свойства операций над матрицами. Матричные выражения. Также заметьте, что в ходе проверки константа (дробь) выносится вперёд и обрабатывается в самом конце – после матричного умножения. Это стандартный приём.
Переходим к более распространенному на практике случаю – матрице «три на три»:
Пример:
Найти обратную матрицу для матрицы
Алгоритм точно такой же, как и для случая «два на два».
Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
1) Находим определитель матрицы.
Здесь определитель раскрыт по первой строке.
Также не забываем, что , а значит, всё нормально – обратная матрица существует.
2) Находим матрицу миноров .
Матрица миноров имеет размерность «три на три» , и нам нужно найти девять чисел.
Я подробно рассмотрю парочку миноров:
Рассмотрим следующий элемент матрицы:
МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:
Оставшиеся четыре числа записываем в определитель «два на два»
Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить:
Всё, минор найден, записываем его в нашу матрицу миноров:
Как вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже.
Ну и для закрепления – нахождение еще одного минора в картинках:
Остальные миноры попробуйте вычислить самостоятельно.
Окончательный результат:
– матрица миноров соответствующих элементов матрицы .
То, что все миноры получились отрицательными – чистая случайность.
3) Находим матрицу алгебраических дополнений .
В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов:
В данном случае:
– матрица алгебраических дополнений соответствующих элементов матрицы .
4) Находим транспонированную матрицу алгебраических дополнений .
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
5) Ответ:
Проверка: 
Таким образом, обратная матрица найдена правильно.
Как оформить решение на чистовик? Примерный образец чистового оформления задания можно найти на страницеПравило Крамера. Метод обратной матрицы в параграфе, где идет речь о матричном методе решения системы линейных уравнений. По существу, основная часть упомянутой задачи – и есть поиск обратной матрицы.
Нахождение обратной матрицы для матрицы «четыре на четыре» не рассматриваем, так как такое задание может дать только преподаватель-садист (чтобы студент вычислил один определитель «четыре на четыре» и 16 определителей «три на три»). В моей практике встретился только один такой случай, и заказчик контрольной работы заплатил за мои мучения довольно дорого =).
В ряде учебников, методичек можно встретить несколько другой подход к нахождению обратной матрицы, однако я рекомендую пользоваться именно вышеизложенным алгоритмом решения. Почему? Потому что вероятность запутаться в вычислениях и знаках – гораздо меньше.
Иногда обратную матрицу требуется найти методом Гаусса-Жордана, но второй способ доступен для студентов с приличной техникой элементарных преобразований.
Желаю успехов!
Автор: Емелин Александр
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Минор матрицы — это… Что такое Минор матрицы?
- Минор матрицы
Минор матрицы A ― определитель матрицы, элементы которой стоят в данной прямоугольной матрице порядка k (который называется также порядком этого минора) на пересечении строк с номерами и столбцов с номерами .
Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.
Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.
Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.
Пример
Например, есть матрица:
Предположим, надо найти дополнительный минор M23. Этот минор — определитель матрицы, получающейся путем вычеркивания строки 2 и столбца 3:
Получаем M23 = 13
См. также
Дополнительный минор
Wikimedia Foundation. 2010.
- Минор Ш. З.
- Минор Шломо Залман
Смотреть что такое «Минор матрицы» в других словарях:
Минор (математич.) — Минор (от лат. minor меньший) k го порядка матрицы, определитель, составленный из элементов, стоящих на пересечении произвольно выделенных k строк и k столбцов матрицы. Так, определитель есть М. 2 го порядка матрицы составленный из ее элементов,… … Большая советская энциклопедия
МИНОР — определитель, составленный из элементов, состоящих на пересечении произвольно выделенных k строк и k столбцов данной матрицы или определителя … Большой Энциклопедический словарь
МИНОР (в математике) — МИНОР, определитель, составленный из элементов, состоящих на пересечении произвольно выделенных k строк и k столбцов данной матрицы или определителя … Энциклопедический словарь
МИНОР — 1. М. элемента aij определителя А есть определитель, полученный из А после вычеркивания элементов i ой строки и j гo столбца. М. m го порядка матрицы А ||aij|| есть определитель m го порядка, составленный из m2 элементов, стоящих на пересечении… … Геологическая энциклопедия
Минор — [minor] см. Определитель матрицы … Экономико-математический словарь
Минор (линейная алгебра) — У этого термина существуют и другие значения, см. Минор (значения). Минор матрицы ― определитель такой квадратной матрицы порядка (который называется также порядком этого минора), элементы которой стоят в матрице на пересечении строк с номерами … Википедия
Минор — I Минор Лазарь Соломонович [17(29).12.1855 1942], советский невропатолог, заслуженный деятель науки РСФСР (1927). В 1879 окончил медицинский факультет Московского университета, работал у А. И. Бабухина, А. Я. Кожевникова. В 1910 17… … Большая советская энциклопедия
минор — а; м. [от итал. minore меньший]. 1. Музыкальный лад, звуки которого образуют аккорд, построенный на малой трапеции (характеризуется звуковой окраской, связанной с настроениями грусти, скорби; противоп.: мажор). Играть в миноре. 2. Разг. О… … Энциклопедический словарь
МИНОР — порядка к определитель матрицы, элементы к рой стоят в данной прямоугольной матрице на пересечении кразных столбцов и кразных строк. Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то М. наз. главным, а есля отмечены первые … Математическая энциклопедия
МИНОР — определитель, составленный из элементов, стоящих на пересечении произвольно выделенных k строк и k столбцов данной матрицы или определителя … Естествознание. Энциклопедический словарь
dic.academic.ru
Базисный минор матрицы. Ранг матрицы.
Как было сказано выше, минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении каких — либо выбранных s строк и s столбцов.
Определение. В матрице порядка mn минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n. Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными. В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.
Определение. Порядок базисного минора матрицы называется рангом матрицы и обозначается Rg А. Очень важным свойством элементарных преобразований матриц является то, что они не изменяют ранг матрицы.
Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными. Надо отметить, что равные матрицы и эвивалентные матрицы — понятия совершенно различные.
Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк. Т.к. элементарные преобразования не изменяют ранг матрицы, то можно существенно упростить процесс нахождения ранга матрицы. Пример. Определить ранг матрицы. , RgA = 2. Пример: Определить ранг матрицы. , Rg = 2. Пример. Определить ранг матрицы. , Rg = 2. Если с помощью элементарных преобразований не удается найти матрицу, эквивалентную исходной, но меньшего размера, то нахождение ранга матрицы следует начинать с вычисления миноров наивысшего возможного порядка. В вышеприведенном примере – это миноры порядка 3. Если хотя бы один из них не равен нулю, то ранг матрицы равен порядку этого минора.
Теорема о базисном миноре. Теорема. В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор. Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице. Если А- квадратная матрица и detA = 0, то по крайней мере один из столбцов – линейная комбинация остальных столбцов. То же самое справедливо и для строк. Данное утверждение следует из свойства линейной зависимости при определителе равном нулю.
Матричный метод решения систем линейных уравнений.
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных. Метод удобен для решения систем невысокого порядка. Метод основан на применении свойств умножения матриц. Пусть дана система уравнений: Составим матрицы: A = ; B = ; X = . Систему уравнений можно записать: AX = B. Сделаем следующее преобразование: A-1AX = A-1B, т.к. А-1А = Е, то ЕХ = А-1В Х = А-1В Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.
Пример. Решить систему уравнений: Х = , B = , A = Найдем обратную матрицу А-1. = det A = 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30. M11 = = -5; M21 = = 1; M31 = = -1; M12 = M22 = M32 = M13 = M23 = M33 = A-1 = ; Cделаем проверку: AA-1 = =E. Находим матрицу Х. Х = = А-1В = = .
Итого решения системы: x =1; y = 2; z = 3. Несмотря на ограничения возможности применения данного метода и сложность вычислений при больших значениях коэффициентов, а также систем высокого порядка, метод может быть легко реализован на ЭВМ.
Метод Крамера. (Габриель Крамер (1704-1752) швейцарский математик) Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных. Для этого необходимо, чтобы определитель матрицы системы не равнялся 0. det A 0; Действительно, если какое- либо уравнение системы есть линейная комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
Теорема. (Правило Крамера): Теорема. Система из n уравнений с n неизвестными в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам: xi = i/, где = det A, а i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi. i =
Пример. A = ; 1= ; 2= ; 3= ; x1 = 1/detA; x2 = 2/detA; x3 = 3/detA;
Пример. Найти решение системы уравнений: = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30; 1 = = (28 – 48) – (42 – 32) = -20 – 10 = -30. x1 = 1/ = 1; 2 = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60. x2 = 2/ = 2; 3 = = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90. x3 = 3/ = 3. Как видно, результат совпадает с результатом, полученным выше матричным методом. Если система однородна, т.е. bi = 0, то при 0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0. При = 0 система имеет бесконечное множество решений. Для самостоятельного решения: ; Ответ: x = 0; y = 0; z = -2.
Метод Гаусса. (Карл Фридрих Гаусс (1777-1855) немецкий математик) В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных. Рассмотрим систему линейных уравнений: Разделим обе части 1–го уравнения на a11 0, затем: 1) умножим на а21 и вычтем из второго уравнения 2) умножим на а31 и вычтем из третьего уравнения и т.д. Получим: , где d1j = a1j/a11, j = 2, 3, …, n+1. dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1. Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Пример. Решить систему линейных уравнений методом Гаусса. Составим расширенную матрицу системы. А* = Таким образом, исходная система может быть представлена в виде: , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
Пример. Решить систему методом Гаусса. Составим расширенную матрицу системы. Таким образом, исходная система может быть представлена в виде: , откуда получаем: z = 3; y = 2; x = 1. Полученный ответ совпадает с ответом, полученным для данной системы методом Крамера и матричным методом. Для самостоятельного решения: Ответ: {1, 2, 3, 4}.
Предел функции при стремлении аргумента к бесконечности.
Определение. Число А называется пределом функции f(x) при х, если для любого числа >0 существует такое число М>0, что для всех х, х>M выполняется неравенство
При этом предполагается, что функция f(x) определена в окрестности бесконечности.
Записывают:
Графически можно представить:
|
Аналогично можно определить пределы для любого х>M и
для любого х<M.
studfiles.net
Вычисление определителей. Миноры, алгебраические дополнения.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Квадратная таблица $$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$$ составленная из четырех действительных или комплексных чисел называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице $A$ (или просто определителем матрицы $A$) называется число $$\det A=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}.$$
Аналогично если $$A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$$
— квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число
$$\det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=$$ $$a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}.$$
Эту формулу называют «правило треугольника»: одно из трех слагаемых, входящих в правую часть со знаком «+», есть произведение элементов главной диагонали матрицы, каждое из двух других — произведение элементов лежащих на параллели к этой диагонали и элемента из противоположного угла матрицы, а слагаемые, входящие в со знаком минус, строятся таким же образом, но относительно второй (побочной) диагонали.
Примеры.
Вычислить определители второго порядка:
3.1. $\begin{vmatrix}-1&4\\-5&2\end{vmatrix}$
Решение.
$\begin{vmatrix}-1&4\\-5&2\end{vmatrix}=-1\cdot 2-(-5)\cdot 4=-2+20=18.$
Ответ: 18.
3.2. $\begin{vmatrix}a+b&a-b\\a-b&a+b\end{vmatrix}$
Решение.
$\begin{vmatrix}a+b&a-b\\a-b&a+b\end{vmatrix}=(a+b)^2-(a-b)^2=a^2+2ab+b^2-a^2+2ab-b^2=4ab.$
Ответ: $4ab.$
3.8. Решить уравнение:
$\begin{vmatrix}x&x+1\\-4&x+1\end{vmatrix}=0.$
Решение.
$\begin{vmatrix}x&x+1\\-4&x+1\end{vmatrix}=x(x+1)-(-4)(x+1)=x^2+x+4x-4=x^2+5x+4.$
Осталось решить квадратное уравнение $x^2+5x+4=0:$
$D=25-16=9$
$x_1=\frac{-5-3}{2}=-4;\qquad x_2=\frac{-5+3}{2}=-1.$
Ответ: $x_1=-4;\,\,\, x_2=-1.$
{jumi[*4]}
3.13. $\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}.$
Решение.
$\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}=3\cdot 7\cdot8+(-5)\cdot 8\cdot(-1)+4\cdot(-2)\cdot2-(-5)\cdot7\cdot2-$
$-4\cdot8\cdot8-3\cdot(-2)\cdot(-1)=168+40-16+70-256-6=0.$
Ответ: $0.$
3.16. $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}.$
Решение.
$\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}=\sin\alpha\cos\beta+\sin\beta\cos\gamma+\cos\alpha\sin\gamma-$
$-\cos\beta\sin\gamma-\sin\alpha\cos\gamma-\cos\alpha\sin\beta=$
$=\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha).$
Ответ: $\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha).$
Свойства определителя:
1) Если матрицу транспонировать, то определитель не изменится: $\det A^T=\det A.$
2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.
3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.
4) Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.
5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.
6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).
Примеры:
3.24. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}.$
Доказательство.
$\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$\begin{vmatrix}a_1&a_1-b_1x&c_1\\a_2&a_2-b_2x&c_2\\a_3&a_3-b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1-b_1x&c_1\\b_2x&a_2-b_2x&c_2\\b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$=\begin{vmatrix}a_1&a_1&c_1\\a_2&a_2&c_2\\a_3&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}b_1x&b_1x&c_1\\b_2x&b_2x&c_2\\b_3x&b_3x&c_3\end{vmatrix}=$
$-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}=$ $-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$
$-2\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}.$
Что и требовалось доказать.
3.31. Проверить, что определитель $\begin{vmatrix}1&1&1\\x&y&z\\x^2&y^2&z^2\end{vmatrix}$ делится на $x-y, y-z$ и $z-x.$
Проверка.
1) Пользуясь 6-м свойством определителей от первого столбца отнимаем второй, а затем используем 2-е свойство и выносим общий множетель за определитель.
$\begin{vmatrix}1&1&1\\x&y&z\\x^2&y^2&z^2\end{vmatrix}=$ $\begin{vmatrix}0&1&1\\x-y&y&z\\x^2-y^2&y^2&z^2\end{vmatrix}=$ $\begin{vmatrix}0&1&1\\x-y&y&z\\(x-y)(x+y)&y^2&z^2\end{vmatrix}=$
$(x-y)\begin{vmatrix}0&1&1\\1&y&z\\x+y&y^2&z^2\end{vmatrix}.$
Таким образом, мы доказали, что определитель делится на $x-y.$ Совершенно аналогично доказываются и два других случая:
2) $\begin{vmatrix}1&1&1\\x&y&z\\x^2&y^2&z^2\end{vmatrix}=$ $\begin{vmatrix}1&0&1\\x&y-z&z\\x^2&y^2-z^2&z^2\end{vmatrix}=$ $\begin{vmatrix}1&0&1\\x&y-z&z\\x^2&(y-z)(y+z)&z^2\end{vmatrix}=$
$(y-z)\begin{vmatrix}1&0&1\\x&1&z\\x^2&y+z&z^2\end{vmatrix}.$
3) $\begin{vmatrix}1&1&1\\x&y&z\\x^2&y^2&z^2\end{vmatrix}=$ $\begin{vmatrix}1&1&0\\x&y&z-x\\x^2&y^2&z^2-x^2\end{vmatrix}=$ $\begin{vmatrix}1&1&0\\x&y&z-x\\x^2&y^2)&(z-x)(z+x)\end{vmatrix}=$
$(z-x)\begin{vmatrix}1&1&0\\x&y&1\\x^2&y^2&z+x\end{vmatrix}.$
Минором $M_{ij}$ элемента $a_{ij}$ матрицы $A$ $n-$ го порядка называется определитель $n-1-$ го порядка, полученного из исходного определителя вычеркиванием $i-$й строки и $j-$го столбца:
$M_{ij}=$\begin{vmatrix}a_{11}&\cdots&a_{1,j-1}&a_{1,j+1}&\cdots&a_{1n}\\\cdots&\cdots&\cdots&\cdots&\cdots&\cdots\\a_{i-1,1}&\cdots&a_{i-1,j-1}&a_{i-1,j+1}&\cdots&a_{i-1,n}\\a_{i+1,1}&\cdots&a_{i+1,j-1}&a_{i+1,j+1}&\cdots&a_{i+1,n}\\\cdots&\cdots&\cdots&\cdots&\cdots&\cdots\\a_{n1}&\cdots&a_{n,j-1}&a_{n,j+1}&\cdots&a_{nn}\end{vmatrix}
Алгебраическим дополнением $A_{ij}$ элемента $a_{ij}$ матрицы $A$ $n-$ го порядка называется число равное произведению минора $M_{ij}$ на $(-1)^{i+j}:$ $A_{ij}=(-1)^{i+j}M_{ij}.$
Определители $n-$го порядка вычисляются с помощью метода понижения порядка — по формуле $\det A=\sum\limits_{j=1}^na_{ij}A_{ij}$ ($i$ фиксированно) — разложение по $i-$й строке.
Из этой формулы и второго свойства определителей — $\det A^T=\det A,$ следует, что верна также формула разложения по $j$ столбцу $\det A=\sum\limits_{i=1}^na_{ij}A_{ij}$ ($j$ фиксированно).
Метод приведения к треугольному виду заключается в преобразовании определителя, когда все элементы, лежащие по одну сторону одной из ее диагоналей, становятся равными нулю. В этом случае определитель равен произведению диагональных элементов.
Примеры.
Вычислить определители, используя подходящее разложение по строке или столбцу.
3.50. $\begin{vmatrix}1&0&2\\0&2&0\\2&0&3\end{vmatrix}.$
Решение.
Вычислим этот определитель с помощью разложения по второй строке: $\begin{vmatrix}1&0&2\\0&2&0\\2&0&3\end{vmatrix}=$ $0\cdot(-1)^{2+1}\begin{vmatrix}0&2\\0&3\end{vmatrix}+$ $2\cdot(-1)^{2+2}\begin{vmatrix}1&2\\2&3\end{vmatrix}+$ $0\cdot(-1)^{2+3}\begin{vmatrix}1&0\\2&0\end{vmatrix}$ $=2(3-4)=-2.$
3.54. (a) $\begin{vmatrix}2&-3&4&1\\4&-2&3&2\\a&b&c&d\\3&-1&4&3\end{vmatrix}.$
Решение.
Вычислим этот определитель с помощью разложения по третьей строке: $\begin{vmatrix}2&-3&4&1\\4&-2&3&2\\a&b&c&d\\3&-1&4&3\end{vmatrix}=$ $a\cdot(-1)^{3+1}$ $\begin{vmatrix}-3&4&1\\-2&3&2\\-1&4&3\end{vmatrix}+$ $b\cdot(-1)^{3+2}\begin{vmatrix}2&4&1\\4&3&2\\3&4&3\end{vmatrix}+$ $+c\cdot(-1)^{3+3}\begin{vmatrix}2&-3&1\\4&-2&2\\3&-1&3\end{vmatrix}+$ $d\cdot(-1)^{3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$
$=a(-27-8-8+3+24+24)-b(18+16+24-9-16-48)+$
$+c(-12-4-18+6+4+36)-d(-16-16-27+24+6+48)=$
$=8a+15b+12c-19d.$
Ответ: $8a+15b+12c-19d.$
{jumi[*4]}
3.61. Вычислить определитель: $\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}.$
Решение.
Вычислим этот определитель с помощью приведения определителя к треугольному виду:
$\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}=$ от каждой из первых четырех строк отнимем пятую $=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\1&1&1&1&6\end{vmatrix}=$ от пятой строки отнимем первую, затем пятую строку умножим на два
$=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&1&1&1&11\end{vmatrix}=$ $\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&2&2&2&22\end{vmatrix}=$ Далее от пятой строки отнимем вторую, после чего пятую строку умножим на $\frac{3}{2}:$ $=\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&2&2&27\end{vmatrix}=$ $\frac{1}{2}\frac{2}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&3&3&40,5\end{vmatrix}=$ Теперь от пятой строки отнимем третью, после чего пятую строку умножим на $\frac{4}{3}:$ $=\frac{1}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&3&45,5\end{vmatrix}=$ $\frac{1}{3}\frac{3}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&4&\frac{182}{3}\end{vmatrix}=$ Отнимем от пятой строки четвертую и перемножив диагональные элементы получаем ответ: $=\frac{1}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&0&\frac{197}{3}\end{vmatrix}=$ $=\frac{1}{4}\cdot2\cdot3\cdot4\cdot\frac{197}{3}=394.$
Ответ: $394.$
Домашнее задание:
Вычислить определители второго порядка:
3.3. $\begin{vmatrix}\cos\alpha&-\sin\alpha\\\sin\alpha&\cos\alpha\end{vmatrix}.$
Ответ: $1.$
3.7. $\begin{vmatrix}\frac{1-t^2}{1+t^2}&\frac{2t}{1+t^2}\\-\frac{2t}{1+t^2}&\frac{1-t^2}{1+t^2}\end{vmatrix}.$
Ответ: $1.$
Решить уравнение:
3.9. $\begin{vmatrix}\cos 8x&-\sin 5x\\\sin 8x&\cos 5x\end{vmatrix}=0.$
Ответ: $x=\frac{\pi}{6}+\frac{\pi k}{3},$ $k\in Z.$
Вычислить определители 3-го порядка:
3.12. $\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix}.$
Ответ: $0.$
3.15. $\begin{vmatrix}\alpha^2+1&\alpha\beta&\alpha\gamma\\\alpha\beta&\beta^2+1&\beta\gamma\\\alpha\gamma&\beta\gamma&\gamma^2+1\end{vmatrix}.$
Ответ: $\alpha^2+\beta^2+\gamma^2+1.$
3.25. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1x+b_1&c_1\\a_2+b_2x&a_2x+b_2&c_2\\a_3+b_3x&a_3x+b_3&c_3\end{vmatrix}=$ $(1-x^2)\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}.$
3.32. Проверить, что определитель $\begin{vmatrix}x&y&x+y\\y&x+y&x\\x+y&x&y\end{vmatrix}$ делится на $x+y$ и $x^2-xy+y^2.$
Вычислить определители, используя подходящее разложение по строке или столбцу.
3.51. $\begin{vmatrix}-1&5&2\\0&7&0\\1&2&0\end{vmatrix}.$
Ответ: $-14.$
3.52. $\begin{vmatrix}2&1&0\\1&2&1\\0&1&2\end{vmatrix}.$
Ответ: $4.$
3.54. (б) $\begin{vmatrix}5&a&2&-1\\4&b&4&-3\\2&c&3&-2\\4&d&5&-4\end{vmatrix}.$
Ответ: $2a-8b+c+5d.$
3.62. Вычислить определитель: $\begin{vmatrix}5&6&0&0&0\\1&5&6&0&0\\0&1&5&6&0\\0&0&1&5&6\\0&0&0&1&5\end{vmatrix}.$
Ответ: $665.$
{jumi[*4]}
mathportal.net

