Как найти все корни уравнения принадлежащие промежутку – Как решать задание 13 | LAMPA

Как решать задание 13 | LAMPA

О чем задача?

Задачи на решение тригонометрических уравнений, более сложных, чем в задании 5. В большинстве задач требуется не только решить уравнение, но и отобрать корни, принадлежащие определенному отрезку.

а) Решите уравнение sinx(2sinx−3ctgx)=3\sin x(2\sin x-3\text{ctg} x)=3sinx(2sinx−3ctgx)=3.
б) Найдите все корни этого уравнения, принадлежащие отрезку [−3π2;π2][-\frac{3\pi }{2};\frac{\pi }{2}][−23π​;2π​].

Как решать?

Шаг 1. Найдите область определения

В первую очередь найдите .

Функция sinx\sin xsinx определена на всей числовой оси, а функция ctgx\text{ctg} xctgx определена, когда sinx≠0\sin x \neq 0sinx≠0 (поскольку ctgx=cosxsinx\text{ctg} x= \frac{\cos x}{\sin x} ctgx=sinxcosx​), то есть x≠πkx\neq \pi kx≠πk, где kkk — любое целое число. Мы нашли область определения уравнения: x≠πkx\neq \pi kx≠πk, где kkk — любое целое число.

Шаг 2. Приведите уравнение к виду простейших тригонометрических уравнений

Для того чтобы привести уравнение к виду простейших тригонометрических уравнений, применяйте следующие стандартные приемы:

• Приведение уравнения к виду квадратного уравнения путем замены переменной;
• Разложение на множители, то есть приведение уравнения к виду (asinx−b)(ccosx−d)=0(a\sin x-b)(c\cos x-d)=0(asinx−b)(ccosx−d)=0 (в таком уравнении может быть сколько угодно множителей, а вместо sinx\sin xsinx и cosx\cos xcosx могут быть и другие тригонометрические функции).

Раскроем скобки: sinx(2sinx−3ctgx)=3⇔sinx(2sinx−3cosxsinx)=3⇔ \sin x(2\sin x-3\text{ctg} x)=3 \,\,\Leftrightarrow \,\,\sin x(2\sin x-3\frac{\cos x}{\sin x})=3 \,\, \Leftrightarrow \,\,sinx(2sinx−3ctgx)=3⇔sinx(2sinx−3sinxcosx​)=3⇔⇔ 2sin2x−3cosx=3.\Leftrightarrow \,\ 2\sin^2 x-3 \cos x=3{.} ⇔ 2sin2x−3cosx=3. Выразим sin2x\sin^2 xsin2x из основного тригонометрического тождества: sin2x=1−cos2x\sin^2 x=1-\cos^2 xsin2x=1−cos2x. Тогда 2−2cos2x−3cosx=3⇔2cos2x+3cosx+1=0.2-2\cos^2 x-3\cos x=3 \,\,\Leftrightarrow \,\,2\cos^2 x+3\cos x+1=0{.}2−2cos2x−3cosx=3⇔2cos2x+3cosx+1=0.
Сделаем замену переменной. Пусть cosx=t\cos x=tcosx=t. Наше уравнение свелось к квадратному уравнению 2t2+3t+1=0.2t^2+3t+1=0{.}2t2+3t+1=0.
Воспользовавшись формулой , получаем два корня: t1=−1t_1=-1t1​=−1 и t2=−12t_2=-\frac{1}{2}t2​=−21​.

Мы свели исходное уравнение к совокупности простейших тригонометрических уравнений [cosx=−1,cosx=−12.\left[\begin{array}{l} \cos x = -1 {,}\\\cos x = -\frac{1}{2} {.}\end{array}\right.[cosx=−1,cosx=−21​.​

Шаг 3. Решите простейшие тригонометрические уравнения

О решении простейших тригонометрических уравнений читайте в отдельной статье.

Убедитесь, что найденные вами корни принадлежат области определения уравнения.

Решим совокупность простейших тригонометрических уравнений, полученную на предыдущем шаге. Заметим, что корни уравнения cosx=−1\cos x =-1cosx=−1 не принадлежат области определения исходного уравнения, потому что при cosx=−1\cos x =-1cosx=−1 имеем sinx=0\sin x=0sinx=0 (а при sinx=0\sin x =0sinx=0 функция ctgx\text{ctg} xctgx в исходном уравнении не определена).

Остается решить уравнение cosx=−12\cos x =-\frac{1}{2}cosx=−21​.

Вспомним, что cosπ3=12\cos \frac{\pi }{3} =\frac{1}{2}cos3π​=21​.

Тогда по cos(π−π3)=cos2π3=−12\cos (\pi -\frac{\pi }{3})=\cos \frac{2\pi }{3}=-\frac{1}{2}cos(π−3π​)=cos32π​=−21​, следовательно arccos(−12)=2π3\text{arccos} (-\frac{1}{2})=\frac{2\pi }{3}arccos(−21​)=32π​.

Получим решение уравнения: x=±2π3+2πk,x=\pm \frac{2\pi }{3}+2\pi k{,}x=±32π​+2πk, где kkk — целое число.

Шаг 4. Выберите корни, принадлежащие отрезку, данному в условии

Корни, принадлежащие данному в условии отрезку, можно найти либо методом перебора, либо путем решения неравенства относительно kkk.

Найдем подходящие корни методом перебора. Для этого рассмотрим две серии корней по отдельности.

Начнем с серии x=2π3+2πkx=\frac{2\pi }{3}+2\pi kx=32π​+2πk. При k=0k=0k=0 корень x=2π3x=\frac{2\pi }{3}x=32π​ не попадает в заданный отрезок, потому что 2π3>π2\frac{2\pi }{3} \gt \frac{\pi }{2}32π​>2π​. При k=−1k=-1k=−1 корень x=2π3−2π=−4π3x=\frac{2\pi }{3}- 2\pi =-\frac{4\pi }{3}x=32π​−2π=−34π​ попадает в заданный отрезок, потому что −3π2<−4π3 -\frac{3\pi }{2} \lt -\frac{4\pi }{3} −23π​<−34π​. Это единственный корень в этой серии, принадлежащий нужному отрезку.

Теперь рассмотрим серию x=−2π3+2πkx=-\frac{2\pi }{3} + 2\pi kx=−32π​+2πk. При k=0k=0k=0 корень x=−2π3x=-\frac{2\pi }{3}x=−32π​ попадает в заданный отрезок. Других корней, принадлежащих нашему отрезку, в этой серии корней нет (это следует из того, что длина отрезка составляет 2π 2\pi2π, а период серии решений также равен 2π 2 \pi2π; значит, если один из корней серии находится внутри отрезка, все остальные корни из этой серии уже не попадают в отрезок).

Итак, отрезку [−3π2;π2][-\frac{3\pi }{2};\frac{\pi }{2}][−23π​;2π​] принадлежат корни x=−4π3x=- \frac{4\pi }{3}x=−34π​ и x=−2π3x=- \frac{2\pi }{3}x=−32π​.

lampa.io

Тригонометрические уравнения с засадой. Задание С1

В этой статье мы разберем две задачи из Задания С1   для  подготовки к ЕГЭ  по математике.

Я хочу рассказать вам о двух своих ошибках, которые я сделала при решении несложных тригонометрических уравнений. Ошибки весьма поучительны.

Первое задание:

а)  Решите уравнение:

б) Найдите все корни на промежутке  []

При решении уравнения я попыталась представить тангенс суммы двух углов по формуле

То есть у меня получилось:

И — внимание! — я потеряла корень. Смотрите внимательно: после этого преобразования я получила отдельно стоящий . Но  не определен при . А в исходном уравнении  вполне мог быть равен .

То есть выполняя это невинное преобразование, я сузила ОДЗ. Но узнала я об этом, только когда посмотрела  ответ. Но на ЕГЭ ответов нет, поэтому выполняя преобразование нужно следить за тем, что происходит с областью допустимых значений.

Итак, мы идем другим путем.

Запишем    и через  и :

Используем формулы синуса и косинуса суммы:

Разделим числитель и знаменатель дроби в левой части уравнения на :

Приведем левую часть уравнения к общему знаменателю:

Перенесем все влево:

Вынесем за скобку общий множитель:

Приведем выражение в скобках к общему знаменателю:

Знаменатель дроби не равен нулю, то есть

и 

Произведение двух множителей равно нулю, если хотя бы один из них равен нулю:

или 

1. 

— вот он, потерянный корень!

2. 

Раскроем скобки, приведем подобные члены:

Итак, мы получили два решения:

б) Найдем корни, принадлежащие промежутку []:

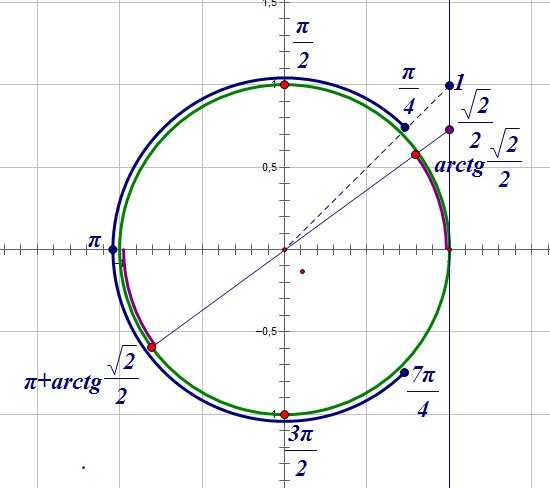
На рисунке красными точками обозначены решения уравнения;

синей дугой обозначен промежуток, которому принадлежат корни;

угловая величина сиреневой дуги равна .

Двигаясь из точки , мы встречаем на пути , ,  — это и есть корни уравнения, принадлежащие промежутку []. Мы видим, что корень  не принадлежит заданному промежутку.

Ответ: а) ;

б) , , 

И второе задание:

а) Решите уравнение:

б) Найдите корни уравнения, принадлежащие промежутку

[]

Засада в этом уравнении такая: когда мы ищем ОДЗ, то записываем

и . Будет ошибкой записать ОДЗ: ,

Нельзя забывать, что  не определен при , то есть в конечном итоге мы получаем такую  ОДЗ: :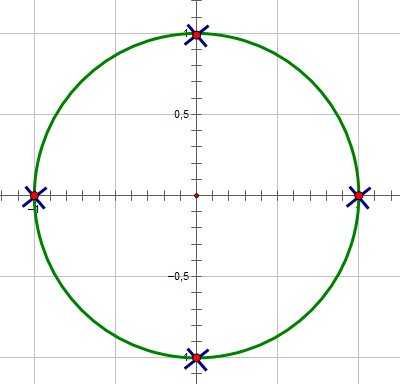

Собственно, больше никаких сложностей в этом уравнении нет.

Умножим обе части на :

Отсюда

или 

И вот в этом месте важно не пропустить, что корень уравнения — посторонний корень, так как не входит в ОДЗ исходного уравнения!

Но у нас еще есть корни уравнения :

или 

Осталось выбрать корни, принадлежащие промежутку []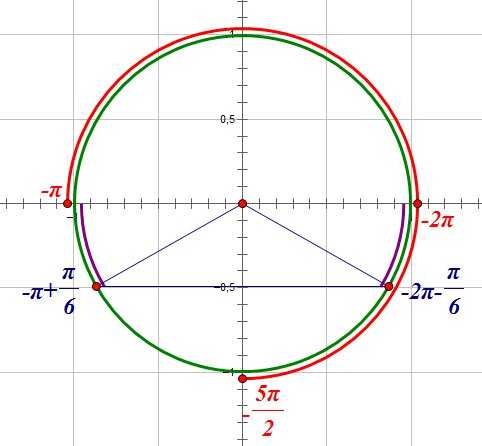

На рисунке красными точками на зеленой окружности обозначены решения уравнения;

красной дугой обозначен промежуток, которому принадлежат корни;

угловая величина сиреневой дуги равна .

Двигаясь из точки , мы встречаем на пути  — это и есть корень уравнения, принадлежащий промежутку .

Ответ: а)  или 

б) 

 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Нахождение корней уравнения, принадлежащих промежутку — «Шпаргалка ЕГЭ»

а) Решите уравнение: .

б) Найдите корни этого уравнения, принадлежащие промежутку  .

Решение задачи

В данном уроке демонстрируется пример решения тригонометрического уравнения, которым можно с успехом воспользоваться при подготовке к ЕГЭ по математике. В частности, при решении задач вида С1 данное решение станет актуальным.

В ходе решения выполняется преобразование тригонометрической функции левой части уравнения с применением формулы двойного аргумента синус. Функция косинус в правой части также записывается как функция синус с упрощенным до аргументом. При этом знак перед полученной тригонометрической функцией меняется на противоположный. Далее все члены уравнения переносятся в его левую часть, где производится вынесение за скобки общего множителя . В результате, полученное уравнение представляется в виде произведения двух множителей. Каждый множитель поочередно приравнивается к нулю, что и позволяет определить корни уравнения. Затем определяются корни уравнения, принадлежащие заданному промежутку. Применяя метод витков, на построенной единичной окружности отмечается виток от левой границы заданного отрезка до правой. Найденные корни на единичной окружности соединяются отрезками с ее центром, а потом определяются точки, в которых эти отрезки пересекают виток. Данные точки пересечения и являются ответом на часть «б» задачи.

shpargalkaege.ru

Отбор корней в тригонометрических уравнениях

Отбор корней в тригонометрических уравнениях

Практика приемных экзаменов в вузы показывает, что при решении тригонометрических уравнений абитуриенты нередко затрудняются как в выборе способа решения уравнения, так и при отборе его корней.

Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений специфична. Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнения. Запись ответа тригонометрического уравнения часто связана с понятиями объединения и пересечения множеств. Обычно при решении таких уравнений получают серии корней, и в окончательном варианте ответ записывают в виде объединения этих серий. Но как быть, если эти серии пересекаются? Надо ли исключать повторяющиеся корни решения или этого можно не делать?

С понятием пересечения множеств связан и еще один важный вопрос: в ответе не должно быть значений переменной, при которых выражения в левой или правой частях уравнения не определены. Такие значения надо исключить. Для этого надо уметь находить пересечение различных серий.

В предлагаемой работе на конкретных примерах рассматриваются различные способы и приемы при выборе ответа. Надеемся, что данная работа поможет учителям старших классов и самим учащимся при подготовке к вступительным экзаменам в вузы.

 1. Отбор чисел на тригонометрическом круге

Проблему отбора корней, отсеивания лишних корней при решении тригонометрических уравнений часто можно решить с помощью изображения чисел на тригонометрическом круге. В ряде случаев этот прием, на наш взгляд, более наглядный и убедительный.

Пример 1. cos x + cos 2x – cos 3x = 1.

Решение.

cos x – cos 3x – (1 – cos 2x) = 0,

2sin x sin 2x – 2sin

2 x = 0,

2sin x (sin 2x – sin x) = 0,

.

Из рис. 1 видно, что серия x₃(*) включает в себя один из корней серии x₁(·).

Ответ:

Пример 2. tg x + tg 2x – tg 3x = 0.

Решение.

Серия x₂(*) не удовлетворяет ОДЗ (рис. 2). Серия x₁(o) входит в серию x₃(·), поэтому ответ можно записать одной формулой: 

Пример 3.

Решение.

sin 4x cos x + sin 2x cos 7x = 0,

sin 2x (2cos 2x cos x + cos 7x) = 0,

sin 2x (cos 3x + cos x + cos 7x) = 0,

sin 2x (cos 3x + 2cos 4x cos 3x) = 0,

sin 2x cos 3x (1 + 2cos 4x) = 0,

Объединяя все три серии корней, ответ можно записать так:

Пример 4. sin² x + sin² 2x = sin² 3x.

Решение.

– (cos 2x + cos 4x) + 1 + cos 6x = 0,

– 2cos 3x cos x + 2cos2 3x = 0,

cos 3x (cos 3x – cos x) = 0,

cos 3x sin 2x sin x = 0,

Серия корней x₂ содержится в серии x₁ и x₃, в чем легко убедиться, изобразив их различными точками на круге, поэтому

ответ:

Пример 5. sin x + sin 7x – cos 5x + cos (3x – 2p) = 0.

Решение.

sin 

x + sin 7x – cos 5x + cos 3x = 0,

2sin 4x cos 3x + 2sin 4x sin x = 0,

sin 4x (cos 3x + sin x) = 0,

Серия x₂ содержится в серии корней x₁, а на круге (рис. 4) изобразим точками серии x₁(·) и x₃(О), которые не совпадают.

Пример 6. ctg 2x + 2ctg x – tg 2x = sin 5x.

Решение.

ОДЗ

Учитывая ОДЗ, получим

Пример 7.

Решение.

Иногда случается, что часть серии входит в ответ, а часть нет.
Нанесем на тригонометрический круг (рис. 6) все числа серии
и выбросим корни, удовлетворяющие условию

Оставшиеся решения из серии x₁ можно объединить в формулу

2. Отбор корней в тригонометрическом уравнении алгебраическим способом

Изображение корней на тригонометрическом круге не всегда удобно, когда период меньше 2p.

Пример 8. sin² 2x + sin² 3x + sin² 4x + sin² 5x = 2.

Решение.

cos 4x + cos 6x + cos 8x + cos 10x = 0,

2cos 5x cos x + 2cos 9x cos x = 0,

cos x cos 2x cos 7x = 0.

«Период» серий равен p. Рассмотрим те корни из серий x₁, x₂, x₃, которые попадают в промежуток [0; p]. Это будут:

Сразу видно, что серия x₁ содержится в серии x₃, а серии x₂ и x₃ не пересекаются. Значит, ответ можно записать в виде .

Способ алгебраический. Общим знаменателем в сериях x₁ и x₂ будет 4:

 

Если x₁ = x₂, то 2 + 4k = 1 + 2l, но слева – четное число, а справа – нечетное. Равенство невозможно, серии x₁ и x₂ не пересекаются. Аналогично получаем, что серии х₃ и х₂ тоже не пересекаются, а вот для серий x₁ и x₃ получаются формулы

Из равенства 7 + 14k = 1 + 2m получаем m = 7k + 3. Это означает, что для всякого k найдется целое m такое, что будет выполняться равенство 7 + 14k = 1 + 2m, т. е. всякий корень из серии x₁ встретится и в серии x₃, поэтому серия x₁ содержится в серии x₃, и в ответе писать ее не надо.

При решении некоторых тригонометрических уравнений их заменяют эквивалентной системой уравнений, а затем находят пересечение множеств решений. Эти пересечения часто найти легко. Но иногда для нахождения решений необходимо решать диафантово уравнение (ax + by = c).

Пример 9.

Решение.

В данном случае сделать отбор решений на тригонометрическом круге неудобно, так как периоды серий разные. Найдем такие целые k, при которых x = p + 2pk имеет посторонние корни, удовлетворяющие условию x № 3pn, n О Z. Пусть p + 2pk = 3pn; 1 + 2k = 3n. Отсюда n = 2m + 1 Ю k = 3m + 1. Итак, посторонние корни в серии x = p + 2pk будет при k = 3m + 1, m О Z.

Ответ: {x = p + 2pk, где k № 3m + 1, m О Z} =   {x = p + 6pm, x = 3p + 6pm, m О Z}.

Пример 10. cos 7x (sin 5x – 1) = 0.

Решение.

Пересекаются ли эти серии? Из равенства

следует 5k = 14n + 1. Выразим ту неизвестную, коэффициент при которой меньше по абсолютной величине:

– целое число.

Пусть

Ответ можно записать в виде

.

Пример 11.

Решение.

Поскольку наибольшее значение функции y = cos t равно 1, уравнение равносильно системе

Решением уравнения является пересечение серий x₁ и x₂, т. е. нам надо решить уравнение

Из него получаем уравнение, имеющее решение k = 8t, n = 3t.

Ответ: {8pt, t О Z}.

Пример 12.

Решение.

Решением уравнения является пересечение серий x₁ и x₂;

,

где – целое число;

Ответ: x = 2p + 8pm, m О Z.

Пример 13.

Решение.

sin 2x sin 4x = sin x (sin 2x + sin 4x),

sin 2x sin 4x = 2sin x sin 3x cos x,

sin 2x sin 4x = sin 2x sin 3x,

sin 2x (sin 4x – sin 3x) = 0,

Остается проверить, лежат ли они в области x О R,

Серию x₁ проверить легко: поскольку ,

а при n, кратных 8, n = 8l (l О Z), получается как раз x № 2pl, вся серия x₁ исключается. Сложнее обстоит дело с серией x₂. Здесь надо выяснить, при каких целых k найдется такое n, что выполняется равенство ,

и исключить такие k. Последнее уравнение приводится к виду 8k + 4 = 7n, причем решать это уравнение надо в целых числах. Из него следует, что n = 4l, поскольку левая часть уравнения делится на 4. Подставляя n = 4l в уравнение, получаем 8k + 4 = 28l, откуда 2k + 1 = 7l. Далее, l должно быть нечетно, l = 2t + 1; поэтому 2k + 1 = 14t + 7, k = 7t + 3. Вот решение и получилось:

k = 7t + 3, n = 4l = 4(2t + 1) = 8t + 4.

Ответ:

3. Отбор корней в тригонометрическом уравнении с некоторыми условиями

Изложенные выше способы отбора корней в тригонометрических уравнениях не всегда применяются в чистом виде: выбор способа зависит от конкретных условий, но иногда эти способы комбинируются.

Пример 14. Найти корни уравнения sin 2x = cos x | cos x |,

удовлетворяющие условию x О [0; 2p].

Решение.

Условию cos x і 0 удовлетворяют

из серии

из серии

Наконец,

Пример 15. Найти все решения уравнения

удовлетворяющие условию

так как то

Ответ: x = 2p + 4pk, k О Z.

Пример 16. Найти все решения уравнения

принадлежащие отрезку .

Решение.

Отметим ОДЗ на тригонометрическом круге (рис. 9):

Отрезку принадлежит только один промежуток из ОДЗ, а именно .

Решим уравнение и выберем корни, принадлежащие этому промежутку:

1 + sin 2x = 2cos² 3x Ю sin 2x = cos 6x,

Из серии при n = 2 имеем

Из серии при n = 5 имеем

Пример 17.

Решение.

а) cos x і 0;

б) cos x < 0;

Ответ:

Пример 18. Найти все корни уравнения

которые удовлетворяют условию .

Решение.

10sin² x = – cos 2x + 3 Ю 10sin²x = 2sin² x – 1 + 3,

Выберем корни, удовлетворяющие условию задачи. Из серии

При

при .

Аналогично выберем корни, удовлетворяющие условию задачи, из второй серии. Это будут .

Пример 19.

Решение.

sin x и cos x должны быть одинакового знака, а, учитывая первое неравенство, только при sin x > 0 и cos x > 0 система совместна. Значит, x оканчивается в первой четверти. Имеем

1 + 2sin x cos x = 4sin x cos x Ю sin 2x = 1,

Ответ:

Пример 20.

Решение.

Ответ:

Пример 21.

Решение.

а)

Но ctg x < 0. Это противоречит условию tg x > 0. Решений нет.

б)

Ответ:

.

Примеры для самостоятельного решения

   7. Найти все решения уравнения, принадлежащие указанным промежуткам:

ОТВЕТЫ

Л. Максименко,
Р. Зинченко,
г. Ангарск

mat.1sept.ru

Нахождение корней уравнения, принадлежащие промежутку — «Шпаргалка ЕГЭ»

a) Решите уравнение  .

б) Найдите все корни этого уравнения, принадлежащие отрезку  . 

Решение задачи

В данном уроке рассматривается пример решения показательно-тригонометрического уравнения, которое можно использовать в качестве примера при решении задач типа С1 при подготовке к ЕГЭ.

Для начала первое слагаемое левой части уравнения раскладывается на множители, используя правило возведения в степень произведения: . Затем общий множитель выносится за скобки. Известно, что произведение равно нулю, когда один из множителей равен нулю. Значит, оба множителя исходного уравнения приравниваются к нулю. Так как область значений показательной функции строго больше нуля, то первое уравнение не имеет решений. Для решения следующего уравнения второе слагаемое переносится в правую часть. Затем, так как основания степеней одинаковы, то основания опускаются. Далее обе части полученного тригонометрического уравнения делятся на , не равное нулю. Решив данное уравнение, определяются корни уравнения. Затем определяются корни уравнения, принадлежащие заданному отрезку, с помощью двойного неравенство с одним неизвестным . Решением полученного неравенства являются только целые значения из полученного промежутка значений . Подставив найденные значения  в корень уравнения , определяется ответ задачи.

shpargalkaege.ru

Решение тригонометрических уравнений на промежутке

Разделы: Математика

---

Цель урока:

а) закрепить умения решать простейшие тригонометрические уравнения;

б) научить выбирать корни тригонометрических уравнений из заданного промежутка

Ход урока.

1. Актуализация знаний.

а)Проверка домашнего задания: классу дано опережающее домашнее задание – решить уравнение и найти способ выбора корней из данного промежутка.

1)cos x = -0,5, где хI [- ]. Ответ: .

2) sin x = , где хI [0;2?]. Ответ: ; .

3)cos 2x = -, где хI [0;]. Ответ:

Ученики записывают решение на доске кто-то с помощью графика, кто-то методом подбора.

В это время класс работает устно.

Найдите значение выражения:

а) tg – sin + cos + sin . Ответ: 1.

б) 2arccos 0 + 3 arccos 1. Ответ: ?

в) arcsin + arcsin . Ответ: .

г) 5 arctg (-) – arccos (-). Ответ:– .

– Проверим домашнее задание, откройте свои тетради с домашними работами.

Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.

См. приложение 1

Приложение 2

Приложение 3

2. Вывод о способах решения данных заданий и постановка проблемы, т. е. сообщение темы и цели урока.

– а) С помощью подбора решать сложно, если задан большой промежуток.

– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.

– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)

– Пример 1. (Ученик выходит к доске)

cos x = -0,5, где хI [- ].

Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске

х = + 2?k, где k R.

– Запишем это решение в виде совокупности:

– Как вы считаете, при какой записи решения удобно выбирать корни на промежутке? (из второй записи). Но это ведь опять способ подбора. Что нам необходимо знать, чтобы получить верный ответ? (Надо знать значения k).

(Составим математическую модель для нахождения k).

Ответ: .

Вывод: Чтобы выбрать корни из заданного промежутка при решении тригонометрического уравнения надо:

1. для решения уравнения вида sin x = a, cos x = a удобнее записать корни уравнения, как две серии корней.
2. для решения уравнений вида tg x = a, ctg x = a записать общую формулу корней.
3. составить математическую модель для каждого решения в виде двойного неравенства и найти целое значение параметра k или n.
4. подставить эти значения в формулу корней и вычислить их.

3. Закрепление.

Пример №2 и №3 из домашнего задания решить, используя полученный алгоритм. Одновременно у доски работают два ученика, с последующей проверкой работ.

4. Самостоятельная работа.

Самопроверка с выбором ответа. Выбрать № правильного ответа, получив закодированное число (312).

1) sin x = -, x

2) 3 tg x = -, x I [0; 2]

3) 2 cos , х [ ]

Приложение. Ответы к примерам

5. Домашнее задание:

1 уровень: № 295 (а,б), № 317 (а,б)

2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).

6. Итог урока.

4.04.2007

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Нахождение корней уравнения, принадлежащих промежутку — «Шпаргалка ЕГЭ»

а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие промежутку .

Решение задачи

В данном уроке рассматривается решение тригонометрического уравнения, которое можно использовать в качестве примера для решения задач типа С1 при подготовке к ЕГЭ по математике.

В ходе решения выполняется преобразование тригонометрической функции синуса в косинус с применением формулы приведения. Далее все члены уравнения переносятся в его левую часть и вводится замена , причем . В полученном квадратном уравнении производится вынесение за скобки общего множителя . Затем каждый множитель поочередно приравнивается к нулю, что и позволяет найти корни уравнения. Выполнив возврат к исходной переменной и решив простейшие тригонометрические уравнения, определяется ответ на первую часть задачи. После этого, с помощью единичной окружности, отбираются те из корней исходного уравнения, которые принадлежат заданному условием промежутку. Для этого на построенной единичной окружности сначала отмечается промежуток, а далее — найденные корни. Вычислив значения корней, входящих в промежуток, и определяется ответ на вторую часть задачи.

shpargalkaege.ru

No related posts.