Как находить производную функции – как найти, вычислить и понять с нуля

Содержание

Производная функции. Геометрический смысл производной.

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Запомним определение:

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

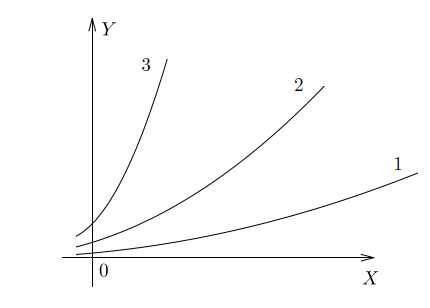
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

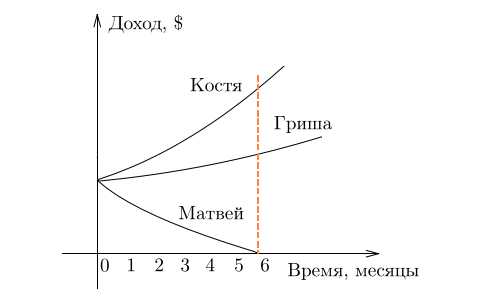
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти с помощью графика.

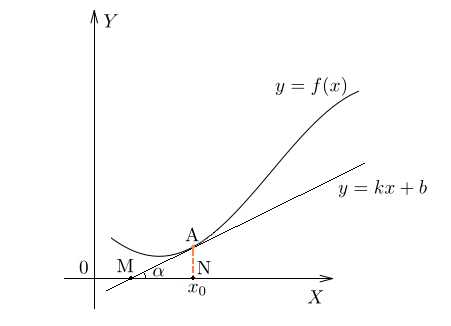
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

Величина в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси .

Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

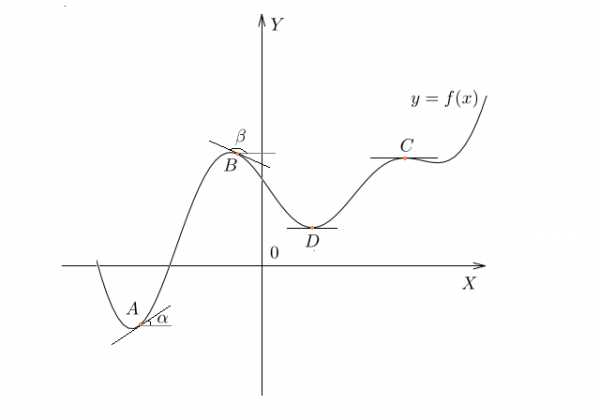
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол ; с положительным направлением оси . Значит, в точке производная положительна.

В точке наша функция убывает. Касательная в этой точке образует тупой угол ; с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.

Вот что получается:

Если функция возрастает, ее производная положительна.

Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».

В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная положительна, то функция возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

	возрастает	точка максимума	убывает	точка минимума	возрастает
	+	0	—	0	+

Ты нашел то, что искал? Поделись с друзьями!

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задачи . Другое — на первом курсе, при более серьезном изучении функций и производных.

Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

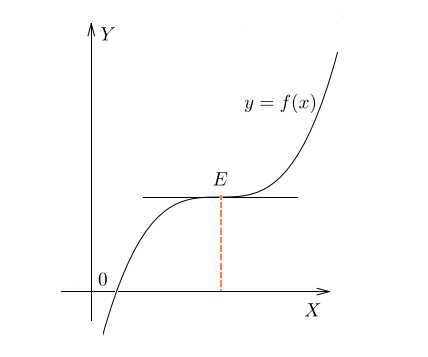
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

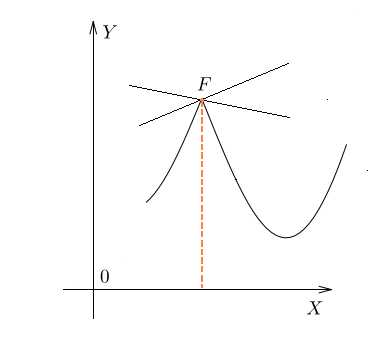
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

как найти производную функции

Здравствуйте!
Давайте для начала разберёмся, что же такое производная и что она характеризует. Производная — понятие, какое характеризует скорость изменения функция в заданной точке.
Но всё-таки, как на мой взгляд, лучше это продемонстрировать на конкретном примере, который Вы нам и предоставили. Итак, приступим.
Первое, что мы должны учесть, чтоб понять как найти производную функции — правила дифференцирования и таблицу производных, без которой сложно найти производную, так как это базовые понятия.
Значит, нам дана функция:

Мы знаем, что производная суммы/разницы равна сумме/разности (соответственно) производных. Из этого получаем такое:

Так как у нас есть постоянные множители, то, учитывая существующие правила дифференцирования, мы можем вынести их за знак производной и получим:

Следующий шаг — выбираем подходящую формулу. Это будет формула для производной степенной функции, из чего мы получим следующее:

Ответ:

ru.solverbook.com

Как найти производную от заданной функции

11 июля 2011

Автор КакПросто!

Задача взятия производной от заданной функции является базовой как для учащихся средних школ, так и для студентов высших учебных заведений. Невозможно в полной мере освоить курс математики без усвоения понятия производной. Но не стоит пугаться раньше времени — любую производную можно вычислить используя простейшие алгоритмы дифференцирования и зная производные элементарных функций.

Статьи по теме:

Вам понадобится

Таблица производных элементарных функций, правила дифференцирования

Инструкция

По определению производной функции является отношение приращения функции к приращению аргумента за бесконечно малый промежуток времени. Таким образом, производная показывает зависимость роста функции от изменения аргумента. Для того чтобы найти производную элементарной функции достаточно воспользоваться таблицей производных. Полная таблица производных элементарных функций приведена на рисунке.

Для того, чтобы найти производную сумму (разности) двух элементарных функций мы используем правило дифференцирования суммы: производная суммы функций равна сумме их производных. Это записывается как:

(f(x)+g(x))’=f'(x)+g'(x). Здесь символом (‘) показывается взятие производной от функции. А далее задача сводится к взятию производных двух элементарных функций, описанная на предыдущем шаге.

Для того чтобы найти производную произведения двух функций, необходимо воспользоваться еще одним правилом дифференцирования:

(f(x)*g(x))’=f'(x)*g(x)+f(x)*g'(x), то есть производная произведения равна сумме произведения производной первого множителя на второй и первого множителя на производную второго. Найти производную частного можно по формуле, представленной на картинке. Она очень похожа на правило взятия производной произведения, только вместо суммы в числителе стоит разность, и добавляется знаменатель, в котором находится квадрат знаменателя заданной функции.

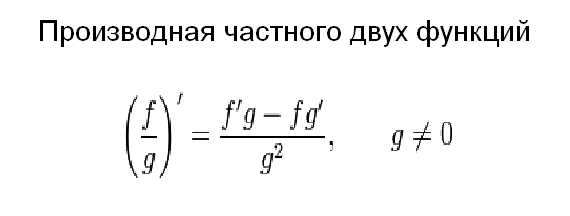
Взятие производной сложной функции — наиболее трудная задача при дифференцировании (сложной функцией называется функция, аргументом которой является какая-либо зависимость). Но и она решается по довольно простому алгоритму. Сначала мы берем производную по сложному аргументу, считая его простым. Затем мы умножаем полученное выражение на производную сложного аргумента. Так мы можем найти производную функции с любой степенью вложенности.

Источники:

Главный математический портал России
найти производные заданных функций

Совет полезен?

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru

Как найти производную?

Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.

Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.

Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.

Для их обозначения будем использовать латинские буквы f, g и др.

Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g’ означает, что мы будем находить производную функции g.

Таблица производных

Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.

С’=0
(sin x)’=cos x
(cos x)’= –sin x
(xⁿ)’=n x^n-1
(e^x)’=e^x
(ln x)’=1/x
(a^x)’=a^xln a
(log_ax)’=1/x ln a
(tg x)’=1/cos²x
(ctg x)’= – 1/sin²x
(arcsin x)’= 1/√(1-x²)
(arccos x)’= — 1/√(1-x²)
(arctg x)’= 1/(1+x²)
(arcctg x)’= — 1/(1+x²)

Пример 1. Найдите производную функции y=500.

Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).

(500)’ = 0

Пример 2. Найдите производную функции y=x¹⁰⁰.

Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).

(x¹⁰⁰)’=100 x⁹⁹

Пример 3. Найдите производную функции y=5^x

Это показательная функция, вычислим ее производную по формуле 4.

(5^x)’= 5^xln5

Пример 4. Найдите производную функции y= log₄x

Производную логарифма найдем по формуле 7.

(log₄x)’=1/x ln 4

Правила дифференцирования

Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для

elhow.ru