Все 10000 комбинаций из 4 цифр. Сложно ли угадать PIN-код
Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.
Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.
Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
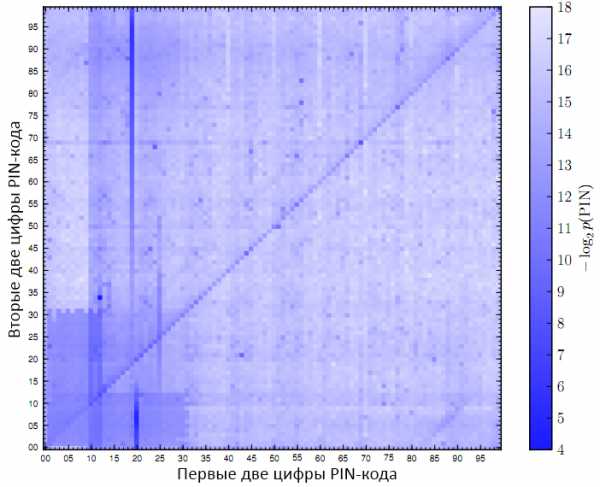
Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
| Фактор | Пример | RockYou | iPhone | Опрос |
|---|---|---|---|---|
| Даты | ||||
| ДДММ | 2311 | 5.26 | 1.38 | 3.07 |
| ДМГГ | 3876 | 9.26 | 6.46 | 5.54 |
| ММДД | 1123 | 10.00 | 9.35 | 3.66 |
| ММГГ | 0683 | 0.67 | 0.20 | 0.94 |
| ГГГГ | 1984 | 33.39 | 7.12 | 4.95 |
| Итого | 58.57 | 24.51 | 22.76 | |
| Клавиатурный паттерн | ||||
| смежные | 6351 | 1.52 | 4.99 | — |
| квадрат | 1425 | 0.01 | 0.58 | — |
| углы | 9713 | 0.19 | 1.06 | — |
| крест | 8246 | 0.17 | 0.88 | — |
| диагональная линия | 1590 | 0.10 | 1.36 | — |
| горизонтальная линия | 5987 | 0.34 | 1.42 | — |
| слово | 5683 | 0.70 | 8.39 | — |
| вертикальная линия | 8520 | 0.06 | 4.28 | — |
| Итого | 3.09 | 22.97 | 8.96 | |
| Цифровой паттерн | ||||
| заканчивается на 69 | 6869 | 0.35 | 0.57 | — |
| только цифры 0-3 | 2000 | 3.49 | 2.72 | — |
| только цифры 0-6 | 5155 | 4.66 | 5.96 | — |
| повторяющиеся пары | 2525 | 4.11 | — | |
| одинаковые цифры | 6666 | 0.40 | 6.67 | — |
| убывающая последовательность | 3210 | 0.13 | 0.29 | — |
| возрастающая последовательность | 4567 | 3.83 | 4.52 | — |
| Итого | 15.16 | 24.85 | 4.60 | |
| Случайный набор цифр | 23.17 | 27.67 | 63.68 | |
Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%. 100 самых популярных PIN-кодов
0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.
P.S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания .
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5 — последнее сочетание, так как все его элементы равны n — m + i. Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Итак, предыстория.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у
droidd.ru
количество комбинаций из 4 цифр
сколько комбинаций можно составить из 4 цифр
В разделе Естественные науки на вопрос Сколько можно составить четырехзначных комбинаций из четырех разных чисел? заданный автором сбросить лучший ответ это Задача не совсем определенная. Если требуется использовать только 4 цифры, то решается так: На первом месте (разряд тысяч) может стоять любая из 4 заданных цифр (если одна из цифр 0, то нужно уточнить, что подразумевается под определением «четырехзначных комбинаций». Если имеется в виду «чисел», то только 3 цифры, так как комбинации с ведущим нулем не являются числами, если же именно «комбинаций» и комбинации не рассматриваются как числа, то даже если одна из цифр заданного набора — 0, то все равно, на первом месте может стоять любая из 4 цифр) , на втором месте (разряд сотен) — любая из оставшихся 3 цифр, на третьем месте (разряд десятков) — любая из оставшихся 2 цифр, на четвертом месте — единственная оставшаяся цифра. Общее количество комбинаций 4*3*2*1=4!=24 (n! — называется n-факториал, и равно произведению 1*2*3*…*n). Если в набор заданных цифр входит 0, а сами комбинации рассматриваются как числа, то общее количество чисел 3*3*2*1=(n-1)*(n-1)!=18.
Если же можно использовать все цифры, то количество комбинаций равно 10*9*8*7=10!/(10-4)!=5040, а количество чисел 9*9*8*7=4536.
Привет! Вот подборка тем с ответами на Ваш вопрос: Сколько можно составить четырехзначных комбинаций из четырех разных чисел?
Ответ от Игрок[новичек]
малыш всего комбинаций 24
Ответ от Европейский[активный]
С пинкодом проще в банк обратиться (или в сотовую компанию) с паспортом ))
Ответ от худосочие[новичек]
байты в Float по ModBUS крутим? )) (я — да — так сюда и попал)
Ответ от Workings[гуру]
4 х 3 х 2 х 1
Это равно 24
Ответ от Марина Мингалимова[новичек]
Здравствуйте уважаемые математики! ПОМОГИТЕ ПОЖАЛУЙСТА. Я забыла пин код там точно есть 1, 7, 0, одна из цифр повторяется дважды. Какие варианты есть. Два раза уже вводила код не верно. Осталась одна попытка. ввела 1170 не помогло, второй раз не помню. Помогите!
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Размещение на Википедии
Посмотрите статью на википедии про Размещение
Ответить на вопрос:
22oa.ru
Сколько комбинаций в пароле из 4 цифр?Ноль тоже учитывать.
0123,0223,0222, до фигища для пароля не используют только цифры)) ) попробуй на майле смени на 4 цифры во первых не надежно во вторых надо буквы добавлять английские
9999 комбинаций
Десять тысяч (если учитывать «0000»)
10^4=10000 комбинаций.
touch.otvet.mail.ru
Надо составить все возможные комбинации из чисел 1, 2, 3. Как подсчитать количество таких возможных комбинаций?
Смотри литературу по комбинаторике. Расчет такой: Пусть «_» будет местом под первую цифру, а «__» — вторую, «___» — третью. Тогда _ может изменяться на все три цифры; __ может изменяться на две цифры, чтобы не повторяться с первой; ___ может быть только одной из цифр. Следовательно: 3 х 2 х1 = число всех вариаций с данными числами без повторов. Их будет 6. 123 132 213 231 312 321
к-во чисел возводится в степень равную их количеству. В твоём варианте надо 3 (1, 2, 3) возвести в куб, то есть предел — 27 комбинаций. Для подсчёта чего-либо подобного, типа цифрового замка, всё делается так же. 4 верньера по 6 цифр. 6 возводим в 4-ю степень и получаем максимум комбинаций.
В данном случае количество доступных чисел в степени длины числа 3 ^ 3 = 27
ты пропустил 223 а вообще формула «количество_цифр»в степени»количество_цифр»(например, 2в степени2,3в степени 3 и т. д.)
А причем тут Программное обеспечение?
Нет не правильно, унего не та формула … Всего 216 Это перемножение всех комбинации для однотипынх чисел из трех таблиц
как решается 1,2,3 123, 321
touch.otvet.mail.ru
Количество комбинаций из трех чисел
Вопрос — сколько существует трехзначных чисел с различными цифрами? Ответ: произвольный набор способов вычисляется по правилам произведения: k1*k2…*kN 10*10*10=1000 комбинаций
10*10*10 = 1000 результатов
Ровно 1000; Начиная с 000—->001——>002….и кончая 997——>998—->999. Удачи
999 комбинаций, по количеству трехзначных чисел, вроде так
Не 999 а правильно 1000 потому что еще есть комбинация 000
как узнать 3 цифры на обратной стороне банковской карточки
touch.otvet.mail.ru
Сколько комбинаций возможно из 7 разных цифр?
Многоооооооооооооо….
оооо… с математикой у меня не очень , но точно скажу МНОГО!!
Берём вначале 1 место (им. в виду цифр) . Там могут стоять 9 цифр. На втором 10. На третьем — 10. На четвертом 10 и т. д. Для решения умножаем. 10 в 6 степени это 10 000 000 и умножаете на 9. Итого ответ: 90 000 000
7! вроде бы так(!-это знак в алгебре)
touch.otvet.mail.ru
Как посчитать максимальное количество комбинаций из трех цифр?
165*160*13 «Эх, молодёжь…» (с)
Так умнож их друг в друга.
165 цветов с одним материалом дадут 165 вариантов. Со 160 материалами 165*160 вариантов. А эти варианты с 13 оттенками каждый дадут (165*160)*13 вариантов
…изучи факториалы!
из 3х чисел а не цыфр. перемножай все числа
touch.otvet.mail.ru
