Как построить параболу в Excel

Построение параболы является одной из известных математических операций. Довольно часто она применяется не только в научных целях, но и в чисто практических. Давайте узнаем, как совершить данную процедуру при помощи инструментария приложения Excel.
Создание параболы
Парабола представляет собой график квадратичной функции следующего типа f(x)=ax^2+bx+c. Одним из примечательных его свойств является тот факт, что парабола имеет вид симметричной фигуры, состоящей из набора точек равноудаленных от директрисы. По большому счету построение параболы в среде Эксель мало чем отличается от построения любого другого графика в этой программе.
Создание таблицы
Прежде всего, перед тем, как приступить к построению параболы, следует построить таблицу, на основании которой она и будет создаваться. Для примера возьмем построение графика функции f(x)=2x^2+7.
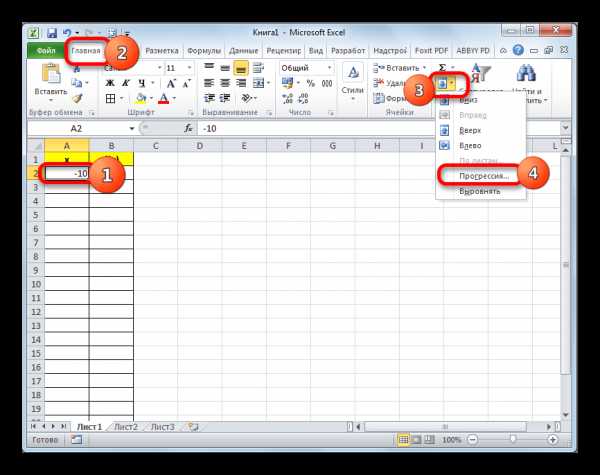
- Заполняем таблицу значениями x от -10 до 10 с шагом 1. Это можно сделать вручную, но легче для указанных целей воспользоваться инструментами прогрессии. Для этого в первую ячейку столбца «X» заносим значение «-10». Затем, не снимая выделения с данной ячейки, переходим во вкладку «Главная». Там щелкаем по кнопке «Прогрессия», которая размещена в группе «Редактирование». В активировавшемся списке выбираем позицию «Прогрессия…».
- Выполняется активация окна регулировки прогрессии. В блоке «Расположение» следует переставить кнопку в позицию «По столбцам», так как ряд «X» размещается именно в столбце, хотя в других случаях, возможно, нужно будет выставить переключатель в позицию «По строкам». В блоке «Тип» оставляем переключатель в позиции «Арифметическая»
В поле «Шаг» вводим число «1». В поле «Предельное значение» указываем число «10», так как мы рассматриваем диапазон x от -10 до 10 включительно. Затем щелкаем по кнопке «OK».
- После этого действия весь столбец «X» будет заполнен нужными нам данными, а именно числами в диапазоне от -10 до 10 с шагом 1.
- Теперь нам предстоит заполнить данными столбец «f(x)». Для этого, исходя из уравнения (f(x)=2x^2+7), нам нужно вписать в первую ячейку данного столбца выражение по следующему макету:
=2*x^2+7Только вместо значения x подставляем адрес первой ячейки столбца «X», который мы только что заполнили. Поэтому в нашем случае выражение примет вид:
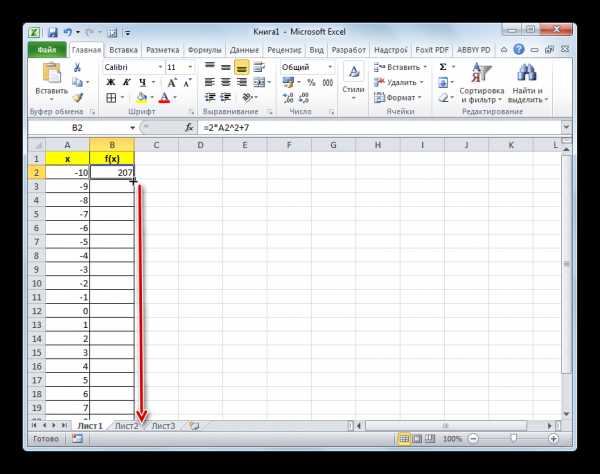
=2*A2^2+7 - Теперь нам нужно скопировать формулу и на весь нижний диапазон данного столбца. Учитывая основные свойства Excel, при копировании все значения x будут поставлены в соответствующие ячейки столбца «f(x)» автоматически. Для этого ставим курсор в правый нижний угол ячейки, в которой уже размещена формула, записанная нами чуть ранее. Курсор должен преобразоваться в маркер заполнения, имеющий вид маленького крестика. После того, как преобразование произошло, зажимаем левую кнопку мыши и тянем курсор вниз до конца таблицы, после чего отпускаем кнопку.
- Как видим, после этого действия столбец «f(x)» тоже будет заполнен.




На этом формирования таблицы можно считать законченным и переходить непосредственно к построению графика.
Урок: Как сделать автозаполнение в Экселе
Построение графика
Как уже было сказано выше, теперь нам предстоит построить сам график.
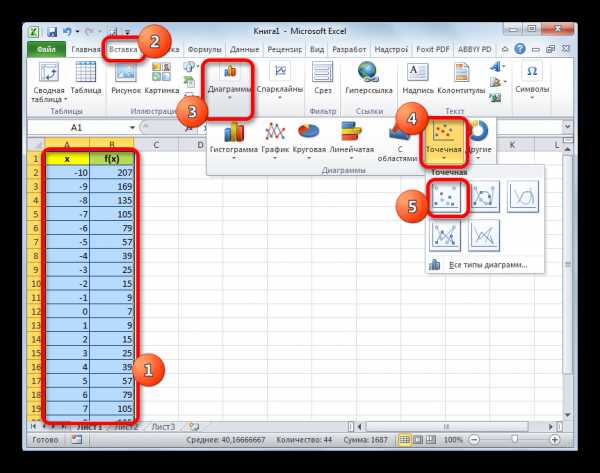
- Выделяем таблицу курсором, зажав левую кнопку мыши. Перемещаемся во вкладку «Вставка». На ленте в блоке «Диаграммы» щелкаем по кнопке «Точечная», так как именно данный вид графика больше всего подходит для построения параболы. Но и это ещё не все. После нажатия на вышеуказанную кнопку открывается список типов точечных диаграмм. Выбираем точечную диаграмму с маркерами.
- Как видим, после этих действий, парабола построена.

Урок: Как сделать диаграмму в Экселе
Редактирование диаграммы
Теперь можно немного отредактировать полученный график.
- Если вы не хотите, чтобы парабола отображалась в виде точек, а имела более привычный вид кривой линии, которая соединяет эти точки, кликните по любой из них правой кнопкой мыши. Открывается контекстное меню. В нем нужно выбрать пункт «Изменить тип диаграммы для ряда…».
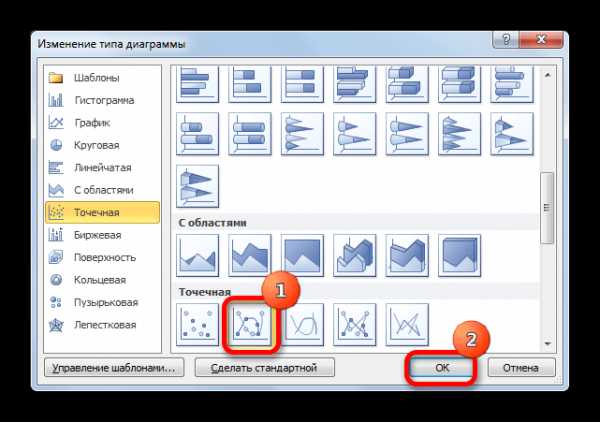
- Открывается окно выбора типов диаграмм. Выбираем наименование «Точечная с гладкими кривыми и маркерами». После того, как выбор сделан, выполняем щелчок по кнопке «OK».
- Теперь график параболы имеет более привычный вид.

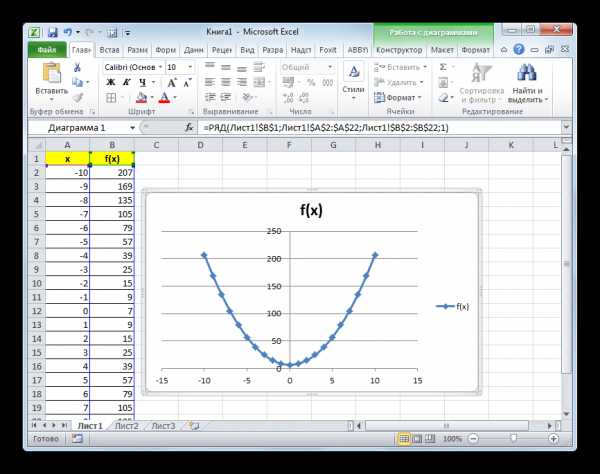
Кроме того, можно совершать любые другие виды редактирования полученной параболы, включая изменение её названия и наименований осей. Данные приёмы редактирования не выходят за границы действий по работе в Эксель с диаграммами других видов.
Как видим, построение параболы в Эксель ничем принципиально не отличается от построения другого вида графика или диаграммы в этой же программе. Все действия производятся на основе заранее сформированной таблицы. Кроме того, нужно учесть, что для построения параболы более всего подходит точечный вид диаграммы.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТlumpics.ru
Построение графика квадратичной функции
Графиком любой квадратичной функции является парабола. У каждой параболы есть вершина, при изображении графика важно знать её координаты. Вершина параболы имеет координаты (m,n).
Определите координаты вершин для парабол:
Определим координаты вершины параболы, которая является графиком квадратичной функции записанной в виде .
Преобразуем квадратный трёхчлен, выделим из него квадрат двучлена:
Второе слагаемое представим в виде удвоенного произведения:
Выделим квадрат суммы:
После сокращения получаем:
Отсюда запишем, что:
Вывод.
Графиком функции является парабола, которую можно получить из параболы с помощью двух параллельных переносов: сдвига относительно оси x и сдвига относительно оси y. Данная парабола имеет вершину с координатами (m,n), где , . Осью симметрии является прямая x=m.
Пример.
Найти координаты вершины параболы .
Вершина будет иметь координаты (m,n), каждую из которых можно получить по формуле. Подставим коэффициенты квадратичной функции в формулу и найдём эти значения:
Вершина параболы имеет координаты (-2,-5).
Воспользуемся наиболее простым способом: сначала найдём m вершины по формуле. И учитывая, что вершина принадлежит графику функции, подставим m вместо аргумента в функцию:
Получили вершину, которая имеет координаты (-2,-5).
Алгоритм построения графика квадратичной функции:
1. Определить направление ветвей парабола. Если a>0, то ветви направлены вверх, если a<0, то — вниз.
2. Найти координаты вершины параболы и отметить её на координатной плоскости. Применив формулу , найдём абсциссу вершины параболы, и, подставив это значение в формулу, задающую функцию, найдем ординату этой точки.
3. Определить ось симметрии x=m.
4. Построить ещё несколько точек принадлежащих параболе, составив таблицу значений функции с учётом оси симметрии.
5. Соединить отмеченные точки плавной линией.
Пример.
Изобразить график функции .
1. Определим направление ветвей параболы:
2. Найдём координаты вершины:
Получили вершину с координатами (-2, -3).
3. Определим ось симметрии:
4. Составим таблицу значений:
Выбранные значения симметричны относительно оси симметрии.
5. Отметим и соединим полученные точки на координатной плоскости:
Получили параболу, которая является графиком функции.
Пример.
Изобразить график функции и описать её свойства.
Изобразим график функции:
1. Определим направление ветвей параболы:
2. Найдём координаты вершины параболы:
Вершина имеет координаты (-2,-4).
3. Определим ось симметрии:
4. Составим таблицу значения функции:
5. Соединив эти точки, получаем:
Определим свойства функции.
Областью определения и областью значений являются:
Определим нули функции:
Перечислим промежутки знакопостоянства функции:
Опишем промежутки монотонности:
videouroki.net
Построение графика квадратичной функции
Построение графика квадратичной функции, заданной формулой
Предмет: алгебра
Класс: 8 «Б»
Тема: Построение графика квадратичной функции, заданной формулой
Тип: комбинированный урок.
Форма организации учебной деятельности: индивидуально-групповая.
Цели
Обучающие
· проверить знания, умения и навыки построения графика квадратичной функции, заданной формулой
· внедрить алгоритм построения графика квадратичной функции, заданной формулой
· отработать алгоритм при построении графиков квадратичной функции.
Развивающая
· продолжить работу по развитию умения работать с книгой, сравнивать; развивать коммуникативные связи, информационную грамотность, логику.
Воспитательная
· стимулировать учащихся к самооценке образовательной деятельности, вызывая чувство самопознания, самоопределения и самореализации.
Оборудование
· Доска, компьютеры, экран с проектором, карточки с алгоритмами.
Ход урока
1) Организационный момент (2 мин)
· Учитель формулирует тему и цели урока, сообщает план работы, который проецируется на экран и по мере выполнения стираются пункты плана. Учащиеся записывают число и тему урока в тетради.
Работа по плану
1) Работая устно, вспоминаем решение уравнений.
2) Учащиеся проверяют свои знания по построению графика квадратичной функции способом перемещения.
3) Знакомство с алгоритмом.
4) Отработка алгоритма при построении графиков функции, заданной формулой
2) Актуализация знаний учащихся (13 мин).
1) Фронтальная устная работа.
1. Что является графиком функции у = аx2. (парабола)
2. Как зависит график функции у = аx2 от коэффициента а.
а) Сформулируйте правило переноса графика функции вдоль оси абсцисс.
б) Сформулируйте правило переноса графика функции вдоль оси ординат.
(если а>0, то происходит растяжение графика функции от оси Ох вдоль оси Оу, ели 0<a<1, то происходит сжатие графика функции к оси Ох вдоль оси Оу)
3. Вспомни алгоритм построения графиков функций , если известен график функции у = аx2.
(График функции является парабола, получаема сдвигом параболы у = аx2:
вдоль оси абсцисс вправо на х0, если х0>0, влево на , если х0<0;
вдоль оси ординат вверх на у0, если у0>0, вниз на , если у0<0).
4. Как определить координаты вершины параболы?
5. Как определить точку, через которую проходит ось симметрии параболы?
6. Как определить направление «ветвей» параболы?
· Заполни пропуски (работа с интерактивной доской): все записывают в тетради. Взаимопроверка.
1. Функция у = aх2 + bx + c, где а, b, c – заданные действительные числа, а ¹ 0,
х – действительная переменная, называется … функцией. (квадратичной)
2. График функции у = ах2 при любом а ¹ 0 называют … .(параболой)
3. Функция у = х2 является … (возрастающей, убывающей) на промежутке
х £ 0. (убывающей)
4. Значения х, при которых квадратичная функция равна нулю, называют … функции (нулями функции)
5. Точку пересечения параболы с осью симметрии называют … параболы. (вершина параболы)
6. При а >0 ветви параболы у = ах2 направлены … . (вверх)
7. Если а< о и х ¹ 0, то функция у = ах2 принимает … (отрицательные)
(положительные, отрицательные) значения.
Работа у доски (индивидуальны карточки у доски)
1. Найдите координаты вершины параболы у=х2-4х+4 Ответ: (2;0)
2.Найдите нули квадратичной функции у=х2+х-2 Ответ: -2; 1
3. Выдели полный квадрат x2 — 4х + 5. И постройте график полученной функции.
Ответ: х2 — 4х + 5 = (х2 — 4х + 4) + 1 = (х — 2)2 + 1
Фронтальная работа с классом. (Презентация)
3.Учитель поясняет задание. Для каждой из функций, графики которых изображены, выберите соответствующее условие и отметьте знаком «+». Ученики выполняют работу на распечатанных листочках, осуществляя самопроверку. Листочки заранее раздать ученикам.
После того, как учащиеся закончили решение теста, выполняем самопроверку: учащиеся по очереди комментируют свои ответы, один ученик выполняет задание на интерактивной доске, на экране с помощью анимации появляются правильные ответы. ( Презентация)
После проверки учащиеся оценивают работу соседа по следующему критерию:
- «5» — нет ошибок;
- «4» — 1 ошибка;
- «3» — 2 ошибки;
- «2» — 3 и более ошибки.
Проверка работ учащихся у доски
4.
Ответ:
(Находим нули функции: =0 х1=0; х2=-5, ветви параболы направлены вверх а>0).
Ответ: (3,0) ;
2) Индивидуальное задание
· Индивидуальная работа на компьютерах. Первая группа, проверяет свои знания по построению графиков функции – в течение 4 минут выполняет теств Excel. (11 человек). Ученикам раздаются по окончанию работы образцы для проверки.
Образец для проверки
· Фронтальная устная работа (проверка работы, анализ и комментирование). Учащиеся второй группы выполняют тест с помощью системы голосования Verdict. На экране появляется изображение соответствующего графика с указанной функцией. (15 человек).
Тест
«Квадратичная функция»
В системе Verdict
10. Функция задана формулой . Найдите .
1) 24 2) 0 3) 8 4) -8
1. График какой функции изображен на рисунке?
1) 2)
3) 4)
4. Найдите нули функции .
1) 2 и 3 2) -6 и -1 3) 1 и 6 4) -3 и -2
2. На каком рисунке изображен график функции ?
1) 2) 3) 4)
0
1
1
х
у
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х
0
1
1
у
х
3. График какой функции изображен на рисунке?
1) 2)
3) 4)
0
1
1
у
х
8. На каком промежутке функция, изображенная на рисунке убывает?1) 2) 3) 4)
5. График какой функции изображен на рисунке?
1) 2)
3) 4)
6. На каком рисунке изображен график функции ?
1) 2) 3) 4)
0
1
1
х
у
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х
0
1
1
у
х
7. График какой функции изображен на рисунке?
1) 2)
3) 4)
0
1
infourok.ru
Построение графика квадратичной функции
Найти Поиск Опубликовать работу Личный кабинет Главная Положение о фестивале и конкурсах- Положение о фестивале
- Краткая информация
- Расчет стоимости участия в фестивале
- Общие положения и ключевые сроки
- Порядок участия в фестивале
- Подготовка мастер-класса и видеоурока
- Соблюдение авторских прав третьих лиц
- Технические требования
- Положение о конкурсе презентаций «Презентация к уроку»
Содержание:
Разделы
Конкурс «Презентация к уроку» Конкурс по экологии «Земля — наш общий дом» Конкурс «Электронный учебник на уроке» Конкурс «История регионов России»Астрономия Биология Начальная школа География Иностранные языки Информатика История и обществознание Краеведение Литература Математика Музыка МХК и ИЗО ОБЖ ОРКСЭ Русский язык Руководство учебным проектом Спорт в школе и здоровье детей Технология Физика Химия Экология Экономика
Администрирование школы Видеоурок Внеклассная работа Дополнительное образование Инклюзивное образование Классное руководство Коррекционная педагогика Логопедия Мастер-класс Общепедагогические технологии Организация школьной библиотеки Патриотическое воспитание Профессия — педагог Работа с дошкольниками Работа с родителями Социальная педагогика Урок с использованием электронного учебника Школьная психологическая служба
xn--i1abbnckbmcl9fb.xn--p1ai
Как начертить параболу 🚩 таблицы параболы 🚩 Математика
Автор КакПросто!
В процессе изучения математики, многие школьники и студенты сталкиваются с построением различных графиков, в частности, парабол. Параболы являются одними из самых часто встречающихся графиков, используемых на многих контрольных, проверочных и тестовых работах. Поэтому знание простейших инструкций по их построению окажет вам значительную помощь.
Статьи по теме:
Вам понадобится
- — линейка и карандаш;
- — калькулятор.
Инструкция
Для начала, начертите на листе бумаги координатные оси: ось абсцисс и ось ординат. Подпишите их. После этого, поработайте над данной квадратичной функцией. Она должна быть такого вида: y=ax^2+bx+c. Самой популярной функцией является y=x^2, поэтому ее можно привести в качестве примера. После построения осей, найдите координаты вершины вашей параболы. Чтобы найти координату по оси X, подставьте известные данные в эту формулу: x=-b/2a, по оси Y — подставьте полученное значение аргумента в функцию. В случае с функцией y=x^2, координаты вершины совпадают с началом координат, т.е. в точке (0;0), так как значение переменной b равно 0, следовательно и x=0. Подставив значение x в функцию y=x^2, нетрудно найти ее значение — y=0. После нахождения вершины, определитесь с направлением ветвей параболы. Если коэффициент a из записи функции вида y=ax^2+bx+c положителен, то ветви параболы направлены вверх, если отрицателен — вниз. График функции y=x^2 направлен вверх, так как коэффицент a равен единице.Следующим шагом будет вычисление координат точек параболы. Чтобы их найти, подставьте в значение аргумента какое-либо число и вычислите значение функции. Для построения графика хватит 2-3 точек. Для большего удобства и наглядности, начертите таблицу со значениями функции и аргумента. Также не забывайте, что парабола обладает симметричностью, следовательно это облегчает процесс создания графика. Самые часто используемые точки параболы y=x^2 — (1;1), (-1;1) и (2;4), (-2;4).
После нанесения точек на координатную плоскость, соедините их плавной линией, придавая ей округлые формы. Не заканчивайте график в верхних точках, а продлите его, так как парабола бесконечна. Не забудьте подписать график на чертеже, а также напишите необходимые координаты на осях, в противном случае, это вам могут посчитать за ошибку и снять определенное количество баллов.
www.kakprosto.ru
Квадратный трехчлен и его график
Рассмотрим многочлен ax2 + bx + c, где a, b, c – коэффициенты, причем a не равно нулю. Его обычно называют квадратным трёхчленом , а графиком функции является парабола. Осью параболы y = ax2 + bx + c служит прямая x= — b/2a (1) . По этой же формуле вычисляется абсцисса x0 вершины параболы. Формулу для нахождения ординаты y0 вершины параболы запоминать не нужно, так как если известна абсцисса, то всегда по формуле y0=f(x0) можно вычислить ординату. Рассмотрим для наглядности два примера построения графиков квадратного трехчлена.
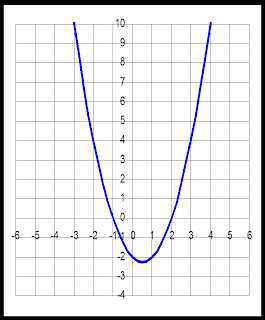
1. Построить график функции y=x2 –x –2.
Ветви параболы направлены вверх, так как a=1 (a>0). Ось симметрии находим по формуле (1) x=0,5. Координаты вершины параболы:Решив квадратное уравнение x2 –x –2=0, находим нули функции: x1=2; x2= -1. Точка пересечения параболы с осью Оy: x=0; y= -2. Для точности построения находим дополнительные точки, задав некоторые значения переменной x. Например точки А(3;4) и В(4;10). По полученным данным строим график параболы (рис.1).
 |
| Рис.1 |
2. Построить график функции y= — x2 +6x –9.
Ветви параболы направлены вниз, так как a= -1 (a<0). Ось симметрии находим по формуле (1) x=3. Координаты вершины параболы: x=3; y=0. Точка пересечения параболы с осью Оy: x=0; y= -9. Дополнительные точки: А(4;-1) и В(2;-1). По полученным данным построим график функции (рис.2).
 |
| Рис 2 |
- Найти координаты вершины параболы (по формуле (1)), отметить на координатной плоскости эту точку и провести ось параболы. Определиться с направлением ветвей параболы (вниз или вверх).
- Отметить на оси x две точки, симметричные относительно оси параболы и найти значения функции в этих точках; построить эти точки.
- Провести параболу через полученные точки ( при необходимости берут ещё пару дополнительных точек, симметричных относительно оси параболы).
Зная алгоритм построения, можно значительно сократить время на дальнейшее исследование графика функции.
solodenkovagalina.blogspot.com
Построение графиков линейной и квадратичной функций
Найти Поиск Опубликовать работу Личный кабинет Главная Положение о фестивале и конкурсах- Положение о фестивале
- Краткая информация
- Расчет стоимости участия в фестивале
- Общие положения и ключевые сроки
- Порядок участия в фестивале
- Подготовка мастер-класса и видеоурока
- Соблюдение авторских прав третьих лиц
- Технические требования
- Положение о конкурсе презентаций «Презентация к уроку»
Содержание:
Разделы
Конкурс «Презентация к уроку» Конкурс по экологии «Земля — наш общий дом» Конкурс «Электронный учебник на уроке» Конкурс «История регионов России»Астрономия Биология Начальная школа География Иностранные языки Информатика История и обществознание Краеведение Литература Математика Музыка МХК и ИЗО ОБЖ ОРКСЭ Русский язык Руководство учебным проектом Спорт в школе и здоровье детей Технология Физика Химия Экология Экономика
Администрирование школы Видеоурок Внеклассная работа Дополнительное образование Инклюзивное образование Классное руководство Коррекционная педагогика Логопедия Мастер-класс Общепедагогические технологии Организация школьной библиотеки Патриотическое воспитание Профессия — педагог Работа с дошкольниками Работа с родителями Социальная педагогика Урок с использованием электронного учебника Школьная психологическая служба
xn--i1abbnckbmcl9fb.xn--p1ai
