Число Пи — значение, история, кто придумал

Все окружности похожи
Если сравнить окружности отличных друг от друга размеров, то можно заметить следующее: размеры разных окружностей пропорциональны. А это значит, что при увеличении диаметра окружности в некоторое количество раз, увеличивается и длина этой окружности в такое же количество раз. Математически это записать можно так:
| C1 | C2 | ||
| = | |||
| d1 | d2 |
где C1 и С2 – длины двух разных окружностей, а d1 и d2 – их диаметры.
Это соотношение работает при наличии коэффициента пропорциональности – уже знакомой нам константы π. Из отношения (1) можно сделать вывод: длина окружности C равна произведению диаметра этой окружности на независящий от окружности коэффициент пропорциональности π:
C = πd.
Также эту формулу можно записать в ином виде, выразив диаметр d через радиус R данной окружности:
С = 2πR.
Как раз эта формула и является проводником в мир окружностей для семиклассников.
Еще с древности люди пытались установить значение этой константы. Так, например, жители Месопотамии вычисляли площадь круга по формуле:
| C2 | |||
| S | = | , | |
| 12 |
где S – площадь круга, C – длина окружности (круга). Если в эту формулу подставить уже знакомые школьнику выражения площади круга S = πr2 и длины окружности С = 2 πR, то мы получим:
| (2πR)2 | ||
| πR2 | = | |
| 12 |
, откуда π = 3.
В древнем Египте значение для π было точнее. В 2000-1700 годах до нашей эры писец, именуемый Ахмесом, составил папирус, в котором мы находим рецепты разрешения различных практических задач. Так, например, для нахождения площади круга он использует формулу:
| 8 | 2 | |||||
| S | = | ( | d | ) | ||
| 9 |
Из каких соображений он получил эту формулу? – Неизвестно. Вероятно, на основе своих наблюдений, впрочем, как это делали и другие древние философы.
По стопам Архимеда
— Какое из двух числе больше 22/7 или 3.14 ?
— Они равны.
— Почему ?
— Каждое из них равно π.
А. А. Власов. Из Экзаменационного билета.
Некоторы полагают, что дробь 22/7 и чисо π тождественно равны. Но это является заблуждением. Помимо вышеприведенного неверного ответа на экзамене (см. эпиграф) к этой группе можно также добавить одну весьма занимательную головоломку. Задание гласит: «переложите одну спичку так, чтобы равенство стало верным».
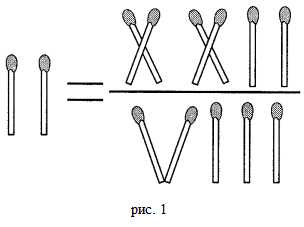
Решение будет таковым: нужно образовать «крышу» для двух вертикальных спичек слева, используя одну из вертикальных спичек в знаменателе справа. Получится визуальное изображение буквы π.
Многие знают, что приближение π = 22/7 определил древнегреческий математик Архимед. В честь этого часто такое приближение называют «Архимедовым» числом. Архимеду удалось не только установить приближенное значение для π, но также найти точность этого приближения, а именно – найти узкий числовой промежуток, которому принадлежит значение π. В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:
| 10 | 6336 | 14688 | 1 | |||||||||
| 3 | < | < | π | < | < | 3 | ||||||
| 71 | 1 | 1 | 7 | |||||||||
| 2017 | 4673 | |||||||||||
| 4 | 2 | |||||||||||
можно записать проще: 3,140 909 < π < 3,1 428 265…
Как видим из неравенств, Архимед нашел довольно-таки точное значение с точностью до 0,002. Самое удивительно то, что он нашел два первых знака после запятой: 3,14… Именно такое значение чаще всего мы используем в несложных расчетах.
Практическое применение
Едут двое в поезде:
− Вот смотри, рельсы прямые, колеса круглые.
Откуда же стук?
− Как откуда? Колеса-то круглые, а площадь
круга пи эр квадрат, вот квадрат-то и стучит!
Как правило, знакомятся с этим удивительным числом в 6-7 классе, но более основательно им занимаются к концу 8-го класса. В этой части статьи мы приведем основные и самые важные формулы, которые пригодятся вам в решении геометрических задач, только для начала условимся принимать π за 3,14 для удобства подсчета.
Пожалуй, самая известная формула среди школьников, в которой используется π, это – формула длины и площади окружности. Первая – формула площади круга – записывается так:
где S – площадь окружности, R – ее радиус, D – диаметр окружности.
Длина окружности, или, как ее иногда называют, периметр окружности, вычисляют по формуле:
С = 2 πR = πd,
где C – длина окружности, R – радиус, d – диаметр окружности.
Понятно, что диаметр d равен двум радиусам R.
Из формулы длины окружности можно легко найти радиус окружности:
| C | C | ||
| R= | = | ||
| 2π | d |
Обозначения для этих формул остаются те же.
Диаметр окружности можно найти по формуле:
где D – диаметр, С – длина окружности, R – радиус окружности.
Это базовые формулы, знать которые должен каждый ученик. Также иногда приходится вычислять площадь не всей окружности, а только ее части – сектора. Поэтому представляем вам её – формулу для вычисления площади сектора окружности. Выглядит она так:
| α | |||
| S | = | πR2 | |
| 360˚ |
где S – площадь сектора, R – радиус окружности, α – центральный угол в градусах.
Такое загадочное 3,14
И правда, оно загадочно. Потому что в честь этих магических цифр устраивают праздники, снимают фильмы, проводят общественные акции, пишут стихи и многое другое.
Например, в 1998 году вышел фильм американского режиссера Даррена Аронофски под названием «Пи». Фильм получил множество наград.
Каждый год 14 марта в 1:59:26 люди, интересующиеся математикой, празднуют «День числа Пи». К празднику люди подготавливают круглый торт, усаживаются за круглый стол и обсуждают число Пи, решают задачи и головоломки, связанные с Пи.
Вниманием это удивительное число не обошли и поэты, неизвестный написал:
Надо только постараться и запомнить всё как есть – три, четырнадцать, пятнадцать, девяносто два и шесть.
Давайте развлечемся!
Вашему вниманию предлагаются интересные ребусы с числом Пи. Разгадайте слова, какие зашифрованы ниже.
1. π р
2. π L
3. π k
Ответы: 1. Пир; 2. Надпил; 3. Писк.
Число Пи — справочные материалы
Чему равно число Пи
Как запомнить число Пи
Число Пи в Excel
Число Пи на клавиатуре и в Word
Фотографии числа Пи
calculator888.ru
Число «Пи»
14 мар 2012
14 марта математики отмечают один из самых необычных праздников — Международный день числа «Пи». Эта дата выбрана неслучайно: числовое выражение π (Пи) — 3,14 (3 месяц (март) 14 число).
Впервые с этим необычным числом школьники сталкиваются уже в младших классах при изучении круга и окружности. Число π — математическая константа, которая выражает отношение длины окружности к длине ее диаметра. Т.е если взять окружность с диаметром равным единице, то длина окружности и будет равна числу «Пи». Число π имеет бесконечную математическую продолжительность, но в повседневных вычислениях используют упрощенное написание числа, оставляя только два знака после запятой, — 3,14.
В 1987 году этот день отмечался впервые. Физик Ларри Шоу из Сан-Франциско заметил, что в американской системе записи дат (месяц / число) дата 14 марта — 3/14 совпадает с числом π (π = 3,1415926…). Обычно празднования начинаются в 1:59:26 дня (π = 3,1415926…).
История числа «Пи»
Предполагается, что история числа π начинается в Древнем Египте. Египетские математики определяли площадь круга диаметром Dкак (D-D/9)2. Из данной записи видно, что в то время число π приравнивали к дроби (16/9)2, или 256/81, т.е. π 3,160…
В VI в. до н.э. в Индии в религиозной книге джайнизма есть записи, свидетельствующие о том, что число π в то время принимали равным квадратному корню из 10, что даёт дробь 3,162…
В III в. до н.э.Архимед в своей небольшой работе «Измерение круга» обосновал три положения:
- Всякий круг равновелик прямоугольному треугольнику, катеты которого соответственно равны длине окружности и её радиусу;
- Площади круга относятся к квадрату, построенному на диаметре, как 11 к 14;
- Отношение любой окружности к её диаметру меньше 3 1/7 и больше 3 10/71.
Последнее положение Архимед обосновал последовательным вычислением периметров правильных вписанных и описанных многоугольников при удвоении числа их сторон. По точным расчётам Архимеда отношение окружности к диаметру заключено между числами 3*10 / 71и 3*1/7, а это означает, что число «пи» равно 3,1419… Истинное значение этого отношения 3,1415922653…
В V в. до н.э. китайский математик Цзу Чунчжи нашёл более точное значение этого числа: 3,1415927…
Впервой половине XV в. астроном и математикал-Каши вычислил π с 16 десятичными знаками.
Спустя полтора столетия в Европе Ф.Виетнашёл число π только с 9 правильными десятичными знаками: он сделал 16 удвоений числа сторон многоугольников. Ф.Виетпервым заметил, что π можно отыскать, используя пределы некоторых рядов. Это открытие имело большое значение, оно позволило вычислить π с какой угодно точностью.
В 1706 г английский математик У.Джонсон ввёл обозначение отношения длины окружности к диаметру и обозначил его современным символом π первой буквой греческого слова periferia—окружность.
На протяжении длительного периода времени учёные всего мира пытались разгадать тайну этого загадочного числа.
В чем же сложность вычисления значения π ?
Число π является иррациональным: его невозможно выразить в виде дроби p/q, где p и q целые числа, данное число не может быть корнем алгебраического уравнения. Нельзя указать алгебраическое или дифференциальное уравнение, корнем которого будет π, поэтому данное число называется трансцендентным и вычисляется путём рассмотрения какого-либо процесса и уточняется за счет увеличения шагов рассматриваемого процесса. Множественные попытки просчитать максимальное количество знаков числа π привели к тому, что сегодня, благодаря современной вычислительной технике, можно рассчитать последовательность с точностью в 10 триллионов цифр после запятой.
Цифры десятичного представления числа π достаточно случайны. В десятичном разложении числа можно найти любую последовательность цифр. Предполагают, что в данном числе в зашифрованном виде есть все написанные и ненаписанные книги, любая информация, которую только можно представить, находится в числе π.
Можете сами попробовать разгадать тайну этого числа самостоятельно. Записать число «Пи» полностью, конечно не получится. Но самым любопытным предлагаю рассмотреть первые 1000 знаковчисла π = 3,
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989
Запоминаем число «Пи»
В настоящее время с помощью вычислительной техники вычислено в десять триллионов знаков числа «Пи». Максимальное число цифр, которое смог запомнить человек составляет сто тысяч.
Чтобы запомнить максимальное количество знаков числа «Пи», используют различные стихотворные «запоминалки», в которых слова с определённым количеством букв располагаются в такой же последовательности, как цифры в числе «Пи»: 3,1415926535897932384626433832795…. Для восстановления числа необходимо подсчитать число символов в каждом из слов и записать по порядку.
Вот и знаю я число, именуемое «Пи». Молодец! (7 цифр)
Вот и Миша и Анюта прибежали
Пи узнать число они желали. (11 цифр)
Это я знаю и помню прекрасно:
Пи многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду. (21 цифра)
Раз у Коли и Арины
Распороли мы перины.
Белый пух летал, кружился,
Куражился, замирал,
Ублажился,
Нам же дал
Головную боль старух.
Ух, опасен пуха дух! (25 знаков)
Можно использовать рифмованные строки, которые помогают запомнить нужное число.
Чтобы нам не ошибиться,
Нужно правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть
Если очень постараться,
Можно сразу пи прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.
Можно просто постараться
И почаще повторять:
«Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять».
Остались вопросы? Хотите знать больше о числе «Пи»?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
www.tutoronline.ru
| ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Таблица значений тригонометрических функций составлена для углов в 0, 30, 45, 60, 90, 180, 270 и 360 градусов и соответствующих им значений углов врадианах. Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций. В таблице значений для тригонометрической функции синус приведены значения для следующих углов: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 в градусной мере, что соответствует sin 0 пи, sin пи/6, sin пи/4, sin пи/3, sin пи/2, sin пи, sin 3 пи/2, sin 2 пи в радианной мере углов. Школьная таблица синусов. В таблице значений тригонометрических функций нестандартных углов приводятся значения синуса, косинуса, тангенса и котангенса для углов в градусах 15, 18, 22,5, 36, 54, 67,5 72 градусов и в радианах пи/12, пи/10, пи/8, пи/5, 3пи/8, 2пи/5 радиан. Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах. |
zadocs.ru
