Тесты по тригонометрии
Разделы: Математика
Вариант № 1
Часть 1
- Выразить в радианах угол α = 20°
1) π/5 2) π/7 3) π/9 4) π/10
- Выразить в градусах угол α = 4π/45
1) 16º 2) 15º 3) 20º 4) 35º
- Какой четверти числовой окружности принадлежит точка t = 19π/4
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 3cos2α — 6 + 3sin2α
1) 1 2) -5 3) 3 4) -3
1) 4,56 2) 3,6 3) 4,6 4) 8,4
- Упростить выражение: sin4α — sin6α + cos2α + cos4α — cos6α
1) cos10α + cos2α 2) 2cos2α 3) cosα — cos6α 4) cos2α + sin10α
- Упростить выражение
1) sinα 2) -sinα 3) 2cosα + sinα 4) cosα + sinα
- Найти область значений функции y = sin2x
1) [-1;1] 2) [-2;2] 3) [0;-2] 4) [-2;0]
- Найти tgα, если cosα = -2/3 и
- Решить уравнение sin2x = 1/2
Часть 2
- Найти значение выражения .
- Решить уравнение 2sin22x + 7cos2x = 3
- Решить уравнение 6sin2x + sinx — cosx — cos2x = 2
- Найти значение выражения 169sin2x, если cosx = -5/13, -π < x < 0
- Сколько корней имеет уравнение
- Найти наименьшее целое значение функции .
Вариант № 2
Часть 1
- Выразить в радианах угол α = 240°
1) 4π/5 2) 2π/3 3) 4π/3 4) 3π/2
- Выразить в градусах угол α = 5π/36
1) 40º 2) 35º 3) 25º 4) 50º
- Какой четверти числовой окружности принадлежит точка t = -23π/6
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 9cos2α — 16 + 9sin2α
1) 2 2) -25 3)-15 4) -7
- Найти значение выражения 3 — 2tg2x · cos2x, если sinx = 0,1
1) 2,8 2) 1,02 3) 2,98 4) 3,02
- Упростить выражение: cos3α — cos2α — cosα — sin3α — sin2α
1) cos5α — cosα 2) 0 3) sinα — cosα 4) cos5α + cosα
- Упростить выражение
- Найти множество значений функции y = sinx — 3
1) [-4;0] 2) [-4;-2] 3) [-3;3] 4) [-3;-2]
- Найти значение выражения
- Решить уравнение
Часть 2
- Найти значение выражения .
- Решить уравнение 2sin2x + 7cosx + 2 = 0
- Решить уравнение 2sin2x -3sinx · cosx + 3cos2x = 2
- Найти значение выражения 5sin2x, если
- Сколько корней имеет уравнение
- Найти наибольшее целое значение функции
Вариант № 3
Часть 1
- Выразить в радианах угол α = 50°
1) 3π/5 2) 6π/7 3) 4π/9 4) 5π/18
- Выразить в градусах угол α = 49π/36
1) 230º 2) 245º 3) 240º 4) 265º
- Какой четверти числовой окружности принадлежит точка t = 37π/4
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: -3cos2α + 8 — 3sin2α
1) 5 2) -5 3)3 4) -3
- Найти значение выражения 3 + 2tg2x · cos2x, если sinx = 0,3
1) 3,18 2) 3,6 3) 4,8 4) 4,82
- Упростить выражение: cos5α · cos7α — cosα + sin5α · sin7α
1) cos12α — cosα 2) sin12α — cosα 3) sin2α — cosα 4) cos2α — cosα
- Упростить выражение
1) sin2α 2) cos2α 3) 3cos2α 4) cos3α
- Найти множество значений функции y = 3sinx — 2
1) [-5;1] 2) [-1;1] 3) (-∞; +∞) 4) [-1;5]
- Найти значение выражения
1) √3 2) √3 + 1 3) 1/2 + 3√3 4) 1
- Решить уравнение 2cos2x — 3sinx = 1/2
Часть 2
- Найти значение выражения
- Решить уравнение 2sin2x + 1 = 5cosx
- Решить уравнение 4sin2x + sinx — cosx + cos2x = 2
- Найти значение выражения 26sin2x, если
- Сколько корней имеет уравнение
- Найти наибольшее целое значение функции
Вариант № 4
Часть 1
- Выразить в радианах угол α = 315°
1) 7π/4 2) 4π/7 3) 5π/9 4) 3π/10
- Выразить в градусах угол α = 13π/9
1) 245º 2) 250º 3) 275º 4) 260º
- Какой четверти числовой окружности принадлежит точка t = 27π/4
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 1,5cos2α — 6,5 + 1,5sin2α
1) 1 2) -5 3)3 4) -3
- Найти значение выражения 7sin2x — 3, если cos 2x = 0,7
1) 1 2) -0,9 3) -1,2 4) -1
- Упростить выражение: 2cosα — cosα + sin2α — sinα — sin(α — 6π)
1) cos3α + sinα 2) 2sinα 3) 0 4) cos3α — sinα
- Упростить выражение
1) sin2x 2) -sin2x 3) 4) cos2x
- Найти множество значений функции y = cosx — 3
1) [-1;1] 2) [2;4] 3) [-4;-2] 4) [-3;-2]
- Найти значение выражения
1)1,5 2) 2√3 3) 1 — √3 4) 0,5
- Решить уравнение 2cos 2x — 3sinx = 0
Часть 2
- Найти значение выражения
- Решить уравнение 2cos 2x + 9sinx = 6
- Решить уравнение 4sin2x — 4sinx — cosx + 6cos2x = 3
- Найти значение выражения 7tg2α, если
- Сколько корней имеет уравнение
- Найти наименьшее значение функции
Вариант № 5
Часть 1
- Выразить в радианах угол α = 210°
1) 7π/5 2) 5π/7 3) 7π/6 4) 4π/5
- Выразить в градусах угол α = 19π/9
1) 320º 2) 365º 3) 380º 4) 375º
- Какой четверти числовой окружности принадлежит точка t = 31π/3
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 10cos2α — 7 + 10sin2α
1) 1 2) -5 3)3 4) -3
- Найти значение выражения 6sin2x — 3, если cos2x = 0,3
1) -1,4 2) -0,2 3) 1,2 4) 0,8
- Упростить выражение: sin3α — cos2α + sin2α — cos3α — cos(2π -α)
1) cos3α + sinα 2) 2sinα 3)0 4) cos3α — sinα
- Упростить выражение
1) -6sinx 2) 2sinx 3) 3cosx — sinx 4) -2sinx
- Найти множество значений функции y = sinx + 2
1) [-1;1] 2) [0;2] 3) [1;3] 4) [2;3]
- Найти значение tgα, если
1) -2 2) 2 3) 0,5 4) -0,5
- Решить уравнение 1 + 2cosx — sin2x = 0
Часть 2
- Найти значение выражения
- Решить уравнение 2cos2x = 11sinx + 7
- Решить уравнение sin2x — 2sinx — cosx = cos2x + 1
- Найти значение выражения
- Сколько корней имеет уравнение
- Найти наибольшее целое значение функции
Вариант № 6
Часть 1
- Выразить в радианах угол α = 330°
1) 11π/6 2) 11π/5 3) 10π/9 4) 9π/10
- Выразить в градусах угол α = 2π/5
1) 72º 2) 75º 3) 65º 4) 52º
- Какой четверти числовой окружности принадлежит точка t = -41π/3
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 13cos2α — 15 + 13sin2α
1) 2 2) -2 3) 0 4) 28
- Найти значение выражения 5cos2x — 3, если sin2x = 0,2
1) 1,2 2) 2,1 3) -1 4) 1
- Упростить выражение: sin2,5α — cos1,5α + sin1,5α — cos2,5α + cos(4π — α)
1) sin4α — cosα 2) sinα + cosα 3) sinα — cosα 4) cosα + sin4α
- Упростить выражение
1) sinα 2) cosα 3) cosα + 2sinα 4) 2cosα + sinα
- Найти наибольшее значение функции y = 2cosx — 14
1) -16 2) 2 3) -14 4) -12
- Найти значение выражения
- Решить уравнение
Часть 2
- Найти значение выражения
- Решить уравнение cos2x + 2 sinx = 2
- Решить уравнение 8sin2x + 3sinx — cosx + cos2x = 3
- Найти значение выражения
- Найти сумму корней уравнения принадлежащих промежутку [0; -2π]
- Найти наименьшее целое значение функции
8.07.2010
xn--i1abbnckbmcl9fb.xn--p1ai
Тест по теме «Основы тригонометрии»
Дисциплина «Математика».
Раздел «Основы тригонометрии».
Тест разработан для учащихся 10-11 классов, а также студентов 1 курса СПО, обучающихся на базе 9 классов.
Вопросы теста
Косинусом называется … точки единичной окружности.
абсцисса
ордината
координата
затрудняюсь ответить
Тангенс углаопределяется отношением
нет правильного ответа
Если угол содержит градусов, то его радианная мера равна
При каких значениях угла (в градусной мере) не существует тангенс?
Установите соответствие между видами тригонометрических уравнений.
Тригонометрическое уравнение, приводимое к квадратному
Однородное тригонометрическое уравнение
Простейшее тригонометрическое уравнение
Тригонометрическое уравнение, решаемое с помощью формул преобразования суммы одноименных тригонометрических функций в произведении
Если существует такое число Т (называемое периодом), что для всех х выполняется равенство и , то функция называется …
периодической
тригонометрической
нечетной
простейшей
Укажите функцию с периодом :
На единичной окружности тангенс – это
ордината
абсцисса
отношение абсциссы к ординате
отношение ординаты к абсциссе
установите соответствие:
основное тригонометрическое тождество
формула половинного аргумента
формула сложения аргументов
формула двойного аргумента
Сжатие функции произойдет, если
Установите соответствие между тригонометрическим уравнением и его решением
При , какое из уравнений не будет иметь решения?
Область определения функции
R
Q
Ординатой точки единичной окружности называется:
косинусом
котангенсом
синусом
тангенсом
Абсциссой точки единичной окружности называется:
котангенсом
синусом
тангенс
косинусом
Основное тригонометрическое тождество имеет вид:
sin2 х — cos2х = 1
sin х + cos x = 0
sin2x + cos 2х= 1
sin x + cos x — 1
Какая из функций является четной:
tg х
Укажите неверное утверждение
 a.
a. b.
b.c.
 d.
d.
Продолжить выражение …
cos 2x
sin 2x
tg 2x
нет ни одного верного
Множество значений функций у = sin x, у = cos x является отрезок:
[-1;1)
(-1;1]
(-1;0)
[-1;1]
Арккосинусом числа а называется такое число из отрезка … косинус которого равен а
Период функций у = cos x, у = sin x равен
Определить соответствие
tga ctga
1
-cos2a — sin2a
cos2a — sin2a
cos2a
-1
Установите соответствие между радианной и градусной мерой
2100
1500
750
2250
При построении графика функции у = sin2x произойдет
растяжение по оси ОУ
сжатие по оси ОУ
сжатие по оси ОХ
растяжение по оси ОХ
Какие из функций являются нечетными
у = tg х, у = ctg x, у = cos х
у = tg x, у = sin x, у = cos х
у = tg х, у = ctg х, y = sin x
у = ctg x , у = sin x, у = cos х
Арктангенсом числа a называется такое число из интервала …, тангенс которого равен α.
Арккотангенсом числа а называется такое число из интервала …, котангенс которого равен α.
Синус двойного аргумента определяется формулой
2sin а + 2cos а
в радианной мере угол в 1200
Выразите в градусах
900
1800
2700
1500
Установите соответствие
При построение графика функции у = 2sin x произойдет:
растяжение функции у = sin x вдоль оси ОХ
сужение функции у = sin x вдоль оси ОХ
растяжение функции у = sin x вдоль оси 0Y
сужение функции у = sin x вдоль оси 0Y
Найдите число arctg 0
0
затрудняюсь ответить
Существует ли arсctg 0
да
нет
затрудняюсь ответить
Продолжить выражение cos cos + sin sin
cos ( — )
sin ( — )
cos ( + )
sin ( + )
Упростите
a.
b.
c.
d.
Укажите выражения, имеющие знак плюс
cos 2500·sin 3300
tg 1750·ctg 2000
cos 1000·sin 1000
cos 1500·sin 1500
Преобразуйте
cos2
sin2
sin ·cos
затрудняюсь ответить
Какая функция на отрезке является возрастающей
sin x
tg x
cos x
ctg x
Ключи к тесту.
1
2
3
4
5
6
7
8
9
10
a
a
b
c
1a, 2d,
3c, 4b
a
b
d
1a, 2c, 3b, 4d
c
11
12
13
14
15
16
17
18
19
20
1c, 2b, 3d, 4a
a
c
c
d
c
b
d
b
d
21
22
23
24
25
26
27
28
29
30
a
c
1a, 2d, 3c, 4b
1b, 2c, 3a, 4d
c
c
d
c
a
b
31
32
33
34
35
36
37
38
39
40
c
1d, 2a, 3c, 4b
c
b
a
a
d
a
b
c
Шарапова Юлия Владимировна,
преподаватель математики
ОАОУ СПО «Астраханский социально педагогический колледж»,
414040 г. Астрахань, ул. Коммунистическая , 48
infourok.ru
Тест по тригонометрии с ответами
Тест по тригонометрии с ответами — Gee Test наверхNotice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 1 из 3
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 2 из 3
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 3 из 3
- 1. -2
- 2. 2sina
- 3. -2sina
- 4. -2cosa
- 1. tg2a
- 2. ctg2a
- 3. 2tg2a
- 4. sin2a
- 1. 2
- 2. 2sina
- 3. 2cosa
- 4. -2
- 1. cos2а
- 2. ctg2a
- 3. tg2a
- 4. -tg2a
- 1. -,+,-
- 2. +,-,-
- 3. -,-,+
- 4. -,-,-
- 1. 2sina
- 2. ctga
- 3. 4tga
- 4. 2tga
- 1. +,+,-
- 2. +,-,+
- 3. -,-,-
- 4. +,-,-
- 1. cosa
- 2. sina
- 3. -cosa
- 4. -2sina
- 1. 0
- 2. √3/2
- 3. 1/2
- 4. √2/2
- 1. 1/3
- 2. -1/2
- 3. -1/3
- 4. 1/2
- 1. 1/4
- 2. 3/8
- 3. 3/4
- 4. √3/2
- 1. √3/2
- 2. 1
- 3. 1/2
- 4. √2/2
- 1. 1/3
- 2. -1/4
- 3. -1/3
- 4. -4
- 1. -,-,-
- 2. -,-,+
- 3. +,-,-
- 4. -,+,-
- 1. -,+,-
- 2. -,+,+
- 3. -,-,-
- 4. +,+,-
- 1. +,+,-
- 2. -,-,-
- 3. +,-,-
- 4. -,+,-
- 1. -,-,-
- 2. +,+,-
- 3. +,-,-
- 4. -,-,+
- 1. +,-,+
- 2. -,+,+
- 3. -,+,-
- 4. +,-,-
- 1. 3ctg2a
- 2. 3tg2a
- 3. 1,5ctg2a
- 4. tg2a
- 1. +,-,+
- 2. -,+,+
- 3. +,+,+
- 4. +,+,-
- 1. 2sina
- 2. tga
- 3. 2ctga
- 4. ctga
- 1. -,+,-
- 2. +,+,-
- 3. +,-,+
- 4. +,+,+
- 1. +,+,-
- 2. -,+,-
- 3. -,+,+
- 4. +,+,+
- 1. +,+,-
- 2. -,+,+
- 3. -,+,-
- 4. -,-,-
- 1. -,-,+
- 2. -,-,-
- 3. +,+,-
- 4. +,-,-
- 1. +,+,-
- 2. +,-,-
- 3. +,+,+
- 4. -,+,-
- 1. +,+,-
- 2. +,-,-
- 3. -,-,-
- 4. +,-,+
- 1. -,+,-
- 2. +,+,-
- 3. +,+,+
- 4. -,-,-
- 1. 1/sina
- 2. 1/2cosa
- 3. 1/cosa
- 4. 1/2sina
- 1. tga
- 2. cosa
- 3. -cosa
- 4. 2sina
- 1. 1/2 sin22a
- 2. sin22a
- 3. cos22a
- 4. 1/2 cos22a
- 1. 1/sin2a
- 2. 1/(2sin2a)
- 3. -1/(2sin2a)
- 4. 1/(2cos2a)
- 1. -sin2a·tg2a
- 2. -sin2a
- 3. cos2a·ctg2a
- 4. -cos2a
- 1. cos2a/2
- 2. 1 / sin2a
- 3. tga/2
- 4. cos2a / 2
- 1. √2/2
- 2. 1
- 3. 0
- 4. √3/2
- 1. -π/6 + πk, k Є Z
- 2. -π/4 + πk, k Є Z
- 3. π/6 + πk, k Є Z
- 4. π/4 + πk, k Є Z
- 1. I или IV
- 2. II или III
- 3. I или II
- 4. I или III
- 1. 2/3
- 2. 1/3
- 3. π/3
- 4. -2/3
- 1. III или IV
- 2. II или III
- 3. I или II
- 4. I ИЛИ III
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 1 из 3
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 2 из 3
Notice: Undefined offset: 3 in /home/o/oldkyx/geetest/public_html/pages/tests/list/list_pages.php on line 35
Страница 3 из 3
geetest.ru
Тест с ответами по тригонометрии старшие классы
Тема: Тригонометрия
1. tg(x)=
+a)sin(x)/cos(x)
б)cos(x)/sin(x)
в)все вышеперечисленное
2. Что такое синус угла в прямоугольном треугольнике?
+а)отношение противолежащего катета к гипотинузе
б)отношение прилежащего катета к противолежащему
в)отношение прилежащего катета к гипотинузе
3. ctg(x)=
а)sin(x)+cos(x)
б)sin(x)/cos(x)
в)cos(x)/sin(x)
г)1/tg(x)
д)нет правильных ответов
+е) ответ в) и г)
4. cos(0)=
а)100
б)0
+в)1
5. sin(0)=
а)100
+б)0
в)1
6.
а)0
+б)1
в)-1
7.
а) sin(2x)
+б) cos(2x)
в)tg(2x)
8. sin(2x)=
+а)2*sin(x)*cos(x)
б) 2*tg(x)*cos(x)
в) 2*tg(x)*ctg(x)
9. tg(x)*ctg(x)=
а)0
+б)1
в)бесконечность
10. 2*cos(x+y)=
а) 2*(cos(x)*cos(y)+sin(x)*sin(y))
+б)2*(cos(x)*cos(y)-sin(x)*sin(y))
в) 2*(cos(x)*sin(y)-sin(x)*cos(y))
11. sin(x+y)=
а) cos(x)*sin(y)-sin(x)*cos(y)
+б) cos(x)*sin(y)+sin(x)*cos(y)
в) cos(x)*cos(y)+sin(x)*sin(y)
12. cos(-x)=
а)-cos(x)
+б)cos(x)
в)0
13. ctg(-x)=
+а)-ctg(x)
б)ctg(x)
в)tg(x)
14. sin(x+π)=
+а)-sin(x)
б)sin(π)
в)cos(x)
15. cos(x+π/2)=
+а)-sin(x)
б)cos(x)
в)sin(π/2)
16. sin(120)=
+а)cos(30)
б)sin(30)
в)tg(30)
17. cos(150)=
+а)-sin(60)
б)sin(60)
в)cos(60)
18. tg(x)*ctg(y)=
+а)1
б)0
в)100000
19. tg(x)+ctg(y)=
а)1
+б)1/(cos(x)*sin(x))
в)0
20. cos(α) может ли быть больше единицы?
а) не знаю
б)да
+в) нет
21. sin(α) может ли быть больше единицы?
а)не знаю
б)да
+в) нет
22. tg(α) может ли быть больше единицы?
а)нет
б)это не возможно
+в)да
23. sin(x)+sin(y)=
+а)2*sin((x+y)/2)*cos((x-y)/2)
б) 2*cos((x+y)/2)*cos((x-y)/2)
в) 2*sin((x+y)/2)*sin((x-y)/2)
24. tg(x)*tg(x)=
а) (1-sin(2x))/(1+cos(2x))
+б)(1-cos(2x))/(1+cos(2x))
в) 1/(1+cos(2x))
25. В каких четвертях cos(x) принимает положительные значения?
+а) I, IV
б)I, II
в)III, II
26. В каких четвертях sin(x) принимает положительные значения?
+а)I, II
б)I, III
в)II, IV
27. В каких четвертях tg(x), ctg(x) принимает положительные значения?
+а)I, III
б)I, II
в)II, IV
28. tg(x+y)=
а) (cos(x)+tg(y))/(1-tg(x)*tg(y))
+б)(tg(x)+tg(y))/(1-tg(x)*tg(y))
в) (ctg(x)+tg(y))/(1-tg(x)*tg(y))
29. Укажите график ctg(x)
а)
+б)
в)
30. Укажите график sin(x)
+а)
б)
в)
testdoc.ru
Тесты по тригонометрии , 4 варианта
ПОВТОРЕНИЕ ТРИГОНОМЕТРИИ.
Вариант 1.
1. Радианная мера двух углов треугольника равна  и
и 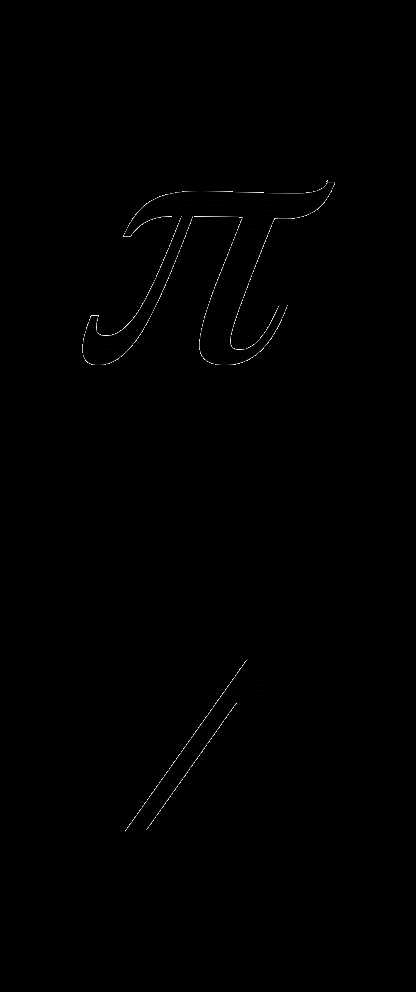 . Найдите градусную меру каждого угла треугольника.
. Найдите градусную меру каждого угла треугольника.
а) 750, 450 и 600; в) 600, 450 и 750;
б) 600, 550 и 650; г) другой ответ.
2. Найдите значение sin 1200.
а)  ; в) —
; в) — ;
;
б) 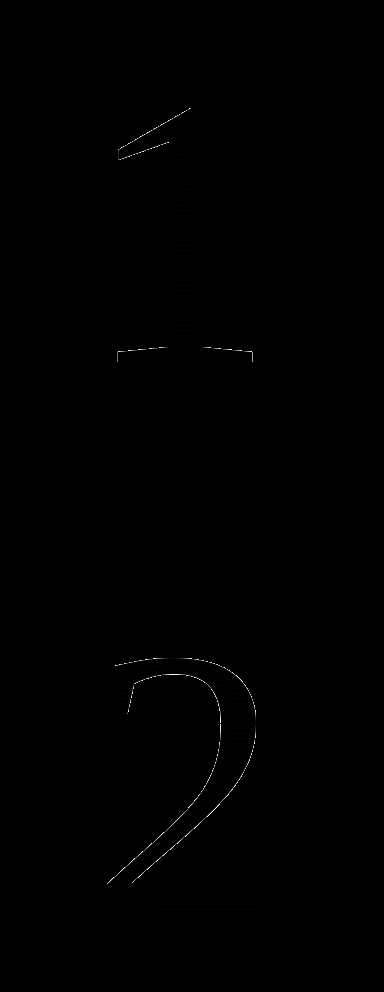 ; г) —
; г) — .
.
3. Какие из условий могут выполняться одновременно.
а) sin =1 и cos
=1 и cos =-1; в) sin
=-1; в) sin =0,3 и cos
=0,3 и cos =-0,7;
=-0,7;
б) sin =
= и cos
и cos =
= ; г) sin
; г) sin =
=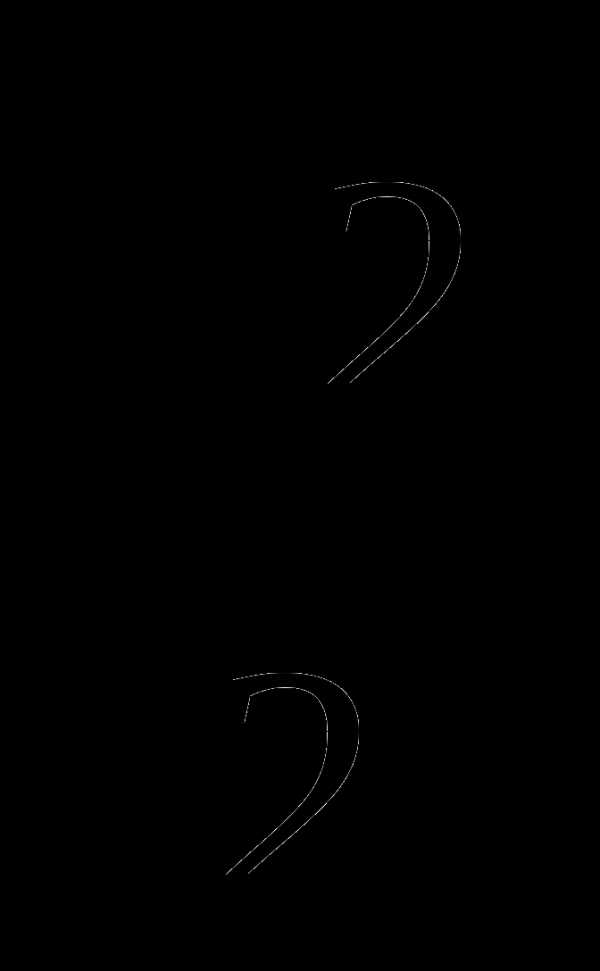 и cos
и cos =
= ?
?
4. Выберите верное утверждение:
а) ctg3,14>ctg3,15; в) ctg3,14=ctg3,15;
б) ctg3,14<ctg3,15; г) ctg3,14 – не имеет смысла.
5. Вычислите значение cos( —
— ), если cos
), если cos =-
=- , sin
, sin =
= ,
,  <
< <
< ;
;  <
< <
< .
.
а) — ; в)
; в)  ;
;
б) — ; г) другой ответ.
; г) другой ответ.
6. Какое из данных выражений положительно, если  =1000?
=1000?
а) sin
 cos
cos ; в) sin
; в) sin +cos
+cos ;
;
б) cos2 — sin2
— sin2 ; г) cos
; г) cos -sin
-sin .
.
7. Упростите выражение 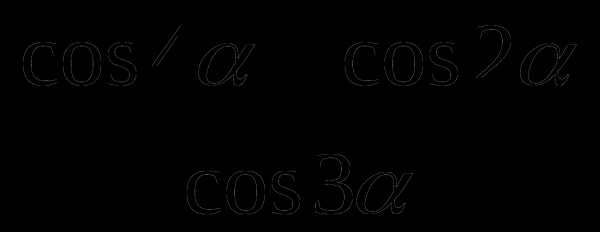 .
.
а) ctg ; в) cos
; в) cos ;
;
б) 2cos ; г) другой ответ.
; г) другой ответ.
8. Найдите tg2x+ctg2x, если tgx+ctgx=2.
а) 3; в) 2;
б) 4; г) другой ответ.
9. Какое из данных выражений равно sin150?
а)  ; в)
; в) 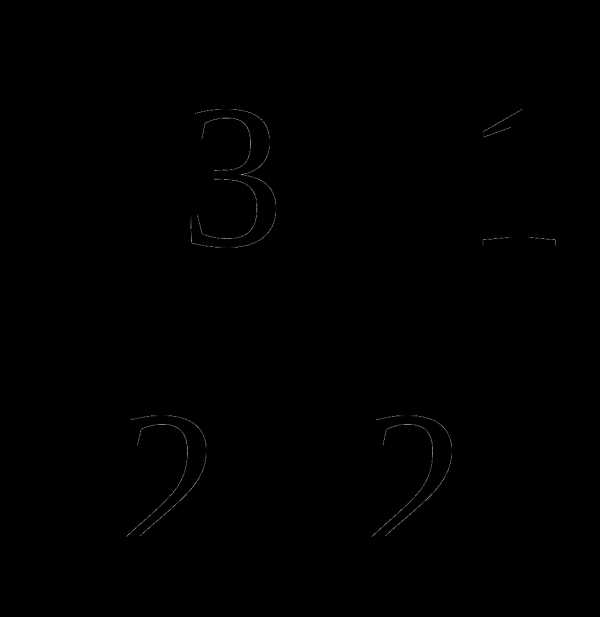 ;
;
б)  ; г) другой ответ.
; г) другой ответ.
10. При каком из данных значений x выражение 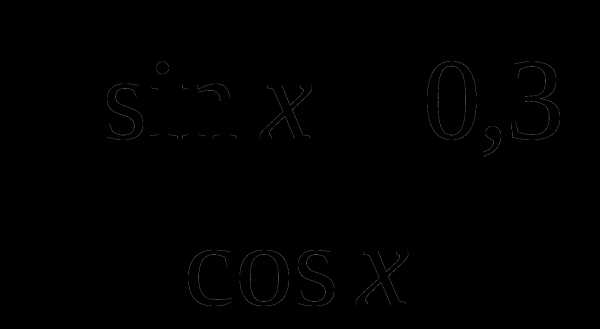 не имеет смысла?
не имеет смысла?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Вариант 2.
1. Градусная мера двух углов треугольника равна 360 и 900. Найдите радианные меры каждого угла треугольника.
а) ,
,  и
и 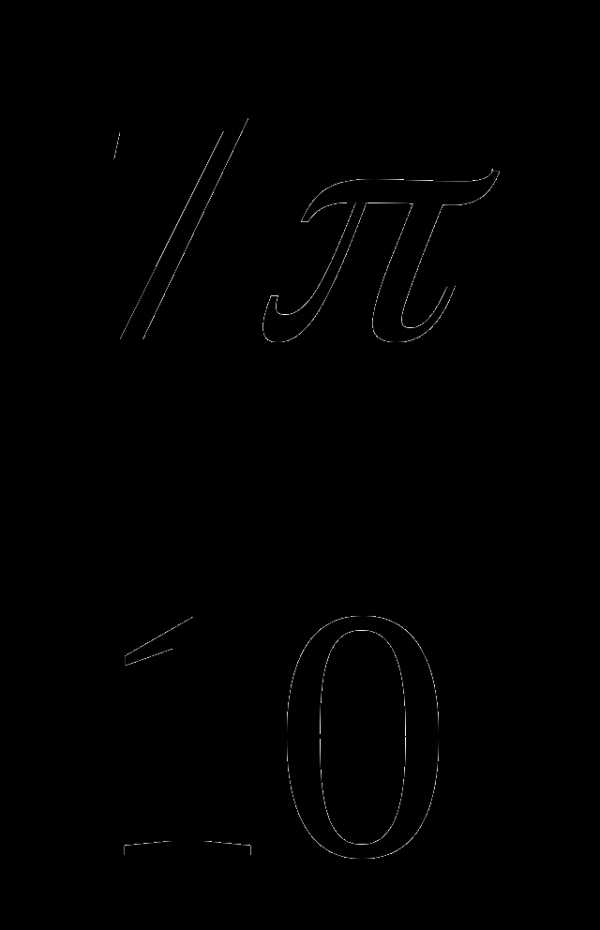 ; в)
; в) ,
,  и
и  ;
;
б) ,
,  и
и  ; г) другой ответ.
; г) другой ответ.
2. Найдите значение sin 1500.
а)  ; в) —
; в) — ;
;
б)  ; г) —
; г) — .
.
3. Какие из условий могут выполняться одновременно, если  угол второй четверти:
угол второй четверти:
а) sin =
= и cos
и cos =-
=- ; в) sin
; в) sin =
= и cos
и cos =
= ;
;
б) sin =
= и cos
и cos =
= ; г) sin
; г) sin =-
=- и cos
и cos =-
=- ?
?
4. Выберите верное утверждение:
а) tg1,57>tg1,58; в) tg1,57=tg1,58;
б) tg1,57<tg1,58; г) tg1,57 – не имеет смысла.
5. Вычислите значение cos( +
+ ), если cos
), если cos =-
=- , sin
, sin =
= ,
,  <
< <
< ; 0<
; 0< <
< .
.
а) ; в)-
; в)-  ;
;
б) -1; г) другой ответ.
6. Какое из данных выражений отрицательно, если  =800?
=800?
а) sin
 cos
cos ; в) sin
; в) sin +cos
+cos ;
;
б) cos2 — sin2
— sin2 ; г) sin
; г) sin — cos
— cos .
.
7. Упростите выражение 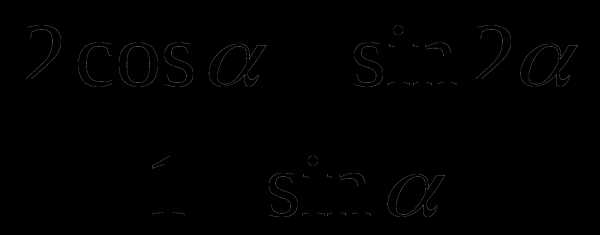 .
.
а) 2cos ; в) 2sin
; в) 2sin ;
;
б) cos ; г) другой ответ.
; г) другой ответ.
8. Найдите sinx cosx, если sinx+cosx=1.
cosx, если sinx+cosx=1.
а) 1; в) 0;
б)  4; г) другой ответ.
4; г) другой ответ.
9. Какое из данных выражений равно ctg750?
а)  -2; в)
-2; в)  ;
;
б)  ; г) другой ответ.
; г) другой ответ.
10. При каком из данных значений x выражение 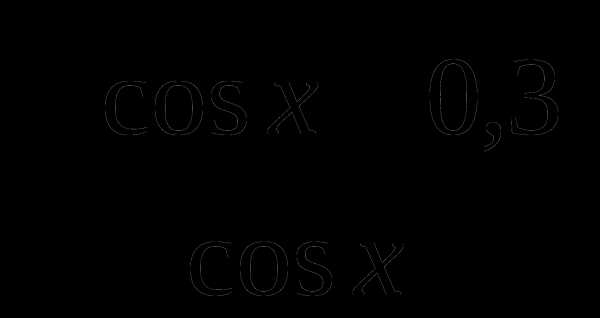 не имеет смысла?
не имеет смысла?
а)  ; б)
; б)  ; в)
; в)  ; г) 0.
; г) 0.
Вариант 3.
1. Радианная мера двух углов треугольника равна  и
и  . Найдите градусную меру каждого угла треугольника.
. Найдите градусную меру каждого угла треугольника.
а) 640, 360 и 800; в) 540, 260 и 1000;
б) 360, 240 и 1200; г) другой ответ.
2. Найдите значение tg1350.
а) -1; в) 1 ;
б) 0; г) — .
.
3. Какие из условий могут выполняться одновременно.
а) tg =1 и ctg
=1 и ctg =-1; в) tg
=-1; в) tg =
= и ctg
и ctg =
= ;
;
б) tg =
= и ctg
и ctg =
= ; г) tg
; г) tg =-
=- и ctg
и ctg =-
=- ?
?
4. Выберите верное утверждение:
а) sin3,14>sin3,15; в) sin3,14=sin3,15;
б) sin3,14г) sin3,14 =0.
5. Вычислите значение sin( —
— ), если cos
), если cos =-
=- , sin
, sin =
= ,
,  <
< <
< ;
;  <
< <
< .
.
а) 0; в)  ;
;
б) 1; г) другой ответ.
6. Какое из данных выражений положительно, если  =1400?
=1400?
а) sin
 cos
cos ; в) sin
; в) sin +cos
+cos ;
;
б) cos2 — sin2
— sin2 ; г) cos
; г) cos -sin
-sin .
.
7. Упростите выражение  .
.
а) 2sin ; в) -2sin
; в) -2sin ;
;
б) sin ; г) другой ответ.
; г) другой ответ.
8. Найдите tgx+ctgx, если tg2x+ctg2x=7, а x (
( ;
; ).
).
а) -3; в) 3;
б) 4; г) другой ответ.
9. Какое из данных выражений равно cos750?
а)  ; в)
; в) 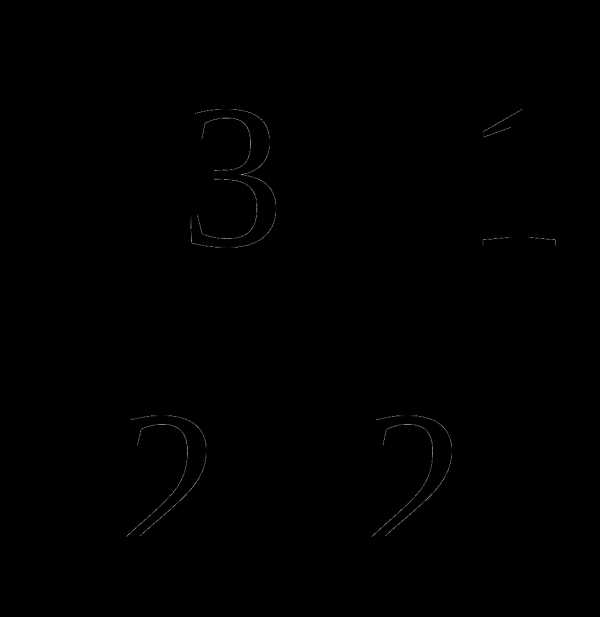 ;
;
б)  ; г) другой ответ.
; г) другой ответ.
10. При каком из данных значений x выражение  не имеет смысла?
не имеет смысла?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Вариант 4.
1. Градусная мера двух углов треугольника равна 1200 и 540. Найдите радианные меры каждого угла треугольника.
а) ,
,  и
и  ; в)
; в) ,
,  и
и  ;
;
б) ,
,  и
и  ; г) другой ответ.
; г) другой ответ.
2. Найдите значение ctg 1200.
а)  ; в) —
; в) — ;
;
б)  ; г) —
; г) — .
.
3. Какие из условий могут выполняться одновременно, если  угол третьей четверти:
угол третьей четверти:
а) tg =
= и ctg
и ctg =-
=- ; в) tg
; в) tg =-
=- и ctg
и ctg =
= ;
;
б) tg =
= и ctg
и ctg =
= ; г) tg
; г) tg =-
=- и ctg
и ctg =-
=- ?
?
4. Выберите верное утверждение:
а) cos1,57>cos1,58; в) cos1,57=cos1,58;
б) cos1,57г) cos1,57 =0.
5. Вычислите значение sin( +
+ ), если cos
), если cos =-
=- , sin
, sin =
= ,
,  <
< <
< ;
;  <
< <
< .
.
а) ; в)-
; в)-  ;
;
б) 0; г) другой ответ.
6. Какое из данных выражений отрицательно, если  =2000?
=2000?
а) sin
 cos
cos ; в) sin
; в) sin +cos
+cos ;
;
б) cos2 — sin2
— sin2 ; г) sin
; г) sin — cos
— cos .
.
7. Упростите выражение  .
.
а) -2sin ; в) 2sin
; в) 2sin ;
;
б) -sin ; г) другой ответ.
; г) другой ответ.
8. Найдите sinx cosx, если sinx-cosx=
cosx, если sinx-cosx= .
.
а) -0,5; в) 0,5;
б) — ; г) другой ответ.
; г) другой ответ.
9. Какое из данных выражений равно tg1050?
а)  +2; в) —
+2; в) — ;
;
б)  ; г) другой ответ.
; г) другой ответ.
10. При каком из данных значений x выражение 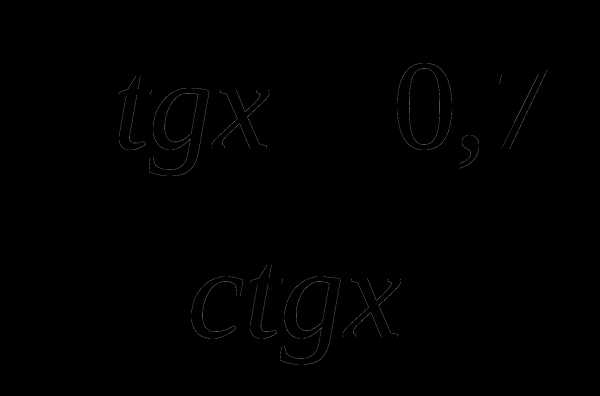 не имеет смысла?
не имеет смысла?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) .
.
№ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
В-1 | в | а | б | б | г | в | б | в | в | г |
В-2 | б | в | а | а | б | б | а | в | в | в |
В-3 | б | а | в | б | а | б | в | а | в | г |
В-4 | в | в | б | а | в | в | а | а | в | а |
www.metod-kopilka.ru
Тест по тригонометрии с ответами
Тест по тригонометрии с ответами — Gee Test наверх Страница 1 из 3Страница 2 из 3Страница 3 из 3- 1. cos2а
- 2. sin-2а
- 3. sin2а
- 4. cos-2а
- 1. -2/3
- 2. 1/4
- 3. π/4
- 4. -1/4
- 1. I или II
- 2. I или III
- 3. I или IV
- 4. II или IV
- 1. 1/2
- 2. 1/3
- 3. -1/2
- 4. 2/3
- 1. sin2a
- 2. sina
- 3. cosa
- 4. cos2a
- 1. ctg2a
- 2. tg2a
- 3. -tg2a
- 4. 1/tga
- 1. tga
- 2. cos2a
- 3. 1/cosa
- 4. ctg2a
- 1. -1/sin2a
- 2. -1/cos2a
- 3. 1/cos2a
- 4. 1/sin2a
- 1. -ctga
- 2. -tga
- 3. tga
- 4. -2cosa
- 1. ctg4a
- 2. 1/2 tg2a
- 3. tg4a
- 4. tg2a
- 1. ctga/2
- 2. ctga
- 3. tga/2
- 4. tga
- 1. 2
- 2. 1/cos2а
- 3. 2tg2а
- 4. 2ctg2а
- 1. 3/4
- 2. 1/4
- 3. 1/16
- 4. 3/8
- 1. -1/sin2x
- 2. -1/cos2x
- 3. 1/sin2x
- 4. 1/cos2x
- 1. tg3а
- 2. tga
- 3. 1
- 4. ctgа
- 1. (-1)k·(π/3) + 2πk, k Є Z
- 2. (-1)k·(π/6) + πk, k Є Z
- 3. (-1)k·(π/4) + 2πk, k Є Z
- 4. (-1)k+1·(π/3) + πk, k Є Z
- 1. π + 2πk, k Є Z
- 2. Ø
- 3. 2πk, k Є Z
- 4. π/4 + πk/2, k Є Z
- 1. 15°
- 2. 45°
- 3. 30°
- 4. 0°
- 1. ±π/3 + 2πk, k Є Z
- 2. π/2 + 2πk, k Є Z
- 3. (-1)k+1·(π/6) + πk; -π/2 + 2πk, k Є Z
- 4. π/2 + 2πk; (-1)k·(π/6) + πk, k Є Z
- 1. ±π/6 + πk, k Є Z
- 2. ±π/4 + πk, k Є Z
- 3. ±π/3 + πk, k Є Z
- 4. ±π/4 + 2πk, k Є Z
- 1. 3πk, k Є Z
- 2. π/2 + (π/3)k, k Є Z
- 3. π/4 + (π/2)k, k Є Z
- 4. (π/3)k, k Є Z
- 1. 45°
- 2. 90°
- 3. 30°
- 4. 60°
- 1. 2πk, k Є Z
- 2. (-1)k (π/6) + πk, k Є Z
- 3. π/2 + 2πk, k Є Z
- 4. π + 2πk, k Є Z
- 1. π/2 + 2πk, k Є Z
- 2. -π/2 + 2πk, k Є Z
- 3. πk, k Є Z
- 4. π + πk, k Є Z
- 1. π/6 + 2πk/3, k Є Z
- 2. ±π/3 + 2πk, k Є Z
- 3. π/4 + πk, k Є Z
- 4. -π/6 + 2πk/3, k Є Z
- 1. πk/2, k Є Z
- 2. πk, k Є Z
- 3. π/2 + πk, k Є Z
- 4. π/4 + (πk)/2, k Є Z
- 1. (π/12 + πk; 5π/12 + πk), k Є Z
- 2. (π/3 + 2πk; 2π/3 + 2πk), k Є Z
- 3. (π/6 + 2πk; 5π/6 + 2πk), k Є Z
- 4. (-7π/12 + πk; π/12 + πk), k Є Z
- 1. πk, k Є Z
- 2. π + 2πk, k Є Z
- 3. 2πk, k Є Z
- 4. π/2 + πk, k Є Z
- 1. 135°
- 2. 120°
- 3. 150°
- 4. 180°
- 1. πk, k Є Z
- 2. πk/5, k Є Z
- 3. πk/2, k Є Z
- 4. πk/4, k Є Z
- 1. Ø
- 2. π/2 + 2πk, k Є Z
- 3. π/2 + πk, k Є Z
- 4. x Є R
- 1. π/6 + 2πk, k Є Z
- 2. ±π/3 + 2πk, k Є Z
- 3. (πk)/2, k Є Z
- 4. ±2π/3 + 2πk, k Є Z
- 1. ±π/6 + πk, k Є Z
- 2. (-1)k+1·(π/6) + πk, k Є Z
- 3. (-1)k·(π/6) + πk/2, k Є Z
- 4. ±π/3 + πk, k Є Z
- 1. 2πk, k Є Z
- 2. πk/2, k Є Z
- 3. π/2 + πk, k Є Z
- 4. Ø
- 1. (-1)k·(π/30) + πk/5, k Є Z
- 2. (-1)k·(π/20) + πk/5, k Є Z
- 3. πk/30, k Є Z
- 4. πk/4, k Є Z
- 1. -4π/3 + 2πk ≤ x ≤ π/3 + 2πk, k Є Z
- 2. π/4 + 2πk ≤ x
- 3. π/4 + 2πk ≤ x ≤ 3π/4 + 2πk, k Є Z
- 4. π/3 + 2πk ≤ x ≤ 2π/3 + 2πk, k Є Z
- 1. π/2 + πk, k Є Z
- 2. πk, k Є Z
- 3. Ø
- 4. πk/2, k Є Z
- 1. π/4; 7π/4
- 2. 3π/4; 5π/4
- 3. 3π/4; 7π/4
- 4. π/6; 11π/6
- 1. π/4 + πk/2, k Є Z
- 2. π/6 + πk, k Є Z
- 3. ±π/6 + 2πk, k Є Z
- 4. ±π/6 + πk/2, k Є Z
geetest.ru
Тематические тесты по тригонометрии (10 класс)
Тригонометрические функции любого угла
Вариант I
1.Найдите значение выражения .
2.Какое из значений может принимать 
3.Углом, какой четверти является угол
4.Какое из данных чисел положительное?
5.Какое из выражений имеет смысл?
8.Найдите наименьшее значение выражения .
Вариант II
1.Найдите значение выражения .
2.Какое из значений может принимать 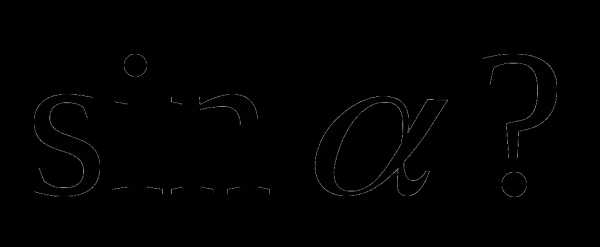
3.Углом, какой четверти является угол
4.Какое из данных чисел отрицательное?
5.Какое из выражений имеет смысл?
4) 
6.Вычислите .
8.Найдите наибольшее значение выражения .
infourok.ru

 a.
a. b.
b. d.
d.