Как вычислять дроби 🚩 простые дроби как 🚩 Математика
Автор КакПросто!
Число, составленное из некоторого количества долей единицы, в арифметике, называется дробью. Оно, как правило, состоит из двух частей — числителя и знаменателя. Каждая из них является целым числом. В буквальном смысле знаменатель показывает на сколько частей разделили единицу, а числитель — сколько из этих частей взяли.
Вам понадобится
- учебное пособие по математике за 5 и 6 классы
Инструкция
Принято разделять обыкновенные и десятичные дроби, знакомство с которыми начинается еще в средней школе. В настоящее время нет такой области знаний, где не применялось бы это понятие. Даже в истории мы говорим первая четверть 17 века, и все сразу понимают, что имеются ввиду 1600-1625 года. Также часто приходится сталкиваться с элементарными действиями над дробями, а также их преобразованием из одного вида в другой.
Приведение дробей к общему знаменателю является, пожалуй, наиболее важным действием над обыкновенными дробями. Это основа проведения абсолютно всех вычислений. Итак, допустим есть две дроби a/b и c/d. Тогда, для того чтобы привести их к общему знаменателю, нужно найти наименьшее общее кратное (М) чисел b и d, и далее умножить числитель первой дроби на (М/b), а числитель второй на (M/d).
Сравнение дробей, еще одна немаловажная задача. Для того чтобы это сделать, приведите заданные простые дроби к общему знаменателю и потом сравните числители, чей числитель окажется больше, та дробь и больше.

Для того чтобы выполнить сложение или вычитание обыкновенных дробей, нужно привести их к общему знаменателю, а после произвести нужное математическое действие с числителями этих дробей. Знаменатель же остается без изменения. Допустим нужно из a/b вычесть c/d. Для этого требуется найти наименьшее общее кратное M чисел b и d, и после вычесть из одного числителя другой, не меняя при этом знаменатель: (a*(M/b)-(c*(M/d))/M
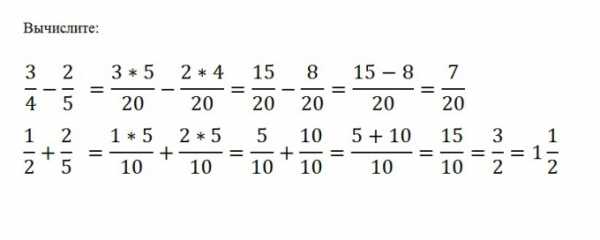
Достаточно просто умножить одну дробь на другую, для этого следует просто перемножить их числители и знаменатели:
(a/b)*(c/d)=(a*c)/(b*d)Чтобы разделить одну дробь на другую, нужно дробь делимого умножить на дробь обратную делителю. (a/b)/(c/d)=(a*d)/(b*c)
Стоить напомнить, что для того чтобы получить обратную дробь, нужно числитель и знаменатель поменять местами.
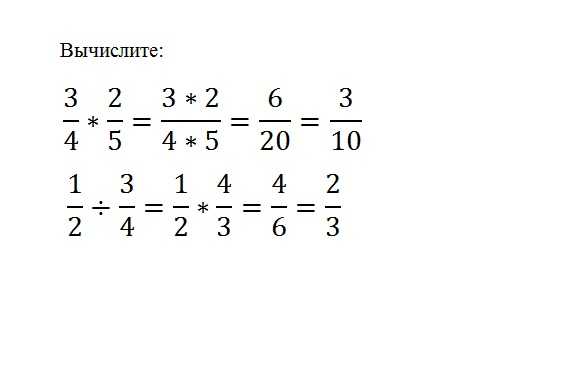
Для того чтобы из обыкновенной дроби перейти к десятичной, нужно числитель поделить на знаменатель. При этом результат может быть как конечным числом так и бесконечным.Если из десятичной дроби нужно перейти к обыкновенной, то разложите ваше число на целую час и дробную, представляя последнюю в виде натурального числа деленного на десять в соответствующей степени.

Видео по теме
Полезный совет
Не забывайте сокращать дроби.
Иногда при выполнении расчетов необходимо разделить дробь на дробь. Причем дроби могут иметь разный вид. И с этим могут возникать всевозможные сложности. Но справиться с ними можно элементарно.
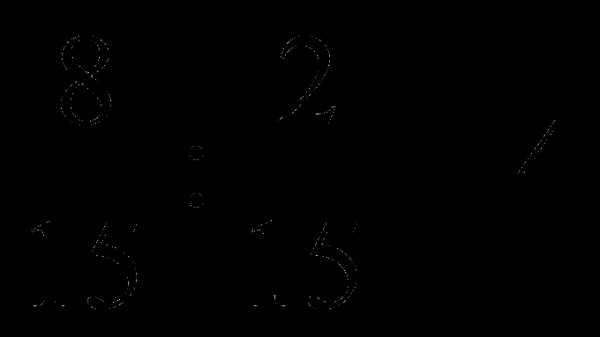
Инструкция
Для того, чтобы разделить обыкновенную дробь на обыкновенную дробь, нужно умножить первую дробь на «перевернутую» вторую дробь. Такая «перевернутая» обыкновенная дробь, где числитель и знаменатель поменяли местами называется обратной.
При делении дробей необходимо обратить внимание на то, чтобы вторая дробь не равнялась нулю. Иногда, если дробь имеет довольно-таки громоздкий вид, это сделать весьма затруднительно. Кроме того, вторая дробь может содержать некоторые переменные (неизвестные) величины, которые при определенных значениях обращают дробь в нуль. Также нужно уделить внимание тем случаям, когда знаменатель второй дроби обращается в нуль. При действиях с переменными все эти случаи необходимо указать в окончательном ответе.
Например: см. рис. 1
Чтобы разделить смешанную дробь на смешанную, смешанную дробь на обыкновенную или обыкновенную на смешанную, нужно привести смешанные дроби к обыкновенному виду. После чего произвести деление, как указано в шаге 1.
Для перевода смешанной дроби к обыкновенной необходимо целую часть смешанной дроби умножить на ее знаменатель и прибавить полученное произведение к числителю.
Пример: см. рис. 2
При делении десятичной дроби на обыкновенную (смешанную) или при делении обыкновенной (смешанной) дроби на десятичную, все дроби приводятся к обыкновенному виду. После этого деление производится согласно шагу 1. Для перевода десятичной дроби в обыкновенную, «выкидываем» из десятичной дроби запятую и записываем в числитель дроби, а в знаменатель пишем единицу и столько нулей, сколько цифр стояло справа от десятичной точки.
Пример: см. рис. 3
Для деления двух десятичных дробей нужно в делимом и делителе перенести десятичную точку на столько цифр вправо, чтобы из второй дроби получилось целое число и разделить полученные числа.Например: 24,68/123,4=246,8/1234=0,2.
Если при этом в делимом для переноса десятичной запятой «не хватает» цифр, то недостающие знаки заменяются нулями.
Например: 24,68/1,234=24680/1234=20
Обратите внимание
Делитель и знаменатели дробей не могут равняться 0.
Дроби имеют практическое значение. Они показывают, на сколько частей делится какой-то объект. И сколько таких частей берется во внимание. Например, дробь 2/4 говорит о том, что арбуз разделили на 4 части. И 2 части из 4-х забрали себе. Принесли 2/4 арбуза домой, а там гости — всего 17 человек. Поэтому разделим дробь 2/4 на число 17, чтобы узнать, какая часть от целого арбуза достанется каждому.
Инструкция
Упростите дробь. И числитель, и знаменатель дроби 2/4 можно одновременно разделить на одно и то же число — 2. После сокращения получаем дробь 1/2. При этом значение дроби не меняется, хотя выглядит она иначе (что 2/4 — пол-арбуза, что 1/2 — пол-арбуза). С ней и будем работать дальше. Пусть она называется «начальная дробь», в отличие от числа, на которое будем ее делить.Представьте число, на которое делим дробь, также в виде дроби. Наше число — 17. В знаменателе напишем цифру 1, получим дробь 17/1. Подобным образом можно представить в виде дроби любое целое число.
Поменяйте местами числитель и знаменатель полученной на 2-м шаге дроби. Вместо 17/1 пишем 1/17. Это называется «обратная дробь».
Умножьте числитель «начальной дроби» на числитель «обратной дроби» и запишите это число в числитель результата. Числитель начальной дроби = 1, числитель обратной дроби = 1. Числитель результата = 1 * 1 = 1.
Умножьте знаменатель «начальной дроби» на знаменатель «обратной дроби» и запишите это число в знаменатель результата. Знаменатель начальной дроби = 2. Знаменатель обратной дроби = 17. Знаменатель результата = 2 * 17 = 34.
Запишите конечный результат. Дробь 1/2 разделить на число 17, равно 1/34. Таким образом, всем находящимся в доме досталась 1/34 часть от целого арбуза.
Видео по теме
Обратите внимание
Кажется, что не было никакого деления. На 4-м и 5-м шаге мы умножали. Но действие умножения происходило с обратной дробью. Поэтому результат является правильным.
Полезный совет
Если дробь надо разделить на нецелое число, то его также представляйте в виде дроби. Например, делим не на число 17, а на число 17,28. В виде дроби оно будет выглядеть как 1728/100. И дальше идем по алгоритму с 3-го шага.
Источники:
- Действия с обыкновенными дробями
Обыкновенная дробь — число капризное. Иногда приходится помучиться, чтобы найти решение задачи с дробью и представить его в должном виде. Научившись решать примеры с дробью, вы легко справитесь с этой неприятной вещью.
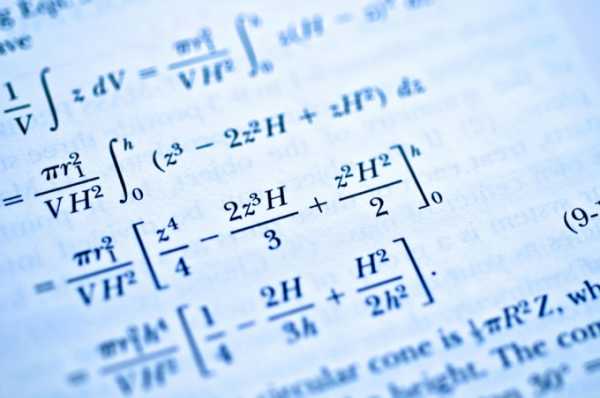
Инструкция
Рассмотрите сложение и вычитание дробей. К примеру, 5/2+10/5. Приведите обе дроби к общему знаменателю. Для этого найдите то число, которое можно разделить без остатка на знаменатель и первой, и второй дроби. В нашем случае это число 10. Преобразуйте вышеуказанные дроби, получается 25/10+20/10.Теперь сложите между собой числители, а знаменатель оставьте неизменным. Получается 45/10.
Можно вычитании дробей.
Рассмотрите умножение дробей. Здесь все просто. Перемножьте между собой числители и знаменатели. К примеру, 2/5 умножить на 4/2 получается 8/10. Сократите дробь, получается 4/5.
Рассмотрите деление дробей. При выполнении этого действия переверните одну из дробей, а затем перемножьте числители и знаменатели. Например, 2/5 разделить на 4/2 — получается 2/5 умножить на 2/4 — получается 4/20. Сократите дробь, получается 1/5.
Источники:
- решить примеры с дробями калькулятор
Делить дробь на дробь нетрудно — нужно всего лишь умножить первую дробь на «перевернутую» вторую. Однако, здесь имеются свои нюансы, учитывать которые все-таки нужно.
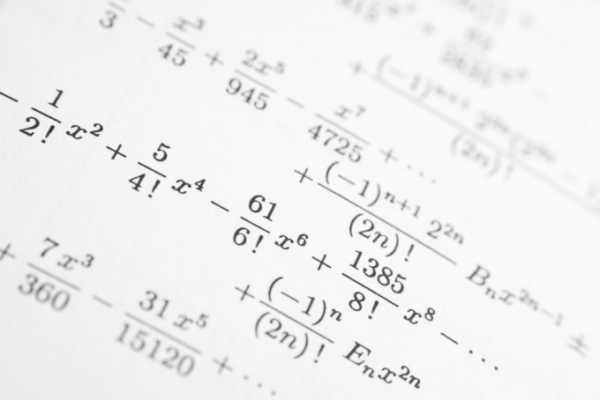
Инструкция
При делении обыкновенных дробей, необходимо умножить первую дробь (делимое) на перевернутую вторую дробь (делитель). Такая дробь, где числитель и знаменатель поменялись местами называют обратной (к исходной).При делении дробей необходимо проконтролировать, чтобы вторая дробь и знаменатели обеих дробей не равнялась нулю (или не принимали нулевых значений при определенных значениях параметров/переменных/неизвестных). Порой, из-за громоздкого вида дроби, это весьма неочевидно. Все значения переменных (параметров), обращающих в нуль делитель (вторую дробь) или знаменатели дробей необходимо указать в ответе.
Пример 1: разделить 1/2 на 2/3
1/2 : 2/3 = 1/2 * 3/2 = (1 * 3) / (2 * 2) = 3/4, или
Пример 2: разделить а/с на х/с
а/с : х/с = а/с * с/х = (а*с)/(с*х) = а/х, где с ? 0, х ? 0.
Чтобы разделить смешанные дроби, нужно привести их к обыкновенному виду. Далее действуем как в п. 1.Для преобразования смешанной дроби к обыкновенному виду нужно ее целую часть умножить на знаменатель, а затем прибавить это произведение к числителю.
Пример 3: преобразовать смешанную дробь 2 2/3 в обыкновенную:
2 2/3=(2 + 2*3)/3=8/3
Пример 4: разделить дробь 3 4/5 на 3/10:
3 4/5 : 3/10 = (3*5+4)/5 :3/10 = 19/5 : 3/10 = 19/5 * 10/3 = (19*10)/(5*3)=38/3=12 2/3
При делении дробей разных типов (смешанных, десятичных, обыкновенных), все дроби предварительно приводятся к обыкновенному виду. Далее — согласно п. 1. Десятичная дробь переводится в обыкновенную очень просто: в числитель записывается десятичная дробь без запятой, а в знаменатель – порядок дроби (десять для десятых, сто для сотых и т.д.).Пример 5: привести десятичную дробь 3,457 к обыкновенному виду:
так как в дроби присутствуют «тысячные» (457 тысячных), то и знаменатель полученной дроби будет равняться 1000:
3,457=3457/1000
Пример 6: разделить десятичную дробь 1,5 на смешанную 1 1/2:
1,5 : 1 1/2 = 15/10 : 3/2 = 15/10 * 2/3 = (15*2)/(10*3) = 30/30 = 1.
При делении двух десятичных дробей обе дроби предварительно умножаются на 10 в такой степени, чтобы делитель стал целым числом. После чего производится деление десятичной дроби «нацело».Пример 7: 2,48/12,4=24,8/124=0,2.
При необходимости (исходя из условий задачи) можно подобрать такое значение множителя, чтобы целыми стали как делитель, так и делимое. Тогда задача деления десятичных дробей сведется к делению целых чисел.
Пример 8: 2,48/12,4=248/1240=0,2
Видео по теме
Под словосочетанием «перевернуть дробь» можно понимать различные математические преобразования. Так или иначе, в результате этих преобразований числитель определенным образом должен меняться местами с знаменателем. В зависимости от вида такого преобразования число может как меняться, так и оставаться прежним.
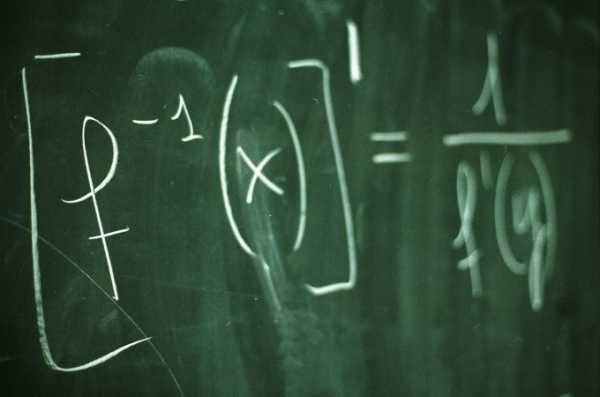
Вам понадобится
- Знание правил преобразования дробей
Инструкция
Самое тривиальное преобразование — это простой «переворот» дроби или перестановка числителя и знаменателя местами. В результате получится число, обратное исходному, а произведение этих двух чисел будет давать единицу. Пример: (2/5)*(5/2) = 1. Как видно из предыдущего примера, если разделить единицу на какое-либо число, то мы получим число, обратное ему. Но деление числа единицы на число — это число х в степени -1. Следовательно, (x/y) = (y/x)^(-1). Пример: (2/3) = (3/2)^(-1).Иногда в результате вычислений можно получить громоздкие, «многоэтажные» дроби. Для упрощения вида дроби их тоже нужно перевернуть. Переворачиваются такие дроби по следующим правилам: x/(y/c) = (x*c)/y, (x/y)/c = x/(y*c), (x/y)/(b/c) = (x*c)/(y*b).
Полезно поменять вид дроби и в случае, когда в знаменателе присутствует иррациональное число. Для этого числитель и знаменатель этой дроби нужно умножить на это иррациональное число. Тогда иррациональное число окажется в числителе дроби. Пример: 1/sqrt(2) = sqrt(2)/(sqrt(2)*sqrt(2)) = sqrt(2)/2.Источник: «Математика: Большой справочник для школьников и поступающих в вузы», Д.И. Аверьянов, П.И. Алтынов, И.И. Баврин и др., 1998
Обратите внимание
Важно помнить, что число в знаменателе дроби должно быть отлично от нуля, иначе все перестановки теряют свою корректность.
В общем виде алгоритм деления обыкновенных дробей таков: сначала та дробь, которая является делителем, заменяется на обратную ей дробь (числитель и знаменатель меняются местами). Затем производится умножение двух дробей, а потом полученный результат упрощается. Если разделить обыкновенную дробь надо на целое число, то это число следует представить в виде обыкновенной дроби с тем же знаменателем, а затем разделить эти две обыкновенные дроби по обычному алгоритму.

Инструкция
Приведите делитель (целое число) к тому же виду, в котором записано делимое (дробь). В знаменателе делителя поставьте то же число, которое использовано в знаменателе делимого. А числителем должен стать знаменатель, умноженный на это самое целое число. Например, если надо разделить дробь 8/15 на число 3, то число надо преобразовать в дробь, у которой в знаменателе будет 15, а в числителе 15 * 3 = 45, то есть 45/15. Теперь исходная задача свелась к делению дроби 8/15 на дробь 45/15.Умножьте делимое (8/15) на дробь, обратную делителю, то есть на 15/45. Поскольку у первой дроби число 15 стоит в знаменателе, а у второй — в числителе, то их можно сократить до 1. В результате исходная задача сведется к умножению дроби 8/1 на дробь 1/45.
Перемножьте числители дробей (8 * 1 = 8) и их знаменатели (1 * 45 = 45). Так вы получите результат, который можно записать в виде обыкновенной дроби 8/45.
Разделите числитель результата на его знаменатель, если решение задачи должно быть представлено не в форме обыкновенной дроби, а в виде десятичной дроби. Разделить можно в столбик или просто воспользоваться калькулятором. Если есть доступ в интернет, то можно, например, использовать калькулятор, встроенный в поисковую систему Google. Для этого перейдите на сайт поисковика и введите в поле поискового запроса «8 делить на 45» или «8 / 45». Нажимать кнопку отправки запроса на сервер не обязательно, ответ с точностью до девяти знаков вы увидите сразу.Если важен только результат в десятичной форме, а сам процесс решения не имеет значения, то можно передоверить все необходимые преобразования дробей и математические операции с ними калькулятору Google. От вас требуется только сформулировать и ввести запрос в поле поиска. Например, для задачи, которая использована как образец в предыдущих шагах, формулировка поискового запроса должна быть такой: «8/15 делить на 3». А результат, который покажет калькулятор Google, будет равен 0,177777778.
Простые дроби (обыкновенные)- это часть единицы или несколько ее частей. Она имеет числитель и знаменатель. Знаменатель – это число равных частей, на которые поделена единица. Числитель — это число взятых равных частей. С простыми дробями можно выполнять простейшие арифметические операции: сложение, вычитание, сравнение, умножение и деление.

Вам понадобится
- Базовые знания по арифметике, таблица умножения
Инструкция
Возьмите две простых (обыкновенных) дроби, которые требуется умножить друг на друга. Для умножения подходят любые простые (обыкновенные дроби).Если дробь содержит целую часть, то ее надо привести к неправильному виду, то есть умножить целую часть на знаменатель дробной части и сложить с числителем дробной части. Знаменатель при этом остается тот же.
Например:
4 1/3 = (4*3+1)/3 = 13/3;
5 3/8 = (5*8+1)/8 = 41/8;
Согласно правилу умножения простых (обыкновенных) дробей, чтобы умножить число на дробь нужно умножить его на числитель дроби и разделить полученное произведение на знаменатель дроби. Таким образом, чтобы получить результат умножения двух простых (обыкновенных) дробей нужно разделить произведение их числителей на произведение их знаменателей.
Например, у нас есть две простых (обыкновенных) дроби 1/4 и 3/5
Возьмите их числители — 1 и 3 и перемножьте их между собой. Для этого используйте таблицу умножения. В столбце, на пересечении двух чисел, находится результат их произведения.
1*3=3
Разделите получившийся числитель на получившийся знаменатель. Ответ — 3/20;
Деление в данном случае подразумевает вид записи простых (обыкновенных) дробей. Для этого используется разделительная черта. Числитель записывается сверху черты, а знаменатель – снизу.Также при записи простой (обыкновенной) дроби может использоваться знак прямой слеш «/»
Если простые (обыкновенные) дроби имеют знаки, то при умножении действуют те же правила, что и с любыми простыми числами. Два отрицательных знака дают минус, два положительных – плюс, если один знак положительный, а другой знак отрицательный, то – минус.
Например:
— 1/3 * 1/6 = -1/18;
— 2/3 *- 5/7 = 10/21;
Видео по теме
Полезный совет
Во время умножения дробей можно сокращать числа в числителе и знаменателе, если они кратны, например3/8 и 2/5
При умножении 2 и 8 можно сократить как 1 и 4, потому что они кратны 2. Это упростит процедуру приведения дроби к нормальному виду.
Источники:
- как умножать дроби с разными знаменателями
Обыкновенные дроби используются, как это ни странно, либо для обучения в самых младших классах, либо для указания самых точных значений чисел. Это связано с тем, что в отличие от более широко применяемых десятичных дробей они не могут быть иррациональными, то есть иметь бесконечное число знаков. Правила деления обыкновенных дробей достаточно просты.

Инструкция
Если делителем тоже является обыкновенная дробь, то начните с ее инвертирования: поменяйте местами числитель и знаменатель. Затем замените знак деления знаком умножения, а все дальнейшие вычисления производите по правилам перемножения двух обыкновенных дробей. Например, если надо разделить 9/16 на 6/8, то записать действие этого шага можно так: 9/16 : 6/8 = 9/16 * 8/6. Сократите числители и знаменатели обеих дробей-множителей, если есть возможность подобрать для них общий делитель. На этот делитель (целое число) надо разделить и числитель и знаменатель. В примере из предыдущего шага числитель первой дроби (9) и знаменатель второй (6) имеют общий делитель 3, а для знаменателя первой (16) и числителя второй (8) таким делителем будет цифра 8. После соответствующего сокращения запись действия примет такой вид: 9/16 : 6/8 = 9/16 * 8/6 = 3/1 * 1/2. Перемножьте попарно числители и знаменатели полученных в результате сокращения дробей — рассчитанное значение и будет искомым результатом. Например, использованный выше образец после этого шага можно будет записать так: 9/16 : 6/8 = 9/16 * 8/6 = 3/2 * 1/2 = (3*1)/(2*2) = 3/4.Если число, стоящее в числителе полученного результата больше числа в его знаменателе, то такая форма записи называется «неправильной» обыкновенной дробью и ее следует перевести в «смешанный» формат. Для этого разделите числитель на знаменатель, полученное целое значение запишите перед дробью, остаток от деления поставьте в числитель, а знаменатель оставьте в прежнем виде. Например, если бы полученный после предыдущего шага результат был равен 9/4, то его следовало бы привести к виду 2 1/4.
Видео по теме
Полезный совет
Если делителем является целое число или десятичная дробь, то его сначала следует перевести в формат обыкновенной дроби, а затем действовать по описанному выше алгоритму. Например, целое число 40 надо записать как 40/1, а десятичную дробь 3,14 — как 314/100.
www.kakprosto.ru
как научиться решать с ними примеры? :: SYL.ru
При слове «дроби» у многих бегут мурашки. Потому что вспоминается школа и задания, которые решались на математике. Это являлось обязанностью, которую необходимо было выполнить. А что если относиться к заданиям, содержащим правильные и неправильные дроби, как к головоломке? Ведь многие взрослые решают цифровые и японские кроссворды. Разобрались в правилах, и все. Так же и здесь. Стоит только вникнуть в теорию — и все встанет на свои места. А примеры превратятся в способ потренировать мозг.
Какие виды дробей существуют?
Для начала о том, что это такое. Дробь — число, которое имеет некоторую часть от единицы. Ее можно записать в двух видах. Первый носит название обыкновенной. То есть такая, у которой есть горизонтальная или наклонная черта. Она приравнивается к знаку деления.
В такой записи число, стоящее над черточкой, называется числителем, а под ней — знаменателем.
Среди обыкновенных выделяют правильные и неправильные дроби. У первых числитель по модулю всегда меньше знаменателя. Неправильные потому так и называются, что у них все наоборот. Значение правильной дроби всегда меньше единицы. В то время как неправильная всегда больше этого числа.
Есть еще смешанные числа, то есть такие у которых имеются целая и дробная части.
Второй вид записи — десятичная дробь. О ней отдельный разговор.
Чем отличаются неправильные дроби от смешанных чисел?
По своей сути, ничем. Это просто разная запись одного и того же числа. Неправильные дроби после несложных действий легко становятся смешанными числами. И наоборот.
Все зависит от конкретной ситуации. Иногда в заданиях удобнее использовать неправильную дробь. А порой необходимо перевести ее в смешанное число и тогда пример решится очень легко. Поэтому, что использовать: неправильные дроби, смешанные числа, — зависит от наблюдательности решающего задачу.
Смешанное число еще сравнивают с суммой целой части и дробной. Причем вторая всегда меньше единицы.
Как представить смешанное число в виде неправильной дроби?
Если требуется выполнить какое-либо действие с несколькими числами, которые записаны в разных видах, то нужно сделать их одинаковыми. Один из методов — представить числа в виде неправильных дробей.
Для этой цели потребуется выполнить действия по такому алгоритму:
- умножить знаменатель на целую часть;
- прибавить к результату значение числителя;
- записать ответ над чертой;
- знаменатель оставить тем же.
Вот примеры того, как записать неправильные дроби из смешанных чисел:
- 17 ¼ = (17 х 4 + 1) : 4 = 69/4;
- 39 ½ = (39 х 2 + 1) : 2 = 79/2.
Как записать неправильную дробь в виде смешанного числа?
Следующий прием противоположен рассмотренному выше. То есть когда все смешанные числа заменяются на неправильные дроби. Алгоритм действий будет таким:
- разделить числитель на знаменатель до получения остатка;
- записать частное на месте целой части смешанного;
- остаток следует разместить над чертой;
- делитель будет знаменателем.
Примеры такого преобразования:
76/14; 76:14 = 5 с остатком 6; ответом будет 5 целых и 6/14; дробную часть в этом примере нужно сократить на 2, получится 3/7; итоговый ответ — 5 целых 3/7.
108/54; после деления получается частное 2 без остатка; это значит, что не все неправильные дроби удается представить в виде смешанного числа; ответом будет целое — 2.
Как целое число превратить в неправильную дробь?
Бывают ситуации, когда необходимо и такое действие. Чтобы получить неправильные дроби с заранее известным знаменателем, потребуется выполнить такой алгоритм:
- умножить целое число на нужный знаменатель;
- записать это значение над чертой;
- разместить под ней знаменатель.
Самый простой вариант, когда знаменатель равен единице. Тогда ничего умножать не нужно. Достаточно просто написать целое число, которое дано в примере, а под чертой расположить единицу.
Пример: 5 сделать неправильной дробью со знаменателем 3. После умножения 5 на 3 получается 15. Это число будет знаменателем. Ответ задания дробь: 15/3.
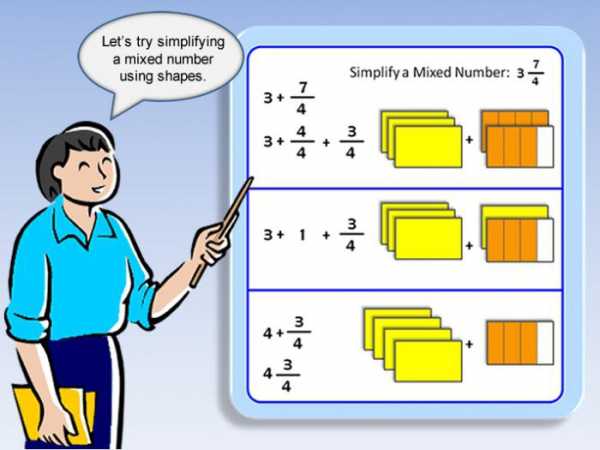
Два подхода к решению заданий с разными числами
В примере требуется вычислить сумму и разность, а также произведение и частное двух чисел: 2 целых 3/5 и 14/11.
В первом подходе смешанное число будет представлено в виде неправильной дроби.
После выполнения действий, описанных выше, получится такое значение: 13/5.
Для того чтобы узнать сумму, нужно привести дроби к одинаковому знаменателю. 13/5 после умножения на 11 станет 143/55. А 14/11 после умножения на 5 примет вид: 70/55. Для вычисления суммы нужно только сложить числители: 143 и 70, а потом записать ответ с одним знаменателем. 213/55 — эта неправильная дробь ответ задачи.
При нахождении разности эти же числа вычитаются: 143 — 70 = 73. Ответом будет дробь: 73/55.
При умножении 13/5 и 14/11 не нужно приводить к общему знаменателю. Достаточно перемножить попарно числители и знаменатели. Получится ответ: 182/55.
Так же и при делении. Для правильного решения нужно заменить деление на умножение и перевернуть делитель: 13/5 : 14/11 = 13/5 х 11/14 = 143/70.
Во втором подходе неправильная дробь обращается в смешанное число.
После выполнения действий алгоритма 14/11 обратится в смешанное число с целой частью 1 и дробной 3/11.
Во время вычисления суммы нужно сложить целые и дробные части по отдельности. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Итоговый ответ получается 3 целых 48/55. В первом подходе была дробь 213/55. Проверить правильность можно, переведя его в смешанное число. После деления 213 на 55 получается частное 3 и остаток 48. Нетрудно заметить, что ответ правильный.
При вычитании знак «+» заменяется на «-». 2 — 1 = 1, 33/55 — 15/55 = 18/55. Для проверки ответ из предыдущего подхода нужно перевести в смешанное число: 73 делится на 55 и получается частное 1 и остаток 18.
Для нахождения произведения и частного пользоваться смешанными числами неудобно. Здесь всегда рекомендуется переходить к неправильным дробям.
www.syl.ru
Как решать алгебраические дроби? Теория и практика
Когда ученик переходит в старшую школу, математика разделяется на 2 предмета: алгебру и геометрию. Понятий становится все больше, задания все сложнее. У некоторых возникают трудности с восприятием дробей. Пропустили первый урок по этой теме, и вуаля. Как решать алгебраические дроби? Вопрос, который будет мучить на протяжении всей школьной жизни.

Понятие алгебраической дроби
Начнем с определения. Под алгебраической дробью понимается выражения P/Q, где P является числителем, а Q – знаменателем. Под буквенной записью может скрываться число, числовое выражение, численно-буквенное выражение.

Прежде чем задаваться вопросом, как решать алгебраические дроби, для начала нужно понимать, что подобное выражение – часть целого.
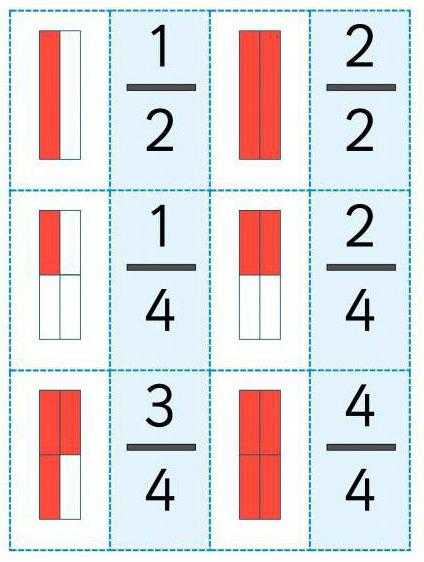
Как правило, целое – это 1. Число в знаменателе показывает, на сколько частей разделили единицу. Числитель необходим для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в качестве математической операции «Деление». В таком случае числитель – делимое, знаменатель – делитель.
Основное правило обыкновенных дробей
Когда учащиеся проходят данную тему в школе, им дают примеры на закрепление. Чтобы правильно их решать и находить различные пути из сложных ситуаций, нужно применять основное свойство дробей.
Оно звучит так: Если умножить и числитель, и знаменатель на одно и то же число или выражение (отличные от нуля), то значение обыкновенной дроби не изменится. Частным случаем от данного правила является разделение обеих частей выражения на одно и то же число или многочлен. Подобные преобразования называются тождественными равенствами.
Ниже будет рассмотрено, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.
Математические операции с дробями
Рассмотрим, как решать, основное свойство алгебраической дроби, как применять его на практике. Если нужно перемножить две дроби, сложить их, разделить одну на другую или произвести вычитание, нужно всегда придерживаться правил.
Так, для операции сложения и вычитания следует найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби даны с одинаковыми выражениями Q, то нужно опустить этот пункт. Когда общий знаменатель найден, как решать алгебраические дроби? Нужно сложить или вычесть числители. Но! Нужно помнить, что при наличии знака «–» перед дробью все знаки в числителе меняются на противоположные. Иногда не следует производить каких-либо подстановок и математических операций. Достаточно поменять знак перед дробью.
Часто используется такое понятие, как сокращение дробей. Это означает следующее: если числитель и знаменатель разделить на отличное от единицы выражение (одинаковое для обеих частей), то получается новая дробь. Делимое и делитель меньше прежних, но в силу основного правила дробей остаются равными изначальному примеру.
Целью этой операции является получение нового несократимого выражения. Решить данную задачу можно, если сократить числитель и знаменатель на наибольший общий делитель. Алгоритм операции состоит из двух пунктов:
- Нахождение НОД для обеих частей дроби.
- Деление числителя и знаменателя на найденное выражение и получение несократимой дроби, равной предшествующей.
Ниже показана таблица, в которой расписаны формулы. Для удобства ее можно распечатать и носить с собой в тетради. Однако, чтобы в будущем при решении контрольной или экзамена не возникло трудностей в вопросе, как решать алгебраические дроби, указанные формулы нужно выучить наизусть.
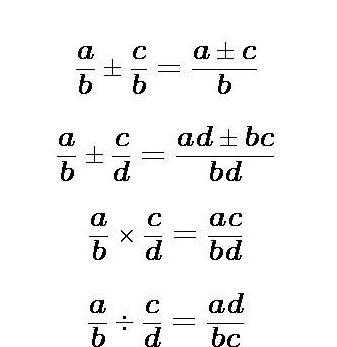
Несколько примеров с решениями
С теоретической точки зрения рассмотрен вопрос, как решать алгебраические дроби. Примеры, приведенные в статье, помогут лучше усвоить материал.
1. Преобразовать дроби и привести их к общему знаменателю.

2. Преобразовать дроби и привести их к общему знаменателю.

3. Сократить указанные выражения (с использованием изученного основного правила дроби и сокращения степеней)
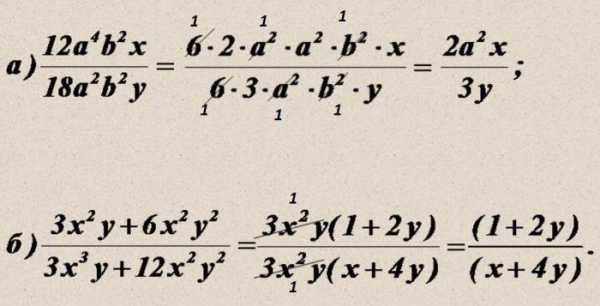
4. Сократить многочлены. Подсказка: нужно обнаружить формулы сокращенного умножения, привести к подобающему виду, сократить одинаковые элементы.
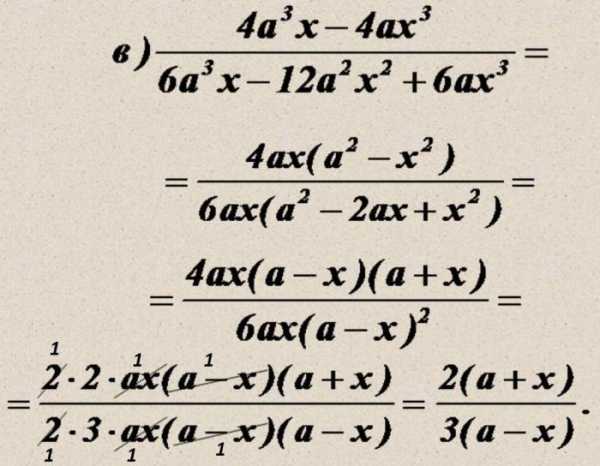
Задание на закрепление материала
1. Какие действия нужно произвести, что найти скрытое число? Решите примеры.

2. Умножьте и поделите дроби, пользуясь основным правилом.

После изучения теоретической части и расссмотрения практической вопросов больше возникнуть не должно.
fb.ru
