Системы логических уравнений в задачах ЕГЭ по информатике
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 18»
городского округа город Салават Республики Башкортостан
Системы логических уравнений
в задачах ЕГЭ по информатике
Автор: Жилина Л.В., учитель информатики высшей категории МБОУ «СОШ № 18» г.Салаватаг
Салават,
2018г.
Раздел «Основы алгебры логики» в заданиях ЕГЭ считается одним из самых сложных и плохо решаемых. Средний процент выполнения заданий по данной теме самый низкий и составляет 43,2.
Раздел курса | Средний процент выполнения по группам заданий |
Кодирование информации и измерение ее количества | 54,7 |
Информационное моделирование | 75,3 |
Системы счисления | 64,7 |
Основы алгебры логики | 43,2 |
Алгоритмизация и программирование | 46,4 |
Основы информационно- коммуникационных технологий | 68,2 |
Исходя из спецификации КИМа 2018 года этот блок включает четыре задания разного уровня сложности.
№ задания | Проверяемые элементы содержания | Уровень сложности задания |
2 | Умение строить таблицы истинности и логические схемы | Б |
17 | Умение осуществлять поиск информации в сети Интернет | П |
18 | Знание основных понятий и законов математической логики | П |
23 | Умение строить и преобразовывать логические выражения | В |
Задание 23 является высоким по уровню сложности, поэтому имеет самый низкий процент выполнения. Среди подготовленных выпускников (81-100 баллов) 49,8% выполнивших, средне подготовленные (61-80 баллов) справляются на 13,7%, оставшаяся группа учеников данное задание не выполняет.
Успешность решения системы логических уравнений зависит от знания законов логики и от четкого применения методов решения системы.
Рассмотрим решение системы логических уравнений методом отображения.
(23.154 Поляков К.Ю.) Сколько различных решений имеет система уравнений?
((x1y1)(x2y2)) (x1x2) (y1y2) =1
((x2y2)(x3y3)) (x2x3) (y2y3) =1
…
((x7y7)(x8y8)) (x7x8) (y7y8) =1
где x1,x2,…,x8, у1,у2,…,у8 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение. Все уравнения, включенные в систему, однотипны, и в каждое уравнение включено четыре переменных. Зная x1 и y1, можем найти все возможные значения x2 и y2, удовлетворяющие первому уравнению. Рассуждая аналогичным образом, из известных x2 и y2 можем найти x3, y3, удовлетворяющее второму уравнению. То есть, зная пару (x1, y1) и определив значение пары (x2, y2) , мы найдем пару (x3, y3), которая, в свою очередь, приведет к паре (x4, y4) и так далее.
Найдем все решения первого уравнения. Это можно сделать двумя способами: построить таблицу истинности, через рассуждения и применение законов логики.
Таблица истинности:
x1 | y1 | x2 | y2 | x1y1 | x2y2 | (x1y1)(x2y2) | (x1x2) | (y1y2) | (x1x2) (y1y2) | |
0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Построение таблицы истинности трудоемко и неэффективно по времени, поэтому применяем второй способ – логические рассуждения. Произведение равно 1 тогда и только тогда, когда каждый множитель равен 1.
(x1y1)(x2y2))=1
(x1x2) =1
(y1y2) =1
Рассмотрим первое уравнение. Следование равно 1, когда 00, 01, 11, значит (x1y1)=0 при (01), (10), то пара (x2y2) может быть любой (00), (01), (10), (11), а при (x1y1)=1, то есть (00) и (11) пара (x2y2)=1 принимает такие же значения (00) и (11). Исключим из этого решения те пары, для которых ложны второе и третье уравнения, то есть x1=1, x2=0, y1=1, y2=0.
Составим связи между парами (x1, y1) и (x2, y2).
(x1, y1) | (x2, y2) |
00 | 00 |
01 | 01 |
10 | 10 |
11 | 11 |
Составим таблицу для вычисления количества пар на каждом этапе.
x1,y1 | x2,y2 | x3,y3 | x4,y4 | x5,y5 | x6,y6 | x7,y7 | x8,y8 | |
00 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
01 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
11 | 1 | 4 | 7 | 10 | 13 | 16 | 19 | 22 |
Общее количество пар 1+1+1+22=25
2) (23.160 Поляков К.Ю.) Сколько различных решений имеет система логических уравнений
(x1 (x2 y2)) (y1 y2) = 1
(x2 (x3 y3)) (y2 y3) = 1
…
(x6 (x7 y7)) (y6 y7) = 1
x7 y7 = 1
Решение. 1) Уравнения однотипные, поэтому методом рассуждения найдем всевозможные пары (x1,y1), (x2,y2) первого уравнения.
(x1 (x2 y2))=1
(y1 y2) = 1
Решением второго уравнения являются пары (00), (01), (11).
Найдем решения первого уравнения. Если x1=0, то x2 , y2 – любые, если x1=1, то x2 , y2 принимает значение (11).
Составим связи между парами (x1, y1) и (x2, y2).
(x1, y1) | (x2, y2) |
00 | 00 |
01 | 01 |
10 | 10 |
11 | 11 |
Составим таблицу для вычисления количества пар на каждом этапе.
x1,y1 | x2,y2 | x3,y3 | x4,y4 | x5,y5 | x6,y6 | x7,y7 | |
00 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
01 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
10 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
11 | 1 | 4 | 8 | 13 | 19 | 26 | 34 |
Учитывая решения последнего уравнения x7 y7 = 1, исключим пару (10). Находим общее число решений 1+7+0+34=42
3)(23.180) Сколько различных решений имеет система логических уравнений
(x1 x2) (x3 x4) = 1
(x3 x4) (x5 x6) = 1
(x5 x6) (x7 x8) = 1
(x7 x8) (x9 x10) = 1
x1 x3 x5 x7 x9 = 1
Решение. 1) Уравнения однотипные, поэтому методом рассуждения найдем всевозможные пары (x1,x2), (x3,x4) первого уравнения.
(x1 x2) (x3 x4) = 1
Исключим из решения пары, которые в следовании дают 0 (10), это пары (01, 00, 11) и (10).
Составим связи между парами (x1,x2), (x3,x4)
3)Составим таблицу для вычисления количества пар на каждом этапе.
Учитывая решения последнего уравнения x1 x3 x5 x7 x9 = 1,
x1 =1, x3 =1, x5 =1, x7 =1, x9 = 1.
(x1,x2) | (x3,x4) | (x5,x6) | (x7,x8) | (x9,x10) | |
00 | 0 | 0 | 0 | 0 | 0 |
01 | 0 | 0 | 0 | 0 | 0 |
10 | 1 | 1 | 1 | 1 | 1 |
11 | 1 | 2 | 3 | 4 | 5 |
Находим общее число решений 0+0+1+5=6.
4)(23.53). Сколько различных решений имеет система уравнений
(X1 X2) (¬X1 ¬X2) (X1 X3) = 1
(X2 X3) (¬X2 ¬X3) (X2 X4) = 1
…
(X7 X8) (¬X7 ¬X8) (X7 X9) = 1
(X8 X9) (¬X8 ¬X9) (X8 X10) = 0
Решение. 1) Уравнения однотипные, поэтому методом рассуждения найдем всевозможные пары (x1,x2), (x2,x3) первого уравнения.
(X1 X2) (¬X1 ¬X2) (X1 X3) = 1
Исключим из решения пары, которые в сумме дают 0, это пары (01), (11) и (10), (00). Составим связи между парами (x1,x2), (x2,x3)
(x1,x2) | (x2,x3) |
00 | 00 |
01 | 01 |
10 | 10 |
11 | 11 |
3)Составим таблицу для вычисления количества пар на каждом этапе, учитывая решения последнего уравнения (x8 x9) (¬x8 ¬x9) (x8 x10) = 0
x8 =0 x9=1, x10=1 и x8 =1 x9=0, x10=0.
(x1,x2) | (x2,x3) | (x3,x4) | (x4,x5) | (x5,x6) | (x6,x7) | (x7,x8) | (x8,x9) | (x9,x10) | |
00 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 8 |
01 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 0 |
10 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 0 |
11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 8 |
Находим общее число решений 8+0+0+8=16.
Успешность решения зависит от уверенного знания метода отображения, чего можно добиться многократным решением систем уравнений. И да осилит дорогу идущий.
Список литературы:
Е.А.Мирончик. Метод отображения // Информатика, № 10, 2013, с. 18-26
Е.А. Мирончик. Люблю ЕГЭ за В15, или Ещё раз про метод отображения // Информатика, № 7-8, 2014, с. 26-32.
К.Ю. Поляков. Преподавание, наука и жизнь. [Электронный ресурс],-
http://kpolyakov.spb.ru/school/ege.htm
xn--j1ahfl.xn--p1ai
Решение логических уравнений
Решение задач с использованием конъюнктивно-нормальной
идизъюнктивно-нормальнойформ
Взадачниках по логике часто встречаются стандартные задачи, где нужно записать функцию, реализующую релейно-контактнуюсхему, упростить ее и построить таблицу истинности для этой функции. А как решать обратную задачу? Дана произвольная таблица истинности, нужно построить функциональную илирелейно-контактнуюсхему. Этим вопросом мы и займемся сегодня.
Любую функцию алгебры логики можно представить комбинацией трех операций: конъюнкции, дизъюнкции и инверсии. Давайте разберемся, как это делается. Для этого запишем несколько определений.
Минтерм — это функция, образованная конъюнкцией некоторого числа переменных или их отрицаний. Минтерм принимает значение 1 при единственном из всех возможных наборов
аргументов, и значение 0 при всех остальных. Пример: x1 x2 x3 x4 .
Макстерм — это функция, образованная дизъюнкцией некоторого числа переменных или их отрицаний. Макстерм принимает значение 0 в одном из возможных наборов, и 1 при всех других.
Пример: x1 + x2 + x3 .
Функция в дизъюнктивной нормальной форме (ДНФ) является логической суммой минтермов.
Пример: x1x2+ x1x2+ x1x2x3.
Конъюнктивная нормальная форма (КНФ) является логическим произведением элементарных дизъюнкций (макстермов).
Пример: (x1+ x2+ x3) (x1+ x2) .
Совершенной дизъюнктивно-нормальнойформойназывается ДНФ, в каждом минтерме которой присутствуют все переменные или их отрицания.
Пример: x1x2x3+ x1x2x3+ x1x2x3
Совершенной конъюктивно-нормальнойформойназывается КНФ, в каждом макстерме которой присутствуют все переменные или их отрицания.
Пример: (x1+ x2+ x3) (x1+ x2+ x3)
Запись логической функции по таблице
Любая логическая функция может быть выражена в виде СДНФ или СКНФ. В качестве примера рассмотрим функцию f, представленную в таблице.
x1 | x2 | x3 | f(x1, x2, x3) | G0 | G1 | G4 | G5 | G7 |
0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
Функции G0, G1, G4, G5, G7 – это минтермы (см. определение). Каждая из этих функций является произведением трех переменных или их инверсий и принимает значение 1 только в одной ситуации. Видно, что для того, чтобы получить 1 в значении функции f, нужен один минтерм. Следовательно, количество минтермов, составляющих СДНФ этой функции, равно количеству единиц в значении функции: f= G0+G1+G4+G5+G7. Таким образом, СДНФ имеет вид:
f (x1, x2, x3) = x1x2x3+ x1x2x3+ x1x2x3+ x1x2x3+ x1x2x3.
Аналогично можно построить СКНФ. Количество сомножителей равно количеству нулей в значениях функции:
f (x1, x2, x3) = (x1+ x2+ x3) (x1+ x2+ x3) (x1+ x2+ x3) .
studfiles.net
Способ решения задачи 23 (решение системы логических уравнений) ЕГЭ по информатики
Искать ошибки у тех, кто идет впереди гораздо легче,
чем пытаться опередить прокладывающих колею…
http://somit.ru
Один из вариантов решения системы логических уравнений.
Задание 23 ЕГЭ по информатики относится к задачам высокой сложности. Процент выполнения учащимися данного задания очень низкий 7-13%. Давайте рассмотрим один из способов решения задачи, предложенный Козловым Александром Ивановичем (нашла случайно и очень благодарна автору). Замечательный сайт http://somit.ru/ (интерактивная анимация для уроков информатики, физики, биологии, математики.)
Задача 23.
Сколько существует различных наборов значений логических переменных x1, x2, … x8, х9,х10, которые удовлетворяют всем перечисленным ниже условиям?
х1 х2 х3 = 1
х2 х3 х4 = 1
…
х6 х7 х8 = 1
х7 х8 х9 = 1
х9 х10 = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x8, х9, х10, при которых выполнена данная система равенств. В качестве ответа нужно указать количество таких наборов.
Решение:
Уравнения 1-7 имеют две особенности : первое — они «одинаковые», второе –существует связь между уравнениями (переменные х2 и х3 из первого уравнения переходят во второе, переменные х3 и х4 из второго уравнения переходят в третье и т.д.)
Берем первое уравнение х1 х2 х3 = 1 и с помощью таблицы истинности находим все его решения (такая же таблица истинности будет и для всех уравнений 1-7). После чего остается выделить (вычеркнуть) все строки, имеющие 0 в итоговой колонке
Анализируя таблицу, строим отображения пар x1x2 в x2x3. Если пара с каким то значением отображается во вторую дважды , то стрелка будет двойная.
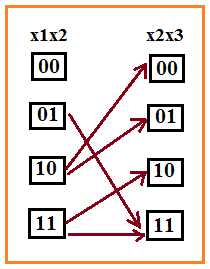
По данному рисунку строим правила отображения, по которым и находим количество решений для первых семи уравнений для чего достаточно заполнить следующую таблицу
Откуда и находим, что первые семь уравнений имеют всего 50 решения.
А нам остается разобраться с оставшимся «добавочным» уравнением х9 х10 = 1
Составим таблицу истинности для этого уравнения.
имеет два решения при значении х9=0, что означает следующее: количество решений для х10 со значениями пары х8х9 равными 00 и 10 — удвоится
имеет одно решение со значениями х9-1 , т.е. количество решений для х10 не изменится (будет таким как для пары х8х9 со значениями 01 и 11) .
Нам остается, найти количество решений для всей системы уравнений, заполнив соответствующие ячейки найденными значениями.
Правильный ответ: 72
Мне кажется, что этот способ решения системы очень понятен и прост.
infourok.ru
Способ решения систем логических уравнений
Решение систем логических уравнений табличным способами преобразованием логических выражений.
Данная методика основана на использование таблиц истинности, рассчитана на учащихся, которые владеют методами преобразования логических выражений. Если учащиеся плохо владеют этими методами, можно использовать и без преобразований. (Мы будем использовать преобразования). Для овладения этим способом решения, необходимы в обязательном порядке знание свойств основных логических операций: конъюнкции, дизъюнкции, инверсии, импликации и эквивалентности.
Алгоритм решения систем уравнений по этому методу:
Преобразовать логическое уравнение, упростить его.
Определить последовательность решения уравнений в системе, так как в большинстве случаев идет последовательное решение уравнений сверху вниз (как они расположены в системе), но есть варианты, когда удобнее, проще начать решать снизу вверх.
Построить таблицу переменных, где задать начальные значения первой переменной (или последней).
Последовательно прописать возможные варианты следующей переменной при каждом значении первой.
После решения предыдущего уравнения, переходя на следующее, обязательно обращать внимание: какие переменные используются в предыдущем и последующем уравнении, так как полученные при решении в предыдущих уравнениях значения переменных переходят как варианты для следующих уравнений.
Обращать внимание на получаемые количества решения при переходе к следующей переменной, т.к. может быть выявлена закономерность в увеличении решений.
Пример1.
¬X1 ˅ X2=1
¬X2 ˅ X3=1
¬X3 ˅ X4=1
….
¬X9 ˅ X10=1
Начнем с Х1 и посмотрим какие значения эта переменная может принимать: 0 и 1.
Затем рассмотрим каждое из этих значений и посмотрим, какое может быть при этом Х2.
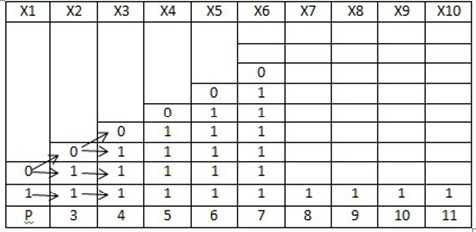
Ответ: 11 решений
Пример 2.
(X1˄ X2)˅(¬X1˄¬X2)˅(X1↔X3)=1
(X2˄ X3)˅(¬X2˄¬X3)˅(X2↔X4)=1
…
(X8˄ X9)˅(¬X8˄¬X9)˅(X8↔X10)=0
Преобразуем по формуле (A˄ B)˅ (¬A ˄ ¬B)= A↔B
Получаем:
(X1↔X2) ˅ (X1↔ X3) =1
(X2↔X3) ˅ (X2↔ X4) =1
…
(X8↔X9) ˅ (X8↔ X10) =0
Возьмем Х1=0 и посмотрим какие значение может принимать Х2. Теперь для каждого Х2 рассмотрим какие значения может принимать Х3 и т.д.
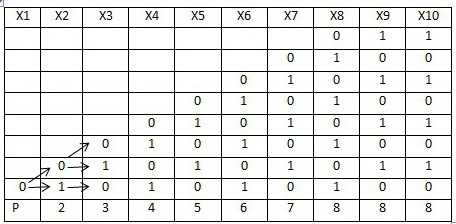
Для Х1 =0 — 8 решений
Возьмем Х1=1 и посмотрим какие значение может принимать Х2. Теперь для каждого Х2 рассмотрим какие значения может принимать Х3 и т.д.
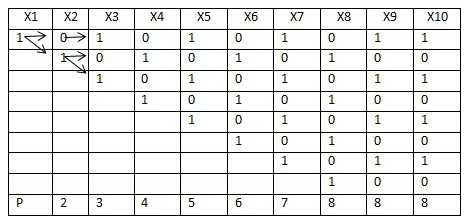
Для Х1=1 – 8 решений
Итого 8+8=16 решений
Ответ. 16 решений
Пример 3.
¬ (X1↔X2) ˄ (X1 ˅ X3) ˄ (¬X1 ˅ ¬X3)=0
¬ (X2↔X3) ˄ (X2 ˅ X4) ˄ (¬X2 ˅ ¬X4)=0
….
¬ (X8↔X9) ˄ (X8 ˅ X10) ˄ (¬X8 ˅ ¬X10)=0
После преобразований (A˅ B) ˄(¬A ˅¬B)= ¬(A ↔B)
получаем:
¬ (X1↔X2) ˄ ¬ (X1↔ X3)=0
¬ (X2↔X3) ˄ ¬ (X2↔ X4)=0
…..
¬ (X8↔X9) ˄ ¬ (X8↔ X10)=0
Возьмем Х1=0 и посмотрим какие значение может принимать Х2. Теперь для каждого Х2 рассмотрим какие значения может принимать Х3 и т.д

Получилось 10 решений для Х1=0
То же самое проделаем для Х1=1. Получим тоже 10 решений
Итого:10+10=20
Ответ: 20 решений.
Пример 4.
(Х1 ˄ Х2) ˅ (¬Х1 ˄ ¬Х2) ˅ (Х2 ˄ Х3) ˅ (¬Х2 ˄¬ Х3)=1
(Х2 ˄ Х3) ˅ (¬Х2 ˄ ¬Х3) ˅ (Х3˄ Х4) ˅ (¬Х3 ˄¬ Х4)=1
….
(Х8 ˄ Х9) ˅ (¬Х8˄ ¬Х9) ˅ (Х9 ˄ Х10) ˅ (¬Х9 ˄¬ Х10)=0
Преобразуем по формулам. (A˄ B)˅ (¬A ˄ ¬B)= A↔B. Получим:
(Х1↔ Х2) ˅ (Х2↔ Х3)=1
(Х2↔ Х3) ˅ (Х3↔ Х4)=1
(Х3↔ Х4) ˅ (Х4↔ Х5)=1
(Х4↔ Х5) ˅ (Х5↔ Х6)=1
(Х5↔ Х6) ˅ (Х6↔ Х7)=1
(Х6↔ Х7) ˅ (Х7↔ Х8)=1
(Х7↔ Х8) ˅ (Х8↔ Х9)=1
(Х8↔ Х9) ˅ (Х9↔ Х10)=0
Начнем с конца, потому что в последнем уравнении переменные определятся однозначно.
Пусть Х10=0, тогда Х9=1, Х8=0, Х7=0, Х6=0, а следующие переменные могут принимать разные значения. Будем рассматривать каждое.

Видим некоторую закономерность: Количество следующих решений равно сумме двух предыдущих.
Итого 21 решение для Х10=0
Теперь рассмотрим для Х10=1. Получаем тоже 21 решение
Итого:21+21=42
Ответ: 42 решения
Пример 5.
(X1 ˄ X2) ˅ (¬X1 ˄ ¬X2) ˅ (¬X3 ˄ X4) ˅ (X3 ˄ ¬X4)=1
(X3 ˄ X4) ˅ (¬X3 ˄ ¬X4) ˅ (¬X5 ˄ X6) ˅ (X5 ˄ ¬X6)=1
(X5 ˄ X6) ˅ (¬X5 ˄ ¬X6) ˅ (¬X7 ˄ X8) ˅ (X7 ˄ ¬X8)=1
(X7 ˄ X8) ˅ (¬X7 ˄ ¬X8) ˅ (¬X9 ˄ X10) ˅ (X9˄ ¬X10)=1
Преобразуем по формулам: (¬A ˄ B) ˅ (A ˄ ¬B)= A↔ ¬B
(A˄ B)˅ (¬A ˄ ¬B)= A↔B
(X1↔ X2) ˅ (X3 ↔ ¬X4)=1
(X3↔ X4) ˅ (X5 ↔ ¬X6)=1
(X5↔ X6) ˅ (X7 ↔ ¬X8)=1
(X7↔ X8) ˅ (X9 ↔ ¬X10)=1
Рассмотрим какие значения могут принимать Х1 и Х2: (0,0), (0,1), (1,0), (1,1).
Рассмотрим каждый вариант и посмотрим какие значения при этом могут принимать Х3, Х4
Начиная с Х7, Х8 будем сразу записывать количество решений, так как сразу видно, что когда значения одинаковые (1,1) и (0,0), то следующие переменные имеют 4 решения, а когда разные (0,1) и (1,0) – 2 решения.
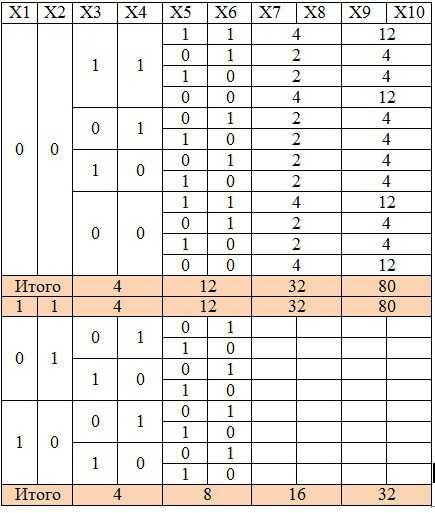
Итого: 80+80+32=192
Ответ:192 решения
Пример 6.
(Х1↔ Х2) ˅ (Х2 ↔Х3)=1
(Х2↔ Х3) ˅ (Х3↔Х4)=1
(Х3↔ Х4) ˅ (Х4 ↔Х5)=1
….
(Х8↔ Х9) ˅ (Х9 ↔Х10)=1
Возьмем Х1=0 и посмотрим какие значение может принимать Х2. Теперь для каждого Х2 рассмотрим какие значения может принимать Х3 и т.д.
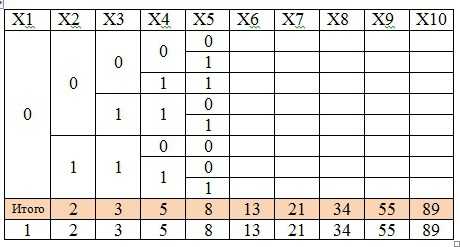
Видим некоторую закономерность: Количество следующих решений равно сумме двух предыдущих.
То же самое для Х1=1 получаем 89 решений
Итого: 89+89=178 решений
Ответ: 178 решений
Решим еще одним способом
(Х1↔ Х2) ˅ (Х2 ↔Х3)=1
(Х2↔ Х3) ˅ (Х3↔Х4)=1
(Х3↔ Х4) ˅ (Х4 ↔Х5)=1
….
(Х8↔ Х9) ˅ (Х9 ↔Х10)=1
Введем замену:
T1=(Х1↔ Х2)
T2=(Х2↔ Х3)
T3=(Х3↔ Х4)
T4=(Х4↔ Х5)
T5=(Х5↔ Х6)
T6=(Х6↔ Х7)
T7=(Х7↔ Х8)
T8=(Х8↔ Х9)
T9=(Х9↔ Х10)
Получаем:
T1 ˅ T2=1
T2 ˅ T3=1
T3 ˅ T4=1
T4 ˅ T5=1
T5 ˅ T6=1
T6 ˅ T7=1
T7 ˅ T8=1
T8 ˅ T9=1
T9 ˅ T10=1
Возьмем T1=1 и используем свойства дизъюнкции:
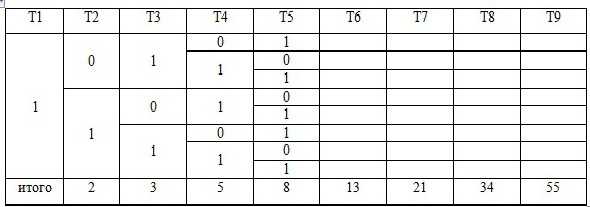
НО Вспомним, что
T1=(Х1↔ Х2)
T2=(Х2↔ Х3) и т.д.
Воспользуемся свойством эквивалентности и убедимся, глядя на таблицу, что
Когда Т =1, то получается два решения. А когда =0 –одно решение.
Следовательно, можно подсчитать количество единиц и умножить их на 2+ количество нулей. Подсчет, так же используя закономерность.
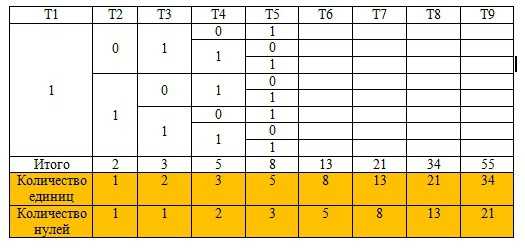
Получается, что количество единиц = предыдущему общему количеству решений Т, а количество нулей равно предыдущему количеству единиц
Итак. Получим. Так как единица дает два решения, то 34*2=68 решений из единицы+21 решение из 0.
Итого 89 решений для Т=1. Аналогичным способом получаем 89 решений для Т=0
Итого 89+89=178
Ответ: 178 решений
Пример 7.
(X1 ↔X2) ˅ (X3↔ X4) ˄ ¬(X1 ↔X2) ˅ ¬(X3↔ X4)=1
(X3 ↔X4) ˅ (X5↔ X6) ˄ ¬(X3 ↔X4) ˅ ¬(X5↔ X6)=1
(X5 ↔X6) ˅ (X7↔ X8) ˄ ¬(X5 ↔X6) ˅ ¬(X7↔ X8)=1
(X7 ↔X8) ˅ (X9↔ X10) ˄ ¬(X7 ↔X8) ˅ ¬(X9↔ X10)=1
Введем замену:
T1=(X1 ↔X2)
T2=(X3↔ X4)
T3=(X5↔ X6)
T4=(X7 ↔X8)
T5=(X9↔ X10)
Получим:
(Т1 ˅ Т2) ˄ ¬( Т1 ˅¬ Т2)=1
(Т2 ˅ Т3) ˄ ¬( Т2˅¬ Т3)=1
(Т3 ˅ Т4) ˄ ¬( Т3 ˅¬ Т4)=1
(Т4 ˅ Т5) ˄ ¬( Т4˅¬ Т5)=1
Рассмотрим какие могут быть Т:
Т1
Т2
Т3
Т4
Т5
Итого
0
1
0
1
0
32
1
0
1
0
1
32
ТK≠ТК+1 И ТK=ТК+2
Получаем: 25=32 для Т
Итого: 32+32=64
Ответ: 64 решения.
infourok.ru
Презентация к уроку по информатике и икт (11 класс) по теме: Логические уравнения и системы логических уравнений в ЕГЭ
Слайд 1
Решение задания В15 (системы логических уравнений) Вишневская М.П., МАОУ «Гимназия №3» 18 ноября 2013 г., г. СаратовСлайд 2
Задание В15 — одно из самых сложных в ЕГЭ по информатике!!! Проверяются умения: преобразовывать выражения, содержащие логические переменные; описывать на естественном языке множество значений логических переменных, при которых заданный набор логических переменных истинен; подсчитывать число двоичных наборов, удовлетворяющих заданным условиям. Самое сложное , т.к. нет формальных правил, как это сделать, требуется догадка.
Слайд 3
Без чего не обойтись!
Слайд 4
Без чего не обойтись!
Слайд 5
Условные обозначения конъюнкция : A /\ B , A B , AB , А &B, A and B дизъюнкция: A \ / B , A + B , A | B , А or B отрицание: A , А, not A эквиваленция : A В, A B, A B исключающее «или»: A B , A xor B
Слайд 6
Метод замены переменных Сколько существует различных наборов значений логических переменных х1, х2, …, х9, х10, которые удовлетворяют всем перечисленным ниже условиям: ((x1 ≡ x2) \/ (x3 ≡ x4)) /\ (¬(x1 ≡ x2) \/ ¬(x3 ≡ x4)) = 1 ((x3 ≡ x4) \/ (x5 ≡ x6)) /\ (¬(x3 ≡ x4) \/ ¬(x5 ≡ x6)) = 1 ((x5 ≡ x6) \/ (x7 ≡ x8)) /\ (¬(x5 ≡ x7) \/ ¬(x7 ≡ x8)) = 1 ((x7 ≡ x8) \/ (x9 ≡ x10)) /\ (¬(x7 ≡ x8) \/ ¬(x9 ≡ x10)) = 1 В ответе не нужно перечислять все различные наборы х1, х2, …, х9, х10, при которых выполняется данная система равенств. В качестве ответа необходимо указать количество таких наборов (демо-версия 2012 г.)
Слайд 7
Решение Шаг 1. Упрощаем, выполнив замену переменных t1 = x1 x2 t2 = x3 x4 t3 = x5 x6 t4 = x7 x8 t5 = x9 x10 После упрощения: (t1 \/ t2) /\ (¬t1 \/ ¬ t2 ) =1 (t2 \/ t3) /\ (¬t2 \/ ¬ t3 ) =1 (t3 \/ t4) /\ (¬t3 \/ ¬ t4 ) =1 (t4 \/ t5) /\ (¬t4 \/ ¬ t5 ) =1 Рассмотрим одно из уравнений: (t1 \/ t2) /\ (¬t1 \/ ¬ t2 ) =1 Очевидно, оно =1 только если одна из переменных равна 0, а другая – 1. Воспользуемся формулой для выражения операции XOR через конъюнкцию и дизъюнкцию: (t1 \/ t2) /\ (¬t1 \/ ¬ t2 ) = t1 t2 = ¬(t1 ≡ t2 ) =1 ¬(t1 ≡ t2 ) =1 ¬(t2 ≡ t3 ) =1 ¬(t3 ≡ t4 ) =1 ¬(t4 ≡ t5 ) =1
Слайд 8
Шаг2. Анализ системы ¬(t1 ≡ t2 ) =1 ¬(t2 ≡ t3 ) =1 ¬(t3 ≡ t4 ) =1 ¬(t4 ≡ t5 ) =1 t1 t2 t3 t4 t5 0 1 0 1 0 1 0 1 0 1 Т.к. tk = x2k-1 ≡ x2k ( t1 = x1 x2 ,…. ), то каждому значению tk соответствует две пары значений x2k-1 и x2k , например: tk =0 соответствуют две пары — (0,1) и (1,0) , а tk =1 – пары (0,0) и (1,1).
Слайд 9
Шаг3. Подсчет числа решений. Каждое t имеет 2 решения, количество t – 5. Т.о. для переменных t существует 2 5 = 32 решения. Но каждому t соответствует пара решений х , т.е. исходная система имеет 2*32 = 64 решения. Ответ: 64
Слайд 10
Метод исключения части решений Сколько существует различных наборов значений логических переменных х1, х2, …, х5, y1,y2,… , y5 , которые удовлетворяют всем перечисленным ниже условиям: (x1→ x2)∧(x2→ x3)∧(x3→ x4)∧(x4→ x5) =1; ( y1→ y2)∧( y2→ y3)∧( y3→ y4) ∧( y4→ y5) =1; y5→ x5 =1. В ответе не нужно перечислять все различные наборы х1, х2, …, х5, y 1 ,y2,… , y5, при которых выполняется данная система равенств. В качестве ответа необходимо указать количество таких наборов .
Слайд 11
Решение. Шаг1. Последовательное решение уравнений х1 1 0 х2 1 0 1 х3 1 0 1 1 х4 1 0 1 1 1 х5 1 0 1 1 1 1 Первое уравнение – конъюнкция нескольких операций импликации, равна 1, т.е. каждая из импликаций истинна. Импликация ложна только в одном случае, когда 1 0, во всех других случаях (0 0, 0 1, 1 1) операция возвращает 1. Запишем это в виде таблицы:
Слайд 12
Шаг1. Последовательное решение уравнений Т.о. получено 6 наборов решений для х1,х2,х3,х4,х5: (00000), (00001), (00011), (00111), (01111), (11111). Рассуждая аналогично, приходим к выводу, что для y1, y2, y3, y4, y5 существует такой же набор решений. Т.к. уравнения эти независимы, т.е. в них нет общих переменных, то решением этой системы уравнений (без учета третьего уравнения) будет 6*6= 36 пар «иксов» и «игреков». Рассмотрим третье уравнение: y5→ x5 =1 Решением являются пары: 0 0 0 1 1 1 Не является решением пара: 1 0
Слайд 13
Сопоставим полученные решения Там, где y5 =1, не подходят x5=0. таких пар 5. Количество решений системы : 36-5= 31 . Ответ: 31 Понадобилась комбинаторика!!!
Слайд 14
Метод динамического программирования Сколько различных решений имеет логическое уравнение x 1 → x 2 → x 3 → x 4 → x 5 → x 6 = 1, где x 1, x 2, …, x 6 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количеств о таких наборов.
Слайд 15
Решение Шаг1. Анализ условия Слева в уравнении последовательно записаны операции импликации, приоритет одинаков. Перепишем: ((((X 1 → X 2 ) → X 3 ) → X 4 ) → X 5 ) → X 6 = 1 NB! Каждая следующая переменная зависит не от предыдущей, а от результата предыдущей импликации!
Слайд 16
Шаг2. Выявление закономерности Рассмотрим первую импликацию, X 1 → X 2. Таблица истинности: X 1 X 2 X 1 → X 2 0 0 1 0 1 1 1 0 0 1 1 1 Из одного 0 получили 2 единицы, а из 1 получили один 0 и одну 1. Всего один 0 и три 1, это результат первой операции.
Слайд 17
Шаг2. Выявление закономерности Подключив к результату первой операции x 3 , получим: F(x 1 ,x 2 ) x 3 F(x 1 ,x 2 ) x 3 0 0 1 0 1 1 1 0 0 1 1 1 1 0 0 1 1 1 1 0 0 1 1 1 Из двух 0 – две 1, из каждой 1 (их 3) по одному 0 и 1 (3+3)
Слайд 18
Шаг 3. Вывод формулы Т.о. можно составить формулы для вычисления количества нулей N i и количества единиц E i для уравнения с i переменными: ,
Слайд 19
Шаг 4. Заполнение таблицы Заполним слева направо таблицу для i = 6, вычисляя число нулей и единиц по приведенным выше формулам; в таблице показано, как строится следующий столбец по предыдущему: : число переменных 1 2 3 4 5 6 Число нулей N i 1 1 3 5 11 21 Число единиц E i 1 2*1+1= 3 2*1+3= 5 11 21 43 Ответ: 43
Слайд 20
Метод с использованием упрощений логических выражений Сколько различных решений имеет уравнение ((J → K) → ( M N L)) (( M N L ) → (¬ J K )) ( M → J ) = 1 где J , K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений J , K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.
Слайд 21
Решение Заметим, что J → K = ¬ J K Введем замену переменных: J → K=А, M N L =В Перепишем уравнение с учетом замены: (A → B) (B → A) (M → J)=1 4. (A B) (M → J)= 1 5. Очевидно, что A B при одинаковых значениях А и В 6. Рассмотрим последнюю импликацию M → J =1 Это возможно, если: M=J=0 M=0, J=1 M=J=1
Слайд 22
Решение Т.к. A B , то При M=J=0 получаем 1 + К=0. Нет решений. При M=0, J=1 получаем 0 + К=0, К=0, а N и L — любые , 4 решения : ¬ J K = M N L K N L 0 0 0 0 0 1 0 1 0 0 1 1
Слайд 23
Решение 10. При M=J=1 получаем 0+К=1 *N * L , или K=N*L, 4 решения: 11. Итого имеет 4+4=8 решений Ответ: 8 K N L 0 0 0 0 0 1 0 1 0 1 1 1
Слайд 24
Источники информации: О.Б. Богомолова, Д.Ю. Усенков. В15: новые задачи и новое решение // Информатика, № 6, 2012, с. 35 – 39. К.Ю. Поляков. Логические уравнения // Информатика, № 14, 2011, с. 30-35. http://ege-go.ru/zadania/grb/b15/ , [ Электронный ресурс ] . http://kpolyakov.narod.ru/school/ege.htm , [ Электронный ресурс ] .
nsportal.ru
Системы логических уравнений в задачах ЕГЭ по информатике
Транскрипт
1 К.Ю. Поляков, М.А. Ройтберг Системы логических уравнений в задачах ЕГЭ по информатике К.Ю. Поляков, М.А. Ройтберг, 0
2 К.Ю. Поляков, М.А. Ройтберг, 0 Постановка задачи ЕГЭ-0 0: Решаемость,% Сколько решений имеет система уравнений: где 0,,, логические переменные.


3 Методы решения замена переменных последовательное подключение уравнений метод отображения Е.А. Мирончик «Информатика. Первое сентября». Е. А. Мирончик, Метод отображения // Информатика, 0, 0, с Е.А. Мирончик, Люблю ЕГЭ за В5, или Еще раз про метод отображения // Информатика, 7-8, 0, с. -. трудоёмко длинная запись решения 0: Решаемость,% К.Ю. Поляков, М.А. Ройтберг, 0
4 Аналогии с алгеброй Алгебра Обычно уравнение имеет одно или несколько решений. Элементарные уравнения: линейные, квадратные. Методы преобразования: законы сложения и умножения, формулы сокращенного умножения, свойства степеней. Логика Уравнение может иметь большое, но конечное число решений. Элементарные уравнения не выделяются. Методы преобразования: законы логики см. далее. К.Ю. Поляков, М.А. Ройтберг, 0
5 Формулы логики I A. Свойства 0, и отрицания Свойства 0 и Свойства отрицания 0 5 К.Ю. Поляков, М.А. Ройтберг, 0
6 К.Ю. Поляков, М.А. Ройтберг, 0 Формулы логики II c c c c c c c c Б. Дизъюнкция и конъюнкция Сочетательный закон Переместительный закон Закон поглощения Распределительный закон Правила де Моргана
7 К.Ю. Поляков, М.А. Ройтберг, 0 Формулы логики III 7 В. Импликация и эквивалентность Определение импликации Свойства импликации Эквивалентность c c c c c c c c
8 Основные идеи Решение системы уравнений это битовая цепочка битовый вектор X {0,} N для любого i i Битовый вектор рассматривается как единый объект. Уравнения это ограничения на битовый вектор ограничения на комбинации битов. Нужно выделить элементарные уравнения и записать ограничения «на русском языке». 5 Количество решений находится по правилам комбинаторики. 8 К.Ю. Поляков, М.А. Ройтберг, 0
9 Типичные ограничения Задача. 5 9 «соседние биты одинаковы» Решения: 00000, Задача. 5 «соседние биты различны» «биты чередуются» Решения: 000, 00 К.Ю. Поляков, М.А. Ройтберг, 0
10 Типичные ограничения Задача. 5 «запрещена комбинация 0» «после первой единицы все следующие биты» «все нули, потом все единицы» Решения: , 00000, 0000, 000, 00, 0, Для уравнения с N переменными: N+ решений. 0 К.Ю. Поляков, М.А. Ройтберг, 0
11 Более сложный пример Задача. 5 «запрещена комбинация 0» «запрещена комбинация» «слева от каждого нулевого бита начиная с -го должны стоять два нуля» «все нули, потом все единицы» Решения: , 00000, 0000, 000, 00, 0, и ещё:, Для уравнения с N переменными: N+ решений. i 0 i i 0 К.Ю. Поляков, М.А. Ройтберг, 0
12 Более сложный пример Задача 5. 5 «запрещена комбинация 00»? Сколько есть цепочек длиной N, в которых нет двух соседних нулей? К.Ю. Поляков, М.А. Ройтберг, 0
13 Более сложный пример K {0, } Все цепочки длиной N K {0, 0, } K N K N 0 K нет 00! N K K N N непересекающиеся множества! К.Ю. Поляков, М.А. Ройтберг, 0

14 Более сложный пример K {0, } K K K {0, 0, } N K N N! Рекурсия: ЕГЭ- B Динамическое программирование: ЕГЭ- B, ЕГЭ-5 B9 K N,,,, 5, 8,,,, Числа Фибоначчи FN K N F N К.Ю. Поляков, М.А. Ройтберг, 0
15 Ещё пример Задача. 5 «запрещена комбинация 0» «после двух единиц подряд следуют только единицы» 5 К.Ю. Поляков, М.А. Ройтберг, 0
16 И снова рекуррентные уравнения Структура решения: «голова» «хвост» m 0 m : m нет комбинации последний бит 0 : одна «голова» пустая m : одна «голова» 0 Fm «голов» N m N K N F m m0 N : K 58 N К.Ю. Поляков, М.А. Ройтберг, 0
17 Последний пример Задача 7. N Последовательность выполнения: N N запрещена комбинация 0 на последнем шаге Сколько решений K N N Z N Z N у уравнения N K N K 0 Начальное значение: N N 0 Z N K N K 7 К.Ю. Поляков, М.А. Ройтберг, 0
18 К.Ю. Поляков, М.А. Ройтберг, 0 Демо-вариант ЕГЭ i i i i i «запрещено 00» «после двух единиц идут только единицы» Если не трогать : Y «хвост» «голова» «запрещено 00 и» «биты чередуются»
19 Демо-вариант ЕГЭ-05 Варианты отличаются местом последнего нуля:, 0, 0, 00, 00, 000, 000, 0000, 0000 Учитываем Y: i i i i i i 0 {0,} i i решение решения 00 нулевых бита, вариантов 0 K 8 9 К.Ю. Поляков, М.А. Ройтберг, 0
20 К.Ю. Поляков, М.А. Ройтберг, 0 Демо-вариант ЕГЭ Как перевести на русский язык??
21 X Системы логических уравнений в задачах ЕГЭ по информатике Демо-вариант ЕГЭ-0 i i i i «очередной бит равен хотя бы одному из -х следующих» «запрещены комбинации 00 и 0» «после 0 или 0 биты чередуются» сначала цепочка нулей, потом биты чередуются /0 сначала цепочка единиц, потом биты чередуются = 0 К.Ю. Поляков, М.А. Ройтберг, 0
22 К.Ю. Поляков, М.А. Ройтберг, 0 Демо-вариант ЕГЭ-0 0
23 К.Ю. Поляков, М.А. Ройтберг, 0 Демо-вариант ЕГЭ-0 5 решений: X = 0000, 000, 00, 0, 5 решений: Y = 0000, 000, 00, 0, i i 0 {0,} i i без ограничений! Связь X и Y:
24 Демо-вариант ЕГЭ-0 X: Y: = 5 К.Ю. Поляков, М.А. Ройтберг, 0
25 К.Ю. Поляков, М.А. Ройтберг, 0 Демо-вариант ЕГЭ Замена переменных:
26 К.Ю. Поляков, М.А. Ройтберг, 0 Демо-вариант ЕГЭ К одному уравнению: Решения: 00, 000 Z Z
27 Демо-вариант ЕГЭ-0 Переход к исходным переменным: i k k i 0 k, k 0,,, 0,0, i k k,0, 7! Каждый бит в Z даёт удвоение вариантов в X! Z 000, Z 00 5 бит 5 бит 5 5 K0 К.Ю. Поляков, М.А. Ройтберг, 0
28 К.Ю. Поляков, М.А. Ройтберг, 0 Ещё одна задача Замена переменных:

29 Ещё одна задача ! Решение: «запрещена комбинация 0» «все единицы, потом все нули» 8 решений: Но в i! К.Ю. Поляков, М.А. Ройтберг, 0
30 Ещё одна задача 05 i i i 0 решения: 0; и ;0 i i! i i i решение: ; i i Z X,Y 8 Каждый 0 удваивает количество решений! Z X,Y = 55 К.Ю. Поляков, М.А. Ройтберг, 0
31 Основные шаги решения упрощение уравнений с помощью эквивалентных преобразований замена переменных если возможно исследование структуры всех решений подсчёт количества решений по формулам комбинаторики К.Ю. Поляков, М.А. Ройтберг, 0
32 Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ, г. Санкт-Петербург РОЙТБЕРГ Михаил Абрамович д.ф.-м.н., зав. кафедрой АТП ФИВТ МФТИ, зам. руководителя Федеральной комиссии по разработке КИМ ЕГЭ по информатике и ИКТ К.Ю. Поляков, М.А. Ройтберг, 0
docplayer.ru
Системы логических уравнений в задачах ЕГЭ по информатике
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: [email protected]
Мы в социальных сетях
Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам
ВКонтакте >
Что такое Myslide.ru?
Myslide.ru — это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями.
Для правообладателей >
myslide.ru
