Пять способов рисования трапеций. | CorelTUTORIALS
В этом уроке вы узнаете пять различных способов, как быстро нарисовать трапецию, используя такие инструменты, как «Основные фигуры», «Форма», «Прямоугольник» а также освоите различные команды для преобразований в CorelDRAW.
Оказывается иногда и простая фигура может поставить начинающего пользователя в тупик. И вправду, как вот так, сразу, нарисовать трапецию.
Рис. 1. Примеры трапеций.
Способ первый. «Простейший».
Активируем инструмент «Основные фигуры». Выбираем подгруппу «Правильные фигуры». В мини–библиотеке, которая появилась на панели свойств, выбираем нужную фигуру и рисуем ее на рабочем листе документа.
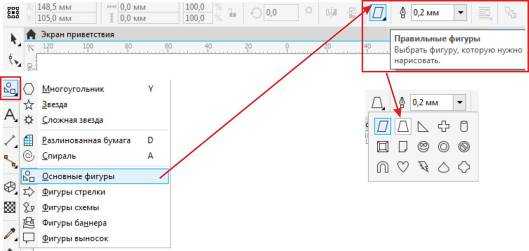
Рис. 2. После активирования инструмента «Основные фигуры», на панели свойств появится список правильных фигур.
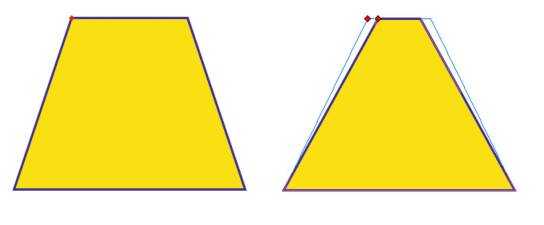
Рис. 3. Перемещение глифа (красного маркера) позволяет редактировать форму объекта.
В левом верхнем углу нарисованной трапеции появляется красный маркер в форме ромба. Этот маркер называется глифом. Вид трапеции или любой другой фигуры из группы основных фигур изменяется, путем перетаскивания глифа инструментом «Форма». При наведении инструмента на глиф, курсор изменится и глиф можно будет переместить.
Способ второй. «Перспективный».
Активируем инструмент «Прямоугольник» и рисуем произвольный прямоугольник. Выделяем его и в меню «Эффекты» выбираем пункт «Добавить перспективу».
Инструментом «Форма» перемещаем верхние маркеры на одной из сторон прямоугольника. Можно перемещать и точку схождения перспективы, добиваясь нужного наклона сторон трапеции.
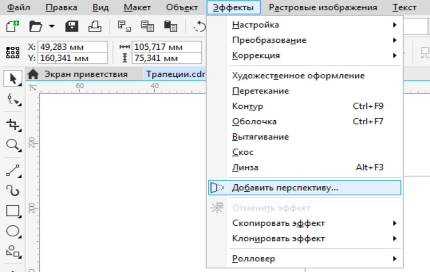
Рис. 4. С помощью меню «Эффекты» можно добавить объекту перспективу.
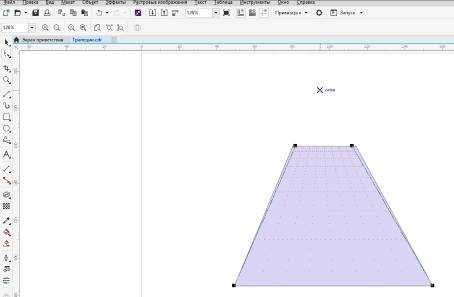
Рис.5. Перемещая маркеры перспективы, или изменяя положение точки схода легко добиться нужного эффекта.
После применения эффекта перспективы, в статусной строке программы появится информация о том, что к объекту был применен эффект перспективы. Можно сразу же преобразовать объект с примененным эффектом в простую кривую командой меню «Объект» > «Преобразовать в кривую». Форма объекта будет сохранена.
Способ третий. «Конструктор».
Инструментом «Прямоугольник» рисуем основной объект — квадрат или прямоугольник.
Удерживаем во время рисования инструментом «Прямоугольник клавишу Сtrl – рисуем квадрат.
Удерживаем во время рисования клавишу «Shift» – рисуем прямоугольник не от угла, а от центра.
Удерживаем во время рисования обе клавиши Сtrl+Shift – рисуем квадрат от центра.
Выставляем по сторонам прямоугольника (квадрата) направляющие. Включаем «привязку к направляющим». Это можно сделать соответствующей командой меню «Вид» > «Привязать к» > «Направляющим».
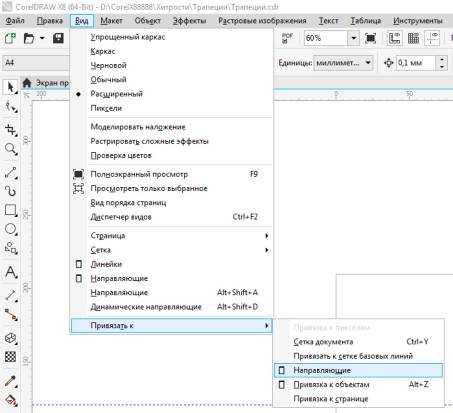
Рис.6. В меню «Вид» можно включить нужный режим привязки объекта.
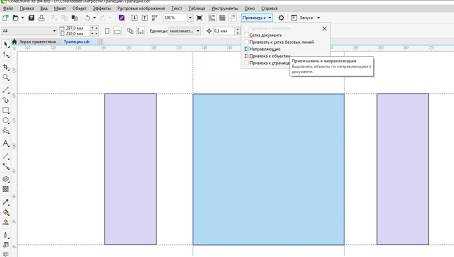
Рис.7. Привязка прямоугольников к направляющим.
Рисуем еще два одинаковых прямоугольника, с высотой, соответствующей высоте базового основного прямоугольника. Размещаем эти объекты слева и справа от основного, базового прямоугольника вплотную к нему. Поскольку включен режим привязки к направляющим, то не составит большого труда правильно расположить объекты.
Преобразуем левый и правый прямоугольники в кривые, командой «Объект» > «Преобразовать в кривую» или используя комбинацию клавиш «Ctrl+ Q».
Инструментом «Форма» удаляем по одному углу во вспомогательных прямоугольниках.
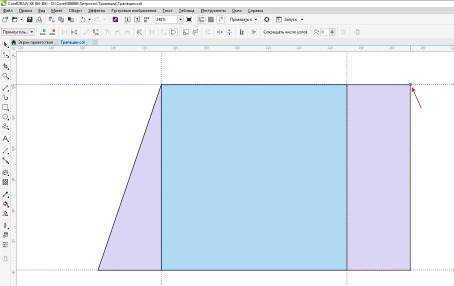
Рис.8. Удаление одного из узлов прямоугольника.
Выделяем инструментом выбора все три фигуры и применяем команду меню «Объект» > «Формирование» > « Объединение» или нажимаем на кнопку этой же команды на панели свойств.
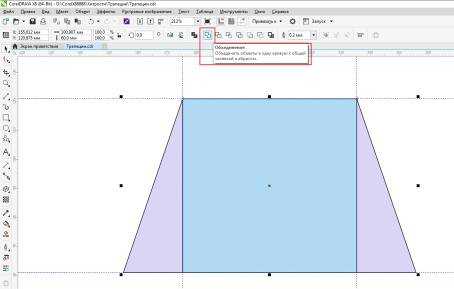
Рис.9. Вызов команды объединения объектов.
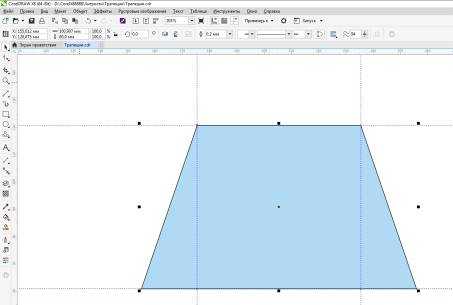
Рис.10. Так выглядит фигура после объединения.
Способ четвертый. «Рисование по сетке или направляющим».
Сначала включаем режим отображения сетки документа. Это можно сделать командой меню «Вид»> «Сетка»> «Сетка документа» либо включить на съемной панели быстрого вызова команд меню.
Рис.11. Включение отображения сетки документа.
На этой же панели находится и кнопка включения различных режимов привязки, включаем режим привязки «сетка документа»
Рис.12. Включение режима привязки объектов.
Теперь можно активировать инструмент «Прямая через две точки» и рисовать трапецию нужного размера. Узлы фигуры будут надежно привязаны к узлам сетки документа. Не забудьте проверить включен ли режим автоматического замыкания полученной кривой.
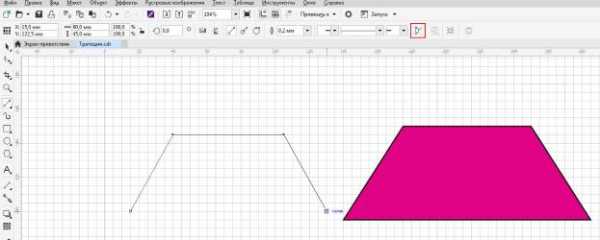
Рис.13. Работа с инструментом «Прямая через две точки».
Кстати если режим привязки к сетке включен, а сама сетка документа невидима, то во время рисования фигуры сохранится способность притяжения к сетке и фигура будет нарисована именно по сетке.
Точно таким же образом можно нарисовать трапецию или любую другую сложную фигуру, используя привязку к направляющим. Сначала выставляются направляющие по размеру будущей фигуры, затем включается режим привязки к направляющим и рисуется собственно фигура.
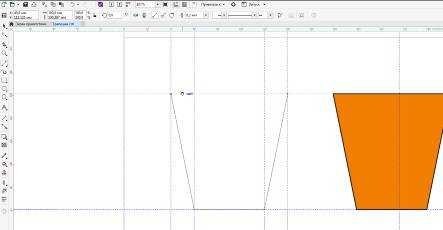
Рис.14. Рисование трапеции по направляющим.
Способ пятый. «Симметричные узелки».
Наверное, самый простой способ рисования трапеции – преобразовать в нее обычный прямоугольник. Сначала придется просто преобразовать прямоугольник в кривую (комбинация клавиш «Ctrl+Q») и, затем, поочередно инструментом «Форма» переместить два параллельных узла на нужное расстояние. Для точности удобно воспользоваться направляющими и включить соответствующий режим привязки.
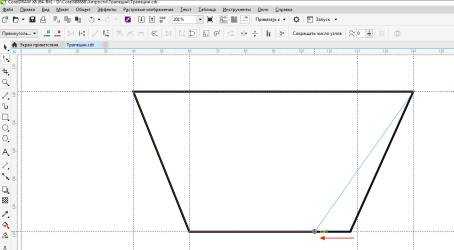
Рис.15. Рисование трапеции из прямоугольника.
Таким способом легко рисовать самые разнообразные трапеции – остроугольные, тупоугольные, прямоугольные.
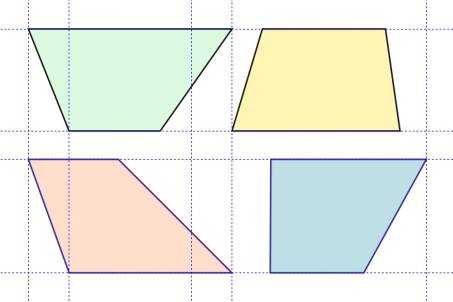
Рис.16. Примеры трапеций.
А вот если необходимо нарисовать равнобедренную трапецию, лучше применить способ симметричного перемещения узлов.
Рисуем прямоугольник, преобразуем его в кривую. Активируем инструмент «Форма», выделяем этим инструментом два параллельных узла. На панели свойств включаем режим «Отразить узлы по горизонтали» и начинаем передвигать выделенные ранее узлы. Оба узла будут перемещаться симметрично до нужного положения.
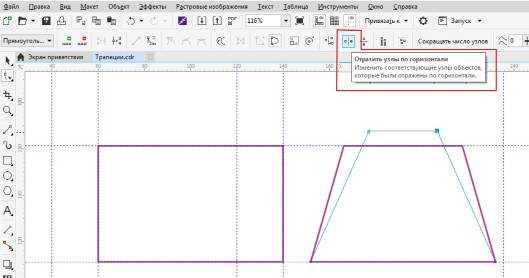
Рис.17. Симметричное перемещение узлов по горизонтали.
Аналогичным образом можно перемещать узлы, включая режим «отразить по вертикали».
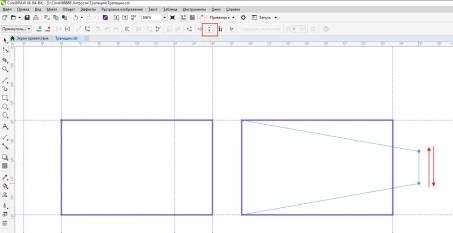
Рис.18. Симметричное перемещение узлов по вертикали.
Работа в режиме отражения узлов по вертикали или горизонтали значительно упрощает работу при рисовании симметричных фигур.
На панели свойств инструмента «Форма» есть еще несколько очень интересных кнопок, позволяющих масштабировать и поворачивать отдельные узлы кривых.
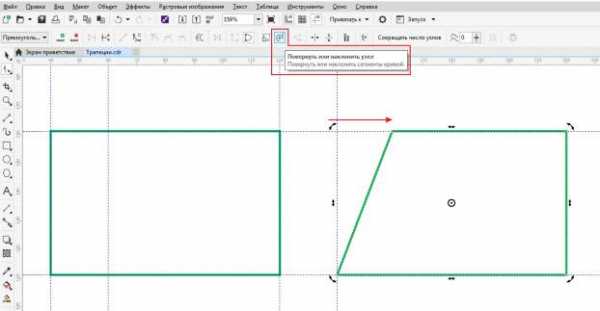
Рис.19. Включение режима «Повернуть или наклонить узел» позволит переместить, наклонить, повернуть один или несколько узлов и создать новую фигуру.
Навыки рисования трапеций различными способами всегда пригодятся при рисовании других простых или сложных фигур.
coreltuts.com
Нарисовать трапецию
← →Pavelnk © (2015-06-02 08:57) [0]
Как нарисовать трапецию в Delphi? Что то не соображу, если известны длины всех её сторон. Как вычислить координаты её углов? Ну не обязательно трапеция, можно сказать и неравносторонний прямоугольник. Но тут помоему мат задача, или как?
← →
кгшзх © (2015-06-02 09:52) [1]
да какая же это математика?
здесь ботаника и зоология с литературой должны рулить.
ты что, в школу не ходил?
← →
Pavelnk © (2015-06-02 09:52
Ну допустим нарисовал я одну линию, как мне найти координаты двух других углов трапеции?
← →
Pavelnk © (2015-06-02 10:00) [3]
Повидимому нужно знать ещё высоту трапеции, и если трапеция не равнобедренная, то повидимому все две высоты.
← →
Pavelnk © (2015-06-02 10:01) [4]
> кгшзх © (02.06.15 09:52) [1]
> да какая же это математика?
>
> здесь ботаника и зоология с литературой должны рулить.
> ты что, в школу не ходил?
Я только на физкультуру ходил.
← →
кгшзх © ( 2015-06-02 10:02) [5]
если известны только длины сторон, то разных прямоугольников с такими сторонами можно нарисовать стопитсот миллионов.
← →
sniknik © (2015-06-02 10:16) [6]
> то повидимому все две высоты.
???
я со школы помню, что у трапеции 1 высота… больше правда ничего о трапециях не помню, особенно формулы. но ведь их можно и загуглить, правда?
← →
кгшзх © (2015-06-02 10:19) [7]
в военное время количество высот у трапеции может доходить до четырех.
← →
sniknik © (2015-06-02 10:22) [8]
> с такими сторонами можно нарисовать стопитсот миллионов.
← →
кгшзх © (2015-06-02 10:25) [9]
Ну не обязательно трапеция,
вроде бы. не математик, но по логике так.
берем четыре палки и сколачиваем концы гвоздями в замкнутую фигуру.
затем начинаем тягать за углы, деформируя первоначальную форму.
получаем стопитсот четырехугольников с точно такими же сторонами.
это я как столяр говорю, а не математик.
← →
sniknik © (2015-06-02 10:26) [10]
о, нагуглил формулу для расчета 1 стороны трапеции, вторая по идее сама «образуется».
https://ru.wikipedia.org/wiki/%D0%93%D0%B8%D0%BF%D0%BE%D1%82%D0%B5%D0%BD%D1%83%D0%B7%D0%B0
← →
sniknik © (2015-06-02 10:27) [11]
> стопитсот четырехугольников
трапеция это четырехугольник, но четырехугольник это не трапеция… © Врунгель.
← →
кгшзх © (2015-06-02 10:28) [12]
Ну не обязательно трапеция,
← →
sniknik © (2015-06-02 10:31) [13]
> © Врунгель.
вернее.
> http://www.03skazki.ru/s405.htm
каждая селедка — рыба, но не каждая рыба — селедка.
> Ну не обязательно трапеция,
а, ну если так, то да.
← →
sniknik © (2015-06-02 10:35) [14]
> Ну не обязательно трапеция,
но это еще проще, ничего считать не надо, подгонка «высотой» как минимум 1 вариант но даст, а больше и нужно ничего. задачи нарисовать все множество нет…
т.е. не знаете математику? — игнорируйте ее! тут это получится.
← →
Jeer © (2015-06-02 11:26) [15]
— рисуем основания трапеции параллельно и на расстоянии друг от друга, равном длине одной из сторон;
— соединяем, скажем левые точки оснований отрезком (выбранной стороной)
— рассматривая, к примеру, левую точку как центр окружности, начинаем вращать отрезок-сторону за которым «тащится» нижнее основание, сохраняя параллельность верхнему основанию до момента когда расстояние между двумя правыми точками станет равным длине второй стороны.
Вот так интереснее, а то формулы, формулы..
← →
icWasya © (2015-06-02 11:53) [16]
Если известны стороны трапеции, и притом известно, какие стороны являются основаниями, а какие боковыми сторонами, то
1) укоротим большее основание на длину меньшего.
2) построим треугольник из укороченого основания и оставшихся боковых сторон
3) из вершины этого треугольника проведём отрезок, параллельный основанию с длиной короткого расстояния.
4) удлиним укороченное основание до его первоначальной длины.
по поводу пункта два — нужно построить точку пересечения двух окружностей с известными центрами и радиусами.
← →
Smile © (2015-06-02 12:58) [17]
> кгшзх © (02.06.15 10:25) [9]
Боюсь, что трапецию (две противоположные стороны параллельны), ты никак деформировать не сможешь. Никаких «стопитсот» ты не получишь. Всего одна для равнобедренной и две для остальных (и то вторая будет зеркальным отображением первой) 🙂
← →
Inovet © (2015-06-02 14:23) [18]
> [15] Jeer © (02.06.15 11:26)
> Вот так интереснее, а то формулы, формулы..
Это слишком просто. Рисуем произвольный квадрат в трёхмерном пространстве. Затем поворачиваем и перемещаем его с учётом перспективы так, чтобы в проекции на плоскость две стороны проекции оставались параллельными, пока не получатся все четыре стороны заданной длины.
← →
Jeer © (2015-06-02 14:36) [19]
Это слишком сложно для ТС.
← →
кгшзх © (2015-06-02 15:59) [20]
Боюсь, что трапецию …..
боюсь что ты русские буквы в русские слова складывать не умеешь.
← →
Smile © (2015-06-02 16:30) [21]
А я рад за тебя, как за столяра, что тебе это удалось «сколачиванием концов гвоздями» и «тяганием за углы» (получить «стопитсот» различных трапеций удовлетворяющих ТС)
Трапецию когда нибудь видел (ощущал)?
🙂
← →
кгшзх © (2015-06-02 16:38) [22]
Ты где там высосал требование рисовать трапецию?
во фразе «можно и не трапецию«?
так она на русский переводится как «можно трапецию, но можно и не трапецию».
← →
Smile © (2015-06-02 16:55) [23]
Я бы посоветовал вернуться к ТС
«Как нарисовать трапецию в Delphi?«
← →
кгшзх © (2015-06-02 16:56) [24]
ну так вернись.
Ну не обязательно трапеция, можно сказать и неравносторонний прямоугольник.
или с тормоза сняться не в силах?
← →
Smile © (2015-06-02 17:12) [25]
возможно что не снялся с тормозов, но грамотнее писать не «неравносторонний прямоугольник», а «не равносторонний четырехугольник»
предлагаю остановиться 🙂
← →
Pavelnk © (2015-06-02 18:00) [26]
Кстати посоветовался с математиками, они настаивают что углы надо знать.
← →
sniknik © (2015-06-02 22:49) [27]
> они настаивают что углы надо знать.
нагло врут, координат стыка линий между собой достаточно (4 точки). и даже их можно не знать, а рандомом «вычислить». вот положи перед собой лист бумаги поставь случайным образом 3 точки (через 3 всегда можно построить треугольник), после поставь четвертую, не совсем случайно, а так чтобы не попала внутрь треугольника. теперь соедени точки линиями, как угодно, каждую с каждой, обведи жирным «внешний контур» (линии не пересекшиеся с другой линией) — вуаля, четырехугольник, и никакого знания углов.
← →
Manaka © (2015-06-03 10:43) [28]
Теорема Пифагора тебе в помощь. Решение сводится к решению системы уравнений:
a+b=A
a^2+b^2=B
где А и В известны из условия
))))))))))))
← →
manaka © (2015-06-03 10:49) [29]
[28] Это для трапеции, у которой таки две стороны параллельны
← →
Manaka © (2015-06-03 10:52) [30]
> Pavelnk © (02.06.15 10:00) [3]
> Повидимому нужно знать ещё высоту трапеции, и если трапеция
> не равнобедренная, то повидимому все две высоты.
> Я только на физкультуру ходил.
заметно )))
(без обиды, но и с математикой, и с русским сплошная физкультура)
← →
manaka © (2015-06-03 11:35) [31]
Ладно…
Опустим две высоты h на нижнее основание. Они «отсекут» от от него отрезки k и l
Зная h,k и l можно вычислить координаты углов? Можно, если знать координаты основания.
Еcли
a — нижнее основание
b — верхнее основание
c,d — боковые стороны
то
h=sqrt(c^2-(((a-b)^2+c^2-d^2)/(2*(a-b)))^2)
k=sqrt(c^2-h^2)
l=k=sqrt(d^2-h^2)
← →
manaka © (2015-06-03 11:40) [32]
> h=sqrt(c^2-(((a-b)^2+c^2-d^2)/(2*(a-b)))^2)
> k=sqrt(c^2-h^2)
> l=k=sqrt(d^2-h^2)
> l=sqrt(d^2-h^2)
← →
Pavia © (2015-06-03 19:28) [33]
Удалено модератором
Примечание: Создание пустых сообщений
← →
Andryk © (2015-06-05 11:14) [34]
> Pavelnk © (02.06.15 10:00) [3]
> Повидимому нужно знать ещё высоту трапеции, и если трапеция
> не равнобедренная, то повидимому все две высоты.
Упс, посыпаю голову пеплом, новое в геометрии!!! У трапеции ДВЕ ВЫСОТЫ?! :)))
← →
Andryk © (2015-06-05 11:36) [35]
> Pavelnk © (02.06.15 18:00) [26]
> Кстати посоветовался с математиками, они настаивают что
> углы надо знать.
>
>
Углы знать не обязательно. Важно знать какие из сторон паралельны. И дальше вооружившись циркулем и линейкой можно нарисовать трапецию.
1. берем большую сторону, принимаем ее за основание.
2. из концов основания строим окружности радиусом равным боковым сторонам.
3. находим точки пересечения на окружностях так чтобы растояние было равно малому основанию, и паралельно большому.
На дельфи, как и на любом другом языке программирования, это тоже можно сделать, но для этого надо составить систему уравнений, т.е. сначала решить математическую задачу.
← →
sniknik © (2015-06-05 13:51) [36]
> Важно знать какие из сторон паралельны.
???
самая длинная, и самая короткая… очевидно же.
← →
Smile © (2015-06-05 14:33) [37]
> sniknik © (05.06.15 13:51) [36]
Далеко не очевидно, и даже неверно …
У трапеции с малой высотой это не так …
← →
sniknik © (2015-06-05 15:21) [38]
> У трапеции с малой высотой это не так …
а, действительно, о такой я почему то подумал.
← →
manaka © (2015-06-09 17:49) [39]
> Smile © (05.06.15 14:33) [37]
> У трапеции с малой высотой это не так …
у трапеции с большой высотой тоже ))) там стороны гораздо длиннее основания
← →
Inovet © (2015-06-09 20:42) [40]
Давайте определимся с определениями. Я предлагаю определения определённые в учебниках школьной геометрии. Ну, и определиться бы с конечным результатом тоже не мешало бы.
delphimaster.net
Как нарисовать 3d рисунок на бумаге карандашом поэтапно
Сейчас посмотрим, как нарисовать 3d рисунок карандашом поэтапно шаг за шагом для начинающих. Будем рисовать трапецию с оптическим обманом. Смотрите внимательно на картинки, там все детально показано. Линии должны быть параллельны друг другу. Если непонятен ход рисования, спрашивайте в комментах, я тогда перепишу урок. Последним этапом в рисовании будет закрашивание трапеции, кто не знает основы штриховки, смотрите уроки в разделе техника рисования. Кликайте на картинку для увеличения изображения.
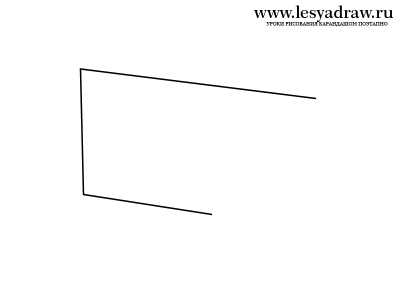
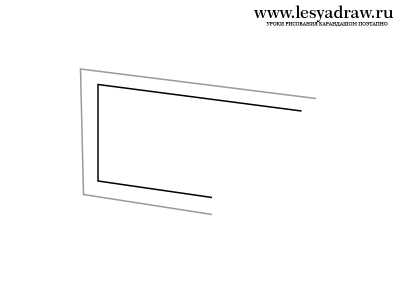
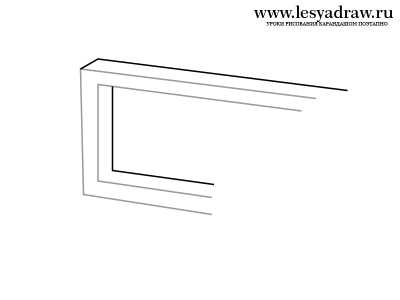
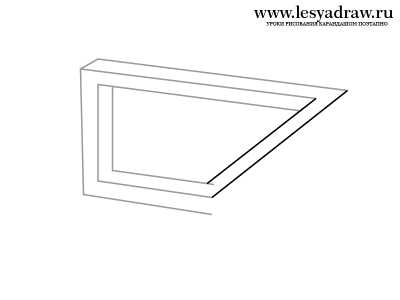
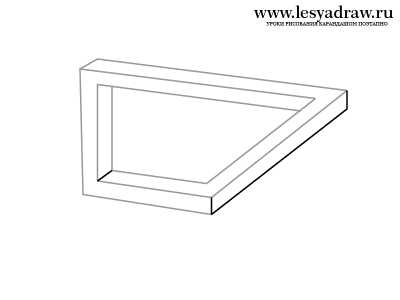
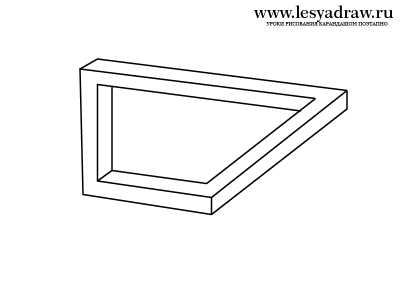
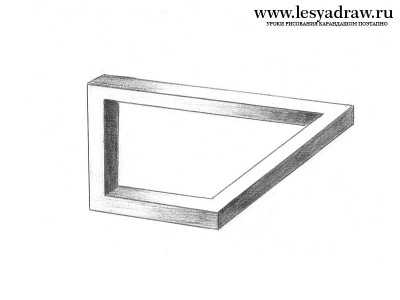
www.lesyadraw.ru
android — как рисовать трапецию для андроидной фигуры?
Ну вот:
Создание макета
<?xml version="1.0" encoding="utf-8"?>
<RelativeLayout xmlns:android="http://schemas.android.com/apk/res/android"
xmlns:tools="http://schemas.android.com/tools"
android:id="@+id/activity_main2"
android:layout_width="match_parent"
android:layout_height="match_parent"
android:paddingBottom="@dimen/activity_vertical_margin"
android:paddingLeft="@dimen/activity_horizontal_margin"
android:paddingRight="@dimen/activity_horizontal_margin"
android:background="@drawable/myshape"
android:paddingTop="@dimen/activity_vertical_margin"
tools:context="com.example.williamkinaan.expresso.Main2Activity">
</RelativeLayout>
Обратите внимание, что в макете есть обратный фон: myshape.xml
myshape.xml
Создайте файл myshape.xml в папке drawbable:
<?xml version="1.0" encoding="utf-8"?>
<vector xmlns:android="http://schemas.android.com/apk/res/android" android:width="100dp" android:height="100dp" android:viewportHeight="100" android:viewportWidth="100">
<group>
<path android:pathData="M0 0 L100 0 L100 50 L75 100 L 25 100 L 0 50 Z"
android:strokeColor="#7e0b0b"
android:strokeWidth="2"/>
<path android:pathData="M100 0 L50 80 L0 0" android:strokeColor="#7e0b0b"
android:strokeWidth="2"/>
<path android:strokeColor="#7e0b0b" android:strokeWidth="2" android:pathData="M80 30 L20 30"/>
<path android:strokeColor="#7e0b0b" android:strokeWidth="2" android:pathData="M50 80 L63 100" />
</group>
</vector>
результат

После редактирования
Измените myshape.xml на:
<?xml version="1.0" encoding="utf-8"?>
<vector xmlns:android="http://schemas.android.com/apk/res/android"
android:width="100dp"
android:height="100dp"
android:viewportHeight="100"
android:viewportWidth="100">
<path
android:pathData="M0 0 L100 0 L75 40 L25 40 Z"
android:strokeColor="#7e0b0b"
android:strokeWidth="2" />
</vector>
Результат
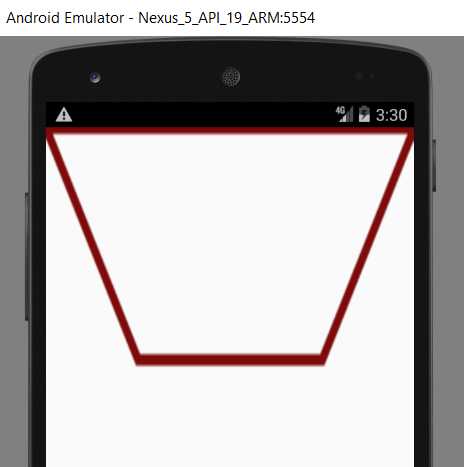
qaru.site
Нарисовать трапецию
← →Pavelnk © (2015-06-02 08:57) [0]
Как нарисовать трапецию в Delphi? Что то не соображу, если известны длины всех её сторон. Как вычислить координаты её углов? Ну не обязательно трапеция, можно сказать и неравносторонний прямоугольник. Но тут помоему мат задача, или как?
← →
кгшзх © (2015-06-02 09:52) [1]
да какая же это математика?
здесь ботаника и зоология с литературой должны рулить.
ты что, в школу не ходил?
← →
Pavelnk © (2015-06-02 09:52) [2]
Ну допустим нарисовал я одну линию, как мне найти координаты двух других углов трапеции?
← →
Pavelnk © (2015-06-02 10:00) [3]
Повидимому нужно знать ещё высоту трапеции, и если трапеция не равнобедренная, то повидимому все две высоты.
← →
Pavelnk © (2015-06-02 10:01) [4]
> кгшзх © (02.06.15 09:52) [1]
> да какая же это математика?
>
> здесь ботаника и зоология с литературой должны рулить.
> ты что, в школу не ходил?
Я только на физкультуру ходил.
← →
кгшзх © (2015-06-02 10:02) [5]
если известны только длины сторон, то разных прямоугольников с такими сторонами можно нарисовать стопитсот миллионов.
← →
sniknik © (2015-06-02 10:16) [6]
> то повидимому все две высоты.
???
я со школы помню, что у трапеции 1 высота… больше правда ничего о трапециях не помню, особенно формулы. но ведь их можно и загуглить, правда?
← →
кгшзх © (2015-06-02 10:19) [7]
в военное время количество высот у трапеции может доходить до четырех.
← →
sniknik © (2015-06-02 10:22) [8]
> с такими сторонами можно нарисовать стопитсот миллионов.
самая длинная это основа, что ограничивает «стопитсот» минимум вчетверо. самая короткая это «крыша» рассуждая логически, отрицательных углов не бывает, и «боковушки» в «воздухе» не висят. т.что все в итоге сводится к 1, и второму зеркальному, варианту. … вроде бы. не математик, но по логике так.
← →
кгшзх © (2015-06-02 10:25) [9]
Ну не обязательно трапеция,
вроде бы. не математик, но по логике так.
берем четыре палки и сколачиваем концы гвоздями в замкнутую фигуру.
затем начинаем тягать за углы, деформируя первоначальную форму.
получаем стопитсот четырехугольников с точно такими же сторонами.
это я как столяр говорю, а не математик.
← →
sniknik © (2015-06-02 10:26) [10]
о, нагуглил формулу для расчета 1 стороны трапеции, вторая по идее сама «образуется».
https://ru.wikipedia.org/wiki/%D0%93%D0%B8%D0%BF%D0%BE%D1%82%D0%B5%D0%BD%D1%83%D0%B7%D0%B0
← →
sniknik © (2015-06-02 10:27) [11]
> стопитсот четырехугольников
трапеция это четырехугольник, но четырехугольник это не трапеция… © Врунгель.
← →
кгшзх © (2015-06-02 10:28) [12]
Ну не обязательно трапеция,
← →
sniknik © (2015-06-02 10:31) [13]
> © Врунгель.
вернее.
> http://www.03skazki.ru/s405.htm
каждая селедка — рыба, но не каждая рыба — селедка.
> Ну не обязательно трапеция,
а, ну если так, то да.
← →
sniknik © (2015-06-02 10:35) [14]
> Ну не обязательно трапеция,
но это еще проще, ничего считать не надо, подгонка «высотой» как минимум 1 вариант но даст, а больше и нужно ничего. задачи нарисовать все множество нет…
т.е. не знаете математику? — игнорируйте ее! тут это получится.
← →
Jeer © (2015-06-02 11:26) [15]
— рисуем основания трапеции параллельно и на расстоянии друг от друга, равном длине одной из сторон;
— соединяем, скажем левые точки оснований отрезком (выбранной стороной)
— рассматривая, к примеру, левую точку как центр окружности, начинаем вращать отрезок-сторону за которым «тащится» нижнее основание, сохраняя параллельность верхнему основанию до момента когда расстояние между двумя правыми точками станет равным длине второй стороны.
Вот так интереснее, а то формулы, формулы..
← →
icWasya © (2015-06-02 11:53) [16]
Если известны стороны трапеции, и притом известно, какие стороны являются основаниями, а какие боковыми сторонами, то
1) укоротим большее основание на длину меньшего.
2) построим треугольник из укороченого основания и оставшихся боковых сторон
3) из вершины этого треугольника проведём отрезок, параллельный основанию с длиной короткого расстояния.
4) удлиним укороченное основание до его первоначальной длины.
по поводу пункта два — нужно построить точку пересечения двух окружностей с известными центрами и радиусами.
← →
Smile © (2015-06-02 12:58) [17]
> кгшзх © (02.06.15 10:25) [9]
Боюсь, что трапецию (две противоположные стороны параллельны), ты никак деформировать не сможешь. Никаких «стопитсот» ты не получишь. Всего одна для равнобедренной и две для остальных (и то вторая будет зеркальным отображением первой) 🙂
← →
Inovet © (2015-06-02 14:23) [18]
> [15] Jeer © (02.06.15 11:26)
> Вот так интереснее, а то формулы, формулы..
Это слишком просто. Рисуем произвольный квадрат в трёхмерном пространстве. Затем поворачиваем и перемещаем его с учётом перспективы так, чтобы в проекции на плоскость две стороны проекции оставались параллельными, пока не получатся все четыре стороны заданной длины.
← →
Jeer © (2015-06-02 14:36) [19]
Это слишком сложно для ТС.
← →
кгшзх © (2015-06-02 15:59) [20]
Боюсь, что трапецию …..
боюсь что ты русские буквы в русские слова складывать не умеешь.
← →
Smile © (2015-06-02 16:30) [21]
А я рад за тебя, как за столяра, что тебе это удалось «сколачиванием концов гвоздями» и «тяганием за углы» (получить «стопитсот» различных трапеций удовлетворяющих ТС)
Трапецию когда нибудь видел (ощущал)?
🙂
← →
кгшзх © (2015-06-02 16:38) [22]
Ты где там высосал требование рисовать трапецию?
во фразе «можно и не трапецию«?
так она на русский переводится как «можно трапецию, но можно и не трапецию».
← →
Smile © (2015-06-02 16:55) [23]
Я бы посоветовал вернуться к ТС
«Как нарисовать трапецию в Delphi?«
← →
кгшзх © (2015-06-02 16:56) [24]
ну так вернись.
Ну не обязательно трапеция, можно сказать и неравносторонний прямоугольник.
или с тормоза сняться не в силах?
← →
Smile © (2015-06-02 17:12) [25]
возможно что не снялся с тормозов, но грамотнее писать не «неравносторонний прямоугольник», а «не равносторонний четырехугольник»
предлагаю остановиться 🙂
← →
Pavelnk © (2015-06-02 18:00) [26]
Кстати посоветовался с математиками, они настаивают что углы надо знать.
← →
sniknik © (2015-06-02 22:49) [27]
> они настаивают что углы надо знать.
нагло врут, координат стыка линий между собой достаточно (4 точки). и даже их можно не знать, а рандомом «вычислить». вот положи перед собой лист бумаги поставь случайным образом 3 точки (через 3 всегда можно построить треугольник), после поставь четвертую, не совсем случайно, а так чтобы не попала внутрь треугольника. теперь соедени точки линиями, как угодно, каждую с каждой, обведи жирным «внешний контур» (линии не пересекшиеся с другой линией) — вуаля, четырехугольник, и никакого знания углов.
← →
Manaka © (2015-06-03 10:43) [28]
Теорема Пифагора тебе в помощь. Решение сводится к решению системы уравнений:
a+b=A
a^2+b^2=B
где А и В известны из условия
))))))))))))
← →
manaka © (2015-06-03 10:49) [29]
[28] Это для трапеции, у которой таки две стороны параллельны
← →
Manaka © (2015-06-03 10:52) [30]
> Pavelnk © (02.06.15 10:00) [3]
> Повидимому нужно знать ещё высоту трапеции, и если трапеция
> не равнобедренная, то повидимому все две высоты.
> Я только на физкультуру ходил.
заметно )))
(без обиды, но и с математикой, и с русским сплошная физкультура)
← →
manaka © (2015-06-03 11:35) [31]
Ладно…
Опустим две высоты h на нижнее основание. Они «отсекут» от от него отрезки k и l
Зная h,k и l можно вычислить координаты углов? Можно, если знать координаты основания.
Еcли
a — нижнее основание
b — верхнее основание
c,d — боковые стороны
то
h=sqrt(c^2-(((a-b)^2+c^2-d^2)/(2*(a-b)))^2)
k=sqrt(c^2-h^2)
l=k=sqrt(d^2-h^2)
← →
manaka © (2015-06-03 11:40) [32]
> h=sqrt(c^2-(((a-b)^2+c^2-d^2)/(2*(a-b)))^2)
> k=sqrt(c^2-h^2)
> l=k=sqrt(d^2-h^2)
> l=sqrt(d^2-h^2)
← →
Pavia © (2015-06-03 19:28) [33]
Удалено модератором
Примечание: Создание пустых сообщений
← →
Andryk © (2015-06-05 11:14) [34]
> Pavelnk © (02.06.15 10:00) [3]
> Повидимому нужно знать ещё высоту трапеции, и если трапеция
> не равнобедренная, то повидимому все две высоты.
Упс, посыпаю голову пеплом, новое в геометрии!!! У трапеции ДВЕ ВЫСОТЫ?! :)))
← →
Andryk © (2015-06-05 11:36) [35]
> Pavelnk © (02.06.15 18:00) [26]
> Кстати посоветовался с математиками, они настаивают что
> углы надо знать.
>
>
Углы знать не обязательно. Важно знать какие из сторон паралельны. И дальше вооружившись циркулем и линейкой можно нарисовать трапецию.
1. берем большую сторону, принимаем ее за основание.
2. из концов основания строим окружности радиусом равным боковым сторонам.
3. находим точки пересечения на окружностях так чтобы растояние было равно малому основанию, и паралельно большому.
На дельфи, как и на любом другом языке программирования, это тоже можно сделать, но для этого надо составить систему уравнений, т.е. сначала решить математическую задачу.
← →
sniknik © (2015-06-05 13:51) [36]
> Важно знать какие из сторон паралельны.
???
самая длинная, и самая короткая… очевидно же.
← →
Smile © (2015-06-05 14:33) [37]
> sniknik © (05.06.15 13:51) [36]
Далеко не очевидно, и даже неверно …
У трапеции с малой высотой это не так …
← →
sniknik © (2015-06-05 15:21) [38]
> У трапеции с малой высотой это не так …
а, действительно, о такой я почему то подумал.
← →
manaka © (2015-06-09 17:49) [39]
> Smile © (05.06.15 14:33) [37]
> У трапеции с малой высотой это не так …
у трапеции с большой высотой тоже ))) там стороны гораздо длиннее основания
← →
Inovet © (2015-06-09 20:42) [40]
Давайте определимся с определениями. Я предлагаю определения определённые в учебниках школьной геометрии. Ну, и определиться бы с конечным результатом тоже не мешало бы.
← →
Германн © (2015-06-10 02:49) [41]
Удалено модератором
Примечание: Создание пустых сообщений
delphimaster.net
