Умножение векторов, формулы и примеры
Для векторов существует три вида умножения векторов: скалярное и векторное произведение двух векторов и смешанное произведение трех векторов. Результатом первого и последнего есть число, а результатом векторного произведения – вектор.
Скалярное умножение векторов
Замечание. Если один из векторов нулевой, то скалярное произведение равно нулю.
Замечание. Из определения скалярного произведения получаем, что угол (а точнее его косинус) между векторами-сомножителями вычисляется по формуле:
Скалярное произведение вектора на самого себя называется скалярным квадратом и обозначается .
Скалярный квадрат вектора равен квадрату его модуля:
Тогда длина вектора может быть найдена по формуле:
Скалярное произведение двух векторов положительно, если угол между векторами острый; и отрицательно, если угол
Критерий ортогональности векторов. Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда угол между ними прямой, то есть когда эти векторы ортогональны (перпендикулярны):
Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:
Векторное умножение векторов
Замечание. Таким образом, длина (модуль) вектора численно равна площади параллелограмма, построенного на векторах и :
Критерий коллинеарности векторов. Два вектора и коллинеарны тогда и только тогда, когда их векторное произведение равно нулю:
Если векторы и заданы своими координатами в пространстве, то их векторное произведение определяется формулой:
Смешанное умножение векторов
Геометрический смысл смешанного произведения. Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами :
Критерий компланарности векторов. Если три вектора компланарны, то их смешанное произведение равно нулю.
Если векторы заданы в пространстве своими координатами: , то их смешанное произведение можно вычислить по формуле:
ru.solverbook.com
определение, сложение, умножение, скалярное и векторное произведение
В статье узнаете что такое вектор, векторные компоненты, единичный вектор, как складывать вектора, умножать вектора на скаляр, скалярное, векторное и смешанное произведение двух векторов.
Сохранение физической величины с вектором обычно означает совершенно иную ситуацию, чем просто сохранение ее скалярной длины. Постоянное значение импульса p (скаляр) может означать совершенно иную ситуацию, чем постоянный вектор p.
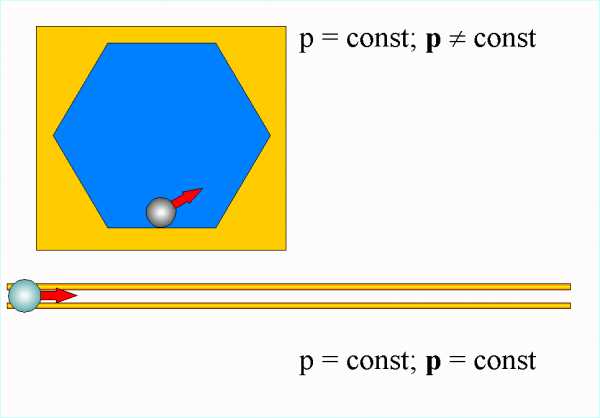
Любое изменение любого из этих признаков — длины, направления или начало с концом — означает, что создан другой вектор. Два вектора равны тогда и только тогда, когда они имеют равную длину, направление и начало с концом.
Векторные компоненты
Компонентами вектора являются его проекции на оси системы координат.
Также в трехмерном пространстве векторы A называются векторами, которые являются проекциями этого вектора A на оси системы координат.
Имея вектор A, мы погружаем его в систему координат x, y, z. Векторы, являющиеся проекциями вектора A на оси системы, называются векторными компонентами вектора A. Вектор A является векторной суммой составляющих векторов Ax, Ay и Az .

Единичный вектор
Единичный вектор, имеющий то же направление, что и вектор, на который он ссылается, важен, но его длина всегда равна 1.
Единичные векторы осей координат. Мы также присваиваем единичные векторы оси системы отсчета. а) относится к правовращающей системе и б) к левосторонней системе.
Сложение векторов
Сумма вектора обычно не совпадает с суммой скалярных величин:
Добавление двух или более векторов друг к другу сводится к добавлению их компонентов, то есть проекций на опорные оси. Результирующий вектор называется случайным вектором. Для двух векторов результирующий вектор является диагональю параллелограмма, построенного на этих векторах. Метод параллелограмма.

В случае большего числа векторов результирующий вектор получается путем рисования одного из этих векторов, затем в конце первого вектора мы начинаем второй, в конце второго мы даем начало третьего и так далее. Полученный вектор является вектором, начало которого находится в начале первого из добавленных векторов. и его конец в конце последнего. При изменении порядка сложения результирующий вектор (красный) не меняет длину, направление:

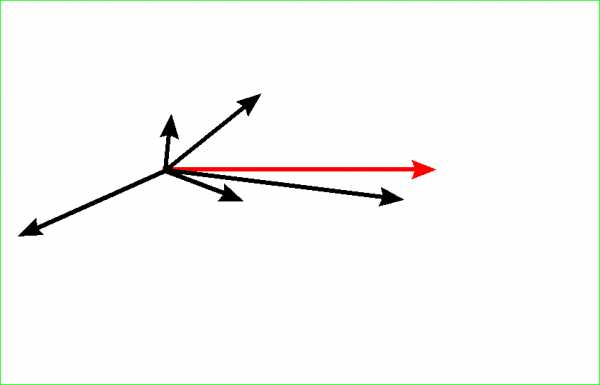
Это правило добавления векторов также действует в трехмерном пространстве:

Умножение вектора на скаляр
Самым простым умножением, выполняемым на векторах, является умножение вектора на скаляр (число). Такое умножение не меняет направление вектора, но, как правило, меняет его длину и может изменить его конец (когда скаляр является отрицательным числом). Когда вектор A умножается на α-скаляр, мы получаем новый вектор B:
Скалярное произведение и векторное произведение двух векторов являются очень важными направления в физике и геометрии. Существует также смешанное произведение трех векторов.
Скалярное произведение двух векторов
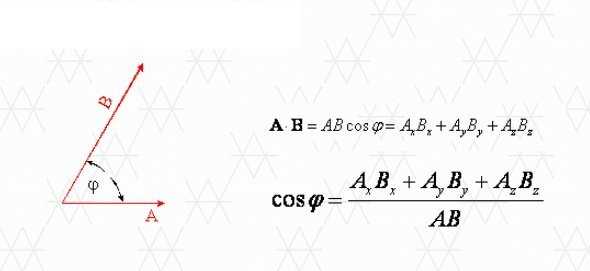
Формально скалярное произведение векторов представляет собой точку, и ее значение определяется зависимостью
Скалярное произведение описывает способ, которым оба вектора видят друг друга, то есть как долго тень (проекция) отбрасывает каждый из векторов в своего партнера, когда угол между ними равен φ
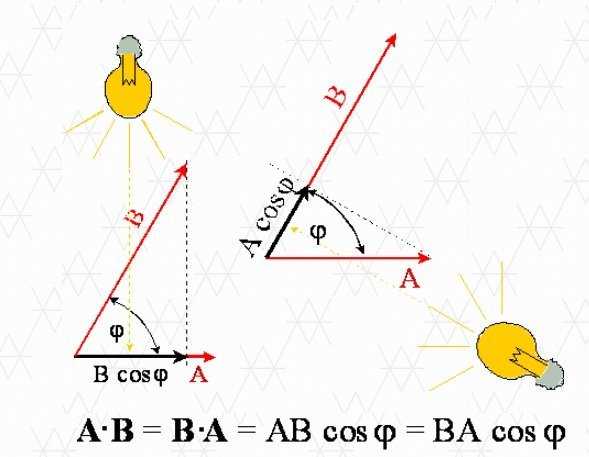
B cos φ — длина тени, которую вектор B выбрасывает в вектор A. Аналогично, A cos φ — длина тени, которую вектор A выбрасывает в вектор B.
Когда длина проекции (тени) одного из векторов равна нулю, тогда длина проекции второго вектора равна нулю, то есть A • B = 0. Это означает, что эти векторы не работают в одном и том же направлении вообще. Работа, которую мы выполняем при движении автомобиля, зависит не только от приложенной силы F, но и от угла, который создает направление силы и направление пути.
Так как единичные векторы оси системы отсчета х, у и z, которые обозначают векторы ех, еY и еz, перпендикулярны друг к другу, то в виду того, что А • В = АВcosφ и что cos 0 = 1 и cos 90o = 0, мы получаем произведение значений этих единичных векторов:
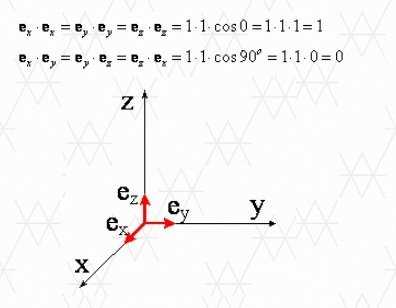
Выполнение аналогичного умножения на векторы A и B
мы получили новое выражение для скалярного произведения двух векторов A и B
Значение скалярного произведения двух векторов A и B можно записать в виде двух эквивалентных выражений:
Сравнивая оба выражения, мы находим выражение для угла между векторами A и B:
Векторное произведение двух векторов
Многие важные величины в науке и технике определяются вектором, который является произведением двух других векторов. В таких случаях произведение этих векторов, называемое векторным произведением , приводит к третьему вектору.
В этом случае задача состоит в том, чтобы определить все три особенности вектора C, являющегося произведением векторного произведения векторов A и B:
- длина
- направление
- начало и конец
Произведение векторов A и B , приводящее к третьему вектору C
Направление
Вектор С такой, что вектор перпендикулярен к плоскости, образованной векторами A и B, которая перпендикулярна как к вектору A и B.
Длина
вектор С равен значению параллелограмма, построенного на векторах А и В. Числовой C = ABsin φ.
Начало и конец
Вектор С определяет правое направление движения шнека во время нанесения первого вектора, а именно А или B.
Изменение порядка применения векторов означает изменение знака векторного произведения.
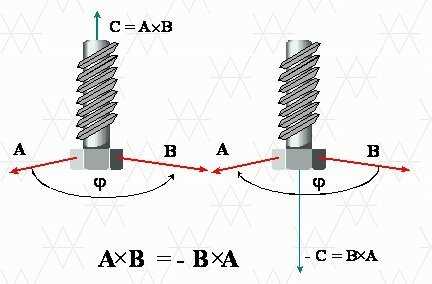
Таким образом, действительное свойство векторного произведения выглядит следующим образом A*B= -B*A
В отличие от скалярного произведения, векторное произведение некоммутативно.
Мы встретимся с векторным произведением на протяжении всего курса физики. Это также часто встречается в механике, а также в науке об электричестве и магнетизме.
В повседневной жизни векторное произведение находится в виде момента силы во вращательном движении. Мы воздействуем на вращательное движение тем эффективнее, чем больше применяем момент силы.
При откручивании гайки гаечным ключом речь идет не только о силе F, но и о способе ее применения (длина рычага R и угол, который создает рычаг с направлением силы).
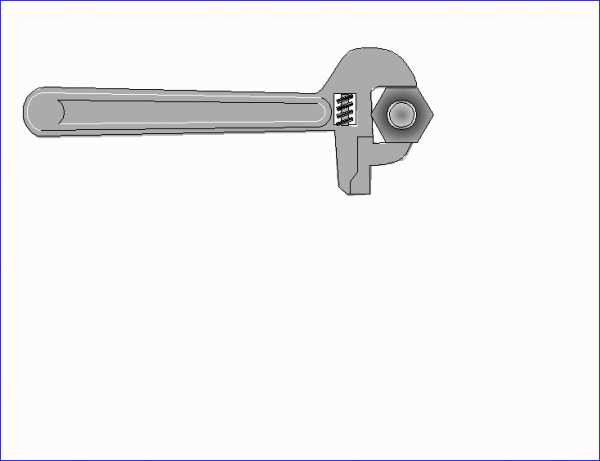
Все эти зависимости элегантно включены в одно выражение в виде векторного произведения:
Хотя составляющие вектора C, который является произведением векторного произведения векторов A и B, уже включены в его длину и направление, но имея данные составляющих векторов A и B, мы можем использовать их для определения компонентов вектора C в форме матрицы:
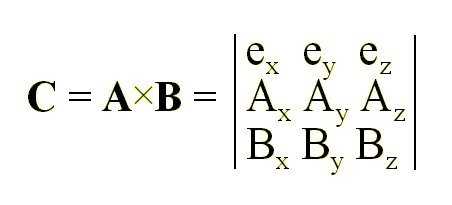
Удобнее всего рассчитать этот определитель, расширив относительно первой строки.
Смешанное произведение трех векторов
Смешанное произведение трех векторов является скалярным значением, равным значению детерминанта
Геометрическая интерпретация: смешанное произведение численно равно объему V параллелепипеда, растянутому по векторам A, B и C:
Циклическая корректировка векторов в смешанном произведении не меняет значение этого произведения, то есть:
meanders.ru
Умножение вектора на число
Откладывание вектора от данной точки
Для того чтобы ввести понятие умножения вектора на число, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Определение 1
Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).
Рисунок 1. $\overrightarrow{a}$ отложенный от точки $A$
Введем следующую теорему:
Теорема 1
От любой точки $K$ можно отложить вектор $\overrightarrow{a}$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
Вектор $\overrightarrow{a}$ — нулевой.
В этом случае, очевидно, что искомый вектор — вектор $\overrightarrow{KK}$.
Вектор $\overrightarrow{a}$ — ненулевой.
Обозначим точкой $A$ начало вектора $\overrightarrow{a}$, а точкой $B$ — конец вектора $\overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Умножение вектора на число
Пусть нам дан вектор $\overrightarrow{a\ }$ и действительное число $k$.
Определение 2
Произведением вектора $\overrightarrow{a\ }$ на действительное число $k$ называется вектор $\overrightarrow{b\ }$ удовлетворяющий следующим условиям:
Длина вектора $\overrightarrow{b\ }$ равна $\left|\overrightarrow{b\ }\right|=\left|k\right||\overrightarrow{a\ }|$;
Векторы $\overrightarrow{a\ }$ и $\overrightarrow{b\ }$ сонаправлены, при $k\ge 0$ и противоположно направлены, если $k
Обозначение: $\ \overrightarrow{b\ }=k\overrightarrow{a\ }$.
Замечание 1
Отметим, что в результате произведения вектора на число всегда получается векторная величина.
Свойства произведения вектора на число
Произведение любого вектора с числом ноль равняется нулевому вектору.
Доказательство.
По определению 2, имеем $\left|\overrightarrow{b\ }\right|=\left|k\right|\left|\overrightarrow{a\ }\right|=0\cdot \left|\overrightarrow{a\ }\right|=0$, следовательно,$\overrightarrow{b\ }=k\overrightarrow{a\ }=\overrightarrow{0}$
Для любого вектора $\overrightarrow{a\ }$ и любого действительного числа $k$ векторы $\overrightarrow{a\ }$ и $k\overrightarrow{a\ }$ коллинеарны.
Доказательство.
Так как по определению 2, векторы $\overrightarrow{a\ }$ и $k\overrightarrow{a\ }$ сонаправлены или противоположно направлены (в зависимости от значения $k$), то они будут коллинеарны.
Для любых действительных чисел $m$ и $n$ и вектора $\overrightarrow{a\ }$ справедлив сочетательный закон:
\[\left(mn\right)\overrightarrow{a\ }=m(n\overrightarrow{a\ })\]Доказательство этого закона иллюстрирует рисунок 3.
Рисунок 3. Сочетательный закон
Для любых действительных чисел $m$ и $n$ и вектора $\overrightarrow{a\ }$ справедлив первый распределительный закон:
\[\left(m+n\right)\overrightarrow{a\ }=m\overrightarrow{a\ }+n\overrightarrow{a\ }\]Доказательство этого закона иллюстрирует рисунок 4.
Рисунок 4. Первый распределительный закон
Для любого действительного числа $m$ и векторов $\overrightarrow{a\ }$ и $\overrightarrow{b\ }$ справедлив второй распределительный закон:
\[m\left(\overrightarrow{a\ }+\overrightarrow{b}\right)=m\overrightarrow{a\ }+m\overrightarrow{b\ }\]Доказательство этого закона иллюстрирует рисунок 5.
Рисунок 5. Второй распределительный закон
Пример задачи на использование понятия произведения вектора на число
Пример 1
Пусть $\overrightarrow{x}=\overrightarrow{a\ }+\overrightarrow{b}$, $\overrightarrow{y}=\overrightarrow{a\ }-\overrightarrow{b}$. Найти векторы:
$2\overrightarrow{x}+2\overrightarrow{y}$
$\overrightarrow{x}+\frac{1}{2}\overrightarrow{y}$
$-\overrightarrow{y}-\overrightarrow{x}$
Решение.
$2\overrightarrow{x}+2\overrightarrow{y}=2\left(\overrightarrow{a\ }+\overrightarrow{b}\right)+2\left(\overrightarrow{a\ }-\overrightarrow{b}\right)=2\overrightarrow{a\ }+2\overrightarrow{b}+2\overrightarrow{a\ }-2\overrightarrow{b}=4\overrightarrow{a\ }$
$\overrightarrow{x}+\frac{1}{2}\overrightarrow{y}=\overrightarrow{a\ }+\overrightarrow{b}+\frac{1}{2}\left(\overrightarrow{a\ }-\overrightarrow{b}\right)=\overrightarrow{a\ }+\overrightarrow{b}+\frac{1}{2}\overrightarrow{a\ }-\frac{1}{2}\overrightarrow{b}=\frac{3}{2}\overrightarrow{a\ }+\frac{1}{2}\overrightarrow{b}=\frac{3\overrightarrow{a\ }+\overrightarrow{b}}{2}$
$-\overrightarrow{y}-\overrightarrow{x}=-\left(\overrightarrow{a\ }-\overrightarrow{b}\right)-\left(\overrightarrow{a\ }+\overrightarrow{b}\right)=-\overrightarrow{a\ }+\overrightarrow{b}-\overrightarrow{a\ }-\overrightarrow{b}=-2\overrightarrow{a\ }$
spravochnick.ru
Умножение вектора на число
Произведением вектора x на число β (x≠0, β≠0) называется вектор, модуль которого равен |x||β| и который направлен в ту же сторону, что и вектор x, если β>0, и в противоположную, если β<0. Если x=0 и (или) β=0, то βx=0.

Рис. 1
На рисунке Рис. 1 вектор x умножен на число 1.5. Полученный вектор y’ имеет то же направление, что и x т.к 1.5>0, и имеет длину 1.5 раз превысшающее длину x.
Вектор q имеет противополжное к p направление, т.к. вектор p умножено на отрицательное число -0.5, и имеет длину 2 раза меньше длины p.
Рассмотрим процесс умножения вектора на число.
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пусть имеется вектор
где координаты вектора x, и пусть β некоторое число. Тогда
То есть для умножения вектора на число достаточно умножить каждый координат данного вектора на это число.
На рисунке Рис. 1 вектор x имеет координаты x=(6,4). Для умножения вектора x на число 1.5, умножим каждый координат вектора x на число 1.5:
Вариант 2. Начальные точки векторов произвольные.
Пусть имеется вектор x, с начальной точкой и конечной точкой . Умножим вектор x на число β. Для этого проще всего параллельно переместить вектор x на начало координат, умножить на число, после чего параллельно переместить началную точку полученного вектора на точку A.
Переместим вектор x на начало координат. Получим новый вектор x’ с начальными и конечными точками:
Умножим x’ на β:
Параллельно переместив начальную точку вектора x’ на точку A, получим вектор x» с начальными и конечными точками:
На рисунке Рис. 1 вектор p=AB имеет координаты A(2,3) и B(8,1). Для умножения вектора p на число -0.5, сначала переместим параллельно вектор p так, чтобы начальная точка вектора p совпала с началом координат. Получим вектор p’=A’B’ с координатами A’(0,0) и B’(8-2, 1-3)=B’(6,-2). Умножим вектор p’ с числом -0.5:
Перемесив начальную точку вектора q’ на точку A, получим вектор q=AE, где точка E имеет координаты:
Операция умножения вектора на число обладает следующими свойствами:
1.β(x+y)=βx+βy (дистрибутивность относительно сложения векторов).
2. (α+β)a=αa+βa (дистрибутивность относительно сложения чисел).
3. α(βa)=(αβ)a (ассоциативность).
4. 1·a=a (умножение на единицу).
Примеры умножения вектора на число
Пример 1. Умножить вектор y=(3,5,-6) на число 2.5.
Для умножения вектора y на число 2.5, просто умножаем каждый координат вектора y на данное число:Пример 2. Умножить вектор x=AB на число 3, где A(2,2), B(7,6).
Переместим вектор AB на начало координат. Начальное и конечное точки перемещенного вектора будут:
Умножив полученный вектор на число 3, изменяется расположение конечной точки B’:
.
Переместив вектор на точку A, получим вектор 3·x, со следующими начальной и конечной точками:
matworld.ru
§8. Умножение векторов
Векторы можно умножать скалярно
и векторно. Скалярным произведением
двух ненулевых векторов  и
и называется число, равное произведению
длин этих векторов на косинус угла между
ними:
называется число, равное произведению
длин этих векторов на косинус угла между
ними:
(8.1).
Эту формулу можно записать в виде
.
Скалярное произведение имеет следующие свойства:
— переместительный закон.
— распределительный закон
 ,
отсюда
,
отсюда
Если
 ,
то
,
то — условие перпендикулярности векторов
— условие перпендикулярности векторов и
и
 ,
, — вектор силы,
— вектор силы, — вектор перемещения,
— вектор перемещения, — работа силы
— работа силы .
.
Если  и
и заданы в прямоугольной системе координат,
то(8.2).
заданы в прямоугольной системе координат,
то(8.2).
Упорядоченная тройка векторов 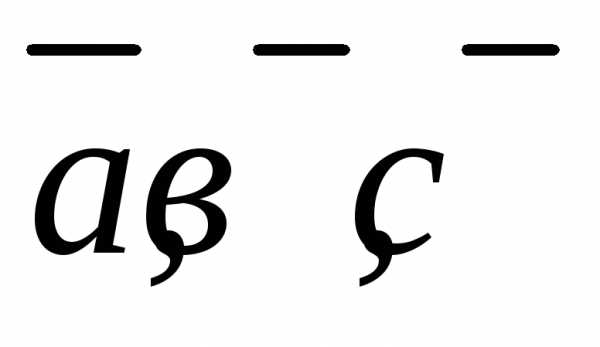 называется правой, если кратчайший
поворот от вектора
называется правой, если кратчайший
поворот от вектора к вектору
к вектору из конца вектора
из конца вектора виден совершающимся против часовой
стрелки. Рис.7.
виден совершающимся против часовой
стрелки. Рис.7.



Рис. 7.
Векторным произведением вектора  на вектор
на вектор называется третий вектор
называется третий вектор ,
длина которого равна,
он перпендикулярен векторам
,
длина которого равна,
он перпендикулярен векторам и
и и направлен в ту сторону, что векторы
и направлен в ту сторону, что векторы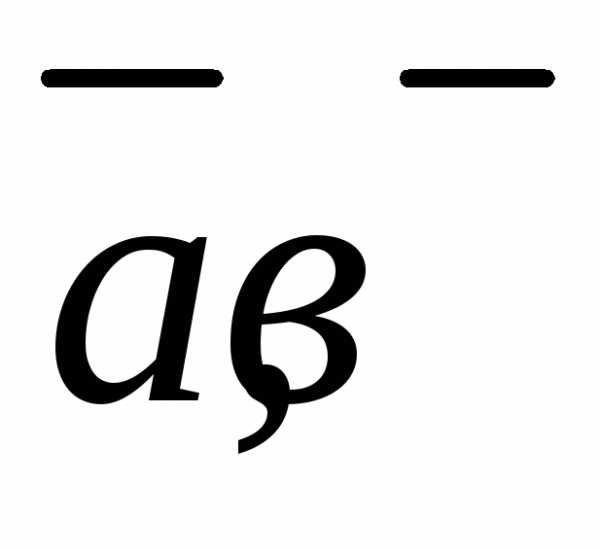 и
и образуют правую тройку.
образуют правую тройку.
Векторное произведение обозначается .
Векторное произведение имеет следующие свойства:
Если
 ,
то
,
то
 ,
где
,
где — площадь параллелограмма, построенного
на этих векторах как на сторонах.
— площадь параллелограмма, построенного
на этих векторах как на сторонах.
Если векторы  и
и заданы в прямоугольной системе координат:и
заданы в прямоугольной системе координат:и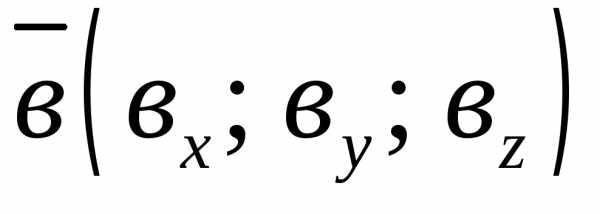 ,
то:
,
то:
(8.3).
Если  вектор силы, приложенной в точке
вектор силы, приложенной в точке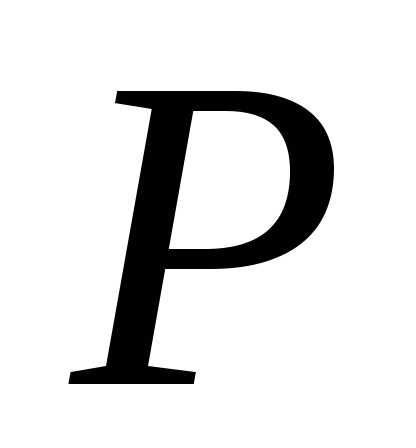 ,
а
,
а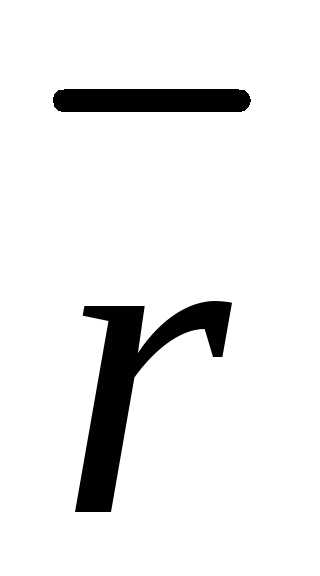 радиус-вектор точки
радиус-вектор точки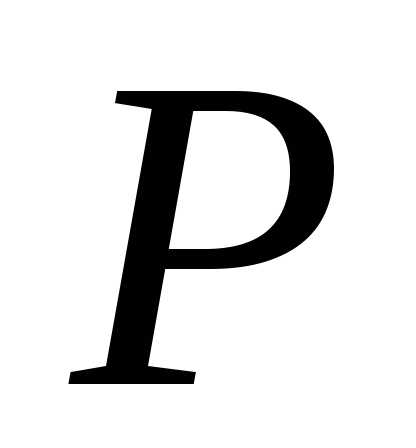 ,
то момент силы
,
то момент силы ,
относительно начала координат
,
относительно начала координат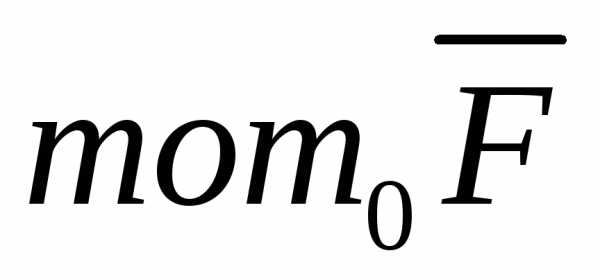 равен:
равен:
.
Смешанным произведением трех
векторов 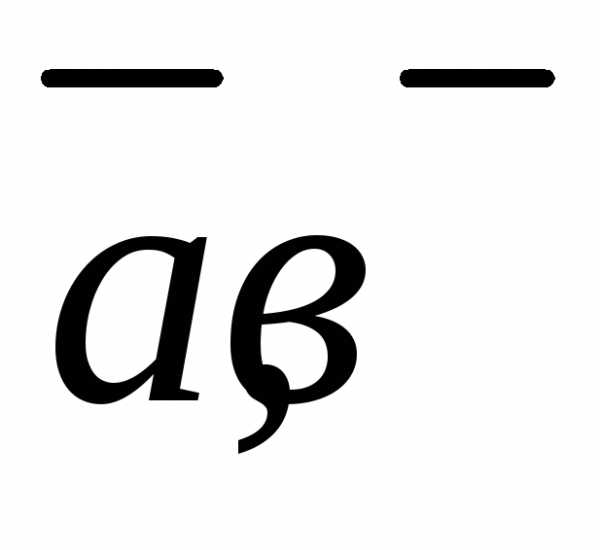 и
и называется их векторно-скалярное
произведение. Обозначается.
называется их векторно-скалярное
произведение. Обозначается.
Если заданы координаты векторов в прямоугольной системе координат, то их смешанное произведение вычисляется по формуле:
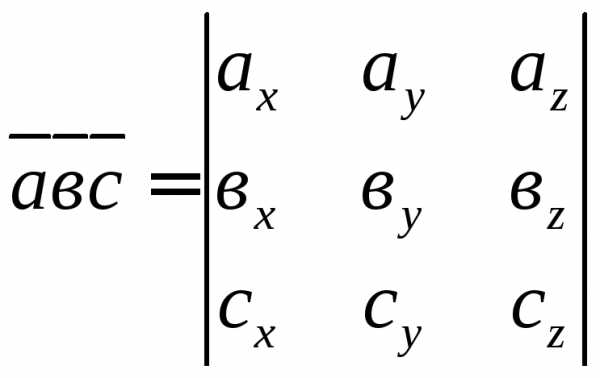 (8.4).
(8.4).
Свойствасмешанного произведения векторов:
 — условие компланарности векторов;
— условие компланарности векторов; — объем параллелепипеда, построенного
на векторах, как на сторонах;
— объем параллелепипеда, построенного
на векторах, как на сторонах;— циклическая перестановка сомножителей не меняет величины смешанного произведения;
Пример 11.Даны вершины
пирамиды.
Найти 1) угол между ребром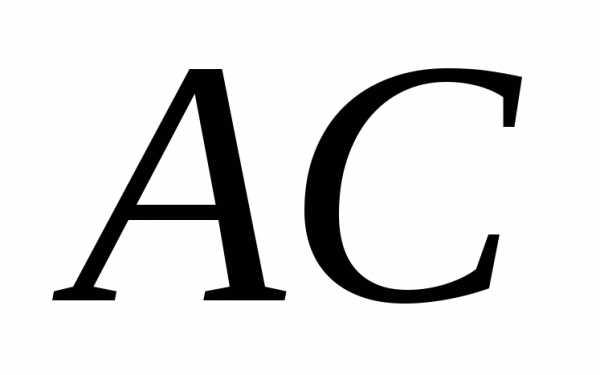 и
гранью
и
гранью ;
2) площадь грани
;
2) площадь грани ;
3) объем пирамиды
;
3) объем пирамиды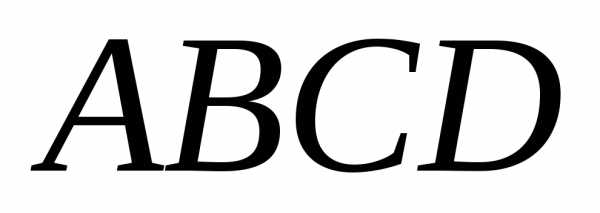 ;
4) длину высоты, опущенной из вершины
;
4) длину высоты, опущенной из вершины на грань
на грань .
.
Решение. Вычислим координаты вектора 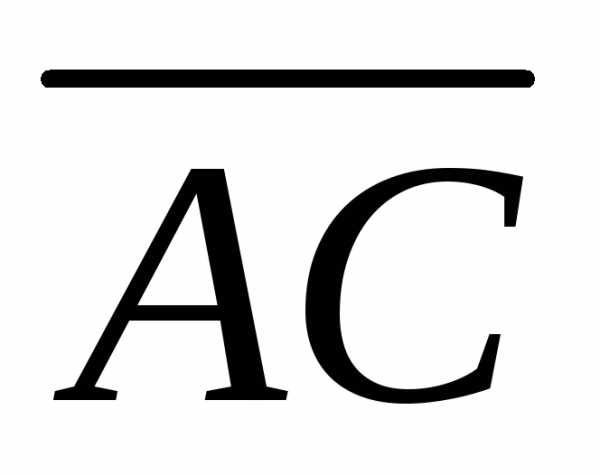 :
:
.
Угол  между ребром
между ребром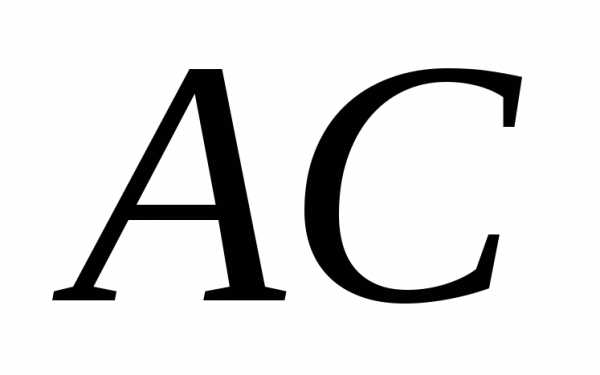 и
гранью
и
гранью является дополнительным углом для угла
является дополнительным углом для угла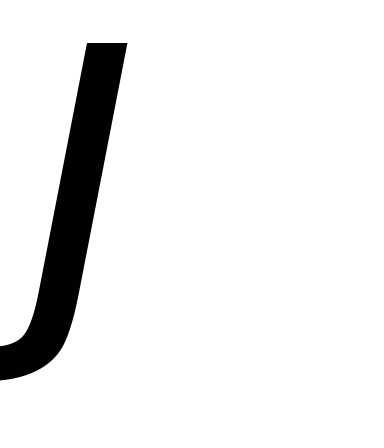 ,
образованного перпендикуляром,
проведенным к плоскости треугольника
,
образованного перпендикуляром,
проведенным к плоскости треугольника и ребром
и ребром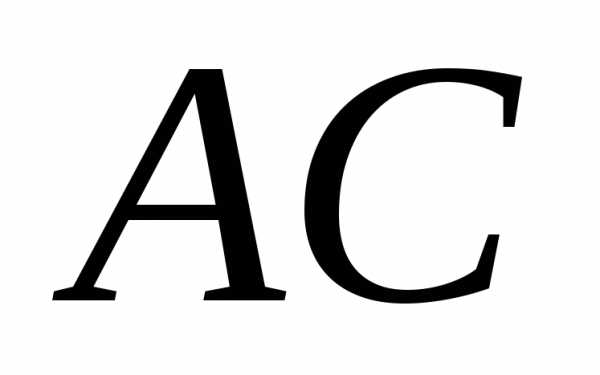 ..
Для нахождения
..
Для нахождения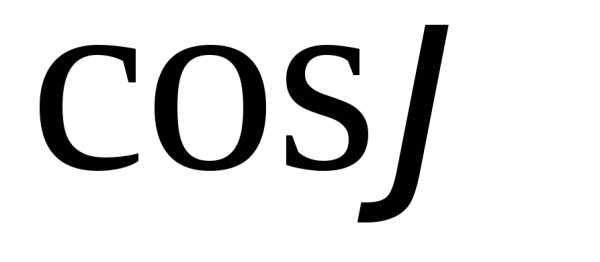 вычислим координаты векторного
произведения векторов
вычислим координаты векторного
произведения векторов и
и :
:
;
.
.
;
.
Площадь грани
 равна половине площади параллелограмма,
построенного на сторонах
равна половине площади параллелограмма,
построенного на сторонах и
и ,
т.е.
,
т.е.
.
Объем пирамиды равен одной трети от объема параллелепипеда,
построенного на ребрах  и
и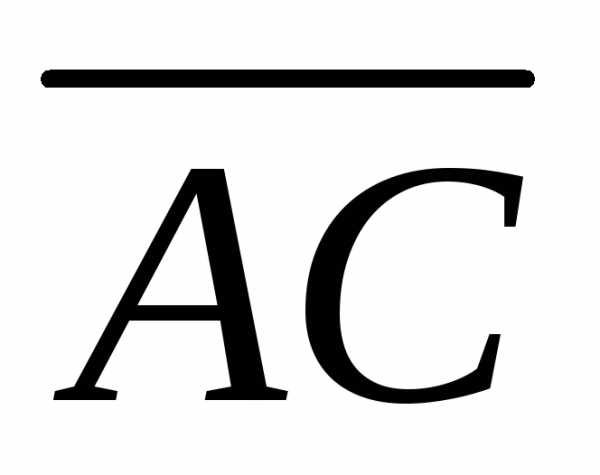 .
Следовательно
.
Следовательно
.
Длина высоты
 определяется из формулы:
определяется из формулы:
;.
Ответ:
; ;
;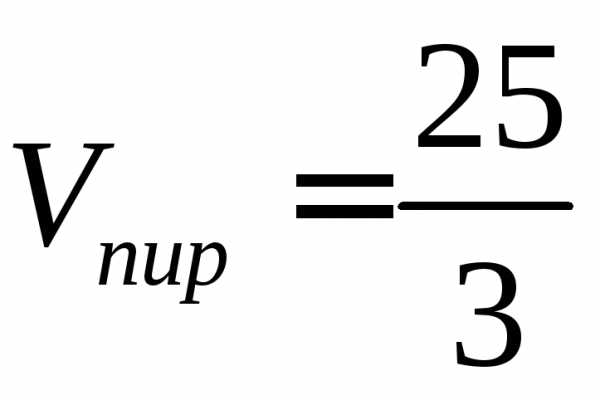 ;
;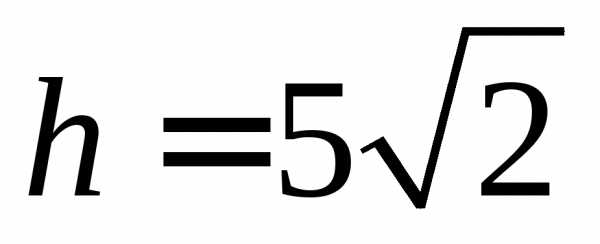 .
.
§9. Комплексные числа
Комплексным числом  называется выражение
называется выражение
(9.1),
где  и
и — действительные числа;
— действительные числа;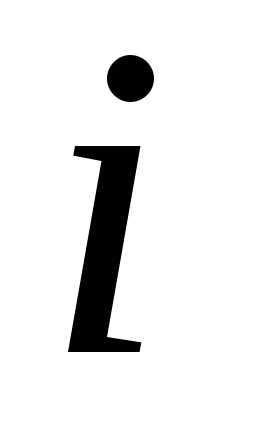 — мнимая единица, определяемая равенством
— мнимая единица, определяемая равенством
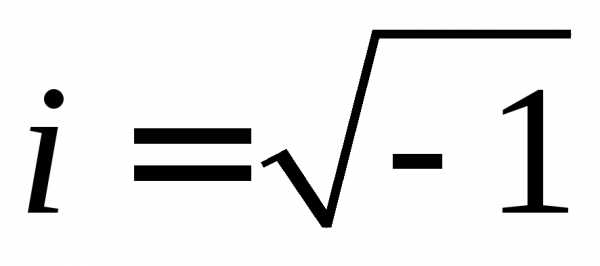 или
или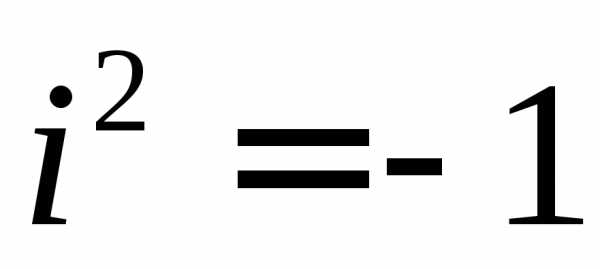 (9.2).
(9.2).
Число  называют действительной частью
комплексного числа
называют действительной частью
комплексного числа и обозначают;
и обозначают; — мнимая часть комплексного числа
— мнимая часть комплексного числа .
Ее обозначают.
Если
.
Ее обозначают.
Если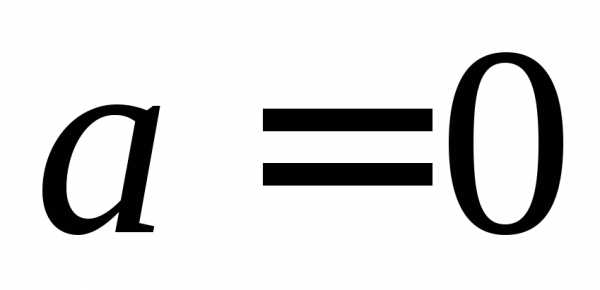 ,
то число
,
то число называют чисто мнимым, если
называют чисто мнимым, если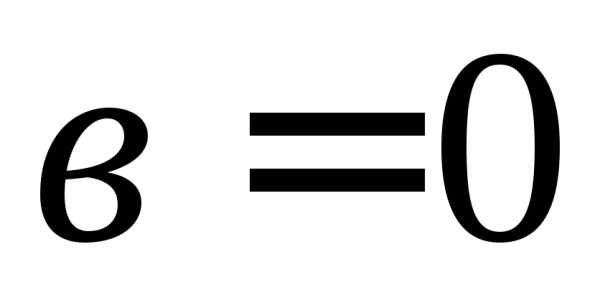 ,
то число
,
то число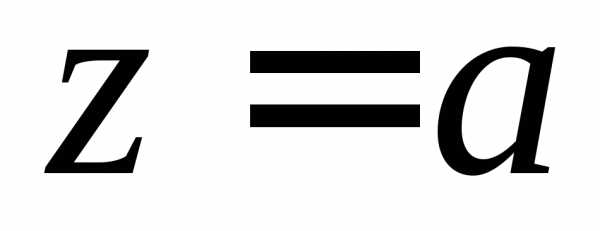 ,
есть действительное число.
,
есть действительное число.
Два комплексных числа иназывают комплексно сопряженными числами.
Два комплексных числа
исчитаются равными, если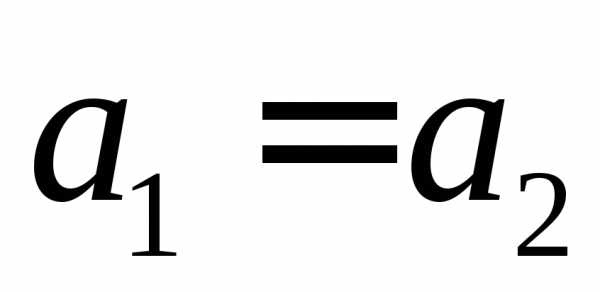 и
и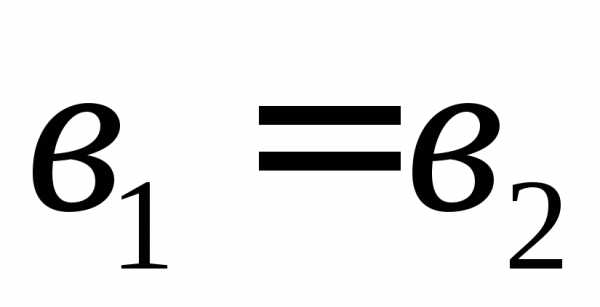 .
Комплексное число
.
Комплексное число ,
если
,
если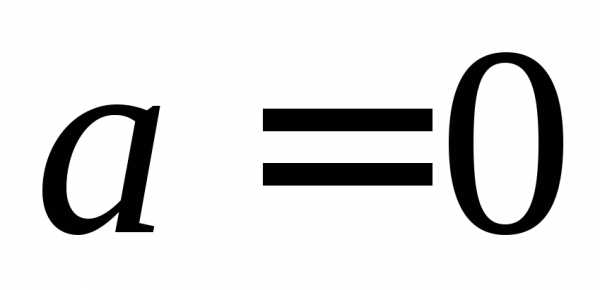 и
и .
Плоскость, точки которой изображают
комплексные числа, называется комплексной
плоскостью.
.
Плоскость, точки которой изображают
комплексные числа, называется комплексной
плоскостью.
Иногда комплексное число  удобнее изображать в виде вектора
удобнее изображать в виде вектора ,
начало которого совпадает с началом
координат, соединяющего точку
,
начало которого совпадает с началом
координат, соединяющего точку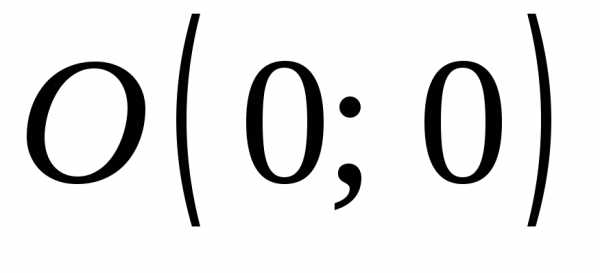 с точкой
с точкой .
Длина этого вектора называется модулем
комплексного числа
.
Длина этого вектора называется модулем
комплексного числа и обозначается
и обозначается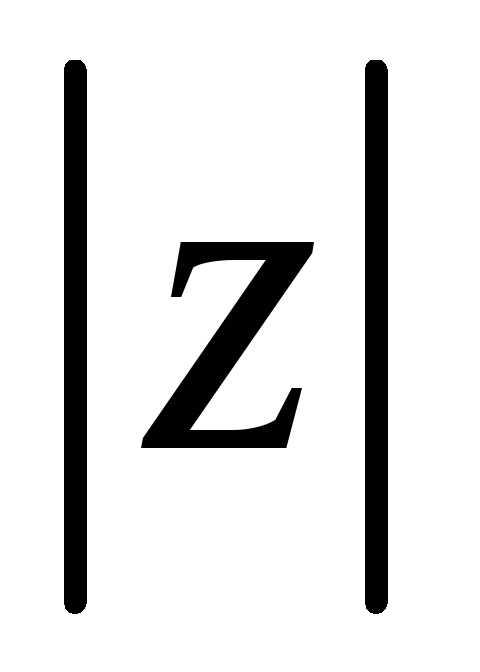 .
.
.
Угол  между осью
между осью и вектором
и вектором ,
отсчитанный против часовой стрелки,
называется аргументом комплексного
числа
,
отсчитанный против часовой стрелки,
называется аргументом комплексного
числа и обозначается
и обозначается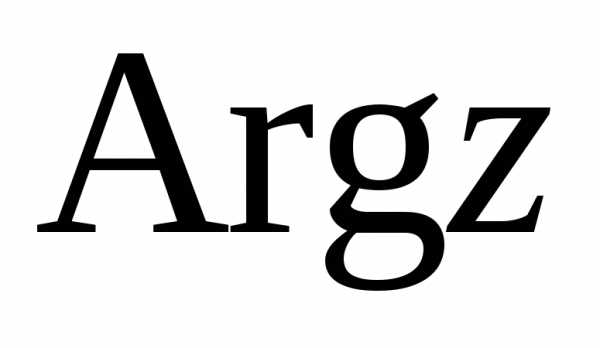 .
.
Аргумент числа  определяется с точностью до слагаемого
определяется с точностью до слагаемого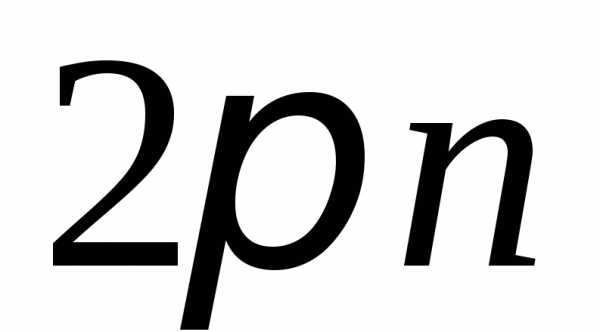 ,
где
,
где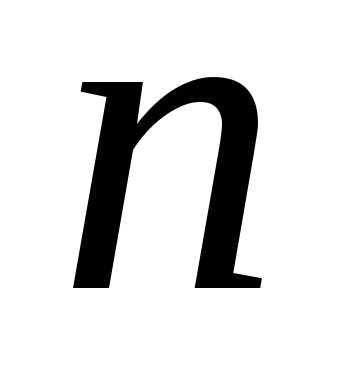 — целое число. Главное значение аргумента
числа
— целое число. Главное значение аргумента
числа — значение аргумента, удовлетворяющее
неравенству.
Главное значение аргумента комплексного
числа
— значение аргумента, удовлетворяющее
неравенству.
Главное значение аргумента комплексного
числа обозначается через
обозначается через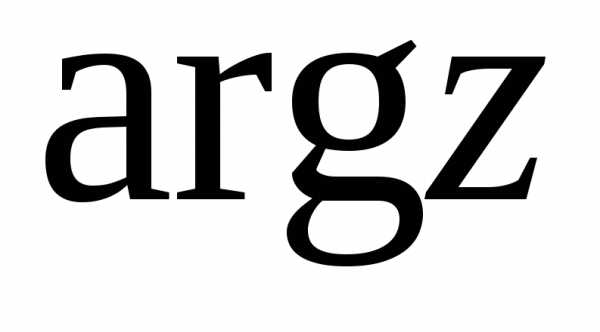 :
: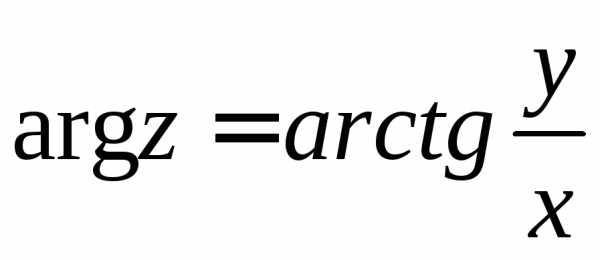 .
.
Запись числа  в виденазывают алгебраической формой записи
комплексного числа.
в виденазывают алгебраической формой записи
комплексного числа.
Сумма, разность комплексных чисел и умножение определяется так же, как действия над соответствующими векторами.
Суммой комплексных чисел 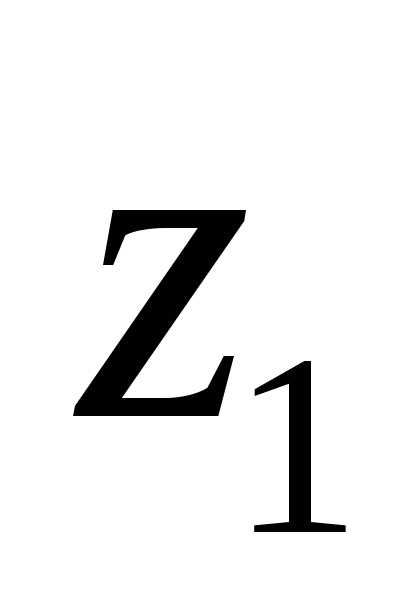 и
и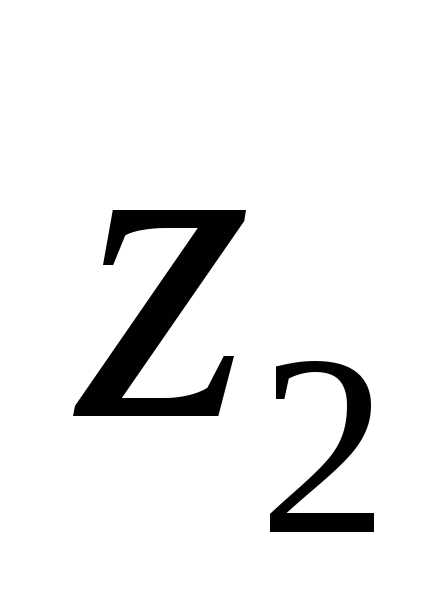 называется комплексное число
называется комплексное число
(9.3).
Разностью комплексных чисел 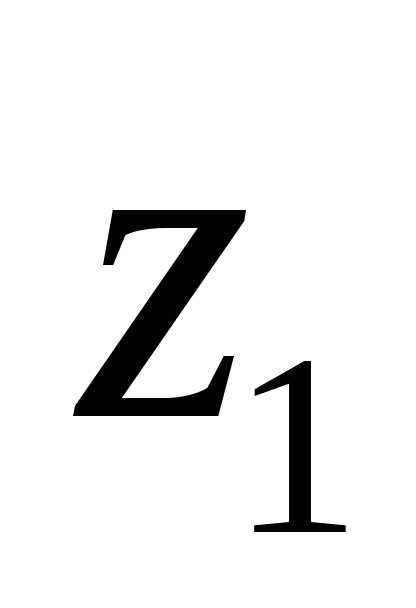 и
и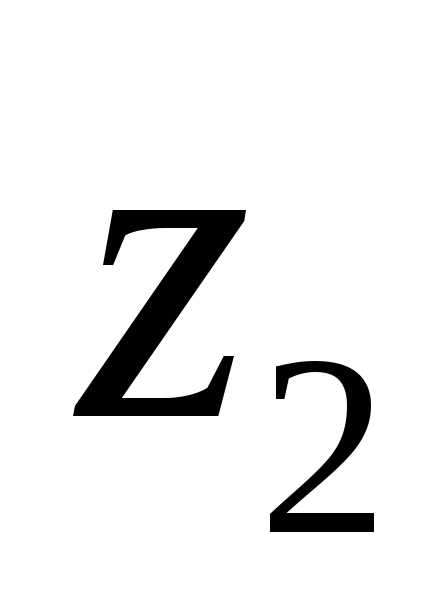 называется комплексное число
называется комплексное число
(9.4).
Произведение комплексного числа  на действительное число
на действительное число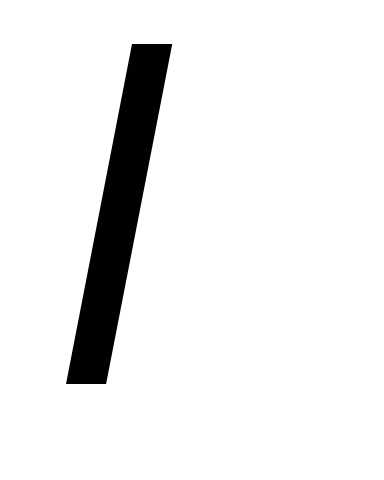 называется комплексное число.
называется комплексное число.
Произведение двух комплексных чисел и, записанных в алгебраической форме определяется как произведение двучленов:
(9.5).
Произведением двух комплексно сопряженных чисел служит действительное число
(9.6).
Деление комплексных чисел определяется, как действие обратное умножению. Частное двух комплексных чисел иопределяется следующим образом:
(9.7).
Наряду с прямоугольной системой
координат 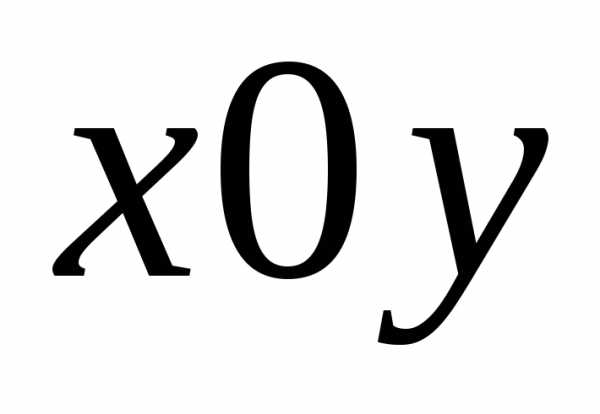 введем полярную систему, начало которой
совпадает с началом прямоугольной
системы, а полярная ось – с положительным
направлением оси
введем полярную систему, начало которой
совпадает с началом прямоугольной
системы, а полярная ось – с положительным
направлением оси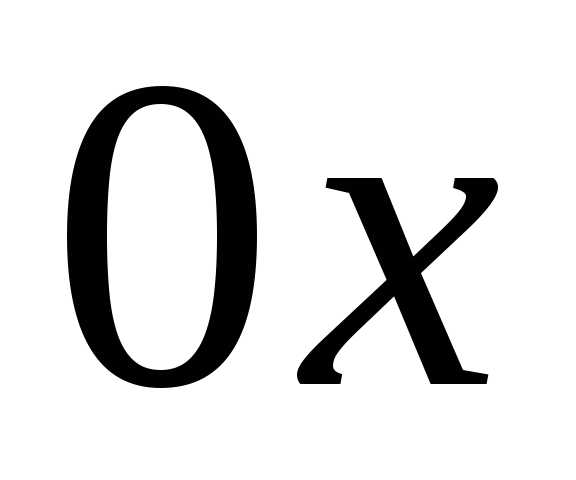 .
Рис. 8.
.
Рис. 8.
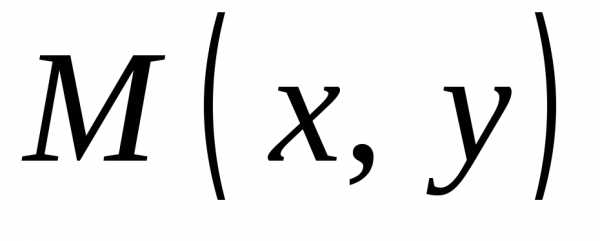

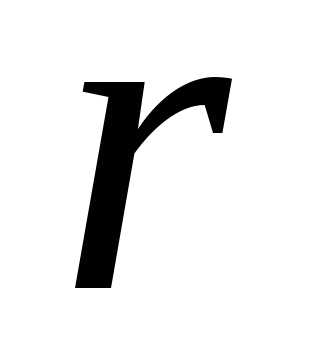
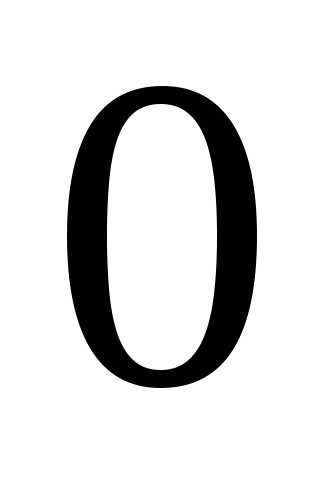
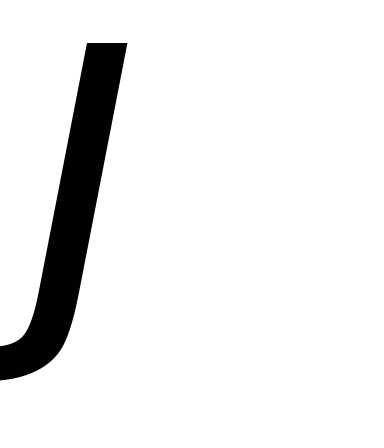
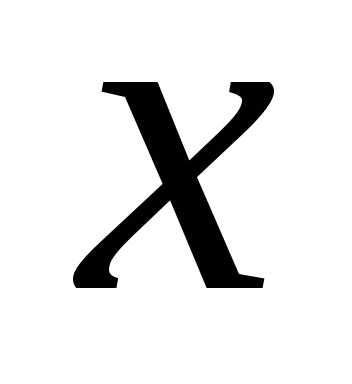
Рис. 8.
Из Рис.8 следует, что:
.
Подставляя 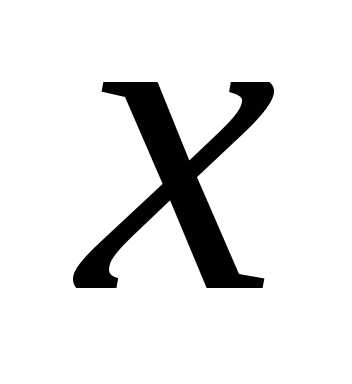 и
и в алгебраическую форму комплексного
числа, получим
в алгебраическую форму комплексного
числа, получим
(9.8).
Выражение (9.8) называют
тригонометрической формой записи
комплексного числа  ,
где.
,
где.
Пусть даны два комплексных числа 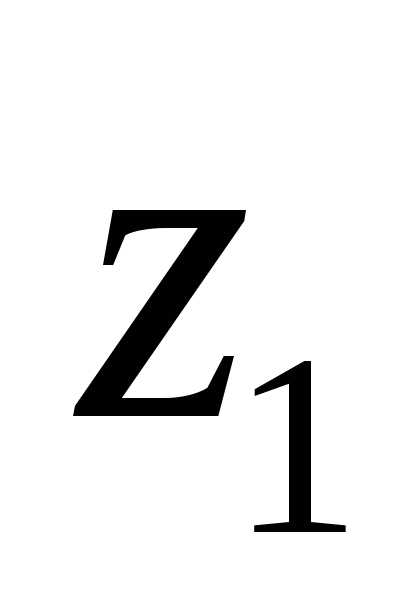 и
и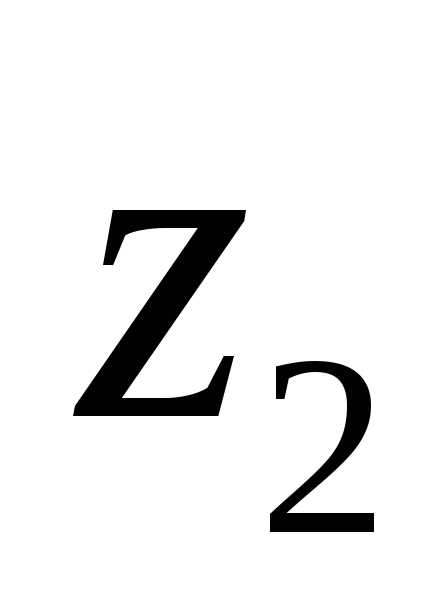 .
Записанные в тригонометрической форме:
.
Записанные в тригонометрической форме:
.
Тогда .
(9.9).
Таким образом, при умножении комплексных чисел их модули перемножаются, а аргументы складываются; при делении комплексных чисел их модули делятся, а аргументы вычитаются.
Если 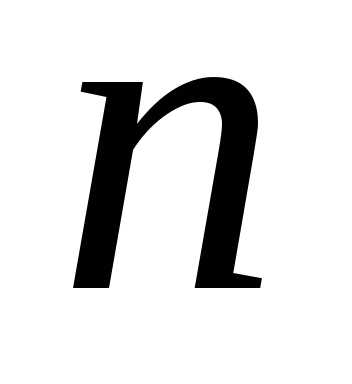 — целое положительное число, то из (9.9)
следует:
— целое положительное число, то из (9.9)
следует:
(9.10).
Корнем 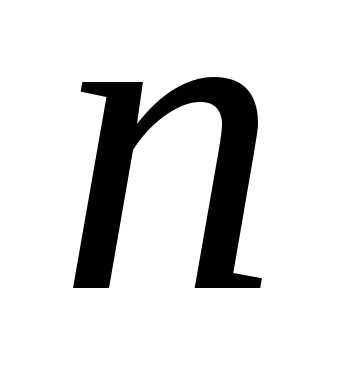 -й
степени из комплексного числа
-й
степени из комплексного числа называется такое комплексное число
называется такое комплексное число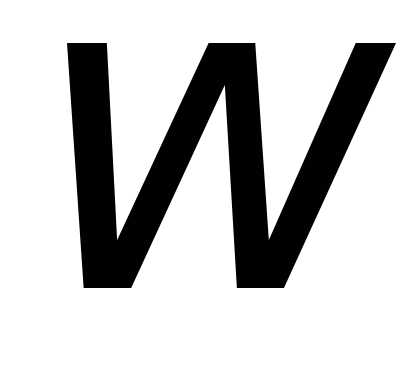 ,
, -я
степень которого равна
-я
степень которого равна ,
т.е.
,
т.е.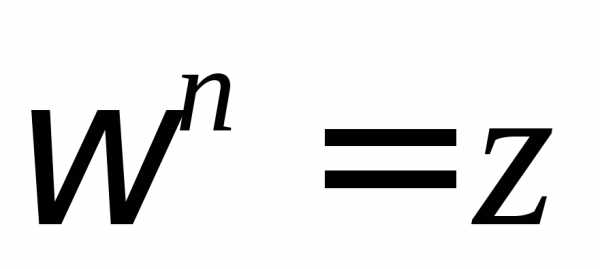 .
.
Корень  -й
степени из
-й
степени из обозначается
обозначается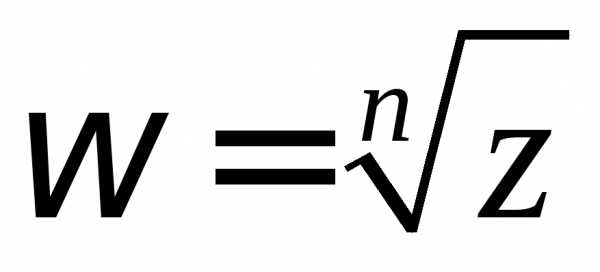 .
.
Если
,
то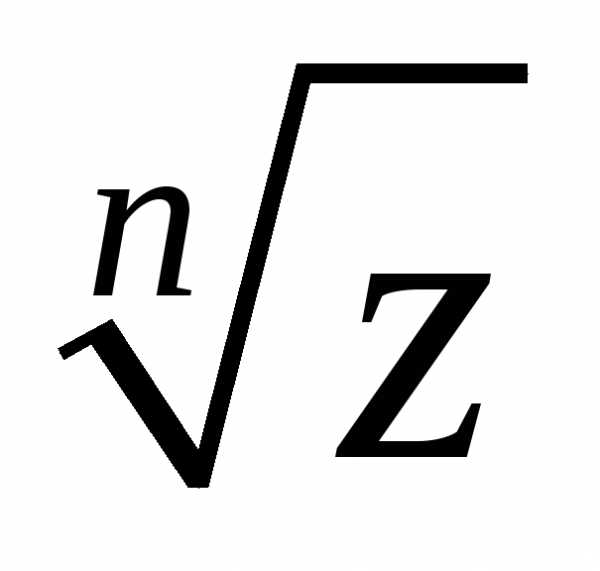 равен:
равен:
(9.11).
Подставляя в (9.11) значения
получим ровно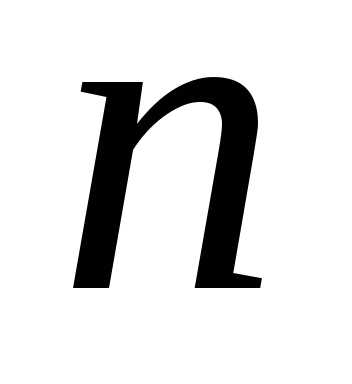 различных корней
различных корней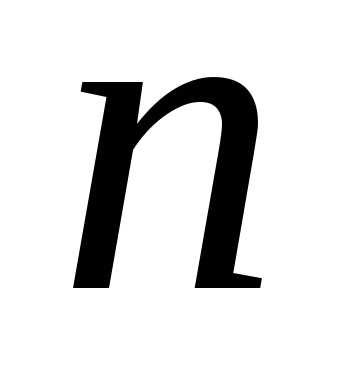 -й
степени из
-й
степени из .
.
Пример 12.Дано комплексное число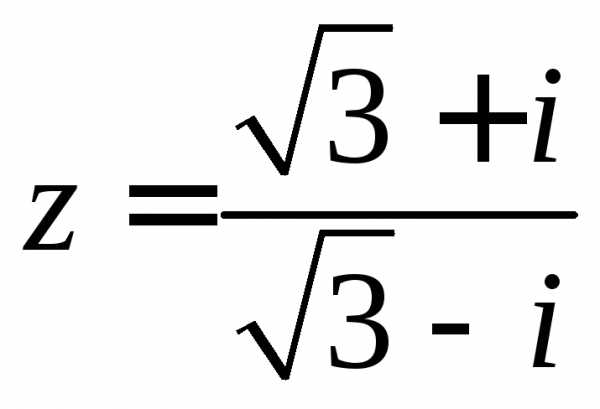 .
.
Записать число  в алгебраической и тригонометрической
формах. Найти все корни уравнения
в алгебраической и тригонометрической
формах. Найти все корни уравнения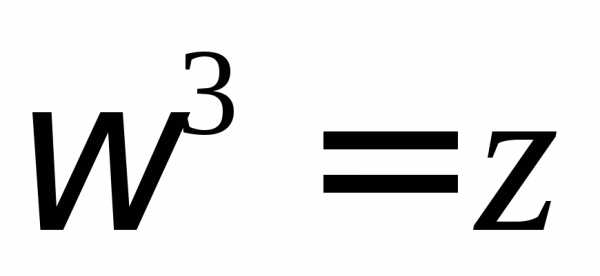 .
.
Решение. Запишем число  в алгебраической форме:
в алгебраической форме:
.
Найдем 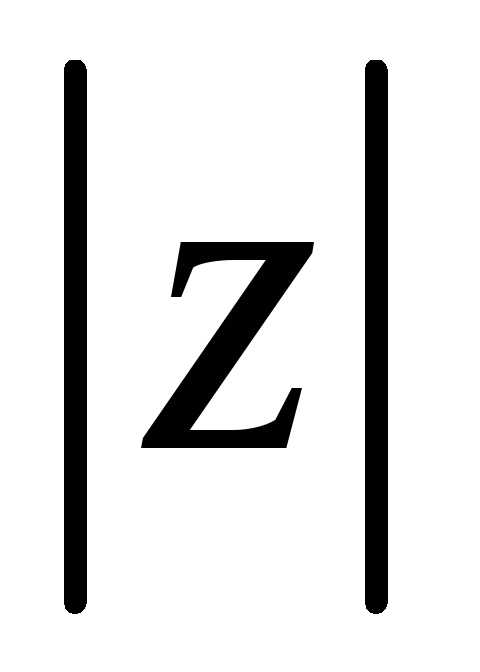 :.
:.
Вычислим
.
Тригонометрическая форма записи
комплексного числа имеет вид:
имеет вид:
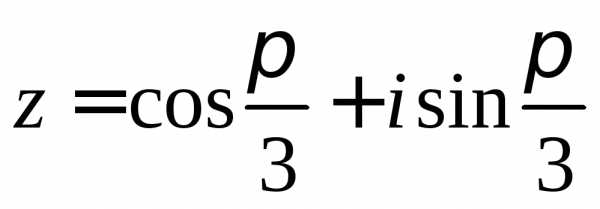 .
.
Вычислим 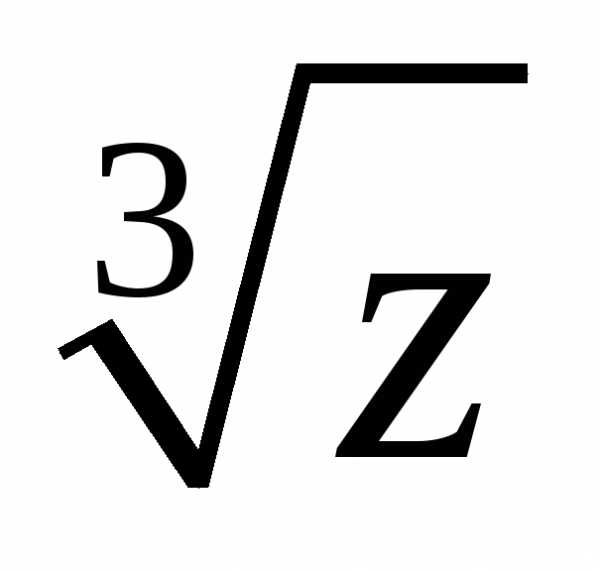 :
:
при
при
при
Кроме алгебраической и
тригонометрической форм записи
комплексного числа  ,
применяется более короткая, так называемая
показательная форма комплексного числа
,
применяется более короткая, так называемая
показательная форма комплексного числа ,
согласно которой
,
согласно которой
.
Пусть 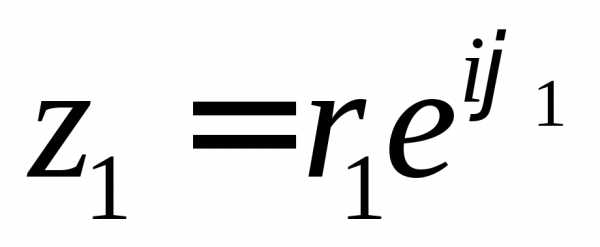 и
и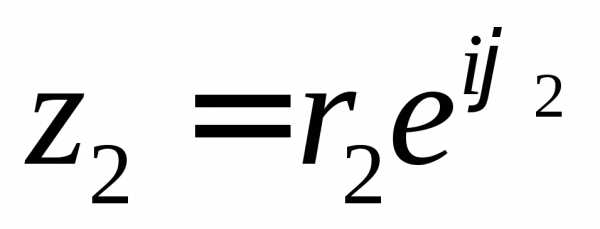 ,
тогда:
,
тогда:
.
studfiles.net
Умножение вектора на число
Произведением вектора u≠0 на число λ≠0 называется вектор w, модуль которого равен |λ||u|, направление которого совпадает с вектором u при λ>0 и противоположно ему при λ
Векторы: \( \mathbf{u} \), \( \mathbf{v} \), \( \mathbf{w} \)
Нулевой вектор: \( \mathbf{0} \)
Координаты векторов: \( X \), \( Y \), \( Z \)
Действительные числа: \( \lambda \), \( \mu \)
Произведением вектора на число
Произведением вектора \( \mathbf{u} \ne \mathbf{0} \) на число \( \lambda \ne 0 \) называется вектор \( \mathbf{w} \), модуль которого равен \( \left| \lambda \right| \cdot \left| \mathbf{u} \right| \), направление которого совпадает с вектором \( \mathbf{u} \) при \( \lambda > 0 \) и противоположно ему при \( \lambda
\(\mathbf{w} = \lambda \mathbf{u},\;\;\left| \mathbf{w} \right| = \left| \lambda \right| \cdot \left| \mathbf{u} \right|\)

Произведение вектора \( \mathbf{u} \) на число \( \lambda \) при \( \lambda = 0 \) и/или \( \mathbf{u} = \mathbf{0} \) равно нулевому вектору \( \mathbf{0} \).
Операция умножения вектора на число обладает следующими линейными свойствами :
Коммутативность умножения вектора на число
\( \lambda \mathbf{u} = \mathbf{u}\lambda \)
Дистрибутивность умножения относительно сложения чисел
\( \left( {\lambda + \mu } \right)\mathbf{u} = \lambda \mathbf{u} + \mu \mathbf{u} \)
Дистрибутивность умножения относительно сложения векторов
\( \lambda \left( {\mathbf{u} + \mathbf{v}} \right) = \lambda \mathbf{u} + \lambda \mathbf{v} \)
Ассоциативность умножения вектора на число
\( \lambda \left( {\mu \mathbf{u}} \right) = \mu \left( {\lambda \mathbf{u}} \right) = \left( {\lambda \mu } \right)\mathbf{u} \)
Умножение вектора на единицу
\( 1 \cdot \mathbf{u} = \mathbf{u} \)
Умножение вектора на число в координатной форме
\( \lambda \mathbf{u} = \left( {\lambda X,\lambda Y,\lambda Z} \right) \)
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
29.Умножение вектора на число. Свойства линейных операций над векторами.
Произведением ненулевого вектора на действительное числоназывается вектор, удовлетворяющий условиям:
1) длина вектора равна, т.е.;
2) векторы иколлинеарные;
3) векторы иодинаково направлены, если, и противоположно направлены, если. (рис. 9). Если среди сомножителей есть 0, то под произведениемпонимается нулевой вектор.
Геометрический смысл операции умножения вектора на число следующий: если , то при умножении векторана числовектор«растягивается» враз, а если– «сжимается» враз. На рис. 9 изображен случай.
Утверждение 1. Если векторы иколлинеарны и, то существует единственное число, что.
Свойства линейных операций над векторами
Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов ,,и любых действительных чиселсправедливы равенства:

30.Угол между векторами. Скалярное произведение векторов

Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

31. Составляющие вектора: на плоскости, по прямой и плоскости, по трем прямым
Проведём a и b,, ,ab, . Из точки О отложим .По правилу парал. сложения векторов устанав, что, гдесост вектора , леж на прямыхa и b, соответственно. Предст вектора равенством назразлож вектора на состав, леж на прямых a и b.Заданы прямая и плоскость , причёмне лежит ви не паралл..
Возьмём и отложим его от О. Получим. Пусть точка– проекцияV на в направлении в направлении, то есть.навыбрана так, что
Тогда(1)
или(2),гдеявл сост, леж наи на.Представлениеравенствами(1) или(2) назывразложна составл, леж на и на.Пусть заданы три прямые a, b, c, пересек в O и не леж в одной плоскости.. Разлаживаем по прямa и плосa:
на составляющие Теперь разложим на составляющие , леж наb и c, в a :В итоге имеем, что.где составляющиеv,леж на a, b, c,соответственно.Представление назыв разлож на сост, леж наa, b, c.
Вопрос32. Разложение вектора по базису
Разложить по базису – это значит представить его.Числкоэфx, y, zв правой части равенства – координаты в базисе .Координаты векторов (как и их сост.) обладают след.св-ми (операции слож. векторов и умн. на число): При слож векторов их координаты складываются. Разл. вектора по базисуимеет вид
, где – действ.числа. Тогда сум., и предст. векторс координатами,,в базисе
При умнож.вектора на число его координаты умнож. на это число. — действ. число. Разлож по базису имеет вид. Тогда.Тройка базисных векторов в пространстве наз. Правой (левой), если эти векторы, отлож. от одной точки, распол. так, как распол. большой, указательный и средний пальцы правой (левой) руки.
Вопрос33.Прямоугольные декартовы координаты в пространстве
Координатами вектора , начало кот. Точка А(), а конец В() в прям. дек. системе координатOxyz наз. числа ,,. Сначала фикс. в прям. дек. сист. координат Охуz точку А(х, у, z). Потом строят точку В(х+, у+, z+). Получаемравн.. Радиусом-вектором – наз. векторс точкой прилож. в нач. координат О, а конец — в А..
studfiles.net

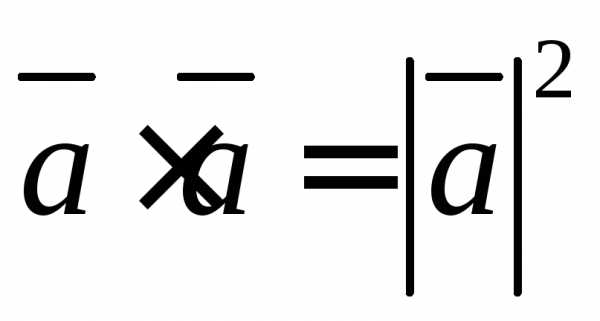 ,
отсюда
,
отсюда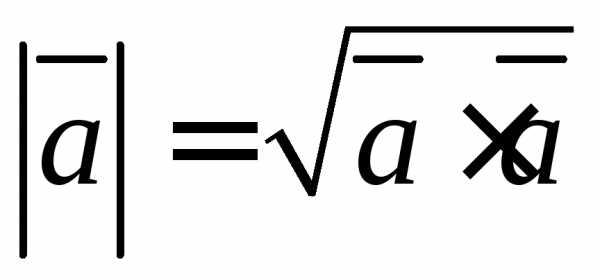
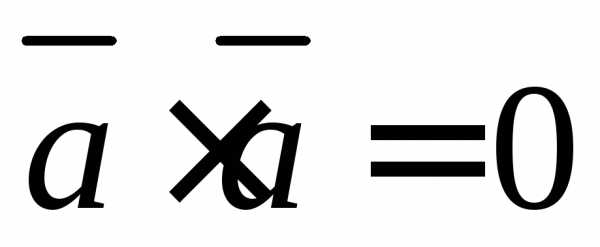 ,
то
,
то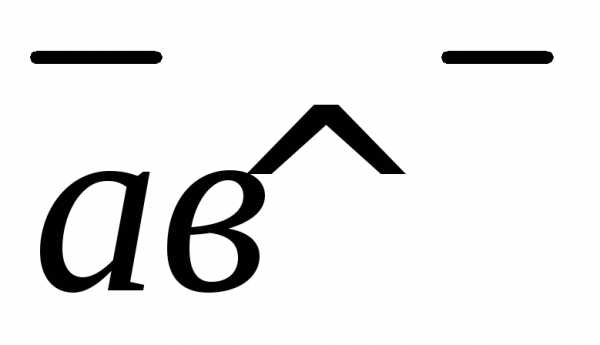 — условие перпендикулярности векторов
— условие перпендикулярности векторов и
и
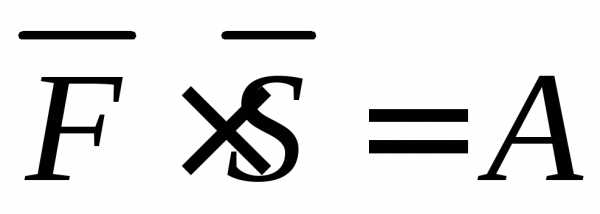 ,
, — вектор силы,
— вектор силы, — вектор перемещения,
— вектор перемещения, — работа силы
— работа силы .
.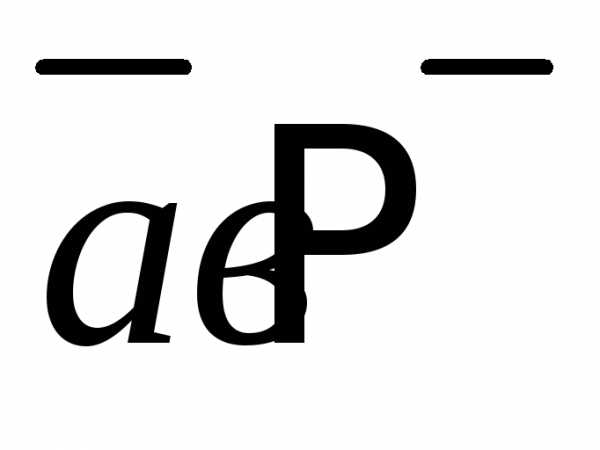 ,
то
,
то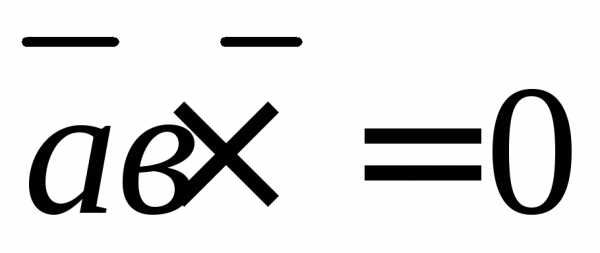
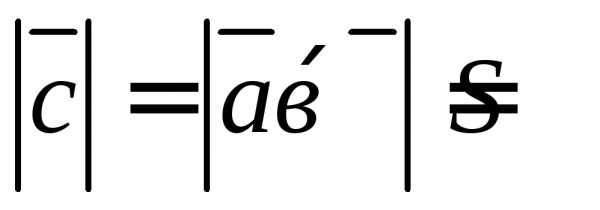 ,
где
,
где — площадь параллелограмма, построенного
на этих векторах как на сторонах.
— площадь параллелограмма, построенного
на этих векторах как на сторонах.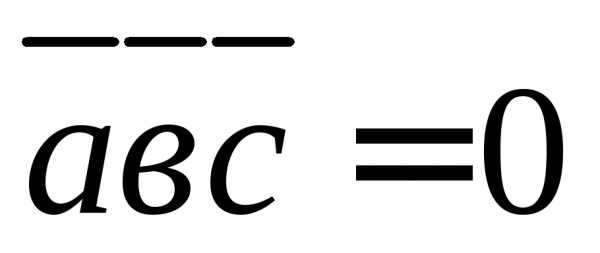 — условие компланарности векторов;
— условие компланарности векторов;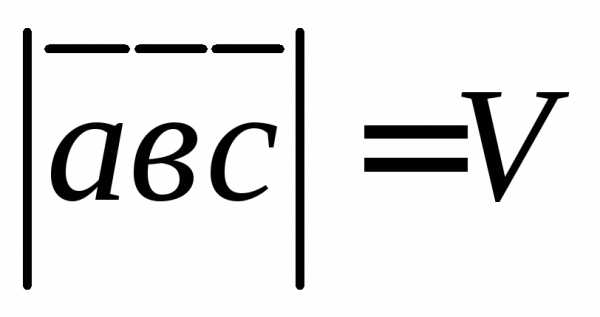 — объем параллелепипеда, построенного
на векторах, как на сторонах;
— объем параллелепипеда, построенного
на векторах, как на сторонах; равна половине площади параллелограмма,
построенного на сторонах
равна половине площади параллелограмма,
построенного на сторонах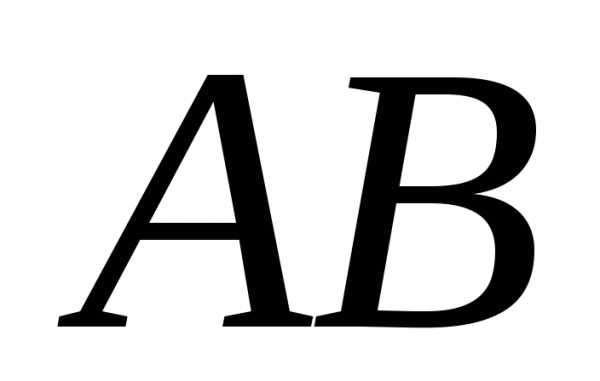 и
и ,
т.е.
,
т.е. определяется из формулы:
определяется из формулы: