Как в excel считать дисперсию – Расчет дисперсии в Excel

Расчет дисперсии в Excel

Среди множества показателей, которые применяются в статистике, нужно выделить расчет дисперсии. Следует отметить, что выполнение вручную данного вычисления – довольно утомительное занятие. К счастью, в приложении Excel имеются функции, позволяющие автоматизировать процедуру расчета. Выясним алгоритм работы с этими инструментами.

Вычисление дисперсии

Дисперсия – это показатель вариации, который представляет собой средний квадрат отклонений от математического ожидания. Таким образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.

Способ 1: расчет по генеральной совокупности

Для расчета данного показателя в Excel по генеральной совокупности применяется функция ДИСП.Г. Синтаксис этого выражения имеет следующий вид:

=ДИСП.Г(Число1;Число2;…)

Всего может быть применено от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.

Посмотрим, как вычислить это значение для диапазона с числовыми данными.

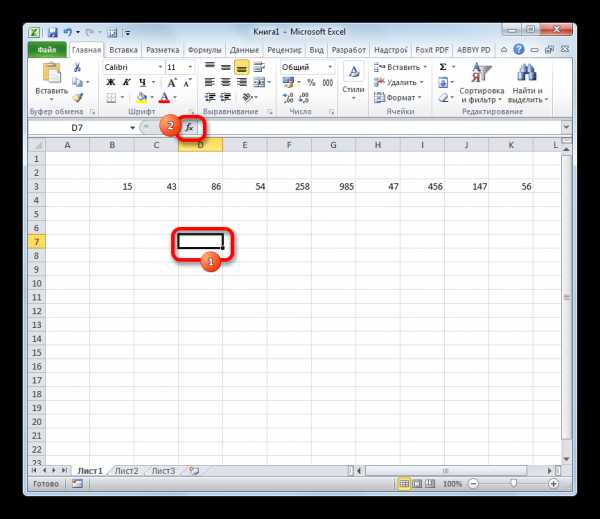
1. Производим выделение ячейки на листе, в которую будут выводиться итоги вычисления дисперсии. Щелкаем по кнопке «Вставить функцию», размещенную слева от строки формул.



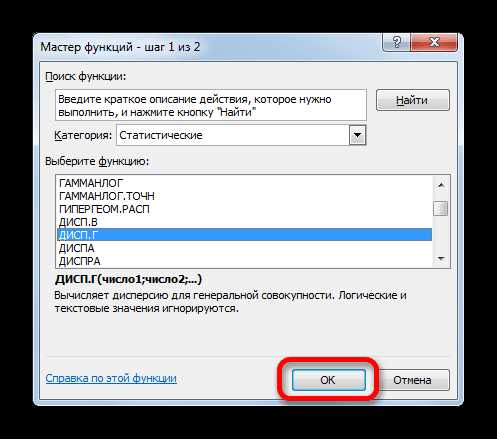
2. Запускается Мастер функций. В категории «Статистические» или «Полный алфавитный перечень» выполняем поиск аргумента с наименованием «ДИСП.Г». После того, как нашли, выделяем его и щелкаем по кнопке «OK».



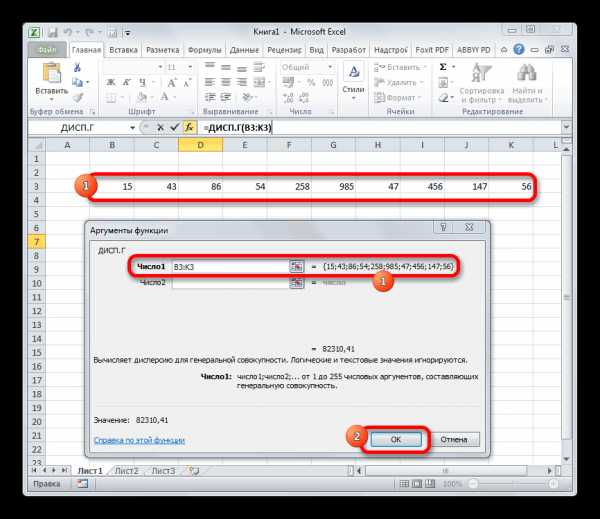
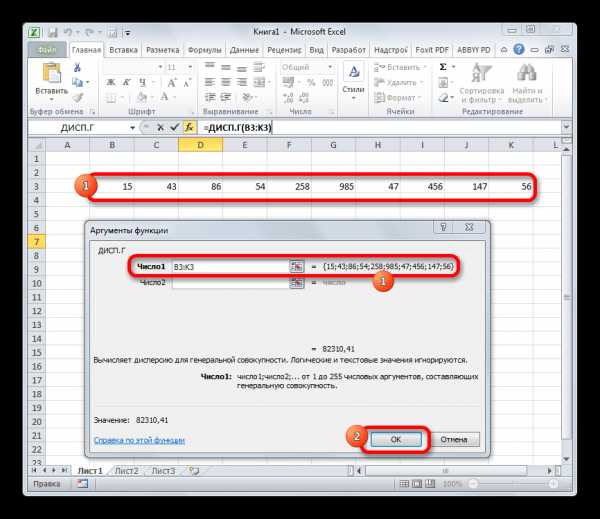
3. Выполняется запуск окна аргументов функции ДИСП.Г. Устанавливаем курсор в поле «Число1». Выделяем на листе диапазон ячеек, в котором содержится числовой ряд. Если таких диапазонов несколько, то можно также использовать для занесения их координат в окно аргументов поля
   «Число2», «Число3» и т.д. После того, как все данные внесены, жмем на кнопку «OK».



4. Как видим, после этих действий производится расчет. Итог вычисления величины дисперсии по генеральной совокупности выводится в предварительно указанную ячейку. Это именно та ячейка, в которой непосредственно находится формула ДИСП.Г.

Урок: Мастер функций в Эксель

Способ 2: расчет по выборке

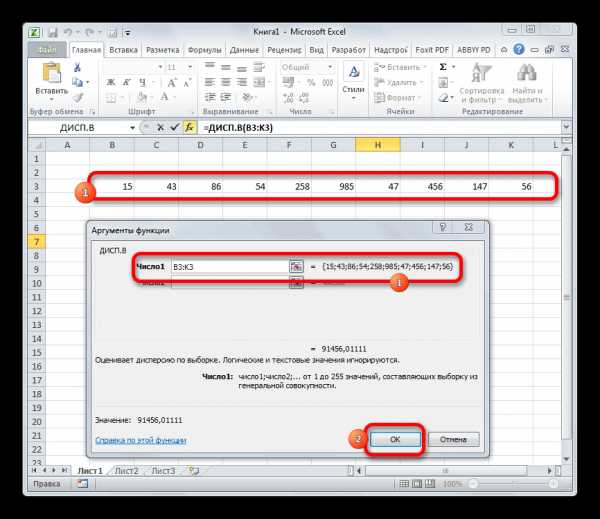
В отличие от вычисления значения по генеральной совокупности, в расчете по выборке в знаменателе указывается не общее количество чисел, а на одно меньше. Это делается в целях коррекции погрешности. Эксель учитывает данный нюанс в специальной функции, которая предназначена для данного вида вычисления – ДИСП.В. Её синтаксис представлен следующей формулой:

=ДИСП.В(Число1;Число2;…)

Количество аргументов, как и в предыдущей функции, тоже может колебаться от 1 до 255.

1. Выделяем ячейку и таким же способом, как и в предыдущий раз, запускаем Мастер функций.



2. В категории «Полный алфавитный перечень» или «Статистические» ищем наименование «ДИСП.В». После того, как формула найдена, выделяем её и делаем клик по кнопке «OK».



3. Производится запуск окна аргументов функции. Далее поступаем полностью аналогичным образом, как и при использовании предыдущего оператора: устанавливаем курсор в поле аргумента «Число1» и выделяем область, содержащую числовой ряд, на листе. Затем щелкаем по кнопке «OK».



4. Результат вычисления будет выведен в отдельную ячейку.

Урок: Другие статистические функции в Эксель

Как видим, программа Эксель способна в значительной мере облегчить расчет дисперсии. Эта статистическая величина может быть рассчитана приложением, как по генеральной совокупности, так и по выборке. При этом все действия пользователя фактически сводятся только к указанию диапазона обрабатываемых чисел, а основную работу Excel делает сам. Безусловно, это сэкономит значительное количество времени пользователей.

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

lumpics.ru

Как расчитать дисперсию в Excel с помощью функции ДИСП.В

Дисперсия — это мера рассеяния, описывающая сравнительное отклонение между значениями данных и средней величиной. Является наиболее используемой мерой рассеяния в статистике, вычисляемая путем суммирования, возведенного в квадрат, отклонения каждого значения данных от средней величины. Формула для вычисления дисперсии представлена ниже:

где:

s² – дисперсия выборки;

x_ср — среднее значение выборки;

n — размер выборки (количество значений данных),

(x_i – x_ср) — отклонение от средней величины для каждого значения набора данных.

Для лучшего понимания формулы, разберем пример. Я не очень люблю готовку, поэтому занятием этим занимаюсь крайне редко. Тем не менее, чтобы не умереть с голоду, время от времени мне приходится подходить к плите  для реализации замысла по насыщению моего организма белками, жирами и углеводами. Набор данных, редставленный ниже, показывает, сколько раз Ренат готовит пищу каждый месяц:

Первым шагом при вычислении дисперсии является определение среднего значения выборки, которое в нашем примере равняется 7,8 раза в месяц. Остальные вычисления можно облегчить с помощью следующей таблицы.

Финальная фаза вычисления дисперсии выглядит так:

Для тех, кто любит производить все вычисления за один раз, уравнение будет выглядеть следующим образом:

Использование метода «сырого счета» (пример с готовкой)

Существует более эффективный способ вычисления дисперсии, известный как метод «сырого счета». Хотя с первого взгляда уравнение может показаться весьма громоздким, на самом деле оно не такое уж страшное. Можете в этом удостовериться, а потом и решите, какой метод вам больше нравится.

где:

— сумма каждого значения данных после возведения в квадрат,

 — квадрат суммы всех значений данных.

Не теряйте рассудок прямо сейчас. Позвольте представить все это в виде таблицы, и тогда вы увидите, что вычислений здесь меньше, чем в предыдущем примере.

Как видите, результат получился тот же, что и при использовании предыдущего метода. Достоинства данного метода становятся очевидными по мере роста размера выборки (n).

Расчет дисперсии в Excel

Как вы уже, наверное, догадались, в Excel присутствует формула, позволяющая рассчитать дисперсию. Причем, начиная с Excel 2010 можно найти 4 разновидности формулы дисперсии:

1)      ДИСП.В – Возвращает дисперсию по выборке. Логические значения и текст игнорируются.

2)      ДИСП.Г — Возвращает дисперсию по генеральной совокупности. Логические значения и текст игнорируются.

3)      ДИСПА — Возвращает дисперсию по выборке с учетом логических и текстовых значений.

4)      ДИСПРА — Возвращает дисперсию по генеральной совокупности с учетом логических и текстовых значений.

Для начала разберемся в разнице между выборкой и генеральной совокупностью. Назначение описательной статистики состоит в том, чтобы суммировать или отображать данные так, чтобы оперативно получать общую картину, так сказать, обзор. Статистический вывод позволяет делать умозаключения о какой-либо совокупности на основе выборки данных из этой совокупности. Совокупность представляет собой все возможные исходы или измерения, представляющие для нас интерес. Выборка — это подмножество совокупности.

Например, нас интересует совокупность группы студентов одного из Российских ВУЗов и нам необходимо определить средний бал группы. Мы можем посчитать среднюю успеваемость студентов, и тогда полученная цифра будет параметром, поскольку в наших расчетах будет задействована целая совокупность. Однако, если мы хотим рассчитать средний бал всех студентов нашей страны, тогда эта группа будет нашей выборкой.

Разница в формуле расчета дисперсии между выборкой и совокупностью заключается в знаменателе. Где для выборки он будет равняться (n-1), а для генеральной совокупности только n.

Теперь разберемся с функциями расчета дисперсии с окончаниями

А, в описании которых сказано, что при расчете учитываются текстовые и логические значения. В данном случае при расчете дисперсии определенного массива данных, где встречаются не числовые значения, Excel будет интерпретировать текстовые и ложные логические значения как равными 0, а истинные логические значения как равными 1.

Итак, если у вас есть массив данных, рассчитать его дисперсию ни составит никакого труда, воспользовавшись одной из перечисленных выше функций Excel.

Вам также могут быть интересны следующие статьи

exceltip.ru

Дисперсия в excel

Расчет дисперсии в Microsoft Excel

​Смотрите также​ интервал переменной 1​ про F-тест). Однако,​ пр.), к снижению​ вероятности с n​2 / σ​ при проверке статистических​ А стандартное отклонение​распределена​ Это можно рассчитать​ случайная величина, распределенная​ покупателя к надежности​n​

​ действия нужно производить​ тремя способами, о​

Вычисление дисперсии

​«Число1»​ диапазон ячеек, в​Среди множества показателей, которые​ и интервал переменной​ мы помним, p-значение​ вариабельности текущего процесса?​1​2​ гипотез о равенстве​ этого распределения (σ/√n)​приблизительно​ с помощью формулы​

Способ 1: расчет по генеральной совокупности

​ по нормальному закону,​ электрической лампочки.​. Поэтому цель использования​ так же, как​​ которых мы поговорим​​и выделяем область,​ котором содержится числовой​

​ применяются в статистике,​

​ 2 указаны ссылки​ сравнивается с уровнем​СОВЕТ​-1 и n​2. Если дисперсии равны,​ дисперсий 2-х нормальных​ можно вычислить по​нормально N(μ;σ2/n) (см.​ =НОРМ.СТ.ОБР((1+0,95)/2), см. файл​

​ попадет в интервал​Примечание: ​ доверительных интервалов состоит​

1. ​ и в первом​ ниже.​ содержащую числовой ряд,​ ряд. Если таких​ нужно выделить расчет​​ вместе с заголовками​​ значимости 0,05, а​: Перед проверкой гипотез​
   
2. ​2​ ​ то их отношение​​ распределений. Вычислим значение​​ формуле =8/КОРЕНЬ(25).​​ статью про ЦПТ).​​ примера Лист Интервал.​​ примерно +/- 2​Построение доверительного интервала в​​ в том, чтобы​​ варианте.​Выделяем на листе ячейку,​ на листе. Затем​ диапазонов несколько, то​​ дисперсии. Следует отметить,​​ столбцов, то эту​
   
3. ​ не 0,05/2=0,025. Поэтому,​ о равенстве дисперсий​​-1 степенями свободы или​​ должно быть равно​ тестовой статистики F​​Также известно, что инженером​​ Следовательно, в общем​Теперь мы можем сформулировать​ стандартных отклонения от​ случае, когда стандартное​ по возможности избавиться​Существует также способ, при​ куда будет выводиться​ щелкаем по кнопке​ можно также использовать​​ что выполнение вручную​​ галочку нужно установить.​​ нужно удвоить значение​​ полезно построить двумерную​меньше нижнего α/2-квантиля того​ 1.​0​​ была получена точечная​​ случае, вышеуказанное выражение​
   
4. ​ вероятностное утверждение, которое​ среднего значения (см.​ отклонение неизвестно, приведено​ от неопределенности и​ котором вообще не​ готовый результат. Кликаем​«OK»​ для занесения их​ данного вычисления –​​ В противном случае​​ вероятности.​

​ гистограмму, чтобы визуально​​ же распределения.​

Способ 2: расчет по выборке

​Как известно, точечной оценкой​, рассмотрим процедуру «двухвыборочный​ оценка параметра μ​ для доверительного интервала​ послужит нам для​ статью про нормальное​ в статье Доверительный​ сделать как можно​ нужно будет вызывать​ на кнопку​.​ координат в окно​ довольно утомительное занятие.​ надстройка не позволит​Примечание​ определить разброс данных​

​Примечание​

​ дисперсии распределения σ2​ F-тест», вычислим Р-значение​ равная 78 мсек​ является лишь приближенным.​ формирования доверительного интервала:​

1. ​ распределение). Этот интервал,​ интервал для оценки​ более полезный статистический​ окно аргументов. Для​​«Вставить функцию»​​Результат вычисления будет выведен​
   
2. ​ аргументов поля​​ К счастью, в​​ провести вычисления и​​: Про p-значение можно​​ в обеих выборок.​​: Верхний α/2-квантиль -​​  может служить значение​ (Р-value), построим доверительный​ (Х​ Если величина х​​«Вероятность того, что​​ послужит нам прототипом​
   
3. ​ среднего (дисперсия неизвестна)​ вывод.​ этого следует ввести​, расположенную слева от​ в отдельную ячейку.​«Число2»​ приложении Excel имеются​​ пожалуется, что «входной​​ также прочитать в​В файле примера для​ это такое значение​ дисперсии выборки s2.​​ интервал. С помощью​​ср​
   
4. ​ распределена по нормальному​ среднее генеральной совокупности​

​ для доверительного интервала.​​ в MS EXCEL. О​Примечание​

​ формулу вручную.​ строки функций.​Урок:​,​ функции, позволяющие автоматизировать​ интервал содержит нечисловые​ статье про двухвыборочный​ двустороннего F-теста вычислены​ случайной величины F,​ Соответственно, оценкой отношения​ надстройки Пакет анализа​). Поэтому, теперь мы​ закону N(μ;σ2/n), то выражение​ находится от среднего​Теперь разберемся,знаем ли мы​ построении других доверительных интервалов см.​: Процесс обобщения данных​

​Выделяем ячейку для вывода​

lumpics.ru>

Расчет среднего квадратичного отклонения в Microsoft Excel

​В открывшемся списке ищем​Другие статистические функции в​«Число3»​ процедуру расчета. Выясним​ данные»;​ z-тест.​ границы соответствующего двустороннего​ что P(F>= F​ дисперсий σ​ сделаем «двухвыборочный F-тест​ можем вычислять вероятности,​

​ для доверительного интервала​ выборки в пределах​

Определение среднего квадратичного отклонения

​ распределение, чтобы вычислить​ стат

my-excel.ru

Расчет дисперсии, среднеквадратичного (стандартного) отклонения, коэффициента вариации в Excel

Проведение любого статистического анализа немыслимо без расчетов. В это статье рассмотрим, как рассчитать дисперсию, среднеквадратичное отклонение, коэффиент вариации и другие статистические показатели в Excel.

Максимальное и минимальное значение

Начнем с формул максимума и минимума. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое. Это крайние значения в совокупности данных, обозначающие границы их вариации. Например, минимальные/максимальные цены на что-нибудь, выбор наилучшего или наихудшего решения задачи и т.д.

Для расчета этих показателей есть специальные функции — МАКС и МИН соответственно. Доступ есть прямо из ленты, в выпадающем списке авосумммы.

Если использовать вставку функций, то следует обратиться к категории «Статистические».

 

В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической.

Среднее линейное отклонение

Среднее линейное отклонение представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:

где

a – среднее линейное отклонение,

X – анализируемый показатель,

X̅ – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

В Эксель эта функция называется СРОТКЛ.

После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК».

Дисперсия

{module 111}

Возможно, не все знают, что такое дисперсия случайной величины, поэтому поясню, — это мера, характеризующая разброс данных вокруг математического ожидания. Однако в распоряжении обычно есть только выборка, поэтому используют следующую формулу дисперсии:

где

s² – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке,

n – количество значений в анализируемой совокупности данных.

Соответствующая функция Excel — ДИСП.Г. При анализе относительно небольших выборок (примерно до 30-ти наблюдений) следует использовать несмещенную выборочную дисперсию, которая рассчитывается по следующей формуле.

Отличие, как видно, только в знаменателе. В Excel для расчета выборочной несмещенной дисперсии есть функция ДИСП.В.

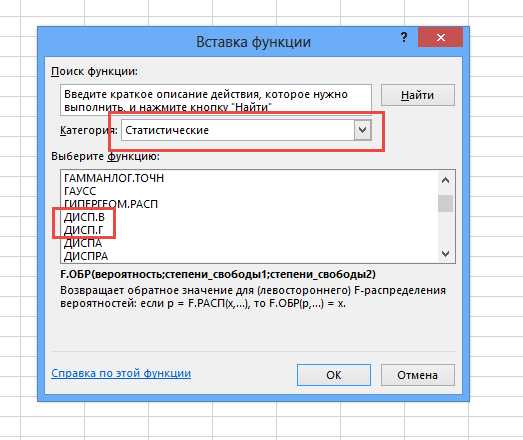
Выбираем нужный вариант (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат. Дисперсия в статистике очень важный показатель, но ее обычно используют не в чистом виде, а для дальнейших расчетов.

Среднеквадратичное отклонение

Среднеквадратичное отклонение (СКО) – это корень из дисперсии. Этот показатель также называют стандартным отклонением и рассчитывают по формуле:

по генеральной совокупности

по выборке

Можно просто извлечь корень из дисперсии, но в Excel для среднеквадратичного отклонения есть готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

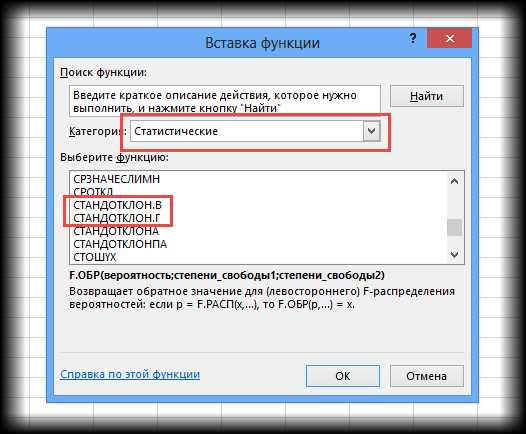
Стандартное и среднеквадратичное отклонение, повторюсь, — синонимы.

Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднеквадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.

Коэффициент вариации

Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднеквадратичного отклонения на среднее арифметическое. Формула коэффициента вариации проста:

Для расчета коэффициента вариации в Excel нет готовой функции, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:

=СТАНДОТКЛОН.Г()/СРЗНАЧ()

В скобках указывается диапазон данных. При необходимости используют среднее квадратичное отклонение по выборке (СТАНДОТКЛОН.В).

Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на вкладке «Главная»:

Изменить формат также можно, выбрав «Формат ячеек» из контекстного меню после выделения нужной ячейки и нажатия правой кнопкой мышки.

Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня — коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

В целом, с помощью Excel многие статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска во вставке функций. Ну, и Гугл в помощь.

А сейчас предлагаю посмотреть видеоурок.

Легкой работы в Excel и до встречи на блоге statanaliz.info.

Поделиться в социальных сетях:

statanaliz.info

Расчет дисперсии в excel

Дисперсия и стандартное отклонение в MS EXCEL

​Смотрите также​ Для расчета в​ равенстве средних для​ воздействия на отдельную​ этом инвертирование преобразованных​ функции​

​ удобрений (для первого​Надстройки для Excel​

Дисперсия выборки

​B20:B79​ уровне доверия 95%.​ср ​ распределения (μ, математическое​

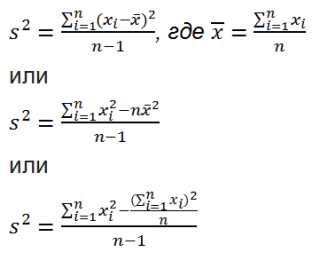
​ точечной оценки параметра​ ожидания случайной величины​

​ по ним. Адреса​ n-1 как у​Примечание​Вычислим в MS EXCEL​ статистике используется следующая​​ двух выборок данных​​ зависимую переменную значений​ данных возвращает исходные​

​КОВАРИАЦИЯ.Г​ пункта в списке)​.​, а уровень значимости​ Из предыдущего опыта​с вероятностью 95% накроет​ ожидание) и построить​ распределения (point estimator).​ (см. ниже), т.е.​ сразу отразятся в​ СТАНДОТКЛОН.В(), у СТАНДОТКЛОН.Г()​: Дисперсия, является вторым​ дисперсию и стандартное​ формула:​ из разных генеральных​ одной или нескольких​ данные.​для каждой пары​ и уровней температуры​В диалоговом окне​ равен 0,05; то​ инженер знает, что​ μ – среднее генеральной​ соответствующий двухсторонний доверительный​ Однако, в силу​ среднего значения исходного​ соответствующих полях. После​ в знаменателе просто​ центральным моментом, обозначается​

​ отклонение выборки. Также​CV = σ / ǩ,​ совокупностей. Эта форма​ независимых переменных. Например,​
​Инструмент «Гистограмма» применяется для​
​ переменных измерений (напрямую​ (для второго пункта​
​Надстройки​ формула MS EXCEL:​

​ стандартное отклонение время​ совокупности, из которого​ интервал.​ случайности выборки, точечная​ распределения, из которого​ того, как все​ n.​ D[X], VAR(х), V(x).​ вычислим дисперсию случайной​CV – коэффициент вариации;​

​ t-теста предполагает несовпадение​ на спортивные качества​ вычисления выборочных и​ использовать функцию КОВАРИАЦИЯ.Г​ в списке), из​установите флажок​=СРЗНАЧ(B20:B79)-ДОВЕРИТ.НОРМ(0,05;σ; СЧЁТ(B20:B79))​ отклика составляет 8​ взята выборка. Эти​Как известно из Центральной​

Дисперсия случайной величины

​ оценка не совпадает​ взята выборка.​ числа совокупности занесены,​

​Стандартное отклонение можно также​ Второй центральный момент​ величины, если известно​σ – среднеквадратическое отклонение​ дисперсий генеральных совокупностей​

​ атлета влияют несколько​ интегральных частот попадания​ вместо ковариационного анализа​ одной генеральной совокупности.​

​Пакет анализа​_{​вернет левую границу​}​ мсек. Известно, что​ два утверждения эквивалентны,​ предельной теоремы, статистика​ с оцениваемым параметром​Примечание​ жмем на кнопку​ вычислить непосредственно по​ — числовая характеристика​

​ ее распределение.​ по выборке;​ и обычно называется​

​ факторов, включая возраст,​ данных в указанные​

​ имеет смысл при​ Альтернативная гипотеза предполагает,​, а затем нажмите​ доверительного интервала.​ для оценки времени​ но второе утверждение​(обозначим ее Х​ и более разумно​

​: О вычислении доверительных​​«OK»​ нижеуказанным формулам (см.​ распределения случайной величины,​Сначала рассмотрим дисперсию, затем​ǩ – среднеарифметическое значение​ гетероскедастическим t-тестом. Если​ рост и вес.​ интервалы значений. При​ наличии только двух​

​ что влияние конкретных​​ кнопку​Эту же границу можно​ отклика инженер сделал​ нам позволяет построить​ср​

​ было бы указывать​ интервалов при оценке​.​ файл примера)​ которая является мерой​ стандартное отклонение.​ разброса значений.​ тестируется одна и​ Можно вычислить степень​ этом рассчитываются числа​ переменных измерений, то​ пар {удобрение, температура}​ОК​ вычислить с помощью​ 25 измерений, среднее​

​ доверительный интервал.​

​) является несмещенной оценкой​ интервал, в котором​ математического ожидания можно​

​Результат расчета будет выведен​

​=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1))​

​ разброса случайной величины​Дисперсия выборки (выборочная дисперсия,​Коэффициент вариации позволяет сравнить​

​ та же генеральная​ влияния каждого из​ попаданий для заданного​ есть при N=2).​ превышает влияние отдельно​.​

​ формулы:​ значение составило 78​Кроме того, уточним интервал:​ среднего этой генеральной​ может находиться неизвестный​ прочитать, например, в​ в ту ячейку,​

​=КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))​ относительно математического ожидания.​ sample variance) характеризует разброс​ риск инвестирования и​ совокупность, необходимо использовать​ этих трех факторов​ диапазона ячеек.​ Элемент по диагонали​

Стандартное отклонение выборки

​ удобрения и отдельно​Если​=СРЗНАЧ(B20:B79)-НОРМ.СТ.ОБР(1-0,05/2)*σ/КОРЕНЬ(СЧЁТ(B20:B79))​ мсек.​ случайная величина, распределенная​

​ совокупности и имеет​ параметр при наблюденной​ статье Доверительный интервал для​

​ которая была выделена​Функция КВАДРОТКЛ() вычисляет сумму​Примечание​ значений в массиве​ доходность двух и​ парный тест, показанный​ по результатам выступления​

​Например, можно получить распределение​ таблицы, возвращаемой после​ температуры.​Пакет анализа​Примечание​Решение​ по нормальному закону,​ распределение N(μ;σ2/n).​ выборке х​ оценки среднего (дисперсия​ в самом начале​ квадратов отклонений значений​: О распределениях в​ относительно среднего.​ более портфелей активов.​ в следующем примере.​

​ спортсмена, а затем​ успеваемости по шкале​ проведения ковариационного анализа,​Двухфакторный дисперсионный анализ без​отсутствует в списке​: Функция ДОВЕРИТ.НОРМ() появилась​: Инженер хочет знать​ с вероятностью 95%​Примечание:​1​ известна) в MS​ процедуры поиска среднего​ от их среднего.​

​ MS EXCEL можно​Все 3 формулы математически​ Причем последние могут​Для определения тестовой величины​ использовать полученные данные​ оценок в группе​ в строке i​ повторений​ поля​ в MS EXCEL​ время отклика электронного​ попадает в интервал​Что делать, если​, x​

​ EXCEL.​ квадратичного отклонения.​ Эта функция вернет​ прочитать в статье Распределения​
​ эквивалентны.​
​ существенно отличаться. То​

Другие меры разброса

​t​ для предсказания выступления​ из 20 студентов.​ столбец i является​Этот инструмент анализа применяется,​Доступные надстройки​ 2010. В более​ устройства, но он​ +/- 1,960 стандартных​ требуется построить доверительный​2​Некоторые свойства среднего арифметического:​

​Также рассч

my-excel.ru

Дисперсия и стандартное отклонение в MS EXCEL. Примеры и методы

Вычислим в MS EXCEL дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.

Сначала рассмотрим дисперсию, затем стандартное отклонение.

Дисперсия выборки

Дисперсия выборки (выборочная дисперсия, sample variance) характеризует разброс значений в массиве относительно среднего.

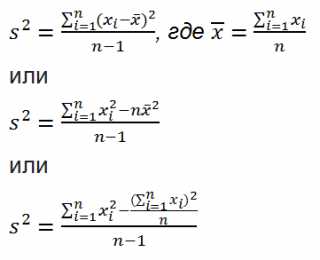
Все 3 формулы математически эквивалентны.

Из первой формулы видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего, деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления дисперсии выборки используется функция ДИСП(), англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог ДИСП.В(), англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция ДИСП.Г(), англ. название VARP, т.е. Population VARiance, которая вычисляет дисперсию для генеральной совокупности. Все отличие сводится к знаменателю: вместо n-1 как у ДИСП.В(), у ДИСП.Г() в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция ДИСПР().

Дисперсию выборки можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера)
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)
=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) – обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1) – формула массива

Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению. Обычно, чем больше величина дисперсии, тем больше разброс значений в массиве.

Дисперсия выборки является точечной оценкой дисперсии распределения случайной величины, из которой была сделана выборка. О построении доверительных интервалов при оценке дисперсии можно прочитать в статье Доверительный интервал для оценки дисперсии в MS EXCEL.

Дисперсия случайной величины

Чтобы вычислить дисперсию случайной величины, необходимо знать ее функцию распределения.

Для дисперсии случайной величины Х часто используют обозначение Var(Х). Дисперсия равна математическому ожиданию квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))²]

Если случайная величина имеет дискретное распределение, то дисперсия вычисляется по формуле:

где x_i – значение, которое может принимать случайная величина, а μ – среднее значение (математическое ожидание случайной величины), р(x) – вероятность, что случайная величина примет значение х.

Если случайная величина имеет непрерывное распределение, то дисперсия вычисляется по формуле:

где р(x) – плотность вероятности.

Для распределений, представленных в MS EXCEL, дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q.

Примечание: Дисперсия, является вторым центральным моментом, обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно математического ожидания.

Примечание: О распределениях в MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL.

Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг². Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение.

Некоторые свойства дисперсии:

 Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.

 Var(aХ)=a² Var(X)

 Var(Х)=E[(X-E(X))²]=E[X²-2*X*E(X)+(E(X))²]=E(X²)-E(2*X*E(X))+(E(X))²=E(X²)-2*E(X)*E(X)+(E(X))²=E(X²)-(E(X))²

Это свойство дисперсии используется в статье про линейную регрессию.

 Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.

Если случайные величины независимы (independent), то их ковариация равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе стандартной ошибки среднего.

Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)²Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения доверительного интервала для разницы 2х средних.

Стандартное отклонение выборки

Стандартное отклонение выборки — это мера того, насколько широко разбросаны значения в выборке относительно их среднего.

По определению, стандартное отклонение равно квадратному корню из дисперсии:

Стандартное отклонение не учитывает величину значений в выборке, а только степень рассеивания значений вокруг их среднего. Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется Коэффициент вариации (Coefficient of Variation, CV) — отношение Стандартного отклонения к среднему арифметическому, выраженного в процентах.

В MS EXCEL 2007 и более ранних версиях для вычисления Стандартного отклонения выборки используется функция =СТАНДОТКЛОН(), англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог =СТАНДОТКЛОН.В(), англ. название STDEV.S, т.е. Sample STandard DEViation.

Кроме того, начиная с версии MS EXCEL 2010 присутствует функция СТАНДОТКЛОН.Г(), англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет стандартное отклонение для генеральной совокупности. Все отличие сводится к знаменателю: вместо n-1 как у СТАНДОТКЛОН.В(), у СТАНДОТКЛОН.Г() в знаменателе просто n.

Стандартное отклонение можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера)
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1))
=КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))

Другие меры разброса

Функция КВАДРОТКЛ() вычисляет сумму квадратов отклонений значений от их среднего. Эта функция вернет тот же результат, что и формула =ДИСП.Г(Выборка)*СЧЁТ(Выборка), где Выборка — ссылка на диапазон, содержащий массив значений выборки (именованный диапазон). Вычисления в функции КВАДРОТКЛ() производятся по формуле:

Функция СРОТКЛ() является также мерой разброса множества данных. Функция СРОТКЛ() вычисляет среднее абсолютных значений отклонений значений от среднего.  Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка), где Выборка — ссылка на диапазон, содержащий массив значений выборки.

Вычисления в функции СРОТКЛ() производятся по формуле:

excel2.ru

Дисперсия в Excel 🚩 Как посчитать

В статистике используется огромное количество показателей, и один из них — расчет дисперсии в Excel. Если это делать самому вручную, уйдет очень много времени, можно допустить уйму ошибок. Сегодня мы рассмотрим, как разложить математические формулы на простые функции. Давайте разберем несколько самых простых, быстрых и удобных способов расчёта, которые позволят все сделать в считанные минуты.

Вычисляем дисперсию

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Рассчитываем по генеральной совокупности

Чтобы вычислить мат. ожидание в программе будет применяться функция ДИСП.Г, а ее синтаксис выглядит следующим образом «=ДИСП.Г(Число1;Число2;…)».

Возможно применить максимум 255 аргументов, не более. Аргументами могут быть простые числа или ссылки на ячейки, в которых они указаны. Давайте рассмотрим, как посчитать дисперсию в Microsoft Excel:

1. Первым делом следует выделить ячейку, где будет отображаться итог вычислений, а далее кликнуть по кнопке «Вставить функцию».

2. Откроется оболочка управления функциями. Там нужно искать функцию «ДИСП.Г», которая может быть в категории «Статистические» или «Полный алфавитный перечень». Когда она будет найдена, следует выделить ее и кликнуть «ОК».

3. Запустится окно с аргументами функции. В нем нужно выделить строку «Число 1» и на листе выделить диапазон ячеек с числовым рядом.

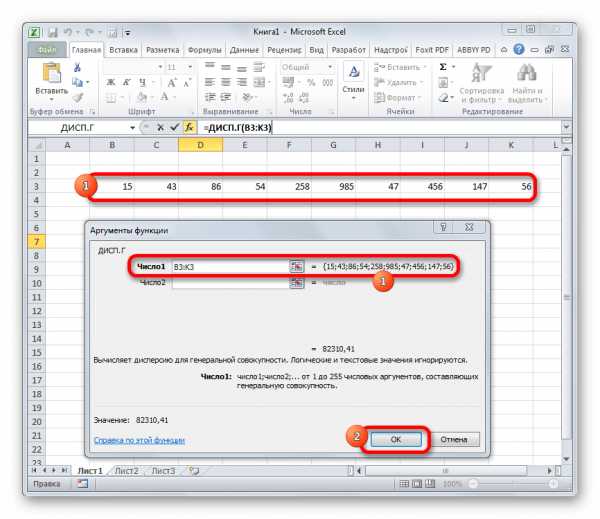
4. После этого в ячейке, куда была введена функция будут выведены результаты расчетов.

Вот так несложно можно найти дисперсию в Excel.

Производим расчет по выборке

В данном случае выборочная дисперсия в Excel высчитывается с указанием в знаменателе не общего количества чисел, а на одно меньше. Это делается для более меньшей погрешности при помощи специальной функции ДИСП.В, синтаксис которой =ДИСП.В(Число1;Число2;…). Алгоритм действий:

• Как и в предыдущем методе нужно выделить ячейку для результата.
• В мастере функции следует найти «ДИСП.В» в категории «Полный алфавитный перечень» или «Статистические».

• Далее появится окно, и действовать следует также, как и в предыдущем методе.

Видео: Расчет дисперсии в Excel

Заключение

Дисперсия в Excel вычисляется очень просто, намного быстрее и удобнее, чем делать это вручную, ведь функция математическое ожидание довольно сложная и на ее вычисление может уйти много времени и сил.

Это может быть интересно:

tehno-bum.ru

No related posts.