Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Данная статья раскрывает вопрос о решении линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Будет рассмотрена теория вместе с примерами приведенных задач. Для расшифровки непонятных терминов необходимо обращаться к теме об основных определениях и понятиях теории дифференциальных уравнений.
Рассмотрим линейное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами вида y»+p·y’+q·y=f(x), где произвольными числами являются p и q, а имеющаяся функция f(х) непрерывная на интервале интегрирования x.
Перейдем к формулировке теоремы общего решения ЛНДУ.
Yandex.RTB R-A-339285-1Теорема общего решения ЛДНУ
Теорема 1Общим решением, находящимся на интервале х, неоднородного дифференциального уравнения вида y(n)+fn-1(x)·y(n-1)+…+f0(x)·y=f(x) с непрерывными коэффициентами интегрирования на x интервале f0(x), f1(x),…, fn-1(x) и непрерывной функцией f(x) равняется сумме общего решения y0, которое соответствует ЛОДУ и каким-нибудь частным решением y~, где исходным неоднородным уравнением является y=y0+y~.
Отсюда видно, что решение такого уравнения второго порядка имеет вид y=y0+y~. Алгоритм нахождения y0 рассмотрен в статье о линейных однородных дифференциальных уравнениях второго порядка с постоянными коэффициентами. После чего следует переходить к определению y~.
Выбор частного решения ЛНДУ зависит от вида имеющейся функции f(x), располагающейся в правой части уравнения. Для этого необходимо рассмотреть отдельно решения линейных неоднородных дифференциальных уравнений второго порядка при постоянных коэффициентах.
Когда f(x) считается за многочлен n-ой степени f(x) = Pn(x), отсюда следует, что частное решение ЛНДУ находим по формуле вида y~=Qn(x)·xγ, где Qn(x) является многочленом степени n, r – это количество нулевых корней характеристического уравнения. Значение y~ является частным решением y~»+p·y~’+q·y~=f(
zaochnik.com
Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами [wiki.eduVdom.com]
Пример 1. $$
\frac{d^{2}y}{dx^{2}}+\frac{dy}{dx}-2y=3x-1$$ Решение:
Пример 2.
Решить уравнение $$ {Y}»+{y}’=4x^{2}e^{x} $$
Решение. Характеристическое уравнение
$$
k^{2}+k=0
\\
k(k+1)=0
\;;\;
k_{1}=0
\;;\;
k_{2}=-1
$$
Общее решение однородных уравнений имеет вид: $y=C_{1}+C_{2}e^{-x}$
Правая часть уравнения $ f(x)=4x^{2}e^{x} \,,\, \alpha=1 $ , т.к. $\alpha=1$ не является корнем характеристического уравнения, то частное решение неоднородного уравнения имеет вид (см. табл. Случай 2/1)
$$ \overline{y}=( A_{1}x^{2}+A_{2}x+A_{3} )e^{x} $$
Подставляя его в исходное уравнение и сокращая обе части уравнения на $e^{x}$ , будем иметь $$ 2A_{1}x^{2} + (6A_{1}+2A_{2})x + 2A_{1} + 3A_{2} + 2A_{3} = 4x^{2} $$
Приравнивая коэффициенты при одинаковых степенях в левой и правой частях равенства, получаем линейную систему уравнений для нахождения коэффициентов $A_{1} \,,\, A_{2} \text{ и } A_{3}$: $$ \left\{\begin{matrix} 2A_{1}=4 &;& A_{1}=2 \\ 6A_{1}+2A_{2}=0 &;& A_{2}=-6 \\ 2A_{1}+3A_{2}+2A_{3}=0 &;& A_{3}=7 \end{matrix}\right. $$ $$ \overline{y}=( 2x^{2}-6x+7 )e^{x} $$
Общее решение данного уравнения $$ y(x)=C_{1}+C_{2}e^{-x}+( 2x^{2}-6x+7 )e^{x} $$
Пример 3.
Найти общее решение уравнения $$ {y}»+{10y}’+25y=4e^{-5x} $$
Решение: характеристическое уравнение $k^{2}+10k+25=0$ имеет двукратный корень $k_{1}=k_{2}=-5$, поэтому $y=( C_{1}+C_{2}x )e^{-5x}$ .
Т.к. $к=-5$ является корнем характеристического уравнения кратности $S=2$, то частное решение неоднородного уравнения ищем в виде ( см. табл., случай 2(2) ):
$$
\overline{y}=Ax^{2}e^{-5x}
\;;\;
{\overline{y}}’=A( 2x-5x^{2} )e^{-5x}
\;;\;
{\overline{y}}»=A( 2-20x+25x^{2} )e^{-5x}
$$
Подставляя выражения для $ y \,,\, {y}’ \,,\, {y}» $ в исходное уравнение, получаем $ 2Ae^{-5x}=4e^{-5x} \,,\, A=2 \,,\, y=2x^{2}e^{-5x} $ . Общее решение данного уравнения $$ y=( C_{1}+C_{2}x )e^{-5x} + 2x^{2}e^{-5x} $$
Пример 4
Найти частное решение уравнения (решить задачу Коши) $$ {y}»+{y}’-2y=\cos{x}-3\sin{x} $$ Начальные условия: $ y(0)=1 \;;\; {y}'(0)=2 \;; $
Решение:
Характеристическое уравнение: $ k^{2}+k-2=0 $;
Корни характеристического уравнения: $ k_{1}=1 \;;\; k_{2}=-2 $;
Общее решение однородного уравнения: $ y=C_{1}e^{-2x}+C_{2}e^{x} $
Частное решение неоднородного дифференциального уравнения будем искать в виде (см.таблицу):
$$
\overline{y}=A\cos{x} + B\sin{x}
\;;\; \\
\overline{{y}’}=-A\sin{x}+B\cos{x}
\;;\; \\
{\overline{y}}»=-A\cos{x}-B\sin{x}
$$
Подставляя выражения для $ y \,,\, {y}’ \,,\, {y}» $ в исходное уравнение, получаем: $(B-3A)\cos{x}+(-3B-A)\sin{x}=\cos{x}–3\sin{x}$ $$ \left\{\begin{matrix} B-3A=1 \\ &\Rightarrow &A=0 &, &B=1 &; \\ -(3B+A)=-3 \end{matrix}\right. $$ Тогда общее решение заданного уравнения будет иметь вид: $$ y=C_{1}e^{-2x}+C_{2}e^{x}+\sin{x} $$
Найдем $С_1$ и $С_2$ , используя начальные условия ( $ y(0)=1 \;;\; {y}'(0)=2 $ ): $$ \left\{\begin{matrix} C_{1}e^{0}-C_{2}e^{0}+\sin{0}=1 \\ 2C_{1}e^{0}+C_{2}e^{0}+\cos{0}=2 \end{matrix}\right. \\ \left\{ \begin{matrix} C_{1}+C_{2}=1 \\ -2C_{1}+c_{2}=1 \end{matrix}\right. \\ C_{1}=0 \;;\; C_{2}=1 \;;\; $$ Задача Коши решена: $y=e^{x}+\sin{x}$
Пример 5.
Решить уравнение: $$ {y}»’+{y}»-{2y}’=x-e^{x} $$
Решение: $$
k^{3}+k^{2}-2k=0
\;;\;
k_{1}=0
\;;\;
k_{2}=1
\;;\;
k_{3}=-2
\;;\;
y=C_{1}+C_{2}e^{x}+C_{3}e^{-2x}
$$
т.к. $k_{1}=0$ – простой корень характеристического уравнения, т.е. S_{1}=1 , то частное решение ищем в виде:
$$
\overline{y}=x(Ax+B)+Cxe^{x}
\;;\; \\
{\overline{y}}’=2Ax+B+Ce^{x}+Cxe^{x}
\;;\; \\
{\overline{y}}»=2A+2Ce^{x}+Cxe^{x}
\;;\; \\
{\overline{y}}»’= 3Ce^{x}+Cxe^{x}
\\ \\
-4Ax+( 2A-3B )+3Ce^{x}=x-e^{x}
\;;\;
A=-\frac{1}{4}
\;;\;
B=-\frac{1}{4}
\;;\;
C=-\frac{1}{3}
$$
Ответ:
$$ y=C_{1}+C_{2}e^{x}+C_{3}e^{-2x}-\frac{1}{4}x( x+1 )-\frac{1}{3}xe^{x} $$
www.wiki.eduvdom.com
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами
Этот тип уравнений характеризуется наличием правой части, то есть имеет вид:
. (17)
Можно доказать, что общее решение уравнения (17) представляется в виде:
, (18)
где 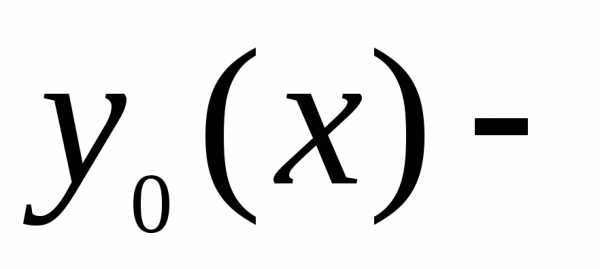 общее
решение уравнения (17), а
общее
решение уравнения (17), а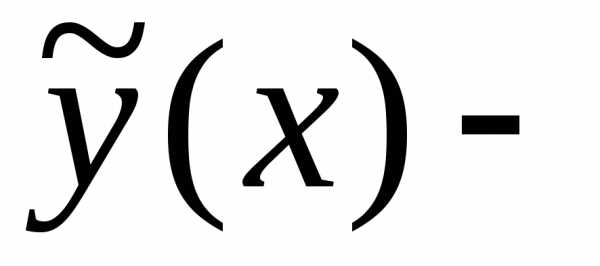 частное
решение уравнения (17). Иными словами,
общее решение линейного неоднородного
уравнения есть сумма общего решения
линейного однородного решения и одного
из частных решений линейного неоднородного
уравнения.
частное
решение уравнения (17). Иными словами,
общее решение линейного неоднородного
уравнения есть сумма общего решения
линейного однородного решения и одного
из частных решений линейного неоднородного
уравнения.
Отметим еще одно важное свойство решений линейных дифференциальных уравнений – принцип суперпозиции решений. Пусть правая часть линейного неоднородного дифференциального уравнения представляется в виде суммы двух (или более) функций:
. (19)
Тогда
решение этого уравнения может быть
представлено в виде
,
где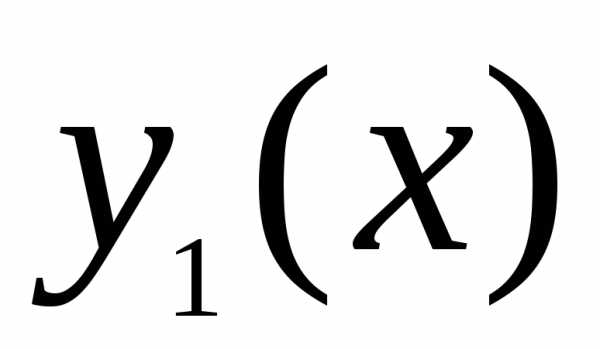 и
и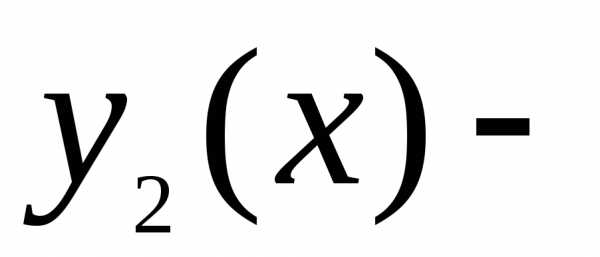 решения
дифференциальных уравнений:исоответственно. Это означает, что, разбив
правую часть линейного неоднородного
дифференциального уравнения на сумму
двух слагаемых, можно свести его решение
к решению двух более простых дифференциальных
уравнений.
решения
дифференциальных уравнений:исоответственно. Это означает, что, разбив
правую часть линейного неоднородного
дифференциального уравнения на сумму
двух слагаемых, можно свести его решение
к решению двух более простых дифференциальных
уравнений.
Заметим, что при формулировке принципа суперпозиции решений не требуется постоянство коэффициентов. Кроме того, этот принцип справедлив и для дифференциальных уравнений более высокого порядка.
Рассмотрим
линейное неоднородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами (17), в котором правая
часть имеет следующий вид:
,
где ,
,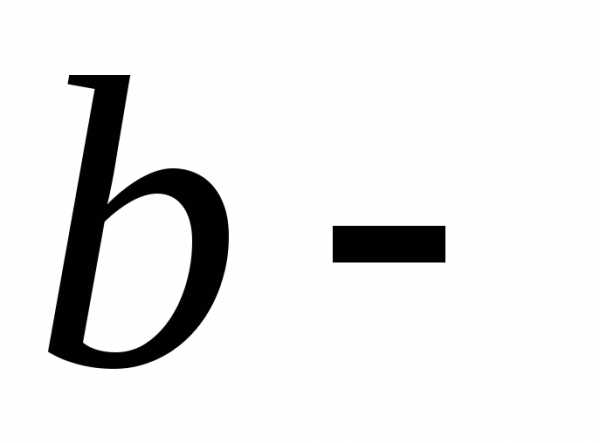 постоянные числа,
постоянные числа, 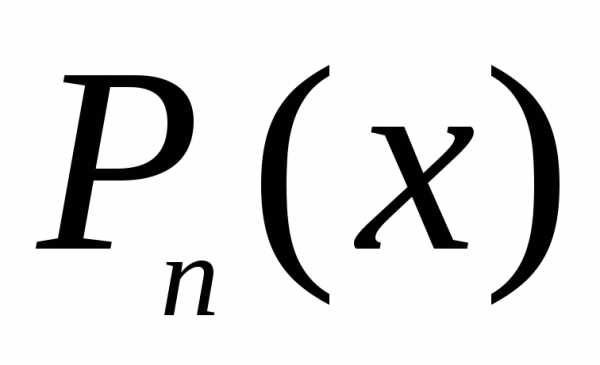 ,
,
 многочлены порядка
многочлены порядка 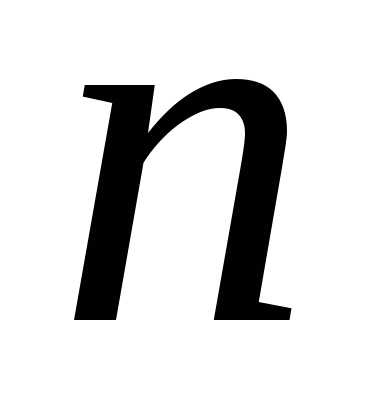 и
и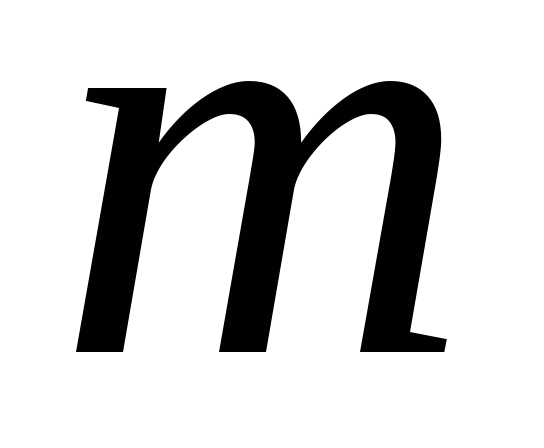 .
.Такие уравнения называют уравнениями со специальной правой частью, и для нахождения их частного решения можно применить метод Эйлера. Согласно этому методу, частное решение ищется в следующем виде:
. (20)
В
правой части равенства (20)
,
а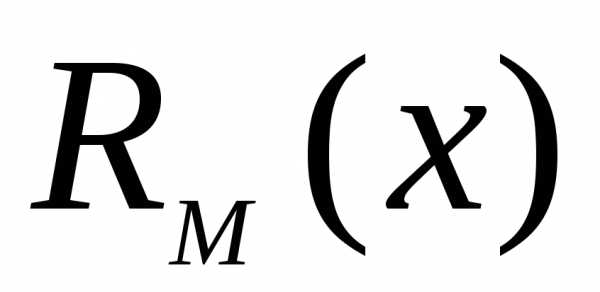 и
и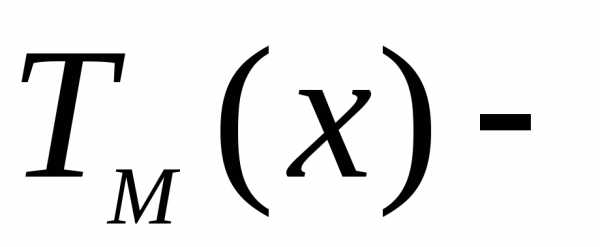 многочлены степени
многочлены степени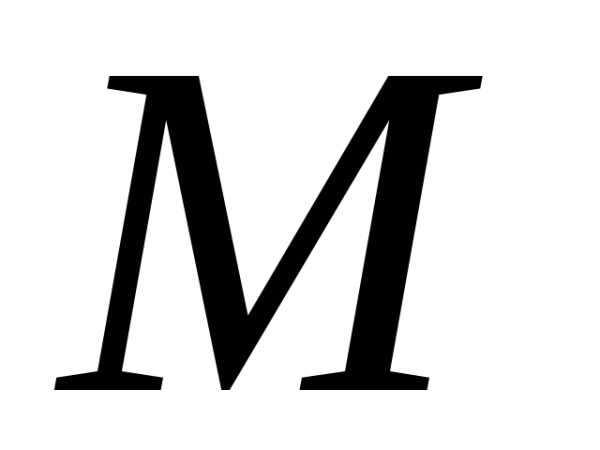
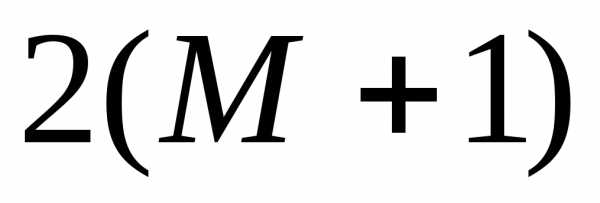 ).
Степень множителя
).
Степень множителя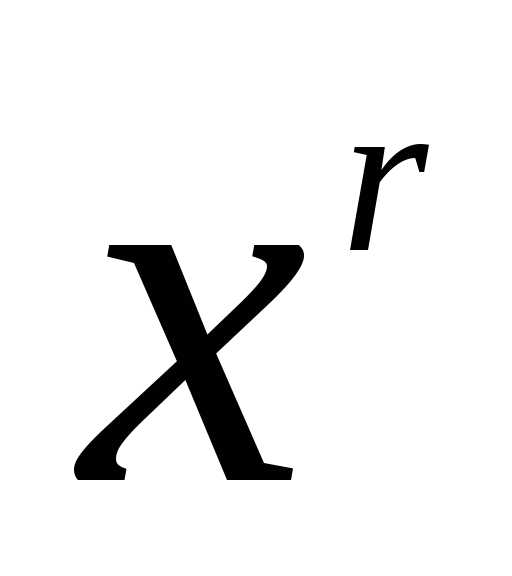 определяется
по следующему правилу.
определяется
по следующему правилу. Если
контрольное число  (комплексное при
(комплексное при не совпадает ни с одним из корней
характеристического уравнения (18), то
не совпадает ни с одним из корней
характеристического уравнения (18), то .
Если контрольное число совпадает с
одним из корней характеристического
уравнения, то
.
Если контрольное число совпадает с
одним из корней характеристического
уравнения, то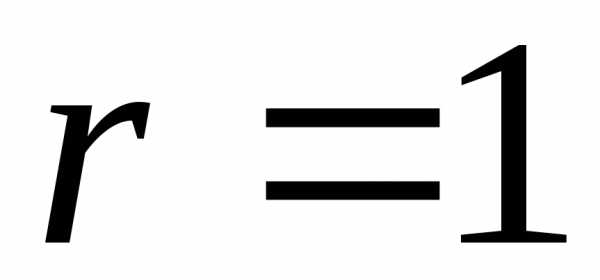
 .
Очевидно, что последний случай возможен
только при
.
Очевидно, что последний случай возможен
только при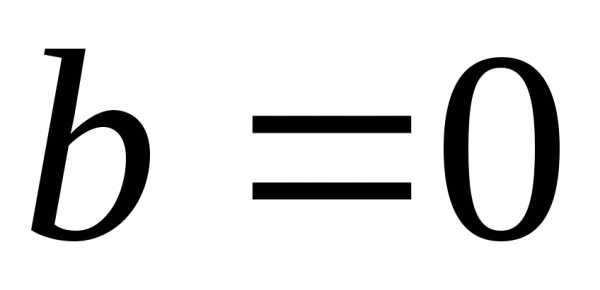 ,
так как кратный корень может быть только
вещественным.
,
так как кратный корень может быть только
вещественным. Для
определения неопределенных коэффициентов
в многочленах 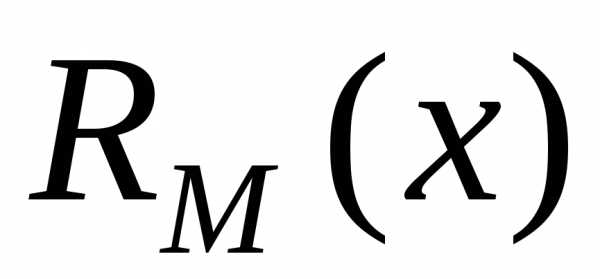 и
и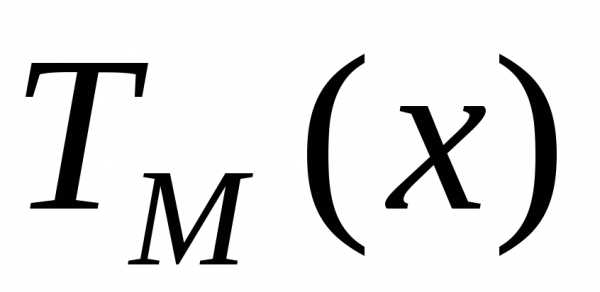 следует подставить выражение (20) в
уравнение (17), предварительно найдя его
производные
следует подставить выражение (20) в
уравнение (17), предварительно найдя его
производные и
и
Пример9. Решить дифференциальное уравнение: .
Решение. Характеристическое уравнение для
однородного дифференциального уравнения
имеет вид:
.
Его корни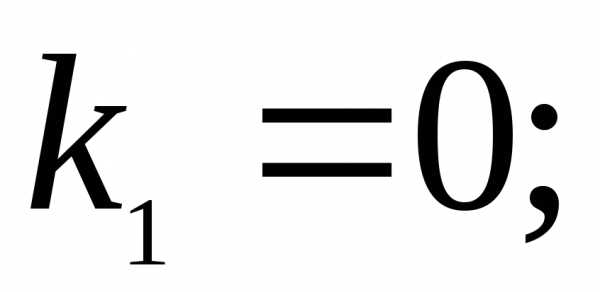
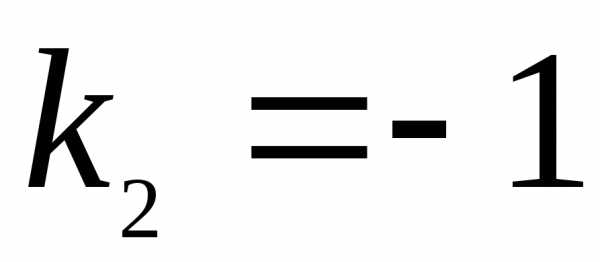 .
Общее решение однородного уравнения
записывается в форме:,
где
.
Общее решение однородного уравнения
записывается в форме:,
где и
и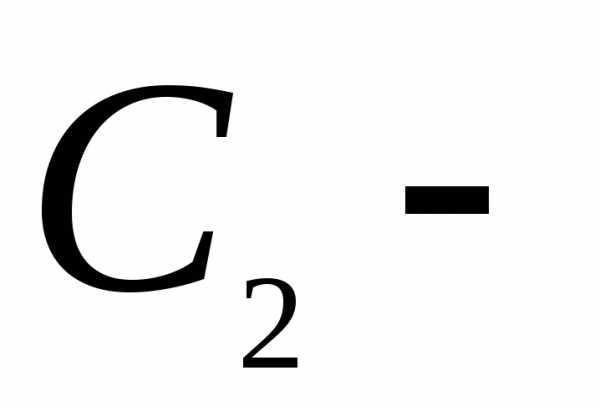 произвольные постоянные.
произвольные постоянные.
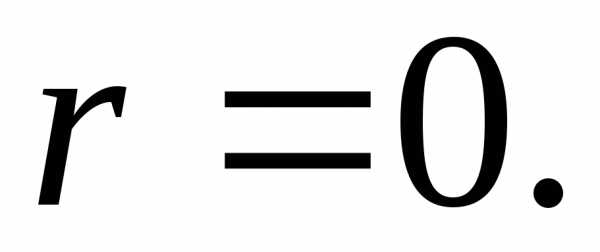 Таким образом, формула (20) дает:.
Найдем производные
Таким образом, формула (20) дает:.
Найдем производные .
.Подставим эти выражения в дифференциальное уравнение:
.
Сокращая
обе части уравнения на 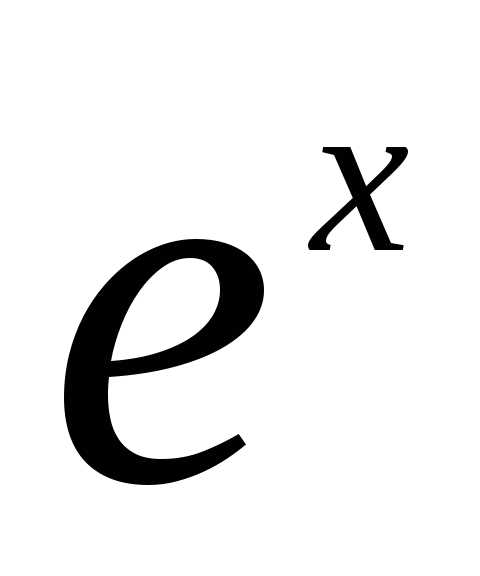 и приводя подобные, получаем:
и приводя подобные, получаем:
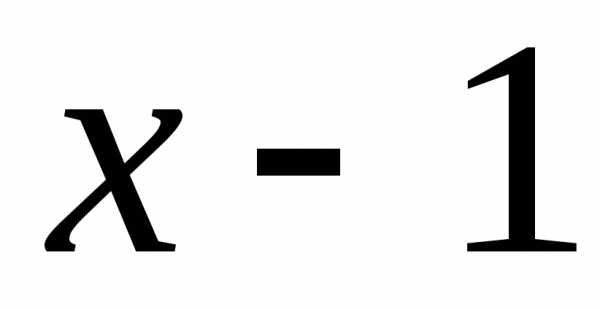 .
.
Последнее
равенство должно выполняться для
произвольных значений 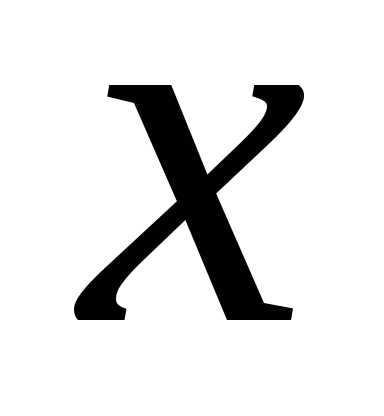
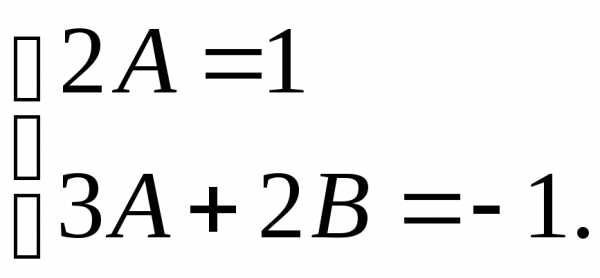
Решая
систему уравнений, находим: 
Следовательно, и общее решение рассматриваемого дифференциального уравнения принимает вид:
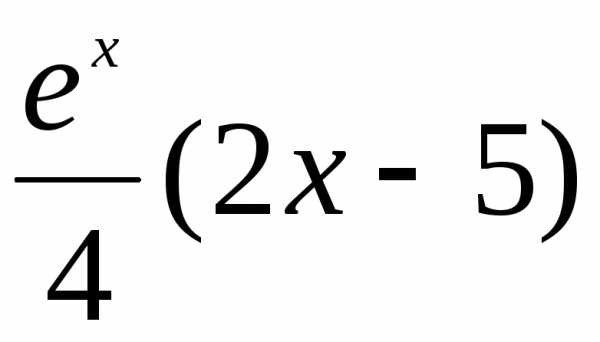 .
.
Пример10. Найти общее решение дифференциального уравнения: .
Решение. Характеристическое уравнение для
однородного дифференциального уравнения
имеет два комплексных корня:Общее решение однородного уравнения
записывается в виде:,
где
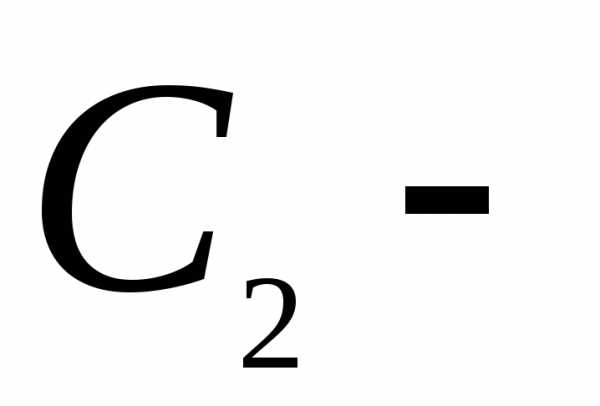 произвольные постоянные.
произвольные постоянные.Найдем частное решение неоднородного уравнения. Заметим, что правая часть уравнения – сумма двух слагаемых, каждое из которых может быть представлено в виде (25). Поэтому, в соответствии с принципом суперпозиции решений, частное решение неоднородного уравнения будем искать в виде:
.
Найдем
производные функции 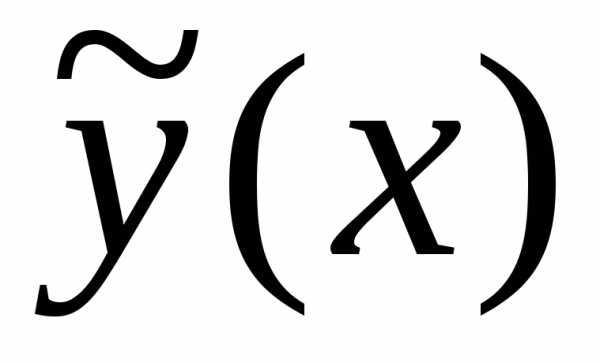 :
:
.
Подстановка этих выражений в исходное уравнение дает:
.
Выполнение
этого уравнения при произвольных
значениях  возможно только в том случае, когда
коэффициенты при функцияхв левой и правой частях уравнения будут
одинаковы. Это условие приводит к системе
уравнений:
возможно только в том случае, когда
коэффициенты при функцияхв левой и правой частях уравнения будут
одинаковы. Это условие приводит к системе
уравнений:
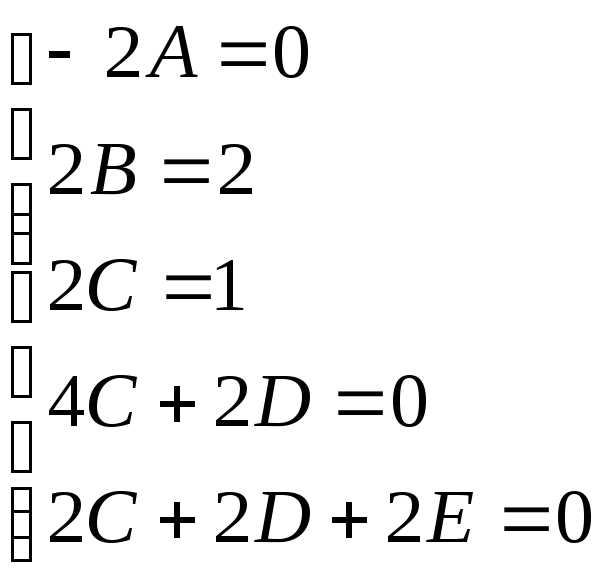
Ее
решение: 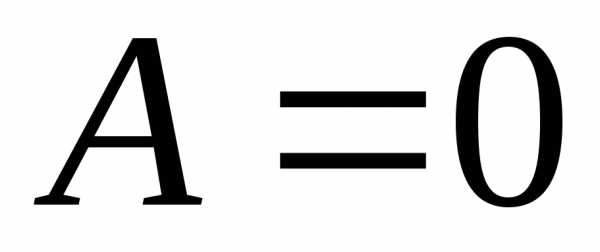 ;
;  ;
; 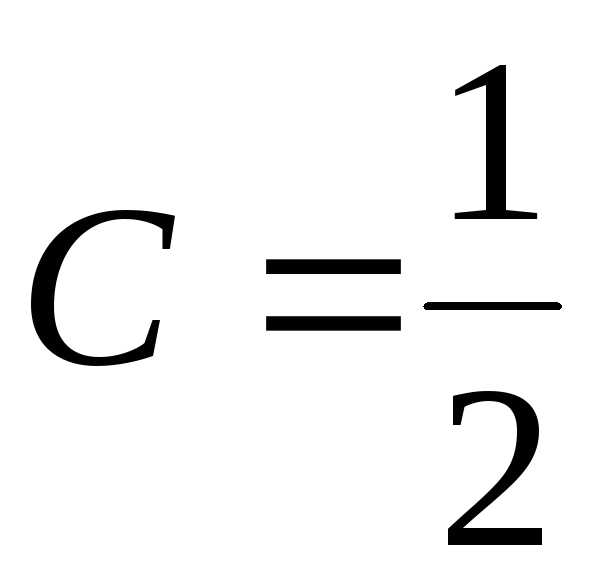 ;;
;;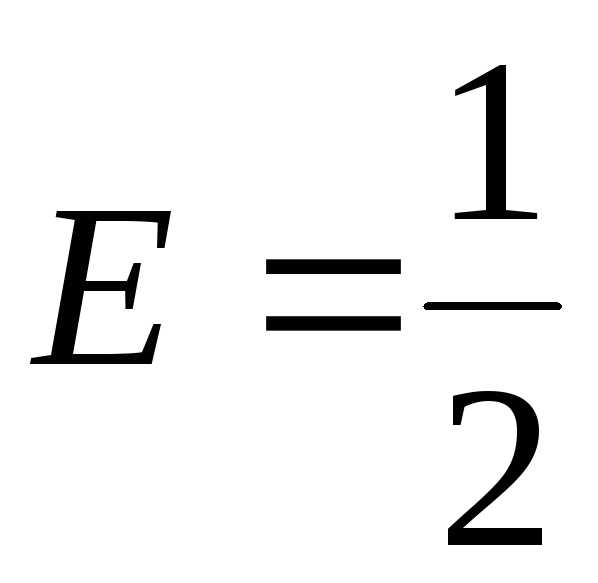
В окончательном виде получаем общее решение неоднородного дифференциального уравнения:
.
Рассмотрим еще один метод нахождения частного решения линейного неоднородного дифференциального уравнения второго порядка. Этот метод применим для уже рассмотренных уравнений с правой частью специального вида, а также для уравнений с правой частью более общего вида. Этот метод называют методом вариации произвольных постоянных, или методом Лагранжа.
Рассмотрим
этот метод применительно к уравнению
(17), хотя он позволяет находить решение
и более общего уравнения с переменными
коэффициентами. Согласно этому методу
сначала находят два линейно- независимых
решения 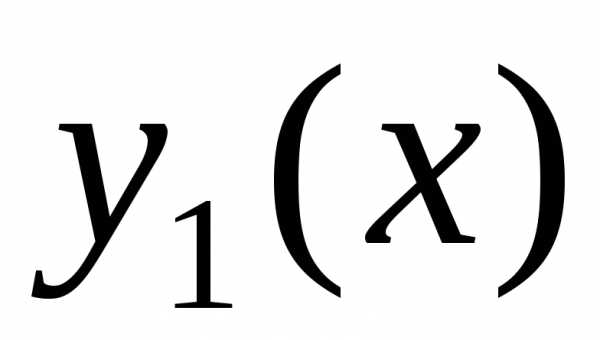 и
и однородного дифференциального уравнения.
Частное решение неоднородного
дифференциального уравнения ищется в
виде их линейной комбинации, в которой
произвольные постоянные
однородного дифференциального уравнения.
Частное решение неоднородного
дифференциального уравнения ищется в
виде их линейной комбинации, в которой
произвольные постоянные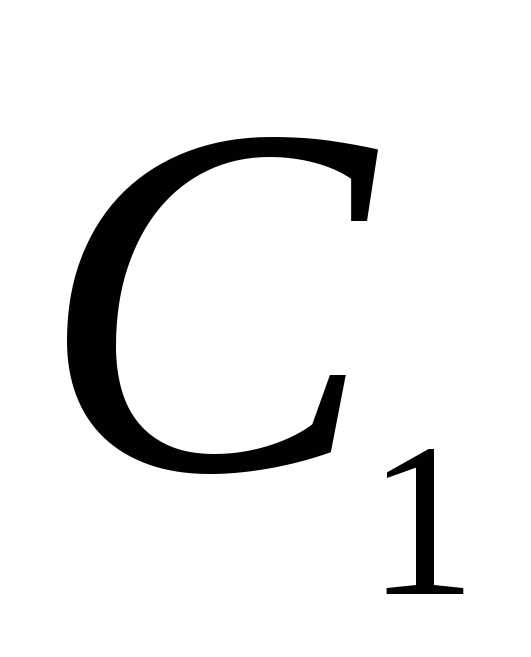 и
и заменяются на неизвестные функции
заменяются на неизвестные функции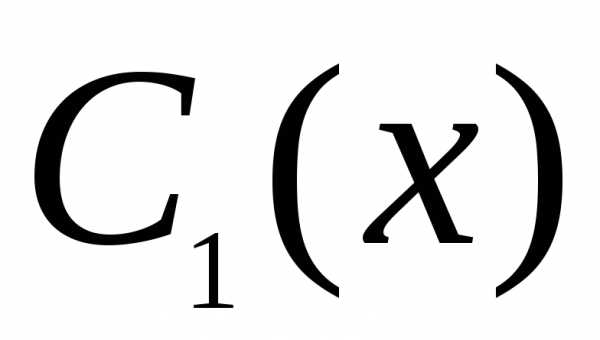 и
и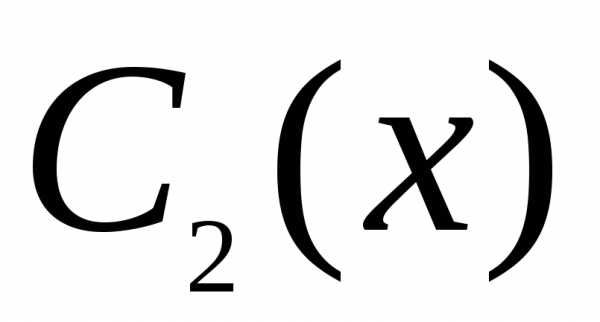 :
:
. (21)
Подстановка этого выражения в неоднородное дифференциальное уравнение (17) приводит к следующему уравнению:

. (22)
Перегруппируем слагаемые в (22):
(23)
Рассмотрим
подробнее уравнение (23). Так как функции 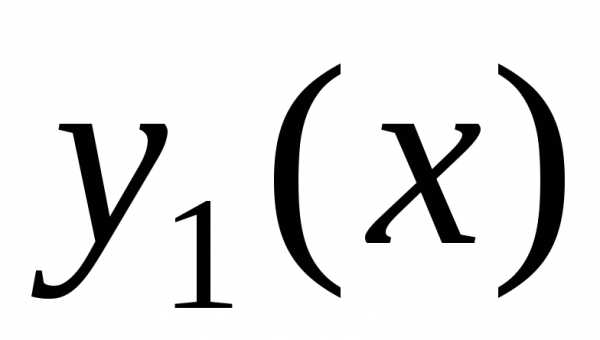 и
и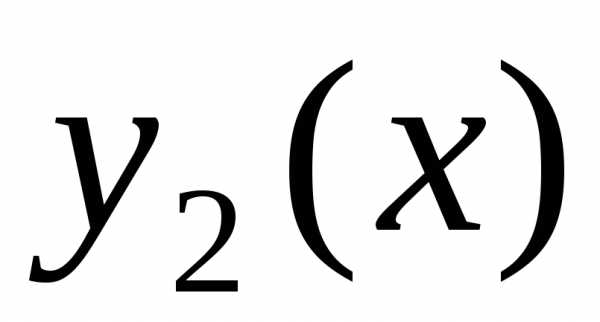 являются решениями однородного
дифференциального уравнения (12), выражения
в третьей и четвертой скобках в (23)
тождественно равны нулю. Наложим на
пока неопределенные функции
являются решениями однородного
дифференциального уравнения (12), выражения
в третьей и четвертой скобках в (23)
тождественно равны нулю. Наложим на
пока неопределенные функции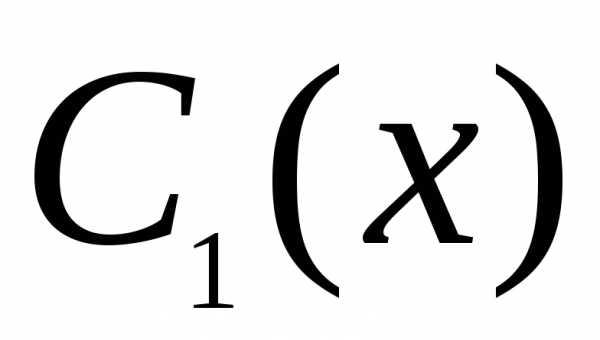 и
и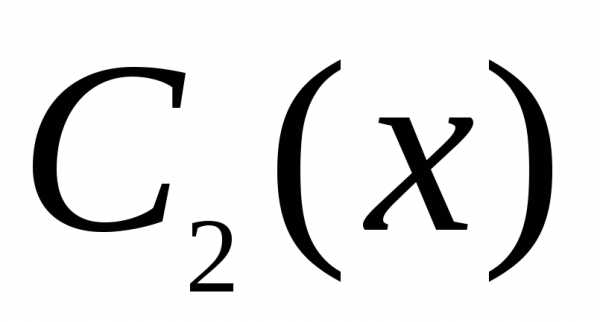 следующее условие:
следующее условие:
(24)
Тогда выражение в пятой скобке в (23) также окажется равным нулю. Продифференцируем обе части равенства (23):
Это соотношение показывает, что и выражение в первой скобке в (23) тождественно равно нулю.
Таким образом, при условии (24) уравнение (23) сводится к следующему: Иными словами, уравнение (23) равносильно системе уравнений:
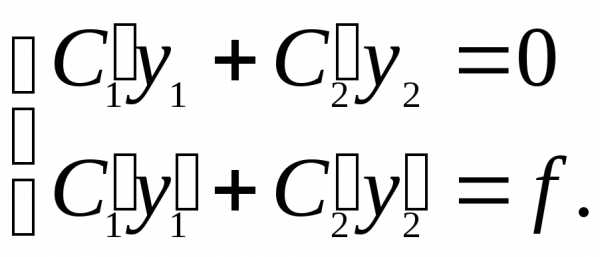 (25)
(25)
Поскольку
определитель этой системы является
вронскианом двух линейно независимых
решений  и
и ,
и отличен от нуля, система всегда имеет
единственное решение.
,
и отличен от нуля, система всегда имеет
единственное решение.
Решив
систему уравнения (25), остается лишь
найти 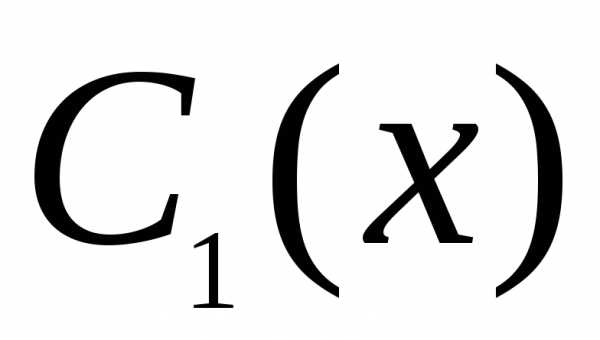 и
и ,
то есть проинтегрировать полученные
из (25) функции
,
то есть проинтегрировать полученные
из (25) функции и
и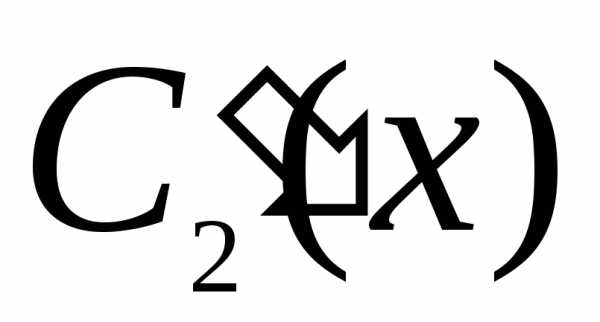 )
и, подставить их в выражение для
)
и, подставить их в выражение для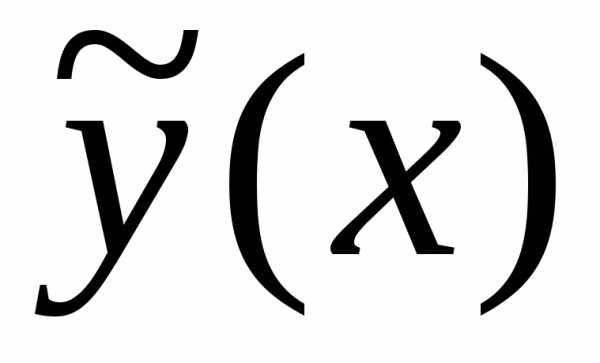 .
.
Пример11. Найти решение дифференциального
уравнения: 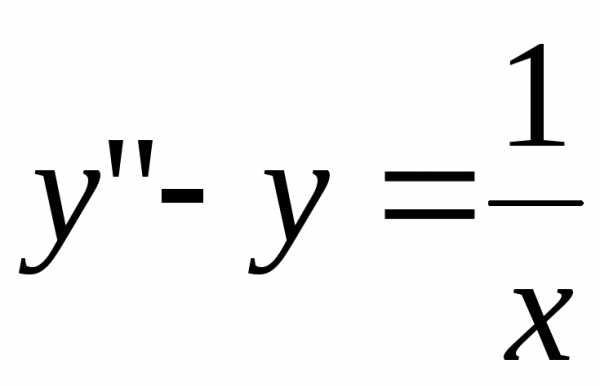 .
.
Решение. В этом уравнении правая часть не подпадает под вид, допускающий применение метода неопределенных коэффициентов.
Поэтому для нахождения частного решения неоднородного дифференциального уравнения воспользуемся методом вариации произвольных постоянных. Но сначала для нахождения фундаментальной системы решений рассмотрим однородное дифференциальное уравнение: .
Характеристическое
уравнение
имеет корни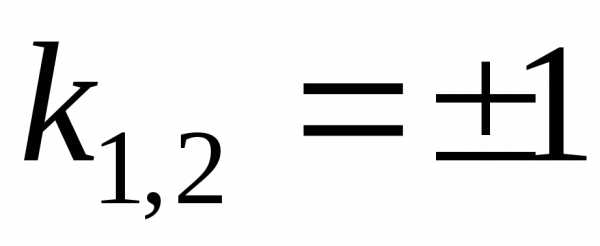 ,
и общее решение записывается в виде:
,
и общее решение записывается в виде:
.
Частное решение неоднородного уравнения ищем в виде:
.
Система (25) приобретает вид:
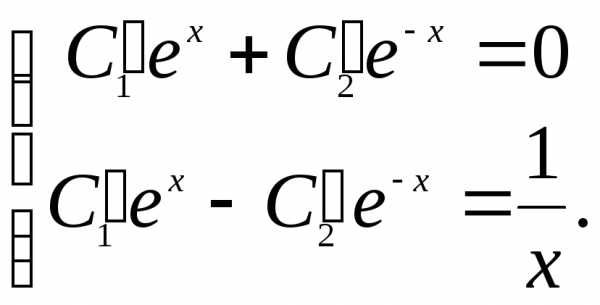
Отсюда находим:
 и
и 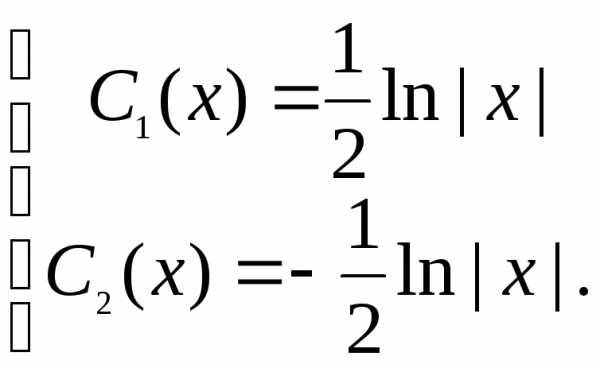
В итоге получаем: .
Общее решение рассматриваемого уравнения принимает вид:
.
studfiles.net
Неоднородные дифференциальные уравнения второго порядка
Задача: найти ОР ЛНДУ-2 $y»-3\cdot y’-18\cdot y=\left(36\cdot x+12\right)\cdot e^{3\cdot x} $. Найти также ЧР, удовлетворяющее начальным условиям $y=6$ при $x=0$ и $y’=1$ при $x=0$.
Записываем соответствующее ЛОДУ-2: $y»-3\cdot y’-18\cdot y=0$.
Характеристическое уравнение: $k^{2} -3\cdot k-18=0$. Корни характеристического уравнения: $k_{1} =-3$, $k_{2} =6$. Эти корни действительны и различны. Таким образом, ОР соответствующего ЛОДУ-2 имеет вид: $Y=C_{1} \cdot e^{-3\cdot x} +C_{2} \cdot e^{6\cdot x} $.
Правая часть данного ЛНДУ-2 имеет вид $\left(36\cdot x+12\right)\cdot e^{3\cdot x} $. В ней необходимо рассматривать коэффициент показателя степени экспоненты $\alpha =3$. Этот коэффициент не совпадает ни с одним из корней характеристического уравнения. Поэтому ЧР данного ЛНДУ-2 имеет вид $U=\left(A\cdot x+B\right)\cdot e^{3\cdot x} $.
Будем искать коэффициенты $A$, $B$ методом НК.
Находим первую производную ЧР:
$U’=\left(A\cdot x+B\right)^{{‘} } \cdot e^{3\cdot x} +\left(A\cdot x+B\right)\cdot \left(e^{3\cdot x} \right)^{{‘} } =$
$=A\cdot e^{3\cdot x} +\left(A\cdot x+B\right)\cdot 3\cdot e^{3\cdot x} =\left(A+3\cdot A\cdot x+3\cdot B\right)\cdot e^{3\cdot x} .$
Находим вторую производную ЧР:
$U»=\left(A+3\cdot A\cdot x+3\cdot B\right)^{{‘} } \cdot e^{3\cdot x} +\left(A+3\cdot A\cdot x+3\cdot B\right)\cdot \left(e^{3\cdot x} \right)^{{‘} } =$
$=3\cdot A\cdot e^{3\cdot x} +\left(A+3\cdot A\cdot x+3\cdot B\right)\cdot 3\cdot e^{3\cdot x} =\left(6\cdot A+9\cdot A\cdot x+9\cdot B\right)\cdot e^{3\cdot x} .$
Подставляем функции $U»$, $U’$ и $U$ вместо $y»$, $y’$ и $y$ в данное ЛНДУ-2 $y»-3\cdot y’-18\cdot y=\left(36\cdot x+12\right)\cdot e^{3\cdot x}. $ При этом, поскольку экспонента $e^{3\cdot x} $ входит как множитель во все составляющие, то её можно опустить. Получаем:
$6\cdot A+9\cdot A\cdot x+9\cdot B-3\cdot \left(A+3\cdot A\cdot x+3\cdot B\right)-18\cdot \left(A\cdot x+B\right)=36\cdot x+12.$
Выполняем действия в левой части полученного равенства:
$-18\cdot A\cdot x+3\cdot A-18\cdot B=36\cdot x+12.$
Применяем метод НК. Получаем систему линейных уравнений с двумя неизвестными:
$-18\cdot A=36;$
$3\cdot A-18\cdot B=12.$
Решение этой системы таково: $A=-2$, $B=-1$.
ЧР $U=\left(A\cdot x+B\right)\cdot e^{3\cdot x} $ для нашей задачи выглядит следующим образом: $U=\left(-2\cdot x-1\right)\cdot e^{3\cdot x} $.
ОР $y=Y+U$ для нашей задачи выглядит следующим образом: $y=C_{1} \cdot e^{-3\cdot x} +C_{2} \cdot e^{6\cdot x} +\left(-2\cdot x-1\right)\cdot e^{3\cdot x} $.
С целью поиска ЧР, удовлетворяющего заданным начальным условиям, находим производную $y’$ ОР:
$y’=-3\cdot C_{1} \cdot e^{-3\cdot x} +6\cdot C_{2} \cdot e^{6\cdot x} -2\cdot e^{3\cdot x} +\left(-2\cdot x-1\right)\cdot 3\cdot e^{3\cdot x} .$
Подставляем в $y$ и $y’$ начальные условия $y=6$ при $x=0$ и $y’=1$ при $x=0$:
$6=C_{1} +C_{2} -1; $
$1=-3\cdot C_{1} +6\cdot C_{2} -2-3=-3\cdot C_{1} +6\cdot C_{2} -5.$
Получили систему уравнений:
$C_{1} +C_{2} =7;$
$-3\cdot C_{1} +6\cdot C_{2} =6.$
Решаем её. Находим $C_{1} $ по формуле Крамера, а $C_{2} $ определяем из первого уравнения:
$C_{1} =\frac{\left|\begin{array}{cc} {7} & {1} \\ {6} & {6} \end{array}\right|}{\left|\begin{array}{cc} {1} & {1} \\ {-3} & {6} \end{array}\right|} =\frac{7\cdot 6-6\cdot 1}{1\cdot 6-\left(-3\right)\cdot 1} =\frac{36}{9} =4; C_{2} =7-C_{1} =7-4=3.$
Таким образом, ЧР данного дифференциального уравнения имеет вид: $y=4\cdot e^{-3\cdot x} +3\cdot e^{6\cdot x} +\left(-2\cdot x-1\right)\cdot e^{3\cdot x} $.
spravochnick.ru
Тема 13. Неоднородные линейные
116 117
дифференциальные уравнения
второго порядка
с постоянными коэффициентами
13.1. Структура решения неоднородного линейного
дифференциального уравнения второго порядка
с постоянными коэффициентами
Уравнение вида
,
где pиq– вещественные числа, называется линейным неоднородным уравнением второго порядка с постоянными коэффициентами.
Общее решение этого уравнения представляет собой сумму частного решения неоднородного уравнения yч.н.и общего решения соответствующего однородного уравненияyо.о., то естьy=yч.н.+yо.о.. Это утверждение составляет содержание теоремы о структуре общего решения неоднородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
Напомним, уравнение является однородным, если f(x) равно нулю. Для того чтобы решить однородное дифференциальное уравнение, необходимо составить характеристическое уравнение. При его решении возможны следующие три случая.
Случай 1. Если корни k1,k2 различны, то общее решение однородного уравнения имеет вид:
.
Случай 2. Если k1 =k2 =k, то общее решение однородного уравнения имеет вид:
.
Случай 3. Если  ,
то общее решение однородного уравнения
имеет вид:
,
то общее решение однородного уравнения
имеет вид:
,
где 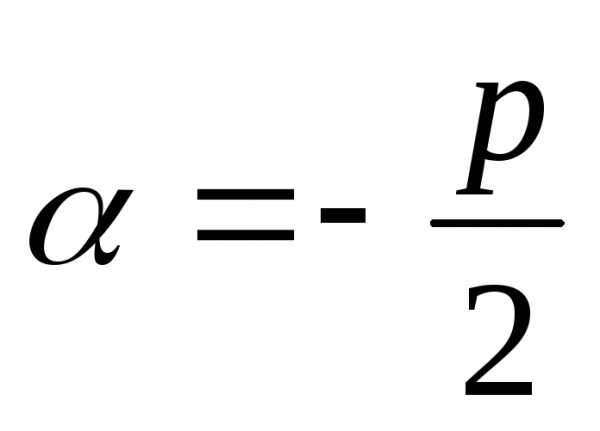 ,
,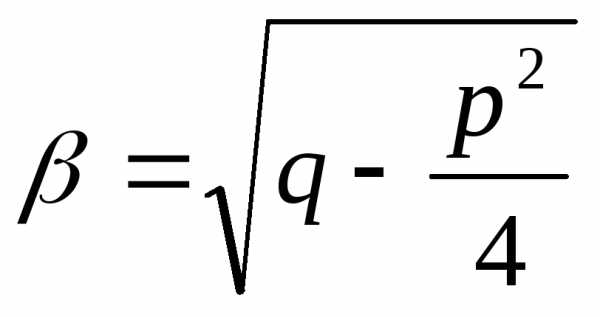 .
.
13.2. Нахождение частных решений неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
Частное решение линейного неоднородного
уравнения зависит от вида правой части
уравнения, то есть от функции  .
.
Если
,
где–данный многочлен степени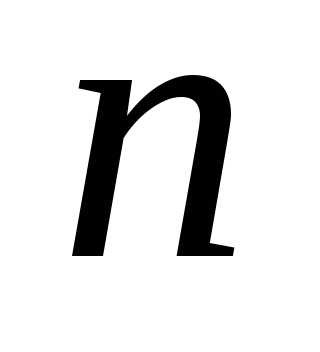 ,
то частное решение линейного неоднородного
уравнения имеет вид:
,
то частное решение линейного неоднородного
уравнения имеет вид:
,
где
– многочлен степени с неизвестными коэффициентами, которые
нужно найти,
с неизвестными коэффициентами, которые
нужно найти,
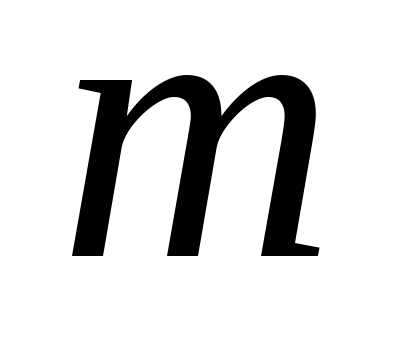 – число корней характеристического
уравнения, равных нулю.
– число корней характеристического
уравнения, равных нулю.
Если , то частное решение линейного неоднородного уравнения имеет вид:
,
где  – многочлен степени
– многочлен степени с неизвестными коэффициентами,
с неизвестными коэффициентами,
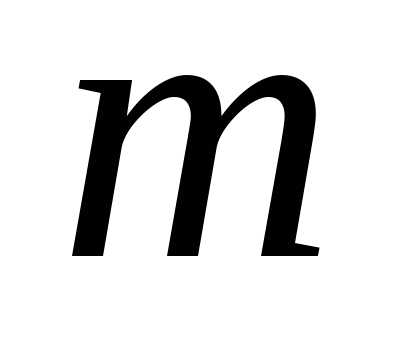 – кратность корня характеристического
уравнения
– кратность корня характеристического
уравнения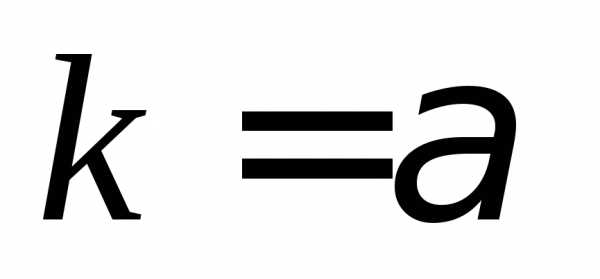 .
.
Если
,
где ,
, и
и – известные числа, то частное решение
линейного неоднородного уравнения
имеет вид:
– известные числа, то частное решение
линейного неоднородного уравнения
имеет вид:
где  ,
, – неизвестные коэффициенты,
– неизвестные коэффициенты,
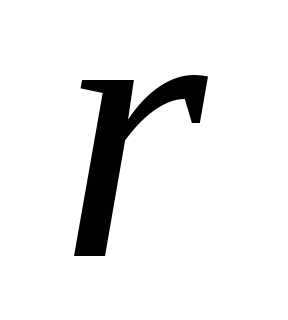 – число корней характеристического
уравнения, равных
– число корней характеристического
уравнения, равных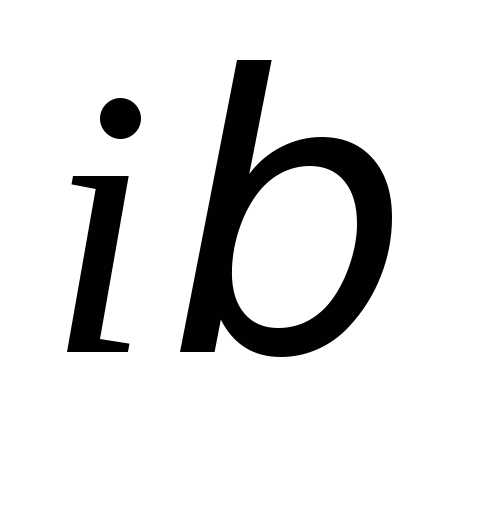 .
.
13.3. Примеры решений неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
Рассмотрим примеры решения неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Пример 1.Найти общее решение уравнения.
Решение.Характеристическое уравнениеимеет корниk1 = 0,k2 = 1. Общее решение однородного уравнения тогда имеет вид:
.
Найдем частное решение неоднородного уравнения. Так как 0 является корнем характеристического уравнения кратности т = 1, то частное решение имеет вид:
.
Найдем  и
и :,
:,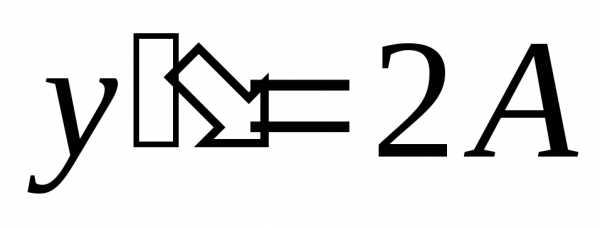 .
.
Теперь подставим производные в исходное уравнение, получим:
.
Приравнивая коэффициенты при одинаковых
степенях 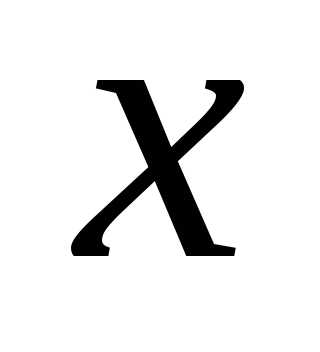 ,
получим систему алгебраических уравнений:
,
получим систему алгебраических уравнений:

Решая систему, находим, что 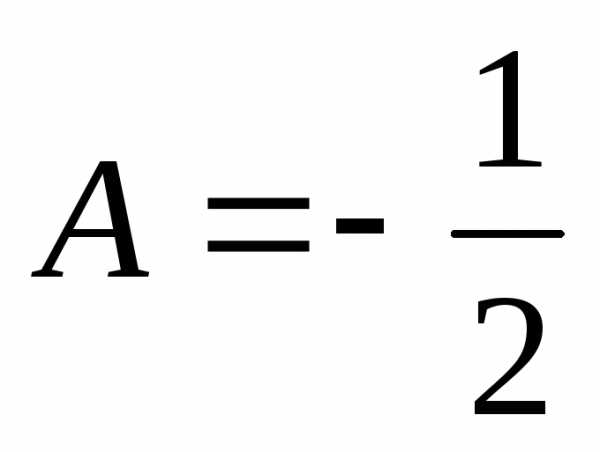 ,
,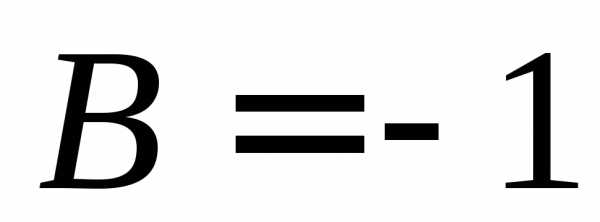 .
Итак,.
Тогда общее решение неоднородного
уравнения примет вид:
.
Итак,.
Тогда общее решение неоднородного
уравнения примет вид:
.
Пример 2.Найти общее решение уравнения.
Решение. Характеристическое уравнение имеет вид:, которое имеет корниk1 = 2,k2 = 3. Следовательно, общее решение однородного уравнения примет вид:
.
Так как  = 1 не является корнем характеристического
уравнения, то частное решение неоднородного
уравнения необходимо искать в виде:.
Подставив
ив исходное уравнение, получим:
= 1 не является корнем характеристического
уравнения, то частное решение неоднородного
уравнения необходимо искать в виде:.
Подставив
ив исходное уравнение, получим:
;
;
;
.
Приравняем коэффициенты при одинаковых
степенях 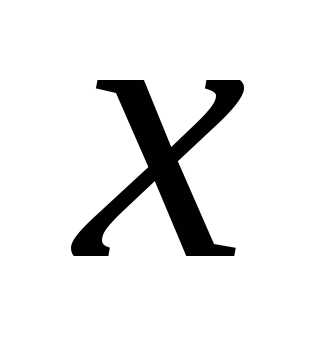 ,
получим систему уравнений:
,
получим систему уравнений:

Откуда находим, что 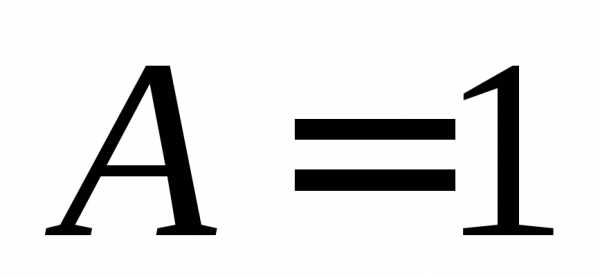 ,
,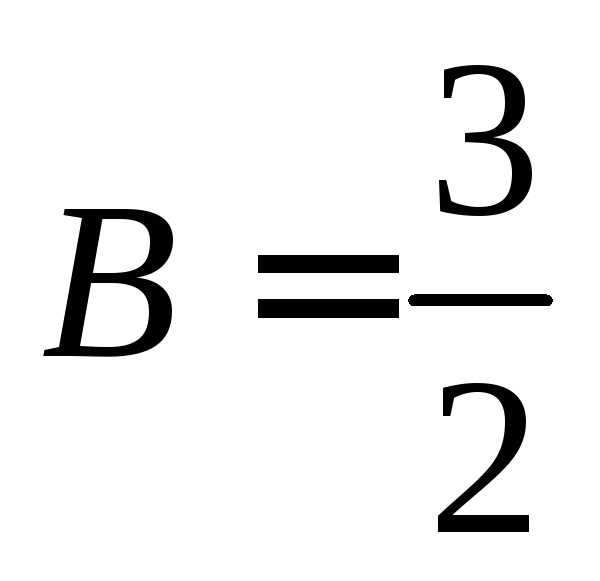 .
.
Находим общее решение неоднородного уравнения:
Пример 3.Найти частное решение
уравнения,
удовлетворяющее начальным условиям ,
,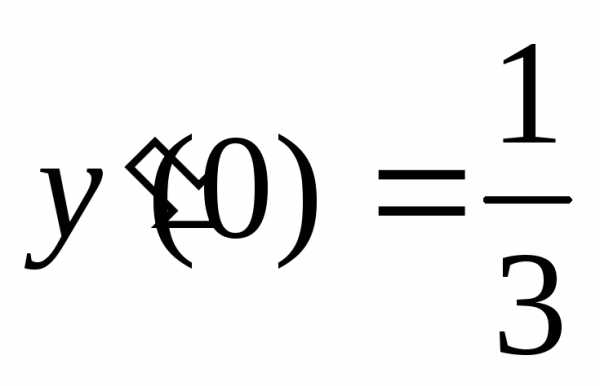 .
.
Решение. Характеристическое уравнениеk2+ 1 = 0 действительных
корней не имеет. Найдем и
и :
:
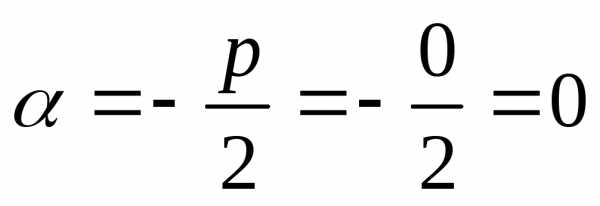 ,.
,.
Общее решение однородного уравнения имеет вид:
.
Найдем частное решение неоднородного уравнения. Так как 2 не является корнем характеристического уравнения, то
;
;
.
Подставим  и
и в исходное уравнение, получим:
в исходное уравнение, получим:
;
.
Из последнего равенства получим систему уравнений:
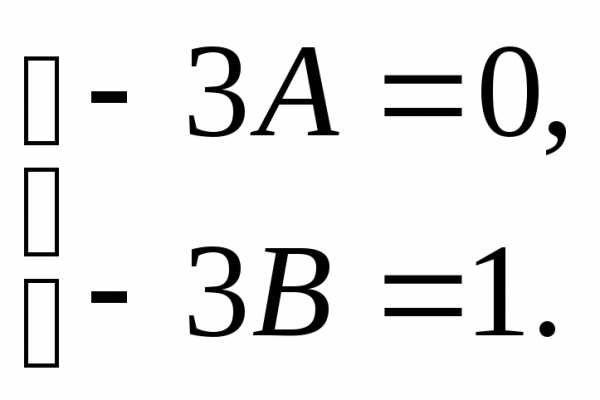
Откуда следует, что 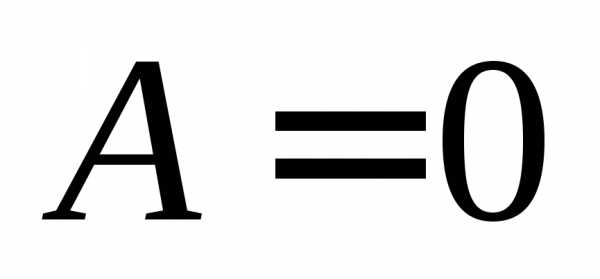 ,
,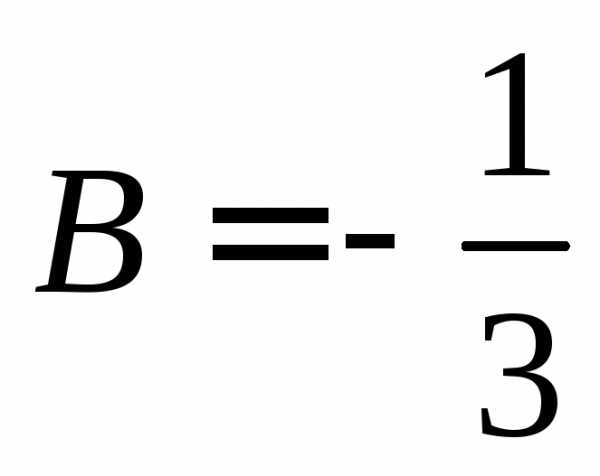 .
.
Тогда общее решение неоднородного уравнения имеет вид:
.
Для того чтобы найти частное решение исходного уравнения, подставим начальные условия в полученное решение. Имеем:
,.
,
,.
Тогда получаем, что частное решение,
удовлетворяющее начальным условиям 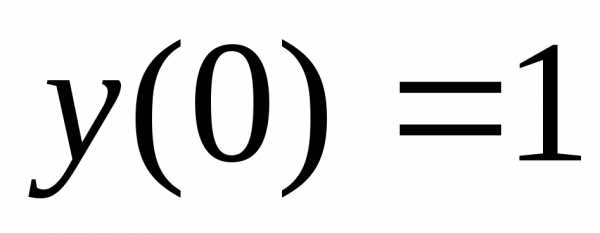 ,
,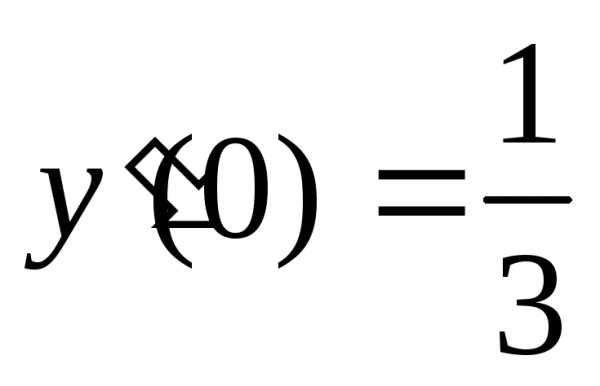 ,
имеет вид:
,
имеет вид:
.
studfiles.net
Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами (лнду)
Скачать с Depositfiles
ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 2-го ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (ЛНДУ)
Такие уравнения имеют вид:
(1)
Структура общего решения уравнения (1) определяется следующей теоремой:
Теорема 1 (о структуре общего решения ЛНДУ)
Общее решение неоднородного уравнения (1) представляется как сумма какого-нибудь частного решения этого уравнения учн(х) и общего решения уоо(х) соответствующего однородного уравнения:
(2)
Теорема 2
Пусть неоднородное уравнение таково, что правая часть его есть сумма двух функций f1(x) и f2(x):
(3)
Если при этом функция у1(х) является частным решением уравнения
(4)
а у2(х) – частным решением уравнения
(5)
то функция у(х)= у1(х)+ у2(х) будет частным решением уравнения (3)
Доказательство: Подставим у(х) в уравнение (3):
= ч.т.д.
1. Пусть правая часть уравнения (1) имеет вид 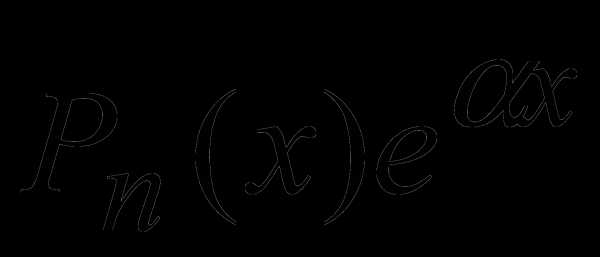 , где
, где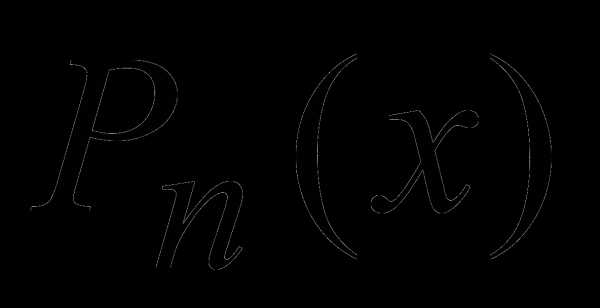 – многочлен n-ной степени:
– многочлен n-ной степени:
(6)
Тогда возможны следующие случаи:
а) Число не является корнем характеристического уравнения
(7)
Тогда частное решение уравнения (6) будем искать в виде
(8)
Подставим его в (6) с учетом вида производных
и сокращая на  , получим:
, получим:
(9)
Если  не является корнем характеристического уравнения, то и слева в уравнении (9) – полином n-ного порядка, приравнивая коэффициенты при равных степенях х слева и справа в (9), получим n+1 уравнение с n+1 неизвестной , найдем их и получим частное решение (8).
не является корнем характеристического уравнения, то и слева в уравнении (9) – полином n-ного порядка, приравнивая коэффициенты при равных степенях х слева и справа в (9), получим n+1 уравнение с n+1 неизвестной , найдем их и получим частное решение (8).
б) Число  есть однократный корень характеристического уравнения (7) (резонанс).
есть однократный корень характеристического уравнения (7) (резонанс).
Тогда в уравнении (9) не будет  , и слева — полином (n+1)-й степени, а справа – n-й степени, и мы не сможем его найти.
, и слева — полином (n+1)-й степени, а справа – n-й степени, и мы не сможем его найти.
В этом случае частное решение ищется в виде
(10)
в) Число  есть двукратный корень характеристического уравнения,
есть двукратный корень характеристического уравнения, 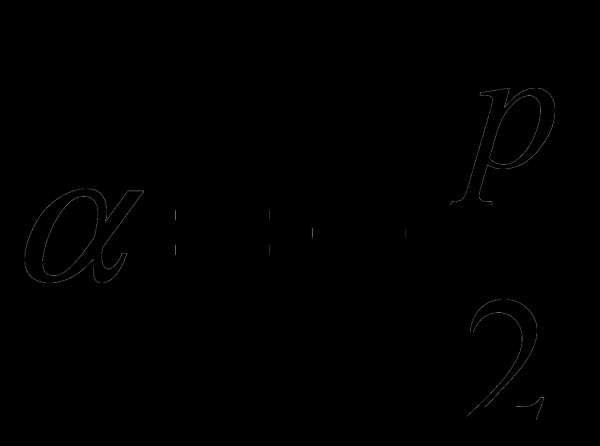 .
.
Тогда в уравнении (9) и слева- полином (n-2) степени, а справа- n-й степени. Частное решение будем искать в виде
(11)
Пример 1
Найти общее решение уравнения .
Характеристическое уравнение имеет корни  ;
;  .
.
Общее решение однородного уравнения .
Правая часть в данном случае: , где =0, а т.к. ноль не является корнем характеристического уравнения, то ищем частное решение в виде многочлена первой степени: . Для нахождения коэффициентов  подставим это решение и его производные ; в уравнение:
подставим это решение и его производные ; в уравнение: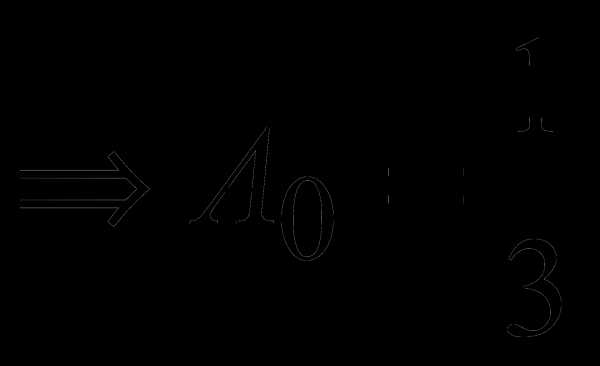 ;
; 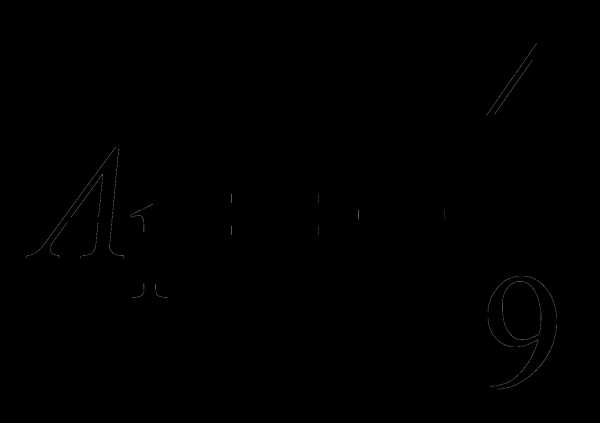 ;
;
Итак, частное решение имеет вид: 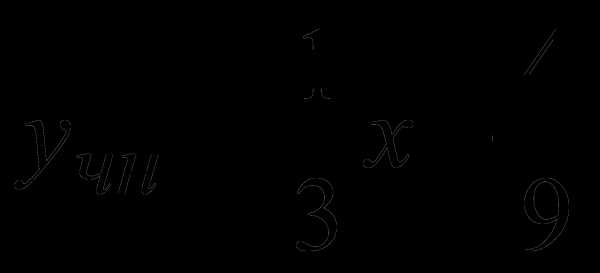 .
.
Общее решение неоднородного уравнения:
.
Пример 2 Найти общее решение уравнения:
Корни характеристического уравнения:  ;
;
; 3 – не является корнем характеристического уравнения- резонанса с правой частью нет, частное решение ищем в виде:
; находим  ;
; 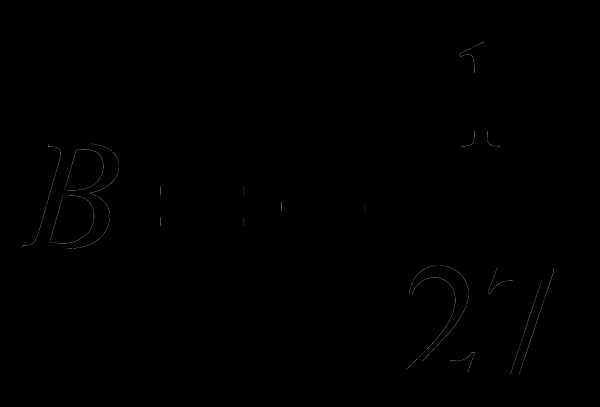 ;
;  .
.
.
Пример 3 ;
;  ;
; 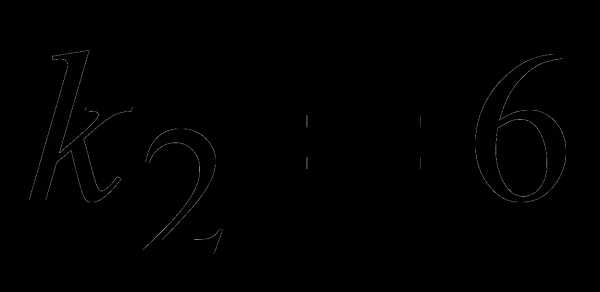 ;
;
Общее решение однородного уравнения: ;
Однократный корень  даёт резонанс
даёт резонанс
; находим  ;
; 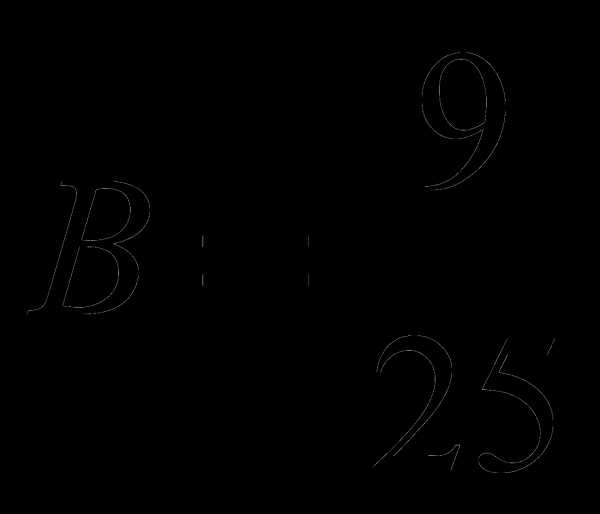 ;
;
.
2. Пусть уравнение (1) имеет вид:
(12)
где — многочлены. Рассмотрим два случая:
а) Если число 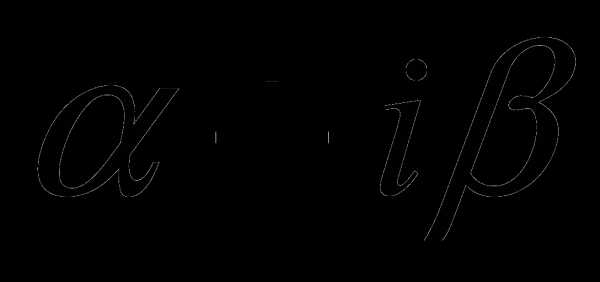 не является корнем характеристического уравнения, то частное решение уравнения (12) надо искать в виде
не является корнем характеристического уравнения, то частное решение уравнения (12) надо искать в виде
(13)
где – многочлены степени, равной наивысшей степени многочленов  и
и 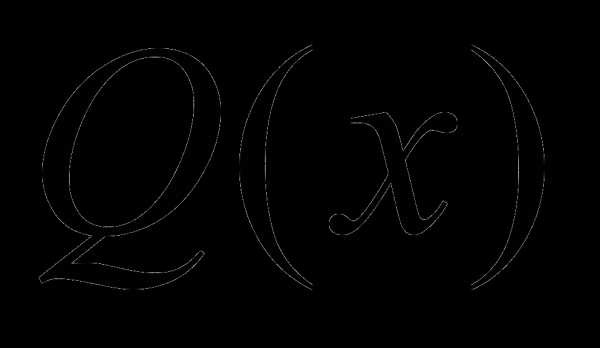 .
.
б) Если число  есть корень характеристического уравнения, то частное решение ищем в виде
есть корень характеристического уравнения, то частное решение ищем в виде
(14)
Важный частный случай: если , где M, N— постоянные числа, т.е.
(15)
а) Если число 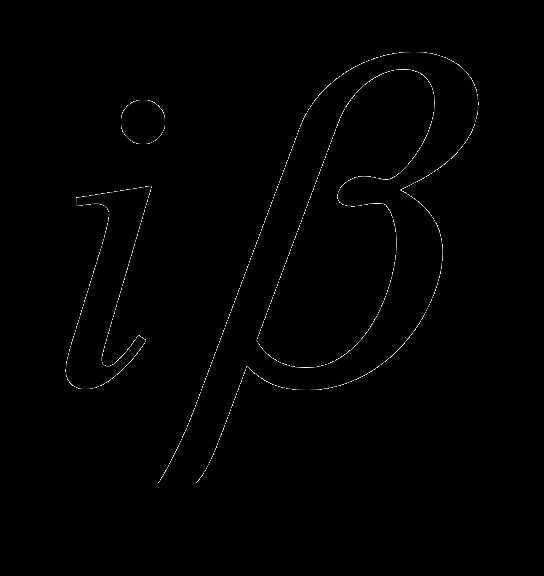 — не является корнем характеристического уравнения, то частное решение ищем в виде
— не является корнем характеристического уравнения, то частное решение ищем в виде
(16)
б) Если  — корень характеристического уравнения, то частное решение уравнения (15) ищем в виде
— корень характеристического уравнения, то частное решение уравнения (15) ищем в виде
(17)
Пример 4
Найти общее решение уравнения: ;
Здесь ; ,
; ;  ;
; ;
;
.
Пример 5 Найти общее решение уравнения ;
Корни характеристического уравнения:  ; корень
; корень  — даёт резонанс с правой частью, ; ;
— даёт резонанс с правой частью, ; ; 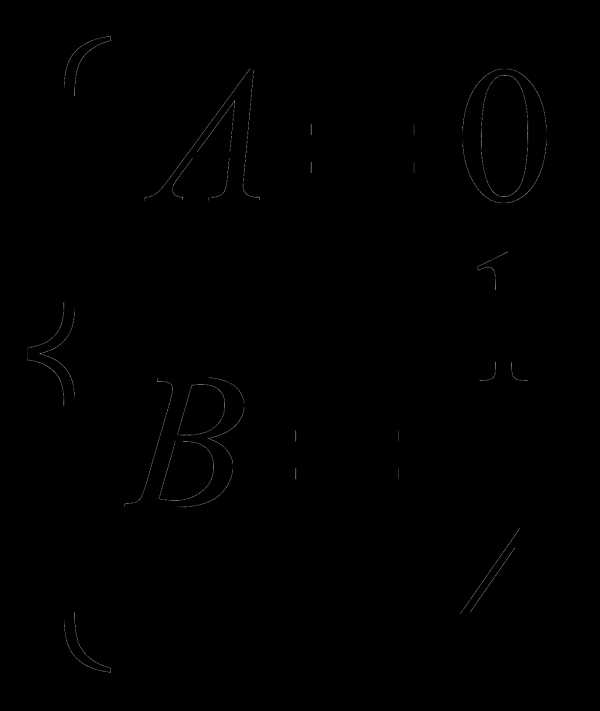
.
Пример 6 ;  ;
; 
Правой части соответствовал бы корень  — но он не является корнем характеристического уравнения, резонанса нет:
— но он не является корнем характеристического уравнения, резонанса нет:
; ; 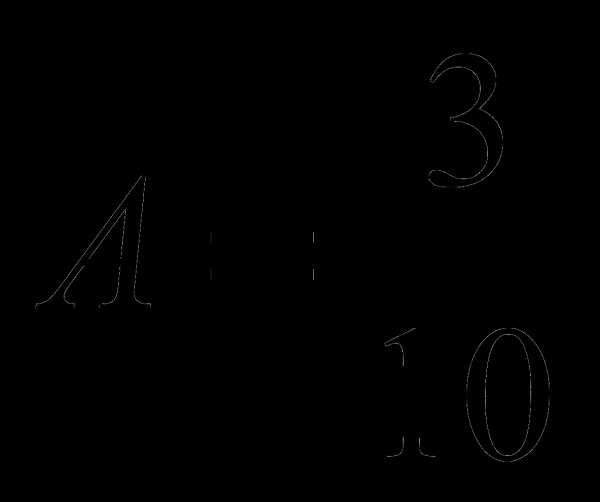 ;
; 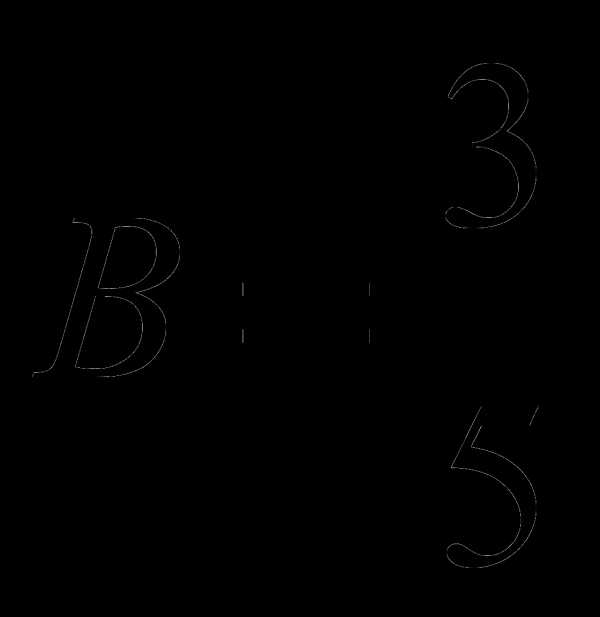 ;
;
.
greleon.ru
§7. Решение лнду 2-го порядка с постоянными коэффициентами со специальной правой частью.
Пусть в уравнении (6.1) коэффициенты постоянны, т.е. уравнение имеет вид:
f(x) (7.1)
где .
Рассмотрим метод отыскания частного решения уравнения (7.1) в случае, когда правая часть f(x) имеет специальный вид. Это метод называется методом неопределенных коэффициентов и состоит в подборе частного решения в зависимости от вида правой части f(x). Рассмотрим правые части следующего вида:
f(x) , где – многочлен степени , причем некоторые коэффициенты, кроме , могут равняться нулю. Укажем вид, в котором надо брать частное решение в этом случае.
Если число не является корнем характеристического уравнения для уравнения (5.1), то частное решение записываем в виде: , где – неопределенные коэффициенты, которые подлежат определению методом неопределенных коэффициентов.
Пример 1. Найти общее решение уравнения .
Решение.
Для уравнения составляем характеристическое уравнение: . Откуда получаем , . Следовательно, общее решение однородного уравнения есть . Правая часть заданного уравнения f(x) имеет специальный вид (случай 1), причем не является корнем характеристического уравнения, поэтому частное решение ищем в виде: , где – неопределенные коэффициенты. Найдем производные первого и второго порядков и подставим их в заданное уравнение:
.
Обе части сокращаем на и приравниваем коэффициенты при одинаковых степенях в левой и правой частях равенства
Из полученной системы уравнений находим: . Тогда , а общее решение заданного уравнения есть:
.
Если является корнем кратности соответствующего характеристического уравнения, то частное решение ищем в виде:
,
где – неопределенные коэффициенты.
Пример 2. Решить уравнение .
Решение.
Соответствующее характеристическое уравнение имеет вид:
, откуда , . Тогда общее решение однородного уравнения есть: .
Правая часть заданного уравнения имеет специальный вид (случай 1). Так как является корнем характеристического уравнения кратности , то частное решение ищется в виде:
. Находим неопределенные коэффициенты методом, изложенным в примере 1. В результате получаем . Окончательно имеем следующее выражение для общего решения:
.
Правая часть f(x) , где хотя бы одно из чисел и отлично от нуля. Укажем вид частного решения в этом случае.
Если число не является корнем характеристического уравнения для уравнения (5.1), то частное решение ищем в виде:
,
где – неопределенные коэффициенты.
Если число является корнем характеристического уравнения для уравнения (5.1), причем его кратность , то записываем частное решение в виде:
,
где – неопределенные коэффициенты.
Пример 3. Решить уравнение .
Решение.
Корни характеристического уравнения для уравнения будут , . Тогда общее решение этого лоду: .
Правая часть заданного в примере 3 уравнения имеет специальный вид: f(x) , где , а . Число является корнем характеристического уравнения кратности , поэтому частное решение лнду имеет вид: .
Для определения и находим , и подставляем в заданное уравнение:
.
Приводя подобные члены, приравнивая коэффициенты при , , получаем следующую систему: , отсюда .
Окончательно общее решение заданного уравнения имеет вид: .
f(x) , где и — многочлены степени и соответственно, причем один из этих многочленов может равняться нулю. Укажем вид частного решения в этом общем случае.
Если число не является корнем характеристического уравнения для уравнения (5.1), то вид частного решения будет:
, (7.2)
где – неопределенные коэффициенты, а .
Если число является корнем характеристического уравнения для уравнения (5.1) кратности , то частное решение лнду будет иметь вид:
, (7.3)
т.е. частное решение вида (7.2) надо умножить на . В выражении (7.3) — многочлены с неопределенными коэффициентами, причем их степень .
Пример 4. Указать вид частного решения для уравнения
.
Решение.
Характеристическое уравнение имеет вид: . Его корни: , . Общее решение лоду имеет вид:
.
Правая часть заданного уравнения имеет специальный вид (случай 3): f(x) . Число является корнем характеристического уравнения кратности . Коэффициент при есть многочлен первой степени, а при — нулевой степени, поэтому степень многочленов с неопределенными коэффициентами надо брать . Итак, вид частного решения:
.
Далее коэффициенты могут быть определены по методу неопределенных коэффициентов.
Замечание. Если правая часть уравнения (7.1) есть сумма двух функций f(x) = f1(x) + f2(x), где каждая из f1(x), f2(x) имеют специальный вид (случаи 1-3), то частное решение подбирается в виде суммы: , где есть частное решение для уравнения с правой частью f1(x), а есть частное решение для уравнения с f2(x). Аналогично находятся частные решения в случае, когда правая часть есть алгебраическая сумма конечного числа функций специального вида, рассмотренного в случаях 1-3.
studfiles.net
