Скалярное произведение векторов
Скалярное произведение векторов (далее в тексте СП). Дорогие друзья! В состав экзамена по математике входит группа задач на решение векторов. Некоторые задачи мы уже рассмотрели. Можете посмотреть их в категории «Векторы». В целом, теория векторов несложная, главное последовательно её изучить. Вычисления и действия с векторами в школьном курсе математики просты, формулы не сложные. Загляните в справочник. В этой статье мы разберём задачи на СП векторов (входят в ЕГЭ). Теперь «погружение» в теорию:
Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты его начала
И ещё:
*Длина вектора (модуль) определяется следующим образом:
Данные формулы необходимо запомнить!!!
Покажем угол между векторами:
Понятно, что он может изменяться в пределах от 0 до 1800 (или в радианах от 0 до Пи).
Можем сделать некоторые выводы о знаке скалярного произведения. Длины векторов имеют положительное значение, это очевидно. Значит знак скалярного произведения зависит от значения косинуса угла между векторами.
Возможны случаи:
1. Если угол между векторами острый (от 00 до 900), то косинус угла будет иметь положительное значение.
2. Если угол между векторами тупой (от 900 до 1800), то косинус угла будет иметь отрицательное значение.
*При нуле градусов, то есть когда векторы имеют одинаковое направление, косинус равен единице и соответственно результат будет положительным.
При 180о, то есть когда векторы имеют противоположные направления, косинус равен минус единице, и соответственно результат будет отрицательным.
Теперь ВАЖНЫЙ МОМЕНТ!
При 90о, то есть когда векторы перпендикулярны друг другу, косинус равен нулю, а значит и СП равно нулю. Этот факт (следствие, вывод) используется при решение многих задач, где речь идёт о взаимном расположении векторов, в том числе и в задачах входящих в открытый банк заданий по математике.
Сформулируем утверждение: скалярное произведение равно нулю тогда и только тогда, когда данные векторы лежат на перпендикулярных прямых.
Итак, формулы СП векторов:
Если известны координаты векторов или координаты точек их начал и концов, то всегда сможем найти угол между векторами:
Рассмотрим задачи:
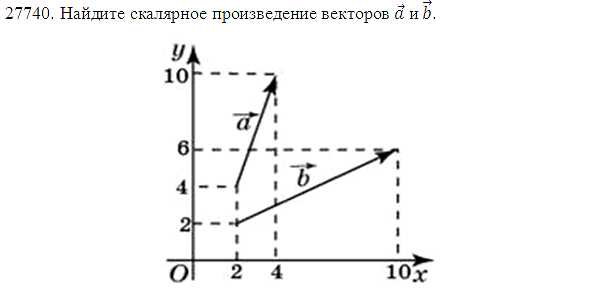
27724 Найдите скалярное произведение векторов a и b.

Скалярное произведение векторов мы можем найти по одной из двух формул:
Угол между векторами неизвестен, но мы без труда можем найти координаты векторов и далее воспользоваться первой формулой. Так как начала обоих векторов совпадают с началом координат, то координаты данных векторов равны координатам их концов, то есть
Как найти координаты вектора изложено в этой статье.
Вычисляем:
Ответ: 40
Найдём координаты векторов и воспользуемся формулой:
Чтобы найти координаты вектора необходимо из координат конца вектора вычесть соответствующие координаты его начала, значит
Вычисляем скалярное произведение:
Ответ: 40
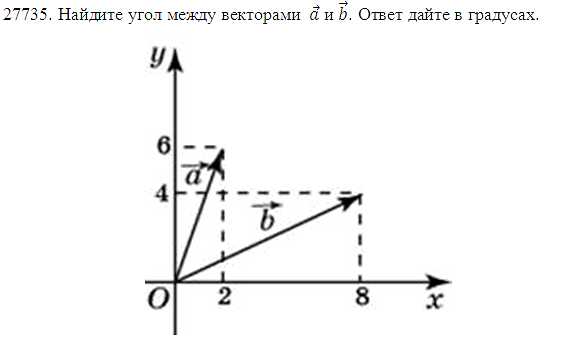
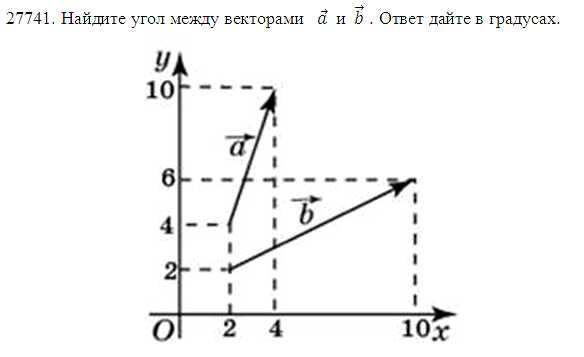
Найдите угол между векторами a и b. Ответ дайте в градусах.
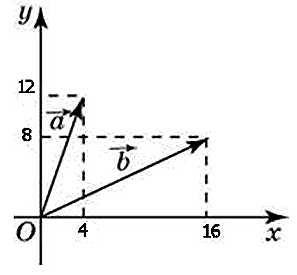
Пусть координаты векторов имеют вид:
Для нахождения угла между векторами используем формулу скалярного произведения векторов:
Косинус угла между векторами:
Следовательно:
Координаты данных векторов равны:
Подставим их в формулу:
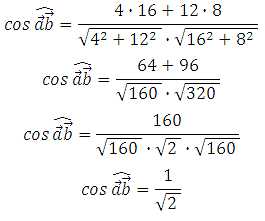
Угол между векторами равен 45 градусам.
Ответ: 45
Посмотреть решение
Посмотреть решение
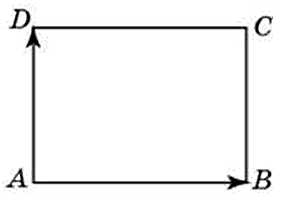
27710. Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов АВ и AD.
Посмотреть решение
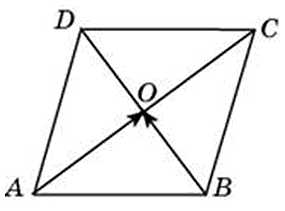
27719. Диагонали ромба ABCD пересекаются в точке О и равны 12 и 16. Найдите скалярное произведение векторов AB и BO.
Посмотреть решение
27719. Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов AB и АС.

Посмотреть решение
На этом всё! Успехов вам!
С уважением, Александр Крутицких.
На уроке физкультуры: — Так, парни, кто из вас курит? Честно! Не врать! Так. … значит, ты… и ты. … Понятно… Значит, так: мы с вами покурим, остальным — пять кругов по стадиону.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Скалярное произведение векторов
Скалярным произведением ненулевых векторов x и y называется произведение
| (1) |
где |·|-модуль вектора, φ -угол между векторами.
Если x=0 или y=0, то скалярное произведение равно нулю.
Пусть в n-мерном пространстве задан ортонормированный базис
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пусть заданы векторы
тогда скалярное произведение (x,y) векторов x и y определяется соотношением:
| (2) |
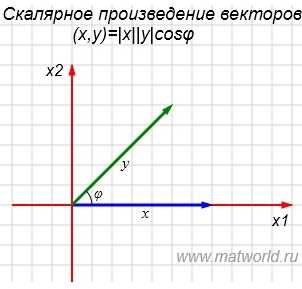
Рис. 1
На рисунке Рис. 1 в двухмерном пространстве представлены векторы
Для вычисления скалярного произведения методом (1), вычислим нормы векторов x и y:
Учитывая что , получим:
Теперь вычислим скалярное произведение векторов x и y используя выражение (2):
Получили одинаковые результаты, но посдедний вариант вычисления проще и не требует знания угла между векторами.
Вариант 2. Начальные точки векторов произвольные.
Пусть заданы векторы x=AB и y=CD, где ,,,.
Переместим векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками):
где
Из выражения (1) видно, что скалярное произведение векторов x и y зависит только от нормы векторов и от угла между ними. Так как |x’|=|x| , |y’|=|y| и угол между векторами x’ и y’ равен углу между векторами x и y, следовательно
Учитывая (2) получаем:
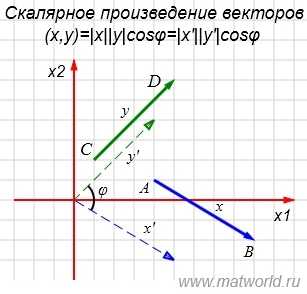
Рис. 2
На рисунке Рис. 2 в двухмерном пространстве представлены векторы x=AB и y=CD, где A(4,1), B(9,-2), C(1,2), D(5,6).
Из выражения (1) видно, что скалярное произведение векторов x и y зависит только от нормы векторов и от угла между ними. Переместим параллельно векторы так, что их начальные точки совпали с началом координат. Тогда x’=(9-4, -2-1)=(5, -3), y’=(5-1, 6-2)=(4,4), |x’|=|x| , |y’
- Скалярное произведение обладает следующими свойствами:
- 1. (x,y)=(y,x) ( коммутативность) .
- 2. (x,y+z)=(x,y)+(x,z) (дистрибутивность относительно сложения векторов).
- 3. λ(x,y)=(λx,y)=(x,λy) (ассоциативность относительно умножения на число).
matworld.ru
Скалярное произведение (a,b)
Скалярным произведением двух векторов (a, b)
называют число равное сумме попарных произведений координат векторов с каждой оси, т.е.
Из формулы видно что вычисление скалярного произведения — это самое простое занятие, которое может выполнить любой школьник.
Например, если есть два вектора в пространстве с координатами
то их скалярное произведение равно 6
В математике есть еще одно определение скалярного произведения.
Согласно второму определению скалярное произведение двух векторов равно числу, которое получают умножением длин векторов (их модулей) на косинус угла между ними
Данное определение используют не столько для нахождения скалярного произведения, как для исчисления значение косинуса угла и уже из таблиц — самого угла между векторами. Из определения получают удобную формулу для вычисления угла между векторами
или в координатной форме
Приведем примеры вычисления скалярного произведения для трехмерных векторов.
———————————————
Примеры.
Задано векторы и . Вычислить их скалярное произведение, если
1)
2)
3)
4)
5)
6)
7)
Решение. Выполним вычисления согласно формул
1)
2)
3)
4)
5)
6)
7)
————————————
Из примеров Вы убедились, что нахождение скалярного произведения попарным перемножением координат векторов, а затем их суммированием не является сложным. В следующих статьях будут рассмотрены другие стороны скалярного произведения и его применение к векторному анализу.
Посмотреть материалы:
yukhym.com
Свойства скалярного произведения векторов
ОПРЕДЕЛЕНИЕ Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:
Замечание. Если хотя бы один из двух векторов нулевой, то их скалярное произведение равно нулю.
Свойства скалярного произведения векторов
1. Скалярное произведение вектора самого на себя называется скалярным квадратом:
Скалярный квадрат вектора равен квадрату его модуля:
2. .
3. .
4. .
5. Длина вектора равна
6. Величина угла (а точнее косинус этого угла) между ненулевыми векторами и равна частному скалярного произведения этих векторов и произведения их длин:
7. Два ненулевых вектора и ортогональны (перпендикулярны) тогда и только тогда, когда их скалярное произведение равно нулю:
8. Угол между двумя ненулевыми векторами и является острым тогда и только тогда, когда их скалярное произведение положительно; и является тупым – когда скалярное произведение отрицательно.
9. Длина проекции вектора на ось, образованную вектором , равна скалярному произведению этих векторов, деленному на модуль вектора :
10. Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:
Примеры решения задач
ПРИМЕР| Задание | Найти модуль вектора , если |
| Решение | Модуль вектора равен корню квадратному из скалярного квадрата этого вектора:
|
| Ответ |
| Задание | Найти скалярное произведение векторов и |
| Решение | Искомое скалярное произведение равно сумме произведений соответствующих координат рассматриваемых векторов, то есть
|
| Ответ |
ru.solverbook.com
Скалярное произведение двух векторов и его свойства
Определение. Скалярным произведением двух векторов  и
и называется
число, равное произведению модулей
векторов
называется
число, равное произведению модулей
векторов и
и на
косинус угла между ними.
на
косинус угла между ними.
Скалярное
произведение векторов  и
и обозначают
обозначают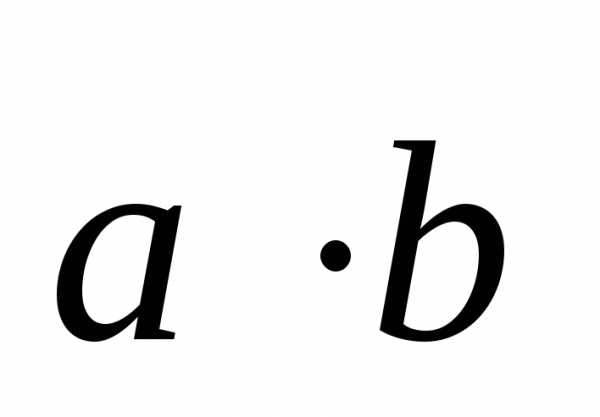
 .
.Итак, по определению
,
где  —
угол между векторами
—
угол между векторами та
та .
.
Если хотя бы один из векторов нулевой, то угол не определен и скалярное произведение по определению считают равным нулю.
Поскольку по формуле

то формулу скалярного произведения можно записать еще и таким образом:
или
.
Таким образом, скалярное произведение двух векторов равно произведению модуля одного из векторов на проекцию второго вектора на направление первого.Скалярное произведение имеет следующие свойства:
1.Скалярное произведение коммутативно, то есть для любых векторов . (2.14)
2.
,
т.е. для произвольного вектора его
скалярный квадрат равняется квадрату
модуля этого вектора. Отсюда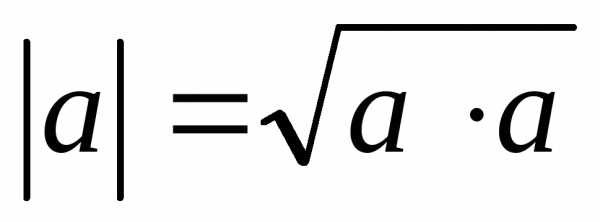 . (2.15)
. (2.15)
3. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них равен нулю.
4. Скалярное произведение ассоциативно относительно скалярного множителя, то есть. (2.16)
5.
Скалярное произведение дистрибутивный
относительно сложения, то есть для
произвольных трех векторов 
.
6. Векторы ортонормального базиса удовлетворяют соотношениям:
,
.
Рассмотрим
теперь два вектора  и
и ,
которые заданы координатами в
прямоугольной системе координат:;,
,
которые заданы координатами в
прямоугольной системе координат:;,
Т.е.,.
Тогда, пользуясь перечисленными свойствами скалярного произведения, получим,
, скалярное произведение двух векторов в ортонормальном базисе равно сумме произведений их соответствующих координат.
, модуль вектора равен корню квадратному из суммы квадратов его координат.
Косинус
угла между двумя векторами 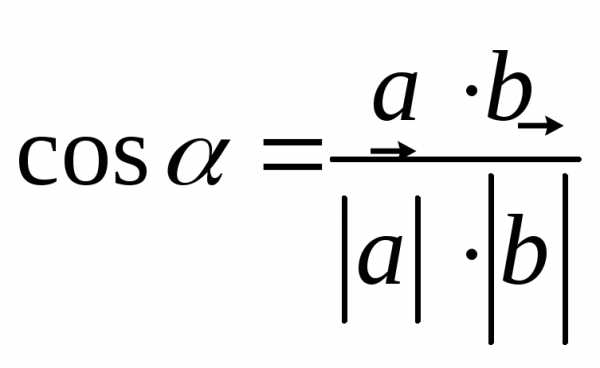 .
.
Для ортонормального базиса получим:
и условие ортогональности двух векторов приобретает вид: .
Если 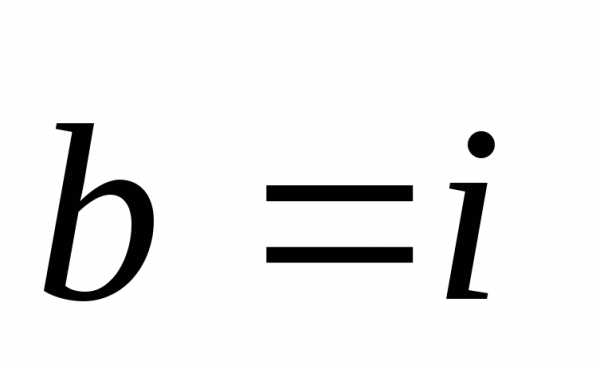 ,
,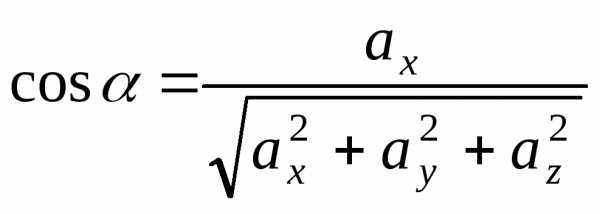 ,
,
при 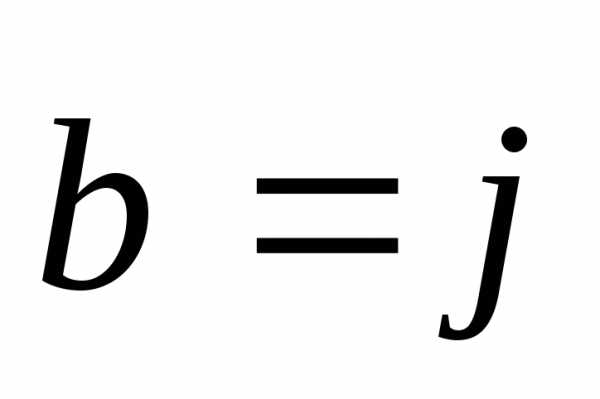
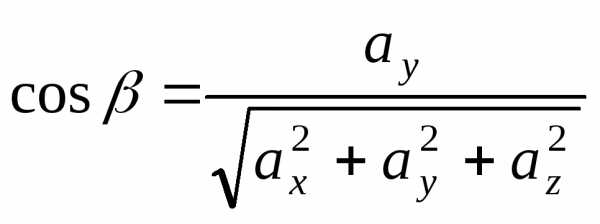 ,
,
при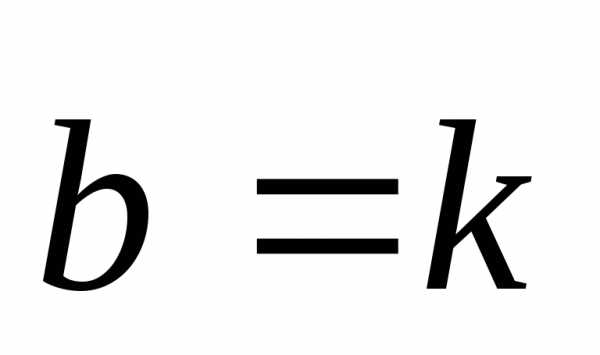
 .
.
Векторное произведение двух векторов, его свойства
Определение
2.21. Векторным произведением вектора  на вектор
на вектор называется вектор
называется вектор
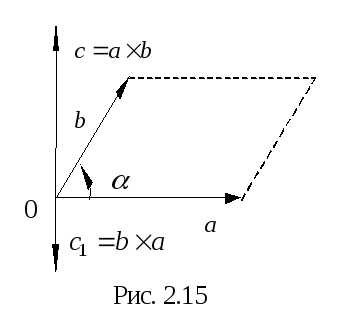 2)
вектор
2)
вектор  перпендикулярен к плоскости, в которой
лежат векторы
перпендикулярен к плоскости, в которой
лежат векторы и
и ,
т.е.
,
т.е. и
и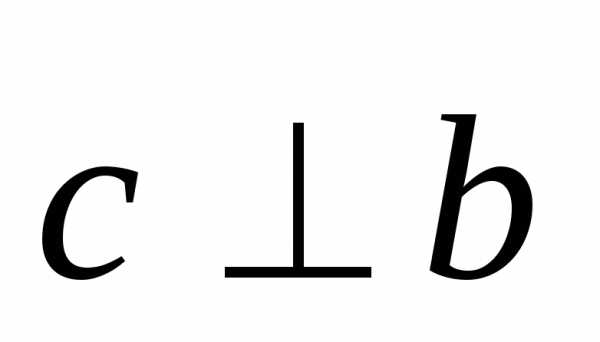 ;
;
3)
вектор  направлен
таким образом, чтобы кратчайший поворот
от вектора
направлен
таким образом, чтобы кратчайший поворот
от вектора к вектору
к вектору осуществлялся против часовой стрелки,
если смотреть на него из конца вектора
осуществлялся против часовой стрелки,
если смотреть на него из конца вектора .
.
Векторное
произведение векторов  и
и обозначается символом
обозначается символом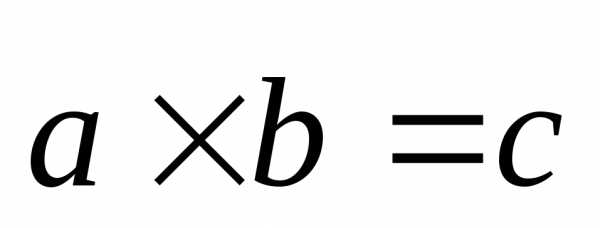 или
или .
.
Из определения вытекает, что .Свойства:
1) — антикоммутативность;
2) — ассоциативность относительно скалярного множителя;
3) — дистрибутивность относительно сложения;
4)  означает коллинеарность векторов
означает коллинеарность векторов и
и .
.
Для
векторного произведения основных ортов 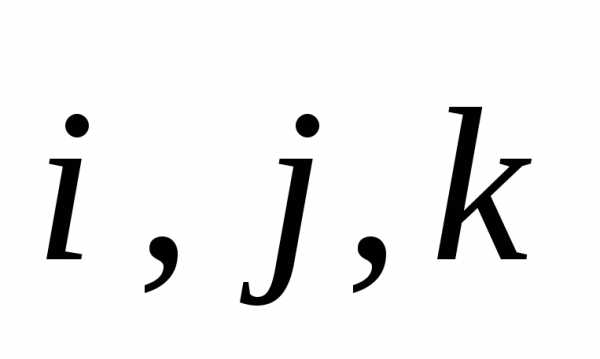 справедлива такая таблица (табл.2.1).
справедлива такая таблица (табл.2.1).
Таблица 2.1
С
использованием этой таблицы можно
доказать, что если векторы  и
и заданные своими координатами в
прямоугольной системе координатт.е.
заданные своими координатами в
прямоугольной системе координатт.е.
; ,
то
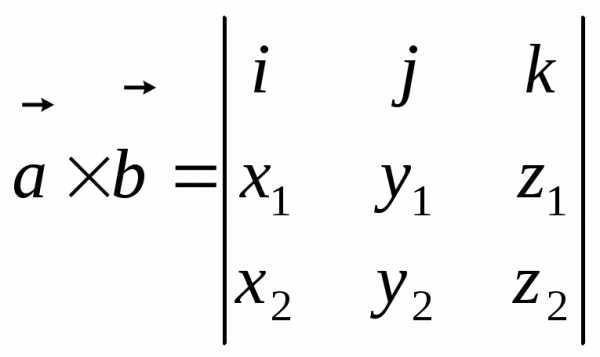 .
.
Если  и
и коллинеарны,
то
коллинеарны,
то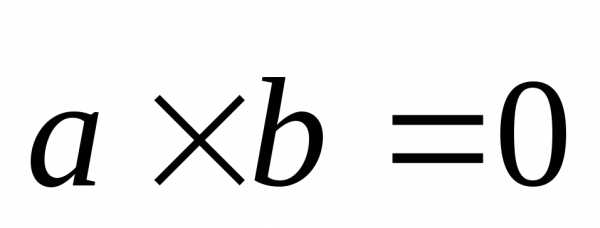 и из (2.31) получим, что
и из (2.31) получим, что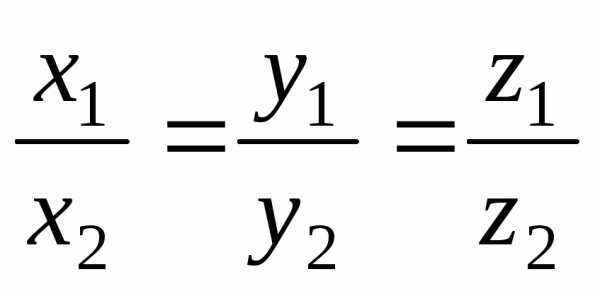 ,
—
условие коллинеарности векторов.
,
—
условие коллинеарности векторов.
Векторное
произведение может использоваться для
вычисления площади параллелограмма, а
значит, треугольника и любого плоского
многоугольника, а также для вычисления
момента силы. В случае, когда тело
неподвижно закреплено в т. ,
а в т.
,
а в т. этого тела приложена сила
этого тела приложена сила ,
тогда момент силы,
а величина момента равна
,
тогда момент силы,
а величина момента равна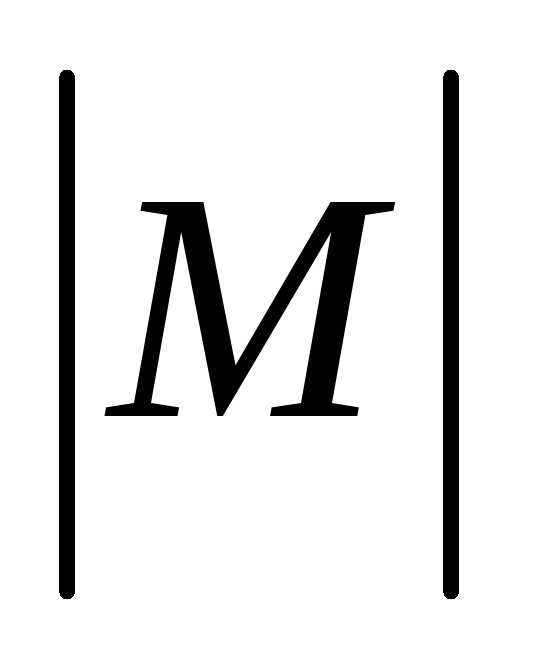 .
.
Пример Сила 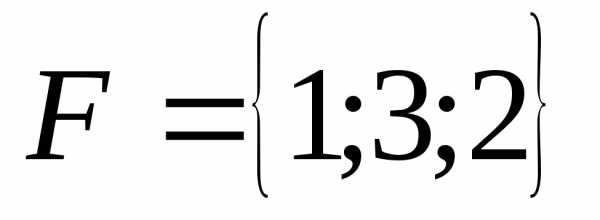 приложена к точке
приложена к точке .
Определить момент этой силы относительно
начала координат.
.
Определить момент этой силы относительно
начала координат.
studfiles.net
Скалярное произведение векторов — GrandKid
Скалярное произведение векторов. Давайте еще немного займемся свойствами векторов. Легко понять, что длина шага в пространстве одинакова во всех координатных схемах. Следовательно, если какому-то шагу r соответствуют составляющие х, у, z в одной системе координат и составляющие х’, у’, z’ в другой системе, то расстояние r = |r| одно и то же в обеих системах. Сначала мы, конечно, должны вывести два расстояния
а затем проверить, что эти обе величины равны. Чтобы не возиться с квадратным корнем, будем сравнивать квадраты расстояний. Мы должны, таким образом, показать, что
Подставив в это уравнение определяемые соотношением (11.5) значения х’, у’, z’, мы увидим, что это действительно так. Значит, кроме уже изученных нами векторных уравнений, существуют еще какие-то соотношения, верные в любой системе координат.
Незаметно мы получили новый тип величин. Мы можем построить функцию х, у и z, называемую скалярной функцией,— величину, которая не имеет направления, и одинакова в обеих системах координат. Из вектора можно построить скаляр. Хорошо бы найти общее правило для этого построения. Собственно говоря, мы уже нашли это правило: надо возвести в квадрат каждую из составляющих вектора и сложить их. Определим теперь новую величину, которую обозначим а·а. Это не вектор, а скаляр; это число, одинаковое во всех координатных системах и определяемое как сумма квадратов трех составляющих вектора:
Вы спросите: «В какой системе координат?» Но раз это число не зависит от системы координат, то ответ одинаков в любой системе координат. Мы имеем дело с новым видом величины, с инвариантом, или скаляром, полученным «возведением вектора в квадрат». Если теперь определить, исходя из векторов а и b, величину
то можно убедиться, что эта величина совпадает в штрихованной и нештрихованной системах координат. Чтобы доказать это, заметим, что это верно для величин а·а, b·b и с·с, где с = а + b. Сумма квадратов (ах + bx)2 + (ау + bу)2 + (аz + bz)2 — инвариант:
Раскроем скобки в обеих сторонах этого уравнения. Перекрестные произведения дадут нам выражения типа (11.19), а суммы квадратов составляющих а и b — выражения (11.18). Инвариантность слагаемых типа (11.18) приводит к инвариантности перекрестных произведений типа (11.19).
Величина а·b называется скалярным произведением двух векторов а и b и имеет много интересных и полезных свойств. Например, легко доказать, что
а • (b + с) = а • b + а • с. (11.21)
Есть еще очень простой геометрический способ вычисления а·b, при котором не надо определять составляющих а и b; просто а·b есть произведение длин векторов а и b на косинус угла между ними. Почему? Предположим, что мы выбрали такую систему координат, в которой вектор а направлен вдоль оси х; в этом случае вектор а имеет единственную ненулевую составляющую ах, которая равна длине вектора а. Таким образом, уравнение (11.19) сводится в этом случае к а·b = ахbх, что равно произведению длины вектора а на составляющую вектора b по направлению а, которая в свою очередь равна b cos θ, т. е. a·b = abcosθ.
Таким образом, в этой частной системе координат мы доказали, что а·b равно произведению длин векторов а и b на косинус угла между ними θ. Но если это верно в одной системе координат, то это верно и во всех системах, потому что а·b не зависит от выбора системы координат.
Что хорошего может дать нам эта новая величина? Нужно ли физику скалярное произведение? Да, оно необходимо ему постоянно. Например, в гл. 4 мы назвали кинетической энергией величину 1/2mv2, но если частица движется в пространстве, то нужно возвести в квадрат отдельно составляющие скорости х, у и z, так что формулу для кинетической энергии можно записать в виде
Энергия не имеет направления. Импульс же направление имеет, это — вектор, и он равен произведению массы на вектор скорости.
Другим примером скалярного произведения может служить работа, произведенная силой при перемещении какого-нибудь предмета с одного места на другое. Мы еще не дали определения работы, она равна изменению энергии, прибавке в весе, после того как сила F поработает вдоль пути s: Работа = F·s. (11.23)
Иногда целесообразно говорить о составляющей вдоль определенного направления (например, вдоль вертикали, потому что это направление силы тяжести). Для этого удобно ввести единичный вектор вдоль интересующего нас направления. Под единичным вектором мы будем понимать вектор, скалярное произведение которого на себя равно единице. Пусть это будет вектор i; тогда i • i = 1. Скалярное произведение i·а равно a cosθ, т. е. оно равно составляющей вектора а вдоль направления i. Это наилучший способ получить составляющую вектора. Поступая так, мы можем найти все составляющие вектора и получить забавную формулу.
Предположим, что нам задана какая-то система координат х, у и z. Введем три вектора: i — единичный вектор вдоль оси х, j — единичный вектор вдоль оси у и к — единичный вектор вдоль оси z. Ясно, что i · i = 1. Чему же равно произведение i·j? Если угол между векторами прямой, то их скалярное произведение равно нулю. Таким образом,
Используя эти свойства векторов i, j, k, можно записать любой вектор а в виде
Таким образом, можно от составляющих вектора легко перейти к самому вектору.
Мы изучили далеко не все свойства векторов. Однако, прежде чем углубиться в этот вопрос, научимся сперва применять обсужденные сейчас идеи в физике. И тогда, когда мы хорошо овладеем основным материалом, будет легче продвинуться дальше, не впадая в ошибки. Позднее мы увидим, что удобно определить еще одно произведение двух векторов, которое называется векторным произведением и записывается в виде а X b. Однако обсуждение этого вопроса лучше отложить до следующей главы.
grandkid.ru
Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов называется число, равное произведению их длин, умноженному на косинус угла между векторами; скалярное произведение двух векторов, хотя бы один из которых нулевой, считается равным нулю. Скалярное произведение векторов и обозначается так: * или . Таким образом, для ненулевых векторов и
и для любого вектора справедливы равенства * = 0 и * = 0.
Из этих формул, в частности, следует, что * = ||2. Скалярное произведение * называется скалярным квадратом вектора и обозначается символом 2. Таким образом,
- скалярный квадрат вектора равен квадрату его длины: 2 = ||2.
Скалярное произведение векторов и можно вычислить, зная координаты {x1; y1} и {x2; y2} этих векторов. В самом деле, если данные векторы не нулевые, то, используя формулу (5) п. 89, получаем:
Эта формула, очевидно, верна и в том случае, когда один из векторов и нулевой. Итак,
- скалярное произведение векторов {x1; y1} и {x2; y2} выражается формулой
* = x1x2 + y1y2. (2)
Сопоставляя это равенство с условием перпендикулярности ненулевых векторов (формула (7), п. 89), приходим к выводу
- скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Из формулы (1) следует, что
- скалярное произведение ненулевых векторов и положительно (отрицательно) тогда и только тогда, когда < 90º ( > 90º).
На рисунке 64
Докажем, что скалярное произведение векторов обладает следующими свойствами.
Доказательство. Справедливость утверждения 1 следует из формулы 2 = ||2, а утверждение 2 — из определения скалярного произведения.
Докажем утверждения 2 и 4. Для этого введем прямоугольную систему координат и обозначим координаты векторов , и так: {x1; y1}, {x2; y2}, {x3; y3}. Используя формулу (2), выражающую скалярное произведение векторов через их координаты, получаем:
Утверждение 3 доказано.
Вектор k имеет координаты {kx1; ky1}, поэтому
Утверждение 4 доказано.
Отметим, что утверждение 3 обобщается на любое число слагаемых. Например,
mthm.ru
