Калькулятор скнф и сднф онлайн – Построение таблицы истинности онлайн | СКНФ | СДНФ | Полином Жегалкина | Таблица истинности булевой функции онлайн

Построение СКНФ и СДНФ по таблице истинности — энциклопедический справочник и словарь для студента от А до Я

1. СКНФ
2. СДНФ

Нормальной форме логической формулы не свойственна эквивалентность, отрицание формул неэлементарного типа и знаки импликации.

Выделяют такие виды формы нормального типа:

• КНФ (конъюнктивная нормальная форма), где подразумевается конъюнкция того или иного количества дизъюнкций, как пример, ;
• ДНФ (дизъюнктивная нормальная форма), где осуществляется дизъюнкция конъюнкций, как пример, .

СКНФ

Совершенная КНФ является разновидностью конъюнктивной нормальной формы, удовлетворяющей такие условия:

• отсутствие одинаковых элементарных дизъюнкций;
• дизъюнкции не содержат одинаковые переменные;
• все дизъюнкции содержат каждую переменную из входящих в конъюнктивную НФ такого типа.

Построение СКНФ согласно таблице истинности

Если функция равна нулю, то в случае каждого набора записывают сумму, причем с отрицанием берутся те переменные, которые равны единице.

СДНФ

Совершенная ДНФ является разновидностью дизъюнктивной нормальной формы, удовлетворяющей следующие условия:

• отсутствие одинаковых элементарных конъюнкций;
• конъюнкции не свойственно обладать одинаковыми переменными;

в случае любой конъюнкции элементарного типа имеет место быть переменная, входящая в такую нормальную дизъюнктивную форму. При этом в одинаковом порядке.

Все формулы булевого типа, которые не относятся к тождественно ложным, могут быть представлены в совершенной разновидности ДНФ, при этом в единственном возможном варианте.

Построение СДНФ согласно таблице истинности

Если функция соответствует единице, то в случае каждого набора записывается произведение, причем с отрицанием берутся те переменные, которые равны нулю.

Нахождение СКНФ и СДНФ: примеры

Пример

Согласно таблице истинности записать логическую функцию:

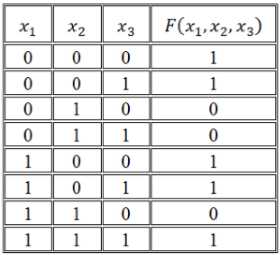
Рисунок 1.

Решение:

Прибегнем к правилу построения совершенной ДНФ

Рисунок 2.

Получаем такую СДНФ

Задействовав правило её построения:

Рисунок 3.

Получаем СКНФ:

Пример

Представить функцию как СДНФ и СКНФ, при том, что она задаётся таблицей истинности.

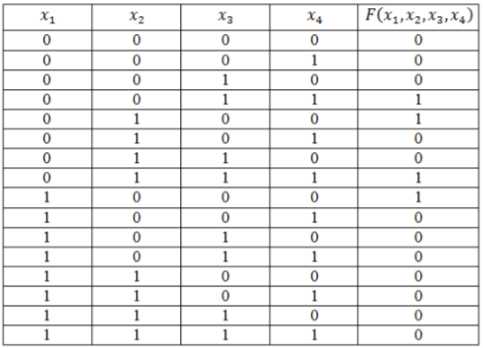
Рисунок 4.

Решение

Для начала нужно записать логическую функцию в СДНФ. Чтобы упростить решение, добавляем к таблице столбец. Прибегнув к правилу составления СДНФ, вводим знак отрицания для переменных с нулевым значением. Инвертирование нулевых значений переменных имеет большое значение, поскольку без этого значения конъюнкций будут преобразованы в нули ключевой функции.

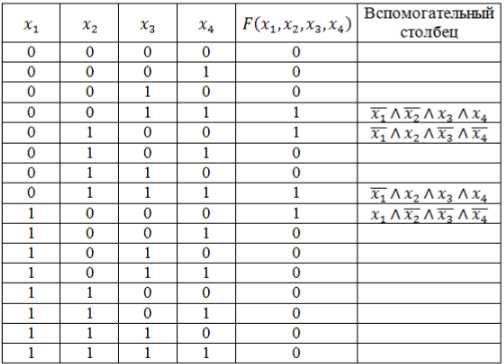
Рисунок 5.

Вычисленные конъюнкции из вспомогательного столбца необходимо объединить знаком дизъюнкции и получим необходимую логическую функцию, имеющую вид совершенной конъюнктивной формы нормального типа:

Запишем логическую функцию в СКНФ.

Прибегнув к правилу, по которому составляется СКНФ, нужно помнить о введения знака отрицания для переменных с единицей. Инвертирование единичных значений имеет большое значение, поскольку без этого значения дизъюнкций будут преобразованы в единицы ключевой функции.

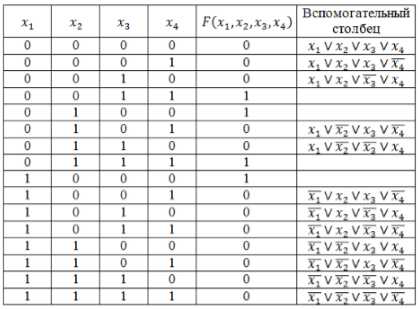
Рисунок 6.

Вычисленные дизъюнкции из вспомогательного столбца необходимо объединить знаком конъюнкции, так как таким образом и можно получить необходимую логическую функцию, имеющую вид совершенной нормальной формы конъюнктивного типа.

sciterm.ru

   &nbsp Примеры приведения формул к СДНФ и СКНФ

   &nbspПример 1. Следующую формулу привести к СДНФ, предварительно приведя ее равносильными преобразованиями к ДНФ: $$A \equiv a ( bc \rightarrow ab) .$$

   &nbspРешение. \(A \equiv a ( bc \rightarrow ab) \equiv a ( \bar{b}\bar{c} \vee ab) \equiv a ( \bar{b} \vee \bar{c} \vee ab) \equiv\)
   &nbsp\(\equiv a \bar{b} \vee a \bar{c} \vee ab \equiv ДНФ A\). $$A \equiv ДНФ A \equiv a\bar{b } ( c \vee \bar{c}) \vee a\bar{c} ( b \vee \bar{b}) \vee ab ( c \vee \bar{c})\equiv$$ $$\equiv a\bar{b} c \vee a \bar{b} \bar{c} \vee ab\bar{c} \vee a \bar{b} \bar{c} \vee abc \vee ab\bar{c} \equiv$$ $$\equiv a\bar{b} c \vee a \bar{b} \bar{c} \vee ab\bar{c} \vee \vee abc \equiv СДНФ A.$$
   &nbspОтвет. \(СДНФ A \equiv a\bar{b} c \vee a \bar{b} \bar{c} \vee ab\bar{c} \vee \vee abc .\)

   &nbspПример 2. Для формулы из примера 1 найти СДНФ путем составления таблицы истинности.
   &nbspРешение. Составим таблицу истинности для формулы \(A \equiv a ( bc \rightarrow ab).\)

\(a\)	\(b\)	\(c\)	\(bc\)	\(ab\)	\(bc\rightarrow ab\)	\(A\)
1	1	1	1	1	1	1
1	1	0	0	1	1	1
1	0	1	0	0	1	1
1	0	0	0	0	1	1
0	1	1	1	0	0	0
0	1	0	0	0	1	0
0	0	1	0	0	1	0
0	0	0	0	0	1	0

   &nbspОтвет. Тогда \(СДНФ A \equiv abc \vee ab \bar{c} \vee a\bar{b}c \vee a\bar{b}\bar{c}.\)

   &nbspПример 3. Для формулы из примера 1 найти СКНФ путем равносильных преобразований, предварительно приведя ее к КНФ.
   &nbspРешение. Из примера 1: \(A \equiv a\bar{b} \vee a \bar{c} \vee ab.\) Далее \(A \equiv a ( \bar{b} \vee \bar{c} \vee b) \equiv a \wedge 1\equiv a\equiv КНФ A.\) $$A \equiv КНФ A \equiv a \vee ( b \wedge \bar{b}) \equiv ( a \vee b) \wedge ( a \vee \bar{b}) \equiv$$ $$\equiv (( a \vee b) \vee c \wedge \bar{c}) \wedge (( a \vee \bar{b}) \vee c \wedge \bar{c}) \equiv$$ $$\equiv ( a \vee b \vee c) \wedge(a \vee b \vee \bar{c}) \wedge ( a \vee \bar{b} \vee c) \wedge ( a \vee \bar{b} \vee \bar{c}) \equiv СКНФ A.$$
   &nbspОтвет. \(СКНФ A \equiv ( a \vee b \vee c) \wedge(a \vee b \vee \bar{c}) \wedge ( a \vee \bar{b} \vee c) \wedge ( a \vee \bar{b} \vee \bar{c}).\)

   &nbspПример 4. Для формулы из примера 1 найти СКНФ, записав предварительно СДНФ ее отрицания, а потом воспользовавшись формулой двойственности.
   &nbspРешение. СКНФ $$\bar{A} \equiv \overline{СДНФ \bar{A}} \equiv \overline{\bar{a}bc \vee \bar{a}b\bar{c} \vee \bar{a}\bar{b}c \vee \bar{a}\bar{b}\bar{c}} \equiv$$ $$\equiv ( a \vee \bar{b} \vee \bar{c} ) \wedge ( a \vee \bar{b} \vee c) \wedge ( a \vee b \vee \bar{c}) \wedge ( a \vee b \vee c) .$$
   &nbspОтвет. СКНФ \(A \equiv ( a \vee \bar{b} \vee \bar{c} ) \wedge ( a \vee \bar{b} \vee c) \wedge ( a \vee b \vee \bar{c}) \wedge ( a \vee b \vee c) .\)

---

2012-11-05 • Просмотров [ 16681 ]

primat.org

Калькулятор логических функций | Обучалки

СКАЧАТЬ ПРОГРАММУ	Размер
LogicCalc.exe (13010)	526 кб

Программа предназначена для получения таблиц истинности логических функций с числом переменных от одной до пяти. Логической (булевой) функцией n переменных y = f(x₁, x₂, …, x_n) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.

Переменные, которые могут принимать только два значения 0 и 1 называются логическими переменными (или просто переменными). Заметим, что логическая переменная х может подразумевать под числом 0 некоторое высказывание, которое ложно, и под числом 1 высказывание, которое истинно.

Из определения логической функции следует, что функция n переменных – это отображение Bⁿ в B, которое можно задать непосредственно таблицей, называемой таблицей истинности данной функции.

Основные функции логики — это функции двух переменных z = f(x,y).

Число этих функций равно 2⁴ = 16. Перенумеруем и расположим их в естественном порядке.

Рассмотрим более подробно эти функции. Две из них f₀ = 0 и f₁₅ = 1 являются константами. Функции f₃, f₅, f₁₀ и f₁₂ являются по существу функциями одной переменной.

Наиболее важные функции двух переменных имеют специальные названия и обозначения.

1) f₁ — конъюнкция (функция И)
Заметим, что конъюнкция – это фактически обычное умножение (нулей и единиц). Эту функцию обозначают x&y;

2) f₇ — дизъюнкция (функция или). Обозначается V.

3) f₁₃ — импликация (следование). Обозначается ->
Это очень важная функция, особенно в логике. Ее можно рассматривать следующим образом: если

х = 0 (т. е. х “ложно”), то из этого факта можно вывести и “ложь”, и “истину” (и это будет правильно), если у = 1 (т. е. у “истинно”), то истина выводится и из “лжи” и из “истины”, и это тоже правильно. Только вывод “из истины ложь” является неверным. Заметим, что любая теорема всегда фактически содержит эту логическую функцию;

4) f₆ — сложение по модулю 2. Обозначается знаком “+” или знаком “+” в кружке.

5) f₉ — эквивалентность или подобие. Эта f₉ = 1 тогда и только тогда, когда х = у. Обозначается х ~ у.

6) f₁₄ — штрих Шеффера. Иногда эту функцию называют “не и” (так как она равна отрицанию конъюнкции). Обозначается x|y.

7) f₈ — стрелка Пирса (иногда эту функцию называют штрих Лукасевича).

Три оставшиеся функции, (f₂ , f₄

и f₁₁) особого обозначения не имеют.

Заметим, что часто в логике рассматриваются функции от функций, т.е. суперпозиции перечисленных выше функций. При этом последовательность действий указывается (как обычно) скобками.

obychalki.ru