График котангенса | Алгебра
Как построить график функции y=ctg x? Для начала рассмотрим график котангенса на интервале (0;π).
Для удобства округлим число π до целого:
Длину единичного отрезка возьмём равной двум клеточкам тетради. В этом случае числу π соответствует отрезок длиной 6 клеточек,числу π/2 — 3 клеточки, π/6 — 1 клеточка, π/4 — 1,5 клеточки, π/3 — 2 клеточки.
В область определения функции y=ctg x не входят числа
Прямые
являются вертикальными асимптотами графика котангенса, то есть график к ним стремиться, но никогда не достигнет. Асимптоты изображают пунктирными линиями.
Составим таблицу значений котангенса на промежутке (0;π/2]:
На координатной плоскости отмечаем полученные точки.
На интервале (0;π) график котангенса симметричен относительно точки (π/2;0):
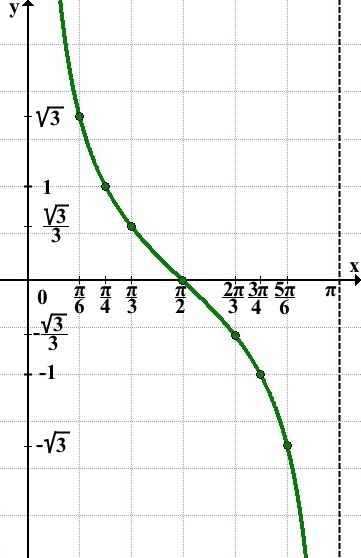
Так как y=ctg x — периодическая функция с периодом T=π, график котангенса, взятый на интервале (0;π), повторяется бесконечное число вправо, на плюс бесконечность, и влево, на минус бесконечность:
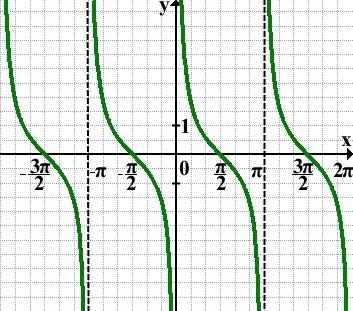
График функции y=ctg x
Графики функций, в том числе, график котангенса, в алгебре используют при решении уравнений, неравенств и других заданий.
www.algebraclass.ru
Формулы тангенсов, с примерами решений
Тангенс половинного угла
Также тангенс половинного угла выражается в виде
Через тангенс половинного угла можно выразить все тригонометрические функции:
Тангенс двойного угла
Тангенс тройного угла
Сумма тангенсов
Разность тангенсов
Тангенс суммы двух углов
Тангенс разности двух углов
Квадрат тангенса
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Формулы котангенсов, с примерами решений
Котангенс связан с тангенсом следующим соотношением:
Котангенса половинного угла
Также котангенс половинного угла выражается в виде
Котангенса двойного угла
Котангенс тройного угла
Сумма котангенсов
Разность котангенсов
Котангенс суммы двух углов
Котангенс разности двух углов
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Функция y=сtgx, ее свойства и график. Нравственное воспитание
Дополнительные сочиненияНа этом уроке мы рассмотрим функцию у = ctg х, ее свойства и график. Вначале вспомним определение котангенса на числовой окружности. И вспомним связь между числовым и угловым аргументом. Дадим определение линии котангенсов – касательной к окружности. Построим график функции котангенса в системе координат и рассмотрим ее основные свойства.
Тема: Тригонометрические функции
Урок: Функция y=ctgt, её свойства и график
1. Определение котангенса
Зададим единственное число Каждому действительному числу соответствует единственная точка на числовой окружности (рис. 1). Точка имеет абсциссу и ординату, абсциссу называют косинусом числа ординату – синусом числа Отношение косинуса к синусу называется котангенсом числа
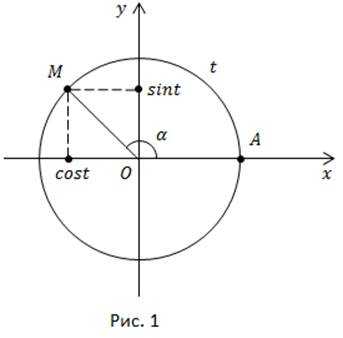
Каждому допустимому значению соответствует единственная точка на окружности, единственная пара её координат, а значит и единственное значение дроби т. е. единственное значение котангенса Таким образом, задаётся функция или
Аргументом функции котангенс может быть число или угол . Вспомним связь между числовым и угловым аргументами.
Радианом называется такой центральный угол, длина дуги которого равна (рис. 2).
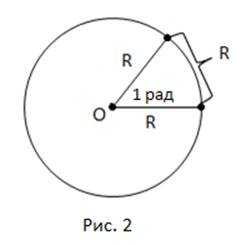
В окружности штук радиан.
Если то
Если есть угол и окружность радиуса 1, то длина этой дуги или аргумент связаны с следующим образом:
2. Котангенс на числовой окружности
Как определить значения котангенса для конкретных значений числового или углового аргумента? Они расположены на линии котангенсов – касательной к окружности в точке B (рис. 3).
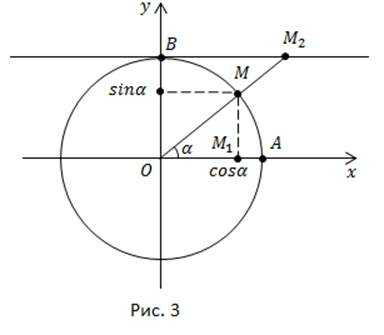
Возьмем аргумент или угол Аргументу или углу в радианах соответствуют синус и косинус. Рассмотрим
3. График функции y=ctgt
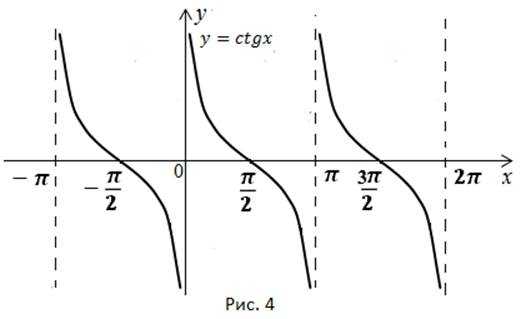
Изобразим график функции в координатной плоскости. По формулам приведения Поэтому для построения графика функции достаточно график функции симметрично отобразить относительно оси х и сдвинуть вдоль оси х на влево (рис. 4).
4. Свойства функции y=ctgt
Исследуем график функции
1) Область определения:
2) Область значений:
a) Каждому допустимому соответствует единственное значение
b) Любой достигается при одном либо нескольких значениях
3) Функция нечетна:
График симметричен относительно начала координат.
4) Наименьший положительный период
Значение периода котангенса также следует из формулы
при том, что нам известен период тангенса.
5) Точки пересечения с осью x:
Точки пересечения с осью y отсутствуют (рис. 4).
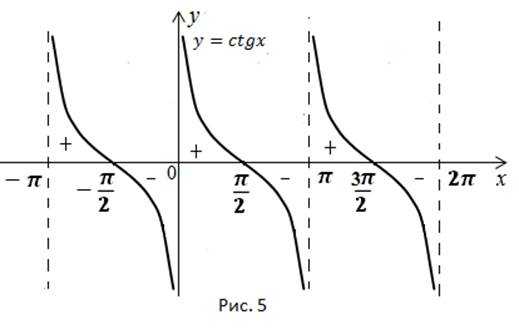
6) Определим интервалы знакопостоянства (рис. 5):
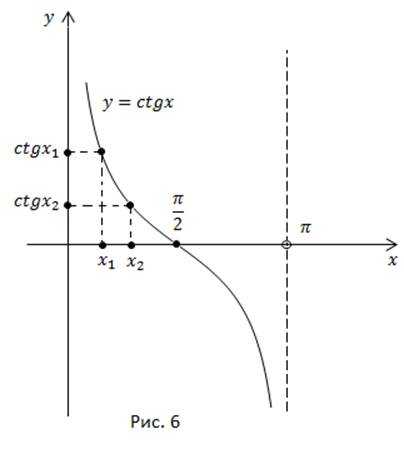
7) Функция монотонно убывает на каждом из интервалов
Покажем это:
Рассмотрим промежуток длиной в период. Функция монотонно убывает от до
Действительно, если мы возьмем две точки из этого промежутка, такие, что то большему значению аргумента соответствует меньшее значение функции (рис. 6).
На каждом из отдельно взятых участков длиной в период функция также монотонно убывает.
8) Функция не имеет ни наибольшего, ни наименьшего значения.
5. Вывод, заключение
Мы изучили функцию её график и свойства. Все они будут использоваться в дальнейшем при решении различных задач, в том числе и при решении тригонометрических уравнений, к изучению которым мы приступим на следующем уроке.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М. Л., Мошкович М. М., Шварцбурд С. И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М. И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А. Г., Полонский В. Б., Якир М. С. Алгебраический тренажер.-К.: А. С.К., 1997.
7. Саакян С. М., Гольдман А. М., Денисов Д. В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А. П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 20.2, 20.3(б, г), 20.5, 20.19.
Дополнительные веб-ресурсы
1. Математика .
2. Интернет-портал Problems. ru .
3. Образовательный портал для подготовки к экзаменам .
dp-adilet.kz
Тангенс угла, теория и примеры
Определение и формула тангенса
ОПРЕДЕЛЕНИЕ Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего к этому углу катета к прилежащему катету. Тангенс угла обозначается .Рассмотрим прямоугольный треугольник (изображен на рисунке) с , гипотенузой и катетами и . Тогда
Рассмотрим тригонометрическую окружность радиуса 1 с центром в начале координат.
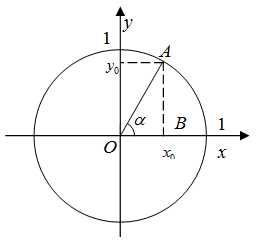
Выберем произвольный угол , которому на окружности соответствует точка . Опустим перпендикуляры на оси координат, тогда
т.е. тангенс угла это отношение ординаты точки А к абсциссе. Так как синус угла равен значению ординаты точки А, а косинус угла равен значению абсциссы, то
Функция периодическая с периодом , т.е.
Примеры решения задач
ПРИМЕР 1| Задание | В прямоугольном треугольнике с катетами см и см найти тангенсы углов и . |
| Решение | Так как тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то можем записать, что
|
| Ответ |
| Задание | Найти , если
|
| Решение | Преобразуем заданное выражение следующим образом:
или
Так как , то получаем, что
|
| Ответ |
Тангенс двойного угла
Тангенс половинного угла
График тангенса
Сумма тангенсов
Разность тангенсов
Тангенс суммы
Тангенс разности
Область определения тангенса
ru.solverbook.com
