Коэффициент парной корреляции — Циклопедия
Коэффициент корреляции — Борис Миркин // ПостНаука [10:50]Коэффициент парной корреляции (Пирсона) — это некоторое число от -1 до 1, характеризующее тесноту линейной корреляционной связи (корреляцию) между зависимой случайной величиной и независимой случайной величиной.
n — число наблюдений;
xi — i-ое наблюдаемое значение независимой случайной величины;
yi — i-ое наблюдаемое значение зависимой случайной величины;
rxy — коэффициент парной корреляции.
- [math]\Leftrightarrow r_{xy}=\frac{\overline{x\cdot y}-\overline{x}\cdot\overline{y}}{\sqrt{\overline{x^2}-\overline{x}^2}\cdot\sqrt{\overline{y^2}-\overline{y}^2}}\Leftrightarrow r_{xy}=\frac{\overline{x\cdot y}-\overline{x}\cdot\overline{y}}{\sigma_x\cdot\sigma_y}\Leftrightarrow[/math]
- [math]\Leftrightarrow r_{xy}=\frac{n\sum\limits_{i=1}^{n}x_iy_i-\sum\limits_{i=1}^{n}x_i\cdot\sum\limits_{i=1}^{n}y_i}{\sqrt{n\sum\limits_{i=1}^{n}x_i^2-\left(\sum\limits_{i=1}^{n}x_i\right)^2}\cdot\sqrt{n\sum\limits_{i=1}^{n}y_i^2-\left(\sum\limits_{i=1}^{n}y_i\right)^2}}[/math]
[править] Другие формулы
[править] Другие разделы
cyclowiki.org
Коэффициент парной корреляции в Excel
Коэффициент корреляции отражает степень взаимосвязи между двумя показателями. Всегда принимает значение от -1 до 1. Если коэффициент расположился около 0, то говорят об отсутствии связи между переменными.
Если значение близко к единице (от 0,9, например), то между наблюдаемыми объектами существует сильная прямая взаимосвязь. Если коэффициент близок к другой крайней точке диапазона (-1), то между переменными имеется сильная обратная взаимосвязь. Когда значение находится где-то посередине от 0 до 1 или от 0 до -1, то речь идет о слабой связи (прямой или обратной). Такую взаимосвязь обычно не учитывают: считается, что ее нет.
Расчет коэффициента корреляции в Excel
Рассмотрим на примере способы расчета коэффициента корреляции, особенности прямой и обратной взаимосвязи между переменными.
Значения показателей x и y:
Y – независимая переменная, x – зависимая. Необходимо найти силу (сильная / слабая) и направление (прямая / обратная) связи между ними. Формула коэффициента корреляции выглядит так:
Чтобы упростить ее понимание, разобьем на несколько несложных элементов.
- Найдем средние значения переменных, используя функцию СРЗНАЧ:
- Посчитаем разницу каждого y и yсредн., каждого х и хсредн. Используем математический оператор «-».
- Теперь перемножим найденные разности:
- Найдем сумму значений в данной колонке. Это и будет числитель.
- Для расчета знаменателя разницы y и y-средн., х и х-средн. Нужно возвести в квадрат.
- Находим суммы значений в полученных колонках (с помощью функции АВТОСУММА). Перемножаем их. Результат возводим в квадрат (функция КОРЕНЬ).
- Осталось посчитать частное (числитель и знаменатель уже известны).
Между переменными определяется сильная прямая связь.
Встроенная функция КОРРЕЛ позволяет избежать сложных расчетов. Рассчитаем коэффициент парной корреляции в Excel с ее помощью. Вызываем мастер функций. Находим нужную. Аргументы функции – массив значений y и массив значений х:
Покажем значения переменных на графике:
Видна сильная связь между y и х, т.к. линии идут практически параллельно друг другу. Взаимосвязь прямая: растет y – растет х, уменьшается y – уменьшается х.
Матрица парных коэффициентов корреляции в Excel
Корреляционная матрица представляет собой таблицу, на пересечении строк и столбцов которой находятся коэффициенты корреляции между соответствующими значениями. Имеет смысл ее строить для нескольких переменных.
Матрица коэффициентов корреляции в Excel строится с помощью инструмента «Корреляция» из пакета «Анализ данных».
- На вкладке «Данные» в группе «Анализ» открываем пакет «Анализ данных» (для версии 2007). Если кнопка недоступна, нужно ее добавить («Параметры Excel» — «Надстройки»). В списке инструментов анализа выбираем «Корреляция».
- Нажимаем ОК. Задаем параметры для анализа данных. Входной интервал – диапазон ячеек со значениями. Группирование – по столбцам (анализируемые данные сгруппированы в столбцы). Выходной интервал – ссылка на ячейку, с которой начнется построение матрицы. Размер диапазона определится автоматически.
- После нажатия ОК в выходном диапазоне появляется корреляционная матрица. На пересечении строк и столбцов – коэффициенты корреляции. Если координаты совпадают, то выводится значение 1.
Между значениями y и х1 обнаружена сильная прямая взаимосвязь. Между х1 и х2 имеется сильная обратная связь. Связь со значениями в столбце х3 практически отсутствует.
Изобразим наглядно корреляционные отношения с помощью графиков.
- Сильная прямая связь между y и х1.
- Сильная обратная связь между y и х2. Изменения значений происходят параллельно друг другу. Но если y растет, х падает. Значения y увеличиваются – значения х уменьшаются.
- Отсутствие взаимосвязи между значениями y и х3. Изменения х3 происходят хаотично и никак не соотносятся с изменениями y.
Скачать вычисление коэффициента парной корреляции в Excel
Для чего нужен такой коэффициент? Для определения взаимосвязи между наблюдаемыми явлениями и составления прогнозов.
exceltable.com
Анализ линейных коэффициентов парной корреляции
Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в уравнении множественной регрессии. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.
Матрицу парных коэффициентов корреляции переменных можно получить, используя инструмент анализа данных Корреляция.
Выполните команду Меню, Данные, Анализ данных, Корреляция и заполните диалоговое окно
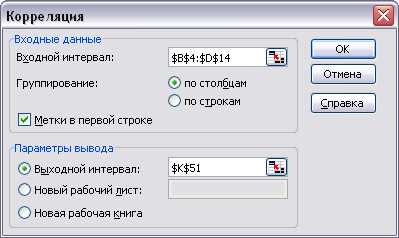
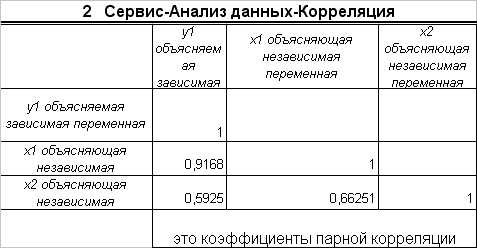
Вывод.
Из анализа коэффициентов парной корреляции следует, что значение ryx1=0,9168 указывает на тесную связь междуyиx1, а значениеrx2x1=0,6625 говорит о тесной связи междуx2иx1, при этомryx2
=0,5925<.rx2x1, т.е.x2 можно пренебречь.Расчёт коэффициентов частной корреляции
В ППП EXCELнет специального инструмента для расчёта линейных коэффициентов частной корреляции. Их можно рассчитать по рекуррентной формуле через коэффициенты парной корреляции
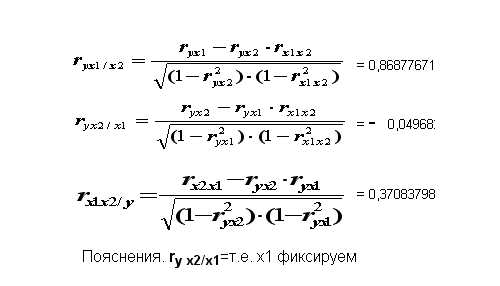
Вывод.
Из анализа частных коэффициентов
множественной корреляции следует, что
значение ryx1/x2=0,8688
(x2 фиксируем) указывает на тесную
связь междуyиx1,
а значениеryx2/x1=—0,04968 (x1 фиксируем) говорит о слабой связи
междуx
В связи с этим, для улучшения данной модели можно исключить из неё фактор x2, как малоинформативный, недостаточно статистически надёжный.
Вычисление методом стандартизации переменных
Стандартизованные частные коэффициенты регрессии – β-коэффициенты — показывают, на какую часть своего среднеквадратического отклонения изменится признак-результатyс увеличением соответствующего фактораxiна величину своего среднеквадратического отклонения при неизменном влиянии прочих факторов модели.
Для вычисления коэффициентов множественной регрессии применим метод стандартизации переменных и построим искомое уравнения в стандартизованном масштабе
ty=β1*tx1+ β2*t
x2Расчёт β-коэффициентов выполняется по формулам:

В результате получаем β-коэффициенты
: β1=0,9343, β2= — 0,0265,
Уравнение в стандартизованном масштабе
Для построения уравнения в естественной форме рассчитаем b1иb2, используя формулы перехода;
В результате получаем: b1=0,9108, b2= — 0,007756.
Значение aопределим из соотношения

Вывод.
В данном примере статистически значимыми являются a иb1, а величинаb2сформировалась под воздействием случайных причин, поэтому факторx2, силу влияния которого оцениваетb2, можно исключить как несущественно влияющий, неинформативный.
Лабораторная работа №6. Вычисление параметров линейного уравнения множественной регрессии с помощью функций регрессия и поиск решения
Вычисление параметров с помощью функции Регрессия
Второй способ получения оценок параметров уравнения множественной регрессии: с помощью инструмента EXCELРегрессия:
Исходный диапазон
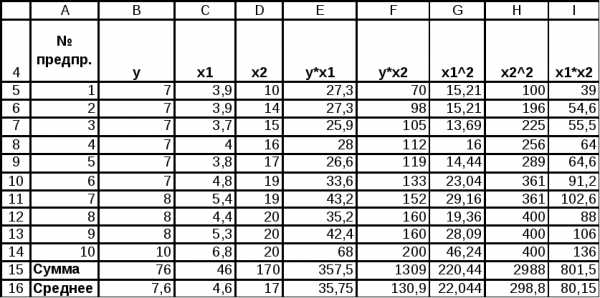
Выполните команду меню Данные, Анализ данных, Регрессия. Заполните диалоговое окно как показано на рисунке ниже;
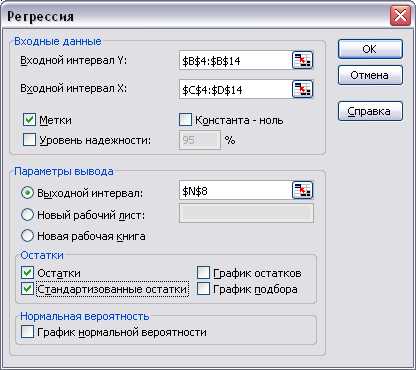
Уравнение регрессии
Результаты анализа:
Значения случайных ошибок параметров a , b1 и b2с учётом округления соответственно равны 0,7996 0,1962 и 0,0589 Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов.
Значения t-критерия Стьюдента соответственно равны 4,4303 4,6417 и -0,1316. Если значениеt-критерия больше 2-3, можно сделать вывод о существенности данного параметра, который формируется под воздействием неслучайных причин. В данном примере статистически значимыми являютсяa иb
Главным показателем качества модели множественной регрессии, как и для парной корреляции, является коэффициент множественной детерминации R2, который характеризует совместное влияние всех факторов на результат.
Расчёт линейного коэффициента множественной корреляции:
Получаем Ryx1x2=0,9170 (сравните с результатами функцииРегрессии). Зависимостьyотx1иx2характеризуется как тесная.
studfiles.net
Коэффициент парной корреляции — МегаЛекции
Корреляционным анализом называется совокупность статистических приемов, с помощью которых исследуются и обобщаются взаимосвязи корреляционно связанных величин.
В эконометрике корреляционный анализ применяется для выявления наличия или отсутствия зависимостей между анализируемыми признаками. И только после утвердительного ответа на этот вопрос имеет смысл определять вид зависимости. В дальнейшем в основном будем иметь дело со случайными величинами, следующими нормальному закону распределения, поэтому, если не будет особо оговорено, будем говорить о линейной зависимости.
Меру линейной зависимости между величинами Y и X определяют с помощью ковариации. Она определяется как
= cov(Y,X) = M{(Y- )(X- )},
где и – соответственно, математические ожидания Y и X. Таким образом, ковариация между случайными переменными – это математическое ожидание произведения отклонений значений случайных переменных от их математических ожиданий. Если X = Y, то имеем дисперсию случайной величины X, т. е.
= = M{(X- )2}.
Корень квадратный из дисперсии называется стандартным отклонением и обозначается как . Если известно, о какой переменной идёт речь, то нижний индекс у стандартного отклонения и дисперсии обычно не ставится.
Чем больше величина ковариации, тем теснее линейная связь между переменными. Но с этой характеристикой не совсем удобно работать, т. к. её величина зависит от единиц измерения анализируемых показателей. Чтобы избавиться от этого недостатка, ковариацию стандартизируют двумя стандартными отклонениям, получая при этом коэффициент корреляции, т. е.
= .
Коэффициент корреляции всегда лежит между –1 и +1 и не зависит от масштаба переменных. Если ковариация cov(Y,X) = 0, то говорят, что случайные переменные некоррелированны, т. е. между ними отсутствует линейная зависимость. То же самое можно говорить и о коэффициенте корреляции. Если случайные величины статистически независимы, то = 0, а в случае нормального распределения из их некоррелированности, когда = 0, следует их независимость. Две случайные переменные Y и X коррелированы полностью ( = 1), если Y = aX для некоторого положительного значения a.
Далее будем пользоваться свойствами дисперсии и ковариации, из которых следует, что дисперсия суммы двух некоррелированных переменных равна сумме дисперсий этих переменных, а ковариация двух переменных равна математическому ожиданию произведения этих переменных, если математическое ожидание хотя бы одной из них равно нулю.
Покажем последнее. Пусть = 0. Тогда cov(Y,X) = M{(Y – )(X – )} = =M{(Y – )(X)} = M{(YX) – X)} = M{(YX) – M X)} = M{(YX) – (X)}= = M{(YX)}– = M{(YX)}. Т. е. в нашем случае cov(Y,X) = M{(YX)}.
До сих пор рассуждения велись по отношению к параметрам генеральной совокупности. Исследователь обычно работает с выборками, на основе которых получает приближённые значения параметров. Эти приближённые значения называют оценками параметров. Для того чтобы оценки были «хорошими», необходимо, чтобы они были несмещёнными, эффективными и состоятельными.
Оценка называется несмещённой, если её математическое ожидание равно самому оцениваемому параметру. Несмещённость оценки означает, что она в среднем соответствует оцениваемому параметру.
Оценка называется эффективной, если она обладает наименьшей дисперсией среди всех альтернативных оценок.
Оценка называется состоятельной, если при увеличении объёма выборки оценка сходится к оцениваемому параметру.
Так, известно, что выборочная средняя арифметическая является несмещённой оценкой генеральной средней. В дальнейшем оценку параметра будем обозначать той же буквой, что и параметр, но сверху будем помечать её знаком «крышки». Тогда можно записать, что = , где – выборочная средняя арифметическая. А выборочная дисперсия – смещённая оценка генеральной дисперсии и первую приходится подправлять, вводя поправочный коэффициент. Так, если выборочную дисперсию обозначить через S2, то несмещённой оценкой генеральной дисперсии будет 2 = S2.
Оценкой коэффициента корреляции генеральной совокупности является выборочный коэффициент корреляции, определяемый из соотношения
= = =
где в числителе стоит выборочная ковариация, а в знаменателе – произведение выборочных стандартных отклонений.
Поскольку речь здесь идёт об оценке, а оценка – величина случайная, то необходимо проверить её надёжность. Осуществляется это с помощью проверки гипотезы о том, что коэффициент корреляции генеральной совокупности равен нулю. Итак, нулевая гипотеза H0 : = 0, альтернативная Ha : 0.
Проверяются статистические гипотезы по стандартному алгоритму. Сначала по выборочным данным вычисляется статистика, закон распределения которой известен, если верна нулевая гипотеза. Затем по фиксированному уровню значимости и известному числу степеней свободы определяются критические точки данного распределения. По критическим точкам определяется область принятия гипотезы и критическая область. Если вычисленное значение статистики попало в область принятия гипотезы, то нулевая гипотеза не отклоняется. В противном случае – отклоняется.
В нашем случае рассчитывается t-статистика вида
t = .
Известно, что если верна нулевая гипотеза, т. е. если = 0, то эта статистика следует распределению Стьюдента с (n–2) степенями свободы. Зафиксировав уровень значимости (обычно его принимают равным 0,05), определяем критические точки ( ) и по ним строим область принятия гипотезы: ( ;+ Если вычисленное значение t-статистики попало в эту область, то говорят, что коэффициент корреляции незначимо отличен от нуля и линейная зависимость между анализируемыми переменными отклоняется. Критические точки обычно определяются по таблице критических значений распределения Стьюдента.
При компьютерных расчётах обычно вычисляется расчётный уровень значимости (их в статистических пакетах обозначают по-разному: p-value, p-level, sign, Prob. и т. д.), это вероятность того что . Т. е. p-value = P( ). Грубо говоря, это вероятность того, что вычисленное значение t-статистика попало в область принятия гипотезы. Расчётный уровень значимости сравнивают с принятым уровнем значимости (у нас это ) и, если p-value , то H0 отклоняется и считается, что переменные x и y коррелированы, Если p-value , то H0 не отклоняется и считается, что переменные не коррелированы.
Если расчётный уровень значимости близок к , то при принятии решения рекомендуется проверять, выполняется ли неравенство .
Для качественной интерпретации значений коэффициентов парной линейной корреляции (в случае их значимого отличия от нуля) можно использовать шкалу Чеддока:
| Величина коэфф. | 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Характеристика силы связи | слабая | Уме-ренная | заметная | высокая | весьма высокая |
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Парный корреляционный анализ — Мегаобучалка
Основные понятия.
В курсе математического анализа одним из основных понятий является понятие функциональной зависимости, при которой каждому значению одной переменной ставится в соответствие единственное вполне определенное значение другой. Такая зависимость на практике встречается достаточно редко и является, как правило, некоторой идеализацией реально существующих зависимостей. Тем не менее функциональная зависимость играет важную роль в тех областях науки, где подобная идеализация не приводит к грубым неточностям и противоречиям (классическая механика, классическая электродинамика и др.). Развитие естественных наук (особенно в XX веке) привело к тому, что стали изучаться явления и процессы, для описания которых функциональные зависимости оказались непригодными.
В математической статистике вводится понятие статистической зависимости.
Определение 1. Зависимость между случайными величинами Y и Х называется статистической (стохастической), если каждому значению одной случайной величины (Х) соответствует определенное условное распределение другой случайной величины (Y).
Статистическую зависимость можно перевести в функциональную, если рассмотреть зависимость условного математического ожидания СВ Y от Х или условного математического ожидания Х от Y.
Определение 2. Корреляционной зависимостью называется функциональная зависимость между значениями одной случайной величины и условным математическим ожиданием другой.
Аналитически корреляционную зависимость можно задать следующим образом
MX(Y) = f(x), MY(X) = g(y), (*)
где f(x) ¹ const и g(y) ¹ const.
Уравнения (*) называются уравнениями регрессии.
Основные задачи данного раздела:
1) выявление связи между случайными величинами и оценка ее тесноты;
2) установление вида регрессии.
Первая задача является основной задачей корреляционного анализа, вторая – регрессионного.
Парный корреляционный анализ.
Решение основной задачи корреляционного анализа можно разбить на следующие этапы.
1. Сбор выборки пар (xi, yj) для характеристики закона распределения двумерной СВ (Х, Y) и ее запись в удобной для работы форме.
2. Расчет численных значений выборочных коэффициентов, характеризующих связь между СВ Х и Y.
3. Проверка гипотезы о значимости связи между Х и Y.
Рассмотрим каждый из этапов подробнее.
1. Данные о статистической зависимости удобно задавать в виде корреляционной таблицы 1.
В данной таблице nij – частота, с которой в опыте встречается пара
(xi, yj), где i = 1, 2, 3, …, k; j = 1, 2, 3, …, m.
Таблица 1.
2. Для оценки тесноты используются коэффициент корреляции rXY (rYX) и корреляционное отношение hXY (hYX).
Коэффициент корреляции служит для характеристики тесноты линейной зависимости между СВ Х и Y.
По данным выборки коэффициент корреляции рассчитывается следующим образом
,
где , , , SX, SY – выборочные средние квадратические отклонения случайных величин Х и Y соответственно.
Свойства коэффициента корреляции.
1) rXY = rYX = r.
2) Коэффициент корреляции принимает значения на отрезке [-1; 1], т.е.
-1 £ r £ 1.
3) При r = ± 1 корреляционная связь является линейной функциональной.
4) При r = 0 линейная корреляционная связь отсутствует.
5) Если случайные величины независимы, то r = 0.
Заметим, что равенство r = 0 говорит об отсутствии только линейной корреляционной связи, а не корреляционной связи вообще
Несложно заметить, что r является выборочной точечной оценкой коэффициента корреляции rГ между случайными величинами Х и Y генеральной совокупности
.
Для проверки значимости выборочного коэффициента корреляции рассматривается гипотеза Н0: rГ = 0 и гипотеза Н1: rГ ¹ 0.
При справедливости гипотезы Н0 статистика
имеет t-распределение Стьюдента с l = n – 2 степенями свободы.
Приведем правило проверки гипотезы о значимости выборочного коэффициента корреляции.
1. По данным выборки рассчитывается величина .
2. Находится значение t(1 — a; n – 2) по таблице IV распределения Стьюдента.
3. Если |tЭ| £ t(1 — a; n – 2), то нет оснований отвергнуть гипотезу Н0:
rГ = 0. Если |tЭ| > t(1 — a; n – 2) гипотеза Н0 отвергается, т.е. rГ ¹ 0.
Коэффициент корреляции r является показателем тесноты линейной связи. Для оценки тесноты нелинейной связи вводится числовая характеристика – корреляционное отношение.
Генеральным корреляционным отношением называется величина
или (*)
В уравнении (*) и – общие дисперсии СВ Y и Х, – межгрупповая дисперсия СВ Y, которая характеризует разброс значений реализаций СВ Y относительно определенных реализаций СВ Х (для — аналогично). Величины hY,X и hX,Y в общем случае являются различными, поэтому там, где это необходимо, мы будем снабжать символ корреляционного отношения соответствующими индексами. Если такой необходимости нет, то будем использовать символ h.
Корреляционное отношение характеризует степень концентрации двумерного распределения (X, Y) вблизи линии регрессии.
Аналогично можно ввести выборочное корреляционное отношение, для чего в уравнении (*) значения и нужно заменить на их выборочные аналоги.
Свойства корреляционного отношения.
1) 0 £ h £ 1.
2) Если h = 0, то корреляционная связь отсутствует.
3) Если h = 1, между переменными Х и Y существует функциональная связь.
4) h ³ |r|.
5) Если h = |r|, то между случайными величинами существует линейная корреляционная зависимость.
Для проверки значимости корреляционного отношения используется статистика
,
где n – объем выборки, m – число интервалов по сгруппированным данным.
Если справедлива гипотеза Н0: h = 0, то СВ F имеет распределение Фишера.
Таким образом, если , где a — выбранный уровень значимости, k1 = n – 1, k2 = n – m, то нет оснований отвергнуть гипотезу Н0. Если , то гипотеза Н0 отвергается и делается вывод о наличии между случайными величинами корреляционной зависимости.
П р и м е р 1. Распределение Х и Y приводится в корреляционной таблице 2.
Таблица 2.
| Y X | nx | |||||||||
| -2 | ||||||||||
| -1 | ||||||||||
| ny |
Найти коэффициент корреляции r, корреляционные отношения hX,Y и hY,X и проверить их значимость.
Решение. Найдем выборочные числовые характеристики случайных величин Х и Y.
.
.
.
.
.
.
.
.
Найдем коэффициент корреляции
.
Полученный результат говорит о том, что между величинами Х и Y нет линейной корреляционной связи. Выясним, есть ли между величинами Y и Х нелинейная корреляционная связь, рассчитав корреляционные отношения и hY,X и hX,Y.
Для расчета hY,X необходимо найти значение межгрупповой дисперсии Y для определенных значений xi
.
Найдем средние значения величины Y, вычисленные по группам
,
,
,
,
.
.
Следовательно,
Таким образом СВ Y не зависит корреляционно от величины Х.
Рассчитаем hX,Y.
Найдем значение межгрупповой дисперсии величины Х для определенных значений yi.
,
,
,
,
,
,
,
,
.
.
.
Проверим значимость hX,Y.
Рассмотрим наблюдаемое значение критерия F
.
Используя таблицу V приложений, найдем значение .
Так как , то величина Х корреляционно зависит от величины Y. Более того, можно сказать, что данная зависимость близка к функциональной, поскольку hX,Y » 1.
Случай, когда корреляционная зависимость Х от Y есть, а зависимости Y от Х нет, не является чем-то экстраординарным. Например, существует зависимость средней урожайности от количества выпавших осадков, однако количество осадков от урожайности не зависит.
Парная регрессия.
Если задачей корреляционного анализа является установление зависимости между величинами Х и Y, то задачей регрессионного анализа является установление формы зависимости между переменными.
В предыдущем пункте мы определили уравнение регрессии как уравнение вида
МХ(Y) = f(x). (*)
Уравнение (*) можно записать следующим образом
у = f(x) + e,
где f(х) – функция регрессии, e — случайная составляющая, характеризующая отклонение у от функции регрессии.
В дальнейшем будем полагать, что величина e удовлетворяет следующим условиям:
1) М(e) = 0;
2) выборочные значения e являются независимыми значениями;
3) величина e имеет нормальное распределение.
Регрессионный анализ не может самостоятельно по данной выборке предложить ту или иную форму регрессионной кривой. Вид регрессии должен быть выяснен с помощью иной теории, в которой рассматривалась бы суть данного явления. Например, утверждение о том, что энергия равновесного излучения пропорциональна четвертой степени температуры, было получено Стефаном и Больцманом из термодинамических соображений, а коэффициент s (U = s T4) был найден в результате обработки опытных данных.
На практике наиболее часто встречается одна из простейших моделей регрессии – линейная. Уравнение линейной регрессии имеет вид
y = а x + b + e.
Сформулируем задачу регрессионного анализа для данного случая.
По выборке объемом n, составленной из реализаций двумерной СВ (Х,Y), найти оценки параметров а и b и проверить, соответствует ли линейная модель экспериментальным данным.
Очевидно, что оценки а и b следует подобрать так, чтобы значения
= a xi + b как можно ближе находились к экспериментальным значениям. В качестве меры близости удобно взять сумму квадратов отклонений экспериментальных данных от теоретических. Можно показать, что в случае, когда e имеет нормальное распределение, наилучшие оценки параметров регрессии получают с помощью метода наименьших квадратов (МНК).
Применим МНК для отыскания оценок параметров а и b.
Составим сумму квадратов отклонений как функцию возможных, но неизвестных параметров а и b:
.
Для минимизации функции F приравняем к нулю ее частные производные по параметрам
Преобразуем полученную систему к более удобному виду
Учитывая, что , и (k = 1, 2), получим
Отсюда
(*)
Заметим, что, если искать уравнение линейной регрессии х от у, т.е.
x = c y + d, то
(**)
Учитывая, что , , rXY = rYX = r = , где SX и SY – выборочные средние квадратические отклонения, преобразуем уравнения (*) и (**) к следующему виду
Таким образом, уравнения линейной регрессии можно записать в виде:
,
или
,
,
где ух, ху – условные (групповые) средние, представляющие выборочные оценки MX(Y) и MY(X) соответственно.
Найдем тангенс угла между прямыми регрессии (см. рис.1) с угловыми коэффициентами а и .
Рис.1.
.
Из полученной формулы видно, что при r = ± 1 уравнения регрессии совпадают. Если r = 0, то прямые регрессии перпендикулярны и их уравнения имеют вид: , .
Значимость уравнения регрессии проверяют, используя дисперсионный анализ. В данном случае общую дисперсию разбивают на дисперсию, которая обусловлена регрессией, и дисперсию, которая обусловлена действием случайных факторов, т.е.
.
Введем обозначения , , .
megaobuchalka.ru
3. Парная корреляция. Оценка значимости коэффициента парной корреляции.
Для двух переменных Х и У теоретический коэффициент корреляции определяется следующим образом:
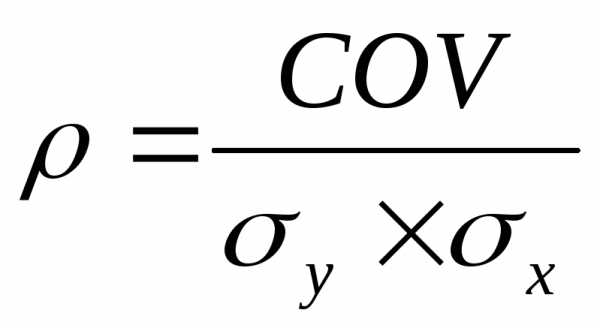 ,
где СOV–
к-т ковариации Х и У, а σyи σx– стандартные
отклонения.
,
где СOV–
к-т ковариации Х и У, а σyи σx– стандартные
отклонения.
Парный коэффициент корреляции является показателем тесноты связи лишь в случае линейной зависимости между переменными и обладает следующими основными свойствами. Коэффициент корреляции принимает значение в интервале (-1, +1). Коэффициент корреляции не зависит от выбора начала отсчета и единицы измерения. В практических расчетах к-т корреляции генеральной совокупности обычно неизвестен. По результатам выборки м.б. найдена его его точечная оценка – выборочн. к-т корреляции r, к-й является случайной величиной (т.к. выборочная совокупность переменных Х и У случайна):
, где ,– оценки дисперсий Х и У.
Для оценки значимости коэффициента корреляции применяется t-критерий Стьюдента. При этом фактическое значение этого критерия определяется по формуле:
Вычисленное по этой формуле значение tпабл сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы.
Если tмабл > tкр, то полученное значение коэффициента корреляции признается значимым (т.е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). Отсюда делается вывод, что между исследуемыми переменными есть тесная статистическая взаимосвязь.
Если значение rу х близко к нулю, связь между переменными слабая. Если случайные величины связаны положительной корреляцией, это означает, что при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать. Если случайные величины связаны отрицательной корреляцией, это означает, что при возрастании одной случайной величины другая имеет тенденцию в среднем убывать.
Коэффициенты парной корреляции используются для измерения силы линейных связей различных пар признаков из их множества. Для множества т признаков п наблюдений получают матрицу коэффициентов парной корреляции R:
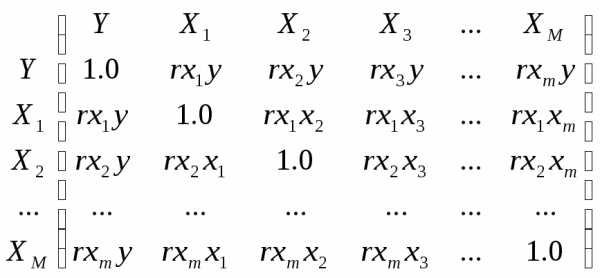
Одной корреляционной матрицей нельзя полностью описать зависимости между величинами. В связи с этим в многомерном коррелицон. анализе рассматриваются 2 задачи:
Определение тесноты связи одной случайной величины с совокупностью остальных величин, включенных в анализ.
Определение тесноты связи между величинами при фиксировании или исключении влияния остальных величин.
Эти задачи решаются с помощью коэффициентов множественной и частной корреляции соответственно.
4. Линейное уравнение регрессии, коэффициенты модели.
Линейная модель парной регрессии есть: у=а0+а1х+
а1 — коэф-т регрессии, показывающий, как изменится у при изменении х на единицу
а0 — это свободный член, расчетная величина, содержания нет.
— это остаточная компонента, т.е. случайная величина, независимая, нормально распределенная, мат ожид = 0 и постоянной дисперсией.
В матричной форме модель имеет вид:
Y=XA+ε
Где Y– вектор-столбец размерности (nx1) наблюдаемых значений зависимой переменной; Х– матрица размерности (nx2) наблюдаемых значений факторных признаков. Дополнительный фактор х0 вводится для вычисления свободного члена; А– вектор-столбец размерности (2х1) неизвестных, подлежащих оценке коэффициентов регрессии; ε– вектор-столбец размерности (nх1) ошибок наблюдений
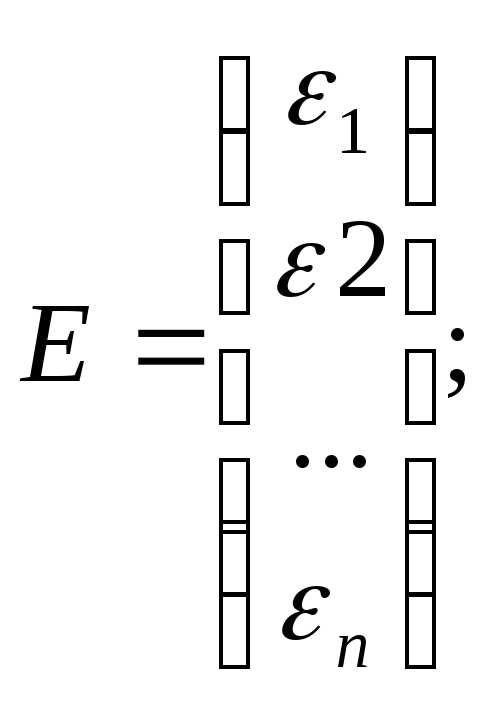
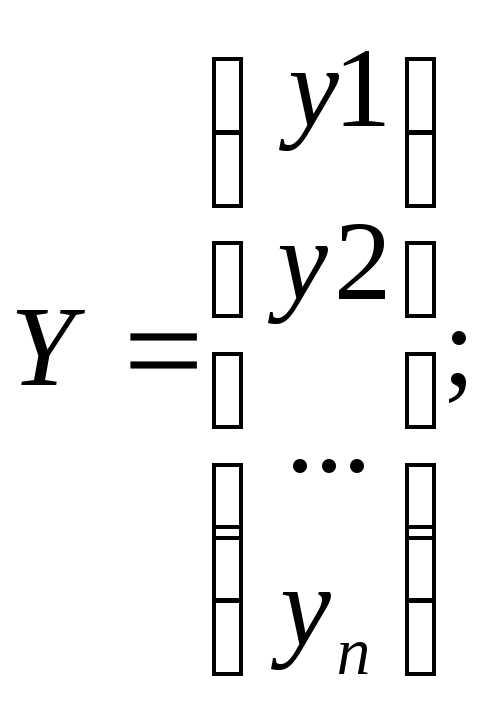

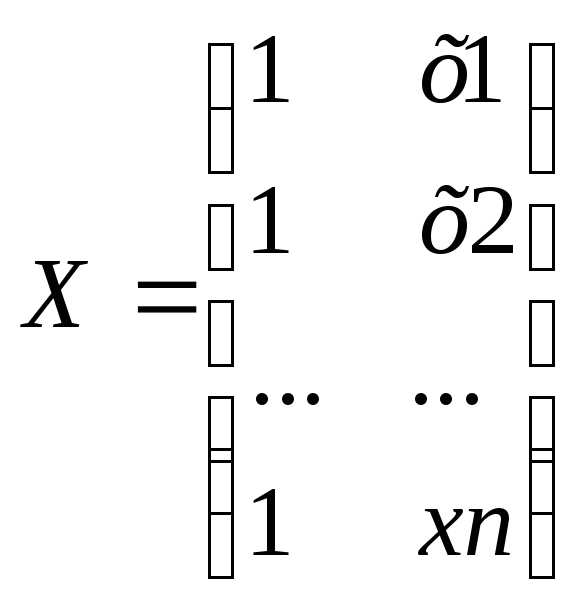 ;
; 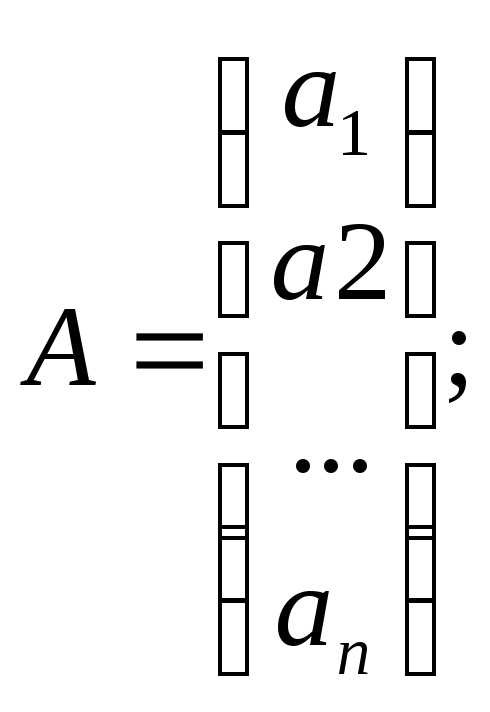
Параметры модели находятся с использованием МНК. Подсчитывается сумма квадратов ошибок наблюдений.
studfiles.net
|
ТОП 10: |
Частные коэффициенты корреляции характеризуют взаимосвязь между двумя выбранными переменными при исключении влияния остальных показателей (т.е. характеризуют «чистую» связь только между этими признаками) и важны для понимания взаимодействия всего комплекса показателей, т.к. позволяют определить механизмы усиления-ослабления влияния переменных друг на друга. Таблица 2.4 Матрица выборочных частных коэффициентов корреляции исследуемых экономических показателей
Теперь необходимо проверить значимость полученных частных коэффициентов корреляции, т.е. гипотезу H0: ρij/{..} = 0. Для этого мы рассчитаем наблюдаемые значения t-статистик для всех коэффициентов по формуле: где l – порядок частного коэффициента корреляции, совпадающий с количеством фиксируемых переменных случайных величин (в нашем случае l=3), а n – количество наблюдений.
Построим матрицу наблюдаемых значений t-статистик для всех коэффициентов rij/{..} Таблица 2.5 Матрица наблюдаемыx значений t-статистик частных коэффициентов корреляции исследуемых экономических показателей
Наблюдаемые значения t-статистик необходимо сравнивать с критическим значением tкр, найденным для уровня значимости α=0,05 и числа степеней свободы ν=n – l – 2=45. Получаем tкр=2,01410336. По результатам, представленным в таблице 2.5, наблюдаемое значение t-статистики больше критического tкр=2,01410336 по модулю для частных коэффициентов корреляции ρyx6, ρyx13 и ρyx14. Следовательно, гипотеза о равенстве нулю этих коэффициентов отвергается с вероятностью ошибки, равной 0,05, т.е. соответствующие коэффициенты значимы. Для остальных коэффициентов наблюдаемое значение t-статистики меньше критического значения по модулю, следовательно, гипотеза H0 не отвергается, т.е. ρyx15, ρx6x13, ρx6x14, ρx6x15, ρx13x14, ρx13x15 и ρx14x15 — незначимы.
Для значимых частных коэффициентов корреляции мы можем построить с заданной надёжностью γ интервальную оценку ρmin ≤ ρ ≤ ρmaxс помощью Z-преобразования Фишера: Алгоритм построения интервальной оценки для частного генерального коэффициента корреляции такой же, как и для парного; единственное отличие заключается в расчёте ΔZ : , где l – порядок частного коэффициента корреляции, совпадающий с количеством фиксируемых переменных случайных величин (в нашем случае l=3), а n – количество наблюдений. Находим ΔZ= 0,2954757. Построим с надёжностью γ=0,95 и с учётом найденного ΔZ= 0,2954757. доверительные интервалы для всех значимых частных коэффициентов корреляции, полученных нами. Расчёты представим в виде таблицы 2.6. Таблица 2.6 Расчёт доверительных интервалов для частных генеральных коэффициентов корреляции исследуемых экономических показателей с надёжностью γ=0,95
Таким образом, доверительные интервалы с надёжностью γ=0,95 для всех значимых частных генеральных коэффициентов корреляции выглядят следующим образом: P(0,101409736≤ ρyx6≤ 0,59972071)=0,95 P(0,329808506≤ ρyx13≤ 0,732251574)=0,95 P(0,122518987≤ ρyx14≤ 0,613234527)=0,95 Теперь построим таблицу сравнения выборочных парных и частных коэффициентов корреляции для всех переменных. Сравнение парных и частных коэффициентов играет важную роль в выявлении механизмов воздействия переменных друг на друга. Парный коэффициент корреляции показывает тесноту связи между двумя признаками на фоне действия остальных переменных, а частный характеризует взаимосвязь этих двух признаков при исключении влияния остальных переменных, т.е. их «личную» взаимосвязь. Таким образом, если оказывается, что парный коэффициент корреляции между двумя переменными по модулю больше соответствующего частного, то остальные переменные усиливают связь между этими двумя признаками. Соответственно, если парный коэффициент корреляции между двумя переменными по абсолютной величине меньше частного, то остальные признаки ослабляют связь между рассматриваемыми двумя. Таблица 2.7 Таблица сравнения выборочных оценок парных и частных коэффициентов корреляции пар исследуемых показателей с выделением значимых коэффициентов (при α=0,05)
По полученным данным можно сделать следующие выводы. Не все значимые корреляционные зависимости, полученные на этапе расчёта парных коэффициентов корреляции, подтвердились и при вычислении частных коэффициентов корреляции. При этом выявлены следующие механизмы воздействия переменных друг на друга:
1. Наиболее тесная связь наблюдается изучаемым признаком Y – производительностью труда(Y) и факторным признаком: «среднегодовой фонд заработной платы ППП» (Х13). Воздействие других переменных (Х6- удельный вес покупных изделий, Х14 –фондовооруженность труда, Х15 – оборачиваемость нормируемых оборотных средств) усиливает взаимосвязь между ними, т.к. абсолютная величина частного коэффициент корреляции ryx13/x6x14x15 = 0,563597012ниже абсолютного значения парного коэффициента корреляции ryx13=0,577299. 2. Между факторным признаком «удельный вес покупных изделий» (Х6) и среднегодовым фондом заработной платы (Х13) наблюдалась прямая не значимая связь, но при воздействии других переменных она перестала быть значимой и стала обратной, rх6х13/уx14x = -0,0787326, rх6х13=0,175528. Аналогично yx15. |
infopedia.su
