Комбинаторные уравнения онлайн – Комбинаторные уравнения | Онлайн калькулятор

Содержание

Комбинаторные уравнения

Для решения комбинаторных уравнений, достаточно знать основные формулы комбинаторики:

формула перестановок $P_n=n!$,
формула сочетаний $A_n^k=\frac{n!}{(n-k)!}$,
формула комбинаций $С_n^k=\frac{n!}{k!(n-k)!}$

и уметь решать алгибраические уравнения.

Задача 1. Решить комбинаторное уравнение:

$$\frac{P_x+3P_{x-1}}{2P_{x+2}+14P_{x+1}}=\frac{2A_{x}^{5}}{5A_{x+2}^{7}}$$

Решение.

Шаг 1. Применяем формулы комбинаторики (перестановки, сочетания) получаем:

$$P_{x+1}= (x+1)!,\: A_{x}^{5}=\frac{x!}{(x-5)!},\: A_{x+2}^{7}=\frac{(x+2)!}{(x+2-7 )!}=\frac{(x+2 )!}{(x-5 )!} $$

Шаг 2. Подставим эти выражения в уравнение и найдем его решение:

$$\frac{x!+3\cdot(x-1)! }{2\cdot (x+2)!+14\cdot (x+1)!}=\frac{2\cdot\frac{x!}{(x-5)!} }{5\cdot\frac{(x+2 )!}{(x-5 )!} }$$

$$x^2-11x+30=0\Rightarrow x_1=5,\: x_2=6$$

Для проверки правильности решения комбинаторного уравнения можно воспользоваться калькулятором комбинаторных уравнений. Формулы набираем как на обычном калькуляторе, знак факториал(!)

Задача 2 Решить комбинаторное уравнение:

$$C_{15}^{14} C_{x+3}^{3}= C_{5}^{1} C_{x+2}^{2} C_{x+1}^{x}+ (C_{5}^{3})^2$$

Решение. Имеем:

$$C_{15}^{14}= \frac{15!}{14!*1!}=1,5$$

$$ C_{x+3}^{3}= \frac{(x+3)!}{x!*3!}= \frac{1}{6}(x^2+6x^2 +11x+6),$$

$$C_{5}^{1}= \frac{(5)!}{1!*4!}=5,$$

$$C_{x+2}^{2}=\frac{(x+2)!}{2!*x!}= \frac{1}{2}(x^2+3x^2+3),$$

$$C_{x+1}^{x}=\frac{(x+1)!}{x!*1!}=x+1,$$

$$(C_{5}^{3})^2=( \frac{(5)!}{3!*2!})^2=100.$$

Подставим эти выражения в уравнение:

$$15*\frac{1}{6}(x^3+6x^2+11x+6)=5*\frac{1}{2}(x+1)+100$$

$$x^2+6x-18=0 \Rightarrow x_1=3,\: x_2=-6$$

Корень $x=-6$ является посторонним, так как не попадает в область определения уравнения.

ЗАДАНИЯ
по контрольной работе
«СПЕЦИАЛЬНАЯ МАТЕМАТИКА»

Все варианты СКАЧАТЬ

В каждом варианте подробно решены все задачи. Контрольные работы выполнены в формате Word. Стоимость решения одного варианта, или аналогичной работы от 300р,, срок выполнения не более 1 дня (можно заказать задачи выборочно, из любого варианта), ЗАКАЗАТЬ

www.reshim.su

Элементы комбинаторики. Перестановки, размещения, сочетания

Ниже калькулятор, подсчитывающий число перестановок, размещений и сочетаний. Под ним, как водится, ликбез, если кто подзабыл.

Число перестановок из n

Число размещений из n по m

Число размещений из n по m с повторениями

Число сочетаний из n по m

Сохранить share extension

Итак, есть множество из n элементов.

Вариант упорядочивания данного множества называется перестановкой (permutation).
Например, есть множество, состоящее из 3 элементов — А, В, и С. Пример перестановки — СВА. Число всех перестановок из n элементов:

Пример: Для случая А, В, С число всех перестановок 3! = 6. Перестановки: АВС, АСВ, ВАС, ВСА, САВ, СВА

Если из множества n элементов выбирают m в определенном порядке, это называется размещением (arrangement).
Пример размещения из 3 по 2: АВ или ВА — это два разных размещения. Число всех размещений из n по m

Пример: Для случая А, В, С число всех размещений из 3 по 2 равно 3!/1! = 6. Размещения: АВ, ВА, АС, СА, ВС, СВ

Также бывают размещения с повторениями, как ясно из названия, элементы на определенных позициях могут повторяться.
Число всех размещений из n по m с повторениями:

Пример: Для случая А, В, С число всех размещений из 3 по 2 с повторениями равно 3*3 = 9. Размещения: AA, АВ, АС, ВА, BB, ВС, СА, СВ, CC

Если из множества n элементов выбирают m, и порядок не имеет значения, это называется сочетанием (combination).
Пример сочетания из 3 по 2: АВ. Число всех сочетаний из n по m

Пример: Для случая А, В, С число всех сочетаний из 3 по 2 равно 3!/(2!*1!) = 3. Сочетания: АВ, АС, СВ

Приведем до кучи формулу соотношения между перестановками, размещениями и сочетаниями:

Обратите внимание, что внизу

planetcalc.ru

Элементы комбинаторики. Перестановки, размещения, сочетания

Данный калькулятор делает подсчет числа перестановок, а также размещений и сочетаний.

Перестановка (permutation) — некий вариант упорядочивания множества.

Глянем на пример: и так, у нас есть множество, состоящее из 3 элементов — А, В, и С. Пример перестановки — СВА.

Количество всех перестановок из n элементов рассчитывается:

Пример: Для случая А, В, С количество всех перестановок 3! = 6. Перестановки: АВС, АСВ, ВАС, ВСА, САВ, СВА

Размещением (arrangement) называется явление, когда из множества n элементов выбирают m в определенном порядке.

Например размещения из 3 по 2: АВ или ВА — это два разных размещения. Количество всех размещений из n по m вычисляется:

Снова пример:

Для случая А, В, С количество всех размещений из 3 по 2 равно 3!/1! = 6. Размещения: АВ, ВА, АС, СА, ВС, СВ

Также бывают размещения с повторениями, как ясно из названия, элементы на определенных позициях могут повторяться.

Количество всех размещений из n по m с повторениями можно высчитать так:

Следующий пример: Для случая А, В, С число всех размещений из 3 по 2 с повторениями равно 3*3 = 9. Размещения: AA, АВ, АС, ВА, BB, ВС, СА, СВ, CC

Сочетание (combination) — когда из множества n элементов выбирают m, и порядок не важно какой.

Пример сочетания из 3 по 2: АВ.

Количество всех размещений из n по m рассчитываем:

Пример: Для случая А, В, С число всех сочетаний из 3 по 2 равно 3!/(2!*1!) = 3. Сочетания: АВ, АС, СВ

Возведем все в 1 формулу соотношения между перестановками, размещениями и сочетаниями

The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 .. %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v.d.

z.d.

yes

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

minutes

minute

minutes

hour

hours

days

day

days

month

months

year

of the year

years

ago

%1 minutes ago

%1 minutesу ago

%1 minutes ago

%1 hour ago

%1 hours ago

%1 days ago

%1 day ago

%1 days ago

%1 month ago

%1 months ago

%1 year ago

%1 of the year ago

%1 years ago

Элементы комбинаторики. Перестановки, размещения, сочетания

Число перестановок из n:

Число размещений из n по m:

Число размещений из n по m с повторениями:

Число сочетаний из n по m:

hostciti.net

Уравнения онлайн. Математика онлайн

Решение любого типа уравнений онлайн на Math34.biz для закрепления изученного материала студентами и школьниками. Пошаговое решение уравнений онлайн на сайте Math34.biz. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений. Math34.biz поможет решить любое уравнение онлайн. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Уравнения онлайн. Решить уравнение онлайн на сайте Math34.biz. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.

math24.biz

кубических, тригонометрических, логарифмических и др. уравнений · Калькулятор Онлайн

Введите уравнение с неизвестным, для которого требуется найти корни.

Решим уравнение с неизвестным x
(если данное уравнение калькулятор способен решить)

Левая и правая части уравнения теперь совмещены в одну.
И знак равенства теперь находится в форме.

Примеры решаемых уравнений

Примеры решаемых уравнений (простых)

Система не умеет решать абсолютно все уравнения из ниже перечисленных, но вдруг Вам повезет 🙂
Решение Алгебраических (по алгебре): Квадратных, кубических и других степеней уравнений x^4-x=0
Решение Тригонометрих уравнений sin(2*x)=1

Правила ввода уравнений

В поле ‘Уравнение’ можно делать следующие операции:

Правила ввода функций

В функции f можно делать следующие операции:

Действительные числа: вводить в виде 7.5, не 7,5
2*x: — умножение
3/x: — деление
x^3: — возведение в степень
x + 7: — сложение
x — 6: — вычитание

Функция f может состоять из функций (обозначения даны в алфавитном порядке):

absolute(x): Функция — абсолютное значение x (модуль x или |x|)
arccos(x): Функция — арккосинус от x
arccosh(x): Функция — арккосинус гиперболический от x
arcsin(x): Функция — арксинус от x
arcsinh(x): Функция — арксинус гиперболический от x
arctan(x): Функция — арктангенс от x
arctanh(x): Функция — арктангенс гиперболический от x
e: Функция — e это то, которое примерно равно 2.7
exp(x): Функция — экспонента от x (тоже самое, что и e^x)
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
log(x) or ln(x): Функция — Натуральный логарифм от x (Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
pi: Число — «Пи», которое примерно равно 3.14
sign(x): Функция — Знак x
sin(x): Функция — Синус от x
cos(x): Функция — Косинус от x
sinh(x): Функция — Синус гиперболический от x
cosh(x): Функция — Косинус гиперболический от x
sqrt(x): Функция — Корень из от x
x^2: Функция — Квадрат x
tan(x): Функция — Тангенс от x
tanh(x): Функция — Тангенс гиперболический от x

www.kontrolnaya-rabota.ru

Онлайн калькулятор: Комбинаторика. Генератор сочетаний.

Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.

Описание алгоритма генерации под калькулятором.

addimport_exportmode_editdelete

Множество

Размер страницы: 5102050100chevron_leftchevron_right

Сохранить share extension

Алгоритм

Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5 — последнее сочетание, так как все его элементы равны n — m + i.

planetcalc.ru

3.8. Решение комбинаторных уравнений

В комбинаторике тоже могут решаться уравнения, особенностью которых является то, что неизвестная принадлежит множеству натуральных чисел. Например, уравнения вида 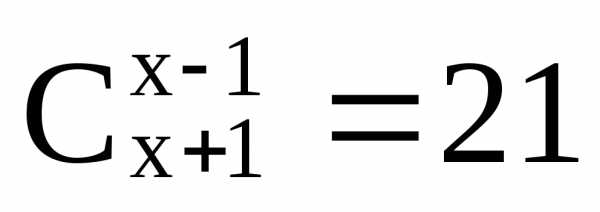,xN, где N – множество натуральных чисел или вида:

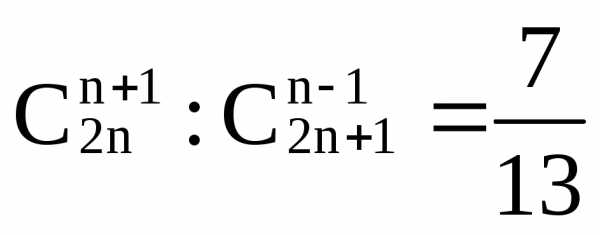, xN (решите!).

При решении комбинаторных уравнений часто необходимо уметь выполнять действия с факториалами типа:

или:

Например, в задаче о сравнении пар записей в базе данных из n записей:

, – что и требовалось доказать.

В комбинаторике рассматриваются и другие типовые комбинаторные комбинации, например, разбиения n-элементного множества на k подмножеств, которые называются блоками разбиения. В информатике вычисления на конечных математических структурах часто называют комбинаторными вычислениями, и они требуют комбинаторного анализа для установления свойств и оценки применимости используемых алгоритмов. На рис. 11 приведен один из возможных вариантов классификации основных комбинаций.

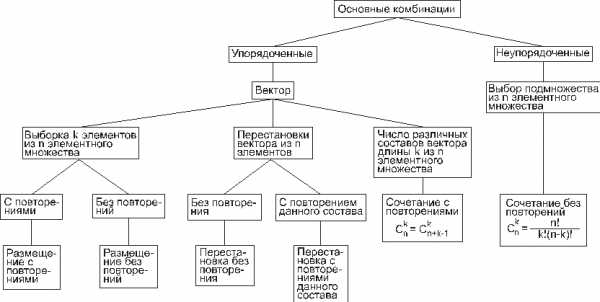
Рис. 11. Основные комбинации

Комбинаторные задачи могут быть решены, например, системой компьютерной математики Matematica (3,4) фирмы Wolfram Research,Inc. – пакет расширения «Дискретная математика» (DiscreteMath) – комбинаторика и ее функции (Combinatorica, CombinatorialFunctions): функции перестановок и сочетаний и др.

4. Основные понятия теории графов

4.1. Способы задания графов

Совокупность множества М с заданным на нем бинарным отношением ТМ² [9] называется графом

G=<M,T>,

где М – носитель графа – множество вершин, изображаемых точками, Т – сигнатура графа – множество линий, обозначающих отношения и называемых ребрами.

Между элементами М и Т определено отношение инцидентности, т.е. связи между двумя элементами множества М через один элемент множества Т. Примеры графов: отношения отцовства и материнства на множестве людей, отношения подчиненности, карты дорог местности, электрические схемы соединений приборов и т.д.

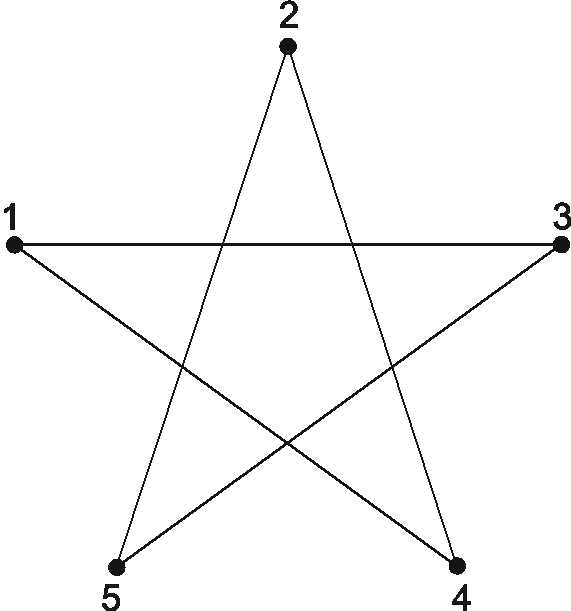
Рис. 12. Пример графа «звезда»

М={1,2,3,4,5},

Т={(1,3),(1,4),(2,4),(2,5),(3,1),(3,5),(4,2),(4,1),(5,3),(5,2}).

Множество линий-ребер в Т задается обозначением пары (i,j), где i,j – инцидентные вершины, отношение Т – «быть связанным».

Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий. В этих задачах несущественно, соединены ли точки конфигурации отрезками прямых или они криволинейны, какова длина линий и другие геометрические характеристики конфигурации. Важно лишь, что каждая линия соединяет какие-либо две из заданных точек [24].

Первые серьезные результаты теории графов связаны с решением задач построения электрических цепей (Г. Кирхгоф) и подсчета числа химических соединений с различными типами молекулярных связей (А. Кэли). Изобразите в виде графа молекулу

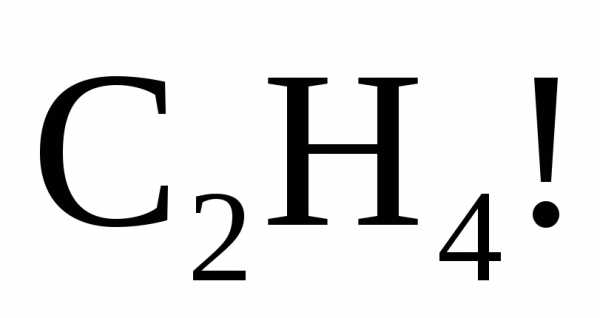
В 30-е годы ХХ века благодаря трудам Д. Кенига [19] теория графов стала развиваться как самостоятельный раздел математики.

Широкое развитие теория графов получила с 50-х годов ХХ века в связи с появлением такой науки, как кибернетика. Графы применяют при анализе функционирования систем. С отдельными компонентами изучаемой системы удобно связывать вершины графа, а с парами взаимодействующих компонент – его ребра. Такой граф называют структурным графом системы.

В некоторых задачах существенно направление ребер графа. Направленные ребра называют дугами, а содержащий их граф – ориентированным (орграфом). Таковым графом может быть изображена диаграмма Хассе. Соответственно граф с неориентированными ребрами называется неориентированным.

Множество ребер может быть пусто. Если же множество вершин пусто, то пусто и множество ребер. Такой граф называется пустым. Линии, изображающие ребра, могут пересекаться на изображении графа, но точки их пересечений не являются вершинами. Различные ребра могут быть инцидентны одной и той же паре вершин, в этом случае они называются кратными. Граф, содержащий кратные ребра, называют мультиграфом (псевдографом). Ребро (дуга) может соединять некоторую вершину саму с собой, такое ребро (дуга) называется петлей. Будем рассматривать конечные графы, содержащие конечные множества вершин и ребер (дуг).

Рассмотрим предложенную фон Нейманом архитектуру ЭВМ, которая состоит из множества устройств М={а,b,c,d,e}, где а – устройство ввода, b – арифметическое устройство (процессор), с – устройство управления, d – запоминающее устройство, е – устройство вывода [9-10].

Информационный обмен между этими устройствами задается графом (рис. 13).

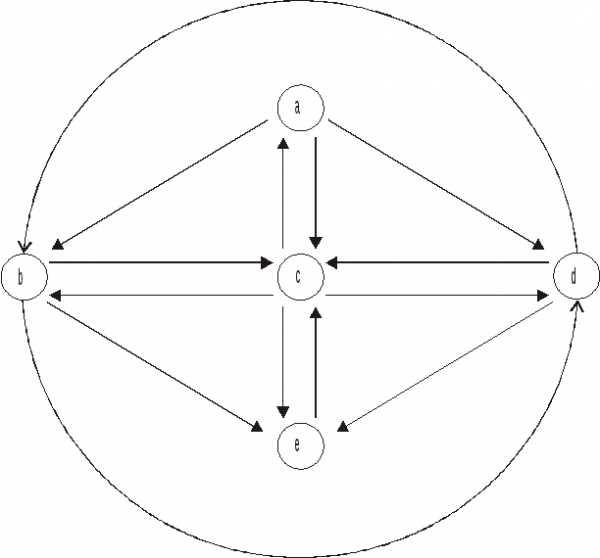
Рис. 13. Граф, описывающий архитектуру

фон Неймановской ЭВМ

Вершины графа на рис. 13 для удобства изображены кружками, а не точками, как на рис. 11.

Граф можно задать так называемой матрицей смежности, каждой i-ой строке (j-му столбцу) которой однозначно сопоставляют элемент множества М, между которыми выполняется отношение смежности. Две вершины, инцидентные одному ребру, смежны. Два ребра, инцидентные одной вершине, тоже смежны. Тогда каждая клетка b_ij взаимно однозначно соответствует элементам множества ММ=М². Клетку b_ij, которая соответствует элементу, принадлежащему бинарному отношению ТМ², отмечают, например, единицей, а в остальные клетки записывают нули.

Рассмотрим матрицу смежности В для графа, изображенного на рис. 13. Устройства i,j находятся в отношении Т, если из устройства i информация поступает в устройство j.

Граф можно задать и с использованием перечисления его дуг, как это сделано на рис. 13:

М={а,b,с,d,е},

Т={(а,b),(а,с),(а,d),(b,с),(b,е),(b,d),(с,а),(с,b),(с,d),(с,е),(d,с),(d,b),(d,е),(е,с)}.

Граф можно задать в виде так называемого фактор-множества, представленного парами «элемент множества М – подмножество М, представляющее собой окрестность единичного радиуса этого элемента»:

[<a,{b,c,d}>,<b,{c,d,е}>,<c,{a,b,d,e}>,<d,{b,c,e}>,<e,{c}>].

Ориентированный граф может быть задан и матрицей инцидентности А размерностью nm: A=a_ij, где n=|M|, m=|Т|, у которой

если вершина a_i является концом дуги t_j;

если вершина a_i является началом дуги t_j;

если вершина a_i не инцидентна дуге t_j,

, .

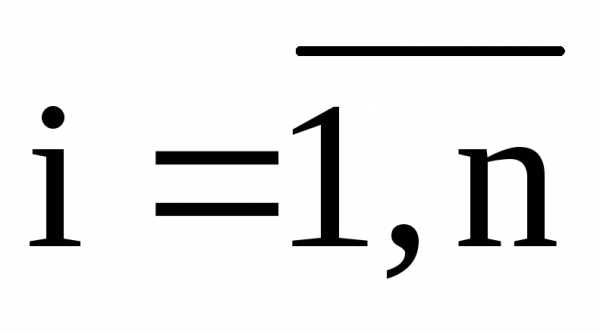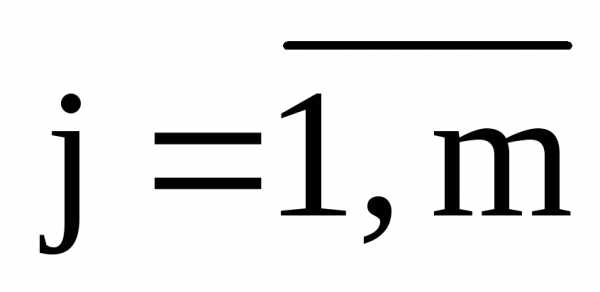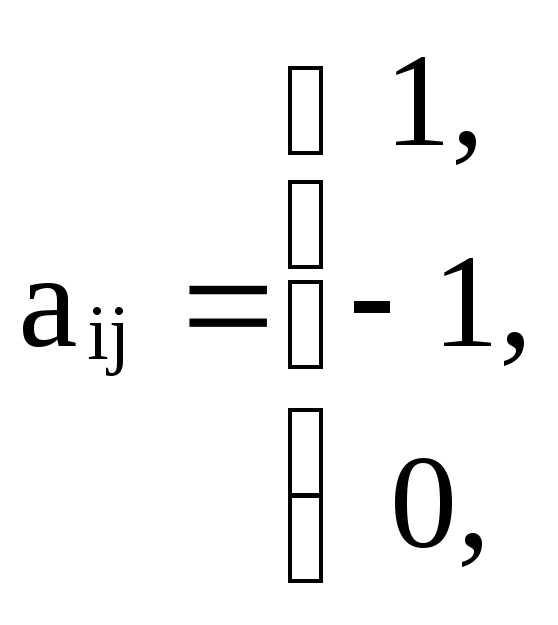
Так, для ориентированного графа (рис. 14) матрица инцидентности имеет вид:

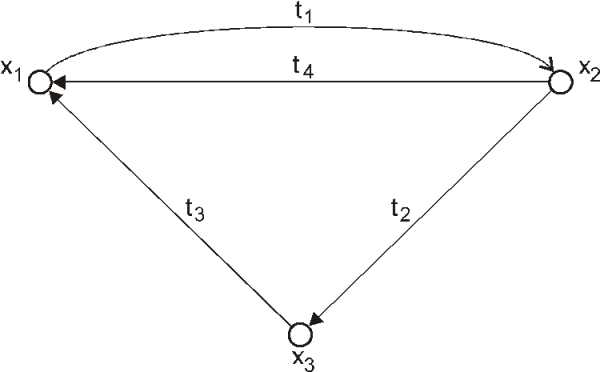
Рис. 14. Некоторый ориентированный граф

В описанном виде матрицы инцидентности применимы только к графам без петель, в случае наличия которых матрицу надо разбить на две полуматрицы: положительную и отрицательную. Ориентированный граф также может быть задан матрицей смежности.

Для графов с кратными ребрами в матрице смежности указывают кратность ребер, например, для графа, изображенного на рис. 15, матрица смежности представляется в виде:

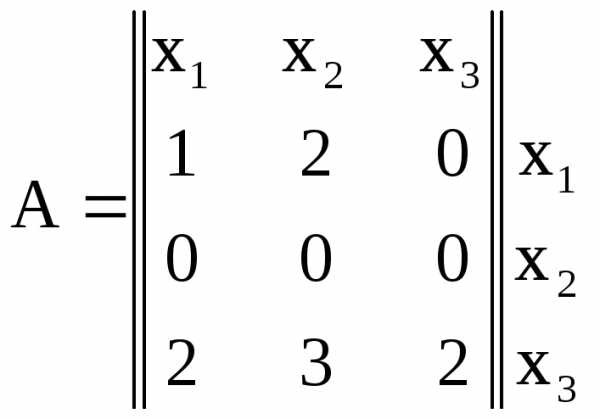
Такой граф называют мультиграфом.

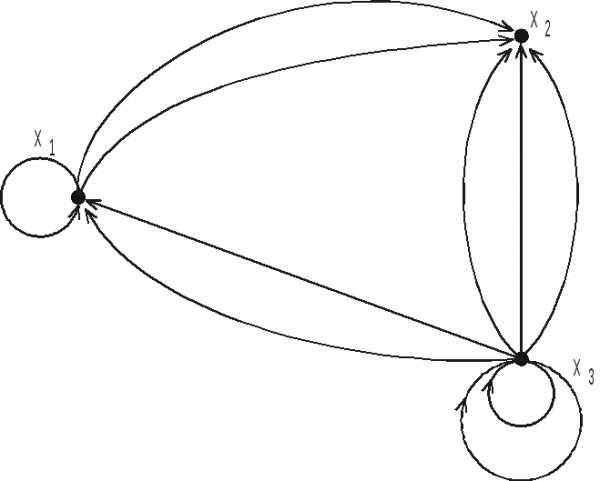
Рис. 15. Некоторый ориентированный мультиграф

Граф называется нагруженным, если каждому ребру (дуге) поставлено в соответствие некоторое действительное число (длина дуги, вес дуги, стоимость дуги и т.д.).

Представим в виде графа некоторые бинарные отношения [9]. Отношение Т в множестве М рефлексивно, как мы уже знаем, если для каждого элемента mМ справедливо (m,m)Т. На графе это изображается петлей (рис. 16а). На матрице смежности графа с рефлексивным отношением все элементы, лежащие на главной диагонали отмечены единицами.

Отношение во множестве М называется симметричным, если из (m_i,m_j)Т следует (m_i,m_j)М, m_im_j (рис. 16б). Матрица смежности симметричного отношения симметрична относительно главной диагонали.

Отношение Т в множестве М называется транзитивным, если из (m_i,m_j)Т, (m_i,m_k)Т следует (m_i,m_k)Т m_i, m_j,m_kМ, m_im_j, m_im_k, m_jm_k (рис. 16в).

В графе, задающем транзитивное отношение Т, для всякой пары дуг таких, что конец первой совпадает с началом второй, существует транзитивно замыкающая дуга, имеющая общее начало с первой и общий конец со второй.

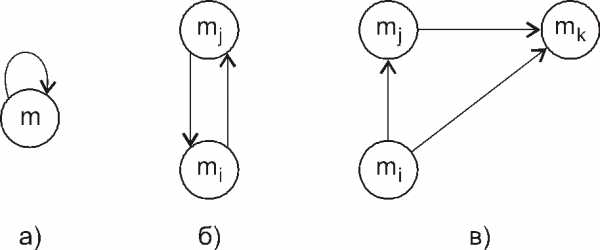
Рис. 16. Изображения бинарных отношений в виде графа

а) рефлексивное отношение, б) симметричное отношение,

в) транзитивное отношение

studfiles.net

Комбинаторные уравнения

Элементы комбинаторики. Перестановки, размещения, сочетания

Элементы комбинаторики. Перестановки, размещения, сочетания

Уравнения онлайн. Математика онлайн

кубических, тригонометрических, логарифмических и др. уравнений · Калькулятор Онлайн

Введите уравнение с неизвестным, для которого требуется найти корни.

Примеры решаемых уравнений

Примеры решаемых уравнений (простых)

Правила ввода уравнений

Правила ввода функций

Онлайн калькулятор: Комбинаторика. Генератор сочетаний.

Множество

Алгоритм

3.8. Решение комбинаторных уравнений

4. Основные понятия теории графов

4.1. Способы задания графов

Добавить комментарий Отменить ответ