Формулы половинного угла: доказательства (вывод) и примеры
Формулы половинного угла (половинного аргумента) – это часть от всех основных тригонометрических формул. Они выражают функции синус, косинус, тангенс, котангенс угла `\frac{\alpha}2` через эти ж функции аргумента `\alpha`. Они, можно сказать, противоположны формулам двойного угла. Ниже приведены все формулы половинных углов, их вывод, а также примеры решения задач с их использованием.
Содержание статьи:
Список всех формул половинного угла
Их можно встретить записанными в двух видах. В первом каждая из тригонометрических функций выражается через радикал:
`sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`
`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`
`tg \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}=` `\frac {sin \ \alpha}{1+cos \ \alpha}=\frac {1-cos \ \alpha}{sin \ \alpha}`
`ctg \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}=` `\frac {sin \ \alpha}{1-cos \ \alpha}=\frac {1+cos \ \alpha}{sin \ \alpha}`
Знак «+» или «-» перед корнями зависит от того, в какую из координатных четвертей попадает угол `\frac{\alpha}2`.
Во втором варианте имеем дело с квадратами тригонометрических функций половинного угла:
`sin^2 \ \frac \alpha 2=\frac {1-cos \ \alpha}2`
`cos^2 \ \frac \alpha 2=\frac {1+cos \ \alpha}2`
`tg^2 \ \frac \alpha 2=\frac {1-cos \ \alpha}{1+cos \ \alpha}`
`ctg^2 \ \frac \alpha 2=\frac {1+cos \ \alpha}{1-cos \ \alpha}`
Формула синуса и косинуса половинного угла имеет место при любом угле `\alpha`.
Формула тангенса половинного угла справедлива для тех углов `\alpha`, при которых определен `tg \frac \alpha 2`, то есть при ` \alpha\ne\pi+2\pi n, \ n \in Z`.
Формула котангенса выполняется для тех `\alpha`, при которых определен `ctg \frac \alpha 2`, то есть при ` \alpha\ne 2\pi n, \ n \in Z`.
С помощью следующего набора формул можно выразить каждую из тригонометрических функций угла `\alpha` через тангенс половинного угла.
`sin \ \alpha= \frac{2tg\frac{\alpha}{2}}{1 + tg^{2}\frac{\alpha}{2}},` ` \alpha\ne \pi +2\pi n, n \in Z`
`cos \ \alpha= \frac{1 — tg^{2}\frac{\alpha}{2}}{1 + tg^{2}\frac{\alpha}{2}},` ` \alpha \ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac{2tg\frac{\alpha}{2}}{1 — tg^{2}\frac{\alpha}{2}},` ` \alpha \ne \pi +2\pi n, n \in Z,` ` \alpha \ne \frac{\pi}{2}+ \pi n, n \in Z`
`ctg \ \alpha = \frac{1 — tg^{2}\frac{\alpha}{2}}{2tg\frac{\alpha}{2}},` ` \alpha \ne \pi n, n \in Z,` `\alpha \ne \pi + 2\pi n, n \in Z`
Вывод формул половинного угла
Формула косинуса и синуса половинного угла выводится из формул косинуса двойного угла `cos \ 2\alpha=1-2 \ sin^2 \alpha` и `cos \ 2\alpha=2 \ cos^2 \alpha-1`. Запишем их в следующем виде: `cos \alpha=1-2 \ sin^2 \frac \alpha 2` и `cos \alpha=2 \ cos^2 \frac \alpha 2-1`. Выразив из первого равенства ` sin \frac \alpha 2` получим `sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`. Аналогично разрешив второе равенство относительно ` cos \frac \alpha 2` в результате будем иметь `cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`.
Формулы тангенса и котангенса половинного угла можно вывести, используя определения этих функций в виде `tg \frac \alpha 2=\frac{sin\frac \alpha 2}{cos \frac \alpha 2}` и `ctg \frac \alpha 2=\frac{cos \frac \alpha 2}{sin \frac \alpha 2}`, а также две уже доказанные выше формулы для синуса и косинуса.
В результате будем иметь: `tg \frac \alpha 2=\frac{sin\frac \alpha 2}{cos \frac \alpha 2}=` `\frac{\pm \sqrt{\frac {1-cos \ \alpha}2}}{\pm \sqrt{\frac {1+cos \ \alpha}2}}=` `\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}` и `ctg \frac \alpha 2=\frac{cos\frac \alpha 2}{sin \frac \alpha 2}=` `\frac{\pm \sqrt{\frac {1+cos \ \alpha}2}}{\pm \sqrt{\frac {1-cos \ \alpha}2}}=` `\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}`.
Примеры использования при решении задач
Пример 1. Найти `cos 15^\circ`, если известно, что `cos 30^\circ=\frac{\sqrt3}2`.
Решение. Формула половинного угла для тригонометрической функции косинус имеет вид `cos^2 \ \frac \alpha 2=\frac {1+cos \ \alpha}2`. Подставив известные значения, имеем `cos^2 15^\circ=\frac {1+cos 30^\circ}2=` `\frac{1+\frac{\sqrt3}2}2=\frac{2+\sqrt3}4`. Имея значение `cos^2 15^\circ`, найдем `cos 15^\circ`. Поскольку угол 15 градусов лежит в первой координатной четверти, а косинус в этой четверти имеет знак «+», то `cos 15^\circ=\sqrt{\frac{2+\sqrt3}4}=` `\frac{\sqrt{2+\sqrt3}}2`.
Ответ. `cos 15^\circ=\frac{\sqrt{2+\sqrt3}}2`.
Пример 2. Вычислить значение выражения `4cos \frac {\alpha}2+2cos \alpha+5`, если `cos \alpha=\frac {1}8`.
Решение. Используя ту же формулу, что и в первом примере (`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`) и известное значение косинуса, упростим выражение: `4\sqrt{\frac {1+cos \ \alpha}2}+2cos \alpha+5=4\sqrt{\frac {1+\frac {1}8}2}+2 \cdot \frac {1}8+5=` `4\sqrt{\frac {9}16}+\frac{1}4+5=8\frac{1}4`.
Ответ. `4cos \frac {\alpha}2+2cos \alpha+5=8\frac{1}4`.
Еще несколько примеров с подробным объяснением посмотрите на видео:
В большинстве случаев формулы половинного угла используются при преобразовании тригонометрических выражений.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Синус половинного угла, формула и примеры
ОПРЕДЕЛЕНИЕ Синус половинного угла выражается формулой, которая связывает функцию угла и функцию угла формуле
Вывод формулы синуса половинного угла
Получить эту формулу можно используя формулу косинуса двойного угла следующим образом:
откуда
Эту формулу еще называют формулой понижения степени синуса.
Примеры решения задач
ПРИМЕР 1| Задание | Вычислить
|
| Решение | Для вычисления данного интеграла воспользуемся формулой половинного угла синуса
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Тригонометрические формулы половинного углаФормулы по геометрии
Рассмотрим прямоугольный треугольник, у которого угол ACB прямой.
a, b – катеты прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
α – угол треугольника, противолежащий стороне a
A, B, C – вершины треугольника
Синус половинного угла sin(α/2) равен:
Косинус половинного угла cos(α/2) равен:
Тангенс половинного угла tg(α/2) равен:
Котангенс половинного угла ctg(α/2) равен:
Все формулы по теме Тригонометрические формулы половинного угла:
formylu.ru
Формулы синус косинус и тангенс половинного угла
Рассмотрены простейшие построения, план решения задач на построение, решаются четыре задачи более сложного уровня, приведены примеры с указаниями к решению некоторых задач. Построить равнобедренный треугольник по углу при основании и высоте, опущенной на основание (слайд 16).
Формулы синус косинус и тангенс половинного угла
Тригонометрические функции: \(\sin \alpha\), \(\cos \alpha\), \(\tan \alpha\), \(\cot \alpha\)
Синус половинного угла
Примечание : Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол \(\alpha/2\) в левой части. Данное правило справедливо также для других формул, приведенных ниже.
Косинус половинного угла
Тангенс половинного угла
Котангенс половинного угла
Выражение синуса через тангенс половинного угла
Выражение косинуса через тангенс половинного угла
Выражение тангенса через тангенс половинного угла
Выражение котангенса через тангенс половинного угла
Сайт оптимизирован для Chrome, Firefox, Safari и Internet Explorer.
Формулы синус косинус и тангенс половинного угла
Формулы половинного угла тригонометрических функций
Формулы половинного угла (половинного аргумента) – это часть от всех основных тригонометрических формул. Они выражают функции синус, косинус, тангенс, котангенс угла `\frac2` через эти ж функции аргумента `\alpha`. Они, можно сказать, противоположны формулам двойного угла. Ниже приведены все формулы половинных углов, их вывод, а также примеры решения задач с их использованием.
Список всех формул половинного угла
Их можно встретить записанными в двух видах. В первом каждая из тригонометрических функций выражается через радикал:
Знак «+» или «-» перед корнями зависит от того, в какую из координатных четвертей попадает угол `\frac2`.
Во втором варианте имеем дело с квадратами тригонометрических функций половинного угла:
Формула синуса и косинуса половинного угла имеет место при любом угле `\alpha`.
Формула тангенса половинного угла справедлива для тех углов `\alpha`, при которых определен `tg \frac \alpha 2`, то есть при ` \alpha\ne\pi+2\pi n, \ n \in Z`.
Формула котангенса выполняется для тех `\alpha`, при которых определен `ctg \frac \alpha 2`, то есть при ` \alpha\ne 2\pi n, \ n \in Z`.
С помощью следующего набора формул можно выразить каждую из тригонометрических функций угла `\alpha` через тангенс половинного угла.
Вывод формул половинного угла
Формула косинуса и синуса половинного угла выводится из формул косинуса двойного угла `cos \ 2\alpha=1-2 \ sin^2 \alpha` и `cos \ 2\alpha=2 \ cos^2 \alpha-1`. Запишем их в следующем виде: `cos \alpha=1-2 \ sin^2 \frac \alpha 2` и `cos \alpha=2 \ cos^2 \frac \alpha 2-1`. Выразив из первого равенства ` sin \frac \alpha 2` получим `sin \ \frac \alpha 2=\pm \sqrt`. Аналогично разрешив второе равенство относительно ` cos \frac \alpha 2` в результате будем иметь `cos \ \frac \alpha 2=\pm \sqrt`.
Формулы тангенса и котангенса половинного угла можно вывести, используя определения этих функций в виде `tg \frac \alpha 2=\frac` и `ctg \frac \alpha 2=\frac`, а также две уже доказанные выше формулы для синуса и косинуса.
Примеры использования при решении задач
Пример 1. Найти `cos 15^\circ`, если известно, что `cos 30^\circ=\frac2`.
Решение. Формула половинного угла для тригонометрической функции косинус имеет вид `cos^2 \ \frac \alpha 2=\frac 2`. Подставив известные значения, имеем `cos^2 15^\circ=\frac 2=` `\frac2>2=\frac4`. Имея значение `cos^2 15^\circ`, найдем `cos 15^\circ`. Поскольку угол 15 градусов лежит в первой координатной четверти, а косинус в этой четверти имеет знак «+», то `cos 15^\circ=\sqrt=` `\frac2`.
Пример 2. Вычислить значение выражения `4cos \frac 2+2cos \alpha+5`, если `cos \alpha=\frac 8`.
Решение. Используя ту же формулу, что и в первом примере (`cos \ \frac \alpha 2=\pm \sqrt`) и известное значение косинуса, упростим выражение: `4\sqrt+2cos \alpha+5=4\sqrt2>+2 \cdot \frac 8+5=` `4\sqrt+\frac4+5=8\frac4`.
Ответ. `4cos \frac 2+2cos \alpha+5=8\frac4`.
Еще несколько примеров с подробным объяснением посмотрите на видео:
В большинстве случаев формулы половинного угла используются при преобразовании тригонометрических выражений.
Формулы синус косинус и тангенс половинного угла
Лекция 14. Синус, косинус, тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла.
Обратимся снова к тригонометрической окружности.
Пусть точка A является концом радиус-вектора, отвечающего углу α. Пусть также OA = 1. Построим прямоугольный треугольник AOC. Применяя к этому треугольнику теорему Пифагора, получаем:
Но OA = 1, OC = cos α, CA = sin α. Значит, непосредственным следствием теоремы Пифагора является равенство Это равенство называется основным тригонометрическим тождеством.
Отсюда следует, что
Знак + или − выбирается в зависимости от того, в какой четверти лежит угол α.
Разделим основное тригонометрическое тождество на Получим:
Разделим основное тригонометрическое тождество на Получим:
Из определений тангенса и котангенса следует:
Найдите sin X и cos X, если и
Для вывода Формул сложения для тригонометрических функций рассмотрим тригонометрическую окруж
poiskvstavropole.ru
Произведение синуса и косинуса половинного угла. Формулы половинного угла в тригонометрии
Самые часто задаваемые вопросы
Возможно ли, изготовить печать на документе по предоставленному образцу? Ответ Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Какие виды оплаты вы принимаете?
Ответ Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами? Ответ В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Что делать при обнаружении в документе опечаток и ошибок?
Ответ Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Что нужно сделать, чтобы заказать диплом в вашей компании?
Ответ Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.
Последние отзывы
Алексей:
Мне нужно было приобрести диплом для устройства на работу по профессии менеджер. И самое главное, что и опыт, и навыки у меня есть, но без документа я не могу, никуда устроится. Попав на ваш сайт, все-таки решился на покупку диплома. Диплом был выполнен за 2 дня!! Теперь у меня есть работа, о которой я раньше и не мечтал!! Спасибо!
Вы можете заказать подробное решение вашей задачи !!!
namvd.ru
Как найти косинус половины угла. Формулы половинного угла в тригонометрии
Самые часто задаваемые вопросы
Возможно ли, изготовить печать на документе по предоставленному образцу? Ответ Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Какие виды оплаты вы принимаете?
Ответ Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами? Ответ В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Что делать при обнаружении в документе опечаток и ошибок?
Ответ Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Что нужно сделать, чтобы заказать диплом в вашей компании?
Ответ Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.
После
namvd.ru
Формулы двойного и половинного угла — МегаЛекции
Формулы двойного угла позволяют выразить тригонометрические функции произвольного угла через функции угла в два раза меньше исходного. Эти формулы являются следствиями формул суммы двух углов, если положить в них углы равными друг другу.
Последнюю формулу можно преобразовать с помощью основного тригонометрического тождества:
или
Таким образом, для косинуса двойного угла существует три формулы:
Следует отметить, что данная формула справедлива только при и , .
Последняя формула справедлива при , .
Аналогично функциям двойного угла могут быть получены функции тройного угла. Здесь данные формулы приводятся без доказательства:
,
,
,
.
Формулы половинного угла являются следствиями формул двойного угла и позволяют выразить тригонометрические функции некоторого угла через функции угла в два раза больше исходного.
Произведем следующие преобразования:
,
и выразим через :
.
Аналогичные преобразования произведем для :
,
.
Последние две формулы носят названия формул понижения степени.
Выведем формулу для :
.
Аналогично
.
Универсальная тригонометрическая подстановка
Эта группа формул позволяет выражать значения всех тригонометрических функций через тангенс половинного угла. Данные формулы часто используются при решении уравнений и произведении преобразований.
Для того, чтобы выразить через воспользуемся ранее выведенной формулой:
,
,
,
при , .
Далее используя формулу и только что выведенное соотношение для косинуса получим зависимость между и :
последняя формула также имеет смысл при , .
Формулы для тангенса и котангенса получаются при помощи формул двойного угла:
при , , ,
при , .
Формулы произведения тригонометрических функций
Данная группа формул является следствием формул суммы и разности двух углов.
Теорема 5. Для любых вещественных и справедливы следующие соотношения:
,
.
Доказательство. Запишем формулы косинуса и синуса суммы и разности для углов и :
, (1)
, (2)
, (3)
. (4)
Произведем следующие преобразования:
((1)-(2))/2:
((1)+(2))/2:
((3)+(4))/2:
Что и требовалось доказать.
Формулы суммы и разности тригонометрических функций
Эти формулы также являются следствием формул суммы и разности двух углов.
Для получения формул суммы и разности функций заметим, что любые углы и можно представить следующим образом:
,
.
Найдем сумму синусов двух произвольных углов и :
Найдем разность синусов двух произвольных углов и :
Найдем сумму косинусов двух произвольных углов и :
Найдем разность косинусов двух произвольных углов и :
Найдем сумму и разность тангенсов двух углов и , таких что , , :
Найдем сумму и разность котангенсов двух углов и , таких что , , :
Формула дополнительного (вспомогательного) аргумента
Рассмотрим выражение вида
,
в котором числа и не равны нулю одновременно. Домножим и поделим каждое из слагаемых на и вынесем общий множитель за скобки:
Нетрудно проверить, что
,
а значит по Теореме 2 существует такой вещественный угол , что
и .
Таким образом, используя формулу синуса суммы, получаем
Формула
где такой угол, что и , носит название формулы вспомогательного аргумента и используется при решении неоднородных линейных уравнений и неравенств.
Обратные тригонометрические функции
Определения
До сих пор мы решали задачу определения тригонометрических функций заданных углов. А что если стоит обратная задача: зная какую-либо тригонометрическую функцию определить соответствующий ей угол.
Арксинус
Рассмотрим выражение , где – известное вещественное число. По определению синуса это есть ордината точки пересечения луча, образующего угол с осью абсцисс и тригонометрической окружности. Таким образом, для решения уравнения надо найти точки пересечения прямой и тригонометрической окружности.
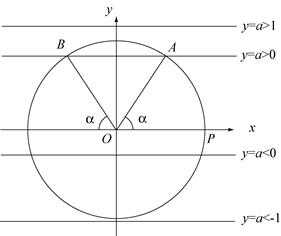
Очевидно, что при прямая и окружность не имеют общих точек, а значит и уравнение не имеет решений. То есть нельзя найти угол, синус которого был бы по модулю больше 1.
При прямая и окружность имеют точки пересечения, например, и (см. рис.). Таким образом, заданный синус будут иметь , и все углы, отличающиеся от них на целое количество полных оборотов, т.е. , , – бесконечное множество углов. Как выбрать один угол среди этого бесконечного множества?
Чтобы однозначно определить угол , соответствующий числу , приходится требовать выполнения дополнительного условия: этот угол должен принадлежать отрезку . Такой угол называют арксинусом числа .
Арксинусом действительного числа называется действительное число , синус которого равен . Такое число обозначают .
Арккосинус
Рассмотрим теперь уравнение вида . Для его решения необходимо найти на тригонометрической окружности все точки, имеющие абсциссу , т.е. точки пересечения с прямой . Как и в предыдущем случае при рассматриваемое уравнение не имеет решений. А если , имеются точки пересечения прямой и окружности, соответствующие бесконечному множеству углов , , .
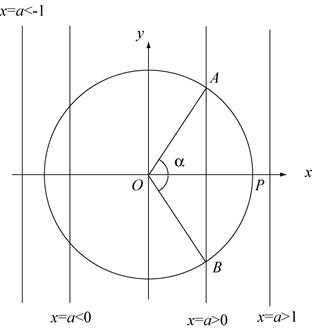
Чтобы однозначно определить угол , соответствующий данному косинусу, вводят дополнительное условие: этот угол должен принадлежать отрезку ; такой угол называют арккосинусом числа .
Арккосинусом действительного числа называется действительное число , косинус которого равен . Такое число обозначают .
Арктангенс и арккотангенс
Рассмотрим выражение . Для его решения надо найти на окружности все точки пересечения с прямой , угловой коэффициент которой равен тангенсу угла наклона прямой к положительному направлению оси абсцисс. Такая прямая при всех действительных значениях пересекает тригонометрическую окружность в двух точках. Эти точки симметричны относительно начала координат и соответствуют углам , , .
Для однозначного определения угла с заданным тангенсом его выбирают из интервала .
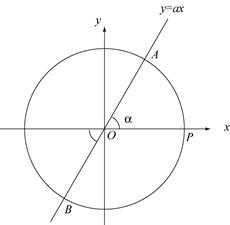
Арктангенсом произвольного действительного числа называется действительное число , тангенс которого равен . Такое число обозначают .
Для определения арккотангенса угла используются аналогичные рассуждения, с той лишь разницей, что рассматривается пересечение окружности с прямой и угол выбирается из интервала .
Арккотангенсом произвольного действительного числа называется действительное число , котангенс которого равен . Такое число обозначают .
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
