Синус (sin x) и косинус (cos x) – свойства, графики, формулы
- Геометрическое определение синуса и косинуса
- Принятые обозначения
- График функции синус, y = sin x
- График функции косинус, y = cos x
- Свойства синуса и косинуса
- Периодичность
- Четность
- Области определения и значений, экстремумы, возрастание, убывание
- Основные формулы, содержащие синус и косинус
- Сумма квадратов
- Формулы синуса и косинуса суммы и разности
- Формулы произведения синусов и косинусов
- Формулы суммы и разности
- Выражение синуса через косинус
- Выражение косинуса через синус
- Выражение через тангенс
- Таблица синусов и косинусов, тангенсов и котангенсов
- Выражения через комплексные переменные
- Формула Эйлера
- Выражения через гиперболические функции
- Производные
- Интегралы
- Разложения в ряды
- Секанс, косеканс
- Обратные функции
- Арксинус, arcsin
- Арккосинус, arccos
Геометрическое определение синуса и косинуса
\( \sin \alpha = \dfrac{|BC|}{|AC|}; \quad \cos \alpha = \dfrac{|AB|}{|AC|} \)
\( |AB| = |AD|; \quad \alpha = \dfrac{|BD|}{|AB|} \)
|BD| — длина дуги окружности с центром в точке A.
α — угол, выраженный в радианах.
Синус (sin α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
\( \sin^2 x \equiv (\sin x)^2; \)\( \quad \sin^3 x \equiv (\sin x)^3; \)\( \quad \sin^n x \equiv (\sin x)^n \)\( \sin^{-1} x \equiv \arcsin x \)\( (\sin x )^{-1} \equiv \dfrac1{\sin x} \equiv \cosec x \).
\( \cos^2 x \equiv (\cos x)^2; \)\( \quad \cos^3 x \equiv (\cos x)^3; \)\( \quad \cos^n x \equiv (\cos x)^n \)\( \cos^{-1} x \equiv \arccos x \)\( (\cos x )^{-1} \equiv \dfrac1{\cos x} \equiv \sec x \).
График функции синус, y = sin x
[ img src=»sin-x.png» alt=»График функции y=sin(x)» title=»График функции y=sin(x)» ]График функции косинус, y = cos x
[ img src=»cos-x.png» alt=»График функции y=cos(x)» title=»График функции y=cos(x)» ]Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
\( \sin(x + 2\pi) = \sin x; \quad \)\( \cos(x + 2\pi) = \cos x \)
Четность
Функция синус – нечетная. Функция косинус – четная.
\( \sin( -x ) = — \sin x; \quad \)\( \cos( -x ) = \cos x \)
Области определения и значений, экстремумы, возрастание, убывание
Основные свойства синуса и косинуса представлены в таблице (n — целое).
| \( \small -\dfrac{\pi}2 + 2\pi n \)\( \small < x < \)\( \small \dfrac{\pi}2 + 2\pi n \) | \( \small -\pi + 2\pi n \)\( \small < x < \)\( \small 2\pi n \) | |
| Убывание | \( \small \dfrac{\pi}2 + 2\pi n \)\( \small < x < \)\( \small \dfrac{3\pi}2 + 2\pi n \) | \( \small 2\pi n \)\( \small < x < \)\( \pi + \small 2\pi n \) |
| Максимумы, \( \small x = \)\( \small \dfrac{\pi}2 + 2\pi n \) | \( \small x = 2\pi n \) | |
| Минимумы, \( \small x = \)\( \small -\dfrac{\pi}2 + 2\pi n \) | \( \small x = \)\( \small \pi + 2\pi n \) | |
| Нули, \( \small x = \pi n \) | \( \small x = \dfrac{\pi}2 + \pi n \) | |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы, содержащие синус и косинус
Сумма квадратов
\( \sin^2 x + \cos^2 x = 1 \)
Формулы синуса и косинуса суммы и разности
\( \sin(x + y) = \sin x \cos y + \cos x \sin y \)
\( \sin(x — y) = \sin x \cos y — \cos x \sin y \)
\( \cos(x + y) = \cos x \cos y — \sin x \sin y \)
\( \cos(x — y) = \cos x \cos y + \sin x \sin y \)
\( \sin( 2x ) = 2 \sin x \cos x \)
\( \cos( 2x ) = \cos^2 x — \sin^2 x = \)\( 2 \cos^2 x — 1 = 1 — 2 \sin^2 x \)
\( \cos\left( \dfrac{\pi}2 — x \right) = \sin x \) ; \( \sin\left( \dfrac{\pi}2 — x \right) = \cos x \)
\( \cos( x + \pi ) = — \cos x \) ; \( \sin( x + \pi ) = — \sin x \)
Формулы произведения синусов и косинусов
\( \sin x \cos y = \)\( \dfrac12 {\Large [} \sin( x — y ) + \sin( x + y ) {\Large ]} \)
\( \sin x \sin y = \)\( \dfrac12 {\Large [} \cos( x — y ) — \cos( x + y ) {\Large ]} \)
\( \cos x \cos y = \)\( \dfrac12 {\Large [} \cos( x — y ) + \cos( x + y ) {\Large ]} \)
\( \sin x \cos y = \dfrac12 \sin 2x \)
\( \sin^2 x = \dfrac12 {\Large [} 1 — \cos 2x {\Large ]} \)
\( \cos^2 x = \dfrac12 {\Large [} 1 + \cos 2x {\Large ]} \)
Формулы суммы и разности
\( \sin x + \sin y = 2 \, \sin \dfrac{x+y}2 \, \cos \dfrac{x-y}2 \)
\( \sin x — \sin y = 2 \, \sin \dfrac{x-y}2 \, \cos \dfrac{x+y}2 \)
\( \cos x + \cos y = 2 \, \cos \dfrac{x+y}2 \, \cos \dfrac{x-y}2 \)
\( \cos x — \cos y = 2 \, \sin \dfrac{x+y}2 \, \sin \dfrac{y-x}2 \)
Выражение синуса через косинус
Далее мы полагаем, что \( n \) – целое число.
\( \sin x = \cos\left( \dfrac{\pi}2 — x \right) = \)\( \cos\left( x — \dfrac{\pi}2 \right) = — \cos\left( x + \dfrac{\pi}2 \right) \)\( \sin^2 x = 1 — \cos^2 x \)\( \sin x = \sqrt{1 — \cos^2 x} \) \( \{ 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \} \)\( \sin x = — \sqrt{1 — \cos^2 x} \) \( \{ -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \} \).
Выражение косинуса через синус
\( \cos x = \sin\left( \dfrac{\pi}2 — x \right) = \)\( — \sin\left( x — \dfrac{\pi}2 \right) = \sin\left( x + \dfrac{\pi}2 \right) \)\( \cos^2 x = 1 — \sin^2 x \)\( \cos x = \sqrt{1 — \sin^2 x} \) \( \{ -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \} \)\( \cos x = — \sqrt{1 — \sin^2 x} \) \( \{ \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \} \).
Выражение через тангенс
\( \sin^2 x = \dfrac{\tg^2 x}{1+\tg^2 x} \)\( \cos^2 x = \dfrac1{1+\tg^2 x} \).
При \( — \dfrac{\pi}2 + 2 \pi n < x < \dfrac{\pi}2 + 2 \pi n \)\( \sin x = \dfrac{\tg x}{ \sqrt{1+\tg^2 x} } \)\( \cos x = \dfrac1{ \sqrt{1+\tg^2 x} } \).
При \( \dfrac{\pi}2 + 2 \pi n < x < \dfrac{3\pi}2 + 2 \pi n \) :
\( \sin x = — \dfrac{\tg x}{ \sqrt{1+\tg^2 x} } \)\( \cos x = — \dfrac1{ \sqrt{1+\tg^2 x} } \).
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
[ img src=»tablitsa.png» alt=»Таблица синусов и косинусов» title=»Таблица синусов и косинусов» ]
Выражения через комплексные переменные
\( i^2 = -1 \)
\( \sin z = \dfrac{e^{iz} — e^{-iz}}{2i} \)\( \cos z = \dfrac{e^{iz} + e^{-iz}}{2} \)
Формула Эйлера
\( e^{iz} = \cos z + i \sin z \)
Выражения через гиперболические функции
\( \sin iz = i \sh z \)\( \cos iz = \ch z \)
\( \sh iz = i \sin z \)\( \ch iz = \cos z \)
Производные
\( ( \sin x )’ = \cos x \)\( ( \cos x )’ = — \sin x \). Вывод формул > > >
Производные n-го порядка:
\( \left( \sin x \right)^{(n)} = \sin\left( x + n\dfrac{\pi}2 \right) \)\( \left( \cos x \right)^{(n)} = \cos\left( x + n\dfrac{\pi}2 \right) \).
Интегралы
\( \int \sin x \, dx = — \cos x + C \)\( \int \cos x \, dx = \sin x + C \)
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
\( \sin x = \sum_{n=0}^{\infty} \dfrac{ (-1)^n x^{2n+1} }{ (2n+1)! } = \)\( x — \dfrac{x^3}{3!} + \dfrac{x^5}{5!} — \dfrac{x^7}{7!} + … \) \( \{- \infty < x < \infty \} \)
\( \cos x = \sum_{n=0}^{\infty} \dfrac{ (-1)^n x^{2n} }{ (2n)! } = \)\( 1 — \dfrac{x^2}{2!} + \dfrac{x^4}{4!} — \dfrac{x^6}{6!} + … \) \( \{ — \infty < x < \infty \} \)
Секанс, косеканс
\( \sec x = \dfrac1{ \cos x } ; \) \( \cosec x = \dfrac1{ \sin x } \)
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
\( y = \arcsin x \) \( \left\{ -1 \leqslant x \leqslant 1; \; — \dfrac{\pi}2 \leqslant y \leqslant \dfrac{\pi}2 \right\} \)
\( \sin( \arcsin x ) = x \) \( \{ -1 \leqslant x \leqslant 1 \} \)
\( \arcsin( \sin x ) = x \) \( \left\{ — \dfrac{\pi}2 \leqslant x \leqslant \dfrac{\pi}2 \right\} \)
Арккосинус, arccos
\( y = \arccos x \) \( \left\{ -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\} \)
\( \cos( \arccos x ) = x \) \( \{ -1 \leqslant x \leqslant 1 \} \)
\( \arccos( \cos x ) = x \) \( \{ 0 \leqslant x \leqslant \pi \} \)
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
Формулы синусов и косинусов, с примерами
Косинусы и синусы связаны между собою следующими тригонометрическими формулами.
Основное тригонометрическое тождество
Тригонометрические формулы косинусов и синусов суммы и разности углов
Тригонометрические формулы косинусов и синусов двойного и тройного аргументов
Формулы понижения степени для косинуса и синуса
Формулы для косинуса и синуса половинного аргумента
Формулы преобразования произведения косинусов и синусов в сумму
Формулы преобразования суммы косинусов и синусов в произведение
Формулы, выражающие синус и косинус через тангенс половинного аргумента
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Синус, косинус и тангенс суммы и разности формулы – тригонометрия
Формулы косинус суммы и разности (cos), синус суммы и разности (sin) и тангенс суммы и разности (tg) часто применяются при решении различных задач по тригонометрии. В первую очередь эти формулы используются при преобразовании тригонометрических числовых и буквенных выражений. Достаточно знать одну из этих формул, остальные можно получить по аналогии.
Запомнить формулы синуса и косинуса суммы и разности просто: в формулах синуса в произведениях находятся разные тригонометрические функции, в формулах косинуса в произведениях находятся одинаковые тригонометрические функции. Главное: запомнить где нужно использовать плюс, а где минус между произведениями.
Формула синус суммы
Синус суммы углов α и β равен сумме произведения синуса угла α на косинус угла β и произведения косинуса угла α на синус угла β.
sin(α + β) = sinα ⋅ cosβ + cosα ⋅ sinβ
Формула синус разности
Синус разности углов α и β равен разности произведения синуса угла α на косинус угла β и произведения косинуса угла α на синус угла β.
sin(α – β) = sinα ⋅ cosβ – cosα ⋅ sinβ
Формула косинус суммы
Косинус суммы углов α и β равен разности произведения косинуса угла α на косинус угла β и произведения синуса угла α на синус угла β.
cos(α + β) = cosα ⋅ cosβ – sinα ⋅ sinβ
Формула косинус разности
Косинус разности углов α и β равен сумме произведения косинуса угла α на косинус угла β и произведения синуса угла α на синус угла β.cos(α – β) = cosα ⋅ cosβ + sinα ⋅ sinβ
Формула тангенс суммы
Тангенс суммы углов α и β равен отношению суммы тангенсов углов к разности единицы и произведения тангенсов углов.
tg(α + β) = (tgα + tgβ) / (1 – tgα ⋅ tgβ)
Формула тангенс разности
Тангенс разности углов α и β равен отношению разности тангенсов углов к сумме единицы и произведения тангенсов углов.
tg(α – β) = (tgα – tgβ) / (1 + tgα ⋅ tgβ)
worksbase.ru
Формулы синусов и косинусов — энциклопедический справочник и словарь для студента от А до Я
Косинусы и синусы связаны между собою следующими тригонометрическими формулами.
Основное тригонометрическое тождество
Тригонометрические формулы косинусов и синусов суммы и разности углов
Тригонометрические формулы косинусов и синусов двойного и тройного аргументов
Формулы понижения степени для косинуса и синуса
Формулы для косинуса и синуса половинного аргумента
Формулы преобразования произведения косинусов и синусов в сумму
Формулы преобразования суммы косинусов и синусов в произведение
Формулы, выражающие синус и косинус через тангенс половинного аргумента
Примеры решения задач
ПРИМЕР 1
Доказать тождество
Распишем выражение в левой части заданного равенства как разность квадратов, получим:
Далее преобразуем разность и сумму косинусов в скобках, используя формулы
Получим:
Учитывая, что косинус функция четная, а также, используя формулу синуса двойного угла , окончательно имеем:
Что и требовалось доказать.
ПРИМЕР 2
Упростить выражение
В числителе и в знаменателе преобразуем, синус двойного угла, используя формулу , получим
Числитель и знаменатель полученной дроби сократим на 4, а из основного тригонометрического тождества выразим и , и, так же подставим в последнюю дробь:
img src=»/public-file/2655/image» alt=»» title=»» data-public-file-id=»2655″>
sciterm.ru
Формулы двойного и тройного угла
Формулы двойного угла — это формулы, связывающие тригонометрические функции угла (синус, косинус, тангенс) с тригонометрическими функциями угла .
Формулы двойного и тройного угла (аргумента) выводятся из формул сложения.
Синус двойного угла
Доказательство. Воспользуемся формулой сложения для синуса
Из этой формулы получаем
Косинус двойного угла
Доказательство. Применим формулу суммы агументов косинуса:
Получим
Тангенс двойного угла
Доказательство этой формулы аналогично, поэтому эту формулу мы предлагаем вам доказать самостоятельно :).
Синус, косинус и тангенс тройного угла
Доказательство. Формулы тройного угла можно получить из формул сложения, зная формулы двойного угла. Покажем это на примере синуса:
Используя основное тригонометрическое тождество и приводя подобные члены, получаем формулу тройного угла для синуса.
Аналогично получаются формулы тройного угла для косинуса и тангенса.
umath.ru
Тригонометрия. Основные формулы — Математика онлайн
Смотрите материал здесь: основные формулы тригонометрии.1. Определения синуса, косинуса, тангенса и котангенса угла.
Синус угла α (обозначается sin α) – ордината точки Pα , полученной поворотом точки P(1; 0) вокруг начала координат на угол α.
Косинус угла α (обозначается cos α) – абсцисса точки Pα , полученной поворотом точки P(1; 0) вокруг начала координат на угол α.
Тангенс угла α (обозначается tg α) – отношение синуса угла α к его косинусу, т.е.
Котангенс угла α (обозначается ctg α) – отношение косинуса угла α к его синусу, т.е.
2. Основное тригонометрическое тождество:
3. Зависимость между синусом, косинусом, тангенсом и котангенсом:
4. Чётность, нечётность и периодичность тригонометрических функций.
Косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции аргумента α:
Синус и косинус – периодические с периодом 2π функции, а тангенс и котангенс – периодические с периодом π функции:Число 2π является наименьшим положительным периодом синуса и косинуса, а число π – наименьшим положительным периодом тангенса и котангенса. Для любого целого n справедливы равенства
5. Формулы сложения:
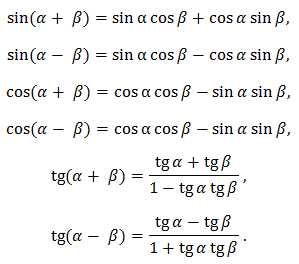
6. Формулы двойного и тройного аргумента:
7. Формулы понижения степени:
8. Формулы приведения:
9. Формулы суммы и разности синусов:
10.
11. Формулы суммы и разности тангенсов:
12. Преобразование произведения синусов и косинусов в сумму (разность):
13. Выражение синуса и косинуса через тангенс половинного аргумента:
Смотреть в PDF
calcs.ucoz.ru
Внеклассный урок — Синус, косинус, тангенс, котангенс
Синус, косинус, тангенс, котангенс
Прежде чем перейти к этому разделу, напомним определения синуса и косинуса, изложенные в учебнике геометрии 7-9 классов.
— Синус острого угла t прямоугольного треугольника равен отношению противолежащего катета к гипотенузе (рис.1):
sin t = b/c.
— Косинус острого угла t прямоугольного треугольника равен отношению прилежащего катета к гипотенузе (рис.1):
cos t = a/c.
Эти определения относятся к прямоугольному треугольнику и являются частными случаями тех определений, которые представлены в данном разделе.
Поместим тот же прямоугольный треугольник в числовую окружность (рис.2).

Мы видим, что катет b равен определенной величине y на оси Y (оси ординат), катет а равен определенной величине x на оси X (оси абсцисс). А гипотенуза с равна радиусу окружности (R).
Таким образом, наши формулы обретают иной вид.
Так как b = y, a = x, c = R, то:
y x
sin t = —— , cos t = ——.
R R
Кстати, тогда иной вид обретают, естественно, и формулы тангенса и котангенса.
Так как tg t = b/a, ctg t = a/b, то, верны и другие уравнения:
tg t = y/x,
ctg = x/y.
Но вернемся к синусу и косинусу. Мы имеем дело с числовой окружностью, в которой радиус равен 1. Значит, получается:
y
sin t = —— = y,
1
x
cos t = —— = x.
1
Так мы приходим к третьему, более простому виду тригонометрических формул.
Эти формулы применимы не только к острому, но и к любому другому углу (тупому или развернутому).
Определения и формулы cos t, sin t, tg t, ctg t.
Косинусом числа t числовой окружности называют абсциссу этого числа: cos t = x Синус числа t – это его ордината: sin t = y Тангенс числа t – это отношение синуса к косинусу: sin t π Котангенс числа t – это отношение косинуса к синусу: cos t |
Из формул тангенса и котангенса следует еще одна формула:
sin t cos t πk |
Уравнения числовой окружности.
Из предыдущего раздела мы знаем одно уравнение числовой окружности: x2 + y2 = 1 Но поскольку x = cos t, а y = sin t, то получается новое уравнение: cos2 t + sin2 t = 1 |
Знаки синуса, косинуса, тангенса и котангенса в четвертях окружности:
| 1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть |
cos t | + | – | – | + |
sin t | + | + | – | – |
tg t, ctg t | + | – | + | – |
Косинус и синус основных точек числовой окружности:
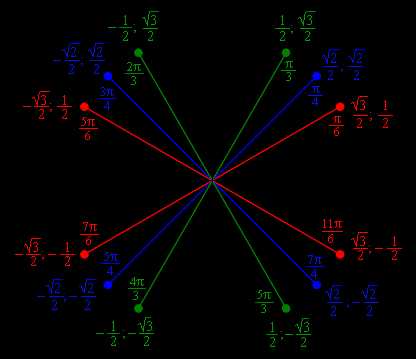
Как запомнить значения косинусов и синусов основных точек числовой окружности.
Прежде всего надо знать, что в каждой паре чисел значения косинуса стоят первыми, значения синуса – вторыми.
1) Обратите внимание: при всем множестве точек числовой окружности мы имеем дело лишь с пятью числами (в модуле):
1 √2 √3
0; —; ——; ——; 1.
2 2 2
Сделайте для себя это «открытие» — и вы снимете психологический страх перед обилием чисел: их на самом деле всего-то пять.
2) Начнем с целых чисел 0 и 1. Они находятся только на осях координат.
Не надо учить наизусть, где, к примеру, косинус в модуле имеет единицу, а где 0.
На концах оси косинусов (оси х), разумеется, косинусы равны модулю 1, а синусы равны 0.
На концах оси синусов (оси у) синусы равны модулю 1, а косинусы равны 0.
Теперь о знаках. Ноль знака не имеет. Что касается 1 – тут просто надо вспомнить самую простую вещь: из курса 7 класса вы знаете, что на оси х справа от центра координатной плоскости – положительные числа, слева – отрицательные; на оси у вверх от центра идут положительные числа, вниз – отрицательные. И тогда вы не ошибетесь со знаком 1.
3) Теперь перейдем к дробным значениям.
— Во всех знаменателях дробей – одно и то же число 2. Уже не ошибемся, что писать в знаменателе.
— В серединах четвертей косинус и синус имеют абсолютно одинаковое значение по модулю: √2/2. В каком случае они со знаком плюс или минус – см.таблицу выше. Но вряд ли вам нужна такая таблица: вы знаете это из того же курса 7 класса.
— Все ближайшие к оси х точки имеют абсолютно одинаковые по модулю значения косинуса и синуса: (√3/2; 1/2).
— Значения всех ближайших к оси у точек тоже абсолютно идентичны по модулю – причем в них те же числа, только они «поменялись» местами: (1/2; √3/2).
Теперь о знаках – тут свое интересное чередование (хотя со знаками, полагаем, вы должны легко разобраться и так).
Если в первой четверти значения и косинуса, и синуса со знаком плюс, то в диаметрально противоположной (третьей) они со знаком минус.
Если во второй четверти со знаком минус только косинусы, то в диаметрально противоположной (четвертой) – только синусы.
Осталось только напомнить, что в каждом сочетании значений косинуса и синуса первое число – это значение косинуса, второе число – значение синуса.
— Обратите внимание еще на одну закономерность: синус и косинус всех диаметрально противоположных точек окружности абсолютно равны по модулю. Возьмем, к примеру, противоположные точки π/3 и 4π/3:
cos π/3 = 1/2, sin π/3 = √3/2
cos 4π/3 = -1/2, sin 4π/3 = -√3/2
Различаются значения косинусов и синусов двух противоположных точек только по знаку. Но и здесь есть своя закономерность: синусы и косинусы диаметрально противоположных точек всегда имеют противоположные знаки.
Важно знать:
Значения косинусов и синусов точек числовой окружности последовательно возрастают или убывают в строго определенном порядке: от самого малого значения до самого большого и наоборот (см. раздел «Возрастание и убывание тригонометрических функций» — впрочем, в этом легко убедиться, лишь просто посмотрев на числовую окружность выше).
В порядке убывания получается такое чередование значений:
√3 √2 1 1 √2 √3
1; ——; ——; —; 0; – —; – ——; – ——; –1
2 2 2 2 2 2
Возрастают они строго в обратном порядке.
Поняв эту простую закономерность, вы научитесь довольно легко определять значения синуса и косинуса.
Тангенс и котангенс основных точек числовой окружности.
Зная косинус и синус точек числовой окружности, легко можно вычислить их тангенс и котангенс. Делим синус на косинус — получаем тангенс. Делим косинус на синус — получаем котангенс. Результаты этого деления — на рисунке.
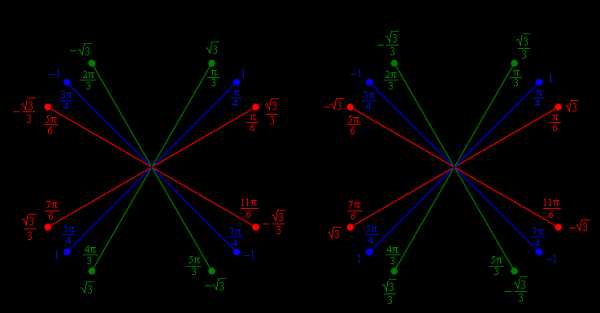
ПРИМЕЧАНИЕ: В некоторых таблицах значения тангенса и котангенса, равные модулю √3/3, указаны как 1/√3. Ошибки тут нет, так как это равнозначные числа. Если числитель и знаменатель числа 1/√3 умножить на √3, то получим √3/3.
Как запомнить значение тангенсов и котангенсов основных точек числовой окружности.
Здесь такие же закономерности, что и с синусами и косинусами. И чисел тут всего четыре (в модуле): 0, √3/3, 1, √3.
На концах осей координат – прочерки и нули. Прочерки означают, что в данных точках тангенс или котангенс не имеют смысла.
Как запомнить, где прочерки, а где нули? Поможет правило.
Тангенс – это отношение синуса к косинусу. На концах оси синусов (ось у) тангенс не существует.
Котангенс – это отношение косинуса к синусу. На концах оси косинусов (ось х) котангенс не существует.
В остальных точках идет чередование всего лишь трех чисел: 1, √3 и √3/3 со знаками плюс или минус. Как с ними разобраться? Запомните (а лучше представьте) три обстоятельства:
1) тангенсы и котангенсы всех середин четвертей имеют в модуле 1.
2) тангенсы и котангенсы ближайших к оси х точек имеют в модуле √3/3; √3.
3) тангенсы и котангенсы ближайших к оси у точек имеют в модуле √3; √3/3.
Не ошибитесь со знаками – и вы большой знаток.
Нелишне будет запомнить, как возрастают и убывают тангенс и котангенс на числовой окружности (см.числовую окружность выше или раздел «Возрастание и убывание тригонометрических функций»). Тогда еще лучше будет понятен и порядок чередования значений тангенса и котангенса.
Тригонометрические свойства чисел числовой окружности.
Представим, что определенная точка М имеет значение t.
Свойство 1:
| | | |
Пояснение. Пусть t = –60º и t = –210º.
cos –60º равен 1/2. Но cos 60º тоже равен 1/2. То есть косинусы –60º и 60º равны как по модулю, так и по знаку: cos –60º = cos 60º.
cos –210º равен –√3/2. Но cos 210º тоже равен –√3/2. То есть: cos –210º = cos 210º.
Таким образом, мы доказали, что cos (–t) = cos t.
sin –60º равен –√3/2. А sin 60º равен √3/2. То есть sin –60º и sin 60º равны по модулю, но противоположны по знаку.
sin –210º равен 1/2. А sin 210º равен –1/2. То есть sin –210º и sin 210º равны по модулю, но противоположны по знаку.
Таким образом, мы доказали, что sin (–t) = –sin t.
Посмотрите, что происходит с тангенсами и котангенсами этих углов – и вы сами легко докажете себе верность двух других тождеств, приведенных в таблице.
Вывод: косинус – четная функция, синус, тангенс и котангенс – нечетные функции.
Свойство 2: Так как t = t + 2πk, то:
| |
Пояснение: t и t + 2πk – это одна и та же точка на числовой окружности. Просто в случае с 2πk мы совершаем определенное количество полных оборотов по окружности, прежде чем приходим к точке t. Значит, и равенства, изложенные в этой таблице, очевидны.
Свойство 3: Если две точки окружности находятся друг против друга относительно центра О, то их синусы и косинусы равны по модулю, но противоположны по знаку, а их тангенсы и котангенсы одинаковы как по модулю, так и по знаку.
| | | |
Пояснение: Пусть точка М находится в первой четверти. Она имеет положительное значение синуса и косинуса. Проведем от этой точки диаметр – то есть отрезок, проходящий через центр оси координат и заканчивающийся в точке окружности напротив. Обозначим эту точку буквой N. Как видите, дуга MN равна половине окружности. Вы уже знаете, что половина окружности – это величина, равная π. Значит, точка N находится на расстоянии π от точки М. Говоря иначе, если к точке М прибавить расстояние π, то мы получим точку N, находящуюся напротив. Она находится в третьей четверти. Проверьте, и увидите: косинус и синус точки N – со знаком «минус» (x и y имеют отрицательные значения).
Тангенс и котангенс точки М имеют положительное значение. А тангенс и котангенс точки N? Ответ простой: ведь тангенс и котангенс – это отношение синуса и косинуса. В нашем примере синус и косинус точки N – со знаком «минус». Значит:
–sin t
tg (t + π) = ———— = tg t
–cos t
–cos t
ctg (t + π) = ———— = ctg t
–sin t
Мы доказали, что тангенс и котангенс диаметрально противоположных точек окружности имеют не только одинаковое значение, но и одинаковый знак.
Свойство 4: Если две точки окружности находятся в соседних четвертях, а расстояние между точками равно одной четверти окружности, то синус одной точки равен косинусу другой с тем же знаком, а косинус одной точки равен синусу второй с противоположным знаком.
π | π |
raal100.narod.ru
